Modelling of interfacial mass transfer in microfluidic solvent extraction: part I. Heterogenous transport

Abstract

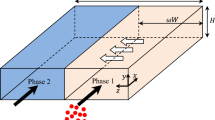
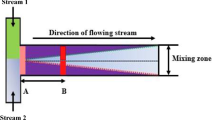
An investigation of molecular diffusion of solutes across water/oil interfaces in a Y-Y-shaped microchannel with an integrated guide structure is presented. Finite volume numerical simulations were compared with experimental literature data. Analytical approaches including an infinite composite medium model, phase-specific mass transfer coefficient models, and a static transfer cell model were also assessed. An increase in accuracy for the mass transfer coefficient models was achieved by using local coefficients as opposed to length-averaged expressions. The static transfer cell model was shown to improve when based on the interfacial contact time, as opposed to the organic phase residence time. The results presented in this work have immediate application to the determination of kinetic rate constants in reactive mass transfer systems, as considered in Part II of this study (Ciceri et al. Microfluid Nanofluid, 2012).

Appendices

Appendix 1: Mass transfer coefficient model

1.1 Derivation

The local flux $J_y$ of solute in the $y$-direction is defined by

$$J_y= k_{\rm {aq}} (\bar{c}_{\rm {aq}} - c_{\rm {aq,int}})$$

(43)

$$J_y= k_{\rm {org}} (c_{\rm {org,int}} - \bar{c}_{\rm {org}}), $$

(44)

where $k_{\rm {aq}}$ and $k_{\rm {org}}$ are the local mass transfer coefficients, $c_{i,{\rm {int}}}$ are the interfacial concentrations (per volume basis) and $\bar{c}_i$ are the velocity-averaged solute concentrations given by

$$\bar{c}_i = \frac{ \int_{{A}_{\perp ,i}} \! c_i u_i \, {\text{d}}A }{ \int_{{A}_{\perp ,i}} \! u_i \, {\text{d}}A } \,, $$

(45)

where ${A}_{\perp ,i}$ is the cross-sectional area of the relevant half of the channel. The distribution constant is defined, using Eq. 11, by

$${c_{\rm org,int}} = K_{\rm D} {c_{\rm aq,int}} \,. $$

(46)

Substituting Eq. 46 into Eq. 44 gives

$$J_y = k_{\rm {org}} (K_{\rm D} c_{\rm {aq,int}} - \bar{c}_{\rm {org}}) \,. $$

(47)

Eliminating $c_{\rm aq,int }$ gives

$$J_y\left( \frac{1}{k_{\rm {aq}}} + \frac{1}{k_{\rm {org}} K_{\rm D} } \right) = \bar{c}_ {\rm {aq}} - \frac{\bar{c}_{\rm {org}}}{K_{\rm D} } \,. $$

(48)

For convenience, the following definitions are introduced:

$$\Updelta \bar{c} \overset{\underset{\text{ def}}{}}{=} \bar{c}_{\rm {aq}} - \frac{\bar{c}_{\rm org}}{K_{\rm D} } $$

(49)

$$K_{\rm eff} \overset{\underset{\text{ def}}{}}{=} \left( \frac{1}{k_{\rm aq}} + \frac{1}{k_{\rm org} K_{\rm D} } \right)^{-1} $$

(50)

so that

$$J_y = K_{\rm eff} \Updelta \bar{c}\,. $$

(51)

From the definition of $J_y$ (Eq. 44),

$$J_y \, {\text{d}A}= F_{\rm aq} \left[\bar{c}_{\rm aq}(A) - \bar{c}_{\rm aq}(A + {\text{ d}A})\right] $$

(52)

$$J_y \, {\text{d}A}= F_{\rm org} \left[\bar{c}_{\rm org} (A + {\rm d} A) - \bar{c}_{\rm aq} (A) \right]\,.$$

(53)

Combining Eqs. 52 and 53 gives

$$J_y\, {\text{d}A} \left(\frac{1}{F_{\rm aq} } + \frac{1}{F_{\rm org} } K_{\rm D} \right) = -\left[ \bar{c}_{\rm aq}(A + {\text{ d}A}) - \bar{c}_{\rm aq}(A) - \left( \frac{\bar{c}_{\rm org}(A + {\text{ d}A})}{K_{\rm D} } - \frac{\bar{c}_{\rm org}(A)}{K_{\rm D} } \right) \right].$$

(54)

Using the definition from Eq. 49 and taking the limit ${\rm d} A \rightarrow 0$ gives

$$J_y \left( \frac{1}{F_{\rm aq}} + \frac{1}{F_{\rm org} K_{\rm D} } \right) = - \frac{{\text{ d}} \Updelta \bar{c}}{{\text{ d}A}} \,. $$

(55)

Substituting Eq. 51 gives

$$\frac{{\text{ d}} \Updelta \bar{c}}{{\text{ d}A}} = - K_{\rm eff} \left( \frac{1}{F_{\rm aq}} + \frac{1}{F_{\rm org} K_{\rm D} } \right) \Updelta \bar{c} \,. $$

(56)

Integrating this expression gives

$$\ln \left( \frac{\Updelta \bar{c}_{\rm outlet}}{\Updelta \bar{c}_{\rm inlet}} \right) = - K_{\rm eff} \left( \frac{1}{F_{\rm aq}} + \frac{1}{F_{\rm org} K_{\rm D} } \right) A_{\rm ref} \,, $$

(57)

where $A_{\rm ref}$ is the total area of the interface. The total amount of solute transferred across the interface is given by

$$\tilde{J}_y A_{\rm ref}= F_{\rm aq} (\bar{c}_{\rm aq,inlet} - \bar{c}_{\rm aq,outlet}) $$

(58)

$$\tilde{J}_y A_{\rm ref}= F_{\rm org} (\bar{c}_{\rm org,outlet} - \bar{c}_{\rm org,inlet}) \,, $$

(59)

where $\tilde{J}_y$ is the average flux of solute. Combining Eqs. 58 and 59 gives

$$\begin{aligned}\tilde{J}_y A_{\rm ref} \left( \frac{1}{F_{\rm aq}} + \frac{1}{F_{\rm org} K_{\rm D} } \right) & = \bar{c}_{\rm aq,inlet} - \bar{c}_{\rm aq,outlet} + \frac{\bar{c}_{\rm org,outlet}}{K_{\rm D} } - \frac{\bar{c}_{\rm org,inlet}}{K_{\rm D} } \\&= \Updelta \bar{c}_{\rm inlet} - \Updelta \bar{c}_{\rm outlet} \,. \end{aligned}$$

(60)

Combing Eqs. 57 and 60 gives

$$\tilde{J}_y= K_{\rm eff} \frac{\Updelta \bar{c}_{\rm outlet} - \Updelta \bar{c}_{\rm inlet}}{ \ln \left( \frac{\Updelta \bar{c}_{\rm outlet}}{\Updelta \bar{c}_{\rm inlet}} \right) } $$

(61)

$$\tilde{J}_y= K_{\rm eff} \left( \Updelta \bar{c} \right)_{\rm LM} \,. $$

(62)

1.2 Solution method

The aim is to solve for $\bar{c}_{\rm org,outlet}$ for a fixed experimental $\Updelta \bar{c}_ {\rm inlet}$. From mass conservation,

$$F_{\rm aq} \bar{c}_{\rm aq,outlet} + F_{\rm org} \bar{c}_{\rm org,outlet} = F_{\rm aq} \bar{c}_{\rm aq,inlet} + F_{\rm org} \bar{c}_{\rm org,inlet}.$$

(63)

Substituting

$$\bar{c}_{\rm org,outlet} = K_{\rm D} (\bar{c}_{\rm aq,outlet} - \Updelta \bar{c}_{\rm outlet}) $$

(64)

into Eq. 63 gives

$$\bar{c}_{\rm aq,outlet} = \frac{1}{F_{\rm aq} + K_{\rm D} F_{\rm org}} \left( F_{\rm aq} \bar{c}_{\rm aq,inlet} + F_{\rm org} \bar{c}_{\rm org,inlet} + F_ {\rm org} \Updelta \bar{c}_{\rm outlet} \right) \,, $$

(65)

where, for constant values of $\tilde{k}_i$ (‘averaged coefficient A & B’), $\Updelta \bar{c}_{\rm outlet}$ is determined from Eq. 57,

$$\Updelta \bar{c}_{\rm outlet} = \Updelta \bar{c}_{\rm inlet} \exp \left[ -K_{\rm eff} \left( \frac{1}{K_{\rm D} F_{\rm aq} } + \frac{1}{F_{\rm org} } \right) A_{\rm ref} \right] \,. $$

(66)

Equation 66 is substituted into Eq. 65 in order to determine $\bar{c}_{\rm aq,outlet}$. $\bar{c}_{\rm org,outlet}$ can then be determined from Eq. 64.

For $x$-dependent $k_i$ values (‘local coefficient A & B’), $\Updelta \bar{c}_{\rm outlet}$ is determined using numerical integration:

$${\Updelta \bar{c}_{\rm outlet} } = {\Updelta \bar{c}_{\rm inlet} } \exp \left[ -\left(\frac{1}{F_{\rm aq} } + \frac{1}{F_{\rm org} K_{\rm D} } \right)\int \limits _0^L \! K_{\rm eff} (x) d\, {\rm d}x \right] \,, $$

(67)

where

$$K_{\rm eff} (x) = \left( \frac{1}{k_{\rm aq}(x)} + \frac{1}{k_{\rm org}(x) K_{\rm D} } \right)^{-1} $$

(68)

and

$$k_i(x) = \frac{{\fancyscript{D}}_{i} }{D_{\rm h} } {Sh}_i(x) \,. $$

(69)

Here, the substitution ${{\rm {d}}A} = d\,{\rm d}x$ has been made, where $d$ is the $z$-height of the interface. The same solution method for determining $\bar{c}_{\rm org,outlet}$ then follows as per the constant $k_i$ case.

Appendix 2: Analytical expression for a heterogeneous thin slit

Building on the approach of Bird et al. (2002), an analytical expression was derived for two immiscible, incompressible liquids flowing in the $y$-direction of a thin slit of length $L$ and effective width $2D_{\rm h}$. The momentum flux for each phase $i$ is given by the differential equation

$$\frac{{\text{ d}} \tau _{yx,i}}{{\text{ d}}y} = \frac{\Updelta p_i}{L} \,, $$

(70)

where $\Updelta p_i$ is the phase-specific pressure difference between the pass-length inlet and outlet. Integrating Eq. 70 for each phase gives

$$\tau _{yx,i} = \left( \frac{\Updelta p_i}{L} \right)y + \alpha _i \,, $$

(71)

where $\alpha _i$ is a constant of integration. The momentum flux across the interface (located at $y=0$) is assumed to be balanced:

$$\tau_{yx,1}|_{y \rightarrow 0^{-}}= \tau_{yx,2}\big |_{y \rightarrow 0^{+}} \Rightarrow \alpha_1 = \alpha_2 \overset{\underset{\rm def}{}}{=} \alpha. $$

(72)

Substituting Newton's law of viscosity and integrating gives

$$u_{x,i} = - \frac{1}{2\mu_{i}} \frac{\Updelta p_{i}}{L} y^2 - \frac{\alpha}{\mu _{i}} y + \beta_{i}.$$

(73)

The solvent velocity was assumed to be continuous across the interface:

$$u_{x,1}\big |_{y \rightarrow 0^-}= u_{x,2}\big |_{y \rightarrow 0^+} \Rightarrow \beta _1 = \beta _2 \overset{\underset{\rm def}{}}{=} \beta. $$

(74)

This gives a set of two equations to be solved simultaneously:

$$u_{x,i} = - \frac{1}{2\upmu _i} \frac{\Updelta p_i}{L} y^2 - \frac{\alpha }{\upmu _i} y + \beta \,. $$

(75)

A no-slip boundary condition was applied on two fictional walls, each a distance $D_{\rm h}$ from the centreline:

$$u_{x,1}\big |_{y = -D_{\rm h} } = 0\,;\quad u_{x,2}\big |_{y = D_{\rm h} } = 0 \,. $$

(76)

Solving for $\alpha$ and $\beta$ gives:

$$\alpha (\Updelta p_1, \Updelta p_2)= \frac{D_{\rm h} }{2L} \left(\frac{{\upmu _2}{\Updelta p_1} - {\upmu _1}{\Updelta p_2}}{{\upmu _1} + {\upmu _2}}\right)$$

(77)

$$ \beta (\Updelta p_1, \Updelta p_2)= \frac{D_{\rm h} ^2}{2L}\left( \frac{\Updelta p_1 + \Updelta p_2}{\upmu _1 + \upmu _2} \right)$$

(78)

The average velocities $\bar{u}_{x,i}$ are then given by:

$$\begin{aligned} \bar{u}_{x,1}&= \frac{1}{D_{\rm h} }\int \limits _{-D_{\rm h} }^0\!u_{x,1}(y) \,{\rm d}y\\&= -\frac{1}{2\upmu _1} \frac{\Updelta p_1}{L}\frac{D_{\rm h} ^2}{3} + {\alpha (\Updelta p_1, \Updelta p_2)}\frac{D_{\rm h} }{2 \upmu _1} + \beta (\Updelta p_1, \Updelta p_2) \end{aligned}$$

(79)

$$\begin{aligned} \bar{u}_{x,2}&= \frac{1}{D_{\rm h} }\int \limits _0^{D_{\rm h} }\!u_{x,2}(y) \,{\rm d}y\\&= -\frac{1}{2\upmu _2} \frac{\Updelta p_2}{L}\frac{D_{\rm h} ^2}{3} - {\alpha (\Updelta p_1, \Updelta p_2)}\frac{D_{\rm h} }{2 \upmu _2} + \beta (\Updelta p_1, \Updelta p_2) \end{aligned}$$

(80)

Equations 78 and 79 are solved simultaneously for $\Updelta p_i$. The interfacial velocity is then given by

$$u_{\rm int} = \beta (\Updelta p_1, \Updelta p_2) \,. $$

(81)