Analysis of tandem polling queues with finite buffers

Abstract

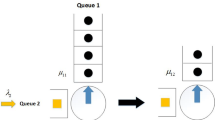
We analyze a tandem polling queue with two stations operating under three different polling strategies, namely: (1) Independent polling, (2) Synchronous polling, and (3) Out-of-sync polling. Under Markovian assumptions of arrival and service times, we conduct an exact analysis using Matrix Geometric method to determine system throughput, mean queue lengths, and mean waiting times. Through numerical experiments, we compare the performance of the three polling strategies and the effect of buffer sizes on performance. We observe that the independent polling strategy generally performs better than the other strategies, however, under certain settings of product asymmetry, other strategies yield better performance.

Appendix

Matrices for IP strategy

The infinitesimal generator ${\mathbb {Q}}_{IP}$ of the IP strategy defined in Eq. (1) is

The sub-matrices used to describe the transitions of infinitesimal generator ${\mathbb {Q}}_{IP}$ are defined in the Eqs. (20)–(23). Note that we suppress the subscripts corresponding to the strategy for notational simplicity in the submatrices.

(20)

(21)

(22)

(23)

where matrices ${\mathbb {S}}_{1}$ and ${\mathbb {S}}_{2}$ are each of dimension $r \times r$, and are represented by Eqs. (24) and (25) respectively.

(24)

(25)

Next, we define the diagonal matrices of ${\mathbb {Q}}_{IP}$, namely, ${\mathbb {B}}_{0}$, ${\mathbb {B}}_{1}$, ${\mathbb {B}}_{2}$, ${\mathbb {B}}_{3}$, and ${\mathbb {B}}_{4}$. First, we define ${\mathbb {B}}_{0}$ and ${\mathbb {B}}_{1}$ in Eqs. (26) and (27) respectively.

(26)

(27)

where matrices ${\mathbb {R}}_{0}$, ${\mathbb {R}}_{1}$, and ${\mathbb {R}}_{2}$ are each of dimensions $r \times r$ and are represented by Eqs. (28)–(30). In these equations, we set $\delta _{0} = {} \lambda _{1}+\lambda _{2}+\mu _{12}$, $\delta _{1} = {} \lambda _{1}+\lambda _{2}+\mu _{11}+\mu _{12}$, and $\delta _{2} = {} \lambda _{2}+\mu _{11}+\mu _{12}$. The matrix $\mathbb {S'}_{1}$ is similar to the matrix ${\mathbb {S}}_{1}$ except for that the state transitions are from the states $\left( l_{11}, l_{21}, 1, *, *, *\right)$ to states $\left( l_{21}-1, l_{21}, 1, *, *, *\right)$ while the matrix $\mathbb {R'}_{0}$ have an additional term $\mu _{11}$ in its diagonal elements when compared to ${\mathbb {R}}_{0}$. The matrix ${\mathbb {B}}_{2}$ is same as matrix ${\mathbb {B}}_{1}$ except that $\lambda _{2}$ is 0 in $\mathbb {R'}_{0}$ , ${\mathbb {R}}_{1}$, and ${\mathbb {R}}_{2}$. Other diagonal matrices ${\mathbb {B}}_{3}$ and ${\mathbb {B}}_{4}$ in the infinitesimal generator can obtained similarly.

(28)

(29)

(30)

Matrices for SP strategy

The infinitesimal generator of the SP strategy ${\mathbb {Q}}_{SP}$ defined in Eq. (2) is

(31)

Table 7 Dimensions of the sub-matrices in ${\mathbb {Q}}_{SP}$

The dimensions of all the matrices used in $\displaystyle \mathop {{\mathbb {Q}}_{SP}}$ are summarized in Table 7. The matrices ${\mathbb {A}}_{1}$, $\mathbb {A'}_{1}$, ${\mathbb {A}}_{2}$, ${\mathbb {A}}_{2}^{'}$, ${\mathbb {D}}_{11, k}$, and ${\mathbb {D}}_{21, k}$ in ${\mathbb {Q}}_{SP}$ are similar to the respective matrices in ${\mathbb {Q}}_{IP}$, and can be obtained using the Eqs. (20)–(23). Next, we define the diagonal matrices of ${\mathbb {Q}}_{SP}$, namely, ${\mathbb {B}}_{0}$, ${\mathbb {B}}_{1}$, ${\mathbb {B}}_{2}$, ${\mathbb {B}}_{3}$, and ${\mathbb {B}}_{4}$. First, we define ${\mathbb {B}}_{0}$ in Eq. (32).

(32)

where matrices ${\mathbb {R}}_{0}$, ${\mathbb {R}}_{1}$, and ${\mathbb {R}}_{2}$ are represented by Equations (33) – (35). In these equations, we set $\delta _{0} = {} \lambda _{1}+\lambda _{2}+\mu _{12}$, $\delta _{1} = {} \lambda _{1}+\lambda _{2}+\mu _{11}+\mu _{12}$, and $\delta _{2} = {} \lambda _{2}+\mu _{11}+\mu _{12}$. The submatrix $\mathbb {S'}_{1}$ can be obtained using Equation (24).

(33)

(34)

(35)

Other diagonal matrices ${\mathbb {B}}_{1}$, ${\mathbb {B}}_{2}$, ${\mathbb {B}}_{3}$, and ${\mathbb {B}}_{4}$ in the infinitesimal generator can obtained similarly. Lastly, we define ${\mathbb {X}}_{1}$ and ${\mathbb {X}}_{2}$ in Eqs. (36) and (37).

(36)

(37)

Matrices for OP strategy

The infinitesimal generator of the OP strategy ${\mathbb {Q}}_{OP}$ defined in Eq. (3) is

Table 8 Dimensions of the sub-matrices in ${\mathbb {Q}}_{OP}$

The dimensions of all the matrices used in $\displaystyle \mathop {{\mathbb {Q}}_{OP}}$ are summarized in Table 8. The matrices ${\mathbb {A}}_{1}$, $\mathbb {A'}_{1}$, ${\mathbb {A}}_{2}$, ${\mathbb {A}}_{2}^{'}$, ${\mathbb {D}}_{11, k}$, and ${\mathbb {D}}_{21, k}$ in ${\mathbb {Q}}_{OP}$ are similar to the respective matrices in ${\mathbb {Q}}_{IP}$, and can be obtained using the Eqs. (20)–(23). Next, we define the diagonal matrices of ${\mathbb {Q}}_{OP}$, namely, ${\mathbb {B}}_{0}$, ${\mathbb {B}}_{1}$, ${\mathbb {B}}_{2}$, ${\mathbb {B}}_{3}$, and ${\mathbb {B}}_{4}$. First, we define ${\mathbb {B}}_{0}$ in Eq. (38).

(38)

Next, we define one of the submatrix, $\displaystyle \mathop {{\mathbb {R}}_{0}}$ of matrix $\displaystyle \mathop {{\mathbb {B}}_{0}}$ in the Eq. (39). In this equation, we set $\delta _{0} = {} \lambda _{1}+\lambda _{2}+\mu _{22}$.

(39)

Similarly, we can define the other diagonal submatrices ${\mathbb {R}}_{1}$ and ${\mathbb {R}}_{2}$ of matrix $\displaystyle \mathop {{\mathbb {B}}_{0}}$. The submatrix $\mathbb {S'}_{1}$ can be obtained using the approach in Eq. (24). Other diagonal matrices ${\mathbb {B}}_{1}$, ${\mathbb {B}}_{2}$, ${\mathbb {B}}_{3}$, and ${\mathbb {B}}_{4}$ in the infinitesimal generator can obtained similarly. Lastly, we define ${\mathbb {X}}_{1}$ and ${\mathbb {X}}_{2}$ for OP strategy in Eqs. (40) and (41).

(40)

(41)