1 Introduction

Cryptocurrencies are well known for their hedging, portfolio diversification, and risk mitigation capabilities across the literature (Bouoiyour et al. 2019; Bouri et al. 2018; Koutmos 2019). Bitcoin, the most popular cryptocurrency, has drawn crucial market players' attention at different hierarchies for accomplishing these activities. Simultaneously, the literature predominantly reports Bitcoin's return behavior as chaotic and multifractal (Al-Yahaee et al. 2018; Filho et al. 2018) and more volatile than other financial assets (Chaim and Laurini 2018).

Several researchers report the critical properties of Bitcoin and its interplay with other assets (Tiwari et al. 2018; Wang et al. 2019; Horra et al. 2019; Poyser 2019; Zhang et al. 2020). The assessment of the price dynamics of Bitcoin remains very challenging due to the high degree of nonstationary, nonlinear, volatile behaviors and the influence of various uncontrollable factors (Matta et al. 2016; Cretarola and Figà-Talamanca 2019). The conventional predictive models like moving average (MA), Autoregressive (AR), autoregressive integrated moving average (ARIMA) fail to produce accurate forecasts (Ghosh et al. 2019). Besides, these models suffer from several shortcomings like the strict requirement of the stationary of datasets, homoscedasticity of errors, etc. (Filho et al. 2018). Researchers propose machine learning, computational intelligence, deep learning, and hybrid models (Ghosh et al. 2017, 2019; Kumar and Ravi 2017) to alleviate these limitations.

This work presents an efficient regression-based predictive modeling framework for forecasting a one-day ahead price of Bitcoin. An accurate estimation of a one-day ahead price forecast may help the daily traders make better investment decisions and more profit. Support vector regression (SVR) and polynomial regression with interactions (PRI) help to learn the inherent governing patterns on the decomposed time series. The maximal overlapping discrete wavelet transformation (MODWT) decomposes the original time series. We use polynomial regression with interactions on linear sub-components and SVR on nonlinear sub-components to generate forecasts. Tuning of hyperparameters of SVR is necessary to ensure superior forecast accuracy from the two regression models. Also, we need to estimate the PRI coefficients. DE helps us to achieve these two tasks. We combine the two regression models' forecasts to generate the final prediction and carry out the proposed approach's comparative performance evaluation with MLP, RF, ANFIS, SVR, MARS, and LASSO, considering the original and five distinct surrogate time series simulated from the original Bitcoin price data.

This research's significant contribution is the proposition of a novel predictive modeling approach by combining the optimization and regression frameworks in a granular set up for time series forecasting. The proposed approach consists of four distinct components—MODWT for granular decomposition, SVR and PRI for learning pattern, and DE for hyperparameter tuning of SVR and the PRI model's estimation. It is different from the existing wavelet decomposition-based approaches in terms of using two distinct predictive modeling algorithms on appropriate granular components (Ghosh et al. 2017a, 2019). This approach is useful for predictive modeling of time series displaying an excess degree of volatility like the Bitcoin for making a more accurate forecast.

The rest of the paper's organization is as follows: Sect. 2 presents the previous research. Section 3 describes data and critical statistical properties of Bitcoin prices. Section 4 presents the research methodology, while Sect. 5 reports the results obtained from the proposed framework. Section 6 concludes the paper.

2 Previous research

This section clusters the pertinent work to inspect Bitcoin's temporal characteristics, interaction dynamics with other assets, and predictive modeling. Several researchers study the temporal characteristics of Bitcoin (Bariviera 2017; Nadarajah and Chu 2017; Takaishi 2018). A section of literature proves that the Bitcoin market is inefficient (Urquhart 2016; Kristoufek et al. 2018; Tiwari et al. 2018). Researchers examine the same market's multifractal nature through multifractal detrended fluctuation analysis (Filho et al. 2018; Kristjanpoller et al. 2020; Takaishi 2018). The findings suggest that the degree of multifractal nature is more substantial in Bitcoin than several other stock market indices. A copula-based Granger causality test explores the causal interplay between Bitcoin's attention manifested through google trends and Bitcoin returns from January 1, 2013, to December to December 31, 2017 (Dastgir et al. 2019). The study reveals the existence of bidirectional causal nexus in the left and right tail of the distribution.

The interaction between Bitcoin returns and economic policy uncertainty (EPU) explores the hedging capacity of Bitcoin (Demir et al. 2018; Paule Vianez et al. 2020). Wang et al. (2019) measure the risk spillover effect from EPU to Bitcoin and selected equity market uncertainty index, US EPU index, and implied volatility index as proxies for EPU. The results indicate the presence of negligible spillover from EPU to Bitcoin. So, Bitcoin may act as a safe asset for investment under EPU shocks. The Bayesian structural time series approach inspects the temporal dynamics and dependence structure of Bitcoin prices on other assets (Poyser 2019). The findings reveal both positive and negative association structures with different foreign exchange rates, gold prices, and stock indices. The LASSO technique identifies EPU, gold returns, and search intensity as the significant drivers of Bitcoin returns (Panagiotidis et al. 2018).

The literature reports various artificial intelligence and predictive modeling approaches for forecasting future movements of financial assets. For example, a combination of radial basis function neural network (RBFN), K-means clustering, and artificial fish swarm algorithm (AFSA) estimates the future movements of the Shanghai stock exchange (Shen et al. 2011). The model performs better than five other approaches. Similarly, a combination of discrete wavelet transforms (DWT), MARS, and SVR predicts stock market returns (Kao et al. 2013). This approach outperforms DWT-MARS, DWT-SVR, ARIMA, standalone SVR, and ANFIS. Similar other hybrid models exist for stock market prediction (Oztekin et al. 2016; Wang et al. 2016; Chen and Hao 2017). These models also perform better compared to the traditional and some other hybrid forecasting approaches. Unfortunately, they are not used to predict the future prices of Bitcoin.

Various techniques like neural network (Jang and Lee 2017), neuro-fuzzy (Atsalakis 2019), machine learning (Mallqui and Fernandes 2019), deep learning (McNally et al. 2018; Wu et al. 2018), and deep neural network (Nakano et al. 2018), deep learning chaotic neural networks (Lahmiri and Bekiros 2019) predict the directional predictive modeling of daily prices of Bitcoin. These techniques produce superior predictive performances over their traditional counterparts and are more useful for nonlinear and chaotic financial markets. The literature reveals that Bitcoin is very closely associated with a myriad of global financial assets. The multifractal interactions and spillovers of Bitcoin with these assets make the temporal dynamics very complicated. It is challenging to identify explanatory variables beforehand due to these associations. The degree of (in)efficiency owing to the Bitcoin bubble and other extreme events further complicates the predictive analysis task. Therefore, developing a robust predictive framework for predicting future prices of Bitcoin can be of paramount importance for practical implications.

Time-series decomposition-based predictive approaches that utilize lagged information as explanatory features for estimating financial assets' future movements emerge to be successful. However, it is rare to find a granular framework-based predictive model driven by lagged information for forecasting Bitcoin prices. The present work contributes to the existing literature by proposing a granular predictive architecture that can recognize Bitcoin price movements' intricate patterns. Wavelet decomposition is an instrumental paradigm for this purpose. SVR works as the learning algorithm. Deployment of DE for optimizing SVR parameters augments the quality of the final forecasts. Wavelet decompositions generate granular linear and nonlinear subseries. Pattern recognition algorithms apply to these subseries for generating forecasts. The use of SVR on all the components may result in overfitting. Thus, we apply metaheuristic driven SVR to the nonlinear component and PRI model to the linear component to reduce this effect. The DE algorithm selects the PRI parameters.

3 Data description

We compile daily closing prices of Bitcoin for January 10, 2013, to February 23, 2019 for conducting the predictive exercise. During late 2017, Bitcoin prevails to be the most dominant cryptocurrency with more than 42% market share capitalization. As a result, we observe a steady upward growth of Bitcoin price during this period. Due to heavy criticism and the Bitcoin bubble, the growth eventually declines afterward. So, we consider the study period consisting of significantly normal, bullish, and bearish phases. Figure 1 portrays the temporal evolutionary dynamics of Bitcoin prices during the considered period. Table 1 reports the results of the statistical tests and additional properties to comprehend the underlying dataset's empirical properties.

Fig. 1
figure 1

Temporal evolutionary pattern of Bitcoin

Full size image
Table 1 Empirical properties of Bitcoin price
Full size table

Financial time series exhibits nonstationary, nonparametric, and chaotic traces (Avdoulas et al. 2018; Guerard et al. 2020). Mere visualization of the temporal evolutionary patterns may not capture such properties distinctly. Throughout the literature, researchers rely upon statistical and econometric tests for decoding such properties (Das et al. 2018; Ghosh et al. 2020; Jana et al. 2019; Boukhatem et al. 2020). The present work follows the same principles for comprehending the fundamental temporal properties of Bitcoin prices.

Outcomes of Jarque–Bera and Frosini tests indicate that daily closing prices of Bitcoin over the considered period do not abide by the normal distribution. Test statistics of Philip-Perron and Augmented Dickey-Fuller tests emerge insignificant, indicating unit-roots' presence in Bitcoin price dynamics. So, the time series under consideration is nonstationary. Therefore, the chosen time series's complex evolutionary pattern implies that the traditional econometric models for forecasting are not appropriate for deriving forecasts. We perform Terasvirta's and White's NN tests to further evaluate the behavioral patterns for gaining more in-depth insights. The test statistic values of both these tests are significant. So, there exists a strong nonlinear trait in the evolutionary patterns of Bitcoin prices. The Hurst exponent identifies the randomness and persistence of the time series. The Hurst exponent value of 0.89404 (> 0.5) implies the presence of fractional Brownian motion with a persistent trend (Ghosh et al. 2017). The persistent trend further indicates the presence of volatility clustering. Thus, the immediate past information on Bitcoin price does play a significant role in explaining future behavior. The present study exploits this property by setting one, two, three, four, and five day back Bitcoin prices as independent variables to predict a one-day ahead price. The partial autocorrelation plots shown in Sect. 5 validates the selection of five lagged variables.

4 Research methodology

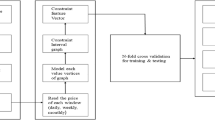
The proposed optimization-based regression approach has four distinct components—MODWT, SVR, PRI, and DE. As the closing prices of Bitcoin are persistent, we select the explanatory variables based on the lagged information. This section elucidates the details of individual components.

4.1 MODWT

MODWT decomposes the original Bitcoin prices into granular subcomponents. It determines the respective wavelet coefficients accounting for different time horizons. Daubechies least asymmetric filter of length eight (la8) helps in the decomposition process. The technique has additional advantages over the conventional 'Haar' wavelet filters in smoother operations (Gencay et al. 2002) and the generation of unrelated coefficients (Cornish et al. 2006). MODWT segregates the Bitcoin price time series into time and frequency space by expressing the sequence as projections of the father (\(\phi \)) and mother (\(\psi \)) wavelets representing approximation and units, respectively. Mean figures of approximation and detail components are one and zero, as shown in the following equations:

$$\int \phi (t)dt=1$$
(1)
$$\int \psi (t)dt=0$$
(2)

We express the long-scale linear component through the father wavelet, whereas the mother wavelet represents the linear component's nonlinear and volatile deviations. Mathematically, we write them as:

$${\phi }_{(j, k)}={2}^{-j/2}\phi \left(\frac{t-{2}^{j}k}{{2}^{j}}\right)$$
(3)
$${\psi }_{\left(j, k\right)}={2}^{-j/2}\psi \left(\frac{t-{2}^{j}k}{{2}^{j}}\right)$$
(4)

From the original time series, we can approximate the coefficients as follows:

$${s}_{\left(j,k\right)}=\int f(t){\phi }_{(j, k)}$$
(5)
$${d}_{\left(j,k\right)}=\int f(t){\psi }_{(j, k)}$$
(6)

The combination of wavelet functions formulates the original time series \(f(t)\) as follows:

$$f\left(t\right)=\sum_{k}{s}_{J,k}{\phi }_{J,k}(t)+\sum_{k}{d}_{J,k}{\psi }_{J,k}(t)+\dots +\sum_{k}{d}_{j,k}{\psi }_{j,k}\left(t\right)+\dots +\sum_{k}{d}_{1,k}{\psi }_{1,k}(t)$$
(7)

We write Eq. (7) as:

$$f\left(t\right)={S}_{J}+{D}_{J}+{D}_{J-1}+\dots +{D}_{j}+\dots +{D}_{1}$$
(8)

where

$${S}_{J}=\sum_{k}{s}_{j,k}{\phi }_{j,k}\left(t\right)$$
(9)
$${D}_{J}=\sum_{k}{d}_{j,k}{\psi }_{j,k}\left(t\right), j=\mathrm{1,2},\dots ,J$$
(10)

The orthogonal constituents \(\left[{S}_{J},{D}_{J},{D}_{J-1},\dots ,{D}_{1}\right]\) are the outcomes of the decomposition process of the original time series \(f\left(t\right)\). \({D}_{J}\) denotes the wavelet detail at \({J}^{th}\) level. \({S}_{J}\) defines the sum of deviations at the detail scales. In the proposed predictive analytics exercise, we carry out six decomposition levels that resulted in one approximation or linear component and six detail components accounting for high frequency or nonlinearity traits of the time series. Subsequently, predictive algorithms applied to the respective components yield predictions. For the MODWT decomposition.

The time series consisting of the closing prices of Bitcoin along with explanatory features become inputs for the decomposition exercise. The outputs comprise of granular decomposed series of Bitcoin prices and other explanatory features.

4.2 Support vector regression (SVR)

SVR (Vapnik, 1995) is an extension of the SVM algorithm applicable for performing nonlinear regression. A nonlinear mapping function \(\theta (x)\) projects the input \({x}_{i}\in {R}^{p}\) to a feature space with a high dimension and establishes a linear relationship between the target and predictor constructs. Mathematically, we represent this as follows:

$$f\left(x\right)={w}^{T} \theta \left(x\right)+b$$
(11)

where w and b are the weight and bias parameters, respectively, account for the decision boundary.

The goal is to estimate the parameters that eventually result in at most \(\varepsilon \) deviation from the target for all training samples. This set up of SVR is known as \(\varepsilon \)-SVR.

$${\left|{y}_{i}-f\left({x}_{i}\right)\right|}_{\varepsilon }=\left\{\begin{array}{l}\begin{array}{cc}0 & if\, \left|{y}_{i}-f\left({x}_{i}\right)\right|\le \varepsilon \end{array}\\ \begin{array}{cc}\left|{y}_{i}-f\left({x}_{i}\right)\right|-\varepsilon & Otherwise\end{array}\end{array}\right.$$
(12)

where \({y}_{i}\) denotes the target variable. We estimate \(f\left(x\right)\) by minimizing the following quadratic optimization problem through determining the parameters w and b using slack constructs, \({\xi }_{i},{\xi }_{i}^{*}\):

$$ Minimize:\frac{1}{2}\left\| w \right\|^{2} + C\sum\limits_{{i = 1}}^{n} {(\xi _{i} } + \xi _{i}^{{\text{*}}} ) $$
(13)

subject to

$$\left\{\begin{array}{l}{w}^{T}{x}_{i}-{y}_{i}\le \varepsilon +{\xi }_{i}\\ {y}_{i}-{w}^{T}{x}_{i}\le \varepsilon +{\xi }_{i}^{*}\\ {\xi }_{i},{\xi }_{i}^{*}\ge 0, i=1,\dots ,n\end{array}\right.$$
(14)

where \(C\) is the regularization parameter represents the trade-off between the fitness of regression and resultant error in training. We write the dual problem with the final solution using Eq. (11) as follows:

$$f\left(x\right)=\sum_{i=1}^{n}\left({\alpha }_{i}-{\alpha }_{i}^{*}\right)k({x}_{i},{x}_{i}^{*})+b$$
(15)

where \(k({x}_{i},{x}_{i}^{*})\) is a kernel function, \({\alpha }_{i}\) and \({\alpha }_{i}^{*}\) are Lagrange multipliers. We use the Radial basis kernel (RBF) defined by \(k\left({x}_{i},{x}_{j}\right)=\mathrm{exp}\left(-{\Vert {x}_{i}-{x}_{j}\Vert }^{2}/2{\sigma }^{2}\right)\) where \(\sigma \) denotes the width of the kernel. The three critical parameters \(C\), \(\sigma \), and \(\varepsilon \) that drive the learning process and affect the prediction performance. The DE provides their optimum values. The SVR-DE learning model applied to the nonlinear decomposed components obtained through MODWT performs the predictive analytics task.

4.3 Polynomial regression with interaction (PRI)

PRI is an extension of simple linear regression. It fits a polynomial to establish the relationship between the target and explanatory variables. Usually, the ordinary least square (OLS) technique estimates the regression coefficients, excluding the predictors' interactions. These two issues lead to the underfitting of the regression curve when time-series movements are highly nonstationary and nonlinear, as in Bitcoin prices. We use a third-order quadratic regression model with one level of interaction with five lagged variables as explanatory variables. The polynomial of order three with one level of interaction is as follows:

$$ \begin{aligned} Y_{t}^{{est}} & = \alpha + \sum _{{i = 1}}^{3} \beta _{i} Y_{{t - 1}}^{i} + \sum _{{j = 1}}^{3} \beta _{{j + 3}} Y_{{t - 2}}^{j} + \sum _{{k = 1}}^{3} \beta _{{k + 6}} Y_{{t - 3}}^{k} + \sum _{{l = 1}}^{3} \beta _{{l + 9}} Y_{{t - 4}}^{l} + \sum _{{m = 1}}^{3} \beta _{{m + 12}} Y_{{t - 5}}^{m} \\ & \quad + {\text{~}}\sum _{{n = 1}}^{4} \delta _{n} Y_{{t - 1}} Y_{{t - n - 1}} + \sum _{{o = 1}}^{3} \delta _{{o + 4}} Y_{{t - 2}} Y_{{t - n - 2}} + \sum _{{p = 1}}^{2} \delta _{{p + 7}} Y_{{t - 3}} Y_{{t - p - 3}} + {\text{~}}\sum _{{q = 1}}^{1} \delta _{{q + 9}} Y_{{t - 4}} Y_{{t - n - 4}} \\ \end{aligned} $$
(16)

where \({Y}_{t}^{est}\) represents the estimated Bitcoin price at time t, \({Y}_{t-i}\) accounts for the previous information of Bitcoin price at \(i (i=\mathrm{1,2},\dots ,5)\) period back, \(\alpha \), \(\beta ,\) and \(\delta \) are the respective coefficients of polynomial and interaction terms.

The DE estimates the regression coefficients \(\alpha , { \beta }_{i}\) and \({\delta }_{i}\) given in the Eq. (16) as follows:

$$\left\{\begin{array}{l}Find: \alpha , {\beta }_{i},{\delta }_{i}\\ Argmin: \sum {\left({Y}_{t}^{act}-{Y}_{t}^{est}\right)}^{2}\end{array}\right.$$
(17)

where \({Y}_{t}^{act}\) represents actual Bitcoin price at time t.

4.4 Differential evolution

The DE is a widely used metaheuristic for solving complex optimization problems in the continuous domain (Storn and Price 1997). It is a population-based searching algorithm that traverses the search space intelligently to obtain local or near-optimal solutions. The following are the detailed procedures of individual phases of the DE.

4.4.1 Initialization

The initial population of the DE comprises of P vectors {\({\stackrel{-}{x}}_{i, G}\),\(i=\mathrm{1,2},\dots ,P\)}, where G denotes the generation number. We randomly generate the initial population from a uniform distribution specified lower and upper bounds. The possible solutions can be represented as a D-dimensional vector as follows:

$${\stackrel{-}{x}}_{i, G}=\left({x}_{i,1, G},{x}_{i,2,G},\dots ,{x}_{i,D,G}\right)$$
(18)

The selection, recombination, and mutation operations subsequently modify the initial population.

4.4.2 Mutation

In traditional DE, three vectors estimate the mutation vector \(\left(\stackrel{-}{v}\right)\). Mathematically, we may represent it as follows:

$${\stackrel{-}{v}}_{i,G}={\stackrel{-}{x}}_{{r}_{1},G}+F*\left({\stackrel{-}{x}}_{{r}_{2},G}-{\stackrel{-}{x}}_{{r}_{3},G}\right)$$
(19)

where \({\stackrel{-}{v}}_{i,G}\) is the donor vector, and \(F\) is the scaling parameter that varies between 0 and 2.

4.4.3 Recombination

In this phase, the components of a donor vector generate a trial offspring vector as follows:

$${u}_{i,j,G}=\left\{\begin{array}{l}{v}_{i,j,G}, \quad if\,{rand}_{j}\le CR\, or\, j=rn\left(j\right)\\ {x}_{i,j,G},\quad otherwise\end{array}\right.$$
(20)

where \({rand}_{j} (j=\mathrm{1,2},\dots ,D)\) denotes random numbers between 0 and 1; \(rn\left(j\right)\) denotes a randomly selected index from \(\mathrm{1,2},\dots ,D\) and \(CR\) is the crossover parameter between 0 and 1.

4.4.4 Selection

The DE uses a greedy approach for selecting candidate vectors for the subsequent generations. It compares trial and target vectors and makes the final selection as follows:

$${\stackrel{-}{x}}_{i,G+1}=\left\{\begin{array}{l}{u}_{i, G}, \quad if\,f\left({\stackrel{-}{u}}_{i,G}\right)<f\left({\stackrel{-}{x}}_{i,G}\right)\\ {\stackrel{-}{x}}_{i,G},\quad otherwise\end{array}\right.$$
(21)

The number of generations can be set depending upon the problem's nature or fixed until the convergence in solutions is noticed.

The DE tunes the hyper-parameters of the SVR model. It randomly initializes the values of different parameters as input and traverses the search space intelligently to yield optimal input parameters. In the PRI model, the DE randomly initializes the value of the coefficients. After completion of the search process, it provides the optimal values of the same as the output.

The combination of SVR-DE and PRI-DE predictions generate the final forecast of the next-day Bitcoin price. The SVR-DE approach yields granular forecasts \({\widehat{Y}}_{t}^{{d}_{i}}(i=\mathrm{1,2},\dots ,6)\) from disentangled nonlinear components provided by MODWT. The PRI-DE approach produces granular forecasts \({\widehat{Y}}_{t}^{{s}_{6}}\) from the approximation component fetched by MODWT. We write the final forecast (\({\widehat{Y}}_{t}^{Final}\)) as follows:

$${\widehat{Y}}_{t}^{Final}={\widehat{Y}}_{t}^{{d}_{1}}+{\widehat{Y}}_{t}^{{d}_{2}}+{\widehat{Y}}_{t}^{{d}_{3}}+{\widehat{Y}}_{t}^{{d}_{4}}+{\widehat{Y}}_{t}^{{d}_{5}}+{\widehat{Y}}_{t}^{{d}_{6}}+{\widehat{Y}}_{t}^{{s}_{6}}$$
(22)

4.5 Predictive performance indicators

Mean squared error (MSE) measures the fitness of the SVR-DE model as follows:

$$MSE=\frac{1}{N}\sum_{t=1}^{N}{\left({\widehat{Y}}_{t}-{Y}_{t}\right)}^{2}$$
(23)

where, \({\widehat{Y}}_{t}\) and \({Y}_{t}\) are predicted and actual figures. The PRI-DE model considers Eq. (17) as the fitness function.

Nash–sutcliffe efficiency (NSE) NSE measures the residual variance's relative strength resulting from a predictive model with the original variance of the dataset.

$$NSE=1-\frac{{\sum }_{t=1}^{N}{\left\{{\widehat{Y}}_{t}-{Y}_{t}\right\}}^{2}}{{\sum }_{i=1}^{N}{\left\{{Y}_{t}-\stackrel{-}{{Y}_{t}}\right\}}^{2}}$$
(24)

The NSE values lie between (\(-\infty )\) to 1. The NSE value close to 1 implies excellent predictive performance by the respective model.

Index of agreement (IA) IA is a measure that considers the magnitude of error generating from a model to assess the predictive capability.

$$IA=1-\frac{\sum_{t=1}^{N}{({\widehat{Y}}_{t}-{Y}_{t})}^{2}}{\sum_{i=1}^{N}{\left\{\left|{\widehat{Y}}_{t}-\stackrel{-}{{Y}_{t}}\right|+|{Y}_{t}-\stackrel{-}{{Y}_{t}}|\right\}}^{2}}$$
(25)

Like NSE, the IA figure should ideally be close to 1 for efficient forecasting.

Theil Index (TI) We can compute the index as follows:

$$TI=\frac{{\left[\frac{1}{N}{\sum }_{t=1}^{N}{\left({\widehat{Y}}_{t}-{Y}_{t}\right)}^{2}\right]}^{1/2}}{{\left[\frac{1}{N}\sum_{i=1}^{N}{\left({\widehat{Y}}_{t}\right)}^{2}\right]}^{1/2}+{\left[\frac{1}{N}\sum_{i=1}^{N}{\left({Y}_{t}\right)}^{2}\right]}^{1/2}}$$
(26)

Unlike NSE and IA, TI values need to be close to 0 to imply a predictive model's effectiveness.

Directional predictive accuracy (DA) For calculating the DA, we use the following relationships:

$$DA=\frac{1}{N}\sum_{t=1}^{N}{D}_{t}, {D}_{t}=\left\{\begin{array}{l}1,\quad ({Y}_{t+1}-{Y}_{t})\left({\widehat{Y}}_{t+1}-{Y}_{t}\right)\ge 0\\ 0,\quad Otherwise\end{array}\right.$$
(27)

The DA values near 1 indicate high accuracy of directional prediction obtained by the model, while DA figures near 0 imply the opposite scenario. As the present paper deals with regression, DA's computation eventually evaluates the presented forecasting framework's directional predictive capacity. Models having high DA values are attractive for traders for profitable trading.

Apart from self-assessment of the proposed forecasting approach's predictive performance, the paper also carries out a comparative study with six advanced predictive modeling algorithms: MLP, ANFIS, RF, SVR, MARS LASSO to justify the usage of the prediction framework. We conduct the Diebold-Mariano Statistical test for inspecting the equal predictive ability to draw inference on comparative assessment.

Diebold-Mariano (DM) test The DM test assesses the predictive accuracy of multiple forecasting models. We use the mean square prediction error (MSPE) as the loss function in the DM test. The DM statistic (DMS) has the following form:

$$DMS=\frac{\bar{D}}{\sqrt{{V}_{\bar{D}}/M}}$$
(28)

where

$$\bar{D}=\frac{1}{M}\sum_{t=1}^{M}{d}_{t}$$
(29)
$${d}_{t}=\frac{1}{M}\sum_{t=1}^{M}\left({\left({Y}_{t}-{\widehat{Y}}_{t}^{test}\right)}^{2}-{\left({Y}_{t}-{\widehat{Y}}_{t}^{bench}\right)}^{2}\right)$$
(30)
$${V}_{\bar{D}}={\gamma }_{0}+2\sum_{q=1}^{\infty }{\gamma }_{q}$$
(31)
$${\gamma }_{q}=cov\left({d}_{t},{d}_{t-q}\right)$$
(32)

\({\widehat{Y}}_{t}^{test}\) and \({\widehat{Y}}_{t}^{bench}\) are predicted values achieved by test and benchmark models. Figure 2 displays the proposed research methodology.

Fig. 2
figure 2

Proposed research methodology

Full size image

The decomposition-based predictive model utilizes two learning methods—SVR-DE and PRI-DE. The DE tunes the hyper-parameters of the SVR model and estimates the coefficients of the PRI model.

5 Results and discussions

We evaluate the proposed approach's performance based on the original Bitcoin price series and five surrogate time series randomly generated through the Monte-Carlo technique from the original Bitcoin price series. The surrogate series are more chaotic and random. Therefore, the performance evaluation based on these series is essential to ascertain the robustness and capability of the proposed forecasting approach. The parameter settings remain constant for both cases.

5.1 Performance evaluation based on the original time series

The proposed framework utilizes one-day, two-day, three-day, four-day, and five-day back lagged closing prices of Bitcoin as explanatory features. The partial autocorrelation function (PACF) plot (Fig. 3) justifies the selection.

Fig. 3
figure 3

PACF plot

Full size image

The first local minima of the PACF plot occurs at lag 5. Subsequently, it exhibits gradual upward and downward movements. The estimated Hurst exponent presented in Table 1 indicates that the series abide by the persistence trend. Therefore, we select the lag at which the PACF value initially reaches close to 0 as the number of lagged variables to form the independent feature set. Then, MODWT applies to the Bitcoin price dataset and explanatory features for six levels of decomposition. Figure 4 displays the original and decomposed series of Bitcoin prices.

Fig. 4
figure 4

MODWT decomposition of Bitcoin price

Full size image

This study utilizes the methodology presented by Bou-Hamad and Jamali (2020) to evaluate in-sample (training) and out-of-sample (validation) forecasting performances. We conduct static one-step ahead and dynamic multiple step-ahead forecasting schemes. For both cases, the validation period is the last 252 observations that reflect the movements of Bitcoin prices of the previous year of the considered sample. A rolling window of 747 observations in the static forecasting scheme estimates the one-day ahead closing price. The considered sample has a total of 1959 observations. To predict the price of 748th observation, samples spanning from observations 1 to 747 constitute the training period's window. The rolling window omits the oldest information and adds the latest observation while traversing from training to validation segments. Training samples 3 to 749 generates the forecast for 750th observation. Similarly, training samples 13 to 759 generates the forecast for 760th observation in the one-step-ahead forecasting framework.

In a multi-step-ahead scheme, the predictive framework uses the entire in-sample segment for training. Then, we partition the decomposed dataset randomly into training (80%) and test (20%) data. The SVR-DE and PRI-DE generate forecasts from the respective components. The DE algorithm estimates the SVR hyperparameters. The number of iterations and the population size are 200 and 20, respectively. Figure 5 depicts the performance of the DE in estimating the three parameters \(C\), \(\sigma \), and \(\varepsilon \). We notice that the DE algorithm converges while determining the three parameters. The DE also estimates the coefficients of the PRI-DE model. As the number of parameters is significantly higher in the PRI model, the number of iterations and population size is 400 and 80, respectively. Figure 6 displays a part of the parameter estimation process betraying iteration wise details for a few selected parameters.

Fig. 5
figure 5

Iteration wise performance of the DE in SVR-DE model

Full size image
Fig. 6
figure 6

Iteration wise performance of the DE in PRI-DE model

Full size image

The presence of convergence is apparent. After completing parameter estimation and component-wise predictions, we compute the final one day ahead forecast of Bitcoin price using Eq. (20). Table 2 reports four performance indicators' estimated values on out-of-sample data points in static and dynamic setups.

Table 2 Forecasting performance of the proposed framework
Full size table

The NSE and IA values of out-of-sample segments in static and dynamic cases are substantially high and close to 1 and show the supremacy of the predictive model. The TI values are low as well, which is ideal for a predictive model. Lastly, the DA statistic is close to 1 for the training and test dataset, which signifies the precise one-day ahead of Bitcoin price predictions. The model has noteworthy performance in estimating the change of price direction of Bitcoin. Hence, the forecasting framework can effectively predict the rise and fall movements, enabling investors to exploit Bitcoin for profitable trading in both short and long terms. The performance of static forecasting is marginally better than that of dynamic forecasting. Thus, the accuracy of the immediate future forecast is comparatively more than the long run futuristic projections. Figure 7 exhibits the actual versus predicted and fitment of actual and forecasted price on out-of-sample data.

Fig. 7
figure 7

Actual and predicted Bitcoin price visualization

Full size image

Both the figures further validate the claims inferred from the values of four performance indicators. The original price and predicted price display very little discriminability between the actual and forecasted. Table 3 summarizes the key parameters of six competing models.

Table 3 Parameters of competing models
Full size table

We generate forecasts from all the competing models in a univariate setup by keeping the same training and test dataset. Subsequently, we calculate the four-performance metrics for comparison. Table 4 furnishes the comparative assessment findings of the proposed approach with the six competing algorithms on test segments of static and dynamic forecasting settings.

Table 4 Forecasting performance evaluation
Full size table

The proposed model outperforms the rest of the models as NSE, IA, and DA figures are higher, while the TI is lower than their counterparts. The competing models' forecasts are above the satisfactory level as the NSE, IA, and DA values are higher than 0.9, and the TI value is considerably low. The performance of competing models degrades in the multi-step ahead dynamic forecasting. The DM derives the statistical significance and gains more in-depth insights into the competing models' performance. Table 5 shows the outcome of the test.

Table 5 The DM test results
Full size table

The DM test is sensitive to the order of constituents of a pair. A positively significant test statistic value implies the statistical superiority of the second model over the first model. A negatively significant test statistic value implies the statistical superiority of the first model over the second model. Finally, an insignificant test statistic value implies that the performance of the models is significant different. A positive significant test statistic associated with the proposed model against all other competing models signifies the proposed model's statistical superiority over the others. From the significance levels, we conclude that all other models outperform MARS and LASSO. There is no significant difference between the predictive performance of MLP, ANFIS, RF, and SVR. Thus, this test offers the statistical validation of the efficacy and effectiveness of the proposed predictive model. The proposed framework is statistically superior to all the six competing models for forecasting one-step ahead and multi-step ahead Bitcoin prices.

5.2 Performance evaluation based on the surrogate time series

We evaluate the efficacy of the surrogate time series to validate and justify the proposed framework's deployment. The present research utilizes 'tseriesEntropy' package of 'R' platform for simulating the surrogate series using Sieve Bootsrap (Buhlmann, 1997). The autoregressive (AR) model resamples the residuals with the replacement for enabling simulation. Using the 'surrogate.AR' function, we generate five such series from the original Bitcoin price series as depicted in Fig. 8. The figure shows that the generated five series are comparatively more volatile than the original one.

Fig. 8
figure 8

Simulated surrogate series

Full size image

As the cryptocurrency market is highly uncertain and chaotic due to various factors, it becomes necessary to examine the proposed predictive model's performance. Tables 6 and 7 show the outcome of the proposed framework's predictive performance and competitive models on static and dynamic forecasting environments on surrogate datasets.

Table 6 Performance on surrogate series in static forecasting
Full size table
Table 7 Performance on surrogate series in dynamic forecasting
Full size table

The performance indicator values imply that the predictive performance is more than satisfactory. Also, the performance is not as good as that of the original Bitcoin price prediction summarized in Sect. 5.1. The validation process applies to a more random and volatile series than the original time series. So, this is an expected outcome. The findings suggest that the proposed predictive framework can predict the future values of cryptocurrencies that are comparatively less stable than Bitcoin. Table 8 reports the results of the DM test on the static and dynamic forecasting setups.

Table 8 The DM test of predictive performance on the surrogate series
Full size table

Table 8 shows that the predictive performance is like that of the original time series. So, the proposed predictive framework is beneficial in an increasingly volatile and random environment. The overall findings of the predictive modeling bring out several interesting results. Both one-step ahead and multi-step ahead forecasting assessments indicate the proposed model's efficiency for estimating Bitcoin prices. Static one-step ahead forecasting performance is marginally better than its counterparts. It is comparatively easier to predict the future figures in the short duration with better accuracy than in the long term. One-step ahead forecasting estimates the closing price of Bitcoin on the next day. It will be useful for daily trading exercise. In multi-step ahead dynamic forecasting, we estimate the Bitcoin price for almost one year. The overall forecast accuracy would naturally be lower in the dynamic case. However, the values of performance indicators suggest that the obtained predictions are very accurate. This will help in long-term portfolio realignment, hedging, etc.

Kristjanpoller et al. (2020) and Zhang et al. (2020) study the dynamic interplay of Bitcoin with other assets. Paule-Vianez et al. (2020) report the safe heaven properties of Bitcoin. Kristoufek et al. (2018) evaluate the inefficiency of the Bitcoin market. However, these works barely throw any light on developing implementable practical predictive architectures capable of predicting short and long-run movements. Interestingly, the literature manifests the multifractal nature of interplay (Kristjanpoller et al. 2020) and sensitivity to volatility contagion (Zhang et al. 2020) that triggers doubt on the predictability of the Bitcoin price with a high degree of precision in the long-range scale. The proposed approach shows that we can predict the Bitcoin price with utmost precision using lagged information of past prices in static and dynamic environments accounting for short and long duration forecasting.

Thus, despite the uncertain nature of Bitcoin prices (Paule Vianez et al. 2020), the proposed approach can model its evolutionary patterns in an efficacious way. Kristoufek et al. (2018) find the inefficiency structure of Bitcoin in the short run. However, the outcomes of the proposed predictive exercises justified that the inefficiency prevailed for long run time horizons. Predictive accuracy of surrogate series rationalizes proposed architecture's effectiveness in modeling Bitcoin price subject to extreme external shocks. As a future endeavor and in connection with the existing literature, the framework can examine Bitcoin price movements during unprecedented events like Covid-19 pandemic with a lagged based architecture.

6 Conclusions

This research proposes a novel DE-based regression framework for forecasting one day ahead price of Bitcoin. It contributes to the forecasting literature by combining a metaheuristic search technique with regression models in a granular setup. The utilization of the DE for optimizing the learning algorithms' performance assists in augmenting the forecast quality. The proposed approach emerges as statistically superior to all other competing models on static and dynamic forecasting situations. LASSO and MARS produce comparatively less accurate forecasts. There is no statistical evidence to discriminate RF, MLP, ANFIS, and SVR's predictive performance. The performance of static one-step ahead is comparatively better than the multi-step ahead dynamic forecasting. The proposed model yields accurate forecasts on the surrogate time series and indicates its efficiency in recognizing intricate patterns. It is useful for estimating future figures of highly volatile cryptocurrencies and other chaotic financial assets.

The diversification benefits of Bitcoin are well known. It has the capability of providing investment security in challenging times. These properties of Bitcoin can help in the precise estimation of its movements in short and long-run horizons. The proposed framework is highly efficient in accomplishing this task. As a result, it will help investors in risk mitigation by estimating the future prices of Bitcoin. The efficacy of the proposed framework on the surrogate series demonstrates the predictive framework's capability to secure noteworthy returns in the crisis period.

This research's scope is limited to examining the predictability of the cryptocurrency having the largest market share. The proposed framework can assess the predictability and efficacy of other cryptocurrencies to infer the market's behavioral characteristics at a holistic level. This work provides the opportunity to offer new forecasting frameworks by integrating appropriate alternate components. We may consider a new forecasting framework by combining the ensemble empirical mode decomposition in place of MODWT. Alternate regression approaches like regression neural network and quantile regression neural network may also work in this setting. Alternate metaheuristics search techniques like PSO, artificial bee colony, and brainstorm optimization may replace the DE. A comparative performance assessment of such predictive frameworks for forecasting highly volatile and chaotic time series may be an interesting research topic.