1 Introduction

In a typical organization, the overall operating costs are primarily comprised of the costs associated with the multi-faceted transportation operations. This implies that, for an organization, a well-designed transportation plan greatly enhances its profitability, competitiveness and credibility. Therefore, one of the key operational decisions is to find the set of optimal vehicle routes, to not only reduce costs but also to improve the service quality. Not surprisingly, many innovative smartphone-based applications have emerged for efficient routing and navigation of vehicles.

Many business situations require a vehicle to undertake several successive pickups of items from pre-determined locations and once all pickups have been completed, the same vehicle has to deliver the items to the respective corresponding delivery location.

The cooperative milk collection is a classic example, wherein a vehicle visits all the collection centers, in a pre-specified order, within a given time window, before delivering the milk so collected to the processing center. Due to the perishability of the product, time windows play a very important role. The other example is Mumbai Dabbawalas,Footnote 1 a homemade food delivery and return system, started in 1890, in the city of Bombay (now renamed as Mumbai) in India. Currently over 200,000 lunchboxes are picked up daily in the morning, delivered before lunchtime and then returned back in the evening.

Such problems, that entail a set of such delivery requests, under time window constraints on the locations, are termed as a Multi Pickup and Delivery Problems with Time Windows (MPDPTW). The MPDPTW has been recently introduced in the literature by Naccache et al. (2018) and Aziez et al. (2020), albeit in its uncapacitated form.

The typical set up for such type of problems fits fully well to the online food ordering applications, which are growing at a fast pace, especially nowadays, where people prefer to order their food online instead of going out to eat at restaurants because of the COVID-19 pandemic. The set up can be understood as follows. Different customers contact a company to request one or several dishes from one or different restaurants. Thereafter, the company, to meet these requirements, has to assign a vehicle to pick up all requested dishes from the selected restaurants prior to delivering them to the customer. The company, of course, may combine the request(s) from different customer(s) for the same vehicle trip and create an overall optimal set of trips for a fleet of vehicles to cater to all customer requests under consideration, based on the operational economics. Moreover, due to the perishability of food products, opening hours of the restaurant for specific food items (breakfast/lunch/dinner) and availability of the customers, the pickup and delivery locations require service/visit during a specific time window. Companies like JUST EAT, Uber eats and SkipTheDishes are the leading companies worldwide, operating under this setting.

In this paper, we consider the capacitated MPDPTW and propose to make three contributions to the body of knowledge. First, we propose an augmented two-index formulation (ATIF) for the MPDPTW, which leads to a more efficient solution algorithm vis-à-vis the higher order formulations, because of the relatively lesser number of variables. The formulation, in variation to the existing two-index formulation for MPDPTW, uses abstract variables representing request-to-request-connectivity. The formulation also captures another operational aspect, i.e. the capacity constraint for each vehicle, which, to the best of the knowledge of the authors, has not been considered in the literature. The number of requests served by a vehicle are often limited because of the capacity limits of the vehicles and considering this constraint makes the problem more practical. Second, we introduce new problem-specific valid inequalities, based on the identified infeasible sets of requests. Third, we report the results on the existing set of benchmark problem instances for MPDPTW and demonstrate that the proposed approach can solve a majority of instances with 25, 35 and 50 nodes, many of which were reported unsolved exactly in the literature.

The proposed study can be a great value addition to the practitioners, especially in the online food delivery business, primarily in two ways. First, by way of providing optimal route plans, especially for the smaller sized problems, and Second, by way of providing solutions for business specific test problems for testing/tuning heuristics-based algorithms, commonly used in practice. Notably, the heuristic algorithms are developed to provide good enough solutions, in almost real time, as against the exact solution methods which can often be time taking. In this context, the study assumes greater practical relevance and can be extremely handy for the practicing managers.

The remainder of this paper is structured as follows. The review of the extant literature, on vehicle routing problems and its relevant extensions, along with the solution approaches is presented in Sect. 2. In Sect. 3, we define the mathematical model, the notations and propose an augmented two-index mathematical formulation for the MPDPTW, along with the proposed valid inequalities. In Sect. 4, we describe the solution methodology. In Sect. 5, we present the results obtained. The conclusions are drawn in Sect. 6 and future scope of work is presented in Sect. 7.

2 Literature review

2.1 The classical vehicle routing problem (VRP)

The VRP was formally introduced by Dantzig and Ramser (1959), which is perhaps the most widely studied operations research problem related to the logistics optimization. The VRP, originally, focused on designing an effective dispatch plan for a set of vehicles for transporting items to serve a group of customers with given demands and an objective to minimize the operational cost. In a typical VRP (see Fig. 1), routes for a fleet of capacitated homogeneous vehicles, located at a base depot, are to be designed such that: (a) a set of customers, each having a known demand, is visited exactly once by a vehicle (b) each vehicle route must begin and terminate at the base depot and (c) the vehicle load on the route, at any point on the designated route, must not exceed the capacity of a vehicle. Due to its wide application in the logistics and transportation industry, VRP is still an intensive research area (Braekers et al., 2016).

Fig. 1
figure 1

Schematics of vehicle routing problem

Full size image

2.2 Extensions to the classical vehicle routing problem (VRP)

The researchers have proposed and studied several variants to the classical VRP, which capture the nuances and distinctive requirements of the evolving logistics processes in practice, like inclusion of time windows for the locations (nodes), fleet of multiple vehicles, backhauls in the supply chain, simultaneous delivery and pick-up, etc.

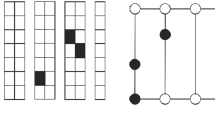
Figure 2 illustrates the broad classification of the VRP family of problems, of our interest.

Fig. 2
figure 2

Classification of VRP related problems

Full size image

In many applications, service time windows are defined, which limit the time period during which the individual location may be serviced by a vehicle. Accordingly, a popular extension to the VRP is the Vehicle Routing Problem with Time Windows (VRPTW). A classic example of VRPTW is collection of currency from parking tolls. To undertake the toll collection, an employee starts her/his journey from a given depot at which she/he is stationed, with a dedicated key for accessing the currency from certain specific tolls eventually to be deposited at a specific delivery location. Although, there is no specific order to visit the set of tolls, but they have to be visited before the employee delivers the currency, only after which the next key will be provided to her/him. Understandably, there are time window restrictions on the completion of the visits.

Another useful extension to VRP includes pickup and delivery at the locations en-route and is termed as Pickup and Delivery Problems (PDP). In PDPs (see Fig. 3), each customer request has its associated pick up (origin) and a corresponding delivery (destination). This entails that the goods, against a pre-determined demand, are to be collected from a specific customer pick-up location before being delivered to a corresponding customer delivery location. The Pickup and Delivery Problems with Time Windows (PDPTW) is the extension of the PDPs with time windows for service at the individual locations (base depot, pickup and delivery). The PDPTW has many practical applications, such as route planning and scheduling for school buses, pooled transportation for lower cost and carbon emissions, urban courier services, less-than-truckload transportation etc.

Fig. 3
figure 3

Schematics of Pickup and Delivery Problems (PDPs)

Full size image

The salient studies on the PDPTW and its variants is given in Table 1 (Table 2).

Table 1 Salient studies on PDPTW
Full size table
Table 2 Exact solution methods used for VRPs and its variants
Full size table

The problem of interest for this study is an extension of the PDPTW, wherein we consider more than one pickups against delivery requests of the customers. The problem is termed as Multi Pickup and Delivery Problem with Time Windows (MPDPTW). The MPDPTW is a relatively recent extension to the VRP (and PDP) family of problems and scarcely studied in the literature (see Table 3).

Table 3 MPDPTW related Work
Full size table

2.3 Solution approaches

VRP is known to be a NP-hard problem (Savelsbergh, 1990). Being an extension of the VRP, the PDPs in general and the MPDPTW in particular are also clearly NP-hard. For NP-hard problems, it is very difficult to obtain exact solutions through mathematical approaches, especially for the large size problem instances. As a result, most research is concentrated on the development of heuristic approaches to attain solutions close to optimal within reasonable time. Adaptive Large Neighborhood Search was used by Pisinger & Ropke (2007), Tabu Search by Nguyen et al. (2017), Parallel Neighborhood Descent by Subramanian et al. (2010) and Particle Swarm Optimization by Ai & Kachitvichyanukul (2009), Goksal et al. (2013) and El-Hajj et al. (2020) for solving pickup and delivery problems. Fischetti et al. (1998) solved the orienteering problem through branch-and-cut algorithm. Whereas, El-Hajj et al. (2016) used cutting plane method to solve the team orienteering problem. However, work on exact methods has been somewhat limited specifically for VRPs and variants. A brief of work done on exact solution approaches for the VRPs and variants can be seen at Table 2.

For an extensive literature survey on exact solution approaches for VRP, readers are referred to Baldacci et al. (2010).

2.4 Work done on MPDPTW

To the best of our knowledge, Naccache et al. (2018) first formally described, modeled and also solved this problem by duly incorporating the associated complicating multi-pickup features. They used 3-index formulation for the problem. They solved the problem using branch-and-bound solution approach, in conjunction with heuristics driven hybrid adaptive large neighborhood search (ALNS). Being the first to introduce MPDPTW, they also developed a benchmark set of problem instances, inspired from the existing instances for the PDPTW. They demonstrated that their approach could solve the problem instances containing up to 400 nodes quiet efficiently, especially vis-à-vis the exact solution approach applied to the mathematical model, using CPLEX solver.

Aziez et al. (2020) made the first attempt to solve the problem with the exact mathematical approach. The authors compared three different formulations (2-index, 3-index and ARF) and concluded that the Asymmetric Representative Formulation (ARF) was the strongest and most efficient formulation. The authors suggest that the ARF overcomes the problem of symmetric solutions, wherein the same set of requests are reassigned to multiple homogeneous vehicles, yielding weak relaxations and as a result, a repetitive branch-and-bound tree. Using the ARF, they solved 60 of the 120 benchmark problem instances of this difficult problem.

2.5 Gaps in the literature

Several gaps can be seen in the extant literature, which are the motivation behind this study. First, only a limited work has been done in the problem area, primarily because it is a recent addition to the research field. This presents an opportunity to extend the body of knowledge. Second, the capacitated form of the problem has not been considered in the literature. This aspect is required to be considered to make the problem practical and relevant. Third, the benchmark problems, used for testing the efficiency of the solution approaches in the literature, remain largely unsolved. This presents a potential to improve the solution approach.

3 Modeling of the problem

The goal of the MPDPTW formulation is to generate route plans under the following constraints:

  1. (a)

    The number of the generated routes is not more than the fleet size, K.

  2. (b)

    Each customer and her/his request is assigned to only one route or vehicle, possibly combined with other requests. It implies that for each request, all its pickups and the corresponding delivery have to be on a single route, undertaken by the same vehicle. This constraint is termed as a coupling constraint.

  3. (c)

    For every request the corresponding pick-up and delivery locations are to be visited once and only once. This constraint is termed as a degree constraint.

  4. (d)

    Within every route, for each request, the visit to the pick-up locations precedes the visit to the corresponding delivery location. This constraint is termed as a precedence constraint.

  5. (e)

    At any point in time, on a route, the load on the vehicle should not exceed its capacity, Q.

  6. (f)

    All pick-up, delivery and the depot (start and terminating) nodes are visited by the assigned vehicles, within the specified time windows for service. The vehicle can wait if it arrives early, but it will be futile for it to reach after the TW closes at any node.

  7. (g)

    The total cost to travel the generated route set is to be minimized. In practice, total distance traveled by all vehicles is considered to represent the cost of travel.

There has been a considerable amount of research related to VRP family of problems and different formulations have been attempted by the researchers, with various extents of success. A summary of related research and formulations used thereof is presented in Table 1.

In this paper, we propose an augmented two-index variables’ based compact mathematical formulation for the capacitated MPDPTW. We strengthen the solution approach in two ways. First, we extend the existing 2-index formulation by introducing additional abstract variables to capture the unique nature of the problem, i.e. more than one pick up point associated with each request. Second, we develop new valid inequalities to improve the lower bounds of the problem. The results, discussed in Sect. 5, indicate that most of the test problem instances (sizes 25, 35 and 50) could be solved using the proposed approach.

3.1 Mathematical model

The MPDPTW can be defined with the set of vertices \(V=P\cup D\cup \{0\}\) on a graph \(G=(V,A)\). \(P=\{1,\dots p\}\) and \(D=\{p+1,\dots p+n\}\) define the pickup and delivery nodes respectively, where \(\left|D\right|=n and |P|\ge n\). We define \(N=P\cup D\) as the set of customer nodes. Node \(0\) is the source as well as the terminating base depot node. \(R=\{{r}_{1},\dots \), \({r}_{n}\)} are the requests required to be routed, wherein each request \(r\in R\) is associated with a set of pickup nodes \({P}_{r}\subseteq P\) and a delivery node \({D}_{r}\in D\). A homogeneous capacitated fleet of \(K\) vehicles is available to serve these requests.

The mathematical model can then be defined with the following decision variables and parameters.

Decision variables

  • \({X}_{ij}\in \left\{\mathrm{0,1}\right\} \forall i,j\in V\): equals to 1, if a vehicle directly goes from node \(i\) to node \(j\), 0 otherwise.

  • \({R}_{mn}\): equals to 1, if requests \(m\in R\) and \(n\in R\) are served by same vehicle, 0 otherwise.

  • \({V}_{rk}\): equals to 1, if a vehicle \(k\in K\) serves the request \(r\in R\), 0 otherwise.

  • \({C}_{j}\): the load immediately after the departure from node \(j\in V\), for the assigned vehicle.

  • \({S}_{j}\): the start time of service at node \(j\in V\)

The \({X}_{ij}\), \({C}_{j}\) and \({S}_{j}\) variables are generic decision variables, used extensively for the VRP family of problems, whereas \({R}_{mn}\) and \({V}_{rk}\) variables have been introduced based on the nature of the problem and are specifically applicable for the MPDPTW type of problem. The latter two are extensively used in this study for incorporating dedicated valid inequalities for the problem.

Parameters

  • \({e}_{j}\),\({l}_{j}\) are the opening and closing times for the service at a node \(j\in V\). The vehicle may arrive at a node \(j\), not later than \({l}_{j}\) but may arrive prior to \({e}_{j}\) and wait until \({e}_{j}\) to service at the node \(j\).

  • \({d}_{j}\) is the service time duration at node \(j\in V\)

  • \({q}_{j}\) is the demand (positive for pick up and negative for delivery) at node \(j\in V\).

  • \({c}_{ij}\) and \({t}_{ij}\) are respectively the cost and time of travel from node \(i\in V\) to node \(j\in V\). In this work, we consider \({c}_{ij }={t}_{ij}\).

  • \(Q\) is the capacity of each vehicle \(k\in K\).

The MPDPTW problem can be mathematically formulated as follows:

$$Min \sum_{i\in V}\sum_{j\in V}{X}_{ij}.{c}_{ij}$$
(1)
$$\mathrm{s}.\mathrm{t}. \sum_{i\in V}{X}_{ij}=1 \forall i\ne j, j\in N$$
(2)
$$\sum_{j\in V}{X}_{ij}=1 \forall i\ne j, i\in N$$
(3)
$$K\ge \sum_{j\in N}{X}_{0j}\ge 1$$
(4)
$${{e}_{j }{\le S}_{j }\le l}_{j} \quad \forall j\in V$$
(5)
$${{S}_{j }+M.\left(1-{X}_{ij}\right)\ge {S}_{i }+{t}_{ij}+d}_{i} \quad \forall i\ne j, i\in N,j\in V$$
(6a)
$${{S}_{j }+M.\left(1-{X}_{0j}\right)\ge {t}_{0j}+d}_{0} \quad \forall j\in N$$
(6b)
$${S}_{{D}_{r}}\ge {S}_{p } p\subseteq \quad P, r\in R$$
(7)
$${R}_{mn}\le 1+{V}_{mk}-{V}_{nk} \quad \forall \mathrm{ k}\in \mathrm{K};\mathrm{m},\mathrm{ n}\in \mathrm{R}$$
(8)
$${X}_{ij} \le {R}_{mn} \quad \forall i\in {P}_{m}\cup {\{D}_{m}\}, j\in {P}_{n}\cup {\{D}_{n}\}, m\ne n, m, n \in R$$
(9)
$$\sum_{k\in K}{V}_{rk}=1 \quad \forall r\in R$$
(10)
$${c}_{j }\le Q \quad \forall j\in N$$
(11)
$${c}_{j }+M.\left(1-{X}_{ij}\right)\ge {c}_{i }+ {q}_{j} \quad \forall i\ne j, i\in N,j\in V$$
(12a)
$${c}_{j }+M.\left(1-{X}_{0j}\right)\ge {q}_{j} \quad \forall j\in N$$
(12b)
$$\sum_{j\in N}{X}_{0j}=\sum_{i\in N}{X}_{i0}$$
(13)

The objective function (1) minimizes the total travel cost (time) for serving the given requests completely. Equations (2) and (3) are the degree constraints associated with the nodes; meaning thereby that there is only one connection coming into and going out of any node. Constraints (4) caps the total vehicles used in the solution at K. Constraints (5) and (6a),(6b) ensure that the service time windows are respected at each node and (6a),(6b) also eliminate sub tours. The precedence order for the nodes of a request is preserved by the precedence constraints (7). Constraints (8) ensure that any number of requests are connected only if they are served by the same vehicle. Constraints (9) ensure that any two requests are directly connected only if they are served by same vehicle. Constraints (10) ensure that a request is served by exactly one vehicle. Constraint (8), (9) and (10) together enforce coupling constraints, i.e. ensuring that the pick-up and delivery nodes of any request are served by one and the same vehicle. Constraints (11) and (12) ensure that capacity of the vehicles is respected at every node. Constraint (13) ensures vehicle consistency, i.e. the number of vehicles starting from the depot (start) node are equal to the number of vehicles terminating at the depot (end) node.

M is a sufficiently big number in constraints (6) and (12). However, the constraints (6) have a detrimental effect on the formulation to the extent that the LP relaxation of model grossly underestimates variable values, hampering the solution performance. To overcome this limitation, as shown by Desrochers and Laporte (1991), the constraints for the \({S}_{j}\)‘s (6), for a given pair of nodes \(i,j\in V\), have been lifted by considering the reverse arc \((j,i\)) for the pair of nodes, as below.

$$ S_{j } \ge S_{i} + d_{i} + t_{ij} - M_{ij } \left( {1 - X_{ij } } \right) + (M_{ij } - d_{i } - t_{ij } - \max \left( {d_{i } + t_{ji } ,e_{i } - e_{j } } \right).X_{ij} \quad \forall i \ne j, i,j \in N $$
(6*a)
$$ S_{j } \ge d_{0} + t_{0j} - M_{0j } \left( {1 - X_{0j } } \right)\quad \forall j \in N $$
(6*b)
$$ S_{0 } \ge S_{i} + d_{i} + t_{i0} - M_{i0 } \left( {1 - X_{i0 } } \right)\quad \forall i \in N $$
(6*c)

Footnote 2We use \(M_{ij } = {\text{max}}(0,l_{i} + d_{i} + t_{ij} - e_{j} )\) in the above equations.

Similarly, lifting for Eqs. (12), is done as below.

$$ C_{j } \ge C_{i} + q_{j} - W_{ij } \left( {1 - X_{ij } } \right) + \left( {W_{ij } - q_{i } - q_{j } } \right)X_{ji } \quad \forall i \ne j, i,j \in N $$
(12*a)
$$ C_{j } \ge q_{j} - W_{0j } \left( {1 - X_{0j } } \right) + \left( {W_{0j } - q_{0 } - q_{j } } \right)X_{j0 } \quad \forall j \in N $$
(12*b)

We use \(W_{ij } = {\text{min}}\left( {Q,Q + q_{i} } \right)\) in the above equations.

In addition to the above constraints, to further improve the bounds, the following constraints are used to remove the set of arcs that are known to lead to infeasible solutions. Equation (14) ensures no node is connected to itself, (15) ensures that no pick up node connects to the depot node, (16) ensures that no delivery node connects to its corresponding pick up node, (17) ensures there is no connection from depot node to any delivery node, (18) ensures that any two nodes are at best connected only one-way, (19) ensures that for each request, only 1 (or none) of the pick-up nodes can be connected from depot node, (20) ensures that for all arcs (\(i,j)\), a vehicle cannot reach node \(j\) before the end of the service time window at node \(j\) from node \(i\), even if the service at node \(i\) had commenced at its start of the service time window (i.e. \(l_{j} < e_{i} + d_{i}\) + \(d_{ij}\)), are inactive.

$$ \mathop \sum \limits_{i \in V} X_{ii} = 0 $$
(14)
$$ \mathop \sum \limits_{{i \in P_{r} ,r \in R}} X_{i0} = 0 $$
(15)
$$ \mathop \sum \limits_{{i \in P_{r} ,r \in R}} X_{{D_{r} i}} = 0 $$
(16)
$$ \mathop \sum \limits_{r \in R} X_{{0D_{r} }} = 0 $$
(17)
$$ X_{ij} + X_{ji} \le 1\quad \forall i,j \in V $$
(18)
$$ \mathop \sum \limits_{{j \in p_{r} }} X_{0j} \le 1\quad \forall r \in R $$
(19)
$$ X_{ij} = 0\quad \forall i,j \in V, l_{j} < e_{i} + d_{i} + d_{ij} $$
(20)

3.2 Valid inequalities

The branch and bound algorithm has to search the entire solution space to find the optimal solution. The time taken to solve, therefore, depends primarily on the contour of the solution space. Researchers strengthen the formulation and therefore the solution algorithm by introducing additional constraints in the form of valid inequalities.

Valid Inequalities are problem specific inequalities which are valid in the feasible solution search space. Cuts are those valid inequalities, which can reduce the solution search space. Cuts can be identified by finding violated valid inequalities in the fractional (LP relaxation) solution and they are expected to improve the lower bound of the problem. The cuts are introduced in the formulation as additional constraints.

Various valid inequalities have been used in the extant literature, across the family of VRP problems, to improve the lower bounds. Following are the valid inequalities used in this work.

3.2.1 Sub Tour Elimination Constraints

The literature suggests that the algorithms for solving pickup and delivery problems suffer from the challenge of sub tours in the solution and the constraints to avoid sub tours are often tight or active constraints. Therefore, it is a common practice to identify potential sub tours and plug in corresponding valid inequalities to ensure that they are avoided in the solution.

The classic sub-tour elimination constraint (CSTECs) have been utilized, using various formulations, to avoid incorrect solutions in the Traveling Salesman Problems and can also be extended to the related problems like MPDPTW. For S, a family of sets, s, for which a sub-tour exists, the CSTECs can be introduced in the form of a valid inequality as under:

$$ \mathop \sum \limits_{i,j \in s} X_{ij} \le \left| s \right| - 1\quad \forall s \in S $$
(21)

3.2.2 Valid Inequalities based on infeasible sets of requests

In an MPDPTW, a vehicle can only serve those combinations of requests together which do not violate any constraints of the problem. A particular combination of requests is strictly infeasible, if there exists no route for a vehicle that does not violate any problem constraint, while serving the requests together. For example, after traversing all intermediate nodes associated with the set of requests under consideration, if the vehicle cannot return to the depot node before the closure of the TW (\(l_{0}\)) at the depot node, such a set will be infeasible. If any such sets of requests are assigned to a single vehicle, along with no or any other request(s), such solutions are bound to be infeasible.

The solution algorithm can be strengthened by adding corresponding valid inequalities (constraints) that do not allow such set of requests, identified as infeasible, to be served by a single vehicle or in other words to be on the same route together. The idea is inspired from the ARF formulation in Aziez et al. (2020), wherein the authors add a constraint to ensure that the infeasible pair of requests are not assigned to same cluster. They defined \( W = \{ \left( {i,j} \right) \in R \times R|i\;and\;j\;are\;infeasible\;to\;be\;served\;together\;by\;one\;vehicle\} , \) which essentially represents the pairs of requests that cannot be served together on the same route because they lead to an infeasible path. We extend this approach to include combination of more than two requests which are infeasible to be served together by a single vehicle. We note that the greater the size of the set of requests, the greater are the chances of it being infeasible.

For W, a family of infeasible sets of requests, w, the valid inequalities are as given by equation as under, which ensures that the requests in the sets under consideration are not served by the same vehicle or are on the same route.

$$ \mathop \sum \limits_{r \in w} V_{rk} \le \left| w \right|\quad \forall k \in K,w \in W $$
(22)

4 Solution methodology

We use branch-and-cut search to solve our mixed integer programming (MIP) model, managing a search tree with several nodes corresponding to variable bounds. Every node on the tree represents the LP sub-problem for the solver to solve and check its integrality. The active nodes are processed in the tree, under the algorithmic constraints. From every parent node, the branching exercise creates two new nodes. For example, branching on a binary variable will create a set of two new nodes, first with a (modified) upper bound of 1 (the only feasible value for the binary variable then becomes 1), and the second with a (modified) lower bound of 0 (the only feasible value for the binary variable then becomes 0). The MIP model has already been discussed in Sect. 3.

Below, we briefly discuss the procedure for identifying the valid inequalities.

4.1 Valid inequalities based on identified sub-tours

Complementing the sub-tour elimination constraints (6(a), (b)), we identify the CSTECs as cuts, as follows. We relax the LP for the MPDPTW on \(X_{ij}\)’s (allowed to take values on a continuum between 0 and 1 instead of being binary), extract the potential sub-tours (a sub tour is said to exist among a set of nodes, \(s\), if the number of connections among the nodes in set \(s\) are equal to \(\left| s \right|\)) in the solution, add the sub-tour elimination constraints in the model and repeat the exercise till we find no additional sub-tours in the LP relaxation problem.

The pseudo code of the algorithm is given below in Table 4. Basically, we run a Relaxation LP, which is the LP set up as per Eqs. (1) to (20). Based on the values that the’s take, we identify all sub-sets s, which form sub-tours. To this extent, we start our search with the best possible pair of nodes in a subset, i.e. edge having max value in the current solution and keep adding nodes to that subset, till we stop getting an increment above a threshold value. We repeat this exercise to identify all sub sets and add them to set. Against each subset of set, found in the current iteration, we then build sub-tour inequalities (21) and add them as constraints of the problem and solve the next iteration of the relaxed LP and repeat the above exercise. We stop, if there is no improvement in the objective function value for the relaxed LP vis-a-vis the previous iteration and no new STECs are obtained in the current iteration.

Table 4 Pseudocode of the algorithm for identifying STECs
Full size table

4.2 Valid inequalities based on identified infeasible set of requests

We run an exploratory search on the unique set (of various sizes) of requests of various sizes. For each exploration, we create a modified problem file, with only the pick-up and delivery nodes associated with the requests contained in the set under consideration. The formulation remains the same (Eqs. 1 to 20; in Sect. 3) except that the objective function is modified with a penalty factor for number of vehicles used.

$$ Min\sum\nolimits_{i \in V} {\sum\nolimits_{j \in V} {X_{ij} \cdot c_{ij} } + M * \sum\nolimits_{k} {Z_{k} } } $$
(23)

We use, i.e. the TW of the depot node. By using the above objective function, if a feasible solution can only be obtained by using more than one vehicle then our set of requests can be taken as infeasible.

The procedure and the pseudocode to identify the infeasible sets of requests (IISOR) is presented in Table 5. Here, W indicates the total set of infeasible requests of all sizes (master). Whereas, indicates infeasible requests of different sizes ranging from 2 to (a carefully chosen number less than or equal to the total number of requests). We begin evaluating the feasibility from the set size of 2 requests (unique; selected from the total requests) and process till we cover the size. For each size, we generate all unique sets of requests of that particular size, at Step 4. For each size, we then identify all such combination of requests which are infeasible and add them in our lists to be used for creating valid inequalities at step 13. Additionally, for all sizes greater than two, we also remove, at step 6, the sets whose sub-sets are already covered in the sets of lower sizes. This saves processing time, as these sets are bound to be infeasible.

Table 4 Pseudocode of the algorithm to find sets of infeasible requests
Full size table

5 Results and discussion

In this section, the results for the proposed approach are presented. In Sect. 5.1, we define the benchmark problem instances for the MPDPTW. In Sect. 5.3, the results obtained against these benchmark problem instances are presented, along with the comparison of the proposed formulation with the existing formulations in the literature.

5.1 Benchmark problem instances

We use the same test instances as used by Aziez et al. (2020) and proposed by Naccache et al. (2018). Notably, these test instances are customizations over the instances used by for Li and Lim (2003) for the PDPTW.

Table 6 defines the basic features of the instances. Each instance type is comprised of three key elements, viz. (a) Request size indicating the maximum dimension of the requests in terms of the number of nodes; (b) Instance size indicating the total nodes in the instance; and (c) TW Type: Without indicates that the TW of the nodes is made significantly wide such that it can be considered as deleted, Normal indicating that the TW for each node is widened somewhat by opening and closing it 150 units earlier and 150 units later respectively, and Large indicating that the TW for each node is further widened by opening and closing it 300 units earlier and later respectively. The requests are designed to contain a maximum of 4 (termed as Short requests) or 8 (termed as Long requests) pick-up and delivery nodes.

Table 6 MPDPTW Instance Types
Full size table

The combinations of request type and time window constitute 6 instance types. For each instance type, five instances are generated against each instance size (25, 35, 50 and 100) to get a total of 20 instances. Overall, we have a total of 120 instances. To understand, for example, the instances of type “l_8 _25” represent an instance with a size of 25 nodes, having large TW and long requests, which are denoted as “l_8 _25” 1 to “l_8_25” 5.

In this study, we solve for problem instances with up to 50 nodes only, because of two reasons. Firstly, the pre-processing required to be done for larger problems becomes rather heavy and perhaps makes it time impractical to obtain an optimal solution using exact solution approach. We propose that in such cases, one can either use heavy duty machines or prefer heuristically attained solutions. Secondly, we expect that this addresses most of the practical situations and may be sufficient to prove the efficacy of the approach.

5.2 Technical settings

The experiments reported in this paper have been performed on a Laptop equipped with a 1.6 GHz CPU, 8 GB of RAM. The LP is coded using the PULP library in Python 3.7 and the CPLEX 12.10 API is called with the default options, for solving the LP.

5.3 Comparison of results

In this section, we evaluate the proposed formulation for MPDPTW in terms of its ability to solve the test instances and also its relative performance against the existing formulations.

Since, the work by Aziez et al. (2020) is the only exact solution work in the literature, we present the comparison of the results, vis-à-vis the formulations used in their work. Further, the comparison is also based on the same instances as used by Aziez et al. (2020), which have proven to be significantly challenging for testing the strength of a formulation. Table 7 gives the results obtained against the various test instances, using the three reference formulations (work by Aziez et al. (2020); i.e. the 2-index, 3-index and ARF) and the proposed augmented 2-Index formulation (say, ATIF). For comparison, we evaluate each formulation in respect of (a) the number of instances that were solved to optimality, for each instance type and (b) the solution time (for the instance solved to optimality). The results demonstrate the efficiency and value of the proposed augmented 2-index formulation.

Table 7 Summary of the results against all MPDPTW test instances—various formulations
Full size table

The results reported in the Table 8 demonstrate that the ATIF outperforms the existing formulation for the number of instances solved (for all test instance sub-groups). Across the sub-groups (Column#1), it can be seen that the ATIF either equals the performance of the best of the existing formulations or is able to outperform them. However, with respect to the time taken, ATIF seems to take more time to solve and is found to be superior only in 4 sub-groups as compared to 11 of existing formulations. However, it is important to note that Aziez et al. (2020) used a desktop compute with 28GM of RAM and 2.67 GHz Intel processor, wheras we used Laptop equipped with a 1.6 GHz Intel processor with only 8 GB of RAM. Therefore, a direct comparison with respect to the solution time perhaps will not be meaningful. Considering that the time taken is well within the time limits of one hour, the results are able to demonstrate the efficiency of the proposed approach.

Table 8 Performance of the formulations against all MPDPTW test instances
Full size table

Summarized results in Table 9, show that the ATIF outperforms the 2-index, 3-index and ARF formulations, as it solves 10% more instances compared the closest competitor (ARF) to optimality.

Table 9 MPDPTW test instances solved by various formulations
Full size table

Here, we briefly present the summary of the comparative analysis given in Tables 7, 8 and 9.

  1. (1)

    We are able to solve 66 out of 90 test instances considered, with the proposed approach. Since, the other formulations, i.e. 2-Index, 3-Index and ARF could solve 47, 49 and 60 test instances respectively, ATIF appears to have outperformed those formulations. The performance is especially superior for the Large and Without TWs test instances.

  2. (2)

    The sub-groups of problem instances, of which not all instances were solved earlier, have been completely solved to optimality now. Barring the 100 nodes instances and the Without TWs type instances, ATIF is able to solve almost all test instances.

    This shows the power of ATIF and the valid inequalities vis-à-vis the existing formulations.

  3. (3)

    The time taken to solve is relatively more than the ARF used in the work by Aziez et al (2020). But, being comfortably in the sub-one-hour category, seems to be reasonable. Moreover, the ATIF consistently outperforms the other formulations.

  4. (4)

    The problem sub-groups of type Without TW (w_4_35, w_4_50, w_8_35 and w_8_50) have proven to be tough to solve. It is noted that the problem instances of Without TWs type are extreme instances and are inherently tough to solve.

As seen in the Fig. 4, none of the formulations have been able to solve the problems with the Without TWs with more than 25 nodes (barring one problem of the w_8_35 group, using ARF). Further, the Fig. 5 demonstrates that, using any of the formulations, the problem instance with Long requests are relatively easier to solve as compared to the problem instances with Small requests.

Fig. 4
figure 4

Sub-Group wise MPDPTW test instances solved by various formulations

Full size image
Fig. 5
figure 5

Request size wise and Problem size wise problem instances solved by any formulation

Full size image

Therefore, the more the picks ups (Longer requests) against each request and tighter the Time Windows for service, the problem becomes that much easier to solve. Intuitively, these conditions result in tighter constraints and resultantly, a shrunken search space.

5.4 Comparison of the characteristics of the formulations

We now review the formulations based on the basic characteristics, i.e. number of variables and constraints. To approximate the calculation in the Tables 9 and 10, the (a) Sub-Tour constraints are not accounted; (b) on an average, three pick up nodes per request have been considered; (c) Vehicles and Requests are assumed to be equal (i.e. |R|= K).

Table 10 Comparative characteristics of the formulations for MPDPTW
Full size table

As we can see, from Table 10 and Fig. 6, in the ATIF.

  1. (a)

    The variable size is a little higher than the 2-Index formulation, but considerably smaller than the other two (three-index and ARF) formulations. The difference is even more significant as the problem size increases. Therefore, the augmented two-index formulation is economical in terms of the variables.

  2. (b)

    The order of constraints is the same (i.e. N.N) as that for the existing 2-Index, ARF and the 3-Index formulations. However, the number of constraints, as in the existing 2-index formulation, are higher than ARF and the 3-Index formulations. Notably, the difference is relatively less for smaller sized problems but grows as the size of the problem increases.

  3. (c)

    The saving in terms of the number of variable (which are significantly less as compared to the ARF and three-index formulations) seems to outweigh the loss in terms of the number of constraints (which are higher as compared to the ARF and three-index formulations).

Fig. 6
figure 6

Formulations—Characteristics vs Problem Instances. There are 40 basic problem instances, with variation in terms of number of nodes (25, 35, 50 and 100) and variation in size of requests (Long and Small) and five problem of each node size-request size combination. These 40 basic problems have different time windows (Without, Large and Normal) which results in a total of 120 problem instances. In Fig. 6, we refer to the 40 basic problem instances.

Full size image

Therefore, we have a benefit of reduced variable size, along with a very limited setback in terms of increased number of constraints, with the proposed ATIF.

6 Conclusions

This paper is focused on the MPDPTW problem, which finds many interesting applications in practice, the most notable in food delivery systems.

In this paper, we have considered the capacitated form of the MPDPTW, making it a more practical and relevant study. We have introduced an augmented two-index formulation for MPDPTW, with the incorporation of abstract request-level variables to the existing two-index formulation. By using these variables, we have also introduced specific valid inequalities based on the identified infeasible sets of requests.

The combination of the ATIF and the valid inequalities seems to be very powerful and produces high quality solutions, within modest computing times. The strength of the approach is clearly illustrated by its capability to solve many of the hitherto unsolved problems. In comparison to the existing formulations/approach, with the ATIF, we solve 10% more benchmark problem instances with problem size of up to 100 nodes and 20% more problem instances with problem size of up to 50 nodes, well within the solution time limit of one hour.

7 Future Research Directions

Many of the valid inequalities available in the extant literature, like Fork Inequalities, Reachability Cuts (Belov and Scheithauer, 2006), etc. have not been utilized in the current work. These inequalities can further strengthen the lower bounds of the problem and render some more problems solvable. The further interest can be to explore them and perhaps solve even the larger sized problem instances in a limited time. One can also apply other solution approaches, like the Lagrangian relaxation technique, by relaxing the service time constraints and/or the degree constraints. It may also be interesting to explore the potential practical extensions to the problem, by way of introducing the heterogeneity of vehicles (in terms of the speed, capacity etc.), time windows of the vehicle etc.