Abstract
Statistical descriptions of coherent flow motions in the atmospheric boundary layer have many applications in the wind engineering community. For instance, the dynamical characteristics of large-scale motions in wall turbulence play an important role in predicting the dynamical loads on buildings, or the fluctuations in the power distribution across wind farms. Davenport (Quarterly Journal of the Royal Meteorological Society, 1961, Vol. 372, 194-211) performed a seminal study on the subject and proposed a hypothesis that is still widely used to date. Here, we demonstrate how the empirical formulation of Davenport is consistent with the analysis of Baars et al. (Journal of Fluid Mechanics, 2017, Vol. 823, R2) in the spirit of Townsend’s attached-eddy hypothesis in wall turbulence. We further study stratification effects based on two-point measurements of atmospheric boundary-layer flow over the Utah salt flats. No self-similar scaling is observed in stable conditions, putting the application of Davenport’s framework, as well as the attached-eddy hypothesis, in question for this case. Data obtained under unstable conditions exhibit clear self-similar scaling and our analysis reveals a strong sensitivity of the statistical aspect ratio of coherent structures (defined as the ratio of streamwise and wall-normal extent) to the magnitude of the stability parameter.
Similar content being viewed by others
1 Introduction and Context
Coherence quantities of atmospheric surface-layer (ASL) turbulence are of great practical significance to the wind-engineering community as these are required for determining the dynamic action of atmospheric turbulence on wind-sensitive structures, such as tall buildings, long span bridges (Isyumov 2012), and wind turbines (Saranyasoontorn et al. 2004), or in predicting peak-power distributions across wind farms (Sørensen et al. 2007, 2008). Ground-breaking work on this subject was carried out by Alan G. Davenport and can be found in Davenport 1961a, b, 2002, Simiu and Scanlan (1996), Pasquill (1971) and Baker (2007). The particular aspect we focus on here is the degree and extent of the coherence of wind fluctuations in the vertical direction, which is quantified via the linear coherence spectrum
where, \(X\left( z;\lambda _x\right) = \mathcal {F}\left[ \psi (z)\right] \) is the Fourier transform of some fluctuating quantity \(\psi (z)\) and \(\lambda _x\) is a streamwise wavelength. The vertical position is z, and \(z_R\) denotes the reference position usually taken close to (or at) the surface. The asterisk * indicates the complex conjugate, \(\langle \rangle \) denotes ensemble averaging and \(\vert \vert \) is the modulus. It is noted that the numerator equals the square of the cross-spectral magnitude, while the two energy spectra of \(\psi (z_R)\) and \(\psi (z)\) form the denominator. Since \(\gamma ^2\) only incorporates the magnitude of the cross-spectrum, the value of \(\gamma ^2\) represents the maximum correlation for a specific scale \(\lambda _x\). Consequently, \(\gamma ^2\) equates to the fraction of common variance shared by \(\chi (z_R)\) and \(\chi (z)\) and we note that, by definition, \(0 \le \gamma ^2 \le 1\). As indicated in Eq. 1, \(\gamma ^2\) generally is a function of the positions z and \(z_R\) and the wavelength \(\lambda _x\) (Note that we restrict the discussion to streamwise scales here as, via Taylor’s hypothesis, this direction is the most accessible experimentally).
Davenport (1961a) hypothesised that the coherence is, (i) a function of the ratio \({\Updelta } z/\lambda _x\) only, where \(\Updelta z = z-z_R\), and (ii) used an exponential decay to fit the dependence. Such a formulation is still widely used in the wind-engineering community to date (e.g., Baker 2007) and we will refer to it as Davenport’s hypothesis.
During the same era as Davenport, A. A. Townsend made his impact in the field of turbulent shear flows (Marusic and Nickels 2011), most notably with his attached-eddy hypothesis (Townsend 1976; Perry and Chong 1982; Marusic and Monty 2019). A central tenet of the attached-eddy hypothesis states that eddying motions in the logarithmic region of wall-bounded flows are self-similar and that their size scales with their distance from the wall z. In the context of the ASL, reference to the attached-eddy hypothesis has been made before, e.g., most recently by Li et al. (2018). Evidence in support of self-similarity and wall-scaling has been reported throughout the boundary-layer community (see, for instance, Jiménez 2012; Hwang 2015; Marusic et al. 2017) and most recently by Baars et al. (2017) who investigated the vertical coherence of the longitudinal velocity fluctuations relative to a reference very close to the wall.
Interestingly, it seems that, regarding the coherence, no cross-work exists between the two respective scientific communities to which Davenport (wind engineering) and Townsend (turbulent shear flow) belonged. To the authors’ knowledge, only Davenport himself noted the early work of Townsend, as Davenport (1961b, p. 209) states: “Some of the possible implications of this have been discussed by Townsend (1957).” In the present study we aim to connect the progress made in these communities regarding the understanding of the self-similar turbulent eddy structures in the ASL, as quantified by the coherence diagnostic. In doing so, we will show that the geometrical self-similarity implied in Davenport’s hypothesis is consistent with the attached-eddy hypothesis. Further, we will demonstrate that also the functional form given in Eq. 2 agrees closely with a logarithmic dependence derived from the attached-eddy model (Baars et al. 2017).
We start out by providing brief reviews of Townsend’s and Davenport’s hypotheses (Sect. 2) and demonstrate their conformity. Subsequently, we describe high-fidelity velocity and temperature data taken along the vertical direction in the ASL over smooth terrain (Sect. 3). These data are used in Sect. 4 to infer the coherence statistics as a function of atmospheric stability. Throughout, we only employ the fluctuating components of the turbulence quantities; the streamwise (or longitudinal), spanwise and wall-normal velocity fluctuations are denoted by u, v and w, respectively, with associated coordinates x, y and z. Temperature fluctuations are denoted with \(\theta \), its mean by \(\Uptheta \).
2 Connecting the Hypotheses of Townsend and Davenport
2.1 Coherence Following Townsend’s Attached-Eddy Hypothesis
Townsend (1976) envisioned that a wall-bounded shear flow encompasses a range of self-similar ‘attached eddies’. The terminology ‘attached’ thereby implies that turbulence statistics scale with their distance from the wall, so-called z-scaling. The exact types of characteristic eddies and whether they are truly attached is of secondary importance. The attached-eddy description is applicable in the inertial region of the turbulent boundary layer, where the scales range from \(\mathcal {O}(100)\) viscous units \(\nu /U_\tau \) to the order of the boundary-layer thickness \(\delta \). In practice, the inertial or ‘logarithmic’ region of the ASL occupies the range from order of millimetres above the ground to \(\mathcal {O}(100\,\mathrm {m})\) and therefore is highly relevant to all wind-engineering applications. The ratio of the two length scales \(\nu /U_\tau \) and \(\delta \) forms the friction Reynolds number, \(Re_\tau \equiv \delta U_\tau /\nu \), where \(\nu \) is the kinematic viscosity and \(U_\tau = \sqrt{\tau _0/\rho }\) is the friction velocity, with \(\tau _0\) and \(\rho \) being the wall-shear stress and fluid density, respectively. Note that throughout the superscript ‘+’ signifies normalization by ‘inner’ scales \(\nu /U_\tau \) and \(U_\tau \). A quantity analogous to the shear velocity, the wall conduction velocity, is given by \(\Uptheta _\tau = -\varepsilon \partial _z \Uptheta \vert _{z=0}/U_\tau \), \(\varepsilon \) being the thermal diffusivity.
Here, we review key results of Baars et al. (2017), who examined two-point measurements in the wall-normal direction for smooth terrain and well-controlled flow conditions. Baars et al. (2017) considered ASL measurements taken at the Utah SLTEST facility over salt flats at \(Re_\tau \approx 1.4 \times 10^6\) (Marusic and Heuer 2007); further details on these types of experimental campaigns to study high-Reynolds-number wall-bounded turbulence can be found in the literature (Metzger et al. 2007; Hutchins et al. 2012; Wang and Zheng 2016; Yang and Bo 2017). A wall-normal array of five sonic anemometers was employed, situated above a wall-shear-stress sensor. This unique set-up made it possible to investigate the coupling between the outer-region turbulence and the near-wall footprint in the fluctuating friction velocity. In most other cases only a near-wall velocity measurement is available, as will be considered later. The coupling of fluctuations at different heights and scales was examined in spectral space using the linear coherence spectrum defined in Eq. 1. One coherence spectrum is obtained per velocity-pair \(u(z_R)\)–u(z), where the height z ranges from \(z^+ {\approx }3500\) up to \(z/\delta \approx 0.03Re_\tau \) (corresponding to physical dimensions of \(z = 2\) to 5 m, Marusic and Heuer 2007). Figure 1a shows the five \(\gamma ^2\) spectra as a function of \(\lambda _x/z\). Note that the streamwise wavelength \(\lambda _x\) has been computed following \(\lambda _x \equiv U(z)/f\), where U(z) is the mean streamwise wind speed and f is the temporal frequency.
a Linear coherence spectra for the neutral ASL (Marusic and Heuer 2007). Five spectra correspond to the five sonic-anemometers (darker shades of grey reflect increasing wall-normal distance). b Coherence spectra of panel a presented as a spectrogram (red contours with levels 0.1:0.1:0.9 from left-to-right). The premultiplied streamwise energy spectrogram is shown with the underlying filled contours (grey contours with levels 0:2:0:2:1.8). The figure is adopted from Baars et al. (2017)
A coherence spectrogram is formed by presenting the five individual coherence spectra as iso-contours of \(\gamma ^2\) in the \((\lambda _x,z)\) plane (Fig. 1b). The iso-contours increase in value with increasing wavelength, and the contours follow lines of constant \(\lambda _x/z\) (slope of 1), reflecting the collapse of the individual spectra in Fig. 1a. For reference, the energy spectrogram of the streamwise velocity fluctuations is shown with filled iso-contours underneath the \(\gamma ^2\) spectrogram. Energy is presented in premultiplied form \(k_x\phi _{uu}/U^2_\tau \), where \(\phi _{uu}\) is the one-sided power spectrum of u. Evidently, only a portion of the energy is statistically coherent with the near-wall measurement (the portion of the energy residing below non-zero contours of \(\gamma ^2\)).
Figure 1 demonstrates that only increasingly larger scales remain coherent with \(z_R\) when z moves upward. This trend is consistent with Townsend’s attached-eddy hypothesis in the formulation of Perry and Chong (1982), where a hierarchy of self-similar eddies is assumed as sketched in Fig. 2a. Each consecutive hierarchy is subject to an arbitrary scaling factor \(\chi \). Figure 2b shows an idealized wall-attached turbulent structure with wall-normal extent l and streamwise scale \(\Updelta x\). In spectral space this relates to the aspect ratio \( \propto \Updelta x/l\). When interpreting the coherence footprint of such a structure, it is important to recall that the coherence metric relates signal contributions at the same scale \(\lambda _x \propto \Updelta x\). In the present application, this implies a parallelogram-like eddy structure as shown in Fig. 2b, for which \(\Updelta x\) is the same at all z. The widely observed phase difference in coherence metrics along the vertical direction (e.g. Panofsky et al. 1974; Marusic and Heuer 2007; Chauhan et al. 2013; Liu et al. 2017; Salesky and Anderson 2018) is equivalent to the inclination angle \(\alpha \) of this structure as indicated in the figure. However, our definition of the aspect ratio only depends on \(\Updelta x\) and l, i.e. the maximum wall-distance at which coherence at scale \(\Updelta x\) is observed. The aspect ratio  is hence solely determined by the magnitude of the coherence and is insensitive to a phase shift (or inclination) between the turbulent fluctuations at z and \(z_R\).
is hence solely determined by the magnitude of the coherence and is insensitive to a phase shift (or inclination) between the turbulent fluctuations at z and \(z_R\).
a A hierarchical range of self-similar wall-attached turbulent eddy structures; for the purpose of this sketch, an arbitrary self-similar scaling factor of \(\chi = 1.5\) is chosen; b Illustration of the eddy geometry. The thick blue line represents the parallelogram-like shape implied by the fact that the linear coherence considers the same wavelength at different z. The structure inclination angle \(\alpha \) can equivalently be expressed as a phase shift \(\Updelta t\) between signals at different wall-normal locations. c Filled iso-contours of \(\gamma ^2\) coherence of four discrete hierarchies (one grey shade per hierarchy \(i = 1,...,4\)), relative to a very near-wall reference position \(z_R\). d Portion of the wall-reference-coherence spectrogram that survives when \(z_R\) is placed at an arbitrary position in the logarithmic region (blue shaded contours)
The implications of the flow organization shown in Fig. 2a on the coherence spectrum with reference at the wall (\(z_R=0\)) is depicted in Fig. 2c. For each eddy hierarchy, there exists a minimum characteristic streamwise wavelength \(\lambda _{x,i} \approx \Updelta x_i\) at which the structure appears coherent. Since eddies within the same hierarchy appear randomly in space (or time) (Woodcock and Marusic 2015), a non-zero coherence (and also turbulent energy) exists for scales larger than \(\lambda _{x,i}\) within that hierarchy. Thus, for hierarchy i with a wall-normal extent of \(\chi ^{(i-1)}l\), a non-zero contribution \(\gamma ^2_i\) to the coherence occurs in the region \(z < \chi ^{(i-1)}l\) and  . The magnitude of \(\gamma ^2_i\) may vary with \(\lambda _x\) and z, but for simplicity we assume a constant magnitude represented by a uniform grey scale per the \(\gamma ^2_i\) iso-contour in Fig. 2c. Our conclusions, however, remain unaffected by eventual variations in \(\gamma ^2_i\) as long as these remain self-similar across hierarchies as implied by the self-similarity of the underlying eddy field. The full coherence spectrogram finally results from superposing the contributions of all hierarchies as reflected by increasing grey scales of the superposed transparent rectangles in Fig. 2c. Within a triangular region in \((\lambda _x,z)\) space, bounded by a minimum wall-normal height \(z = l\), a constant \(\lambda _x/z\) limit (at small wavelengths) and a constant \(\lambda _x\) limit (large wavelengths), the \(\gamma ^2\) iso-contours align with lines of constant \(\lambda _x/z\). Within this region, the magnitude of \(\gamma ^2\) increases linearly with \(\ln (\lambda _x)\) (for constant z) and decreases with \(\ln (z)\) (for constant \(\lambda _x\)): a direct consequence of a geometrically self-similar structure. This implies that as a consequence of the attached-eddy hypothesis assumptions, the coherence magnitude within the self-similar region adheres to
. The magnitude of \(\gamma ^2_i\) may vary with \(\lambda _x\) and z, but for simplicity we assume a constant magnitude represented by a uniform grey scale per the \(\gamma ^2_i\) iso-contour in Fig. 2c. Our conclusions, however, remain unaffected by eventual variations in \(\gamma ^2_i\) as long as these remain self-similar across hierarchies as implied by the self-similarity of the underlying eddy field. The full coherence spectrogram finally results from superposing the contributions of all hierarchies as reflected by increasing grey scales of the superposed transparent rectangles in Fig. 2c. Within a triangular region in \((\lambda _x,z)\) space, bounded by a minimum wall-normal height \(z = l\), a constant \(\lambda _x/z\) limit (at small wavelengths) and a constant \(\lambda _x\) limit (large wavelengths), the \(\gamma ^2\) iso-contours align with lines of constant \(\lambda _x/z\). Within this region, the magnitude of \(\gamma ^2\) increases linearly with \(\ln (\lambda _x)\) (for constant z) and decreases with \(\ln (z)\) (for constant \(\lambda _x\)): a direct consequence of a geometrically self-similar structure. This implies that as a consequence of the attached-eddy hypothesis assumptions, the coherence magnitude within the self-similar region adheres to
where \(C_1\), \(C_2\) are fit constants. The aspect ratio then follows from

Based on laboratory data at \(Re_\tau \approx 14{,}000\), Baars et al. (2017) obtained \(C_1 \approx 0.302\) and \(C_2 \approx -\,0.796\), which results in  . These values were seen to be consistent with numerical data at \(Re_\tau \approx 2000\) (Sillero et al. 2013) and the ASL data at \(Re_\tau \approx 1.4 \times 10^6\) (Marusic and Heuer 2007) (see the corresponding trend line in Fig. 1). All cases represent the turbulent boundary layer under neutral stability conditions and were performed over smooth walls/terrain. Since (2) holds for three orders of magnitude in \(Re_\tau \), it can be concluded that a wall-attached, self-similar structure is indeed ingrained in the u velocity field. Similar conclusions for more isolated ranges in \(Re_\tau \) were made by Morrison and Kronauer (1969) and Bullock et al. (1978) for pipe flow and more recently by del Álamo et al. (2004) for channel flow. Generally, all these results explicitly show the (wall-)coherent nature of the turbulence in the logarithmic region (at
. These values were seen to be consistent with numerical data at \(Re_\tau \approx 2000\) (Sillero et al. 2013) and the ASL data at \(Re_\tau \approx 1.4 \times 10^6\) (Marusic and Heuer 2007) (see the corresponding trend line in Fig. 1). All cases represent the turbulent boundary layer under neutral stability conditions and were performed over smooth walls/terrain. Since (2) holds for three orders of magnitude in \(Re_\tau \), it can be concluded that a wall-attached, self-similar structure is indeed ingrained in the u velocity field. Similar conclusions for more isolated ranges in \(Re_\tau \) were made by Morrison and Kronauer (1969) and Bullock et al. (1978) for pipe flow and more recently by del Álamo et al. (2004) for channel flow. Generally, all these results explicitly show the (wall-)coherent nature of the turbulence in the logarithmic region (at  ). In particular, for all ASL-type applications (\(Re_\tau \sim 10^5\) to \(10^6\)), where the relative range of scales that are coherent will grow, these results reflect large-scale turbulent structures comprising significant lifetimes in the streamwise direction (Cantwell 1981; Robinson 1991; Hutchins and Marusic 2007).
). In particular, for all ASL-type applications (\(Re_\tau \sim 10^5\) to \(10^6\)), where the relative range of scales that are coherent will grow, these results reflect large-scale turbulent structures comprising significant lifetimes in the streamwise direction (Cantwell 1981; Robinson 1991; Hutchins and Marusic 2007).
Thus far, the coherence trend has been discussed only relative to the wall such that \(z_R\rightarrow 0\). However, in typical tower micrometeorological studies, the reference measurement is taken at \(z_R \sim 1\) m (which is well within the logarithmic region for typical atmospheric conditions). To illustrate how an off-wall position at height \(z_R\) affects the idealized coherence trend in the attached-eddy picture envisioned by Townsend, we increased the number of discrete hierarchies to 10 in Fig. 2d. For any given \(z_R\), only the wall-attached turbulent structures that extend beyond \(z_R\) are coherent with \(z_R\) (their corresponding coherence contours are blue-shaded). The coherence trend above \(z_R\) remains unaffected if only wall-attached structures are considered.
As a final remark, we point out that the above considerations made for the streamwise velocity component should also apply to the spanwise velocity field and temperature (Perry and Chong 1982; Krug et al. 2018).
2.2 Comparing Davenport’s Hypothesis to Townsend’s
Davenport (1961a) presented a trend in the wall-normal coherence of streamwise velocity fluctuations u based on observations from typical tower micrometeorological data. It was evident from the data that both a decreasing wavelength \(\lambda _x \equiv U/f\) and an increase in vertical separation \(\Updelta z = z - z_R\) made the turbulent quantities less coherent. He hypothesized that for a given stability, the coherence should only depend on the ratio of \(\Updelta z\) and \(\lambda _x\). The implied geometrical self-similarity is obviously equivalent to the attached eddy framework discussed above if \(\Updelta z \approx z \), which is approached either for \(z_R \rightarrow 0\) or for \(z \gg z_R\) in experiments. The Davenport formulation, however, also entails self-similarity for any reference point, not just the wall, and therefore additionally encompasses also self-similarity of ‘detached’ structures. Noting that the drop-off in coherence with increasing \(\Updelta z/\lambda _x\) resembles an exponential decay, Davenport (1961a) gave the following empirical expression
where a is a decay parameter. Here, a factor of two is added in the exponent compared to the original formulation, as Davenport proposed the relation for \(\gamma \) (root-coherence) and we use \(k \equiv 2a\) for brevity. Just as in other later works, we prefer \(\gamma ^2\), since the squared coherence is proportional to the fraction of energy that is coherent over \(\Updelta z\). With respect to the fitting constant in (4), Davenport initially quoted \(a = 7.7\) for the ‘vertical coherence’ (\(\Updelta z\) separations) of the u component in neutral conditions. Slightly updated values and extensions of the formulation to other velocity components and the temperature field have been reported in the ensuing literature (Pielke and Panofsky 1971; Davison 1976; Berman and Stearns 1977). It is generally accepted that a varies with surface-layer stability in the sense that it is small in strong convection and large in neutral or stable air, and we address this aspect in the following. A representation of (4) with \(k = 23\) (Panofsky 1973; Naito and Kondo 1974) is included in Fig. 1a and is seen to match closely with (2) and the data for neutral conditions.
Parametrizations of the coherence spectrogram according to (2) with \(C_1 = 0.302\) and \(C_2 = -0.796\) (solid blue line) and (4) with \(k = 23\) (thick dashed red line). Panel a shows \(\gamma \) vs. \(z/\lambda _x\) on linear axes as commonly plotted in the wind-engineering community, in b\(\gamma ^2\) is plotted vs. \(\lambda _x/z\) on semi-logarithmic axes. Additional thinner dashed lines in varying shades of red illustrate the effect of varying k in (4) over a range \(k=5\) to \(k=39\) in increments of 3
Since the introduction of (4) in 1961, many researchers have tested their data against Davenport’s hypothesis. Studies range from research focusing on the vertical coherence of various velocity components in tower micrometeorological data (Davenport 1961a; Panofsky and Singer 1965; Pielke and Panofsky 1971; Naito and Kondo 1974; Panofsky et al. 1974; Brook 1975; Seginer and Mulhearn 1978; Kanda and Royles 1978; Soucy et al. 1982; Bowen et al. 1983; Saranyasoontorn et al. 2004), investigations including the lateral/spanwise coherence (Kristensen and Jensen 1979; Ropelewski et al. 1973; Panofsky and Mizuno 1975; Perry et al. 1978; Kristensen 1979; Kristensen et al. 1981; Schlez and Infield 1998), the coherence of temperature fluctuations (Davison 1976) and even mesoscale applications (typically in the horizontal directions) (Hanna and Chang 1992; Woods et al. 2011; Vincent et al. 2013; Larsén et al. 2013; Mehrens et al. 2016). Together, these measurements cover a great variety of terrain and topography. Here we wish to restrict the discussion to the effect of stability and limit the analysis to the base case over smooth terrain, where high fidelity data are available from experiments at the Utah salt flats.
Before we introduce this dataset (see Sect. 3), we briefly consider stability effects in more detail. For this purpose, we have replotted the parametrizations according to (2) and (4) already included in Fig. 1a in Fig. 3 along with the Davenport parametrizations at varying k. As mentioned before, increasing stability corresponds to increasing k and the linear plot of \(\gamma \) vs. \(z/\lambda _x\) in Fig. 3a clearly illustratres how this leads to a faster decay of coherence. From the plot of \(\gamma ^2\) vs. \(\lambda _x/z\) in Fig. 3b it becomes apparent that a change in k approximately leads to a horizontal shift of the curves. In the framework of Baars et al. (2017), such a shift implies a change in aspect ratio of the wall-attached structures and we investigate this aspect in more detail below.
3 Dataset
The experimental dataset employed herein has been recorded by Marusic and Heuer (2007), Marusic and Hutchins (2008) and was previously employed in a study of the neutral ASL by Hutchins et al. (2012) and investigation of the stability dependence of the structure inclination angle by Chauhan et al. (2013). We refer to these papers for details beyond the short overview provided here.
The complete dataset consists of a continuous recording over several days (26 May to 4 June 2005) at the Surface Layer Turbulence and Environmental Science Test (SLTEST) facility in the salt flats of western Utah. A measurement tower held nine logarithmically-spaced sonic anemometers (Campbell Scientific CSAT3) at distances ranging from 1.42 m to 25.69 m above ground, which recorded all three velocity components along with temperature. All measurements were synchronized and recorded at a sampling rate of 20 Hz. In addition, there was a spanwise array at \(z_s = 2.14\) m above ground with nine anemometers of the same type evenly spaced over 30 m from the tower. Data from this array are only employed here to characterize the stability of the ASL.
Prior to further analysis, the data are corrected for wind direction and a de-trending procedure is applied (see Hutchins et al. 2012, for details). While the de-trending is necessary to remove slow temporal trends in the data, it inherently also compromises the coherence at very long scales, which needs to be kept in mind when interpreting the data. After data selection a total of 63 1-h long segments, corresponding to the dataset used in Chauhan et al. (2013), remains. The stability of each segment is characterized using the Monin–Obukhov stability parameter \(z_s/L\) with the Obukhov length scale
where the von Kármán constant \(\kappa = 0.41\), g is the acceleration due to gravity, and \(U_\tau = (-\overline{uw})^{1/2}\) is the friction velocity. All quantities are evaluated from an average of the total of 10 sonic anemometers at \(z_s = 2.14\) m. Most of our data lie in the unstable regime \(z_s/L<0\) but a few data points also have \(z_s/L>0\).
Next, we will employ the SLTEST dataset to investigate how stability affects the self-similarity of coherent structures and how this changes the aspect ratio of the structures in the flow. We use the lowest measurement point as reference throughout, i.e. \(z_R = 1.41\) m from now on.
4 Results
4.1 Stability Dependence of the Self-Similar Scaling
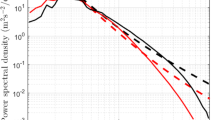
We start out by considering a representative case with stable stratification \(z_s/L>0\) in Fig. 4a. Evidently, the stable stratification has a significant effect on the spectral energy distribution of the streamwise velocity fluctuations. Even more importantly, however, these changes are seen to also propagate to the coherence spectrogram. While the coherence levels are generally lower, the isolines are also seen to deviate notably from a slope of 1, which would be expected for self-similarity as discussed above (recall Fig. 1). This equally holds for plotting \(\gamma ^2\) vs. z (as implied by the attached-eddy hypothesis), as well as vs. \(\Updelta z\) following Davenport’s hypothesis. The same observations could be made for the other stable data points (in total we have 11), other velocity components and temperature (not shown here). Remarkably, this is already the case for relatively moderate values of \(z_s/L\). In fact, the case at \(z_s/L= 0.10\) shown in Fig. 4 corresponds to the most stable conditions in the dataset. Based on these findings, the application of both (2) and (4) does not appear justified for stable stratification and will not be pursued further.
The situation is different for unstable configurations, where the heat flux is directed upward, as can be seen from Fig. 4b. Also, here, the turbulence field is significantly affected by buoyancy as evidenced by considerably higher fluctuation levels. In contrast to the stable case, however, the coherence isocontours in this case are observed to follow a slope of 1 for large enough \(z^+\) consistent with the presence of self-similar wall-attached structures. The fact that such a scaling is only obtained for sufficiently large \(z^+\) is to be expected since, for small separations, also structures that are not attached to the wall will be coherent (trivially \(\gamma ^2 = 1\) at all scales \(z = z_R\)) and pure wall-scaling is only recovered once their influence has decayed. For large \(\Updelta z\), there is no difference between plotting \(\gamma ^2\) as a function of z and \(\Updelta z\), consistent with the expectation at \(\Updelta z\gg z_R\). A more interesting observation can be made at smaller \(\Updelta z\), for which \(\Updelta z\gg z_R\) does not hold. Even for this range, the slope of the \(\gamma \) isocontours is now approximately one, indicative of self-similar scaling, all the way to the smallest vertical separation distance (noting that \(\Updelta z = 0\) is not shown due to the logarithmic axis). This means that self-similarity is now also observed where it was compromised by the contribution of non-attached structures when plotting with reference to the wall. The extended scaling region is therefore, in fact, indicative of self-similarity of non-wall-attached structures as suggested by the formulation of Davenport. Judging by the fact that the red lines for the ramp-up in coherence are relatively straight, detached and wall-attached structures have the same aspect ratios. As a side note to the discussion here, we point out that the eventual decay of coherence for \(\lambda _x>10^6\) is likely an artefact of the de-trending procedure since a similar effect was not observed in laboratory data (see Baars et al. 2017).
Our dataset allows us to investigate self-similar scaling also in the spanwise velocity component and the temperature fields. Such data are not commonly available in laboratory experiments and have therefore not been are used previously in this context. We plot the results corresponding to the unstable case in Fig. 4b but now for v and \(\theta \) in Figs. 5a, b, respectively. With maybe some minor limitations in the scaling vs. \(z^+\) in the v-component, the situation is very similar to that observed in the plot for the streamwise component in Fig. 4b. This provides evidence of self-similar scaling also in the spanwise velocity component and the temperature field. Especially the fact that the temperature field adheres to a similar geometrical organization appears remarkable in view of how different the energy spectrogram looks in this case. Compared to the velocity counterparts, the relative contributions at high \(\lambda _x\), as well as further away from the wall, are considerably lower for the scalar spectrogram.
Same as Fig. 4 but for the spanwise velocity component v (a), and temperature \(\theta \) (b)
A more quantitative analysis is best achieved by replotting the data in the style of Fig. 1a. This is done in Fig. 6 for the two velocity components and the temperature in the unstable case with \(z_s/L = -2.80\). Note that here we use the normalization with \(\Updelta z\) as this provides a more extensive scaling region. Using z instead provides similar results—albeit with larger uncertainties. Plotting the results as presented in Fig. 6 scrutinises the aspect of self-similarity, since for this case a collapse of curves at different \(\Updelta z\) is expected. As can be seen from the figure, such a nominal collapse is indeed observed for all quantities plotted. Identifying the scaling region by the range of this collapse (marked in red in the figure) allows us to fit the expression (2) to the data and to extract the statistical aspect ratio. These results are also included in Fig. 6 and it is obvious that the resulting  to
to  is significantly lower than the value of
is significantly lower than the value of  obtained under neutrally stable conditions. It therefore seems that unstable conditions drastically reduce the aspect ratio of coherent structures in the flow.
obtained under neutrally stable conditions. It therefore seems that unstable conditions drastically reduce the aspect ratio of coherent structures in the flow.
\(\gamma ^2\) in the range \(1.58\,\text {m}\le \Updelta z \le 11.10\,\text {m} \) (with increasing \(\Updelta z\) indicated by lighter shades of grey) for the streamwise (a), and spanwise (b) velocity components as well as temperature (c) for the case with \(z_s/L = -2.80\). The blue line is a fit according to Eq. 2 with \(C_1=0.302\) fixed; the fitting region used here is bounded by \(\gamma ^2>0.1\) and \(\lambda _x <100\,\text {m}\) and is indicated in red
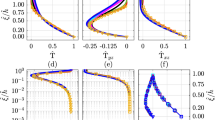
We systematically investigate this trend by applying the same fitting procedure to all unstable datasets available. The results obtained from doing so are presented for u, v, and \(\theta \) in Fig. 7a–c. In all three cases, there is a clear trend of decreasing  with increasing magnitude of the stability parameter up to \(-z_s/L \approx 1\). For even higher values of \(-z_s/L\), the aspect ratio consistently attains approximately constant values in all three quantities in the range 2 to 3. It is worth highlighting how sensitive the aspect ratio is to even only weakly unstable conditions. Indeed, the data appear well represented by an entirely empirical, logarithmic fit for \(-z_s/L <1\). The grey-shaded region corresponds to \(|z_s/L|<0.1\), which is a commonly used limit for approximately neutral conditions (e.g. Högström et al. 2002; Metzger et al. 2007; Hutchins et al. 2012). As our results show,
with increasing magnitude of the stability parameter up to \(-z_s/L \approx 1\). For even higher values of \(-z_s/L\), the aspect ratio consistently attains approximately constant values in all three quantities in the range 2 to 3. It is worth highlighting how sensitive the aspect ratio is to even only weakly unstable conditions. Indeed, the data appear well represented by an entirely empirical, logarithmic fit for \(-z_s/L <1\). The grey-shaded region corresponds to \(|z_s/L|<0.1\), which is a commonly used limit for approximately neutral conditions (e.g. Högström et al. 2002; Metzger et al. 2007; Hutchins et al. 2012). As our results show,  varies by up to 50% in this region, lending support to more stringent criteria such as \(|z/L|<0.06\) applied in Wang and Zheng (2016) at least for certain statistical quantities. We do note, however, that the precise value of the stability parameter depends on the choice of the reference height z (we use \(z = 2.14\) m) as L is determined by wall quantities only. This choice is somewhat arbitrary for the multipoint statistics presented here and was motivated by data availability and consistency with previous studies in the present case. The dependence is linear however, and the values can therefore easily be transformed to other reference heights.
varies by up to 50% in this region, lending support to more stringent criteria such as \(|z/L|<0.06\) applied in Wang and Zheng (2016) at least for certain statistical quantities. We do note, however, that the precise value of the stability parameter depends on the choice of the reference height z (we use \(z = 2.14\) m) as L is determined by wall quantities only. This choice is somewhat arbitrary for the multipoint statistics presented here and was motivated by data availability and consistency with previous studies in the present case. The dependence is linear however, and the values can therefore easily be transformed to other reference heights.
Results for the aspect ratio as a function of the stability parameter \(z_s/L\) for velocity components u (a) and v (b), as well as temperature (c). Lines and the equations in a–c represent the results from fitting a linear relation for \(z_s/L<0.1\) and a constant for \(z_s/L>0.1\), respectively. Panel d compares the aspect ratios obtained from different quantities by showing the ratios  (blue triangles) and
(blue triangles) and  (green diamonds). The region shaded in grey denotes the \(-z_s/L <0.1\), a range widely considered as near-neutral
(green diamonds). The region shaded in grey denotes the \(-z_s/L <0.1\), a range widely considered as near-neutral
Finally, we briefly comment on the differences in the aspect ratios obtained from the three different quantities. We already established from Fig. 7a–c that the general trends are consistent across u, v and \(\theta \). In Fig. 7d, we plot  and
and  with respect to
with respect to  , and in general all ratios are close to 1. It will require further research to determine whether the slight deviations from 1, e.g., both
, and in general all ratios are close to 1. It will require further research to determine whether the slight deviations from 1, e.g., both  and
and  tend to be slightly < 1 for \(-z_s/L<1\), are statistically significant or simply owed to inaccuracies in determining
tend to be slightly < 1 for \(-z_s/L<1\), are statistically significant or simply owed to inaccuracies in determining  . Differences between the coherence decay in different velocity components have nevertheless also been reported in the wind-engineering community where Berman and Stearns (1977) and similarly Pielke and Panofsky (1971) report somewhat smaller decay rates (lower k) for the v-component as compared to the u-component.
. Differences between the coherence decay in different velocity components have nevertheless also been reported in the wind-engineering community where Berman and Stearns (1977) and similarly Pielke and Panofsky (1971) report somewhat smaller decay rates (lower k) for the v-component as compared to the u-component.
4.2 Relationship Between  and k
and k
The relationship between the statistical aspect ratio  derived based on (2) and the parameter k in (4) is addressed in the following. An analytical relationship is readily derived by setting (2) and (4) equal at a reference point \(\xi \equiv {\lambda _x}/{z}\large |_{\text {ref}}\) and assuming \(z = \Updelta z\). In this case, we obtain
derived based on (2) and the parameter k in (4) is addressed in the following. An analytical relationship is readily derived by setting (2) and (4) equal at a reference point \(\xi \equiv {\lambda _x}/{z}\large |_{\text {ref}}\) and assuming \(z = \Updelta z\). In this case, we obtain

and from Fig. 6, \(\xi = 20\) is a reasonable choice for the present data as it corresponds to \(\gamma ^2 \approx 0.5\). A representation of (6) with this parameter is included in Fig. 8a along with results for \(k_i\) obtained from fitting (4) to the same data points used to determine  (here and in the following \(i = u,v,\theta \)). Overall, the agreement of (6) with the data is very good and there is little scatter even between different components and the scalar. For the region of interest, the somewhat unwieldy relation (6) is very well approximated by a linear function and the corresponding linear dependence is included in Fig. 8a. Figure 8b and c compare our results for \(k_u\) and \(k_v\) to values reported in the wind-engineering literature and collected by Panofsky (1973). In these figures the region corresponding to stable conditions is shaded as our detailed analysis revealed a lack of self-similar scaling as implied by both (2) and (4). The scatter in the literature data is considerable between different observation sites likely reflecting differences in topography. In this sense, our data from the SLTEST can be considered as a reference case with minimal roughness and topographical effects. Consequently, the scatter in the present data is significantly lower. For both, u and v, the new data points are largely consistent with the dashed lines labelled ‘Trend others’, which is a trend line (by eye) for all measurements but those at the Kennedy Space Center drawn by Panofsky (1973). The data from the Kennedy Space Center (and the corresponding trend lines) lie at consistently and significantly higher values of \(k_i\) than our results. Nonetheless, the fact that \(k_i\) levels off at an approximately constant value beyond \(-z_s/L=1\) is a feature that appears to be shared by all available datasets. Once again, we emphasize that the exact values of the stability parameter might change slightly depending on which reference height is chosen; unfortunately, information on the reference heights could not be retrieved for all literature datasets introducing an element of uncertainty.
(here and in the following \(i = u,v,\theta \)). Overall, the agreement of (6) with the data is very good and there is little scatter even between different components and the scalar. For the region of interest, the somewhat unwieldy relation (6) is very well approximated by a linear function and the corresponding linear dependence is included in Fig. 8a. Figure 8b and c compare our results for \(k_u\) and \(k_v\) to values reported in the wind-engineering literature and collected by Panofsky (1973). In these figures the region corresponding to stable conditions is shaded as our detailed analysis revealed a lack of self-similar scaling as implied by both (2) and (4). The scatter in the literature data is considerable between different observation sites likely reflecting differences in topography. In this sense, our data from the SLTEST can be considered as a reference case with minimal roughness and topographical effects. Consequently, the scatter in the present data is significantly lower. For both, u and v, the new data points are largely consistent with the dashed lines labelled ‘Trend others’, which is a trend line (by eye) for all measurements but those at the Kennedy Space Center drawn by Panofsky (1973). The data from the Kennedy Space Center (and the corresponding trend lines) lie at consistently and significantly higher values of \(k_i\) than our results. Nonetheless, the fact that \(k_i\) levels off at an approximately constant value beyond \(-z_s/L=1\) is a feature that appears to be shared by all available datasets. Once again, we emphasize that the exact values of the stability parameter might change slightly depending on which reference height is chosen; unfortunately, information on the reference heights could not be retrieved for all literature datasets introducing an element of uncertainty.
a Fit results for \(k_i\) vs. those for  (same symbols as in Fig. 7), with \(i = u,v,\theta \). Black dashed line represents the relation (6) with \(\xi = 20\), solid lines are linear fits to the data as labelled in the legend. Panels b and c respectively compare our results for \(k_u\) and \(k_v\) to literature values obtained from Panofsky (1973). The fits to the current data shown here are obtained from the fits to
(same symbols as in Fig. 7), with \(i = u,v,\theta \). Black dashed line represents the relation (6) with \(\xi = 20\), solid lines are linear fits to the data as labelled in the legend. Panels b and c respectively compare our results for \(k_u\) and \(k_v\) to literature values obtained from Panofsky (1973). The fits to the current data shown here are obtained from the fits to  in Fig. 7(a, b) along with the linear relations in panel a of this figure
in Fig. 7(a, b) along with the linear relations in panel a of this figure
5 Concluding Remarks
The main findings of the present study are summarized as follows:
-
We have demonstrated that implications of Townsend’s attached-eddy hypothesis for the coherence trend are consistent with Davenport’s hypothesis. This applies to the geometrical self-similarity of wall-attached structures as well as to the fact that the empirically derived exponential decay in Davenport’s formulation matches closely with a logarithmic expression that follows directly from the aspect of self-similarity.
-
The self-similarity implied by Davenport is even more comprehensive and also encompasses structures that are not attached to the wall. Evidence of such a self-similar behaviour could indeed be observed for the high \(Re_\tau \) SLTEST data employed herein.
-
The self-similarity assumptions/hypotheses do not seem to hold for stable data. Neither z- nor \(\Updelta z\)-scaling is observed in this case, which implies that there is no self-similarity for stable data. This is clearly observed in our results since we compute the coherence spectrum (a continuous function of scale with a finely frequency-discretized fast Fourier transform approach). In the literature, the coherence is often computed at coarsely spaced frequency discretizations with fits based on a few data points only. Our results provide clear evidence that the stable ASL has no self-similar coherence and hypotheses of Townsend and Davenport should not be applied in this case. We point out that it is predominantly the self-similarity aspect that fails in the stable regime while there is still non-zero coherence. The departure from self-similarity occurs far from extreme (‘z-less’) conditions at relatively weak stratification, for which Monin–Obukhov similarity theory holds. While we do not observe self-similarity for any of our stable data, it appears likely that for very weak stable stratification self-similarity may be recovered. Unfortunately, we cannot determine such a threshold from the present dataset.
-
Consistent with expectations based on the attached-eddy hypothesis framework, self-similar scaling was not only observed for the u-component, but also for spanwise velocity fluctuations v and temperature fluctuations \(\theta \).
-
Even relatively weak unstable stratifications drastically reduce the statistical aspect ratio
 for all quantities investigated here. Based on our results, we were able to parametrize this trend in terms of a logarithmic decay for \(z_s/L<1\) and constant values for \(z_s/L>1\).
for all quantities investigated here. Based on our results, we were able to parametrize this trend in terms of a logarithmic decay for \(z_s/L<1\) and constant values for \(z_s/L>1\). -
Generally, the trend of decreasing
 with decreasing stability is intuitively consistent with the fact that buoyancy supports the upward motion of structures from the wall. The question remains as to whether the nature of the structures themselves changes under very unstable conditions (e.g. towards convection cell-type motion) as may be suspected based on the change in trend for
with decreasing stability is intuitively consistent with the fact that buoyancy supports the upward motion of structures from the wall. The question remains as to whether the nature of the structures themselves changes under very unstable conditions (e.g. towards convection cell-type motion) as may be suspected based on the change in trend for 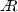 around \(z_s/L =1\). A conclusive answer in this regard cannot be provided from the present analysis. It is, however, remarkable that the slope \(C_1\) is largely insensitive to \(z_s/L\) in our data. Physically, the parameter \(C_1\) can be interpreted as a measure for the relative contribution of attached structures to the overall turbulence intensity. The fact that this quantity remains unaltered seems to indicate that, at least in the parameter range accessed here, the fundamental flow organization does not change significantly. This notion is substantiated by the observation that also self-similarity still holds in the unstable regime.
around \(z_s/L =1\). A conclusive answer in this regard cannot be provided from the present analysis. It is, however, remarkable that the slope \(C_1\) is largely insensitive to \(z_s/L\) in our data. Physically, the parameter \(C_1\) can be interpreted as a measure for the relative contribution of attached structures to the overall turbulence intensity. The fact that this quantity remains unaltered seems to indicate that, at least in the parameter range accessed here, the fundamental flow organization does not change significantly. This notion is substantiated by the observation that also self-similarity still holds in the unstable regime. -
We established a simple linear relation between the aspect ratio
 and k in the Davenport formulation, such that the fit parameter k can be interpreted as an aspect ratio. Comparison of our results for the stability dependence of k with the literature reveals significantly lower scatter for the high-fidelity ASL data over smooth-terrain presented here. As such, the present dataset serves as a base-case for the vertical coherence over any other type of terrain.
and k in the Davenport formulation, such that the fit parameter k can be interpreted as an aspect ratio. Comparison of our results for the stability dependence of k with the literature reveals significantly lower scatter for the high-fidelity ASL data over smooth-terrain presented here. As such, the present dataset serves as a base-case for the vertical coherence over any other type of terrain.
As a final remark, we point out that even though the present study is limited to vertical coherence, connecting Davenport’s to Townsend’s framework for this case also places predictions and applications to horizontal coherence on a stronger footing.
References
Baars WJ, Hutchins N, Marusic I (2017) Self-similarity of wall-attached turbulence in boundary layers. J Fluid Mech 823:R2
Baker CJ (2007) Wind engineering: past, present and future. J Wind Eng Ind Aero 95(9):843–870
Berman S, Stearns CR (1977) Near-earth turbulence and coherence measurements at Aberdeen proving ground, Md. Boundary-Layer Meteorol 11:485–506
Bowen AJ, Flay RGJ, Panofsky HA (1983) Vertical coherence and phase delay between wind components in strong winds below 20 m. Boundary-Layer Meteorol 26:313–324
Brook RR (1975) A note on vertical coherence of wind measured in an urban boundary layer. Boundary-Layer Meteorol 9:11–20
Bullock KJ, Cooper RE, Abernathy FH (1978) Structural similarity in radial correlations and spectra of longitudinal velocity fluctuations in pipe flow. J Fluid Mech 88:585–608
Cantwell BJ (1981) Organized motion in turbulent flow. Annu Rev Fluid Mech 13:457–515
Chauhan K, Hutchins N, Monty J, Marusic I (2013) Structure inclination angles in the convective atmospheric surface layer. Boundary-Layer Meteorol 147(1):41–50
Davenport A (1961a) The spectrum of horizontal gustiness near the ground in high winds. Q J R Meteorol Soc 87(372):194–211
Davenport AG (1961b) A statistical approach to the treatment of wind loading on tall masts and suspension bridges. Ph.D. thesis, Department of Civil Engineering, University of Bristol, United Kingdom
Davenport AG (2002) Past, present and future of wind engineering. J Wind Eng Ind Aero 90(12):1371–1380
Davison DS (1976) Geometric similarity for the temperature field in the unstable atmospheric surface layer. Boundary-Layer Meteorol 10:167–180
del Álamo JC, Jiménez J, Zandonade P, Moser RD (2004) Scaling of the energy spectra of turbulent channels. J Fluid Mech 500:135–144
Hanna SR, Chang JC (1992) Representativeness of wind measurements on a mesoscale grid with station separations of 312 m to 10 km. Boundary-Layer Meteorol 60:309–324
Högström U, Hunt J, Smedman A (2002) Theory and measurements for turbulence spectra and variances in the atmospheric neutral surface layer. Bound-Layer Meteorol 103(1):101–124
Hutchins N, Marusic I (2007) Evidence of very long meandering structures in the logarithmic region of turbulent boundary layers. J Fluid Mech 579:1–28
Hutchins N, Chauhan K, Marusic I, Monty J, Klewicki J (2012) Towards reconciling the large-scale structure of turbulent boundary layers in the atmosphere and laboratory. Boundary-Layer Meteorol 145(2):273–306
Hwang Y (2015) Statistical structure of self-sustaining attached eddies in turbulent channel flow. J Fluid Mech 767:254–289
Isyumov N (2012) Alan G. Davenport’s mark on wind engineering. J Wind Eng Ind Aerodyn 104–106:12–24
Jiménez J (2012) Cascades in wall-bounded turbulence. Annu Rev Fluid Mech 44:27–45
Kanda J, Royles R (1978) Further consideration of the height-dependence of root-coherence in the natural wind. Build Environ 13:175–184
Kristensen L (1979) On longitudinal spectral coherence. Boundary-Layer Meteorol 16:145–153
Kristensen L, Jensen NO (1979) Lateral coherence in isotropic turbulence and in the natural wind. Boundary-Layer Meteorol 17(3):353–373
Kristensen L, Panofsky HA, Smith SD (1981) Lateral coherence of longitudinal wind components in strong winds. Boundary-Layer Meteorol 21:199–205
Krug D, Zhu X, Chung D, Marusic I, Verzicco R, Lohse D (2018) Transition to ultimate Rayleigh-Bénard turbulence revealed through extended self-similarity scaling analysis of the temperature structure functions. J Fluid Mech 851:R3
Larsén XG, Vincent C, Larsen S (2013) Spectral structure of mesoscale winds over the water. Q J R Meteorol Soc 139:685–700
Li Q, Gentine P, Mellado JP, McColl KA (2018) Implications of nonlocal transport and conditionally averaged statistics on Monin–Obukhov similarity theory and townsend’s attached eddy hypothesis. J Atmos Sci 75(10):3403–3431
Liu H, Bo T, Liang Y (2017) The variation of large-scale structure inclination angles in high Reynolds number atmospheric surface layers. Phys Fluids 29(3):035104
Marusic I, Heuer W (2007) Reynolds number invariance of the structure inclination angle in wall turbulence. Phys Rev Lett 99(11):114504
Marusic I, Hutchins N (2008) Study of the log-layer structure in wall turbulence over a very large range of Reynolds number. Flow Turbul Combust 81(1–2):115–130
Marusic I, Monty JP (2019) Attached eddy model of wall turbulence. Annu Rev Fluid Mech 51(1):49–74
Marusic I, Nickels T (2011) A.A. Townsend, chap 9. In: Davidson P, Kaneda Y, Moffatt H, Sreenivasan K (eds) A voyage through turbulence. Cambridge University Press, Cambridge
Marusic I, Baars WJ, Hutchins N (2017) Scaling of the streamwise turbulence intensity in the context of inner-outer interactions in wall-turbulence. Phys Rev Fluids 2:100502
Mehrens AR, Hamann AN, Larsén XG, von Bremen L (2016) Correlation and coherence of mesoscale wind speeds over the sea. Q J R Meteorol Soc 142:3186–3194
Metzger M, McKeon B, Holmes H (2007) The near-neutral atmospheric surface layer: turbulence and non-stationarity. Philos Trans R Soc A 365(1852):859–876
Morrison WRB, Kronauer RE (1969) Structural similarity for fully developed turbulence in smooth tubes. J Fluid Mech 39:117–141
Naito G, Kondo J (1974) Spatial structure of fluctuating components of the horizontal wind speed above the ocean. J Meteorol Soc Jpn 52(5):391–399
Panofsky HA (1973) Tower micrometeorology. In: Haugen DA (ed) Workshop on micrometeorlogy. American Meteorologial Society, pp 151–174
Panofsky HA, Mizuno T (1975) Horizontal coherence and Pasquill’s beta. Boundary-Layer Meteorol 9:247–256
Panofsky HA, Singer IA (1965) Vertical structure of turbulence. Q J R Meteorol Soc 91(389):339–344
Panofsky HA, Thomson DW, Sullivan DA, Moravek DE (1974) Two-point velocity statistics over lake Ontario. Boundary-Layer Meteorol 7:309–321
Pasquill F III (1971) Effects of buildings on the local wind. Philos Trans R Soc A 269:439–456
Perry A, Chong M (1982) On the mechanism of wall turbulence. J Fluid Mech 119:173–217
Perry SG, Norman JM, Panofsky HA (1978) Horizontal coherence decay near large mesoscale variations in topography. J Atmos Sci 35:1884–1889
Pielke RA, Panofsky HA (1971) Turbulence characteristics along several towers. Boundary-Layer Meteorol 1:115–130
Robinson SK (1991) Coherent motions in turbulent boundary layers. Annu Rev Fluid Mech 23:601–639
Ropelewski CF, Tennekes H, Panofsky HA (1973) Horizontal coherence of wind fluctuations. Boundary-Layer Meteorol 5:353–363
Salesky S, Anderson W (2018) Buoyancy effects on large-scale motions in convective atmospheric boundary layers: implications for modulation of near-wall processes. J Fluid Mech 856:135–168
Saranyasoontorn K, Manuel L, Veers PS (2004) A comparison of standard coherence models for inflow turbulence with estimates from field measurements. J Sol Energy Eng 126:1069–1082
Schlez W, Infield D (1998) Horizontal, two point coherence for separations greater than the measurement height. Boundary-Layer Meteorol 87:459–480
Seginer I, Mulhearn PJ (1978) A note on vertical coherence of streamwise turblence inside and above a model plant canopy. Boundary-Layer Meteorol 14:515–523
Sillero J, Jiménez J, Moser R (2013) One-point statistics for turbulent wall-bounded flows at Reynolds numbers up to \(\delta ^+\approx 2000\). Phys Fluids 25(10):105102
Simiu E, Scanlan R (1996) Wind effects on structures: fundamentals and applications to design. Wiley, New York
Sørensen P, Cutululis NA, Vigueras-Rodríguez A, Jensen LE, Hjerrild J, Donovan MH, Madsen H (2007) Power fluctuations from large wind farms. IEEE Trans Power Syst 22(3):958–965
Sørensen P, Cutululis NA, Vigueras-Rodríguez A, Madsen H, Pinson P, Jensen LE, Hjerrild J, Donovan M (2008) Modelling of power fluctuations from large offshore wind farms. Wind Energy 11(1):29–43
Soucy R, Woodward R, Panofsky HA (1982) Vertical cross-spectra of horizontal velocity components at the boulder observatory. Boundary-Layer Meteorol 22:57–66
Townsend A (1976) The structure of turbulent shear flow. Cambridge University Press, Cambridge, UK
Vincent CL, Larsén XG, Larsen SE (2013) Corss-spectra over the sea from observations and mesoscale modelling. Boundary-Layer Meteorol 146:297–318
Wang G, Zheng X (2016) Very large scale motions in the atmospheric surface layer: a field investigation. J Fluid Mech 802:464–489
Woodcock J, Marusic I (2015) The statistical behaviour of attached eddies. Phys Fluids 27(1):015104
Woods MJ, Davy RJ, Russell CJ, Coppin PA (2011) Cross-spectrum of wind speed for meso-gamma scales in the upper surface layer over South-Eastern Australia. Boundary-Layer Meteorol 141:93–116
Yang H, Bo T (2017) Scaling of wall-normal turbulence intensity and vertical eddy structures in the atmospheric surface layer. Boundary-Layer Meteorol 166(2):199–216
Acknowledgements
The authors acknowledge financial support by the Australian Research Council and by the University of Melbourne through the McKenzie fellowship program. We further thank Dr. Kapil Chauhan for making the de-trended data available to us.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Krug, D., Baars, W.J., Hutchins, N. et al. Vertical Coherence of Turbulence in the Atmospheric Surface Layer: Connecting the Hypotheses of Townsend and Davenport. Boundary-Layer Meteorol 172, 199–214 (2019). https://doi.org/10.1007/s10546-019-00445-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10546-019-00445-4










 and k
and k

 for all quantities investigated here. Based on our results, we were able to parametrize this trend in terms of a logarithmic decay for
for all quantities investigated here. Based on our results, we were able to parametrize this trend in terms of a logarithmic decay for  with decreasing stability is intuitively consistent with the fact that buoyancy supports the upward motion of structures from the wall. The question remains as to whether the nature of the structures themselves changes under very unstable conditions (e.g. towards convection cell-type motion) as may be suspected based on the change in trend for
with decreasing stability is intuitively consistent with the fact that buoyancy supports the upward motion of structures from the wall. The question remains as to whether the nature of the structures themselves changes under very unstable conditions (e.g. towards convection cell-type motion) as may be suspected based on the change in trend for 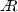 around
around  and k in the Davenport formulation, such that the fit parameter k can be interpreted as an aspect ratio. Comparison of our results for the stability dependence of k with the literature reveals significantly lower scatter for the high-fidelity ASL data over smooth-terrain presented here. As such, the present dataset serves as a base-case for the vertical coherence over any other type of terrain.
and k in the Davenport formulation, such that the fit parameter k can be interpreted as an aspect ratio. Comparison of our results for the stability dependence of k with the literature reveals significantly lower scatter for the high-fidelity ASL data over smooth-terrain presented here. As such, the present dataset serves as a base-case for the vertical coherence over any other type of terrain.