Optimal Pollution Control in a Dynamic Multi-echelon Supply Chain

Abstract

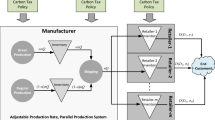
Today supply chains must internalize the impact of transport on the environment in their cost models. Therefore, managers must reduce green house gas emissions while striving to increase cost efficiency and satisfy demand. Our multi-echelon supply chain model minimizes pollution and cost while trying to achieve the best match between supply and demand over time. Three supply chain network configurations are investigated. Two of them are two-echelon: the first involves several suppliers and one warehouse, while the second involves one warehouse and several retail stores. The third network configuration is a three-echelon supply chain including multiple suppliers, one distribution center, and several retail stores. Using optimal control theory, we derive closed form solutions in such multi-echelon supply chain planning problems with consideration of pollution. This approach extends in a new direction the literature in operations and transport management by simultaneously addressing demand, supply as well as the greenhouse gas emissions that continuously vary in time and location. The proposed model provides a decision maker with the optimal choice of right deliveries, right times, while minimizing green house gas emissions. A numerical illustration presents some insights.

Appendix

1.1 Proof of Theorem 1

Proof

This is the proof of Theorem 1. The Hamiltonian associated with the problem is:

$$\begin{aligned} H&(x_{1}(t),x_2(t), \ldots,x_N(t),P(t),\lambda (t))\\ = & \ \sum _{j=1}^N c_{j}(t) x_{j}(t) + \frac{1}{2} \sum _{j=1}^N \alpha _j(t) \left( x_{j}(t) - s_j(t)\right) ^2 \\&+\frac{1}{2} \beta (t) \left( \sum _{j=1}^N x_{j}(t) - \xi (t)\right) ^2 dt \\&+ \lambda (t)\left[ \sum _{j=1}^N \gamma _{j}(t) x_{j}(t) - \delta _P P(t)\right] \end{aligned}$$

(33)

The optimality conditions read as:

$$\begin{cases} \begin{aligned} \frac{\partial H}{\partial x_{i}} =& \ c_{i}(t) + \alpha _i(t) \left( x_{i}(t) - s_i(t)\right) \\ & + \beta (t) \left( \sum _{j=1}^N x_{j}(t) - \xi (t)\right) + \lambda (t) \gamma _{i} = 0, \ \ i=1\ldots N, \\ \dot{\lambda }(t) =& - \frac{\partial H}{\partial P} = \delta _P \lambda (t), \\ \dot{P}(t) =& \ \sum _{i=1}^N \gamma _{i}(t) x_{i}(t) - \delta _P P(t), \\ P(0) =& \ P_0\ge 0, \\ \lambda (T) =& \ \theta . \end{aligned} \end{cases}$$

(34)

The differential equation for $\lambda$ with terminal condition $\lambda (T)=\theta$, namely

$$\begin{aligned} \dot{\lambda }(t) = \delta _P \lambda (t) \end{aligned},$$

(35)

is linear and can be easily solved, leading to $\lambda (t) = \theta e^{\delta _P (t-T)}$. If we plug the expression of $\lambda$ into the maximum principle, we get:

$$\begin{aligned} \alpha _i(t) x_{i}(t)+ \beta (t) \sum _{j=1}^N x_{j}(t) = - c_{i}(t) - \theta \gamma _{i} e^{\delta _P (t-T)} + s_i(t) \alpha _i(t) + \xi (t) \beta (t). \end{aligned}$$

(36)

If we define the matrix

$$\begin{aligned} \Omega (t):= \left( \begin{array}{cccc} \alpha _1(t) + \beta (t) &{} \beta (t) &{} \ldots &{} \beta (t) \\ \beta (t) &{} \alpha _2(t) + \beta (t) &{} \ldots &{} \beta (t) \\ \ldots &{} \ldots &{} \ldots &{} \ldots \\ \beta (t) &{} \beta (t) &{} \ldots &{} \alpha _N(t) + \beta (t) \end{array} \right) \end{aligned}$$

and the vectors

$$\begin{aligned} X(t) := \left( \begin{array}{c} x_1(t) \\ x_2(t)\\ \ldots \\ X_N(t) \end{array} \right) , \ \ \ \ C(t):=\left( \begin{array}{c} c_{1}(t) \\ c_{2}(t) \\ \ldots \\ c_{N}(t) \end{array}\right) , \ \ \end{aligned}$$

$$\begin{aligned} S(t):=\left( \begin{array}{c} s_{1}(t)\alpha _{1}(t)+\xi (t)\beta (t) \\ s_{2}(t)\alpha _{2}(t)+\xi (t)\beta (t) \\ \ldots \\ s_{N}(t)\alpha _{N}(t)+\xi (t)\beta (t) \end{array} \right) ,\, \text {and} \ \, \Gamma (t):=\left( \begin{array}{c} \gamma _{1}(t) \\ \gamma _{2}(t) \\ \ldots \\ \gamma _{N}(t) \end{array} \right) . \end{aligned}$$

This equation can be written in vectorial form as:

$$\begin{aligned} \Omega (t) X(t) = - C(t) - \theta e^{\delta _P (t-T)} \Gamma (t) + S(t) \end{aligned}$$

(37)

and, using the fact that the matrix $\mathbf{\Omega (t)}$ is invertible, we get

$$\begin{aligned} X(t) = - \Omega (t)^{-1} C(t) - \theta e^{\delta _P (t-T)} \Omega (t)^{-1} \Gamma (t) + \Omega (t)^{-1} S(t). \end{aligned}$$

(38)

The equation of P boils down to:

$$\begin{aligned} \dot{P}(t) = \Gamma (t)^T X(t) - \delta _P P(t) \end{aligned}$$

(39)

and this differential equation has a closed form given by:

$$\begin{aligned} P(t) = e^{-\delta _P t} \left[ \int \limits _0^t \Gamma (s)^T X(s) e^{\delta _P s} ds + P_0\right] . \end{aligned}$$

(40)

$\blacksquare$

1.2 Proof of Theorem 2

The proof of this theorem is very similar to the one of Theorem 1 and is therefore omitted.

1.3 Proof of Theorem 3

The Hamiltonian associated with the problem is:

$$\begin{aligned} H&(x_{1}(t),x_2(t), \ldots ,x_N(t),y_1(t), y_2(t),\ldots ,y_M(t), P(t),\lambda (t)) \\ =& \sum _{i=1}^N c_{i}(t) x_{i}(t) + \sum _{j=1}^M \bar{c_{j}}(t) y_{j}(t) + \frac{1}{2} \sum _{i=1}^N \alpha _i(t) \left( x_{i}(t) - s_i(t)\right) ^2\\&+ \ \frac{1}{2} \sum _{j=1}^M \bar{\alpha }_j(t) \left( y_{j}(t) -\xi _j(t)\right) ^2+ \frac{1}{2} \beta (t) \left( \sum _{i=1}^N x_{i}(t) - \xi (t)\right) ^2 \\&+\frac{1}{2} \bar{\beta }(t) \left( \sum _{j=1}^M y_{j}(t) - \sum _{i=1}^N x_{i}(t)\right) ^2\\ & + \lambda (t)\left[ \sum _{i=1}^N \gamma _{i}(t) x_{i}(t) +\sum _{j=1}^M \bar{\gamma }_{j}(t) y_{j}(t)- \delta _P P(t)\right] . \end{aligned}$$

(41)

The optimality conditions read as:

$$\begin{cases} \begin{aligned}\frac{\partial H}{\partial x_{i}} = & \ c_{i}(t) + \alpha _i(t) \left( x_{i}(t) - s_i(t)\right) + \beta (t) \left( \sum _{i=1}^N x_{j}(t) - \xi (t)\right) \\ & \ -\bar{\beta }(t) \left( \sum _{j=1}^M y_{j}(t) - \sum _{i=1}^N x_{i}(t)\right) + \lambda (t) \gamma _{i} (t) = 0, \ \ i=1\ldots N\\ \frac{\partial H}{\partial y_{j}} = & \ \bar{c_{j}}(t) + \bar{\alpha }_j(t) \left( y_{j}(t) - \xi _j(t)\right) +\bar{\beta }(t) \left( \sum _{j=1}^M y_{j}(t) - \sum _{i=1}^N x_{i}(t)\right) \\ & + \lambda (t) \bar{\gamma }_{j} (t)= 0, \ \ i=j\ldots M\\ \dot{\lambda }(t) =& \ - \frac{\partial H}{\partial P} = \delta _P \lambda (t), \\ \dot{P}(t) =& \ \sum _{i=1}^N \gamma _{i}(t) x_{i}(t) +\sum _{j=1}^M\bar{\gamma }_{j} (t) y_{j}(t) - \delta _P P(t), \\ P(0) =& \ P_0\ge 0, \\ \lambda (T) =& \ \theta . \end{aligned}\end{cases}$$

(42)

The differential equation for $\lambda$ with terminal condition $\lambda (T)=\theta$, namely

$$\begin{aligned} \dot{\lambda }(t) = \delta _P \lambda (t), \ \ \lambda (T)=\theta \end{aligned},$$

(43)

is linear and can be easily solved, leading to $\lambda (t) = \theta e^{\delta _P (t-T)}$. If we plug the expression of $\lambda$ into the maximum principle, we get:

$$\begin{aligned} \alpha _i(t) x_{i}(t)&+ (\beta (t)+\bar{\beta }(t)) \sum _{i=1}^N x_{i}(t) - \bar{\beta }(t) \sum _{j=1}^M y_{j}(t) = - c_{i}(t) \\ &- \theta \gamma _{i} (t) e^{\delta _P (t-T)} + s_i(t) \alpha _i(t) + \xi (t) \beta (t), \ \ i=1 \ldots N \end{aligned}$$

(44)

$$\begin{aligned} -\bar{\beta }(t) \sum _{i=1}^N x_{i}(t) + & \ \bar{\alpha }_j(t) y_{j}(t)+ \bar{\beta }(t) \sum _{j=1}^M y_{j}(t) =- \bar{c_{j}}(t) \\ -& \ \theta \bar{\gamma }_{j} (t) e^{\delta _P (t-T)} + \xi _j(t) \bar{\alpha }_j(t) , \ \ j=1\ldots M. \end{aligned}$$

(45)

If we define the matrix

$$\begin{aligned} \Omega 1(t):= \left( \begin{array}{cc} A(t) &{} B(t) \\ C(t) &{} D(t) \\ \end{array} \right) \end{aligned}$$

(46)

with

$$\begin{aligned} A(t):= \left( \begin{array}{cccc} \alpha _1(t) +\beta (t) +\bar{\beta }(t) &{} \beta (t)+\bar{\beta }(t) &{} \ldots &{} \beta (t)+\bar{\beta }(t) \\ \beta (t)+\bar{\beta }(t) &{} {\alpha }_2(t) +\beta (t)+ \bar{\beta }(t) &{} \ldots &{} \beta (t)+\bar{\beta }(t) \\ \ldots &{} \ldots &{} \ldots &{} \ldots \\ \beta (t)+\bar{\beta }(t) &{} \beta (t)+\bar{\beta }(t) &{} \ldots &{} \alpha _N(t)+\beta (t)+\bar{\beta }(t) \end{array} \right) , \end{aligned}$$

$$\begin{aligned} B(t):= \left( \begin{array}{ccc} -\bar{\beta }(t) &{} \ldots &{} -\bar{\beta }(t) \\ -\bar{\beta }(t) &{} \ldots &{} -\bar{\beta }(t) \\ \ldots &{} \ldots &{} \ldots \\ -\bar{\beta }(t) &{} \ldots &{} -\bar{\beta }(t) \\ \end{array} \right) , \end{aligned}$$

$$\begin{aligned} C(t):= \left( \begin{array}{cccc} -\bar{\beta }(t) &{} -\bar{\beta }(t) &{} \ldots &{} -\bar{\beta }(t) \\ \ldots &{} \ldots &{} \ldots &{} \ldots \\ -\bar{\beta }(t) &{} -\bar{\beta }(t) &{} \ldots &{} -\bar{\beta }(t) \\ \end{array} \right) , \end{aligned}$$

$$\begin{aligned} D(t):= \left( \begin{array}{ccc} \bar{\alpha }_1(t) + \bar{\beta }(t) &{} \ldots &{} \bar{\beta }(t) \\ \bar{\beta }(t) &{} \ldots &{} \bar{\beta }(t) \\ \bar{\beta }(t) &{} \ldots &{} \bar{\alpha }_M(t) + \bar{\beta }(t) \end{array} \right) , \end{aligned}$$

and the vectors

$$\begin{aligned} U(t) := \left( \begin{array}{c} x_1(t) \\ x_2(t)\\ \ldots \\ x_N(t)\\ y_1(t)\\ y_2(t)\\ \ldots \\ y_M(t)\\ \end{array} \right) , \, \, \qquad C1(t):=\left( \begin{array}{c} c_{1}(t) \\ c_{2}(t) \\ \ldots \\ c_{N}(t)\\ \bar{c_{1}}(t) \\ \bar{c_{2}}(t) \\ \ldots \\ \bar{c_{M}}(t)\\ \end{array}\right) , \end{aligned}$$

$$\begin{aligned} S1(t):=\left( \begin{array}{c} s_{1}(t)\alpha _{1}(t)+\xi (t)\beta (t) \\ s_{2}(t)\alpha _{2}(t)+\xi (t)\beta (t) \\ \ldots \\ s_{N}(t)\alpha _{N}(t)+\xi (t)\beta (t)\\ \bar{\alpha }_{1}(t)\xi _{1}(t)\\ \bar{\alpha }_{2}(t)\xi _{2}(t)\\ \ldots \\ \bar{\alpha }_{M}(t)\xi _{M}(t)\\ \end{array} \right) , \, \text {and} \, \ \Gamma 1(t):=\left( \begin{array}{c} \gamma _{1}(t) \\ \gamma _{2}(t) \\ \ldots \\ \gamma _{N}(t) \\ \bar{\gamma }_{1}(t)\\ \bar{\gamma }_{2}(t) \\ \ldots \\ \bar{\gamma }_{M}(t) \end{array} \right) . \end{aligned}$$

This equation can be written in vectorial form as:

$$\begin{aligned} \Omega 1(t) U(t) = - C1(t) - \theta e^{\delta _P (t-T)} \Gamma 1(t) + S1(t) \end{aligned}$$

(47)

and, using the fact that the matrix $\mathbf{\Omega 1(t)}$ is invertible, we get

$$\begin{aligned} U(t) = - \Omega 1(t)^{-1} C1(t) - \theta e^{\delta _P (t-T)} \Omega 1(t)^{-1} \Gamma 1(t) + \Omega 1(t)^{-1} S1(t). \end{aligned}$$

(48)

The equation of P boils down to:

$$\begin{aligned} \dot{P}(t) = \Gamma 1(t)^T U(t) - \delta _P P(t) \end{aligned}$$

(49)

and this differential equation has a closed form given by:

$$\begin{aligned} P(t) = e^{-\delta _P t} \left[ \mathop{\int} _0^t \Gamma 1(s)^T U(s) e^{\delta _P s} ds + P_0\right] . \end{aligned}$$

(50)

1.4 Proof of Theorem 4

The proof of this theorem is very similar to the one of Theorem 1, and it can be obtained from it by introducing a time shift of L units.

1.5 Proof of Theorem 5

The proof of this theorem is very similar to the one of Theorem 3, and it can be obtained from this one by adding an exogenous inventory variable.