An efficient implementation of a phase field model for fatigue crack growth

Abstract

Recently, phase field modeling of fatigue fracture has gained a lot of attention from many researches and studies, since the fatigue damage of structures is a crucial issue in mechanical design. Differing from traditional phase field fracture models, our approach considers not only the elastic strain energy and crack surface energy, additionally, we introduce a fatigue energy contribution into the regularized energy density function caused by cyclic load. Comparing to other type of fracture phenomenon, fatigue damage occurs only after a large number of load cycles. It requires a large computing effort in a computer simulation. Furthermore, the choice of the cycle number increment is usually determined by a compromise between simulation time and accuracy. In this work, we propose an efficient phase field method for cyclic fatigue propagation that only requires moderate computational cost without sacrificing accuracy. We divide the entire fatigue fracture simulation into three stages and apply different cycle number increments in each damage stage. The basic concept of the algorithm is to associate the cycle number increment with the damage increment of each simulation iteration. Numerical examples show that our method can effectively predict the phenomenon of fatigue crack growth and reproduce fracture patterns.

1 Introduction

In the last decade, the phase field method was developed to simulate fracture processes (Francfort and Marigo 1998; Bourdin et al. 2000; Bourdin 2007). The core idea of the phase field model is to represent a discrete discontinuous phenomenon by a smooth function. The biggest advantage of phase field modeling is its unified framework, in which the entire fracture evolution (nucleation, propagation, branching, kinking) is covered. Griffith (1921) initially proposes the idea of using an energetic criterion to predict the onset of crack propagation. Later, Francfort and Marigo (1998) generalize the classical Griffith theory by a variational formulation of brittle fracture, but it is nevertheless numerically difficult. A regularized approximation of the model is presented by Bourdin (Bourdin 2007; Bourdin et al. 2008), which is more suitable for numerical implementation. This regularized version gives birth to the so-called fracture phase field models, building a simple path to model fracture phenomenon. The phase field method has been successfully established for quasi-static fracture (Kuhn and Müller 2010; Miehe et al. 2010; Borden et al. 2014), dynamic brittle fracture (Schlüter et al. 2014), ductile fracture (Ambati et al. 2015; Kuhn et al. 2016), hydraulic fracture (Wilson and Landis 2016; Yoshioka and Bourdin 2016) so far. However, the real manufacturing processes usually involve oscillating loads, which usually do not lead to an immediate failure, but rather a failure caused by fatigue crack growth after numerous loading cycles. In this spirit, a phase field model that can handle complex cyclic fatigue process is required.

Some research contributions are given to find phase field models for the fatigue fracture process. On the one hand, Boldrini et al. (2016) proposed a phase field model to describe the fracture behavior coupling thermal and fatigue problems, where fatigue behavior is related to an additional scalar variable. On the other hand, fatigue fracture can be modeled by adopting the Ginzburg-Landau formalism (Gurtin 1996): In Caputo and Fabrizio (2015) and Amendola et al. (2016), the fatigue damage evolution is derived by incorporating a fatigue potential to degrade the material under cyclic loading. However, those methods fail to reproduce the important known feature of fatigue behavior like the Paris’ law, the Wöhler curve with the transition between low- and high-cyclic fatigue, and the Palmgren-Miner law. Recently, (Alessi et al. 2018; Carrara et al. 2020; Seiler et al. 2020; Seleš et al. 2021; Hasan and Baxevanis 2021) advance the fatigue phase field model by taking both degradation of stiffness and reduction of fracture energy in the fatigue damage evolution, where the major feature of fatigue behavior can be recovered into account. Differing from the above approaches, Schreiber et al. (2020a, 2020b) extend the model from Kuhn and Müller (2010), where an additional energy density contribution is proposed as an additional driving forces caused by the increasing number of load cycles. In Schreiber et al. (2020a, 2020b), a realistic fatigue crack growth behavior, including the mean stress effects and different stress ratios, can be predicted.

In phase field simulation of fatigue fracture, huge computational effort is usually required before crack nucleation or propagation can be observed on a macroscopic level. As an efficient scheme, the computing time must be kept below a reasonable limit with respect to a large number of load cycles. In this work, we provide an efficient adaptive cycle number adjustment algorithm based on the work of Schreiber et al. (2020a, 2020b). The platform FEniCS (Alnæs et al. 2015) is used for the implementation.

Fig. 1

A quadratic geometry is loaded at the top of the surface and the pre-defined crack $a_0$ is with length of 0.05L. The model parameter $\varepsilon$ controls the width of the transition zone (${\mathbf {a}}$: $\epsilon =0.001$; ${\mathbf {b}}$: $\epsilon =0.002$; ${\mathbf {c}}$: $\epsilon =0.003$; ${\mathbf {d}}$: $\epsilon =0.004$; ${\mathbf {e}}$: $\epsilon =0.005$ ${\mathbf {f}}$: $\epsilon =0.006$)

2 Phase field modeling for cyclic fatigue cracks

2.1 Phase field modeling

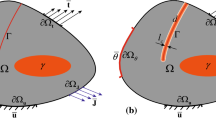
A phase field fracture model introduces an additional field variable to represent cracks. In the phase field model from Kuhn and Müller (2010), the crack field s is 1 if the material remains undamaged and is 0 where cracks occur. Furthermore, it is to postulate that the displacement field ${\mathbf {u}}$ and crack field s locally minimize the total energy of a loaded body $\varOmega$. The total energy E is given as

$$\begin{aligned} \begin{aligned} E&= \int _\varOmega {\dfrac{1}{2}\biggl ((s^2+\eta ){\varvec{\varepsilon }}:[{\mathbb {C}}{\varvec{\varepsilon }}]\biggr )}\mathrm {d}V \\&\quad \, +\int _\varOmega {{\mathcal {G}}_c \biggl (\dfrac{(1-s)^2}{4{\epsilon }} + {\epsilon } |\nabla s|^2\biggr )}\mathrm {d}V \end{aligned} \end{aligned}$$

(1)

with the infinitesimal strain tensor ${\varvec{\varepsilon }}=\dfrac{1}{2}(\nabla {\mathbf {u}}+\nabla ^T {\mathbf {u}})$ and stiffness tensor ${\mathbb {C}}$. The dimensionless parameter $\eta$ is used to avoid numerical difficulties, and ${\mathcal {G}}_c$ is the cracking resistance. The parameter $\epsilon$ controls the width of the transition zone between the broken and undamaged material. Figure 1 shows the influence of $\epsilon$ to the crack width. The internal length parameter $\epsilon$ is taken as four times the mesh size in order to solve the phase field governing equation in the presented examples of this work.

In a classical phase field fracture mode, e.g. Kuhn and Müller (2010), only the elastic energy and the fracture surface energy is considered in the total free energy. The crack will propagate in such a way that the total energy is minimized. However, this is not suitable in a fatigue fracture simulation. The cyclic loading involved in the fatigue simulation is much lower than the other fracture simulation cases, thus, with this load it is not effective to minimize the total energy. Additionally, the continuous loading and unloading process consumes also much energy as shown in Mughrabi (2015) and this is not included in the Kuhn and Müller’s model. Different from the work proposed in  (Alessi et al. 2018; Carrara et al. 2020; Hasan and Baxevanis 2021), where a fatigue degradation function related to a history variable is applied directly on the fracture energy term and the fracture toughness of the material is reduced during the fatigue process, we keep the surface energy term untouched and extend the phase field model from Kuhn and Müller (2010) by an additional term for cyclic fatigue. The total energy now reads

$$\begin{aligned} \begin{aligned} E({\varvec{\varepsilon }}, s, \nabla s) =&\int _\varOmega \psi ({\varvec{\varepsilon }}, s, \nabla s)\mathrm {d}V \\ =&\int _\varOmega {\dfrac{1}{2}\biggl ((s^2+\eta ){\varvec{\varepsilon }}:[{\mathbb {C}}{\varvec{\varepsilon }}]\biggr )}\mathrm {d}V + \\&\int _\varOmega {{\mathcal {G}}_c \biggl (\dfrac{(1-s)^2}{4{\epsilon }} + {\epsilon } |\nabla s|^2\biggr )}\mathrm {d}V+ \\&\int _\varOmega \psi ^{ac}\mathrm {d}V, \end{aligned} \end{aligned}$$

(2)

Among them, $\psi$ is the total energy density, and $\psi ^{ac}$ is the energy density, standing for the sum of additional driving forces caused by fatigue damage. The energy density for fatigue crack $\psi ^{ac}$ is given as (Schreiber et al. 2020b)

$$\begin{aligned} \begin{aligned} \psi ^{ac}&= h(s)q\biggl \langle D -D_c\biggr \rangle ^b\\&= h(s)q \biggl \langle D_0 + \dfrac{\mathrm {d}N}{n_D}\biggl (\dfrac{{\hat{\sigma }}(1-L)}{f(L)}\biggr )^k -D_c\biggr \rangle ^b, \end{aligned} \end{aligned}$$

(3)

which is related to a new introduced parameter D, representing the damage related to fatigue.

Fig. 2

A higher number of c increases the crack growth rate

The function $f(L)=A_D(1-L)^c$ is a threshold, where L is the ratio of the mean external load and the maximum external load; and the parameter c is a constant. In general, the function f(L) can be chosen arbitrarily as long as it captures the mean stress effect of a specific material. Fig. 2 shows the influence of the parameter c on the crack growth rate by unidirectional cyclic load, where a higher value of c increases mean stress effect. The increments with load amplitude below this threshold is not taken into damage accumulation. The term ${\hat{\sigma }}({\varvec{\varepsilon }})$ is the driving force, corresponding to the first principal stress of the stress tensor ${\varvec{\sigma }}={\mathbb {C}}{\varvec{\varepsilon }}$ in this case, of which we only consider positive entries and negative entries are neglected. However, it is not claimed that this choice of driving force is generally valid for all materials with complex properties or effects. Other effective stress quantities, as e.g. the von-Mises stress, might be more suitable in different cases. The parameters $A_D$, k and $n_D$ can be obtained from the S-N curve (see Fig. 3). Here, the mathematical model of the phase field is coupled with the fatigue parameters from experiments, which allows for a general and elegant incorporation of influences, like the temperature effect or ambient environment into the fatigue propagation behavior. Furthermore, $D_0$ is the previous state of fatigue damage; $D_c$ is a threshold to determine the critical fatigue damage stage. The idea, to use a damage parameter D, is inspired by Miner’s rule from Miner (1945). Miner’s rule describes the mechanism of damage accumulation until macro crack initiation. The connection between Paris’ law and Miner’s rule is shown in Ciavarella et al. (2018). Thus, we define the damage parameters in cooperation with fatigue parameters from the S-N curve. The regularization parameters q and b determine the speed of fatigue damage energy growth, which should be chosen appropriately to ensure a stable energy growth speed. Figure 4 shows the influence of different parameter settings on the crack length and crack growth rate. It is to notice that the parameters q and b are merely numerical parameters, which are only used to construct the fatigue energy term from the damage parameter D. The crack growth rate is mostly determined by the fatigue parameters from the S-N curve with the help of experiments, as shown in Fig. 5

Fig. 3

A simplified explanation of S-N curve

Fig. 4

The influence of the model parameters q, b and $D_c$ on the crack length and crack growth rate

The degradation function $h(s)=s^2$ models the loss of stiffness in broken material caused by cyclic fatigue. This choice of degradation function is for the sake of simplicity. For a comprehensive overview of the model parameters, we provide a summary in Table 1.

With the Macauley brackets, which is defined by

$$\begin{aligned} \langle x \rangle ^n = {\left\{ \begin{array}{ll} 0&{} \text{ if } \quad x \le 0 \\ x^n &{} \text{ if } \quad x > 0, \end{array}\right. } \end{aligned}$$

(4)

the fatigue crack will only occur after the damage D reaches the threshold $D_c$. After that, the fatigue energy grows rapidly controlled by parameters q and b; and it eventually decreases again due to the degradation function.

The fatigue damage D is updated for every simulation iteration

$$\begin{aligned} D_{n+1} = D_n + \mathrm {d}D_n \end{aligned}$$

(5)

with

$$\begin{aligned} \mathrm {d}D_n=\dfrac{\mathrm {d}N}{n_D}\biggl (\dfrac{{\hat{\sigma }}_n(1-L)}{f(L)}\biggr )^k. \end{aligned}$$

(6)

With the help of variational principle, Eq. (2) yields the equilibrium of the displacement field ${\mathbf {u}}$ and the evolution of the crack field s.

2.2 Paris’ law

The crack growth behavior is the main focus of the present investigation. The growth behavior of a macro crack can be described by Paris’ law (Paris and Erdogan 1963). The Paris’ law describes the fatigue crack growth rate in relation to the stress intensity factor range, it reads

$$\begin{aligned} \dfrac{\mathrm {d}a}{\mathrm {d}N} = C (\Delta K)^m, \end{aligned}$$

(7)

where C and m are material dependent parameters. The stress intensity factor K (Irwin 1997) is an intensity parameter, which describes the stress singularity near the tip of a crack. It is determined by the specimen geometry, the size and location of the crack, the magnitude and the distribution of loads applied on the material. The crack growth rate is discretized as

$$\begin{aligned} \biggl ( \dfrac{\mathrm {d}a}{\mathrm {d}N} \biggr )_p \approx \dfrac{a_p - a_{p-1}}{N_p - N_{p-1}}, \end{aligned}$$

(8)

where $a_p$ and $N_p$ denote the crack length and cycle number from the p-th data point. According to Paris’ law, the crack growth rate has a linear behavior with scope m in a diagram with logarithmic scales (see Fig 6).

Fig. 5

The influence of the fatigue parameters on the crack growth rate

Table 1 Model parameters

Fig. 6

The crack growth rate has a linear behavior in a diagram with logarithmic scales

3 FEniCS implementation of the phase field fatigue fracture model

3.1 Simulation settings

Let ${{{\varvec{t}}}}^*$ be the external traction on the part ${\partial \varOmega }_{{{{\varvec{t}}}}}$ of the boundary of the domain $\varOmega$. The variational formulation of our problem reads

$$\begin{aligned} \int _\varOmega \delta E ~ \mathrm {d}V + \int _{\partial \varOmega _{{{\varvec{t}}}}} {{{\varvec{t}}}}^* \cdot \delta {\mathbf {u}} ~\mathrm {d} A = 0. \end{aligned}$$

(9)

Computing the variation of total energy E with regard to displacement field ${\mathbf {u}}$ and fracture field s yields

$$\begin{aligned} \begin{aligned} \delta E =&\int _\varOmega \biggl ( \dfrac{\partial \psi }{\partial {\varvec{\varepsilon }}}:\delta {\varvec{\varepsilon }} + \dfrac{\partial \psi }{\partial s}\delta s + \dfrac{\partial \psi }{\partial \nabla s} \cdot \delta \nabla s \biggr ) \mathrm {d}V. \end{aligned} \end{aligned}$$

(10)

Employing the product rule

$$\begin{aligned} \begin{aligned} \dfrac{\partial \psi }{\partial {\varvec{\varepsilon }}} : \delta {\varvec{\varepsilon }} = - \mathrm {div} \biggl ( \dfrac{\partial \psi }{\partial \nabla {\mathbf {u}}} \biggr ) \delta {\mathbf {u}} + \mathrm {div} \biggl ( \biggl ( \dfrac{\partial \psi }{\partial \nabla {\mathbf {u}}} \biggr )^T \delta {\mathbf {u}} \biggr ) \end{aligned} \end{aligned}$$

(11)

and

$$\begin{aligned} \begin{aligned} \dfrac{\partial \psi }{\partial \nabla s} \cdot \delta \nabla s = - \mathrm {div} \biggl ( \dfrac{\partial \psi }{\partial \nabla s} \biggr ) \delta s + \mathrm {div} \biggl ( \dfrac{\partial \psi }{\partial \nabla s} \delta s \biggr ) \end{aligned}, \end{aligned}$$

(12)

as well as the divergence theorem on Eq. (10) results in

$$\begin{aligned} \begin{aligned} \delta E&= \int _\varOmega - \mathrm {div} \biggl ( \dfrac{\partial \psi }{\partial \nabla {\mathbf {u}}} \biggr ) \delta {\mathbf {u}} ~ \mathrm {d}V \\&\quad + \int _\varOmega \biggl ( \dfrac{\partial \psi }{\partial s} - \mathrm {div}\dfrac{\partial \psi }{\partial \nabla s} \biggr ) \delta s ~ \mathrm {d}V \\&\quad + \int _{\partial \varOmega } \dfrac{\partial \psi }{\partial \nabla s} \cdot {\mathbf {n}} ~ \delta s ~ \mathrm {d} A \\&\quad + \int _{\partial \varOmega } \biggl ( \dfrac{\partial \psi }{\partial \nabla {\mathbf {u}}} \biggr )^T \cdot {\mathbf {n}} ~ \delta {\mathbf {u}} ~ \mathrm {d} A \end{aligned} \end{aligned}$$

(13)

Thus, Eq. (9) yields four coupled Euler-Lagrange equations of the variational principle

$$\begin{aligned}&{\mathrm {div}} \dfrac{\partial \psi }{\partial \nabla {\mathbf {u}}} =0 \end{aligned}$$

(14)

$$\begin{aligned}&\dfrac{\partial \psi }{\partial s} - {\mathrm {div}}\dfrac{\partial \psi }{\partial \nabla s} = 0 \end{aligned}$$

(15)

$$\begin{aligned}&\dfrac{\partial \psi }{\partial \nabla s} \cdot {\mathbf {n}} = 0 \quad \text{ on }~ {\partial \varOmega }_{\nabla s} \end{aligned}$$

(16)

$$\begin{aligned}&\biggl (\dfrac{\partial \psi }{\partial \nabla {\mathbf {u}}} \biggr )^T \cdot {\mathbf {n}} + {{{\varvec{t}}}}^* = 0 \quad \text{ on }~ {\partial \varOmega }_{{{\varvec{t}}}}. \end{aligned}$$

(17)

With the constitutive law $\frac{\partial \psi }{\partial \nabla {\mathbf {u}}}={\varvec{\sigma }}$, Eq. (14) represents the equilibrium condition

$$\begin{aligned} \mathrm {div} {\varvec{\sigma }} = 0. \end{aligned}$$

(18)

Eq. (15) provides the evolution equation of the crack field. As shown in Gurtin (1996), the most general form of the evolution of the crack field s, which is in consistent with a mechanical view of the second law of thermodynamics reads

$$\begin{aligned} \dfrac{\mathrm {d} s}{\mathrm {d} N} = -M \dfrac{\delta \psi }{\delta s}=-M \biggl ( \dfrac{\partial \psi }{\partial s}-\mathrm {div}\dfrac{\partial \psi }{\partial \nabla s} \biggr ), \end{aligned}$$

(19)

where $M>0$ is the mobility parameter, which models the “viscosity”(rate dependency) of the phase field fracture model. The $M \rightarrow \infty$ approximates the quasi static limit case with $\dfrac{\delta \psi }{\delta s}=0$. Therefore, the evolution of crack field is modeled by

$$\begin{aligned} \begin{aligned} \dfrac{\mathrm {d} s}{\mathrm {d} N} =&-M \biggl \{ g(s)' \dfrac{1}{2}{\varvec{\varepsilon }}:[{\mathbb {C}}{\varvec{\varepsilon }}] \\&-{\mathcal {G}}_c \biggl (2\epsilon \nabla \cdot \nabla s - \dfrac{s-1}{2\epsilon } \biggr ) \\&+ h(s)'\psi ^{ac}(D) \biggr \}. \end{aligned} \end{aligned}$$

(20)

Eqs. (16) and  (17) are the Neumann boundary conditions for the crack field

$$\begin{aligned} \nabla s \cdot {\mathbf {n}} = 0 \quad \text{ on }~ {\partial \varOmega }_{\nabla s} \end{aligned}$$

(21)

and the stress field

$$\begin{aligned} {\varvec{\sigma }} {\mathbf {n}} = {{{\varvec{t}}}}^* \quad \text{ on }~ {\partial \varOmega }_{{{{\varvec{t}}}}}. \end{aligned}$$

(22)

Solving Eqs. (18) and  (20) by means of the Newton method yields the displacement field ${\mathbf {u}}$ and fracture field s.

3.2 Adaptive cycle number adjustment algorithm

To reduce the total number of load cycles, we transfer the simulation step to cycles: The simulation step is defined as the incremental change of “time” in one simulation iteration, and each simulation step represents a certain increment of load cycles. Furthermore, the real cyclic loading is approximated with its envelope loading. In general, this “time-cycle” transfer concept is also suitable for any arbitrary loading process. Noting Eq. (6), the cycle number increment can be rewritten as

$$\begin{aligned} \mathrm {d}N=n_D\biggl (\dfrac{{\hat{\sigma }}_n(1-L)}{f(L)}\biggr )^{-k}\mathrm {d}D. \end{aligned}$$

(23)

The choice of the cycle number increment is a crucial point in the phase field model: not only because it determines the computational time; it also strongly influences the shape of the crack pattern. The crack trace is wide and irregular when the cycle number increment is too large. Besides, the fatigue energy grows dramatically by over-large cycle number increments, and it might result in a simulation with an unstable energy state. Several crack patterns from unsuitable cycle number increment are demonstrated in Fig. 7.

Fig. 7

The crack pattern is strongly influenced by the cycle number increment $\mathrm {d}N$; ${\mathbf {a}}$: $\mathrm {d}N$ chosen by our algorithm; ${\mathbf {b}}$: crack pattern is wide and irregular ($\mathrm {d}N=50$); ${\mathbf {c}}$: unstable state ($\mathrm {d}N=500$)

Additionally, the displacement field ${\mathbf {u}}_n$, the crack field $s_n$ and the cycle number $N_n$ from the previous simulation step are stored as reference values. These values will be reused if the simulation needs to be restarted. In Alg. 2, we provide the details of the restart-algorithm.

The simulation of fatigue fracture is divided into three stages: the damage D is below the threshold $D_c$. In this stage, it behaves in a pure static mechanical state. Thus, the cycle number increment should be chosen as large as possible. the damage D is at the limit threshold $D_c$. The fatigue crack is about to begin and the cycle number increment $\mathrm {d}N$ should be chosen suitable to ensure $\mathrm {d}D$ small enough to simulate the transient process. the damage D is bigger than $D_c$. We control the maximum damage increment $\mathrm {max}[\mathrm {d}D]$ between a control parameter $D_{\beta }$ and $D_{\gamma }$ to obtain a moderate growth rate of the fatigue energy. Since the damage increment $\mathrm {d}D$ is controlled by this algorithm, the fatigue damage at the previous step and current step will not change much. As a result, it is suitable to take the stress from the previous step as the driving force even if the cycle number increment $\mathrm {d}N$ is large. This adaptive algorithm will stop once the cycle number increment $\mathrm {d}N$ reach a minimal cycle number increment. Figure 8 reports the maximum damage increment $\mathrm {max}[\mathrm {d}D]$ and cycle number increment $\mathrm {d}N$ by applying the adaptive cycle increment adjustment algorithm. The cyclic loading is applied within four phases in this example, where both the influence of the maximum external load and mean stress are taken into consideration. According to our algorithm, small cyclic loading increases the increment of cycle number of one simulation step. It is to noticed that in this algorithm only two global values (the maximum damage increment $\mathrm {max}[\mathrm {d}D]$ and cycle number increment $\mathrm {d}N$) are involved. The algorithm is suitable for a fatigue fracture scenario with only one crack or multiple cracks are simultaneously at the same stage.

Fig. 8

Illustration of the proposed adaptive cycle adjustment. The upper figure is a schematic illustration of the approximation for cyclic loading in four phases; ${\mathbf {a}}$: damage within the simulation; ${\mathbf {b}}$: cycle number within the simulation

For a better comprehension of our algorithm, we summarize this in Alg. 1.

4 Numerical examples

For validation of the introduced implementation of the proposed model, several simulations are used. The compact tension (CT) specimen is widely used as testing sample in the field of fracture mechanics. The definition of the geometry is given in the ASTM E 399 standard (ASTM 2009).

Fig. 9

${\mathbf {a}}$: The geometry definition of CT specimen; ${\mathbf {b}}$: the crack length in relation to cycle number obtained from a simulation with vertical loads on the upper bolt hole; ${\mathbf {c}}$: the evolution of crack field at cycle $N_1$, $N_2$ and $N_3$; ${\mathbf {d}}$: the field value (${\hat{\sigma }}$, D and s) at cycle $N_1$, $N_2$ and $N_3$

For the CT specimen, the stress intensity factor can be approximated by

$$\begin{aligned} \begin{aligned} \Delta K&= \dfrac{\Delta F}{\mathrm {B}\sqrt{\mathrm {L}}}\dfrac{2+\dfrac{a}{\mathrm {L}}}{\biggl (1-\dfrac{a}{\mathrm {L}}\biggr )^{3/2}} \cdot \\&\quad \biggl [0.886 + 4.64\biggl (\dfrac{a}{\mathrm {L}}^2\biggr ) - 13.32\biggl (\dfrac{a}{\mathrm {L}}\biggr )^3 \\&\quad + 14.72\biggl (\dfrac{a}{\mathrm {L}}\biggr )^4 - 5.69\biggl (\dfrac{a}{\mathrm {L}}\biggr )^5 \biggr ]. \end{aligned} \end{aligned}$$

(24)

This equation was proposed in Srawley (1976). Here F is the applied force, and $\mathrm {B}$ is the thickness of the specimen. The simulation result is depicted in Fig. 9, where the upper semi-circle of the bolt hole is loaded with a distributed vertical pulsating load. The evolution of the crack field is demonstrated in Fig. 9$\mathrm{{b}}$ and $\mathrm{{c}}$. Figure 9$\mathrm{{d}}$ shows the evolution of the field values (driving force ${\hat{\sigma }}$, damage D and crack field s) along the crack ligament at cycle $N_1$, $N_2$ and $N_3$. It is recognized, the driving force ${\hat{\sigma }}$ increases at the crack tip as the crack propagates; as a consequence, the specimen is easier to break than the early stage. In other words, the fatigue crack will propagate faster, and the crack growth rate will be higher. The fatigue damage parameter D is accumulated continuously during the crack propagation, whereas the crack field s decreases from 1 to 0. Figure 10 shows the comparison using cycle adjustment against the “classical” simulation scheme. As depicted in Fig. 10$\mathrm{{a}}$, our algorithm can accelerate the simulation process significantly. The computing time has dropped to nearly $3\%$ using our method, compared to constant cycle number increment $\mathrm {d}N=5$. Figure 10$\mathrm{{b}}$ and $\mathrm{{c}}$ show, although the cycle number is adjusted, the proposed method yields almost the same crack growth rate and crack pattern. Using the applied forces as a variable, Fig. 11 shows the crack growth rate related to the stress intensity factor for different simulations. In Fig. 11$\mathrm{{a}}$, we present the crack growth rate for different levels of maximum external load. The result matches Paris’ law with parameters $C=3.724 \times 10^{5} \dfrac{\mathrm {mm}/\mathrm {cycle}}{(\mathrm {MPa}\sqrt{\mathrm {m}})^m}$ and $m=5.548$ very well. It is to observe that even though different force amplitudes for the simulation are applied, the rate of crack growth can be described with the same Paris’ law. Figure 11$\mathrm{{b}}$ displays the effect of mean stress on the crack growth rate, where the stress ratio R is defined as the ratio between the minimum stress and the maximum stress. The depicted diagram reflects the fact that higher mean stress increases the rate of crack growth.

Fig. 10

Our method compared to the classical simulation scheme in ${\mathbf {a}}$: the computational time; ${\mathbf {b}}$: the crack growth rate; ${\mathbf {c}}$: the crack pattern

Fig. 11

The crack growth rate related to the stress intensity factor from simulations with the CT specimen. ${\mathbf {a}}$: constant stress ratio with different force amplitudes; ${\mathbf {b}}$: different stress ratio with the same force amplitude

In the next example, we consider a block geometry with initial boundary values as proposed in Müller and Kuhn (2020). This example is straightforward and disregards special problems of distinction between tension and compression, since the cracks should only occur in tension region (Kuhn 2013). A half of its top surface is loaded with a displacement load, whereas the bottom of the block is fixed. Furthermore, we assume this upper half of the block will never break, given as a Dirichlet boundary condition $s=1$ in the indicated area (in red) of width 0.5L (see Fig. 12). As seen in Fig. 12, the crack begins at the top of the surface, which is different from the pure elastic case shown in Müller and Kuhn (2020). The reason is that the fatigue crack is triggered at areas where the maximum first principal stress is found, which is the driving force for the fatigue crack propagation in our model.

Fig. 12

The left figure is the definition of the block geometry; in the right figure, ${\mathbf {a}}$: the evolution of crack field; ${\mathbf {b}}$: the magnitude of the first principal stress ${\hat{\sigma }}$ (driving force) with color-map

Different loads, deformations and crack interactions can lead to complex crack propagation behavior, depending on the applied load conditions on the geometry. A specimen of a rectangular geometry is set up to validate our model under mixed mode loading in traction conditions. The rectangular geometry is loaded with a purely alternating ($R=-1$) displacement load in the vertical direction on the upper edge, and the lower edge is fixed. Sharp notches on both vertical edges are defined for different situations. Figure 13 shows that the presented method is robust under mixed load situation. The first row at cycle number $N_1$ is the initial state of the crack pattern, where the predefined cracks are located at different positions. The simulation results at cycle number $N_2$ can be verified with the crack patterns illustrated in Yates et al. (2008). In the last row at cycle number $N_3$, we demonstrate the results at the last feasible simulation stages. At the early stage, the crack extends purely horizontal in all simulation settings. After this stage, the cracks begin to deviate from each other (see Fig. 13$\mathrm{{b}}$ and $\mathrm{{c}}$), caused by the fatigue driving force. After this period, the cracks intend to change their directions to the horizontal level and grow towards each other again. The deviation of the crack paths is influenced by the crack interaction, as shown in Fig. 13$\mathrm{{d}}$. The crack propagation remains almost straight during the whole crack evolution due to the higher distance of the cracks. These crack paths simulated by the finite element method using our model is very similar comparing to experiments.

Fig. 13

The left figure is the definition of the rectangular specimen; the right figure (${\mathbf {a}}$-${\mathbf {e}}$) shows the evolution of the crack field loaded with different conditions (${\mathbf {a}}$: f=0; ${\mathbf {b}}$: f=0.05L; ${\mathbf {c}}$: f=0.1L; ${\mathbf {d}}$: f=0.15L; ${\mathbf {e}}$: f=0.2L)

5 Conclusion

We present a phase field fracture model to predict the fracture behavior caused by fatigue damage. In the phase field modeling framework, the entire fatigue fracture behavior is simply derived by a single regularized energy density function. Differing from alternative fatigue phase field models (Alessi et al. 2018; Carrara et al. 2020; Seiler et al. 2020; Seleš et al. 2021), we introduce an additional energy term related to the fatigue damage into the total energy density function. The new method incorporates the experiment data directly into the phase field energy term, which is best to the author’s knowledge, the first work to combine the experimental findings with the phase field fatigue model. Thus the proposed simulation setup has the potential to compactly simulate the fatigue propagation under complex circumstances. This fatigue energy part represents the accumulated driving force caused by fatigue damage. Furthermore, the fatigue energy is related to a damage parameter, which represents the damage caused by cyclic fatigue. The results show that our model is able to reproduce the significant properties of fatigue crack growth, as e.g. the mean stress effect. The main contribution of our study is to develop an adaptive cycle increment adjustment algorithm. The entire simulation is split into three stages: elastic stage; transient stage and fatigue stage. During the simulation, the damage increment is controlled to obtain a moderate fatigue energy growth, where the cycle number increment is chosen adaptively according to the damage increment. This algorithm can reduce the computational cost of simulation without sacrificing accuracy. The implementation of the phase field model is done on the open-source platform FEniCS. Thanks to its flexibility and simplicity, it enables elaborate and efficient simulations of complex problems. As a future work, the phase field fatigue damage model will be extended to three dimensions.