Stable and unstable viscoelastic crack growth: experimental validation of nonlinear theory for rubber

Abstract

A theory of viscoelastic crack growth that accounts for global and local (crack-tip) viscoelasticity, as well as continuum nonlinearity, is used to analyze stable and unstable crack growth data on carbon black-filled rubber. First, we briefly review relevant results from a recently published linear theory that compares the effect of various models of the failure zone (fracture process zone) on crack growth. Then, it is shown that an extension of this theory to include nonlinearity is in very good agreement with experimental data on crack opening displacement and crack speed for rubber with three different volume fractions of carbon black.

Appendix

1.1 Constitutive equation

The constitutive equation used in large deformation ${J_{v}}$ theory is based on a strain energy density W that is a function of pseudo quantities, in which the Piola stress tensor ${{\varvec{\upsigma}}}$ (whose transpose is called the Lagrangian stress tensor by Fung (1965)), satisfies

$${{\varvec{\upsigma}}} = \frac{\partial W}{{\partial (\nabla {\mathbf{u}}^{R} )}},$$

(34)

where $\nabla {\mathbf{u}}^{R}$ is the pseudo displacement gradient and ${\mathbf{u}}^{R}$ is the pseudo displacement vector,

$${\mathbf{u}}^{R} \equiv \frac{1}{{G_{e} }}\int\limits_{{0^{ - } }}^{t} {G(t - \tau )} \frac{{\partial {\mathbf{u}}}}{\partial \tau }d\tau$$

(35)

in terms of the displacement vector ${\mathbf{u}}$. Although other relaxation moduli could be used, we use here the shear relaxation modulus, G(t), and its equilibrium value, $G_{e}$. The stresses and displacements are defined in terms of coordinates in the initial, undeformed body.

The inverse of Eq. (35) is

$${\mathbf{u}} = G_{e}\int\limits_{{0 - }}^{t} {Cs(t - \tau )\frac{{\partial {\mathbf{u}}^{R} }}{\partial \tau }d\tau }$$

(36)

in which Cs(t) is the shear creep compliance.

We should add that Eqs. (34) and (35) have been shown to be a special case of constitutive theory based on nonequilibrium thermodynamics (Schapery 1990, Sect. 3) if the stress therein is interpreted as the Piola stress tensor and strain as the displacement gradient; this is valid because these are conjugate thermodynamic variables. However, rotations in viscoelastic continua may affect the stresses unless the deformation is small (Schapery 1984). Thus, this formulation in not fully frame indifferent.

The mechanical state of an elastic body will be independent of rigid rotation if the strain energy depends on the displacement gradient through Green’s strains (Fung 1965). However, for now, we require only that W depends on the pseudo displacement gradient. Because this means that the stresses and displacements in the viscoelastic body may be affected by rotations when the deformation is large, the excellent agreement found here between theory and experiment for the COD and crack speed is believed to show that this effect is not significant here. This insignificance is apparently at least partly due to the high applied stretching strain, which results in even higher stretching strains, relative to local rotation, in the neighborhood of P and, for points $\varepsilon_{1} \;{\text{and}}\;\varepsilon_{2}$, in the entire singular-field. Additionally, viscoelasticity reduces the amount of near-tip rotation.

Analysis of viscoelastic crack growth is reduced essentially to elastic analysis when Eq. (34) can be used. One may check this aspect of the constitutive model experimentally by expressing displacement gradients (“nominal strains”) in terms of pseudo variables. The resulting stress-pseudo strain behavior will be (essentially) independent of the strain history if the model is valid. Undoubtedly, it will not be valid for all histories with large strains.

1.2 Effective compliance

Convolution integrals such as Eqs. (35) and (36) do not converge when evaluated numerically by standard methods if there are many decades over which the compliance and modulus vary. However, by changing the variable of integration to its logarithm, an excellent approximation becomes apparent, as originally shown by Schapery (1975a). Specifically, using Eq. (36) to illustrate this, let

$$d\tau = 10^{z} \ln (10)dz$$

(37)

showing that, for most functions ${\mathbf{u}}^{R}$, the lower limit of the integral, $- \infty ,$ can be replaced by a finite value because of the cutoff function $10^{z}$. When the pseudo COD, $v^{R}$, obeys a power law in time, as it does for the present class of problems,

$$v^{R} = ct^{p}$$

(38)

where c does not depend on time; then, the integral can be found analytically if the curvature of C is small in logarithmic coordinates. Equation (36) becomes, with $c = 1$ for simplicity,

$$v = \int\limits_{ - \infty }^{0} {\overline{C}(Lt + z)} w(z,\;p)dz,$$

(39)

where w is the weight function,

$$w = p\ln (10)10^{z} (1 - 10^{z} )^{p - 1}$$

(40)

which is plotted in Fig. 

Fig. 9

Weight functions

9 for the smallest and largest p-values needed here. Figure 

Fig. 10

Normalized creep compliance for CB = 0.05

10 shows that it is sufficient to use − 3 as the lower limit in Eq. (39). The compliance for CB = 0.05 is used in Fig. 10 because it exhibits the largest curvature of the three CB-filled elastomers.

Now, we define an effective compliance when Eq. (38) applies,

$$\overline{C}_{ef} (t) = \frac{1}{{t^{p} }}\int\limits_{0}^{t} {\overline{C}(t - \tau )\frac{{d\tau^{p} }}{d\tau }} d\tau .$$

(41)

Inasmuch as the creep master curve can be approximated by a power law over any one-decade time range (the effective width of the weight function), one may use

$$C(t) \sim t^{n}$$

(42)

to evaluate the effective modulus, where

$$n = \frac{dLC}{{dLt}}$$

(43)

is the local slope. This approximation used in Eq. (41) yields,

$$\overline{C}_{ef} = \overline{C}\left( {t/s_{f} } \right),$$

(44)

where $s_{f}$ given by Eq. (18). Thus,

$$u_{i} = \overline{C}(t/s_{f} )u_{i}^{R} .$$

(45)

Figure 

Fig. 11

Shift factors for CB = 0.05

11 shows the variation of $s_{f}$ with Lt; the “bumpiness” is due to cubic spline interpolation of the compliance.

Figure 12 shows how well Eq. (44) agrees with the “exact” (using numerical integration) Eq. (41) for p = 0.4 and 2, respectively. Furthermore, one would not be able to see easily in Fig. 12 the effect of using constant vs. varying shift factors.

Fig. 12

Master curves of normalized creep and effective compliances for CB = 0.05. Dashed line is creep compliance; solid and dotted lines are exact and approximate effective compliances, respectively

1.3 Power law nonlinearity

When the elastic strain energy density is a homogeneous function of degree N + 1 in the pseudo displacement gradient, then

$$W(c(\nabla {\mathbf{u}}^{R} )) = \left| c \right|^{N + 1} W(\nabla {\mathbf{u}}^{R} ),$$

(46)

where c is a scalar and N is a constant. Let us define

$$\nabla {\mathbf{u}}^{Rc} \equiv c\nabla {\mathbf{u}}^{R} {,}\quad W^{c} \equiv W(\nabla {\mathbf{u}}^{Rc} ),\quad {\text{sgn}} (c) \equiv {\text{sign}}\;{\text{of}}\;c.$$

(47)

Equation (46) becomes,

$$W^{c} = \left| c \right|^{N + 1} W$$

(48)

and we find,

$$\frac{{\partial W^{c} }}{{\partial \nabla {\mathbf{u}}^{Rc} }} = \frac{{\partial W^{c} }}{{\partial \nabla {\mathbf{u}}^{R} }}\frac{{\partial \nabla {\mathbf{u}}^{R} }}{{\partial \nabla {\mathbf{u}}^{Rc} }} = {\text{sgn}} (c)\left| c \right|^{N} \frac{\partial W}{{\partial \nabla {\mathbf{u}}^{R} }}$$

(49)

which yields the simple result,

$${{\varvec{\upsigma}}}^{c} = {\text{sgn(c)}}\left| c \right|^{N} {{\varvec{\upsigma}}}$$

(50)

which, in turn, implies that the pure shear stress–strain behavior has the form $\sigma = {\text{sgn}} (\varepsilon )\sigma_{0} \varepsilon^{N}$, where $\sigma_{0}$ is a constant with stress dimensions.

The homogeneity assumption excludes dependence on displacement gradients through Green’s strains unless the nonlinear component in the latter is negligible or dominant.

Stresses and displacements in a plane-strain or plane-stress singular-field, defined in polar coordinates $(r,\;\theta )$, are (Rice and Rosengren 1968)

$${{\varvec{\upsigma}}} = \sigma_{0} \left( {\frac{J}{{\sigma_{0} r}}} \right)^{{\frac{N}{N + 1}}} {\mathbf{g}}(\theta ,\;N),\quad {\mathbf{u}} = \left( {\frac{{r^{N} J}}{{\sigma_{0} }}} \right)^{{\frac{1}{N + 1}}} {\mathbf{h}}(\theta ,\;N)$$

(51)

in which ${\mathbf{g(}}\theta ,\;N{\mathbf{)}}$ and ${\mathbf{h}}(\theta ,\;N)$ are a dimensionless tensor and vector that depend on only $\theta$ and N; $\theta$ = 0 is the line of crack prolongation and $r = 0$ at P; they may be found by solving the equilibrium equations in terms of ${\mathbf{u}}$. The stresses and displacements are uniquely defined by J, N and $\sigma_{0}$, apart from rigid body displacements. Extension to viscoelasticity is easily performed using substitutions $J \to J_{v} \;{\text{and}}\;{\mathbf{u}} \to {\mathbf{u}}^{R}$.

Equation (51) was derived using small strain theory. However, with large deformations, Piola stresses and pseudo displacements obey the same r-behavior because the equilibrium equations and boundary traction conditions are identical to those of small strain theory, apart from a possibly nonsymmetrical stress tensor (Schapery 1984).

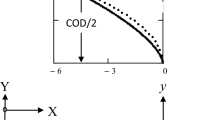
Inasmuch as the FZ serves to remove the singularity, the stresses deviate from Eq. (51)within some radius that is proportional to $\alpha$. Along the line of crack growth $X$(see Fig. 1) the normal stress $\sigma_{y}$ is assumed to be continuous at P; and therefore equal to $\sigma_{m}$, regardless of the value of $J_{v}$. This continuity at P is a reasonable assumption because it is true for linear theory (Schapery 1975a). Inasmuch as $\alpha$ and r are the only local dimensions, this stress must have the form

$$\sigma_{y} = \sigma_{m} f\left( {\frac{X - a}{\alpha }} \right),$$

(52)

where $X \ge a$, and $f(0) = 1$. It must also blend into the singular solution when ${\text{X}} - a \gg \alpha$. Suppose, for example, it is essentially equal to the singular solution at $X - a = 10\alpha$. Thus, from Eq. (51),

$$\sigma_{m} f(10) = \sigma_{0} \left( {\frac{{J_{v} }}{{\sigma_{0} 10\alpha }}} \right)^{{\frac{N}{N + 1}}}$$

(53)

which obviously means that $\alpha$ must be proportional to $J_{v}$ since the left side does not depend on $\alpha$. This proportionality was proven in Schapery (1986), but not as directly as it is here.

1.4 Singular-field COD

Using notation for a viscoelastic material, the pseudo COD at a fixed spatial point x within the singular-field follows from Eq. (51). It is useful to write it using normalized variables,

$$\overline{v}^{R} = k_{d} \overline{x}^{{\frac{N}{N + 1}}} \left( {\overline{J}_{v} } \right)^{{\frac{1}{N + 1}}} ,$$

(54)

where $k_{d}$ is a dimensionless constant. For a crack propagating at constant speed $\dot{a}$, the COD at $x = \dot{a}t$ follows from Eq. (45), assuming $x \gg \alpha$,

$$\overline{v} = \int\limits_{0}^{t} {\overline{C}(t - \tau )\frac{{\partial \overline{v}^{R} }}{\partial \tau }d\tau = } k_{d} \overline{C}\left( {\frac{x}{{s_{f} \dot{a}}}} \right)\overline{x}^{{\frac{N}{N + 1}}} \left( {\overline{J}_{v} } \right)^{{\frac{1}{N + 1}}} .$$

(55)

This result may be compared to the linear viscoelastic displacement in Eq. (9) after using Eq. (17),

$$\overline{v} = 4 \cdot \overline{C}\left( {\frac{{\overline{x}}}{{s_{f} \overline{\dot{a}}}}} \right)\sqrt {\overline{x}\overline{J}_{v} } .$$

(56)

It is helpful to replace $k_{d}$ with the constant $k_{D}$, which is unity for a linear material,

$$\overline{v} = 4k_{D} \overline{C}\left( {\frac{{\overline{x}}}{{s_{f} \overline{\dot{a}}}}} \right)\overline{x}^{{\frac{N}{N + 1}}} \left( {\overline{J}_{v} } \right)^{{\frac{1}{N + 1}}} .$$

(57)

1.5 Definition of $J_{v}$

A line integral version of the two-dimensional $J_{v}$ is

(58)

where ${\mathbf{T}}$ is the traction vector and S is the path of counterclockwise integration surrounding the crack tip, which starts on one crack face and ends on the opposite face, for a crack along the $x_{1}$ axis. Additionally, $n_{1}$ is the $x_{1}$ component of the outer unit normal to the path.