1 Introduction

Nowadays, digital data transmission (images, documents, audios) has become increasingly and more manageable and faster because of the popularization of high-definition photography technology and the considerable development of communication technologies. Thanks to these technologies, a large volume of digital data is stored and shared on open platforms such as LinkedIn. Along with the rapid development of internet technology, image data have been widely used in various social networks, Facebook, Twitter, and Flickr [38]. Digital images are the most frequently used, shared/communicated on these platforms and it has been used widely in all aspects of life and work. It has played an increasingly important role in modern society in recent years [5, 12, 21, 22, 40].

Furthermore, in the age of big data, many digital images, particularly color images, are widespread in people’s lives, making them significantly convenient for storage applications and information processing. However, many digital images can be stored, copied, and distributed without distortion, falsification, or arbitrary spread without the copyright owner’s permission, posing a severe threat to the healthy development of the information industry.

Moreover, digital images can be reprinted indiscriminately on the Internet, resulting in many piracy cases and infringement of copyright owners’ legitimate rights and interests of digital images.

Therefore, the problem with copyright protection of digital color images is also becoming increasingly severe at the same time and has become an urgent problem to be solved. Digital watermarking has emerged as an effective technology and a potential solution for digital images’ copyright protection and content authentication. Digital watermarking technology can effectively prevent illegal copying, tampering, and digital content distribution [57].

Digital watermarking, based on its purposes, is categorized into three types- Semi-fragile [32], Fragile [28], and Robust watermarking [1]. A semi-fragile watermarking is suited for content authentication, while a fragile watermark is detectable and can be altered or erased; thus, it is used for integrity authentication. On the other side, a robust watermark is detectable and not erasable, and it is most suitable for copyright protection.

In recent years, significant progress has been made in robust image watermarking technology, and consequently, many outstanding research achievements have been made. Robust image watermarking technology is the leading way to protect digital image content copyrights [30, 39]. The main challenges [23] in watermarking schemes are to provide robustness against modification, compression, scaling, filtering, etc. Nowadays, the most robust image watermarking algorithms can effectively resist common attacks. Still, the effect of watermark extraction becomes unideal after a watermarked image is subjected to geometric attacks such as rotation, scaling, and flipping. Currently, geometric invariant methods are effective in resisting geometric attacks [58]. Constructing stable geometric invariants to resist global geometric attacks and improving the robustness of watermarking algorithms has become a key issue in robust image watermarking. Many researchers have focused on moment invariants-based watermarking in recent years. Alghoniemy et al. [2] introduced the first robust watermarking algorithm using the geometric moment invariants (i.e., Hu moments) in the digital watermarking technology. Since then, numerous research efforts have designed and introduced robust watermarking schemes using image moments and invariants [6, 20, 25, 48, 56]. A few of the abovementioned works have performed well in resisting various attacks, especially in resisting geometric attacks. However, these invariant watermarking methods have been developed for grayscale images. Color images, as compared to grayscale images, contain more information and are thus more attractive. Therefore, color image watermarking becomes one of the active research topics. Color image watermarking has become more critical than the watermarking of grayscale images. Due to their image representation capacity and geometric invariance, several watermarking schemes for color images based on quaternion moments have been proposed. Many invariant robust watermarks for color images have been presented [26, 29, 41, 44, 50, 53, 54]. However, these methods have some limitations:

  1. (1)

    The inaccurate traditional method, zero-order approximation (ZOA), is used to compute the quaternion moments.

  2. (2)

    There are instabilities and numerical errors, especially at big moment orders.

  3. (3)

    Because of inaccurate quaternion moments, there is low robustness and poor imperceptibility.

  4. (4)

    Some methods have weak resistance to geometric distortion.

  5. (5)

    The basis orthogonal functions are restricted to integer orders.

  6. (6)

    It isn’t easy to obtain the favorable trade-off between robustness and imperceptibility.

These moment-based methods for image watermarking were limited to the use of orthogonal moments of integer orders. These limitations motivated Hosny et al. to introduce quaternion Legendre–Fourier moments (QLFMs) [7] and quaternion radial-substituted Chebyshev moments (QRSCMs) [8] based watermarking methods for color images. Recently, moment-based watermarking algorithms with different chaotic maps were presented to increase security [3, 27, 34, 45,46,47]. Ma et al. [5] proposed a robust watermarking of gray-level images by combining a chaotic map with invariant accurate polar harmonic Fourier moments. Recent studies [13,14,15,16,17] have proved that polynomials with fractional orders better represent functions than their corresponding integer orders. Yamni et al. [51] used fractional-order Charlier moments for reconstructing and watermarking gray-level images. Yamni et al. [52] proposed a zero-watermarking scheme based on a new set of quaternion moments called Quaternion Radial Fractional Charlier Moments (QRFrCMs) for copyright protection color medical images. Recently, Hosny et al. [11] proposed a novel robust watermarking scheme of color images based on new accurate fractional-order multi-channel fractional polar harmonic transforms and a chaotic map.

With the remarkable characteristics of the new fractional-order orthogonal moments [11, 13,14,15,16,17], in this paper, we propose a robust watermarking algorithm to embed multiple watermark images in the host color image simultaneously. Firstly, basis functions of three types of fractional new multi-channel orthogonal moments are derived. Then an accurate three types of fractional new multi-channel orthogonal moments, namely, fractional-order exponent moments (MFrEMs), fractional-order polar harmonic transforms (MFrPHTs), and fractional-order radial harmonic Fourier moments (MFrRHFMs), are constructed using an exact integration and Gaussian numerical integration methods to compute the angular and radial kernels, respectively. Finally, a color image robust watermarking algorithm based on the multiple fractional multi-channel orthogonal moments, MFrEMs, MFrPHTs, and MFrRHFMs, and chaotic sine map is proposed, which has good robustness to various attacks and has high security. Experimental results show that the proposed algorithm can effectively resist geometric attacks and common image processing attacks. Compared with other existing robust watermarking algorithms, the proposed algorithm performs better and outperforms the existing algorithms.

The main contributions of this paper are as follows:

  • We proposed accurate multiple multi-channel orthogonal moments, MFrEMs, MFrPHTs, and MFrRHFMs.

  • We utilized the accurate multiple multi-channel orthogonal moments to develop a multiple-robust watermarking approach for color images.

  • We used 1D Sine chaotic map for scrambling the multiple watermarks to improve the security of the proposed scheme.

  • Solving the contradiction between robustness and imperceptibility, which improves the robustness of the watermarking

  • Experimental results show that the proposed scheme has a better trade-off between robustness and imperceptibility and superior robustness to image processing and geometric and attacks.

  • The proposed algorithm has superiority in terms of imperceptibility and robustness.

The remainder of this paper is organized as follows. Section 2 presents the proposed fractional-order multi-channel orthogonal moments and their geometric invariance. Section 3 describes the detailed process of the proposed watermarking algorithm. In Section 4, the experimental results are discussed in detail. Section 5 concludes this paper.

2 Fractional-order orthogonal moments

2.1 The definition of MFrEMs for RGB color images

The Exponent moments of integer-order are circular orthogonal moments [18]:

$$ {M}_{pq}=\frac{1}{4\pi }{\int}_0^{2\pi }{\int}_0^1f\left(r,\theta \right){\left[{E}_{pq}\left(r,\theta \right)\right]}^{\ast } rdrd\theta \kern2.25em $$
(1)

where Mpq is the EMs of order p (| p | ≥ 0) with repetition q (| q | ≥ 0), \( \hat{\mathrm{i}}=\sqrt{-1} \); [∙]∗ the complex conjugate; and basis function Epq(r, θ) is

$$ {E}_{pq}\left(r,\theta \right)={T}_P^{EM}(r)\ {e}^{-\kern.3em \hat{i}\kern.6em q\theta}\kern1.75em $$
(2)

with

$$ {T}_P^{EM}(r)=\sqrt{\frac{2}{r}}\ {e}^{-\kern.3em \hat{i}\kern.6em 2\ \pi p\ r}\kern0.5em $$
(3)

The integer-order EMs are extended to FrEMs. The key to the construction of FrEMs is to construct the fractional-order radial polynomials; \( {T}_P^{FrEM}\left(r,\alpha \right) \), therefore, the extension of the orthogonal radial polynomial \( {T}_P^{EM}(r) \), is considered. The integer-order EMs are extended to FrEMs. Such extension mainly involves the modification of radial basis functions, \( {T}_P^{EM}(r) \). The radial basis functions of FrEMs are defined as [17]:

$$ {T}_P^{FrEM}\left(r,\alpha \right)={r}^{\alpha -1}\sqrt{\frac{2}{r^{\alpha }}}\kern.3em {e}^{-\kern.3em \hat{i}\kern.6em 2{\pi pr}^{\alpha }} $$
(4)

Then the basis function \( {H}_{pq}^{FrEM}\left(r,\theta \right) \) of the FrEMs is:

$$ {H}_{pq}^{FrEM}\left(r,\theta \right)={T}_P^{FrEM}\left(r,\alpha \right)\kern.3em {e}^{-\hat{i}\kern.5em q\theta} $$
(5)

with a real-values parameter α ϵ R+.

The basis functions of fractional-order, \( {H}_{pq}^{FrEM}\left(r,\theta \right) \), are orthogonal within the range of [0, 1] × [0, 2π]:

$$ {\int}_0^{2\pi }{\int}_0^1{H}_{pm}^{FrEM}\left(r,\theta \right){\left[{H}_{qn}^{FrEM}\left(r,\theta \right)\right]}^{\ast } rdrd\theta =\frac{4\pi }{\alpha }{\delta}_{pm}{\delta}_{qn}\kern3em $$
(6)

Assuming that gc(r, θ) is an RGB color image in polar coordinates, which is represented according to the multi-channel approach [9, 35], where the R−, G− & B−channels expressed using gR(r, θ), gG(r, θ) & gB(r, θ) respectively. The definition of the multi-channel orthogonal fractional-order exponent moments MFrEMs are:

$$ {FM}_{pq}^{FrEM}=\frac{\alpha }{4\pi }{\int}_0^{2\pi }{\int}_0^1{g}_c\left(r,\theta \right)\ {r}^{\alpha -1}\sqrt{\frac{2}{r^{\alpha }}}\ {e}^{-\kern.3em \hat{i}\kern.6em 2\pi p{r}^{\alpha }}{e}^{- iq\theta} rdrd\theta \kern3em $$
(7)

The image function, gC(r, θ), reconstructed as:

$$ {g}_C^{recons.}\left(r,\theta \right)=\sum \limits_{p=-\infty}^{\infty}\sum \limits_{q=-\infty}^{\infty }{FM}_{pq}^{FrEM}\left({g}_C\right){H}_{pq}^{FrEM}\left(r,\theta \right)\approx \sum \limits_{p=- pmax}^{pmax}\sum \limits_{q=- qmax}^{qmax}{FM}_{pq}^{FrEM}\left({g}_C\right){H}_{pq}^{FrEM}\left(r,\theta \right)\kern1.75em $$
(8)

The reconstructed color image \( {g}_C^{recons.}\left(r,\theta \right) \) obtained using \( {g}_R^{recons.}\left(r,\theta \right),\kern0.5em {g}_G^{recons.}\left(r,\theta \right), \) and \( {g}_B^{recons.}\left(r,\theta \right) \). The quality of the reconstructed image improved as pmax & qmax increased.

2.2 The definition of MFrPHTs for RGB color images

Polar Complex Exponential Transform (PCET) of integer-order are circular orthogonal moments [55]:

$$ {D}_{pq}=\frac{1}{\pi }{\int}_0^{2\pi }{\int}_0^1f\left(r,\theta \right){\left[{L}_{pq}\left(r,\theta \right)\right]}^{\ast } rdrd\theta $$
(9)

where Dpq is the PCET of order p (| p | ≥ 0) with repetition q (| q | ≥ 0), \( \hat{\mathrm{i}}=\sqrt{-1} \); [∙]∗ the complex conjugate; and basis function Lpq(r, θ) is

$$ {L}_{pq}\left(r,\theta \right)={T}_P^{PCET}(r)\ {e}^{-\hat{i}\kern.6em q\theta}, $$
(10)

With

$$ {T}_P^{PCET}(r)={e}^{-\hat{i}\kern.6em 2\pi p{r}^2} $$
(11)

The integer-order PCETs are extended to FrPCETs where the fractional-order radial polynomials; \( {T}_P^{FrPCET}\left(r,\alpha \right) \), is the extension of the orthogonal radial polynomial \( {T}_P^{PCET}(r) \). The radial basis functions of FrPCETs, \( {T}_P^{FrPCET}\left(r,\alpha \right) \) are defined as [13]:

$$ {T}_P^{FrPCET}\left(r,\alpha \right)=\sqrt{r^{\alpha -2}}{e}^{-\hat{i}\kern.4em 2\pi p{r}^{\alpha }} $$
(12)

Then the basis function \( {H}_{pq}^{FrPCET}\left(r,\theta \right) \) of the FrEMs is:

$$ {H}_{pq}^{FrPCET}\left(r,\theta \right)={T}_P^{FrPCET}\left(r,\alpha \right)\kern.3em {e}^{-\hat{i}\kern.4em q\theta} $$
(13)

The basis functions of fractional-order, \( {H}_{pq}^{FrPCET}\left(r,\theta \right) \), are orthogonal within the range of [0, 1] × [0, 2π]:

$$ {\int}_0^{2\pi }{\int}_0^1{H}_{pm}^{FrPCET}\left(r,\theta \right){\left[{H}_{qn}^{FrPCET}\left(r,\theta \right)\right]}^{\ast } rdrd\theta =\frac{2\pi }{\alpha }{\delta}_{pm}{\delta}_{qn} $$
(14)

The MFrPCET of gc(r, θ) are:

$$ {FM}_{pq}^{FrPCET}=\frac{\alpha }{2\pi }{\int}_0^{2\pi }{\int}_0^1{g}_c\left(r,\theta \right)\kern1em \sqrt{r^{\alpha -2}}{e}^{-\kern.3em \hat{i}\kern.6em 2\pi p{r}^{\alpha }}{e}^{- iq\theta} rdrd\theta $$
(15)

The image function, gC(r, θ), reconstructed as:

$$ {g}_C^{recons.}\left(r,\theta \right)=\sum \limits_{p=-\infty}^{\infty}\sum \limits_{q=-\infty}^{\infty }{FM}_{pq}^{FrPCET}\left({g}_C\right){H}_{pq}^{FrPCET}\left(r,\theta \right)\approx \sum \limits_{p=- pmax}^{pmax}\sum \limits_{q=- qmax}^{qmax}{FM}_{pq}^{FrPCET}\left({g}_C\right){H}_{pq}^{FrPCET}\left(r,\theta \right) $$
(16)

The reconstructed color image \( {g}_C^{recons.}\left(r,\theta \right) \) obtained using \( {g}_R^{recons.}\left(r,\theta \right),\kern0.5em {g}_G^{recons.}\left(r,\theta \right), \) and \( {g}_B^{recons.}\left(r,\theta \right) \). The quality of the reconstructed image improved as pmax & qmax increased.

2.3 The definition of MFrRHFMs for RGB color images

Radial harmonic Fourier moments (RHFMs) of integer-order are circular orthogonal moments is as follows [31]:

$$ {F}_{pq}=\frac{1}{2\pi }{\int}_0^{2\pi }{\int}_0^1f\left(r,\theta \right){\left[{G}_{pq}\left(r,\theta \right)\right]}^{\ast } rdrd\theta $$
(17)

where Fpq is the RHFM of order p (p ≥ 0) with repetition q (| q | ≥0), \( \hat{\mathrm{i}}=\sqrt{-1} \); [∙]∗ the complex conjugate; and basis function Gpq(r, θ) is

$$ {G}_{pq}\left(r,\theta \right)={T}_P^{RHFM}(r)\ {e}^{-\hat{i}\kern.6em q\theta}, $$
(18)

With

$$ {T}_P^{RHFM}(r)=\left\{\begin{array}{c}\ \sqrt{\frac{1}{r}},\kern9.25em p=0\\ {}\ \sqrt{\frac{2}{r}}\mathit{\cos}\left(\pi pr\right),\kern3.25em p\ is\ even\\ {}\sqrt{\frac{2}{r}}\mathit{\sin}\left(\pi \left(p+1\right)r\right),\kern1.5em p\ is\ odd\end{array}\right.\kern1.25em $$
(19)

The integer-order RHFMs are extended to FrRHFMs where the fractional-order radial polynomials; \( {T}_P^{FrRHFM}\left(r,\alpha \right) \), is the extension of the orthogonal radial polynomial \( {T}_P^{RHFM}(r) \). The radial basis functions of FrRHFMs, \( {T}_P^{FrRHFM}\left(r,\alpha \right) \) are defined as [14]:

$$ {T}_P^{FrRHFM}\left(r,\alpha \right)=\Big\{{\displaystyle \begin{array}{c}\sqrt{\alpha }{r}^{\alpha -1}\sqrt{\frac{1}{r^{\alpha }}},\kern9.25em p=0\\ {}\sqrt{\alpha }{r}^{\alpha -1}\sqrt{\frac{2}{r^{\alpha }}}\cos \left(\pi p{r}^{\alpha}\right),\kern3.25em p\kern.3em is\kern.3em even\\ {}\sqrt{\alpha }{r}^{\alpha -1}\sqrt{\frac{2}{r^{\alpha }}}\sin \left(\pi \left(p+1\right){r}^{\alpha}\right),\kern1.5em p\kern.3em is\kern.3em odd\end{array}}\operatorname{} $$
(20)

Then the basis function \( {H}_{pq}^{FrRHFM}\left(r,\theta \right) \) of the FrRHFMs is:

$$ {H}_{pq}^{FrRHFM}\left(r,\theta \right)={T}_P^{FrRHFM}\left(r,\alpha \right)\kern.3em {e}^{-\hat{i}\kern.4em q\theta} $$
(21)

The basis functions of fractional-order, \( {H}_{pq}^{FrRHFM}\left(r,\theta \right) \), are orthogonal within the range of [0, 1] × [0, 2π]:

$$ {\int}_0^{2\pi }{\int}_0^1{H}_{pm}^{FrRHFM}\left(r,\theta \right){\left[{H}_{qn}^{FrRHFM}\left(r,\theta \right)\right]}^{\ast } rdrd\theta =2\pi {\delta}_{pm}{\delta}_{qn} $$
(22)

The multi-channel orthogonal fractional-order radial harmonic Fourier moments are:

$$ {FM}_{pq}^{FrRHFM}=\frac{1}{2\pi }{\int}_0^{2\pi }{\int}_0^1{g}_c\left(r,\theta \right)\kern0.5em {T}_P^{FrRHFM}\left(r,\alpha \right){e}^{- iq\theta} rdrd\theta $$
(23)

The image function, gC(r, θ), reconstructed as:

$$ {g}_C^{recons.}\left(r,\theta \right)=\sum \limits_{p=0}^{\infty}\sum \limits_{q=-\infty}^{\infty }{FM}_{pq}^{FrRHFM}\left({g}_C\right){H}_{pq}^{FrRHFM}\left(r,\theta \right)\approx \sum \limits_{p=0}^{pmax}\sum \limits_{q=- qmax}^{qmax}{FM}_{pq}^{FrRHFM}\left({g}_C\right){H}_{pq}^{FrRHFM}\left(r,\theta \right) $$
(24)

The reconstructed color image \( {g}_C^{recons.}\left(r,\theta \right) \) obtained using \( {g}_R^{recons.}\left(r,\theta \right),\kern0.5em {g}_G^{recons.}\left(r,\theta \right), \) and \( {g}_B^{recons.}\left(r,\theta \right) \). The quality of the reconstructed image improved as pmax & qmax increased.

2.4 Rotation, scale, and translation (RST) invariants

2.4.1 Rotation invariance

For the original color image, gC(r, θ), the rotated image with an angle β is while \( {g}_C^{\beta}\left(r,\theta \right) \), where:

$$ {g}_C^{\beta}\left(r,\theta \right)={g}_C\left(r,\theta -\beta \right) $$
(25)

The MFrEMs of \( {g}_C^{\beta}\left(r,\theta \right) \) is [17]:

$$ {FM}_{pq}^{FrEM}\left({g}_C^{\beta}\right)=\frac{\alpha }{4\pi }{\int}_0^{2\pi }{\int}_0^1{g}_C^{\beta}\left(r,\theta \right){\left[{H}_{pq}^{FrEM}\left(r,\theta \right)\right]}^{\ast } rdrd\theta \kern0.5em =\frac{\alpha }{4\pi }{\int}_0^{2\pi }{\int}_0^1{g}_C\left(r,\theta -\beta \right){T}_P^{FrEM}\left(\alpha, r\right){e}^{- iq\theta} rdrd\theta =\frac{\alpha }{4\pi }{\int}_0^{2\pi }{\int}_0^1{g}_C\left(r,\theta \right){T}_P^{FrEM}\left(\alpha, r\right){e}^{- iq\left(\theta +\beta \right)}\kern.3em rdrd\theta =\frac{\alpha }{4\pi }{\int}_0^{2\pi }{\int}_0^1{g}_C\left(r,\theta \right){T}_P^{FrEM}\left(\alpha, r\right){e}^{- iq\theta}{e}^{- iq\beta} rdrd\theta ={FM}_{pq}^{FrEM}\left({g}_C\right){e}^{- iq\beta} $$
(26)

Simply, we could write:

$$ {FM}_{pq}^{FrEM}\left({g}_C^{\beta}\right)={e}^{- iq\beta}{FM}_{pq}^{FrEM}\left({\mathrm{g}}_C\right)\kern0.5em ,\kern1em C\in \left\{R,G,B\right\} $$
(27)

where \( {FM}_{pq}^{FrEM}\left({g}_C\right) \) and \( {FM}_{pq}^{FrEM}\left({g}_C^{\beta}\right) \) are the MFrEMs of, gC(r, θ)and \( {g}_C^{\beta}\left(r,\theta \right) \), respectively.

Since, |e−iqβ| = 1, for any value of q and β; therefore:

$$ \mid {FM}_{pq}^{FrEM}\left({g}_C^{\beta}\right)\mid =\mid {e}^{- iq\beta}{FM}_{pq}^{FrEM}\left({g}_C\right)\mid $$

Then:

$$ \mid {FM}_{pq}^{FrEM}\left({g}_C^{\beta}\right)\mid =\mid {FM}_{pq}^{FrEM}\left({g}_C\right)\mid $$
(28)

Equation (28) proves the MFrEMs are rotation invariant.

Similarly, the MFrPCET and MFrRHFM moments of the two images \( {g}_C^{\beta}\left(r,\theta \right) \) and gC(r, θ), are rotation invariant.

2.4.2 Scaling invariance

The scaling invariance of the multi-channels orthogonal circular moments is valid if these circular moments are computed in polar coordinates [43]. In the proposed method, the MFrEMs, the MFrPCETs, and MFrRHFMs are defined and calculated on the unit circle where input RGB color images are mapped. (See Fig. 1).

Fig. 1
figure 1

a Cartesian pixels, b Polar pixels

Full size image

2.4.3 Translation invariance

Invariance to translation means shifting the coordinate origin to coincides with image centroid (xc, yc) [37] where xc & yc defined using geometric moments as:

$$ {\displaystyle \begin{array}{c}{x}_c=\left({m}_{10}\left({g}_R\right)+{m}_{10}\left({g}_G\right)+{m}_{10}\left({g}_B\right)\right)/{m}_{00},\\ {}{y}_c=\left({m}_{01}\left({g}_R\right)+{m}_{01}\left({g}_G\right)+{m}_{01}\left({g}_B\right)\right)/{m}_{00}\\ {}{m}_{00}={m}_{00}\left({g}_R\right)+{m}_{00}\left({g}_G\right)+{m}_{00}\left({g}_B\right).\end{array}} $$
(29)

The central MFrEMs are:

$$ {\overset{\hbox{--} \hbox{--} \hbox{--} \hbox{--} \hbox{--} }{FM}}_{pq}^{FrEM}=\frac{\alpha }{4\pi }{\int}_0^{2\pi }{\int}_0^1{g}_C\left(\overset{\hbox{--} }{r},\overset{\hbox{--} }{\theta}\right){\left[{H}_{pq}^{FrEM}\left(\overset{\hbox{--} }{r},\overset{\hbox{--} }{\theta}\right)\right]}^{\ast}\overset{\hbox{--} }{r}d\overset{\hbox{--} }{r}d\overset{\hbox{--} }{\theta }=\frac{\alpha }{4\pi }{\int}_0^{2\pi }{\int}_0^1{g}_C\left(\overset{\hbox{--} }{r},\overset{\hbox{--} }{\theta}\right){T}_P^{FrEM}\left(\alpha, \overset{\hbox{--} }{r}\right){e}^{\hbox{--} iq\overset{\hbox{--} }{\theta }}\overset{\hbox{--} }{r}d\overset{\hbox{--} }{r}d\overset{\hbox{--} }{\theta } $$
(30)

Similarly, the central MFrPCETs and MFrRHFMs are invariant to translation and defined as follows:

$$ {\overset{\hbox{--} \hbox{--} \hbox{--} \hbox{--} \hbox{--} }{FM}}_{pq}^{FrPCET}=\frac{\alpha }{2\pi }{\int}_0^{2\pi }{\int}_0^1{g}_C\left(\overset{\hbox{--} }{r},\overset{\hbox{--} }{\theta}\right){\left[{H}_{pq}^{FrPCET}\left(\overset{\hbox{--} }{r},\overset{\hbox{--} }{\theta}\right)\right]}^{\ast}\overset{\hbox{--} }{r}d\overset{\hbox{--} }{r}d\overset{\hbox{--} }{\theta }=\frac{\alpha }{2\pi }{\int}_0^{2\pi }{\int}_0^1{g}_C\left(\overset{\hbox{--} }{r},\overset{\hbox{--} }{\theta}\right){T}_P^{FrPCET}\left(\alpha, \overset{\hbox{--} }{r}\right){e}^{\hbox{--} iq\overset{\hbox{--} }{\theta }}\overset{\hbox{--} }{r}d\overset{\hbox{--} }{r}d\overset{\hbox{--} }{\theta } $$
(31)
$$ {\overset{\hbox{--} \hbox{--} \hbox{--} \hbox{--} \hbox{--} }{FM}}_{pq}^{FrRHFM}=\frac{1}{2\pi }{\int}_0^{2\pi }{\int}_0^1{g}_C\left(\overset{\hbox{--} }{r},\overset{\hbox{--} }{\theta}\right){\left[{H}_{pq}^{FrRHFM}\left(\overset{\hbox{--} }{r},\overset{\hbox{--} }{\theta}\right)\right]}^{\ast}\overset{\hbox{--} }{r}d\overset{\hbox{--} }{r}d\overset{\hbox{--} }{\theta }=\frac{1}{2\pi }{\int}_0^{2\pi }{\int}_0^1{g}_C\left(\overset{\hbox{--} }{r},\overset{\hbox{--} }{\theta}\right){T}_P^{FrRHFM}\left(\alpha, \overset{\hbox{--} }{r}\right){e}^{\hbox{--} iq\overset{\hbox{--} }{\theta }}\overset{\hbox{--} }{r}d\overset{\hbox{--} }{r}d\overset{\hbox{--} }{\theta } $$
(32)

2.5 Accurate computation of fractional-order orthogonal moments

The proposed watermarking algorithm’s cornerstone is to compute accurate fractional-order orthogonal moments, MFrEMs, MFrPCETs, and MFrRHFMs using the highly accurate kernel-based approach [10], where the color images interpolated [49]. The MFrEMs computed as follows:

$$ {FM}_{pq}^{FrEM}=\frac{\alpha }{4\pi }\ \sum \limits_i\sum \limits_j{K}_{pq}^{FrEM}\left({r}_i,{\theta}_{ij}\right)\kern0.5em {\hat{g}}_C\left({r}_i,{\theta}_{i,j}\right)\kern1em $$
(33)

With:

$$ {K}_{pq}^{FrEM}\left({r}_i,{\theta}_{ij}\right)={I}_p^{FrEM}\left({r}_i\right)\ {J}_q\left({\theta}_{ij}\right) $$
(34)

The angular and radial kernels are defined as:

$$ {J}_q\left({\theta}_{ij}\right)=\underset{V_{ij}}{\overset{V_{i,j+1}}{\int }}{e}^{-\hat{i}\kern.5em q\ \theta } d\theta $$
(35)
$$ {I}_p^{FrEM}\left({r}_i\right)=\underset{U_i}{\overset{U_{i+1}}{\int }}{T}_p^{FrEM}\left(\alpha, r\right)\kern.3em rdr=\underset{U_i}{\overset{U_{i+1}}{\int }}{R}^{FrEM}(r) dr\kern1.25em $$
(36)

With:

$$ {R}^{FrEM}(r)={T}_p^{FrEM}\left(\alpha, r\right)\kern.3em r $$
(37)

The limits, Vi, j + 1, Vi, j, Ui + 1 & Ui are:

$$ {V}_{i,j+1}={\theta}_{i,j}+\Delta {\theta}_{i,j}/2\kern0.5em ;{V}_{i,j}={\theta}_{i,j}-\Delta {\theta}_{i,j}/2 $$
(38)
$$ {U}_{i+1}={R}_i+\Delta {R}_i/2\kern0.5em ;\kern0.5em {U}_i={R}_i-\Delta {R}_i/2 $$
(39)

Based on the principles of Calculus, Jq(θij) computed in the exact form:

$$ {J}_q\left({\theta}_{i,j}\right)=\left\{\begin{array}{c}\frac{\hat{i}}{q}\left({e}^{-\hat{i}\ q\ {V}_{i,j+1}}-{e}^{-\hat{i}\ q\ {V}_{i,j}}\right),\kern2.75em q\ne 0\ \\ {}{V}_{i,j+1}-{V}_{i,j}\kern0.5em ,\kern7.75em q=0\ \end{array}\right. $$
(40)

Unlike Jq(θij), calculating \( {I}_p^{FrEM}\left({r}_i\right); \) requires numerical integration. Accurate Gaussian integration [4] is our choice. The \( {I}_p^{FrEM}\left({r}_i\right) \) computed using as:

$$ {I}_p^{FrEM}\left({r}_i\right)=\underset{U_i}{\overset{U_{i+1}}{\int }}{R}^{FrEM}\left(\mathrm{r}\right) dr\approx \frac{\left({U}_{i+1}-{U}_i\right)}{2}\sum \limits_{l=0}^{c-1}{w}_l{R}^{FrEM}\left(\frac{U_{i+1}+{U}_i}{2}+\frac{U_{i+1}-{U}_i}{2}{t}_l\right)\kern0.5em $$
(41)

The symbols, wl & tl, refer to weights and the location l = 0, 1, 2, …. . c − 1 of sampling points; c is the order of the numerical integration. The values of wl are fixed and \( \sum \limits_{l=0}^{c-1}{w}_l=2 \). The values of tl can be expressed in terms of the limits of the integration Ui and Ui + 1.

Similar computational steps are derived to compute the MFrPCETs and MFrRHFMs of order p and repetition q as follow:

$$ {FM}_{pq}^{FrPCET}=\frac{\alpha }{2\uppi}\ \sum \limits_i\sum \limits_j{K}_{pq}^{FrPCET}\left({r}_i,{\theta}_{ij}\right)\kern0.5em {\hat{g}}_C\left({r}_i,{\theta}_{i,j}\right)\kern1em $$
(42)
$$ {FM}_{pq}^{FrRHFM}=\frac{1}{2\pi }\ \sum \limits_i\sum \limits_j{K}_{pq}^{FrRHFM}\left({r}_i,{\theta}_{ij}\right)\kern0.5em {\hat{g}}_C\left({r}_i,{\theta}_{i,j}\right)\kern1em $$
(43)

With:

$$ {K}_{pq}^{FrPCET}\left({r}_i,{\theta}_{ij}\right)={I}_p^{FrPCET}\left({r}_i\right)\ {J}_q\left({\theta}_{ij}\right) $$
(44)
$$ {K}_{pq}^{FrRHFM}\left({r}_i,{\theta}_{ij}\right)={I}_p^{FrRHFM}\left({r}_i\right)\ {J}_q\left({\theta}_{ij}\right) $$
(45)

Where:

$$ {I}_p^{FrPCET}\left({r}_i\right)=\underset{U_i}{\overset{U_{i+1}}{\int }}{T}_p^{FrPCET}\left(\alpha, r\right)\kern.3em rdr=\underset{U_i}{\overset{U_{i+1}}{\int }}{R}^{FrPCET}(r) dr\kern1.25em $$
(46)
$$ {I}_p^{FrRHFM}\left({r}_i\right)=\underset{U_i}{\overset{U_{i+1}}{\int }}{T}_p^{FrRHFM}\left(\alpha, r\right)\kern.3em rdr=\underset{U_i}{\overset{U_{i+1}}{\int }}{R}^{FrRHFM}(r) dr\kern1.25em $$
(47)

The definite integral in eqs. (46) and (47) is evaluated by using the eq. (41) as follows:

$$ {I}_p^{FrPCET}\left({r}_i\right)=\underset{U_i}{\overset{U_{i+1}}{\int }}{R}^{FrPCET}(r) dr\approx \frac{\left({U}_{i+1}-{U}_i\right)}{2}\sum \limits_{l=0}^{c-1}{w}_l{R}^{FrPCET}\left(\frac{U_{i+1}+{U}_i}{2}+\frac{U_{i+1}-{U}_i}{2}{t}_l\right)\kern1.25em $$
(48)
$$ {I}_p^{FrRHFM}\left({r}_i\right)=\underset{U_i}{\overset{U_{i+1}}{\int }}{R}^{FrRHFM}(r) dr\approx \frac{\left({U}_{i+1}-{U}_i\right)}{2}\sum \limits_{l=0}^{c-1}{w}_l{R}^{FrRHFM}\left(\frac{U_{i+1}+{U}_i}{2}+\frac{U_{i+1}-{U}_i}{2}{t}_l\right)\kern0.75em $$
(49)

3 Proposed watermarking scheme

The proposed watermarking algorithm will be described in two main stages in this section. The first stage describes the procedure of multiple watermark embedding, which will be described in detail. The second stage describes the procedure of multiple watermark extraction, which will be explained.

For the color image, gc, and multiple binary watermark images, the MFrEMs, MFrPCETs, and MFrRHFMs of the original image, respectively, are combined with a 1D Sine map to design new color images watermarking algorithm. This algorithm selected MFrEMs, MFrPCETs, and MFrRHFMs magnitudes, which are TSR invariants used to construct multiple robust watermarks. In contrast, the sine map is used in scrambling the multiple watermark images. Through the following subsection, we consider the host color image, gc, of size N × N while the multiple binary watermark images, W1, W2, and W3 of size P × Q where W1 = {w1(i, j) ∈ {0, 1}, 0 ≤ i < P, 0 ≤ j < Q}, W2 = {w2(i, j) ∈ {0, 1}, 0 ≤ i < P, 0 ≤ j < Q} and W3 = {w3(i, j) ∈ {0, 1}, 0 ≤ i < P, 0 ≤ j < Q}.

3.1 Multiple watermark embedding

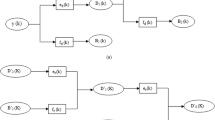
The process of multiple embedding is achieved through three steps. First, for the original image, the MFrEMs, MFrPCETs, and MFrRHFMs are computed, respectively. Second, the most significant TSR MFrEMs, MFrPCETs, and MFrRHFMs invariant are selected. Third, the multiple watermarks are embedded in the Red, Green, and Blue channels, gR, gG, and gB of the original image by using the selected moment invariants, MFrEMs, MFrPCETs, and MFrRHFMs. Figure 2 shows an illustrated flowchart of the embedding process, which can be summarized as the following steps:

Fig. 2
figure 2

Watermark embedding framework

Full size image
  1. 1)

    The multiple watermark images, W1, W2, and W3, converted to a one-dimensional vector, OW1 = {ow1(i) : 0 ≤ i < P × Q}, OW2 = {ow2(i) : 0 ≤ i < P × Q} and OW3 = {ow3(i) : 0 ≤ i < P × Q}, respectively. Then a chaotic sequence C of the length P × Q generated by using the Sine chaotic map [19] with the initial value of x0. This map is defined as follows:

$$ {x}_{n+1}= rsin\left(\pi {x}_n\right) $$
(50)

The variable r is the control parameter of the Sine map, r ∈ [0, 1]. The chaotic sequence C = {c(i) : 0 ≤ i < P × Q} can be obtained using key K1 as the initial value of the Sine chaotic mapping, where the initial value of the Sine chaotic mapping multiple watermark sequence scrambled using Sine chaotic mapping [11] and a binarized chaotic sequence \( \hat{C}=\left\{\hat{c}(i),0\le i<P\times Q\right\} \) is obtained by binarizing C as follows:

$$ \hat{C}(i)=\left\{\begin{array}{c}1,\kern1.5em if\kern0.5em \hat{c}(i)\ge T\kern2.75em \\ {}0,\kern1.25em if\kern0.75em \hat{c}(i)<T\kern2.25em \end{array}\right.,\left(0\le i<P\times Q\right) $$
(51)

Where T refers to the threshold, which is defined as the mean of C. Then, XOR operation is performed on OW1, OW2 and OW3 respectively with the binarized chaotic sequence \( \hat{\mathrm{C}} \) to obtain a chaotic scrambled multiple watermark sequence, \( {\hat{W}}_1 \), \( {\hat{\mathrm{W}}}_2 \) and \( {\hat{W}}_3 \):

$$ {\displaystyle \begin{array}{c}{\hat{W}}_1={OW}_1\oplus \hat{\kern.3em C},\\ {}{\hat{W}}_2={OW}_2\oplus \hat{\kern.3em C},\\ {}{\hat{W}}_3={OW}_3\oplus \hat{\kern.3em C}.\end{array}} $$
(52)
  1. 2)

    For each Red, Green, and Blue channel of the host image, the MFrEMs, MFrPCETs, and MFrRHFMs are computed according to a maximum moment order equals to P × Q [6].

  2. 3)

    The magnitude values of MFrEMs, MFrPCETs, and MFrRHFMs are computed to assure the invariances. The MFrEMs, MFrPCETs, and MFrRHFMs with positive repetitions, q = 4m, m ∈ Z, are removed. The selected MFrEMs, MFrPCETs, and MFrRHFMs, SFrEM, SFrPCET, SFrRHFM, respectively are:

$$ {\displaystyle \begin{array}{c}{S}^{FrEM}=\left\{\left|{FM}_{pq}^{FrEM}\right|,q\ne 4m,m\in Z\right\},\\ {}{S}^{FrPCET}=\left\{\left|{FM}_{pq}^{FrPCET}\right|,q\ne 4m,m\in Z\right\},\\ {}{S}^{FrRHFM}=\left\{\left|{FM}_{pq}^{FrRHFM}\right|,q\ne 4m,m\in Z\right\}.\end{array}} $$
(53)

A P × Q number of MFrEMs, MFrPCETs, and MFrRHFMs coefficients, are randomly selected from the accurate coefficients MFrEMs, MFrPCETs, and MFrRHFMs set SFrEM, SFrPCET, SFrRHFM and their amplitudes are respectively MFrEM, MFrPCET and MFrRHFM.

  1. 4)

    The multiple watermark bits embedded in the Red, Green, and Blue channels of the host color image using modulate selected MFrEMs, MFrPCETs, and MFrRHFMs, using the dither modulation function [48].

$$ {\displaystyle \begin{array}{c}{m_{FrEM}}^{\prime}\left(\mathrm{i}\right)=\left[\frac{m_{FrEM}\left(\mathrm{i}\right)-{\mathrm{d}}_{\mathrm{i}}\left({\hat{\mathrm{w}}}_1\left(\mathrm{i}\right)\right)}{\Delta }\right]\ast \Delta +{\mathrm{d}}_{\mathrm{i}}\left({\hat{\mathrm{w}}}_1\left(\mathrm{i}\right)\right),\kern0.5em 0\le \mathrm{i}<\mathrm{P}\times \mathrm{Q}\\ {}{m_{FrPCET}}^{\prime}\left(\mathrm{i}\right)=\left[\frac{m_{FrPCET}\left(\mathrm{i}\right)-{\mathrm{d}}_{\mathrm{i}}\left({\hat{\mathrm{w}}}_2\left(\mathrm{i}\right)\right)}{\Delta }\right]\ast \Delta +{\mathrm{d}}_{\mathrm{i}}\left({\hat{\mathrm{w}}}_2\left(\mathrm{i}\right)\right),\\ {}\begin{array}{c}{m_{FrRHFM}}^{\prime}\left(\mathrm{i}\right)=\left[\frac{m_{FrRHFM}\left(\mathrm{i}\right)-{\mathrm{d}}_{\mathrm{i}}\left({\hat{\mathrm{w}}}_3\left(\mathrm{i}\right)\right)}{\Delta }\right]\ast \Delta +{\mathrm{d}}_{\mathrm{i}}\left({\hat{\mathrm{w}}}_3\left(\mathrm{i}\right)\right)\\ {}{d}_i(1)=\frac{\Delta }{2}+{d}_i(0),\kern0.5em {d}_i(0)\in \left[0,1\right].\end{array}\end{array}} $$
(54)

where mFrEM(i), mFrPCET(i) and mFrRHFM(i) refers to a vector that contains these magnitude values of selected MFrEMs, MFrPCETs, and MFrRHFMs, respectively. The vector length is equal to the number of multiple watermark bits; mFrEM′(i), mFrPCET′(i) and mFrRHFM′(i) refer to the modulated one; the [·] is the rounding operator; Δ refer to watermark quantization step; di(.) refers to the dither function where the elements of the dither vector are uniformly distributed over [0, ∆] and randomly generated.

  1. 5)

    The inverse operation of MFrEMs, MFrPCETs, and MFrRHFMs applied to obtain the watermarked color image, \( {g}_c^w\left(r,\theta \right) \), as:

$$ {g}_c^w\left(r,\theta \right)={g}_c\left(r,\theta \right)-{g}_c^M\left(r,\theta \right)+{g}_c^{M^{\prime }}\left(r,\theta \right) $$
(55)

where gc(r, θ) denotes the original image, \( {g}_c^M\left(r,\theta \right) \) and \( {g}_c^{M^{\prime }}\left(r,\theta \right). \) The image components contributed by using unmodified and modified MFrEMs, MFrPCETs, and MFrRHFMs.

Based on the above steps, the pseudo-code of the embedding of the multiple watermarks can be described as follows.

figure a

3.2 Multiple watermark extraction

The process of multiple watermark extraction is an inverse process of the embedding one, where the multiple binary watermarks are extracted. First, the MFrEMs, MFrPCETs, and MFrRHFMs were computed for the watermarked image Red, Green, and Blue channels using the same accurate method. Second, a similar selection process was applied. Third, the same secret keys are employed. Finally, the multiple binary watermarks were extracted. Figure 3 shows a flowchart for the extraction process, which the detailed process of watermark extraction is described below.

Fig. 3
figure 3

Watermark extraction framework

Full size image
  1. 1)

    The MFrEMs, MFrPCETs, and MFrRHFMs of this attacked watermarked image were calculated using the same accurate method as described in sec. 2.5.

  1. 2)

    The P × Q feature vector of MFrEMs, MFrPCETs, and MFrRHFMs,\( {M}_{FrEM}^{\ast }=\left\{{m}_{FrEM}^{\ast }(i),\kern0.5em 0\le i<P\times Q\right\} \), \( {M}_{FrPCET}^{\ast }=\left\{{m}_{FrPCET}^{\ast }(i),\kern0.5em 0\le i<P\times Q\right\} \) and \( {M}_{FrRHFM}^{\ast }=\left\{{m}_{FrRHFM}^{\ast }(i),\kern0.5em 0\le i<P\times Q\right\} \) respectively are selected by using the same secret key, K2, which is a symmetric key for the embedding and extraction processes.

  1. 3)

    The selected MFrEMs, MFrPCETs, and MFrRHFMs magnitudes were extracted using the same quantization process as:

$$ {\displaystyle \begin{array}{l}{\left|{\mathrm{m}}_{FrEM}^{\ast}\left(\mathrm{i}\right)\right|}_{\mathrm{j}}=\left[\frac{\left|{\mathrm{m}}_{FrEM}^{\ast}\right|-{\mathrm{d}}_{\mathrm{i}}\left(\mathrm{j}\right)}{\Delta }\right]\ast \Delta +{\mathrm{d}}_{\mathrm{i}}\left(\mathrm{j}\right),\kern0.75em \mathrm{j}=0,1\\ {}{\left|{\mathrm{m}}_{FrPCET}^{\ast}\left(\mathrm{i}\right)\right|}_{\mathrm{j}}=\left[\frac{\left|{\mathrm{m}}_{FrPCET}^{\ast}\right|-{\mathrm{d}}_{\mathrm{i}}\left(\mathrm{j}\right)}{\Delta }\right]\ast \Delta +{\mathrm{d}}_{\mathrm{i}}\left(\mathrm{j}\right),\kern0.75em \mathrm{j}=0,1\\ {}{\left|{\mathrm{m}}_{FrRHFM}^{\ast}\left(\mathrm{i}\right)\right|}_{\mathrm{j}}=\left[\frac{\left|{\mathrm{m}}_{FrRHFM}^{\ast}\right|-{\mathrm{d}}_{\mathrm{i}}\left(\mathrm{j}\right)}{\Delta }\right]\ast \Delta +{\mathrm{d}}_{\mathrm{i}}\left(\mathrm{j}\right),\kern0.75em \mathrm{j}=0,1\end{array}} $$
(56)

A bit \( {\hat{\mathrm{w}}}_1^{\ast}\left(\mathrm{i}\right) \), \( {\hat{\mathrm{w}}}_2^{\ast}\left(\mathrm{i}\right) \) and \( {\hat{\mathrm{w}}}_3^{\ast}\left(\mathrm{i}\right) \) are either 0 or 1 based on the value \( {\mathrm{m}}_{FrEM}^{\ast}\left(\mathrm{i}\right) \), \( {\mathrm{m}}_{FrPCET}^{\ast}\left(\mathrm{i}\right) \) and \( {\mathrm{m}}_{FrRHFM}^{\ast}\left(\mathrm{i}\right) \) where:

$$ {\displaystyle \begin{array}{l}\underset{\kern3em \mathrm{j}\in \left[0,1\right]}{{\hat{\mathrm{w}}}_1^{\ast}\left(\mathrm{i}\right)=\mathrm{argmin}}{\left({\left|{\mathrm{m}}_{FrEM}^{\ast}\left(\mathrm{i}\right)\right|}_{\mathrm{j}}-|{\mathrm{m}}_{FrEM}^{\ast}\left(\mathrm{i}\right)|\right)}^2,\\ {}\underset{\kern3em \mathrm{j}\in \left[0,1\right]}{{\hat{\mathrm{w}}}_2^{\ast}\left(\mathrm{i}\right)=\mathrm{argmin}}{\left({\left|{\mathrm{m}}_{FrPCET}^{\ast}\left(\mathrm{i}\right)\right|}_{\mathrm{j}}-|{\mathrm{m}}_{FrPCET}^{\ast}\left(\mathrm{i}\right)|\right)}^2,\\ {}\underset{\kern3em \mathrm{j}\in \left[0,1\right]}{{\hat{\mathrm{w}}}_3^{\ast}\left(\mathrm{i}\right)=\mathrm{argmin}}{\left({\left|{\mathrm{m}}_{FrRHFM}^{\ast}\left(\mathrm{i}\right)\right|}_{\mathrm{j}}-|{\mathrm{m}}_{FrRHFM}^{\ast}\left(\mathrm{i}\right)|\right)}^2.\kern6.25em \end{array}} $$
(57)

The \( {\hat{\mathrm{w}}}_1^{\ast}\left(\mathrm{i}\right) \), \( {\hat{\mathrm{w}}}_2^{\ast}\left(\mathrm{i}\right) \) and \( {\hat{\mathrm{w}}}_3^{\ast}\left(\mathrm{i}\right) \) called a minimum distance decoder.

  1. 4)

    The multiple one-dimensional watermarks, \( {OW}_1^{\ast } \), \( O{W}_2^{\ast } \) and \( {OW}_3^{\ast } \) obtained by performing reverse Sine mapping and scrambling of \( {\hat{W}}_1^{\ast }=\left\{{\hat{w}}_1^{\ast }(i),0\le i<P\times Q\right\} \) using key K1. Then, \( {OW}_1^{\ast }=\left\{{ow}_1^{\ast }(i),0\le i<P\times Q\right\} \), \( O{W}_2^{\ast }=\left\{\mathrm{o}{w}_2^{\ast }(i),0\le i<P\times Q\right\} \) and \( {OW}_3^{\ast }=\left\{{ow}_3^{\ast }(i),0\le i<P\times Q\right\} \) are transformed into a two-dimensional binary multiple watermarks \( {W}_1^{\ast }=\left\{{w}_1^{\ast}\left(i,j\right)\in \left\{0,1\right\},0\le i<P,0\le j<Q\right\} \), \( {W}_2^{\ast }=\left\{{w}_2^{\ast}\left(i,j\right)\in \left\{0,1\right\},0\le i<P,0\le j<Q\right\} \) and \( {W}_3^{\ast }=\left\{{w}_3^{\ast}\left(i,j\right)\in \left\{0,1\right\},0\le i<P,0\le j<Q\right\} \).

Based on the above steps, the pseudo-code of the extraction of the multiple watermarks can be described as follows:

figure b

4 Experiments

This section performs various experiments to evaluate the proposed watermarking algorithm regarding visual imperceptibility and the robustness analysis against potential attacks. We conducted all experiments on selected color images from the dataset of birds [24] which contains 600 images (100 samples each) of six different classes of birds (Egret, Mandarin, owl, puffin, toucan, and wood duck). The images are RGB color JPEG with different dimensions (e.g., 539 × 570, 400 × 600).

All selected color images are resized with unified dimensions, 512 × 512, as shown in Fig. 4a–e. Besides, we selected five standard color images from the USC-SIP image database [42] with the size 512 × 512 as host images, as shown in Fig. 4f–j. Binary images as watermark images with the size 64 × 64 as shown in Fig. 5. All experiments are implemented in MATLAB (R2015a) on a personal computer with 1.9 GHz Core (™) i7 and 8 GB RAM.

Fig. 4
figure 4

Standard Color images (Host images)

Full size image
Fig. 5
figure 5

Binary images (watermarks)

Full size image

4.1 Watermark imperceptibility

The peak signal-to-noise ratio (PSNR) is a standard quantitative measure used to evaluate visual imperceptibility.

The PSNR of the watermarked image, \( {g}_c^w \), and the original image, gc, is [33]:

$$ PSNR\left(\ {g}_c,{g}_c^w\right)=10{\mathit{\log}}_{10}\frac{255^2}{MSE} $$
(58)

where

$$ MSE=\frac{1}{N^2}\left(\sum \limits_{i=1}^N\sum \limits_{j=1}^N{\left[\ {g}_c^w\left(i,j\right)-{g}_c\left(i,j\right)\right]}^2\right) $$
(59)

For a fair comparison, the compared methods [7, 8, 44, 50] are used to embed a single watermark in the host color images. Therefore, the imperceptibility of the proposed watermark algorithm is evaluated by embedding a 128-bit watermark sequence into the ten standard color images with Δ ∈ [0.2,0.4,0.6,0.8,1.0]. In which, we compute the proposed, MFrEMs, MFrPHTs and MFrRHFMs with α = 1.7 and the existing compared methods [7, 8, 44, 50] then, we used the amplitude of MFrEMs, MFrPHTs and MFrRHFMs and the existing compared methods [7, 8, 44, 50] in the embedding a 128-bit watermark sequence in host color images. For each generated watermarked image, the average PSNR values are calculated for the proposed algorithm.

The compared algorithms [7, 8, 44, 50] and the relationship between the average PSNR of watermarked images and the quantization step are shown in Fig. 6. Table 1 reports the average PSNR for different quantization steps.

Fig. 6
figure 6

PSNR using different values of (Δ)

Full size image
Table 1 The average PSNR (dB) using different amounts of (Δ)
Full size table

As shown in Fig. 6 and Table 1, the average PSNR decreases as the watermark quantization step increases. As we know, when the PSNR is>38 dB, the watermarking algorithms can achieve superb imperceptibility. The watermarking algorithm achieved the highest values of PSNR, where all PSNR values PSNR >38 dB, which means that the proposed algorithm achieves outstanding watermark imperceptibility and the proposed watermark algorithm outperformed those in [7, 8, 44, 50].

4.2 Watermark robustness analysis

The most used performance evaluation metrics to test the robustness of digital watermarking against attacks are the bit error rate (BER) and the normalized correlation (NC). The BER and NC describe the similarity of two images, the original and extracted watermark. The larger NC and the smaller BER denote that the original and extracted watermark is more similar. When the original and extracted watermark is the same, the watermarking algorithms have an NC and BER are 1 and 0, respectively, and the watermark is more robust. The BER and NC, respectively defined as [36]:

$$ BER=\frac{1}{P\times Q}\left(\sum \limits_{i=1}^P\sum \limits_{j=1}^Q{\left[w\left(i,j\right)-{w}^{\ast}\left(i,j\right)\right]}^2\right) $$
(60)
$$ NC=\frac{\sum \limits_{i=1}^P\sum \limits_{j=1}^Q\left[w\left(i,j\right)\times {w}^{\ast}\left(i,j\right)\right]}{\sum \limits_{i=1}^P\sum \limits_{j=1}^Q{\left[w\left(i,j\right)\right]}^2} $$
(61)

Where W & W∗ refer to original and extracted watermarks.

4.2.1 Multiple watermark extraction

In this subsection, we perform various experiments to evaluate the robustness of the proposed watermarking algorithm to various attacks, including JPEG compression, Salt and Peppers noise, Gaussian noise, filtering, and median filtering, Rotation, Scaling, and Flipping. As the proposed algorithm embeds multiple watermarks in the Red, Green, and Blue channels, gR, gG, and gB, of an original color image using the MFrEMs, MFrPCETs, MFrRHFMs, BER, and NC defined by Eqs. (60) and (61), respectively, are used to measure the robustness of the algorithm where the multiple watermarks are extracted from the Red, Green, and Blue channels, gR, gG, and gB, of the original color image.

  1. 1.

    JPEG compression attack

To test the robustness of the proposed algorithm against the JPEG compression attack, we use compression quality factors, QF = 50, 70, and 90, on the color image. Figure 7 shows represent color images after JPEG compression attacks of different compression quality factors. Table 2 reports the obtained results of BER and NC values under the JPEG compression attacks for the multiple extracted watermarks from the three channels, Red, Green, and Blue of the color image, simultaneously. It can be seen from Table 2 that the extracted watermarks have a higher quality with lower BER and higher NC values.

Fig. 7
figure 7

JPEG compression attacks: a JPEG 30, b JPEG 50, c JPEG 70, d JPEG 90

Full size image
Table 2 Extracted watermarks with the BER and NC values under JPEG compression attack
Full size table

The results of this experiment prove that the proposed algorithm can effectively resist JPEG compression attacks.

  1. 2.

    Noise attack

To test the robustness of the proposed algorithm against the noise attacks, Matlab statements, C = imnoise(C, ‘gaussian’, m, v), is used to add Gaussian white noise of mean m and variance v to the image C and B = imnoise (B, ‘salt & pepper”, d), is used to add salt and pepper noise to the image B, where d is the noise density. In this experiment, Gaussian noise with (m = 0, v = 0.02), (m = 0, v = 0.04) for mean and variance value, pepper & salt noise with (d = 0.02) and (d = 0.04) are added to the original color image. Figure 8 shows the color image after adding different noises. Table 3 shows the obtained results of BER and NC values under the noise attacks for the extracted watermarks from the three channels, Red, Green, and Blue, of the color image, simultaneously. It can be seen from Table 3 that the extracted watermarks are closer to the original ones with lower BER and higher NC values. The results of this experiment ensure that the proposed algorithm is highly robust to noise attacks.

Fig. 8
figure 8

Noise attacks: a Gaussian noise 0.02, b Gaussian noise 0.04, c Salt & peppers noise 0.02, d Salt & peppers noise 0.04

Full size image
Table 3 Extracted watermarks and the corresponding BER and NC values to Noise attack
Full size table
  1. 3.

    Filtering attack

Here, three kinds of filtering are used to test the robustness of the proposed algorithm to filtering attacks. We perform median filtering, Gaussian filtering, and average filtering on the original color image with a filtering window of 3 × 3, respectively. The color images after the filtering attacks are displayed in Fig. 9. The obtained results of extraction watermarks with their corresponding BER and NC values are shown in Table 4. It can be seen from the results that the proposed algorithm has good robustness to filtering attacks.

Fig. 9
figure 9

Filter attacks: a Median Filtering 3 × 3, b Gaussian Filtering 3 × 3, c Average Filtering 3 × 3

Full size image
Table 4 Extracted watermarks and the corresponding BER and NC values under Filtering attack
Full size table
  1. 4.

    Rotation attack

As one of the geometric attacks, rotation attacks are used to test the robustness of the proposed algorithm. We rotate the original color image by the rotation angles, θ = 15o, 30o, 45o. Figure 10 shows the color images after being subjected to rotation attacks; the BER and NC values for each extracted watermark are reported in Table 5.

Fig. 10
figure 10

Rotation attacks: a Original image, b Rotation 15, c Rotation 30, d Rotation 45

Full size image
Table 5 Extracted watermarks and the corresponding BER and NC values under Rotation attack
Full size table

It can be seen from the results in Table 5 that extracted watermarks are recognizable with values of BER and NC approaches to the optimum values 0 and 1, respectively. These results ensure the robustness of the proposed algorithm against rotation.

  1. 5.

    Scaling attack

Here, a scaling attack, a common one of the geometric attacks, is used to test the robustness of the proposed algorithm. We scaled the color images by scaling factors S = 0.75, 1.5, 2.0. Figure 11 shows the scaled color images. Table 6 presents the obtained results of BER and NC values for each extracted watermark under scaling attacks. As shown from Table 6, the extracted watermarks are closer to the original one in Fig. 5. The results confirm the proposed algorithm has good robustness against scaling attacks with reduction and magnification scaling factors.

Fig. 11
figure 11

Scaling attacks: a Original image, b Scaling 0.75, c Scaling 1.5, d Scaling 2.0

Full size image
Table 6 Extracted watermarks and the corresponding values of BER and NC under Scaling attack
Full size table
  1. 6.

    Flipping attack

To test the robustness of the proposed algorithm toward the flipping attacks. We perform flipping horizontally and vertically to the original color image. Figure 12 shows the color images after flipping attacks. Table 7 shows the values of BER and NC for the extracted watermarks. As shown in Table 7, the proposed algorithm can effectively extract multiple watermarks even with flipping attacks. It can be shown from the results in Table 7 that extracted watermarks are recognizable with values of lower BER, and higher NC values approach to the optimum values 0 and 1, respectively. These results ensure the robustness of the proposed algorithm against flipping attacks.

Fig. 12
figure 12

Flipping attacks: a Horizontal flipping, b Vertical flipping

Full size image
Table 7 Extracted watermarks and the corresponding BER and NC values under Flipping attack
Full size table

4.3 Comparison of robustness with similar algorithms

In this section, the experiment was performed to verify the superiority of the proposed algorithm; the proposed algorithm was compared with other robust watermarking algorithms [7, 8, 26, 44, 50]. The existing algorithms [7, 8, 26, 44, 50] are used to embed a single watermark in the host color images, while the proposed algorithm can be used for single and multiple watermarks.

We perform all comparisons to embed a single watermark in the host color images for a fair comparison. Ten binary watermarks of 32 × 32 pixels are embedded in the ten host images using the proposed scheme and another quaternion moment-based watermarking algorithm [7, 8, 26, 44, 50]. Then, a total of 10 × 10 = 100 watermarked color images are generated. For each watermarked color image, the average values of BER and NC are computed for extracted watermark under geometric distortions and different common attacks. Tables 8 and 9 reports the average values of BER and NC, respectively.

Table 8 Average BER comparison between the proposed algorithm and other watermarking methods [7, 8, 26, 44, 50]
Full size table
Table 9 Average NC comparison between the proposed algorithm and other watermarking methods [7, 8, 26, 44, 50]
Full size table

It can be seen from the results in Tables 8 and 9 that the robust watermarking scheme based on fractional multi-channels orthogonal moments proposed in this paper has significantly better performance in resisting standard image processing and geometric attacks than the compared methods in [7, 8, 26, 44, 50]. The better performance of the proposed algorithm occurs because of the highly accurate computation method used to compute the new fractional multi-channels orthogonal moments, which has numerical stability and better accuracy. Besides, the new fractional multi-channels orthogonal moments have a remarkable characteristic in image description and representation compared to the others with integer orders in [7, 8, 26, 44, 50].

As a result, the proposed robust method is more robust and resistant to various attacks. On the other side, most quaternion moments-based watermarking algorithms utilize the zeroth-order approximation (ZOA) method in Cartesian coordinate. This traditional method has poor accuracy and produces two standard errors, numerical integration and geometric errors. Therefore, the watermarking schemes have a result in poor robustness of the extracted watermark. The experimental results and the above analysis show that the proposed robust watermarking scheme has better robustness towards typical geometric and image processing attacks. The proposed algorithm is better than other compared watermarking schemes in terms of robustness and imperceptibility.

5 Conclusion

In this paper, a novel robust watermarking algorithm for color image based on multiple accurate MFrEMs, MFrPHTs, and MFrRHFMs and a 1D Sine mapping has been proposed. The proposed scheme uses a 1D Sine chaotic map for enhancing the security by scrambling the multiple watermarks images where these scrambled multiple watermarks bits are embedded into original color images by adapting the magnitudes of MFrEMs, MFrPHTs, and MFrRHFMs. Experimental results have shown that the performance of the proposed scheme is superior to existing methods in terms of imperceptibility and watermark robustness.

Additionally, it is demonstrated by experimental results that the robust watermarking scheme provides resistance against the different common geometric and image processing attacks. Moreover, it proved that the proposed scheme achieves a good trade-off between robustness and imperceptibility. We will improve the proposed algorithm to deal with dual and multiple color images simultaneously in future work.

Extension of this approach to robust zero watermarking to solve the problem of conflicting between discriminability and robustness. Moreover, in our plan, we will extend the proposal to medical applications.