1 Introduction and Literature Review of Immiscible Viscous Fingering

Viscous instability (also known as viscous fingering) is an important physical phenomenon which occurs during fluid displacements in porous media when the displacement is unstable due to the displacing phase viscosity being much lower than the displaced fluid viscosity. Viscous fingering is observed in both miscible and immiscible displacements and has been extensively described in the literature (e.g. Van Meurs and Van der Poel 1958; Homsy 1987; Peters and Hardham 1989, 1990; Pavone 1992; Calderon et al. 2007; Daripa and Ding, 2012). The classical review by Homsy (1987) has recently been updated by Pinilla et al (2021a) who present a well-organized survey the entire field of viscous instability in porous media to date.

In this work, we focus on immiscible viscous fingering since this has proven particularly difficult to model and to date no very convincing direct numerical simulation of well-developed viscous fingering has appeared which directly matches experiment.

Several approaches to the study of immiscible viscous fingering have been taken in the literature, which we broadly group under the following headings:

  1. (i)

    Linear stability analysis of the initial growth of the immiscible fingers;

  2. (ii)

    Direct numerical simulation of immiscible fingering;

  3. (iii)

    Experimental studies at the core/slab scale of immiscible fingering;

  4. (iv)

    Discrete and pore-scale modelling and experiments on viscous fingering.

1.1 Linear Stability Analysis of Immiscible Fingering

Since the original linear stability analysis of two-phase immiscible fingering by Chuoke et al. 1959, more than 100 papers on this topic have appeared in the literature typified over recent years by, for example, Huang et al. 1984; Yortsos and Huang 1986; Alemán and Slattery 1988; Chikhliwala et al. TIPM, 1988; Yortsos and Hickernell 1989; Riaz and Tchelepi 2004. This widely applied type of analysis uses linear stability theory to examine the early time growth of the unstable modes or wave numbers of a small perturbation on the unstable “interface” between the immiscible fluids. This has been very useful to provide an analysis of what parameters appear to be “driving” the instability. This approach has little in detail to say about the later time behaviour of the viscous fingers. However, it has given us an important clue that some studies have shown the larger the total mobility, the more unstable is the fingering. In this work, we also build on the result that Yortsos and Huang (1986) show that, for certain model views of the step displacement front, then the relationship between the relative permeabilities (RPs) and the fractional flow function is important in determining the stability of the displacement.

1.2 Direct Numerical Simulation of Immiscible Fingering

This is most important area of review since this is where the current paper seeks to make a contribution. Our central claim for this work is that it is the first paper to present a very good (if not perfect!) direct comparison between a continuum numerical modelling method and all the data for a wide range of experimental immiscible viscous fingering 2D experiments (see below) for a wide range of viscosity ratios, (μo/μw).

One of the earliest continuum numerical simulation papers to show immiscible viscous fingering with well-resolved fingering was that of Blunt et al. (1994). These simulations were actually for unstable compositional displacements, and to this day, they have not been significantly improved upon, until the present work. Riaz and Tchelepi (2006a) used very accurate spectral methods to solve the two-phase equations for cases where immiscible fingering occurs. Their simulations do show some of the qualitative features of observed fingering. However, they point out (in Fig. 7) that their methods do not reproduce some of the important features observed in experiments. In particular, they note that the length and growth rates of real observed fingers are not correctly reproduced. They comment (correctly, in our view) that this disagreement with experiment may be due to the lack of correct input experimental relative permeabilities (RPs) or capillary pressure functions (Pc). In another paper, Riaz and Tchelepi (2006b) go on to examine the effect of the RP functions on the immiscible fingering patterns by carrying out some sensitivities simulations for unstable flows. They used a limited range of RP functions, but they did find that enhanced fingering was observed for the RP functions with the highest total mobility. They defined total mobility in the conventional manner using the end point RPs (i.e. M in this paper). This is an important observation in the context of this work since our method uses a maximum mobility approach to model detailed fingering (Sorbie et al. 2020). The limited finger growth seen by Riaz and Tchelepi (2006a) is also evident in the CO2 /water displacement simulations presented by Berg and Ott (2012) who also used “conventional” RPs derived from experiment. The simulations in the latter paper certainly showed indications of the onset of instability, but again we believe that the (numerical) fingers were not fully developed.

Extensive numerical studies of immiscible fingering were published in a series of papers by the Imperial College (London) group and their collaborators (Mostaghimi et al. 2016; Adam et al. 2017; Hamid and Muggeridge, 2018; Kampitsis et al. 2019, 2020). In this work, they used very sophisticated adaptive meshing numerical techniques to model immiscible fingering. Although immiscible fingering was clearly reproduced in these simulations, it again showed the lack of discrete finger growth and formation of many early time fingers as observed experimentally. Bakharev et al. (2020) presented a good recent example of the direct simulation approach of viscous unstable immiscible displacement which again showed many of the features already discussed above.

Erandi et al. (2015) studied immiscible fingering in heavy oil using the porous medium formulation of a commercially available CFD package. They claim that they validated the model by comparing their simulations with results from the resin displacing oil experiments of Pavone (1992). Two of Pavone’s experimental cases were simulated (in3D) in which the viscosity ratios (μo/μresin) were reported as 6.82 and 2.27 for cases 1 and 2, respectively. Some fingers were observed in the simulations and breakthrough times were poorly reproduced, and so the comparison is far from being a validation of the model.

Pinilla et al. (2021b) presented 3D simulations of core flood tests from the literature (Doorwar and Mohanty, 2017) focussing on the best grid (structured or unstructured) to model the 3D fingering. The core flood oil recoveries can be matched in some simulations, and plausible 3D viscous fingering is produced in their simulations. However, no experimental images of the 3D figures are actually available for direct comparison with these simulations. An initial stricter test of the approach of Pinilla et al. (2021b) would simply be to simulate the same (2D) data as we are modelling in this paper (see below).

Chaudhuri and Vishnudas (2018) presented a very well-executed field study of waterflooding and polymer flooding in a field scale 5-spot model of a 500cP oil reservoir. Again their simulations show some degree of immiscible fingering during the waterflood and also miscible fingering the polymer postflush with water. However, in our view, the immiscible fingering is still “suppressed” for the same reasons as in the studies discussed above.

Many of the previously reviewed papers all have great merit as numerical studies and method development, but we believe that the reason that they did not see fully developed fingers of the type reported in this paper (experiments and simulations) was that their RPs functions were “over-stable”. That is, the presence of the sometimes wispy frontal fingering was an indicator that the system is unstable, but the chosen RP functions suppressed or stabilized this fingering. From the review above, we do not see the realistic modelling of immiscible viscous fingering as a “problem of numerics”, but of the physics, as explained in detail in Sorbie et al. (2020). In that work, we demonstrated that detailed, realistic resolved fingering can be reproduced using our fraction flow (fw*)/ maximum total mobility (λT(Sw)) approach using a reasonably fine grid with single point upstreaming, and this is demonstrated further in this paper. Indeed, if any of the numerical approaches reviewed above simply employed the “pseudo RPs” in our work here, we are quite sure that they would produce realistic and highly resolved viscous fingering.

For further discussion of the role of RPs, we refer the reader to Appendix A: Some Comments on “Experimentally Measured” Relative Permeabilities (RPs) for Unstable Immiscible Displacements.

1.3 Experimental Results on Immiscible Fingering

The first mention of the term “viscous fingering” appeared in Engelberts and Klinkenberg (1951), and this referred to immiscible (oil/water) fingering. This was followed by the analysis of Hill (1952) and the early classical work of Saffman and Taylor (1958). One of the earliest studies showing immiscible fingering experimentally was by van Meurs and van der Poel (1958) in which refractive index matched oil and beads were used to construct high permeability bead packs. When water was injected into the oil (viscosity ratio, \((\mu_{o} /\mu_{w} ) = 80\)), the resulting fingers could be clearly observed and photographed directly. Although experimental work should be the most important activity in the study of immiscible viscous fingering, there are very few complete experimental studies which allow us to do direct numerical simulations to test our various theoretical and numerical models. By “complete”, we mean having access to the time lapsed finger patterns of the immiscible fingers, along with the oil recovery, watercut and pressure drop profiles (vs. PV). Much more work on the theory (e.g. stability analysis, numerical simulation, average modelling, etc.) than on experiments has appeared in the literature.

Doorwar and Mohanty (2011, 2014b, 2017) studied immiscible viscous fingering in a remarkably thorough series of experimental and modelling papers. They used pore-scale model experiments to derive a dimensionless parameter to correlate the results from viscous unstable displacements at the core scale at various viscosity ratios (μo/μw) and flow rates. From this, they derived a “finger function”, in the general manner carried out some time ago by Fayers and Newley (1988) for miscible unstable flow. This also led them to develop pseudo-RP functions both the oil and water phases which could capture the averaged behaviour of the system very well. In this work, it was also recognised that the fractional flow for describing fingering required some modification /adjustment, which is an important point of contact with the current work. In a later paper, Doorwar and Ambastha (2020) review much of the early work on immiscible fingering, drawing particular attention to Maini’s (Maini 1998) warning about the difficulty (futility?) of trying to “measure” (or even define) RPs for very viscous oils (see Appendix A). Doorwar and Ambastha (2020) then went on to describe a procedure for developing pseudo-RPs for unstable immiscible displacement in viscous oils. This body of work has made a significant contribution to both our understanding of immiscible fingering and to the “averaging” (correlations and finger function development) approach to modelling unstable immiscible displacements. This certainly contributes practical methods and work flows to the task of modelling unstable water–oil displacements in viscous oils in the field. In contrast, the current work takes the alternative approach of trying to do these calculations by direct numerical simulation of the fingers (Sorbie et al. 2020).

The explicit effects of the system wettability on immiscible viscous fingering are considered by several authors (Doorwar and Mohanty 2014b; Worawutthichanyakul and Mohanty 2017; Jamaloei 2021). Wettability will principally determine the forms of the relative permeabilities (RPs) and the capillary pressure functions, which in turn will affect the details of the finger formation and growth or suppression. This will be considered in some detail by the authors in a future publication.

Recently, Beteta et al. (2022) published a series of water and polymer core floods where the oil/water viscosity ratio was (μo/μw) ~ 100. Both the viscous unstable water floods and the (secondary and tertiary) polymer floods were simulated by the method used here to model the unstable immiscible fingering (Sorbie, et al. 2020). Good matches were obtained for the unstable waterfloods, and the subsequent performance of the polymer floods was predicted with no further assumptions. However, although viscous fingering was predicted to occur in these floods (in the simulations), no in situ images of the viscous fingers were available and this is remedied in the work reported in this paper.

Over the last decade or so, a very extensive body of experimental work has been published on unstable (water oil) displacements in 2D sandstone slabs by researchers at the University of Bergen, Norway. This work has provided some excellent datasets suitable for testing models of immiscible viscous fingering in porous media (Skauge et al. 2009; Skauge et al. 2011; Skauge et al. 2012; Skauge et al. 2013; Skauge and Salmo 2015; Bondino et al. 2011; Fabbri et al. 2015; Salmo et al. 2017; Skauge et al. 2014; Fabbri et al. 2020). Both water/viscous oil displacement experiments (and tertiary polymer floods) were performed on 2D slabs of Bentheimer sandstone. Since oil recovery, watercut and pressure drop profiles and in situ X-ray images of the finger patterns (all vs. PV injected) were reported, the great value and utility of this work are that it provides virtually all of the data required to test numerical models (as discussed above). Hitherto, such “complete” datasets have not been available. The current study has access to all of this data, and it provides a very testing dataset for immiscible viscous fingering with oil/water viscosity ratios over the range, (μo/μw) ~ 400−7000. Further details of these immiscible viscous fingering experiments are provided below, since it is these data which are modelled directly in this work.

1.4 Discrete and Pore-Scale Modelling

We will say little about this topic although it covers a large and interesting area of discrete methods such as pore-scale experiments/ modelling, network modelling, lattice Boltzmann methods and other discrete particle methods for modelling unstable flows. None of the extensive work on immiscible fingering in Hele-Shaw cells is referenced here.

The classical study of pore-scale immiscible displacements (drainage) and modelling is that of Lenormand et al. (1988). This work elucidates the main aspects of the pore-scale drainage physics by laying out the phase diagram of viscosity ratio vs. capillary number showing the regions of viscous fingering, capillary fingering and compact (stable) flow. Recent work by Patmonoaji et al. (2020) has presented a detailed CT small core study of the viscous fingering to capillary fingering transition at the small scale, which extends this earlier work to 3D. An interesting pore network experimental and modelling study by Rabbani et al. (2018) discusses the physics of suppressing viscous fingering in structured porous media. Sharma et al. (2012) present some novel results on imbibition flow regimes in small micromodels as functions of the viscosity ratio and capillary number, which as expected governs the observed flow regimes. Interesting observations include non-equilibrium and apparent non-Darcy type flows.

However, the most recent work in this area of relevance to the subject of this paper is by Doorwar and Mohanty (2014a). They developed a pore-scale model of their own experiments (see references above) based on the physics of dielectric breakdown which correctly described the various flow regimes (stable, fingering, etc.) observed. Indeed, they note (their Fig. 11) that there are combinations of parameter which do lead to fingers which resemble those in the μo = 2000 and 7000cP unstable displacements in the work of Skauge et al. (2012); direct simulations of these floods are presented in this paper. In addition, this work has helped to build the bridge between the pore scale and core scale physics in a practical way, referred to above, which other work has not previously succeeded in doing.

2 The Approach to the Direct Numerical Modelling of Immiscible Viscous Fingering

The governing equations for two-phase flow in porous media for incompressible immiscible two phases (water and oil) flow can be written as the following 2 coupled equations:

$$\nabla \bullet \left[\left({\lambda }_{o}+{\lambda }_{w}\right){\varvec{K}}.\nabla {P}_{o}-{\lambda }_{w}{\varvec{K}}.{\nabla P}_{c}\right]=0$$
(1.1)

and

$$\phi \left(\frac{{\partial S}_{o}}{\partial t}\right)=\nabla \bullet [{\lambda }_{o}{\varvec{K}}.\nabla {P}_{o}]$$
(1.2)

where Eq. 1.1 is the pressure equation, and Eq. 1.2 is the transport equation describing the change in local fluid (water and oil) saturations, \({S}_{w}\) and \({S}_{o}\) (where \({S}_{w}+{S}_{o}=1\)); the quantities \({\lambda }_{w}\) and \({\lambda }_{o}\) are the phase mobilities, which are given by \({\lambda }_{w}={k}_{rw}/{\mu }_{w}\) and \({\lambda }_{o}={k}_{ro}/{\mu }_{o}\), where the \({k}_{rw}\) and \({k}_{ro}\) are relative permeabilities (RPs) which depend on \({S}_{w}\) (subscripts w = water and o = oil). \(\phi\) is the porosity of the porous media. \({\varvec{K}}\) is the permeability tensor, which is generally assumed to be diagonal, although this is not necessary. Equations 1.1 and 1.2 include both viscous and capillary forces (not gravity) where capillary pressure, \({P}_{c}\left({S}_{w}\right)={P}_{o}-{P}_{w}\). Capillarity in these equations acts like a non-linear diffusion term and essentially defines a lower length scale or “capillary dispersivity” below which fingers cannot form since they are dispersed (Stephen et al. 2001). However, we have shown that in the viscous-dominated case, where \({P}_{c}=0\), then this lower length scale can be determined by the numerical grid itself using numerical dispersion, as discussed in Sorbie et al. (2020).

However, although the equations above are quite well known, it has been challenging to reproduce the observed immiscible fingering patterns through direct numerical simulation, by discretizing these equations and solving them numerically in the usual manner. The main reason for this lack of ability to mimic the viscous fingers is often attributed to numerical issues (e.g. Kampitsis et al. 2019; Bakharev et al. 2020 and other paper reviewed in Sect. 1). However, recent work by the authors (Sorbie et al. 2020) has identified the problem of reproducing “realistic” immiscible fingering patterns as being due to the physics and mathematical formulations. This approach suggested a methodology for the modelling of two-phase immiscible viscous fingering that can simulate water displacing oil in porous media when \({\mu }_{o}\gg {\mu }_{w}\); where \({\mu }_{o}\) and \({\mu }_{w}\) are the oil and water viscosities, respectively. This type of displacement is described as being at “adverse mobility ratio”, \(M\), where \(M={\lambda }_{w}/{\lambda }_{o}\). In this paper, we will avoid this term and will instead refer to “adverse viscosity ratio” where \({\mu }_{o}/{\mu }_{w}\gg 1\), when referring to unstable immiscible displacements. However, we will use the local value of M, particularly at the saturation shock front where, \({S}_{w}={S}_{wf}\), where \(M=M({S}_{wf})\). The reason for this will become evident later in the paper.

This paper is based on the procedure proposed in Sorbie et al. (2020) for modelling viscous fingering in two-phase unstable displacements in porous media. This work presented the following 4-step approach to the problem, although it is the first 2 steps that provide the core of the method:

  1. 1.

    Identify and choose a water fractional flow value, \({f}_{w}^{*}\), from direct observations of experimental data. This value corresponds to,\({S}_{wf }^{*}\), a shock front water saturation higher than is typically found for conventional relative permeability curves, to account for high water saturations in the fingers. From \({f}_{w}^{*}\), the ratio of relative permeabilities can be calculated as:

    $$\frac{{k}_{ro}^{*}}{{k}_{rw}^{*}}=\left(\frac{{\mu }_{o}}{{\mu }_{w}}\right)\left(\frac{1}{{f}_{w}^{*}\left({S}_{w}\right)}-1\right)$$
    (1.3)
  2. 2.

    Using selected \({f}_{w}^{*}\), one can generate infinite number of corresponding relative permeability sets. The optimum set for the purpose is taken as the set that yields maximum total mobility,\({\lambda }_{T} ({\lambda }_{T}={\lambda }_{w}+{\lambda }_{o})\), which is the sum of water and oil mobilities, shown in Eq. 1.4. The maximum \({\lambda }_{T}\) leads to an unstable displacement giving the minimum pressure drop across the fingering system at any value of injected pore volumes.

    $${\lambda }_{T}={\lambda }_{o}+{\lambda }_{w}=\frac{{k}_{ro}^{*}}{{\mu }_{o}}+\frac{{k}_{rw}^{*}}{{\mu }_{w}}$$
    (1.4)
  3. 3.

    Generate a random correlated permeability field with a given average permeability. This field has both its heterogeneity and structure quantified; thus, its permeability variance range can be described by the ratio of maximum to minimum permeability in a correlation structure. The structure is characterized by a dimensionless correlation length (\({\lambda }_{D}\)) defined as the ratio between correlation length (\(\lambda\)) of the permeability field and the total system length, \(L\), i.e. \({\lambda }_{D}=(\lambda /L)\).

  4. 4.

    Lastly, an adequately fine spatial gridding scheme is selected in a 2D (or 3D) system, where the ratio of both \(\Delta x\) and \(\Delta y\) to the total system length is sufficiently smaller than the selected correlation length from the previous step.

A full discussion of the method outlined above is given in Sorbie et al. (2020), and the reader is referred there for further detail, in particular, the discussion and resolution of the “M-paradox”. This earlier paper shows results for modelling water–oil adverse viscosity ratio displacements (with \({\mu }_{o}=\) 1600 cP and \({\mu }_{w}=\) 1cP) and the viscous fingering examples are much more “realistic” than have hitherto been produced. In addition, the simulations show all the qualitative features observed recently reported viscous fingering experiments ( Skauge et al. 2009; Skauge et al. 2011; Skauge et al. 2012; Skauge et al. 2013; Skauge et al. 2014). However, the results presented in this earlier paper (Sorbie et al. 2020) were generic results, and no attempt was made to simulate any specific experiment data. In the current paper, we apply this approach to directly simulate all of the laboratory data for four immiscible viscous fingering floods over a wide range of adverse viscosity ratios where water (\({\mu }_{w}=\) 1 cP) displaces various viscous oils (\({\mu }_{o}=\) 412 cP, 616 cP, 2000 cP and 7000 cP). Four experiments previously presented in the literature ( Skauge et al. 2014) have been modelled using the proposed procedure, where we attempt to reproduce all of the experimental data including (i) the oil recovery; (ii) the effluent water cut (% produced water); (iii) the pressure drop across the system, \(\Delta P\), and (iv) the viscous fingering patterns, from the initial period of finger initiation and development to the late time of the displacement; where all of these quantities are functions of pore volume (PV) injected. To our knowledge, no publication has appeared in the literature which succeeds in reproducing all of these experimental features in systems showing severe immiscible fingering in a fully satisfactory manner. The simulation matches to the experiments in this paper show from very good to excellent quantitative agreement for all observed data, and the main features of the complex viscous fingering patterns are well reproduced and observed finger patterns are well resolved.

3 Experimental Details

The experimental data used to test the modelling approach to viscous fingering during waterflooding are given in the publication by Skauge et al. (2014). Four experiments are chosen with oil viscosities of \({\mu }_{o}=\) 412 cP, 616 cP, 2000 cP and 7000 cP, thus spanning a wide range of displacement conditions from adverse to extremely adverse values of the viscosity ratio (\({\mu }_{o}/{\mu }_{w}\)), i.e. over the range (\({\mu }_{o}/{\mu }_{w}\)) \(\sim\) 400 to 7000. These 2D sandstone slab experiments were performed as a part of a study to analyse the implementation of polymer flooding for oil viscosity at adverse viscosity conditions, where water was injected first, and then, polymer was injected as a tertiary process. In this paper, we will only focus on the unstable water/oil displacements. The modelling and analysis of the more complex fluid mechanics of the polymer displacements will be presented in a later paper.

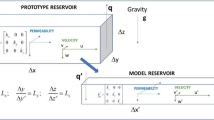
All experiments were conducted on 2D sandstone slabs with dimensions, of 30 cm × 30 cm × 2 cm for the three more adverse oil viscosities (\({\mu }_{o}=\) 616 cP, 2000 cP and 7000 cP,), while the 412 cP experimental sandstone slab had dimensions, 15 cm × 15 cm × 2 cm. The rock material used was Bentheimer sandstone with an average permeability of approximately 2500 mD. The rock material is thought to be quite homogeneous at the large scale, although it has some degree of heterogeneity in permeability at the smaller scale. Bentheimer sandstone has been used very extensively in porous media studies and its depositional setting and petrophysical properties are quite well described in the papers by Peksa et al. (2015) and De Boever et al. (2016). More information on the different experiments is presented in Table 1. Water was injected over the whole length of the slab from the bottom and fluids were produced from the top also over the whole length (see Fig. 1). This was done to try to ensure a uniform pressure across the model by activating both edges. In these experiments, water and oil had approximately the same density, and thus, gravity effects did not influence the displacements.

Table 1 Petrophysical data for the four 2D adverse viscosity ratio (\({\mu }_{o}/{\mu }_{w}\)) experiments modelled in this work; from Skauge et al. (2014)
Full size table
Fig. 1
figure 1

Tubing placement for horizontal injection and production ports in the 2D Bentheimer sandstone slab used in the water oil displacement experiments. Differential pressure was measured between inlet and outlet lines; from T. Skauge et al. (2014)

Full size image

X-ray images were captured at many times during water injection in all of the experiments T. Skauge et al. (2014). To avoid repetition, all experimental data — both production profiles, pressure drops and in situ images, are shown together with the corresponding numerical simulations in the results section of this paper. The visualization of the immiscible fingers during all displacements was captured in the 2D X-ray scanning rig, where the slabs were mounted vertically. Further information about the details of X-ray image filtering and processing can be found in the previous papers by A. Skauge et al. (2009, 2012). The production data are also given in the results section; this includes the oil recovery, the effluent water cut (fraction produced water) and the pressure drop across the system, \(\Delta P\), all as a function of pore volumes injected. A summary of the main experimental production data is given in Table 2, but full profiles are not presented until the results section where the experimental results are compared directly with the numerical modelling.

Table 2 Production data for viscosity ratio (\({\mu }_{o}/{\mu }_{w}\)) experiments (water viscosity is \({\mu }_{w}=\) 1 cP, in all cases); from Skauge et al. (2014)
Full size table

4 The Simulation Model

A 2D square numerical simulation model was created to simulate the adverse viscosity ratio flooding experiments. Water was injected (produced) from a horizontal injection (production) well at the bottom (top) of the model and perforated along the entire bottom (top) edge to mimic the experimental setup in Fig. 1. Capillary forces are neglected as the viscous forces dominate in the experiments.

The approach which we are testing here for modelling immiscible viscous fingering is described above. The crucial steps in modelling immiscible viscous fingering in this approach are the choice of fractional flow, \({f}_{w}^{*}\), and the subsequent derivation of the maximum mobility relative permeabilities, \({k}_{rw}\) and \({k}_{ro}\), which must honour this chosen \({f}_{w}^{*}\) function. The relative permeability correlation used in this paper is the correlation of Lomeland et al. (2005), which we denote as the LET relative permeabilities after its authors. This is as just as flexible as the correlation used in the paper by Sorbie et al. (2020) and these models provide a good alternative when the Corey correlation for \({k}_{rw}\) and \({k}_{ro}\) does not give a sufficient flexible description of two-phase flow functions. The LET correlation is described by three parameters: L, E and T, where L controls the lower part, E the middle part and T the top part of the relative permeability curve to the respective phase. The LET correlation is given in Eqs. 3.1 and 3.3, for the water and oil relative permeabilities, respectively:

$${k}_{rw}={k}_{rw}^{0}\frac{{{S}_{wn}}^{{L}_{w}^{o}}}{{{S}_{wn}}^{{L}_{w}^{o}}+{E}_{w}^{o}(1-{S}_{wn}{)}^{{T}_{w}^{o}}}$$
(3.1)
$${k}_{ro}={k}_{ro}^{0}\frac{(1-{{S}_{wn})}^{{L}_{o}^{w}}}{(1-{{S}_{wn})}^{{L}_{o}^{w}}+{E}_{o}^{w}{{S}_{wn}}^{{T}_{o}^{w}}}$$
(3.2)

For the water relative permeability, the subscript denotes the oil phase, and the superscript denotes the water phase. The normalized water saturation, \({S}_{wn}\), is given by Eq. 3.3:

$${S}_{wn}=\frac{{S}_{w}-{S}_{wi}}{1-{S}_{wi}-{S}_{or}}$$
(3.3)

where \({S}_{w}\) is the water saturation, \({S}_{wi}\) is the initial water saturation, and \({S}_{or}\) is the residual oil saturation.

The two last steps of the approach involve generating the permeability field and choosing a sufficiently fine spatial grid. From a numerical simulation point of view, the two last parts need to be established first. We therefore start with a sensitivity analysis of the grid size. A grid size sensitivity study was also included in the paper by Sorbie et al. (2020). However, we also need to conduct such a sensitivity in order to find the optimal grid size resolution for our experimental simulations, with respect to both finger development and computational time.

Figure 2 shows the system dispersivity as a function of length scale as reviewed from the literature review by Arya et al. (1988). The red dashed line was used as the scaling of dispersivity in our work, and since the system length is \(L \sim\) 0.3 m (30 cm), we obtain an approximate dispersivity of 0.001 m (1 mm). This suggests a grid resolution of 300 × 300 × 1 grid blocks, where each block is 1 mm × 1 mm × 2 mm. However, we also examine grid resolutions of 100 × 100 × 1 and 600 × 600 × 1 and 1000 × 1000 × 1, while respecting the actual size of the model. For the grid size sensitivity study, the relative permeability curves and fractional flow curve were the same for all three cases.

Fig. 2
figure 2

Field and lab data of dispersivity as a function of length scale; modified from Arya et al. (1988)

Full size image

The permeability fields were generated using a random Gaussian field distribution, and these are shown in Fig. 3. All cases have an average permeability in the range 2000 ± 100 mD, i.e. \({k}_{min}=\) 1900 mD and \({k}_{max}=\) 2100 mD. The correlation length is \(\lambda =\) 9 mm for all fields, which gives a dimensionless correlation length of \({\lambda }_{D}=\) 0.03, where the dimensionless correlation length, \({\lambda }_{D}=\left(\frac{\lambda }{L}\right),\) and \(L=\) system length. According to Sorbie et al. (2020), \({\lambda }_{D}\) has a significant impact on the number of total initial fingers as well as on the emergent number of later time dominant fingers. They also found that the ratio between minimum and maximum permeability (\({{k}_{max}/k}_{min}\)) did not affect the results in terms of both fingering pattern and production data, over the range \({{k}_{max}/k}_{min}=\) 100 to 2.

Fig. 3
figure 3

Random correlated permeability field for model size 1000 × 1000 × 1, 600 × 600 × 1, 300 × 300 × 1 and 100 × 100 × 1, showing the average permeability, Kavg

Full size image

5 Numerical Sensitivities

Before modelling the experimental results directly, we present some numerical sensitivities to both the grid size and also the correlation length. In these unstable water oil displacement simulations, we take an oil viscosity of \({\mu }_{o}=\) 2000, and a water viscosity of \({\mu }_{w}=\) 1 cP. The set of flow functions used (\({f}_{w}^{*}\), \({k}_{rw}\) and \({k}_{ro}\)) in these sensitivity calculations is the same as will be developed for the \({\mu }_{o}=\) 2000cP example below, but the actual functions will be presented and discussed later.

5.1 Grid Resolution

Figure 4 shows the (a) oil recovery, (b) water cut, (c) differential pressure and (d) dimensionless differential pressure (differential pressure divided on maximum value of differential pressure, \(\Delta P/{\Delta P}_{max}\)), all vs. pore volumes (PV) injected for the four grid resolutions. The oil recoveries are all very close, although it is slightly higher for the coarser grid resolution (100 × 100 × 1) and slightly lower for the finest grid resolution (1000 × 1000 × 1). There is only a small difference in the oil recovery curve for the 600 × 600 and the 300 × 300 cases, which can be a result of the particular permeability field distribution itself, and the somewhat higher average permeability in the 600 × 600 case. Water cut has approximately the same trend as the oil recovery, while both differential pressure and dimensionless differential pressure are close for all grid resolutions.

Fig. 4
figure 4

a Oil recovery, b water cut, c differential pressure and d dimensionless differential pressure for the three grid cases in the grid resolution sensitivity study

Full size image

Numerical images of the finger development are given in Fig. 5 as snapshots at different values of pore volumes injected, as indicated in the figure. In all cases presenting simulated finger saturation distributions as in Fig. 5, (effectively of \({S}_{w}(x,y)\) vs. PV injected), the saturation range goes from initial water saturation, \({S}_{wi}\) (black), through shades of red to white at or above the max \({S}_{w}\) (i.e. 0.5 in this case); indeed, the white shading is at \({S}_{w}\ge\) 0.5 for all cases except the 7000cP case where white denotes \({S}_{w}\ge\) 0.3. In Fig. 5, the 1000 × 1000 case is at the top, followed by the 600 × 600 case, then the 300 × 300 with the 100 × 100 case at the bottom. The fingers are clear and are quite similar until breakthrough for the finer grid resolutions. After breakthrough, the rest of the area is swept by the injected water and there are a few bypassed zones in the simulation. The coarsest grid (100 × 100) has more fingers developing at an early stage and does not represent the finger development as well as the three other cases. This, and further sensitivities indicated that it was sufficient to use the 300 × 300 × 1 case for modelling immiscible viscous fingers for all the cases presented here.

Fig. 5
figure 5

Local water saturation development at different pore volumes injected for grid with size 600 × 600 × 1, 300 × 300 × 1 and 100 × 100 × 1

Full size image

5.2 Permeability Field Correlation Length

Another important aspect of the random correlated permeability field is the correlation length. The 300 × 300 grid resolution case was chosen for the correlation length analysis, where the correlations length was \(\lambda =\) 9 mm (\({\lambda }_{D}=\) 0.03). All three generated permeability fields are shown in Fig. 6, the base case with \({\lambda }_{D}=\) 0.03 together with correlation length of \(\lambda =\) 4.5 mm (\({\lambda }_{D}=\) 0.015) and \(\lambda =\) 18 mm (\({\lambda }_{D}=\) 0.06).

Fig. 6
figure 6

Random correlated permeability fields for model size 300 × 300 × 1 with dimensionless correlation length of \({\lambda }_{D}=\) 0.015, 0.03 and 0.06, showing the average permeability, \({K}_{\mathrm{avg}}\)

Full size image

Figure 7 shows the (a) oil recovery, (b) water cut, (c) differential pressure and (d) dimensionless differential pressure, all vs. pore volumes injected, for the three correlations lengths in Fig. 6. The short length of 4.5 mm (\({\lambda }_{D}=\) 0.015) gives slightly higher oil recovery, while the 9 mm (\({\lambda }_{D}=\) 0.03) and 18 mm (\({\lambda }_{D}=\) 0.06) cases give approximately equal oil recovery. The corresponding water cut vs. PV and differential pressure vs. PV and dimensionless differential pressure vs. PV profiles for all three cases are almost indistinguishable (see Fig. 7b, c and d).

Fig. 7
figure 7

a Oil recovery, b water cut, c differential pressure and d dimensionless differential pressure for the three correlation length cases in the correlation length sensitivity study

Full size image

The previous work by Sorbie et al. (2020) indicated that, the longer correlation length case showed fewer but thicker fingers and the shorter correlation length gave more, but thinner fingers. The same observation was found for miscible viscous fingering by Mossis et al. (1993). This is also seen in this work as shown in Fig. 8, which shows the local water saturation at various pore volumes injected for the three different correlation length cases. As expected, both more and thinner fingers observed for the dimensionless correlation length of 0.015, while as the correlation length increases, the fingers are fewer and thicker (see Fig. 8). Evaluating the X-ray images of the experiments will help in deciding the correlations length to use for arriving at an accurate match to the experimental data.

Fig. 8
figure 8

Local water saturation development at different pore volumes injected for grid with size 300 × 300 × 1 with random correlated permeability field with dimensionless correlation length of 0.015, 0.03 and 0.06

Full size image

6 Direct Simulations of the Experimental Viscous Fingering Results

In this section, we now present the direct simulation matches of experimental data for the four experiments, referred to as: #412, #616, #2000 and #7000, where the number refers to the oil viscosity, \({\mu }_{o}\). Each of these cases will be presented showing the comparison between the numerical simulation and experiment for the profiles (values vs. pore volumes, PV, injected) of oil recovery, water cut and differential pressure, together with finger development and growth patterns. The corresponding fractional flow, relative permeability curves, and total mobility, i.e. the functions \({f}_{w}^{*}\), \({k}_{rw}\), \({k}_{ro}\) and \({\lambda }_{T}\), will also be presented for each case. After showing the results of simulation and experimental comparisons, these flow description curves will then be compared and discussed in the following section.

The grid with dimensions of 300 × 300 × 1 was used to model the two lower oil viscosity experiments (#412 and #616) as it has sufficiently fine spatial resolution to capture both the early and later finger patterns in these cases. The lower oil viscosity experiments (#412 and #616) show fewer and thicker fingers compared to more viscous oil experiments, as reported below. As water relative permeability is the key parameter for the total mobility, all four experiments were modelled with an end point relative permeability to water as high as possible in order to obtain a high total mobility. The final residual oil, \({S}_{or}\), which in practice is never reached in any of the viscous oil displacement experiments, was set to \({S}_{or}=\) 0.2 in all the relative permeability curves for all simulations.

6.1 Simulation of Experiment with Oil Viscosity \({{\varvec{\mu}}}_{{\varvec{o}}}=\) 412 cP (#412)

The first experiment to be modelled in this study was the \({\mu }_{o}=\) 412 cP oil experiment, with the 2D slab dimensions, 15 cm × 15 cm × 2 cm, i.e. this slab is ¼ of the size of the other experiments. The injection rate was also reduced accordingly, see Table 2. The numerical simulated match to the profiles of oil production, water cut, and differential pressure are shown in Fig. 9. Both oil recovery and water cut are very well modelled and show very good quantitative agreement between experiment and simulation. The oil recovery at 1 PV of injection is \(\sim\) 32.8% at 1PV, and this is very well matched; we will note this quantity for each flood since it shows a systematic trend with viscosity ratio. The differential pressure vs. PV profile shows the correct early time sharp drop (as the fingers break through), but it is slightly underestimated.

Fig. 9
figure 9

Experimental data and simulated a Oil recovery vs. PV, b water cut vs. PV, c differential pressure vs. PV and d dimensionless differential pressure vs. PV for the \({\mu }_{o}=\) 412 cP experiment

Full size image

The experimental fingers in the #412 case were observed to be thicker (from the X-ray scans) than the more viscous oils, and therefore, the permeability field with \({\lambda }_{D}=\) 0.06 was chosen (see permeability field on the right of Fig. 6). A larger \({\lambda }_{D}\) gives thicker fingers during simulation, see Fig. 8. The simulated fingers in Fig. 10 are similar to the experimental ones, with high water saturation being observed experimentally and reproduced numerically in the fingers. The earlier time behaviour of the fingers is matched quite satisfactorily, with approximately the correct number of emergent fingers and the right water saturation (\({S}_{w}\)) levels in the main fingers themselves. However, in the later stages of the flood, somewhat more of the fingers are swept compared to the experimental observations at the end of waterflooding.

Fig. 10
figure 10

Finger development during water injection for the \({\mu }_{o}=\) 412 cP experiment and the corresponding simulated match

Full size image

The fractional flow, \({f}_{w}^{*}\), and the relative permeability curves derived for the #412 case are presented in Fig. 11. The water shock front saturation from the fractional flow curve is \({S}_{wf}=\) 0.434, as shown in the dashed construction line in Fig. 11 (b). It is this \({S}_{wf}\) value that determines the water saturation in the emergent fingers, where the value of \({S}_{w}\) in the finger is \({S}_{w}\) > \({S}_{wf}\). The \({f}_{w}^{*}\) is chosen to get this latter quantity (\({S}_{wf}\)) correct and this is the main factor in obtaining the correct overall recovery, finger saturation patterns, etc. The total mobility \({\lambda }_{T}\) (given by Eq. 1.4) is also shown for this case in Fig. 11 (b). As the viscosity ratio is still adverse, the total mobility is dominated by the water relative permeability curve.

Fig. 11
figure 11

a Relative permeability curves and b Fractional flow and total mobility for the simulated match of the \({\mu }_{o}=\) 412 cP experiment

Full size image

6.2 Simulation of Experiment with Oil Viscosity \({{\varvec{\mu}}}_{{\varvec{o}}}=\) 616 cP (#616)

Figure 12 shows the comparison between the numerical simulation and the \({\mu }_{o}=\) 616 cP experiment. The oil recovery is matched very well up to 1 PV of injection, with a slight overestimation in the middle part (between \(\sim\) 0.2—\(\sim\) 0.6 PV). In addition, the breakthrough time and the subsequent water cut profile vs. PV injected are both very well modelled. The oil recovery at 1 PV of injection is \(\sim\) 25.5% at 1PV and again this is very well matched. The differential pressure vs. PV profile is matched reasonably well, especially over the initial period, although the longer time plateau is lower in the simulation.

Fig. 12
figure 12

Experimental data and simulated matched a Oil recovery, b water cut, c differential pressure and d dimensionless differential pressure for the \({\mu }_{o}=\) 616 cP experiment

Full size image

As the fingers in the X-ray images (see top of Fig. 13) are fewer and thicker compared to the more viscous oil experiments, the dimensionless correlation length here was taken to be \({\lambda }_{D}=\) 0.06 (as in the #412 case). This corresponds to the permeability field on the right of Fig. 6. In the finger development in Fig. 13, clear fingers develop in the simulation, like the ones observed during the experiment. The late-time fingers in the simulation after breakthrough are also broadly similar to the experiment in the lower part of the system. However, there are some detailed differences where the experiment here shows just 2 dominant fingers close to the outlet, presumably due to some feature in the system such as a lower permeability region in the slab or possibly a restriction in flows near the outlet. Our simulation could not be expected to reproduce these detailed (unknown) features, but they capture the overall experimental results very well.

Fig. 13
figure 13

Finger development during water injection for the \({\mu }_{o}=\) 616 cP experiment and the corresponding simulated match

Full size image

The fractional flow, \({f}_{w}^{*}\), for the \({\mu }_{o}=\) 616cP case and the derived relative permeabilities are shown in Fig. 14. The fractional flow for this case has a shock front water saturation of \({S}_{wf}=\) 0.36 which, as expected, is a little lower than the \({\mu }_{o}=\) 412cP case (for which \({S}_{wf}=\) 0.434). The relative permeability curves are similar to the previous reported relative permeability curves; however, the oil relative permeability decreases at a lower water saturation (see Fig. 14). The increase in water relative permeability is sharper here than in the more viscous oil matches (see below). Again, the total mobility is dominated by the water relative permeability.

Fig. 14
figure 14

a Relative permeability curves and b fractional flow and total mobility for the simulated match of the \({\mu }_{o}=\) 616 cP experiment

Full size image

6.3 Simulation of Experiment with Oil Viscosity \({{\varvec{\mu}}}_{{\varvec{o}}}=\) 2000 cP (#2000)

The numerical simulation match to the experimental data for the oil viscosity of \({\mu }_{o}=\) 2000 cP is presented in Fig. 15. The match on the oil recovery vs. PV, and the water cut vs. PV is both excellent for this case. Note that at 1 PV injection, the oil recovery is \(\sim\) 22.3%, which is lower than both the \({\mu }_{o}=\) 412 cP (32%) and 616cP (26%) cases, as expected. The differential pressure profile is satisfactorily reproduced.

Fig. 15
figure 15

Experimental data and simulated a Oil recovery, b water cut, c differential pressure and d dimensionless differential pressure for the \({\mu }_{o}=\) 2000 cP case

Full size image

At the early time, the fingers are both more abundant and also thinner in the more viscous oil experiments. To reflect this, the correlation length is taken as \({\lambda }_{D}=\) 0.03 and the grid resolution in increased to 1000 × 1000 (permeability field on the left side of Fig. 3). Figure 16 shows the experimental fingers together with the simulated fingers from the direct numerical simulation of the \({\mu }_{o}=\) 2000 cP experiment. The finger trend is well captured both before and after breakthrough. However, after breakthrough at the later time, it appears from the finger patterns that a little less bypassed oil is left behind in the simulations.

Fig. 16
figure 16

Finger development during water injection for the \({\mu }_{o}=\) 2000 cP experiment and the corresponding simulated match

Full size image

The relative permeabilities for the #2000 numerical simulation match are given in Fig. 17 (a). These were derived as explained from the fractional flow (\({f}_{w}^{*}\)) shown in Fig. 17 (b) along with the total mobility (\({\lambda }_{T}\)) function. The fractional flow gives a water shock front saturation of approximately \({S}_{wf}=\) 0.2, as shown by the dashed line construction in Fig. 17 (b). This indicates that due to the high viscosity ratio, the water saturations in the fingers will be lower for this case than for the lower oil viscosity cases described above, and this is indeed what is observed experimentally. Figure 17 (a) shows high oil relative permeability until higher water saturations and a rapid increase in water relative permeability occurs above \({S}_{w} \sim\) 0.3. Again, the total mobility is still strongly dependent on the water relative permeability due to the high viscosity oil.

Fig. 17
figure 17

a relative permeability curves and b fractional flow and total mobility for the simulated match of the \({\mu }_{o}=\) 2000 cP experiment

Full size image

6.4 Simulation of Experiment with Oil Viscosity \({{\varvec{\mu}}}_{{\varvec{o}}}=\) 7000 cP (#7000)

The last comparison presented between simulation and experiment is for the most viscous oil displacement experiment where \({\mu }_{o}=\) 7000 cP. This highly adverse viscosity ratio provides a very severe test of out modelling approach (Sorbie et al. 2020). The 1000 × 1000 grid permeability field with \({\lambda }_{D}=\) 0.03 was used in this case (left case in Fig. 3).

Figure 18 shows the oil recovery and water cut profiles (vs. PV) together with the differential pressures vs. PV injected. The match between the simulation and experiment is excellent for all these quantities, although oil production is slightly overestimated in the early stages of the flood (0 – 1 PV) and marginally underestimated towards the end (\(\sim\) 4–5 PV). Water cut and differential pressure are modelled very well. At 1 PV injection, the oil recovery is \(\sim\) 14.7%, which is lower than all the three previous cases where the \({\mu }_{o}=\) 412 cP (32%), 616 cP (26%) and 2000cP (22%) cases. As expected, all four cases show lower oil recovery at 1 PV as viscosity increases, and this is captured very well in the direct numerical simulations.

Fig. 18
figure 18

Experimental data and simulated a oil recovery, b water cut, c differential pressure and d dimensionless differential pressure for the \({\mu }_{o}=\) 7000 cP experiment

Full size image

Figure 19 shows the local water saturation from the experiment together with the numerical simulation results at various pore volumes injected. Note that the white shade is for \({S}_{w}\ge\) 0.3, in this case, and black is for initial water saturation, \({S}_{wi}=\) 0.07 (Table 1). Very good early time agreement is observed in terms of the number of fingers and their “wispy” form; that is, the water saturation in the fingers is relatively low (see \({S}_{wf}\) results below; \({S}_{wf} \sim\) 0.1). At intermediate time (e.g. 0.72 PV in Fig. 19), the finger structure is well reproduced with a few main channels of slightly higher \({S}_{w} \sim\) 0.3. At later time, the simulated fingers are somewhat more dispersed than in the experiment. Thus, the total amounts of fluid (oil and water) in place are accurately modelled since all recoveries and water cut are accurately reproduced and mass balance is exactly maintained. Therefore, there is some small discrepancy in the precise distribution of water in the system.

Fig. 19
figure 19

Finger development during water injection for the \({\mu }_{o}=\) 7000 cP experiment and the corresponding simulated match

Full size image

Figure 20 shows (a) the relative permeability curves (\({k}_{rw}\) and \({k}_{ro}\)) and (b) the water fractional flow (\({f}_{w}^{*}\)) and the total mobility (\({\lambda }_{T}\)), which were used to match the \({\mu }_{o}=\) 7000 cP experimental data above. In this case, we found that a satisfactory match could not be obtained with end point relative permeability to water as high as 1, and it was therefore reduced to 0.5 (see Fig. 20 (a)). The tangent line on \({f}_{w}^{*}\) is also drawn in order to calculate the shock front water saturation which is very low; \({S}_{wf}=\) 0.1, in this case (note that the initial water saturation, \({S}_{wi}\), was very low for this case, \({S}_{wi}=\) 0.07). The relative permeability curves have a high oil relative permeability until water saturation of \(\sim\) 0.2. The water fractional flow curve increases rapidly after \({S}_{wi}\), with a shock front saturation of approximately \({S}_{wf} \sim\) 0.1. From Fig. 20 (b), the total mobility is dominated by the water relative permeability, due to the very high oil viscosity.

Fig. 20
figure 20

a Relative permeability curves and b fractional flow and total mobility for the simulated match of the \({\mu }_{o}=\) 7000 cP experiment

Full size image

7 Comparison of the Matched Flow Functions (\({{\varvec{f}}}_{{\varvec{w}}}^{*}\), \({{\varvec{k}}}_{{\varvec{r}}{\varvec{w}}}\), \({{\varvec{k}}}_{{\varvec{r}}{\varvec{o}}}\) and \({{\varvec{\lambda}}}_{{\varvec{T}}}\))

The results above show that we can obtain very good quantitative matches to all of the observed experimentally measured data (profiles of oil recovery, watercut, pressure drop and finger patterns – all vs. PV) for the four experiments at highly adverse viscosity ratios; with (\({\mu }_{o}/{\mu }_{w}\)) \(\sim\) 400 to 7000. We now compare the flow functions which gave rise to these matches to establish if they show a clear pattern, as functions of viscosity ratio, (\({\mu }_{o}/{\mu }_{w}\)).

The fractional flow curves (\({f}_{w}^{*}\)) for all four experimental matches in this paper are shown in Fig. 21 (a). The shock front water saturation heights (\({S}_{wf}\)) corresponding to each of these fractional flow curves are summarized in Table 3. All of the “base case” fractional flow curves have a similar shape; however, the \({S}_{wf}\) systematically increases as the oil viscosity decreases, corresponding to higher water saturations in the fingers and thus later water breakthrough; that is, the \({f}_{w}^{*}\) for the lower μo cases systematically move to the right in Fig. 21a. The total mobility (\({\lambda }_{T}\)) curves corresponding to the \({f}_{w}^{*}\) curves are shown in Fig. 21b. The \({\lambda }_{T}\) curves continuously reduce as the oil viscosity increases. The water saturation shock front height (\({S}_{wf}\)) increases more rapidly in the lower oil viscosity oil simulations, and this is also observed as the fingers have higher water saturation, and a sharper boundary between finger and outside the finger is observed. The parameters in the simulation match to all experiments vary in a very consistent manner as the viscosity ratio changes. We note that the corresponding RP functions themselves do not show a systematic shift with viscosity ratio (see Figs. 11a, 14a, 17a and 20a). However, we believe that we should consider the actual form of the RP functions much like we consider “pseudo–RPs” which often show such behaviour. It is the fractional flow (fw*) and the maximum mobility curves (\({\lambda }_{T}\)(Sw)) that contain the important physics of viscous fingering here and these change very systematically as shown in Fig. 21.

Fig. 21
figure 21

a Fractional flow and b total mobility as a function of water saturation for all four modelled experiments

Full size image
Table 3 Water shock front height (\({S}_{wf}\)) and fractional flow (\({f}_{w}^{*}\)) and the mobility ratio at the front (\({M(S}_{wf})\)); note that \({f}_{w}^{*}= M/(M+1)\) where \(M\) is the mobility ratio at the shock front
Full size table

We now reconsider the use of the term “mobility ratio”, as it is applied in two-phase flow through porous media. In this work, we have focussed on the mobility ratio at the shock front saturation (\({S}_{wf}\)) for the immiscible finger, denoted by \({M(S}_{wf})\); this is defined above as \(M={\lambda }_{w}{/\lambda }_{o}\) at \({{S}_{w}=S}_{wf}\) and we note that is this a local quantity. As shown in Table 3, this quantity (M) decreases as the oil viscosity, or more accurately the viscosity ratio (\({\mu }_{o}/{\mu }_{w}\)), increases. However, the quantity, “mobility ratio”, is very often defined at the end point saturation of the relative permeability curves, i.e. this specific version of mobility ratio is defined as:

$${\varvec{M}}=\left(\frac{{\lambda }_{w}({S}_{w1}=1-{S}_{or})}{{\lambda }_{o}({S}_{w2}={S}_{wi})}\right)=\left(\frac{{{k}_{rw}\left({S}_{w1}\right). \mu }_{o}}{{{k}_{ro}\left({S}_{w2}\right). \mu }_{w}}\right)$$
(6.1)

This more conventional “mobility ratio” (here denoted by M) is also given in Table 3 and it is clear that this quantity is anti-correlated with the frontal value of this quantity, \({M(S}_{wf})\). These two versions of “mobility” ratio are shown in the log/log plot in Fig. 22 for the simulated matches of the four experiments. The conventional M is in some applications a useful number, although it has two simple drawbacks physically, (i) firstly, as shown in Table 3, it expresses the obvious and simply reflects the viscosity ratio, (\({\mu }_{o}/{\mu }_{w}\)), which is already clear, and (ii) there is of course no local point in the system where M is actually achieved, since it refers to two different values of \({S}_{w}\) (\({S}_{w}={S}_{wi}\) and \({S}_{w}={1-S}_{or}\)). The value \({M(S}_{wf})\), on the other hand, must, by definition, occur in the system and it plays a key role in the displacement, since it is directly related to actual fractional flow of the water phase at the front, since \({{f}_{w}^{*}\left({S}_{wf}\right)=M(S}_{wf})/({M(S}_{wf})+1)\); this is indeed the case for any \({S}_{w}\ge {S}_{wf}\) (above the shock front saturation). To illustrate this point, the relation between our local definition of mobility ratio and local fractional flow is emphasized in Table 3. Following the discussion above, it should be noted that “adverse mobility ratio” usually means a high value of M, and this should really refer to a high value of (\({\mu }_{o}/{\mu }_{w}\)). Also, when using this preceding definition of “adverse” (either M or \({\mu }_{o}/{\mu }_{w}\)), the frontal mobility ratio \({M(S}_{wf})\) is actually decreasing. This is why we prefer to refer to these unstable immiscible floods as “adverse viscosity ratio (\({\mu }_{o}/{\mu }_{w}\))” displacements rather than as “adverse mobility ratio” displacements.

Fig. 22
figure 22

Plot of the conventional “mobility ratio”\(,\) M (which should be replaced by viscosity ratio, (\({\mu }_{o}/{\mu }_{w}\))) vs. the mobility ratio at the displacement shock front, \(M({S}_{wf})\)

Full size image

Figure 23 shows a plot of the calculated \({S}_{wf}\) and \({f}_{w}^{*}\) values vs. the oil viscosity (\({\mu }_{o}\)) for the four experimental matches in Table 3; this is shown as both a linear plot and also as a log/linear plot with the oil viscosity (or \({\mu }_{o}/{\mu }_{w}\)) on a log scale. This again illustrates the systematic reduction in \({S}_{wf}\) and \({f}_{w}^{*}\) as the oil viscosity (or \({\mu }_{o}/{\mu }_{w}\)) increases. As the viscosity ratio (\({\mu }_{o}/{\mu }_{w}\)) increases, more severe fingering is observed, but internally in the fingers the water saturation is lower (\({S}_{wf}\) decreases) and, at the frontal tip of the finger, \({M(S}_{wf})\) decreases. As a result of this, the initial finger numbers increase, but then they become more “wispy” and have a lower water saturation within the fingers.

Fig. 23
figure 23

Plot of the calculated \({S}_{wf}\) and \({f}_{w}^{*}\) values for the four experimental matched in Table 3 showing the systematic reduction in \({S}_{wf}\) and \({f}_{w}^{*}\) as the oil viscosity (or \({\mu }_{o}/{\mu }_{w}\)) increases. a As linear plot and b As log/linear plot

Full size image

We also note that the form of the plot in Fig. 23(b) leads us to the following tentative conjecture: since the system is viscous dominated, then it is possible that this figure may be “universal”. By this, we mean that it is possible that for a given \({\mu }_{o}\) (in fact (\({\mu }_{o}/{\mu }_{w}\)) ratio), then this diagram may be used to read off that \({S}_{wf}\) required from the corresponding \({f}_{w}^{*}\). Hence, this may provide either the answer or at least an excellent starting point based on \({S}_{wf}\) to match any immiscible fingering experiment for a given (\({\mu }_{o}/{\mu }_{w}\)) ratio. This addresses an important question that has been put to the authors on several occasions: how does one go about finding the “correct” \({f}_{w}^{*}\) to match a given two-phase immiscible fingering system? This conjecture is currently being tested.

8 Summary and Conclusions

This paper applies a recently published method proposed by Sorbie et al. (2020) for modelling immiscible viscous fingering to four sets of experimental data on water displacing viscous oils (\({\mu }_{o}=\) 412 cP, 616 cP, 2000 cP and 7000cP), where the porous medium was a 2D sandstone slab. The data modelled include the time profiles of oil recovery, water cut, and differential pressure drop (all vs. PV injected), as well as the actual finger patterns (i.e. the \({S}_{w}\) distributions) at various PV injected. These finger patterns were measured by calibrated X-ray scanning of the slabs during the unstable water oil displacement experiments. For reasons explained previously (Sorbie et al. 2020) and referred to in the literature review in this paper, it has proved to be very difficult to model well-resolved viscous fingering using conventional numerical simulation approaches. However, this new approach involves starting from the fractional flow (\({f}_{w}^{*}\)) which gives the correct water saturations in the fingers, and then working back to the underlying relative permeabilities which give the maximum total mobility while still honouring the chosen \({f}_{w}^{*}\) function. This approach has been shown previously, and in the results presented in this paper, to lead to very well-resolved fingers in these unstable displacements (Sorbie et al. 2020).

In all four experiments modelled, from very good to excellent agreement is found when comparing the direct numerical modelling and experimental results for all quantities measured, including the production and differential pressure profiles (vs. PV) as well as the specific characteristics of the finger patterns themselves.

From our analysis of the matched parameters to the four sets of unstable water displacements (Table 3 and Figs. 22 and 23), a clear picture emerges. This again supports our claim that the \({f}_{w}^{*}\)/maximum \({\lambda }_{T}\) approach can predict clearly defined emergent viscous fingering in unstable immiscible displacements and can quantitatively reproduce all the features observed in the experimental data. The observed trends of higher water saturations in the fingers (higher \({S}_{wf}\)) at lower (\({\mu }_{o}/{\mu }_{w}\)), ratio to successively lower finger \({S}_{w}\) values as this ratio increases are quantitatively reproduced. The result in the immiscible finger patterns is that more fingers are initially produced leading to lower saturation “wispy” fingers at the highest viscosity ratio of (\({\mu }_{o}/{\mu }_{w}\)) \(\sim\) 7000 is reached.

We believe that the very good quantitative agreement between all the simulated and experimental results across a very wide range of (\({\mu }_{o}/{\mu }_{w}\)) viscosity ratios from \(\sim\) 400 to 7000 as reported in this paper, fully validates this new approach to the modelling of immiscible viscous fingering. Furthermore, we present a conjecture based on the results in Fig. 23(b), that this result may be “universal” and that this may point us towards a systematic and general way to establish the correct \({S}_{wf}\), and hence \({f}_{w}^{*}\), required to match any 2 phase unstable immiscible fingering system, given the value of the (\({\mu }_{o}/{\mu }_{w}\)) ratio. Some guidelines are presented in the final section of Sorbie et al. (2020) on how to proceed to match a given set of experiments in terms of choosing the fractional flow function (fw*), developing the maximum mobility RPs and tuning the correlations structure and heterogeneity of the flow field.

In a future paper, we will show that, with no further assumptions, the response of the 2D system to a viscous polymer flood can be readily predicted.

9 Appendix A: Some Comments on “Experimentally Measured” Relative Permeabilities (RPs) for Unstable Immiscible Displacements

Some issues were raised by reviewers of this paper concerning various features of both the mathematical method used in this work and the resulting relative permeabilities (RPs) which arise in the application of this method (Sorbie et al. 2020). The questions arising specifically related to:

  1. (i)

    Why the forms of the RPs that result are “strange” or unfamiliar?;

  2. (ii)

    Are the RPs unique, or indeed is the proposed development of RPs actually ill-posed?;

  3. (iii)

    The issue of what exactly “drives” the immiscible fingering instability; is it viscosity ratio (μo/μw) or “mobility ratio”? And if the latter, which mobility ratio, M or M(Swf)? ( see main text for a clear distinction).

To some extent, when we consider the concept of RP in viscous unstable displacement experiments, we are revisiting the matters discussed by Maini (1998), who posed the question: It is futile to measure relative permeabilities for heavy oil reservoirs? To understand the viewpoint of this paper and also the issues listed above, we first need to remind the reader that we never directly “ measure” relative permeabilities (RPs) experimentally. Instead, we actually measure pressures and pressure drops, volumetric flows and (sometimes) in situ saturations – the latter by calibration, not quite directly. There is no machine like an ammeter or pressure transducer that “measures” RP. We then use a model based on the multiphase Darcy Law incorporating the concept of RP to decide what the actual RP should be. Which model we use, and the assumptions we make using it, will determine what the resulting RP functions looks like. We may do this by (a) history matching using a numerical simulator (including or omitting capillary pressure, Pc), (b) we may use the JBN method or some variant of this, (c) we may use a 1D SCAL model (neglecting or allowing for capillary end effects); and other model choices can be made. The process is known to be highly non-unique and indeed can often be ill-posed, especially for viscous unstable process. What the RP actually “looks like” depends on the data that is collected, how accurate it is, a number of experimental artefacts and the actual model that is used to process the data. Incidentally, this issue is not averted by determining the RPs by a “steady-state” experimental RP method since these have been found by experiment not to agree with the unsteady-state method for viscous oils (Maini et al. 1990).

When viscous fingering occurs, some of the assumption made in conventional RP experiments are clearly wrong e.g. assumptions such as: the system is 1D, a Buckley-Leverett model describes the saturation profiles, etc. Therefore, in the approach used for modelling viscous instability in our current work (Sorbie et al. 2020) starting with fw*, maximising mobility (λT(Sw)) etc., we have made our assumptions quite clear. Firstly, we assume fingering does occur (since we can see is clearly present from in-situ monitoring). We then continue applying our procedure and we obtain the “strange” RPs shown in this work. Like any normal consistent model, when we put these RPs back into the simulator, it reproduces the observations (as it must), consistent with the underlying assumptions. Therefore, however “strange” these RPs are, they are at least as valid as “normal” RP measurements. We would say they are more valid since we already know that viscous instability is present, which conventional RPs do not reproduce very well (as discussed in the literature review and elsewhere in this paper). In other words, the RPs we derive, using the procedure described in the core flooding paper by Beteta et al. (2022) and in this present paper are actually “experimentally derived” RPs; note that we avoid the word “measured”. However, we have shown that these RPs also have the added advantage of having some predictive value in that, (a) they clearly show viscous fingering patterns very consistent with the experimental observations, and (b) with no additional assumptions they are able to predict the polymer response.

Can we be sure that our resulting RPs are “unique” or indeed that our method of obtaining them is actually “ill posed”? The answer here is that they are no more unique (or ill posed) than any other approach to “calculating” RPs. The RPs we derive are probably somewhat better constrained than most “conventional” RP measurements since so much data is matched in deriving them. However, our RP functions are affected in a major way by the actual method/assumptions used to derive them, exactly like all other methods.

Having said the above and given that there is certainly some degree of non-uniqueness in the system, then we can address the issue of whether it is viscosity ratio (μo/μw) or mobility ratio ( M or M(Swf)?) that “drives” the instability in the system. We claim that for our model it appears to be the viscosity ratio (μo/μw) which drives the instability, since the RPs are already maximum mobility RPs (as explained in Sorbie et al. 2020). The RPs in our model are the experimental RPs, under our assumption and they match all the data. And since we calculate and present both the viscosity ratio (μo/μw) and the values of M here, and they are not much different except for the 7000cP case (see Table 3), it is simply our preference here to use the former. Our reasons for doing so are clearly explained in the discussion in Sect. 7.

However, if one takes the “conventional” model (e.g. using Corey type RPs), we would not be too surprised if one could find some combinations of RP with highly adjusted end point values and much lower viscosity ratio that might give “genuine” developed fingering. By “genuine” we mean highly ramified fingering of the type observed in the experiments and our modelling of them in this paper. For such a “conventional” model, then under the assumptions of this model, it may appear that the mobility ratio (including RP end points) was actually the driving parameter of immiscible viscous instability. However, we note that to date, no cases like this have yet been reported in the literature, and we pose the question: Where are these cases if this is possible? We believe the results discussed in our literature review (e.g. Riaz and Tchelepi (2006), Berg and Ott (2012) etc.) support this view.