Introduction

Manganese reactivity has attracted particular attention since its ions are present in the active sites of many enzymes and participate in very important biological processes [1, 2]. A key topic in this field is the oxidation of water into molecular oxygen, which is catalyzed by a CaMn4 cluster in photosystem II [3]. Although recent progress in solar energy research has led to an increased interest in photosynthesis and artificial photosynthesis [4, 5], the structure of this cluster is still unknown [6–9] and very few manganese-based homogeneous catalysts have been reported to evolve oxygen upon oxidation [10, 11]—an observation that, however, has recently been questioned [12]. The ability to catalyze the heterolytic cleavage of the O–O bond in hydrogen peroxide and molecular dioxygen by manganese has been recently intensively studied [13]. Despite the mechanism of these processes catalyzed by heme oxygenases, such as cytochrome P450, cytochrome c oxidase, peroxidases, and catalase being known [14–19], direct observation of the O–O bond cleavage has been difficult due to the complex catalytic cycles, short-lived iron intermediates, and required cryogenic conditions. High-valent manganese oxo intermediates are more stable and can be functional analogs of heme proteins appearing in many biological systems using hydrogen peroxide and molecular dioxygen [13]. Recently, a bridged manganese(V) porphyrin dimer was shown to oxidize water into dioxygen, [20] and reversible O–O bond cleavage was observed for a manganese corrole system [21, 22], and the design of novel, long-lived manganese(III) complexes, which can be a model of the precursor of the endogenous high-valent peroxo and oxo intermediates, has been published recently [23]. A special emphasis has been focused on manganese species as effective catalysts in the degradation reactions of many organic species [24, 25]. In this study, a detailed account of the mechanistic features as well as the kinetic parameters for the oxidative transformation of phenothiazines by manganese(III) is provided. Details of the powerful and environmentally friendly manganese(III) complexes that act as very efficient oxidants for many oxidative degradation processes, were sought in an effort to develop new methods for the clean oxidation of pharmacologically active phenothiazines, and select the most effective methods with potential applications in green chemistry for the disposal of this class of pharmaceuticals.

Experimental

Materials

Manganese acetate (Mn(CH3COO)3·H2O, Aldrich), promazine, chlorpromazine, promethazine, trifluoperazine (Sigma-Aldrich), and all other chemicals were analytical grade reagents. Water purified in a Millipore Milli-Q system was used to prepare all the solutions. The stock solutions of manganese(III) were prepared by dissolving manganese acetate in 0.1 M Na4P2O7 and 1.0 M H3PO4. The concentration of a stock solution of manganese(III) was determined iodometrically. The solution was stable for a few days when stored at 5 °C. The stability of manganese(III) has been analyzed in different pyrophosphate and phosphate media by Klewicki [26]. Manganese(III)-pyrophosphate is unstable at higher temperatures and undergoes a disproportionation reaction, which can be facilitated by OH− ions, as well as by lower than 10 molar ratio of L T /MnT, where T is a total concentration of pyrophosphate and manganese, respectively [26]. The desired solutions of manganese(III) were prepared before each series of kinetic measurements. Aqueous solutions of chlorpromazine (Sigma-Aldrich) and other phenothiazine derivative were stored in the dark because of their photosensitivity.

Kinetic measurements

The kinetic measurements were performed on a Shimadzu UV-1601 PC spectrophotometer equipped with a six-position cell-holder. Kinetic data were acquired and processed using the UVPC personal spectroscopy software. In all measurements, the solutions were thermostated to the desired temperature (±0.1 °C) with an external Julabo F25 ultrathermostat. The reaction rate was recorded by monitoring the disappearance of the phenothiazines radicals visualized by the decrease in absorbance at 514 nm for phenothiazines radicals electron transitions in accordance with literature data: λmax, nm (εmax, dm3 mol−1 cm−1): promazine radical, 513(9200) [27], chlorpromazine radical, 525(10200) [27], promethazine radical, 515(9300) [27], and trifluoperazine radical, 502(9000) [28]. In the same visible spectral region, the characteristic electronic transition of the manganese(III)-pyrophosphate ion is observed, λmax, nm (εmax, dm3 mol−1 cm−1): 513(85). On account of the marked difference in molar absorption coefficients for reactants, the changes in absorbance, which were monitored as a function of reaction time and resulted from the change of oxidant concentration, were low, ca. 0.01. The reaction rate was determined as a function of the manganese(III) concentration: [PTZ] = 5 × 10−5 M, [MnIII] = (0.5–4.5) × 10−3 M, [P2O7 4−] T  = 0.1 M, [Na4P2O7] T  = 0.1 M, [H3PO4] T  = 1.0 M, [H+] = 0.04 M, I = 0.45 M (H+, H2PO4 −, Na+, H3P2O7 −, and H2P2O7 2−), T = 288–308 K. In another series of experiments, the reaction rate dependence on the H+ concentration was determined: [PTZ] = 5 × 10−5 M, [MnIII] = 1.5 × 10−3 M, [P2O7 4−] = 0.1 M, [H3PO4] = 0.3–1.0 M, [H+] = 0.005–0.04 M, I ≠ const, T = 298 K. The time scale was 4,800–200 and 5,800–500 s (95%) for chlorpromazine and trifluoperazine, respectively. The pseudo-first-order rate constants were calculated using a non-linear fitting procedure to the first-order absorbance dependence versus time. At least three kinetic runs were recorded for every set of the reagent concentrations, and the reported rate constants represent the average values. The relative standard errors of the pseudo-first-order rate constants for a single kinetic trace were ca. 0.5–1%, and relative standard errors of the mean value were usually ca. 1–2%. Additionally, the kinetic traces for the first-order and second-order radical decay at higher pH > 1 were analyzed by the integral solution derived from the differential equation of the concentration derivative of radical dependence versus time using the Mathematica 7 program.

The kinetics of radical disproportionation were studied spectrophotometrically at 514 nm in acidic sulphate media. The phenothiazine radicals were generated in situ in 0.01 M phenothiazine derivatives dissolved in concentrated acid solution (95%, Aldrich). This process did not lead to the complete conversion to the stable phenothiazine radicals (ca. 25–50% yield). The phenothiazine derivatives are photosensitive, and free radicals were stabilized by sulphate or by the H+ ion in concentrated acid solution. The free radicals appear also in non-oxidizing concentrated HCl acid, but this process proceeds with lower yield than in the sulphuric acid solution. The concentrated HNO3 acid oxidized phenothiazines directly to phenothiazine 5-oxide. The reaction rate in acidic sulphate media was determined in dependence of the H+ concentration: [PTZ] = 1 × 10−2 M, [PTZ+.] = (0.2–1.2) × 10−4 M, [H2SO4] = (0.35–1.65) M, I ≠ const, T = 298 K. In a few cases, the reaction rate was measured at different concentrations of phenothiazines: [PTZ] = 1 × 10−2 M, [PTZ+.] = (0.2–1.2) × 10−4 M, [H2SO4] = 1.0 M, [H+] = 1.2 M, I = 1.4 M (H+, HSO4 −, SO4 2−), T = 298 K. The second-order rate constants were calculated by fitting to the linear inverse of concentration derivative of radical dependence versus time.

Results and discussion

The kinetics of the oxidative transformation of phenothiazine derivatives by manganese(III) complexes have been studied in acidic phosphate—pyrophosphate media ([PTZ] = 5 × 10−5 M, [MnIII] = (0.5–4.5) × 10−3 M, [Na4P2O7] T  = 0.1 M, [H3PO4] T  = 1.0 M, [H+] = 0.04 M, I = 0.45 M (H+, H2PO4 −, Na+, H3P2O7 −, H2P2O7 2−), T = 288–308 K). Manganese(III) ions are more stable in pyrophosphate media and slowly decompose with rate constants ranging from 3 × 10−7 to 1.5 × 10−8 s−1 and half-lives of 25–530 days in the pH range 7–9 [26]. The stability decreases with increasing pH as well as with decreasing the molar ratio of L T /Mn T . At values of L T /Mn T lower than 10, decomposition half-lives decrease to only 5 h at pH = 8 [26]. For pH > 9, disproportionation and precipitation of a MnO2 oxide is observed. At pH < 7, stability decreases mainly by protonation of the ligand and liberation of protonated pyrophosphate resulting in MnO2 precipitation, which begins to occur after 7 days at pH = 1–2. There are large discrepancies in stability constants published in the literature [29, 30], and it is not obvious that these data can be assumed to be useful in the determination of molar percentage of manganese(III) ions with pyrophosphate. Taking into account, the values of the acidity constants for pyrophosphoric acid (pK1a = 0.91, pK2a = 2.10, pK3a = 6.70, and pK4a = 9.32) [31], we could show that the manganese(III) is coordinated with H2P2O7 2− ion at pH = 1.4 and exists mainly as the [Mn(H2P2O7)2]− ion. The acidity constants of proton active groups that are present in free ligands decrease usually after coordination to transition metal ions.

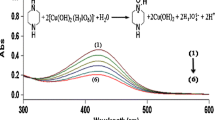
The oxidative degradation of phenothiazine derivatives proceeds via two consecutive reaction steps, in which transformation of a PTZ radical is followed by faster oxidation of PTZ to the radical intermediate. In acidic solution, only one final product was detected, phenothiazine oxide. As can be seen in Fig. 1, the characteristic spectral changes in UV–vis. spectra are consistent with a consecutive increase in absorbance in the n–π* band at 500 nm for the trifluoperazine radical and 525 nm for the chlorpromazine radical. These spectral changes are consistent with the appearance of an intensively colored cationic radical intermediate. The cationic phenothiazine radical is known to be very stable in acidic solution [32, 33] and is only slowly transformed to the final product. The latter process is consistent with the decrease in absorbance in the n–π* band at 500–525 nm and is accompanied by the subsequent increase in absorbance in the π–π* band in the range 300–400 nm. The final product was characterized on the basis of the known positions of the electronic transition band at 340 nm, characteristic for chlorpromazine oxide, and at 347 nm, for trifluoperazine oxide [34].

Fig. 1
figure 1

Spectral changes during chlorpromazine degradation by manganese(III). Experimental conditions: [PTZ] = 5 × 10−5 M, [MnIII] = 5 × 10−4 M, [Na4P2O7] T  = 0.1 M, [H3PO4] T  = 1.0 M, pH = 1.4 (phosphate buffer), I = 0.45 M (H+, H2PO4 −, Na+, H3P2O7 −, H2P2O7 2−), T = 298 K, 2, t = 5,616 s, Δt = 216 s

Full size image

Although oxidative degradation of phenothiazines proceeds in accordance with a two-step consecutive reaction scheme, the first-order approximation has been applied. It can be justified by the significant differences in the rates of the two processes mentioned above. Kinetic measurements apply mainly to the second, much slower PTZ+. radical oxidation reaction, leading to PTZ+2, which then hydrolyzes to phenothiazine oxide (Scheme 1). Pseudo-first-order rate constants were calculated from the first-order dependence of absorbance versus time using a non-linear least-square method. The relatively low standard deviations in the determination of rate constants for the single kinetic trace and the good convergence between experimentally and theoretically determined absorbance values seem to confirm the use of this approximation. Pseudo-first-order rate constants are presented in Table 1; clearly the dependence of manganese(III) is linear with significant non-zero intercepts (Fig. 2). The linear regression data are presented in Table 2 and can be expressed as follows:

$$ k_{\text{obs}} = k_{ - 2}^{\prime } + k_{2}^{\prime } [{\text{Mn}}^{\text{III}} ] $$
(1)

in which the intercept and slope have been determined as the pseudo-first-order (k′−2) and second-order rate constants (k′2), respectively. In fact, the values of the intercepts should be close to zero as is expected for strong oxidants, for example, cerium(IV). These data mean that another process takes place at lower concentration of H+ ion and pH > 1. Under such conditions, a competing reaction to the oxidation process might be disproportionation of phenothiazines radicals [32]. In that case, the kinetic traces should be characterized by the first-order and second-order radical decay according to the following concentration dependences versus time:

$$ A = 1/((1/A_{\text{o}} )\exp (k_{2} t) + (2k_{3} /k_{2} )(\exp (k_{2} t) - 1)) $$
(2)

as a result of integration of the differential equation, d[A]/dt = −k 2[A] − 2k 3[A]2, where A is the concentration of radical, k 2 is the first-order, and k 3 is the second-order rate constant for dismutation. Preliminary tests showed that only at the lowest manganese(III) concentration, small deviations from first-order kinetics occurred in the first few percent of conversion; therefore, the highest but statistically low (ca. 2%) value of standard deviation of the rate constant for a single kinetic trace has been evaluated. A statistically significant decreasing trend in standard deviation was observed for higher oxidant concentrations (ca. 1%). In the case of more stable radicals, such as promazine, chlorpromazine, and trifluoperazine, slow disproportionation influences only the intercept (Fig. 2) in the observed rate constant dependence on [MnIII]. In the case of more reactive radicals like promethazine (data not shown), the observed rate constants should be fitted by Eq. 2.

Scheme 1
scheme 1

The mechanism of the reaction between phenothiazine derivatives and the manganese(III) ion

Full size image
Table 1 Observed pseudo-first-order rate constants for the reaction between phenothiazine radicals (k obs) and the manganese(III) ion
Full size table
Fig. 2
figure 2

Plots of k obs versus [PTZ] for the electron-transfer reaction between chlorpromazine and manganese(III) at different temperatures. Experimental conditions: [PTZ] = 5 × 10−5 M, [Na4P2O7] T  = 0.1 M, [H3PO4] T  = 1.0 M, pH = 1.4 (phosphate buffer), I = 0.45 M (H+, H2PO4 −, Na+, H3P2O7 −, H2P2O7 2−), T = 288 (filled square), 298 (filled circle), 308 (filled triangle) K

Full size image
Table 2 Linear regression data for the plots of kobs versus [MnIII] (Fig. 2) for the reaction between phenothiazine radical and the manganese(III) ion
Full size table

However, when the pH is increased, an increasingly important influence of the disproportionation process is detected even for the most stable trifluoperazine and chlorpromazine radicals. In 0.2 M (pH = 4.0) phosphoric acid solution, the value of the observed first-order rate constant differs significantly from the other results (Fig. 3). In other cases, k obs values are similar to each other. Due to the fact that the increase in the value of the observed rate constant with increasing pH for both trifluoperazine and chlorpromazine is similar and covers the pH range outside the pKa of these compounds (9.2 for chlorpromazine) [35], changes might be attributed to either changes in the coordination sphere of the complex of manganese(III) or a change in rate of disproportionation. At pH > 2, manganese(III) undergoes a further coordination reaction with pyrophosphates; this process causes the blue-shift of the transition band from 513 to 479 nm (pH = 5.5). An increasing concentration of the manganese(III) complexes with two and three coordinated pyrophosphates will cause a decrease in the redox potential, which at pH = 1.5 is 1.25 V. This will reduce the rate of oxidation reaction proceeding with an outer-sphere mechanism. Thus, the changes observed and increase in the overall degradation rate with increasing pH can be attributed to the increased rate of disproportionation. The kinetic trace at higher pH corresponds to the function characterized by the first- and second-order decay (Eq. 2). The rate constants of oxidative degradation calculated for kinetic traces at pH = 1.4, do not differ from the values calculated from the first-order dependence, while for pH = 4.0 they varied in the same trend as the redox potential of the MnIII/MnII couple (Table 2).

Fig. 3
figure 3

Plots of [PTZ+·] versus time for the reaction between chlorpromazine radical and the manganese(III) ion. Experimental conditions: [PTZ] = 5 × 10−5 M, [MnIII] = 1.5 × 10−3 M, I ≠ const (H+, H2PO4 −, Na+, H3P2O7 −, H2P2O7 2−), T = 298 K, A pH = 4.0, 1st order fit, Chi2 = 6 × 10−13, k 2 = 0.0041 ± 0.0001; B pH = 4.0, 1st + 2nd order fit, Chi2 = 1 × 10−14, k 2 = 0.00058 ± 0.00001, k 3 = 157 ± 1; C pH = 1.4, Chi2 = 6 × 10−14, k 2 = 0.0026 ± 0.00001; D pH = 1.4, Chi2 = 2 × 10−14, k 2 = 0.00231 ± 0.00002, k 3 = 6.6 ± 0.3

Full size image

Levy et al. [32] reported the stability of 10-alkylphenothiazine free radicals in response to the Hammett acidity function in sulphuric acid solutions [36]. Because the Hammett function is more convenient for concentrated acid solutions and no detailed data for more dilute solutions are available, we decided to measure the rate of the disproportionation reaction of these phenothiazine derivatives in sulphuric acid solution in the range of 0.35–1.65 M. Phenothiazine free radicals were produced directly in concentrated sulphuric acid (95%), in which they are very stable. The choice of acidic sulphate media resulted in the highest yield of phenothiazine free radicals. The second-order rate constants were calculated from the reciprocal of concentration versus time according to the following equation:

$$ 1/A-1/A_{\text{o}} = 2k_{3} t $$
(3)

where A, as before, is concentration of radical and A o, is initial concentration at time t = 0. The second-order rate constants are presented in Table 3. The rate of radical disproportionation decreases with increasing H+ concentration, and phenothiazine radicals are more stable at higher acid concentration. The plot of the second-order rate constants versus [H+] is non-linear (Fig. 4). This characteristic trend is not affected by ionic strength because the positively charged radicals should react with a higher rate at increased ionic strength. The hydrogen ion concentration increases the stability of the free radical and decreases the rate of the disproportionation not directly, but probably via interaction of cationic radicals with sulphate or other negatively charged ions of electrolyte present in aqueous solution. The second-order rate constants were found to be inversely proportional to the initial concentration of free radical, although this tendency was not so significant as for the decreasing rate dependence on the H+ concentration (see Table 3). It may be a consequence of the reversibility of the disproportionation process, and the reverse comproportionation reaction takes place. Thus, the observed rate constant is expected to be the sum of the second-order rate constant for disproportionation and the second-order rate for the reverse process with regeneration of reactant in the reaction mixture. The second-order rate constants, calculated from linear regression data (first few experimental points), at [H+] = 0.04 M, in which the reaction with manganese(III) has been studied, are 8.8 and 9.2 M−1 s−1 for chlorpromazine and trifluoperazine radical, respectively. These variables are close to the values of k′−2/[PTZ+·] for the reaction with manganese(III), which were estimated as 12.8 and 25 M−1 s−1, respectively. The similarity of these quantities confirms the hypothesis that the oxidative degradation proceeds simultaneously with the disproportionation as a competing reaction. Nevertheless, this latter process should proceed with a higher rate in phosphate than in sulphate media.

Table 3 Selected second-order rate constants for disproportionation of phenothiazine free radicals in acidic sulphate media
Full size table
Fig. 4
figure 4

Plots of k 3 versus [H+] for the disproportionation of chlorpromazine free radicals. Experimental conditions: [PTZ] = 1 × 10−2 M, [PTZ+·] = 1.2 × 10−4 M, [H2SO4] T  = 0.35 − 1.15 M, [H+] = 0.4 − 1.4 M, I ≠ const, T = 298 K

Full size image

The reaction with manganese(III) proceeds according to an outer-sphere mechanism. This conclusion is supported by the fact that the rate of the electron-transfer process can be correlated with the reduction potential, E +·PTZ /PTZ = 0.6 V and E +·PTZO/PTZ  = 1.0 V for chlorpromazine and E +·PTZ /PTZ = 0.7 V and E +·PTZO/PTZ  = 1.0 V for trifluoperazine [37]. The very similar reactivities of phenothiazine free radicals with manganese(III) are consistent with the similar values of reduction potential of E +·PTZO/PTZ . These similarities result from the similar electronic structures of the radicals as seen from the ionization energy of HOMO orbitals. As can be seen, the relevant electron-transfer reaction proceeds with a similar negative entropy of activation. The negative values of ΔS≠ indicate that this process is accompanied by extensive solvation related to charge creation in the activation process and with similar changes of charge and solvation effects for creating a 2+ cationic phenothiazine transient in the activation process.

Manganese(III)-pyrophosphate complexes act as very efficient oxidants for phenothiazine derivative degradation processes, and can be useful in an effort to develop new methods for the clean oxidation of pharmacologically active phenothiazines, and selecting the most effective and environmentally friendly manganese(III) oxidants with potential applications in green chemistry for the disposal of this class of pharmaceuticals. Compared to manganese(III)-pyrophosphate, the green oxidants, such as oxygen or hydrogen peroxide, react slowly and require the use of transition metal complexes as catalysts for the oxidation process [38, 39].