3D Human Pose Tracking Priors using Geodesic Mixture Models

Abstract

We present a novel approach for learning a finite mixture model on a Riemannian manifold in which Euclidean metrics are not applicable and one needs to resort to geodesic distances consistent with the manifold geometry. For this purpose, we draw inspiration on a variant of the expectation-maximization algorithm, that uses a minimum message length criterion to automatically estimate the optimal number of components from multivariate data lying on an Euclidean space. In order to use this approach on Riemannian manifolds, we propose a formulation in which each component is defined on a different tangent space, thus avoiding the problems associated with the loss of accuracy produced when linearizing the manifold with a single tangent space. Our approach can be applied to any type of manifold for which it is possible to estimate its tangent space. Additionally, we consider using shrinkage covariance estimation to improve the robustness of the method, especially when dealing with very sparsely distributed samples. We evaluate the approach on a number of situations, going from data clustering on manifolds to combining pose and kinematics of articulated bodies for 3D human pose tracking. In all cases, we demonstrate remarkable improvement compared to several chosen baselines.

Appendices

Appendix 1: Derivation of Mixture Models on Riemannian Manifolds

We follow the standard expectation-maximization approach to maximize the log-likelihood of our model adapting it to Riemannian manifolds. For simplicity, we will not consider the Minimum Message Length criteria for model selection. We start out by defining the log-likelihood of the model $\lambda (x,\theta )$ and bounding it by Jensen’s equality:

$$\begin{aligned} \lambda (x,\theta )&= \sum _{i=1}^N \log \sum _{k=1}^K \alpha _k p(x^{(i)}|\theta _k) \nonumber \\&\ge \sum _{i=1}^N \sum _{k=1}^K w^{(i)}_k \log \frac{ \alpha _k p(x^{(i)}|\theta _k) }{ w^{(i)}_k } = B(x,\theta )\;. \end{aligned}$$

(37)

with $w_k^{(i)}$ as auxiliary variables that represent membership probabilities. We can maximize over the lower bound $B(x,\theta )$ instead of the untractable full likelihood.

1.1 E-step

The E-step consists of maximizing the auxiliary terms $w_k^{(i)}$ which are the membership probabilities of the samples. This is done by solving:

(38)

This is straight forward to do by computing the derivative and equating it to 0 to obtain the update rule for step t:

$$\begin{aligned} w_k^{(i)}(t) = \frac{\alpha _k(t-1) p(x_i|\theta _k(t-1))}{\sum _{k=1}^K\alpha _k(t-1)p(x_i|\theta _k(t-1))}\;. \end{aligned}$$

(39)

1.2 M-step

In this step, we have fixed w and are updating the other parameters $\theta =(\mu ,\varSigma )$ and $\alpha$ by solving:

$$\begin{aligned} \begin{aligned}&{\mathop {\hbox {arg max}}\limits _{{\theta ,\alpha }}}&B(x,\theta ) \\&\text {subject to}&\sum _{i=1}^K \alpha _k = 1 \\&&\alpha _k \ge 0 , k=1,\ldots ,K \;. \end{aligned} \end{aligned}$$

(40)

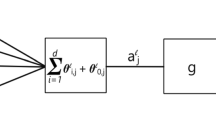
We shall follow the same approach as in the E-step and compute the partial derivatives to obtain the update rules. In particular, both $\alpha$ and $\varSigma$ are straight forward to compute, and do not significantly deviate from the standard formulation. Thus for $\alpha$ we obtain:

$$\begin{aligned} \alpha _k(t) =\frac{1}{N}\sum _i^N w_k^{(i)}=\frac{w_k}{N} \;, \end{aligned}$$

(41)

and for $\varSigma$:

$$\begin{aligned} \frac{\partial B(x,\theta )}{\partial \varSigma _k} = \frac{1}{2} \sum _{i=1}^N w_k^{(i)} \left( \log _{\mu _k}(x^{(i)})\log _{\mu _k}(x^{(i)})^\top - \varSigma _k \right) \;, \end{aligned}$$

(42)

and thus,

$$\begin{aligned} \varSigma _k(t) = \frac{ \sum _{i=1}^{N} w_k^{(i)} \log _{\mu _k}(x^{(i)})\log _{\mu _k}(x^{(i)})^\top }{ \sum _{i=1}^{N} w_k^{(i)} } \;. \end{aligned}$$

(43)

For the mean $\mu _k$ we can follow the same approach, however, due to the logarithmic map, it is slightly different to resolve. We start out by computing the partial derivative:

$$\begin{aligned} \frac{\partial B(x,\theta )}{\partial \mu _k} = \sum _{i=1}^{N} w_k^{(i)} \varSigma ^{-1}_k \log _{\mu _k}(x^{(i)}) \frac{\partial \log _{\mu _k}(x^{(i)})}{\partial \mu _k} \;. \end{aligned}$$

(44)

In general, there is no analytic solution to $\frac{\partial \log _{\mu _k}(x^{(i)})}{\partial \mu _k}$. However, under the assumption that $\frac{\partial \log _{\mu _k}(x^{(i)})}{\partial \mu _k} = c$ where $c \ne 0$ is a constant, and equating the partial derivative to 0, we can obtain:

$$\begin{aligned} \sum _{i=1}^N w_k^{(i)} \log _{\mu _k}(x^{(i)}) = 0 \;. \end{aligned}$$

(45)

For simply connected and complete manifolds whose curvature is non-positive (i.e., Hadamard manifolds) and bounded from below, there exists one and only one Riemannian center of mass which is characterized by $E[\log _{\mu }(x)]=0$ Darling (1996). Note that a compact and simply connected manifold with a non-positive and bounded from below curvature has no cut locus. In this case, as Eq. (45) is the discrete expectation of the weighted sum, we can establish the update rule for the mean by:

$$\begin{aligned} \mu _k(t) = {\mathop {\hbox {arg min}}\limits _{p}} \sum _{i=1}^N d\left( \frac{N}{w_k} w_k^{(i)} x^{(i)},\; p\right) ^2. \end{aligned}$$

(46)

Note that this does not hold for the case in which there is a cut locus, in which case there may not be only one Riemannian center of mass. However, in practice, this approach will generally converge to the center of mass. We will use Eq. (46) in all cases.

Finally, we perform a numerical analysis of the error for the $S^2$ sphere by numerically computing $\frac{\partial \log _{\mu _k}(x^{(i)})}{\partial \mu _k}$ and visualizing the results. In particular we visualize the change of Frobenius norm of the Jacobian in Fig. 10. We can see that points near the origin have very little change in the derivative. Again, the use of multiple tangent planes favors configurations in which the points are close to the center, and thus, keeps the error produced by approximating the partial derivative to a constant within reasonable bounds.

Fig. 10

Plot of the change Frobenius norm of $\frac{\partial \log _{\mu _k}(x^{(i)})}{\partial \mu _k}$. We compute the derivative numerically using a first order approximation as there is no analytic form. We can see for points near the center there is small change in the derivative and thus little error in the approximation we make by considering the derivative to be constant. For visualization purposes we only display points with a change of under 10 units

Appendix 2: Clustering with Von Mises–Fisher Distributions

Given a random vector x on the unit hypersphere of dimension $q-1$, the probability density function of a von Mises–Fisher distribution with mean direction $\mu$ and concentration $\kappa$ can be written as:

$$\begin{aligned} f_q(x | \mu ,\kappa ) =&c_q(\kappa ) e^{\kappa \mu ^\text {T} x } \quad , \nonumber \\ c_q(\kappa ) =&\frac{\kappa ^{q/2-1}}{(2\pi )^{q/2}I_{q/2-1}(\kappa )} \quad , \end{aligned}$$

(47)

where $\Vert \mu \Vert =1$, and $I_{q/2-1}$ is the modified Bessel function of first kind and order $q/2-1$. Note that the concentration parameter $\kappa$ is a single scalar that represents a uniform distribution on the sphere for $\kappa =0$ and is unimodal for $\kappa >0$.

The algorithm from Figueiredo and Jain (2002) can be modified to use von Mises–Fisher distributions by adapting the way the distributions are recalculated in the M-step. This can be computed by:

$$\begin{aligned} r_k =&\sum _{i=1}^N w_k^{(i)} x^{(i)} \quad , \end{aligned}$$

(48)

$$\begin{aligned} \mu _k(t) =&\frac{r_k}{\Vert r_k\Vert } \quad , \end{aligned}$$

(49)

$$\begin{aligned} \kappa _k(t) =&\frac{\Vert r_k\Vert (q-\Vert r_k\Vert ^2)}{1-\Vert r_k\Vert ^2} \quad . \end{aligned}$$

(50)

As there exists no analytic form of $I_{q/2}(\kappa _k(t))/I_{q/2-1}(\kappa _k(t))=r_k$, the computation of $\kappa _k(t)$ is indeed an approximation Banerjee et al. (2005).