On the seismic stability of soil slopes containing dual weak layers: true failure load assessment by finite-element limit-analysis

Abstract

Seismic stability analyses of soil slopes in the presence of weak interlayers are rather challenging within the framework of plasticity theory, due to the construction of kinematically admissible velocity fields and statically allowable stress fields at limit state. Finite-element limit-analysis procedures including finite-element upper-bound (FEUB) and finite-element lower-bound (FELB) approach are introduced in this study, retaining the merits of FEM and limit analysis theory to tackle above issues. Incorporating modified pseudo-dynamic approach, seismic slope stability analyses are transformed to linear programming models, in terms of lower- and upper-bound formulations. Pseudo-static and modified pseudo-dynamic solutions of the factor of safety (FoS) are sought through optimization with an interior-point algorithm. An appealing merit of the proposed procedure is that both lower and upper bounds are searched, aiding to better estimate the true solution of FoS. Limit equilibrium and Abaqus are applied to validate FEUB and FELB results. Effects of dual weak interlayers’ position and dimension on seismic slope stability are investigated. Critical failure surface and velocity field are plotted by post-processing, demonstrating a rotational-translational failure mechanism. Based on less than 5% difference between lower- and upper-bound solutions, the proposed procedure is capable of providing a reliable guidance for slope design and assessment.

1 Introduction

Layering soils widely exist in site, due to complex geological conditions and formation processes. There are some cases where soil strength parameters of certain layers are much smaller than neighboring soils, behaving as weak interlayers. Performing a slope stability analysis in the presence of weak interlayers is a rather tough issue in geotechnical engineering. Therefore, such issue has not been comprehensively investigated till now, although it is not uncommon in engineering practice. Numerical simulation, physical modelling and limit equilibrium are commonly used approaches for slope stability analysis. Comparatively, adoption of numerical techniques, such as FLAC [8], MPM [1], and FEM [9], is relatively straightforward to account for complex weak interlayers. The efficacy of numerical modeling is satisfactory, but the reliability of numerical results is suggested to be further verified, for example by experiments. The response of slopes under rainfall and earthquake conditions can be truly estimated by experiments [20, 25, 29]. Undoubtedly, physical modelling aids to reveal the deformation and failure mechanisms of slope models in the presence of weak interlayers. However, relevant research has been rarely conducted because it is rather challenging to perform such test and even costly and time-consuming. Widespread use of limit equilibrium for the calculation of FoS is due to its simplicity and accumulated experience [27, 29]. It is found that the use of limit equilibrium raises a concern on the reliability of calculated results which are neither upper nor lower bounds. Comparatively, limit analysis is capable of providing a reliable manner for the assessment of slope stability. Note that, in the literature mentioned above, a long weak interlayer layer was discussed only, and multiple weak interlayers and effects of weak interlayer dimension and position on slope stability were not comprehensively investigated.

Limit analysis provides a sound avenue to evaluate geotechnical stability problems including slope stability. It has two bifurcations: upper- and lower-bound theorem, based on which the true solution of slope stability can be well estimated. Prior to specific limit analysis, construction of a kinematically admissible velocity field (KAVF) and a statically allowable stress field (SASF) is a prerequisite. Since KAVF is easier to be constructed than SASF, the upper-bound theorem is more commonly used in stability analyses [4, 12, 14, 18, 28, 31]. Note that the above analyses considered a pre-defined failure mechanism, which is merely appropriate for simple problems such as homogeneous and/or isotropic slopes. However, for complex issues such as in the presence of weak interlayers, a demanding work is necessitated or it is nearly impossible to construct velocity or stress fields. For example, a pioneering work was carried out by Huang et al. [10, 11], assuming a rotational-translational failure mechanism to discuss the effects of a weak interlayer on slope stability. In a similar manner, Zhou et al. [32] performed a pseudo-static stability analysis of a pile-reinforced slope with a weak layer beneath slope toe elevation. On the one hand, relevant research was seldom found with a pre-defined mechanism. On the other hand, the above analyses only estimated the slope stability from the upper-bound theorem, with/without considering earthquake forces (pseudo-static only). This is attributed to the complexity of weak interlayers in the construction of velocity and stress fields and in latter stress equilibrium and work rates calculations. In an effort to overcome these issues, Sloan combined the limit analysis theory with finite element method, forming FELB [21] and FEUB [22] methods. Slope stability analysis under complex conditions can be readily performed by FEUB and FELB modelling. For example, the stability of a soil slope in the presence of a weak interlayer was analyzed by FEUB [23] or FELB [3]. However, no relevant studies have been further performed to better estimate weak interlayers’ effects on seismic slope stability, which is the motivation of this study.

It is widely acknowledged that earthquakes are one of major triggering factors for the occurrence of slope failure. In seismic analysis of slope stability, selecting a proper manner to characterize earthquake inputs is vital to not only facilitate the analysis but also produce reliable solutions. The use of actual seismic signal, e.g., acceleration time-history, tends to yield most reliable results, but is principally suited to numerical simulations such as DEM [26], FEM and MPM [2]. The simplest way is to adopt pseudo-static approach [13], which provides a quick but maybe not reliable estimate for seismic slope stability analyses. In order to balance the extremely complex earthquake time-history and overly simplified pseudo-static approach, the pseudo-dynamic approach was proposed by Steedman and Zeng [24] and applied to seismic slope stability analysis [6, 16, 30]. Notwithstanding, it has some intrinsic drawbacks which were overcome by the modified pseudo-dynamic approach. An attempt was made to seismic slope stability analysis with discretization-based kinematic analysis [17]. Owing to its complexity, no relevant research has been performed to investigate the effects of both modified pseudo-dynamic earthquake and weak interlayers on seismic slope stability.

In this study, a powerful procedure including FEUB and FELB will be introduced to evaluate the seismic stability of a soil slope containing weak interlayers within soil strata, aiming to better understand weak interlayers’ effects on seismic slope stability. Meanwhile, pseudo-static and modified pseudo-dynamic approach are used to represent earthquake inputs. In the presence of weak interlayers, the scientific challenge is to construct KAVF and SASF, in upper- and lower-bound analyses. Resorting to finite element method, such challenge is ultimately tackled by satisfying corresponding conditions within each element and boundary. Pseudo-static and modified pseudo-dynamic solutions of FoS are sought by optimization. After having performed such analysis, the crux is to estimate the true solution of seismic slope stability under the effects of weak interlayers, by lower and upper bounds, which can be applied to slope design and assessment in engineering practice.

2 Methodologies

In an effort to estimate seismic slope stability at limit state, two main methodologies include: (1) methods for representing earthquake inputs and (2) finite-element limit-analysis approach. Selecting an appropriate manner to characterize seismic inputs is imperative under earthquake effects, aiding to derive a closed-form or semi-analytical solution to seismic slope stability. Modified pseudo-dynamic approach is mainly considered herein. The latter methodology is inclusive of finite-element upper-bound and finite-element lower-bound analyses, aiming to evaluate the true failure load from upper and lower bounds.

2.1 Earthquake inputs

In seismic slope stability analyses, there exist three commonly used approaches for representation of earthquake inputs. Pseudo-static approach was initially introduced to represent seismic accelerations, due to the lack of in-depth understanding of dynamic earthquakes and sophisticated methods available. It is straightforward to use constant horizontal and vertical accelerations to describe seismic forces, being capable of providing a quick estimate to seismic slope stability. Although pseudo-static approach has been widely adopted in existing literature, its essential drawback lies in the extreme simplicity of dynamic earthquakes without considering time- and space-dependent effects. In contrast, acceleration time-history provides a detailed information of a specific earthquake, including amplitude, frequency and duration. This in turn demonstrates that such acceleration profile is rather complicated and hence mainly suited to advanced numerical simulations. As a compromise, pseudo-dynamic approach was developed, with specific expressions to represent time- and space-dependent seismic accelerations. Although acceleration time-history can also be accounted for with the proposed procedure, focus of this study is placed onto the use of pseudo-static and modified pseudo-dynamic approach. A brief introduction of the modified pseudo-dynamic approach is introduced as below.

For the case of a plane wave propagating vertically in a Kelvin–Voigt soil medium, the equations of motion can be expressed by horizontal and vertical displacement, respectively. A closed-form solution of horizontal and vertical displacement is then derived after the satisfaction of zero stress boundary and prescribed displacement boundary conditions. Thereafter, the shear and primary wave-induced seismic acceleration can be obtained by double differential calculation [15, 17, 19]. In this study, the place of action of the base seismic acceleration (or displacement) is located at slope toe elevation. Accordingly, the seismic horizontal acceleration induced by shear wave gives

$$a_{h} (y_{i} ,\;t) = \frac{{k_{h} g}}{{C_{S}^{2} + S_{S}^{2} }}\left[ \begin{gathered} \left( {C_{S} C_{SZ} + S_{S} S_{SZ} } \right)\cos \left( {\varpi t} \right) \hfill \\ + \left( {S_{S} C_{SZ} - C_{S} S_{SZ} } \right)\sin \left( {\varpi t} \right) \hfill \\ \end{gathered} \right]$$

(1)

where k_h is horizontal seismic coefficient at slope toe, g is gravitational acceleration, $\varpi$ denotes angular velocity of harmonious shaking (with period $T = 2\pi {/}\varpi$), t is time, and intermediate variables $y_{s1} ,\;y_{s2} ,\;C_{S} ,\;S_{S} ,\;C_{SZ} ,\;S_{SZ}$ present the following form:

$$\begin{aligned} & y_{s1} = \frac{\varpi H}{{Vs }}\left[ {\frac{{\sqrt {1 + 4\xi^{2} } + 1}}{{2\left( {1 + 4\xi^{2} } \right)}}} \right]^{1/2} ,\;\;y_{s2} = - \frac{\varpi H}{{Vs }}\left[ {\frac{{\sqrt {1 + 4\xi^{2} } - 1}}{{2\left( {1 + 4\xi^{2} } \right)}}} \right]^{1/2} \\ & C_{S} = \cos \left( {y_{s1} } \right)\cosh \left( {y_{s2} } \right),\;\;\;\;\;\;S_{S} = - \sin \left( {y_{s1} } \right)\sinh \left( {y_{s2} } \right) \\ & C_{SZ} = \cos \left[ {\frac{{y_{s1} \left( {H - y_{i} } \right)}}{H}} \right]\cosh \left[ {\frac{{y_{s2} \left( {H - y_{i} } \right)}}{H}} \right],\;\;S_{SZ} = - \sin \left[ {\frac{{y_{s1} \left( {H - y_{i} } \right)}}{H}} \right]\sinh \left[ {\frac{{y_{s2} \left( {H - y_{i} } \right)}}{H}} \right] \\ \end{aligned}$$

(2)

with H being slope height, $Vs$ shear wave velocity, $\xi$ soil damping ratio, and $y_{i}$ the ordinate of a point in the domain of interest. The use of coordinates is for the ease of representing accelerations at different locations, when using the finite-element limit-analysis method as introduced later.

As for seismic motion induced by primary wave, the corresponding vertical acceleration can be expressed as

$$a_{v} (y_{i} ,\;t) = \frac{{k_{v} g}}{{C_{P}^{2} + S_{P}^{2} }}\left[ \begin{gathered} \left( {C_{P} C_{PZ} + S_{P} S_{PZ} } \right)\cos \left( {\varpi t} \right) \hfill \\ + \left( {S_{P} C_{PZ} - C_{P} S_{PZ} } \right)\sin \left( {\varpi t} \right) \hfill \\ \end{gathered} \right]$$

(3)

where k_v denotes vertical seismic coefficient at slope toe, and variables $y_{p1} ,\;y_{p2} ,\;C_{P} ,\;S_{P} ,\;C_{PZ} ,\;S_{PZ}$ have the following form:

$$\begin{gathered} y_{p1} = \frac{\varpi H}{{Vp }}\left[ {\frac{{\sqrt {1 + 4\xi^{2} } + 1}}{{2\left( {1 + 4\xi^{2} } \right)}}} \right]^{1/2} ,\;\;y_{p2} = - \frac{\varpi H}{{Vp }}\left[ {\frac{{\sqrt {1 + 4\xi^{2} } - 1}}{{2\left( {1 + 4\xi^{2} } \right)}}} \right]^{1/2} \hfill \\ C_{P} = \cos \left( {y_{p1} } \right)\cosh \left( {y_{p2} } \right),\;\;\;\;\;S_{P} = - \sin \left( {y_{p1} } \right)\sinh \left( {y_{p2} } \right) \hfill \\ C_{PZ} = \cos \left[ {\frac{{y_{p1} \left( {H - y_{i} } \right)}}{H}} \right]\cosh \left[ {\frac{{y_{p2} \left( {H - y_{i} } \right)}}{H}} \right],\;\;S_{PZ} = - \sin \left[ {\frac{{y_{p1} \left( {H - y_{i} } \right)}}{H}} \right]\sinh \left[ {\frac{{y_{p2} \left( {H - y_{i} } \right)}}{H}} \right] \hfill \\ \end{gathered}$$

(4)

with $Vp$ being primary wave velocity.

It is worthwhile highlighting that stiffness parameters are assumed to be constant in the above derivation. This assumption is also made in the later analysis where single and dual weak interlayers are discussed. Moreover, weak interlayers’ effects on reflection and transmission of seismic waves are not considered in this study, for the ease of simplification.

2.2 Finite-element upper-bound analysis

In an upper-bound analysis, it involves three main issues: generation of a kinematically admissible velocity field, calculations of external and internal rates of work, derivation and optimization of upper-bound solutions. A kinematically admissible velocity field is a prerequisite and constructed following an associated flow rule. Based on this, the rates of work done by external forces and internal energy dissipation are computed. If external rates of work are no less than internal energy dissipation (e.g., in slopes), slope instability is imminent or occurs. At limit state, upper-bound formulations are derived, in the form of limit bearing capacity on slope crest, factor of safety, etc. An effective algorithm is then necessitated to seek optimal upper-bound solutions. Broadly speaking, the upper-bound analysis is achieved based on the virtual work principle with a general equation expressed as below,

$$\int_{V} {\sigma_{ij} \dot{\varepsilon }_{ij}^{U} } dV \le \int_{V} {\sigma_{ij}^{U} \dot{\varepsilon }_{ij}^{U} } dV = \int_{S} {T_{i}^{U} v_{i}^{U} } dS + \int_{V} {X_{i}^{U} v_{i}^{U} } dV$$

(5)

where $\sigma_{ij}$ is stress field corresponding to true failure load, $\dot{\varepsilon }_{ij}^{U}$ is strain rate field, $\sigma_{ij}^{U}$ is stress field pertaining to applied external forces, $T_{i}^{U}$ represents surface loading on surface S, $X_{i}^{U}$ is body force within potential failure block volume V, $v_{i}^{U}$ denotes velocity field and is kinematically compatible with $\dot{\varepsilon }_{ij}^{U}$. It is noted that the true failure load is equal to or less than the load calculated from the work rate balance equation in a kinematically admissible velocity field.

Two commonly used approaches to construct a kinematically admissible velocity field are based on: (1) an assumed failure mechanism, and (2) numerical techniques such as finite element method. There are some well-defined failure mechanisms for slope stability under simplified scenarios. For instance, a log-spiral mechanism is suited to a homogeneous and isotropic c-φ soil slope, a circular one for a purely cohesion clayey slope and a translational mechanism for a cohesionless sand slope. As for some cases such as under complex geological structure and non-homogeneity of soil properties, the use of an assumed failure mechanism is deemed unreliable and inaccurate. In such case, an alternative and effective way is resorting to numerical treatments, such as finite element method. Combining the finite element with the upper-bound theorem forms the FEUB method, which is to be adopted in this study for the analysis of seismic slope stability.

2.2.1 Generation of a kinematically admissible velocity field

In FEUB analyses, a potential velocity field is generated after discretizing the soil mass into finite elements. The core principle for the generation of such field is to satisfy the flow rule, velocity discontinuities and velocity boundary conditions. Mathematically, the associated flow rule within each element is expressed as

$$\begin{gathered} F = \left( {\sigma_{x} - \sigma_{y} } \right)^{2} + \left( {2\tau_{xy} } \right)^{2} - \left[ {2c\cos \varphi - \left( {\sigma_{x} + \sigma_{y} } \right)\sin \varphi } \right]^{2} \hfill \\ \dot{\varepsilon }_{x} = \frac{\partial u}{{\partial x}} = \dot{\lambda }\frac{\partial F}{{\partial \sigma_{x} }},\;\dot{\varepsilon }_{y} = \frac{\partial v}{{\partial y}} = \dot{\lambda }\frac{\partial F}{{\partial \sigma_{y} }},\;\dot{\gamma }_{xy} = \frac{\partial u}{{\partial y}} + \frac{\partial v}{{\partial x}} = \dot{\lambda }\frac{\partial F}{{\partial \tau_{xy} }} \hfill \\ \end{gathered}$$

(6)

in which F denotes generalized Mohr–Coulomb (MC) failure criterion in a plane strain analysis, $\sigma_{x} ,\;\sigma_{y} ,\;\tau_{xy}$ are planar stress components, c and φ represent MC strength parameters (soil cohesion and internal angle of soil friction, respectively), $\dot{\varepsilon }_{x} ,\;\dot{\varepsilon }_{y} ,\;\dot{\gamma }_{xy}$ correspond to plastic strain rates, u and v are horizontal and vertical nodal velocities, $\dot{\lambda }$ is plastic multiplier rate which is assumed to be constant and non-negative. When a plane strain problem is discretized to linear three-nodded constant-strain triangular finite elements, u and v in each element can be expressed with a linear function of nodal velocities by shape functions.

On the velocity discontinuities, the following conditions are supposed to be satisfied,

$$\begin{aligned} & f = \left| {\tau_{s} } \right| + \sigma_{n} \tan \varphi - c \\ & \Delta u_{s} = \dot{\xi }\frac{\partial f}{{\partial \tau_{s} }},\;\Delta v_{n} = \dot{\xi }\frac{\partial f}{{\partial \sigma_{n} }} \\ \end{aligned}$$

(7)

where f is MC failure criterion expressed by shear stress ($\tau_{s}$) and normal stress ($\sigma_{n}$) on a discontinuous edge, $\Delta u_{s} ,\;\Delta v_{n}$ represent velocity jumps parallel and normal to the edge shared by two adjacent elements, separately, and non-negative $\dot{\xi }$ is plastic discontinuity multiplier.

In addition, velocity boundary conditions are

$$u_{s} = \overline{u}_{s} ,\;v_{n} = \overline{v}_{n}$$

(8)

in which $\overline{u}_{s} ,\;\overline{v}_{n}$ denote prescribed velocities which are parallel and normal to a specific boundary, respectively.

Based on the above elementary analysis (Fig. 1), it is found that four variables including u and v, $\dot{\lambda }$ and $\dot{\xi }$, are required to satisfy the above kinematically compatible conditions. After explicitly expressing u and v with nodal velocities and assembling all elements together, a potential kinematically admissible velocity field should satisfy the following constraints:

$$\begin{gathered} A_{11}^{{}} X_{1}^{{}} - A_{12}^{{}} X_{2}^{{}} = 0 \hfill \\ A_{23}^{{}} X_{3}^{{}} - A_{24}^{{}} X_{4}^{{}} = 0 \hfill \\ A_{3}^{{}} X_{5}^{{}} = B_{3}^{{}} \hfill \\ \end{gathered}$$

(9)

where $A_{11}^{{}} ,\;A_{12}^{{}} ,\;A_{23}^{{}} ,\;A_{24}^{{}} ,\;A_{3}^{{}} ,\;B_{3}^{{}}$ are matrices of constraint coefficients which are assembled from $A_{11}^{e} ,\;A_{12}^{e} ,\;A_{23}^{d} ,\;A_{24}^{d} ,\;A_{3}^{b} ,\;B_{3}^{b}$, in elementary analysis, with specific expressions shown in Appendix A. $X_{1} = \left[ {u_{1} \;\;v_{1} \;\;u_{2} \;\;v_{2} \;\; \cdots \;\;u_{np} \;\;v_{np} } \right]^{T}$ is the vector of nodal velocities for np nodes and assembled from $X_{1}^{e} = \left[ {u_{1}^{e} \;\;v_{1}^{e} \;\;u_{2}^{e} \;\;v_{2}^{e} \;\;u_{3}^{e} \;\;v_{3}^{e} } \right]^{T}$. $X_{2} = \left[ {\dot{\lambda }_{11} \;\;\dot{\lambda }_{12} \;\; \cdots \;\;\dot{\lambda }_{1p} \;\;\dot{\lambda }_{21} \;\;\dot{\lambda }_{22} \;\; \cdots \;\;\dot{\lambda }_{2p} \;\; \cdots \;\;\dot{\lambda }_{ne1} \;\;\dot{\lambda }_{ne2} \;\; \cdots \;\;\dot{\lambda }_{nep} \;\;} \right]^{T}$ is the vector of plastic multiplier rates for ne elements, with MC criterion linearized with a p-polygon, and assembled by non-negative $X_{2}^{e} = \left[ {\dot{\lambda }_{1}^{e} \;\;\dot{\lambda }_{2}^{e} \;\; \cdots \;\;\dot{\lambda }_{k}^{e} \;\; \cdots \;\;\dot{\lambda }_{p}^{e} } \right]^{T}$. $X_{3} = \left[ {u_{11} \;\;v_{11} \;\;u_{12} \;\;v_{12} \;\;u_{13} \;\;v_{13} \;\;u_{14} \;\;v_{14} \;\; \cdots \;\;u_{nd1} \;\;v_{nd1} \;\;u_{nd2} \;\;v_{nd2} \;\;u_{nd3} \;\;v_{nd3} \;\;u_{nd4} \;\;v_{nd4} } \right]^{T}$ is the vector of nodal velocities for a total of nd discontinuity edges and assembled from $X_{3}^{d} = \left[ {u_{1}^{d} \;\;v_{1}^{d} \;\;u_{2}^{d} \;\;v_{2}^{d} \;\;u_{3}^{d} \;\;v_{3}^{d} \;\;u_{4}^{d} \;\;v_{4}^{d} } \right]^{T}$. $X_{4} = \left[ {\dot{\xi }_{11} \;\;\dot{\xi }_{12} \;\;\dot{\xi }_{13} \;\;\dot{\xi }_{14} \;\;\dot{\xi }_{21} \;\;\dot{\xi }_{22} \;\;\dot{\xi }_{23} \;\;\dot{\xi }_{24} \;\; \cdots \;\;\dot{\xi }_{nd1} \;\;\dot{\xi }_{nd2} \;\;\dot{\xi }_{nd3} \;\;\dot{\xi }_{nd4} } \right]^{T}$ is the vector of plastic discontinuity multipliers for nd discontinuity edges and assembled from $X_{4}^{d} = \left[ {\dot{\xi }_{1}^{d} \;\;\dot{\xi }_{2}^{d} \;\;\dot{\xi }_{3}^{d} \;\;\dot{\xi }_{4}^{d} } \right]^{T}$. $X_{5} = \left[ {u_{11} \;\;v_{11} \;\;u_{12} \;\;v_{12} \;\;u_{21} \;\;v_{21} \;\;u_{22} \;\;v_{22} \;\; \cdots \;\;u_{nb1} \;\;v_{nb1} \;\;u_{nb2} \;\;v_{nb2} } \right]^{T}$ is the vector of nodal velocities for nb velocity boundaries and assembled from $X_{5}^{b} = \left[ {u_{1}^{b} \;\;v_{1}^{b} \;\;u_{2}^{b} \;\;v_{2}^{b} } \right]^{T}$. Specific expressions can be found in Appendix A.

Fig. 1

A schematic view of elementary analysis and linearized MC criterion for the generation of a kinematically admissible velocity field

After having introduced the finite element method, it plays a key role in two major aspects: (1) aiding to generate a kinematically admissible velocity field satisfying Eq. (9), and (2) facilitating the considerations of complex soil properties and external loadings in the following work rate calculations. Consequently, the upper-bound analysis combining with the finite element method is capable of accounting for complicated cases in slope stability, such as weak interlayers and modified pseudo-dynamic forces as discussed in this study.

2.2.2 Calculations of external and internal rates of work

Prior to work rate calculations, understanding the driving forces that could potentially affect slope stability is essential. In the presence of earthquakes, the applied forces acting on a slope include soil weight, surface tractions, and seismic forces. Accordingly, the total rates of work produced by soil weight ($\dot{W}_{e1}$), by surface tractions ($\dot{W}_{e2}$), and by earthquake forces ($\dot{W}_{e3}$), are expressed through the integral of elementary rates of work, as below:

$$\begin{gathered} \dot{W}_{e1} = \int_{A} {\left( {\gamma v} \right)} d{A} \hfill \\ \dot{W}_{e2} = \int_{s} {\left( {qv} \right)} ds \hfill \\ \dot{W}_{e3} = \int_{A} {\left[ {k_{h} (t,y) \cdot \gamma u} \right]} d{A}\begin{array}{*{20}c} + \\ \end{array} \int_{A} {\left[ {k_{v} (t,y) \cdot \gamma v} \right]} d{A} \hfill \\ \end{gathered}$$

(10)

where γ denotes soil unit weight, A is cross-sectional area of a failure block, q is vertical surface loading acting on boundary s, $k_{h} (t,y)$ and $k_{v} (t,y)$ represent time- and position-dependent seismic coefficients, horizontally and vertically. Herein, the positive directions are defined as horizontal acceleration towards outside of sloping surface and vertical acceleration downwards.

In a kinematically admissible velocity field, internal energy would dissipate along velocity discontinuities and within the failure block. The source of internal energy dissipation comes from plastic deformation. Based on elementary analysis and after integral calculations, the total internal rates of work dissipated within all elements ($W_{i1}$) and along velocity discontinuities ($W_{i2}$) yield

$$\begin{gathered} W_{i1} = \int_{A} {\left( {\dot{\varepsilon }_{x} \sigma_{x} + \dot{\varepsilon }_{y} \sigma_{y} + \dot{\gamma }_{x} \tau_{xy} } \right)}dA \hfill \\ W_{i2} = \int_{0}^{l} {c(\dot{\xi }_{a} + \dot{\xi }_{b} )dl} \hfill \\ \end{gathered}$$

(11)

in which l denotes total length of velocity discontinuities.

2.2.3 Derivation and optimization of upper-bound solutions

After having obtained external rates of work and internal energy dissipation rates in a velocity field, the next step is to derive upper-bound formulations. Note that there exist numerous velocity fields; therefore, infinite upper-bound solutions can be obtained, which satisfy Eq. (5). Thereof, a group of upper-bound solutions is derived when the equality condition in Eq. (5) is satisfied, i.e., work rate balance equation at limit state. Taking the limit surcharge load ($q_{{{\text{limit}}}}$) as the objective function and defining $q_{{{\text{limit}}}} = \lambda_{q}^{U} \overline{q}_{n}$, where $\lambda_{q}^{U}$ represents the overload coefficient from an upper-bound analysis, and $\overline{q}_{n}$ is the prescribed loading acting on boundary s, the upper-bound formulation gives

$$\lambda_{q}^{U} = \frac{{q_{{{\text{limit}}}} }}{{\overline{q}_{n} }} = \frac{{W_{i1} + W_{i2} - W_{e1} - W_{e3} }}{{\int_{s} {\overline{q}_{n} v} ds}}$$

(12)

Optimization of Eq. (12) could yield an optimal upper-bound solution. Notice that, however, a non-linear programming technique is required for the direct optimization, which is somewhat challenging and demanding. In an effort to make Eq. (12) easier to be optimized, it is alternatively transformed to

$$\lambda_{q}^{U} = W_{i1} + W_{i2} - W_{e1} - W_{e3}$$

(13)

by adding an additional constraint, i.e., $\int_{s} {\overline{q}_{n} v} ds = 1$.

It is more straightforward and efficient to seek the optimal upper-bound solution of limit surcharge load (expressed by $\lambda_{q}^{U}$), with a linear programming technique. In combination with the constraint conditions required for the generation of a kinematically admissible failure mechanism, the slope stability analysis can be explicitly expressed as:

$$\begin{gathered} \min \left( {\lambda_{q}^{U} = C_{i1}^{{}} X_{2} + C_{i2}^{{}} X_{4} - C_{e1}^{{}} X_{1} - C_{e3}^{{}} X_{1} } \right) \hfill \\ s.t.\;\;\left\{ \begin{gathered} A_{11} X_{1} - A_{12} X_{2} = 0 \hfill \\ A_{23} X_{3} - A_{24} X_{4} = 0 \hfill \\ A_{3} X_{5} = B_{3} \hfill \\ C_{e2}^{{}} X_{6} = 1.0 \hfill \\ X_{2} \ge 0 \hfill \\ X_{4} \ge 0 \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered}$$

(14)

where $C_{i1}^{{}}$, $C_{i2}^{{}}$, $C_{e1}^{{}}$, $C_{e2}^{{}}$ and $C_{e3}^{{}}$ are the vectors of coefficients pertaining to components of the objective function, which are assembled from $C_{i1}^{e}$, $C_{i2}^{d}$, $C_{e1}^{e}$, $C_{e2}^{q}$ and $C_{e3}^{e}$, respectively. $X_{6} = \left[ {u_{11} \;\;v_{11} \;\;u_{12} \;\;v_{12} \;\;u_{21} \;\;v_{21} \;\;u_{22} \;\;v_{22} \;\; \cdots \;\;u_{nq1} \;\;v_{nq1} \;\;u_{nq2} \;\;v_{nq2} } \right]^{T}$ is the vector of nodal velocities for nq boundaries to which surface tractions are applied and is assembled from $X_{6}^{q} = \left[ {u_{1}^{q} \;\;v_{1}^{q} \;\;u_{2}^{q} \;\;v_{2}^{q} } \right]^{T}$. It is worth pointing out that the components of X₃, X₅ and X₆ can also be found in X₁. Specific expressions are listed in Appendix A for completeness.

It is worthwhile highlighting that Eq. (14) is suited to a pseudo-static analyses of seismic slope stability or pseudo-dynamic analyses at a specific time instant t. This is demonstrated by the time-dependent coefficient $C_{e3}^{{}}$. If dynamic accelerations are accounted for, there exist a series of $\lambda_{q}^{U} (t)$ values calculated at various time instants. The best upper-bound solution is sought by minimizing $\lambda_{q}^{U} (t)$ values. In other words, the linear programming model, Eq. (14), can be rectified as:

$$\begin{aligned} & \mathop {\min }\limits_{{t,\;t \in \left[ {t_{start} ,t_{end} } \right]}} \;\;\mathop {\min }\limits_{{X_{1} ,X_{2} ,X_{3} ,X_{4} ,X_{5} ,X_{6} }} \left( {\lambda_{q}^{U} (t) = C_{i1}^{{}} X_{2} + C_{i2}^{{}} X_{4} - C_{e1}^{{}} X_{1} - C_{e3}^{{}} X_{1} } \right) \\ & s.t.\;\;\left\{ \begin{gathered} A_{11} X_{1} - A_{12} X_{2} = 0 \hfill \\ A_{23} X_{3} - A_{24} X_{4} = 0 \hfill \\ A_{3} X_{5} = B_{3} \hfill \\ C_{e2}^{{}} X_{6} = 1.0 \hfill \\ X_{2} \ge 0 \hfill \\ X_{4} \ge 0 \hfill \\ \end{gathered} \right. \\ \end{aligned}$$

(15)

Based on the above mathematical programming model, the optimal pseudo-dynamic solution to seismic slope stability is to be searched with an optimization technique. The interior-point algorithm is implemented into MATLAB to achieve this specific purpose.

2.3 Finite-element lower-bound analysis

In a lower-bound analysis, it mainly contains two steps: generation of a statically allowable stress field, derivation and optimization of lower-bound solutions. Unlike upper-bound analyses that are carried out from the perspective of work (work rates), lower-bound analyses are based on stresses (forces). Accordingly, a statically allowable stress field is necessitated, aiming to derive the lower-bound failure load from stress equilibrium analysis. Its core principle lies in the lower-bound theorem, stating that the true failure load is equal to or greater than the applied load computed from the virtual work principle in a statically allowable stress field. Thereof, the virtual work principle is expressed as:

$$\int_{V} {\sigma_{ij} \dot{\varepsilon }_{ij} } dV \ge \int_{V} {\sigma_{ij}^{L} \dot{\varepsilon }_{ij} } dV = \int_{S} {T_{i}^{L} v_{i} } dS + \int_{V} {X_{i}^{L} v_{i} } dV$$

(16)

in which σ_ij is stress field corresponding to true failure load, stress field $\sigma_{ij}^{L}$ is to be determined and theoretically equivalent to external forces, including traction force $T_{i}^{L}$ acting on surface S and body force $X_{i}^{L}$ within volume V, $\dot{\varepsilon }_{ij}$ and $v_{i}$ are strain rate field and velocity field, respectively, both belonging to the compatible set. Since stress equilibrium and no violation of yield criterion are both satisfied, a geotechnical structure (e.g., slopes) is capable of adapting itself to sustain the applied external loading calculated from a lower-bound analysis.

Generating a statically allowable stress field is more challenging than a kinematically admissible velocity field, thereby demonstrating the popularity and widespread use of upper-bound analyses in geotechnical stability problems. A few stress fields were constructed for extremely simplified cases, particularly for not considering soil self-weight. Note that, however, soil stresses at various depths vary significantly in site, which is directly attributed to the effects of soil weight. Therefore, soil self-weight cannot be ignored in the lower-bound analysis of geotechnical problems. In an effort to tackle this issue, sophisticated numerical techniques are introduced to generate a statically allowable stress field, especially under complicated cases such as in the presence of weak interlayers. Similar to FEUB analyses, finite element method is also adopted to achieve this specific purpose. In combination with the lower-bound theorem, a FELB procedure is therefore formed and will be used in this study.

2.3.1 Generation of a statically allowable stress field

In FELB analyses, a soil mass is discretized into finite three-nodded triangular elements for the case of a plane strain problem. Stress variables are adopted herein, in contrast to velocity variables used in FEUB analyses. Correspondingly, stresses within an element or on an edge can be linearly expressed by nodal stresses and shape functions. In the process of generating a statically allowable stress field, the following four conditions must be satisfied: (1) stress equilibrium within each element; (2) stress continuity at the interface; (3) stress boundary conditions; and (4) no violation of yield criterion. A schematic view of nodal variables and linearized MC criterion is presented in Fig. 2, serving to better demonstrate the conditions required in lower-bound analyses.

Fig. 2

A schematic view of elementary analysis and linearized MC criterion for the generation of a statically allowable stress field

Stress equilibrium within a soil mass implies the stress distribution in a constructed stress field is equivalently compatible with external loadings (body stress). Mathematically, it gives

$$\frac{{\partial \sigma_{x} }}{\partial x} + \frac{{\partial \tau_{xy} }}{\partial y} = X_{x}^{{}} ,\;\;\;\frac{{\partial \sigma_{y} }}{\partial y} + \frac{{\partial \tau_{xy} }}{\partial x} = X_{y}^{{}}$$

(17)

where $\sigma_{x} ,\;\sigma_{y} ,\;\tau_{xy}$ are stress components of the stress state at a point within an element, $X_{x}^{{}} ,\;X_{y}^{{}}$ are components of body forces per unit volume in x- and y-directions. Thereof, stress components can be explicitly expressed with linear combinations of two nodal normal stresses and one nodal shear stress, using shape functions.

After having discretized the soil mass into a series of triangular elements, there exist many interfaces formed by two adjacent elements. Continuity of normal and shear stresses on the interface is supposed to be satisfied, i.e.

$$\sigma_{na} = \sigma_{nb} ,\;\;\;\tau_{sa} = \tau_{sb}$$

(18)

where $\sigma_{na} ,\;\sigma_{nb}$ are the normal stress perpendicular to the edge shared by two adjacent elements a and b, $\tau_{sa} ,\;\tau_{sb}$ are the shear stress along this edge.

For the case of free boundaries or boundaries subject to tractions, stress boundary conditions are:

$$\sigma_{n} = q_{n} ,\;\;\;\tau_{s} = t_{s}$$

(19)

in which $\sigma_{n} ,\;\tau_{s}$ are stress components normal and tangential to a boundary, $q_{n} ,\;t_{s}$ are prescribed stresses normal and tangential to this boundary.

The above three items serve to guarantee a stress field satisfying stress equilibrium within the entire soil mass and along all boundaries or interfaces. Besides, the stress state of any point in the domain of interest is not allowed to violate the yield criterion. When Mohr–Coulomb yield criterion is adopted in this study, this condition is given as

$$F = \left( {\sigma_{x} - \sigma_{y} } \right)^{2} + \left( {2\tau_{xy} } \right)^{2} - \left[ {2c\cos \varphi - \left( {\sigma_{x} + \sigma_{y} } \right)\sin \varphi } \right]^{2} \le 0$$

(20)

where F is the generalized Mohr–Coulomb yield criterion in a plane strain analysis.

2.3.2 Derivation and optimization of lower-bound solutions

After having constructed a statically allowable stress field satisfying the above four conditions, a lower-bound formulation, for example limit surcharge load Q on slope crest, can be derived in closed form. Based on stress equilibrium and integral calculation, load Q can be calculated as

$$Q = \int_{s} {q_{n} } ds = \int_{s} {\lambda_{q}^{L} \overline{q}_{n} } ds$$

(21)

where s denotes the portion of the boundary to which $q_{n}$ is applied, $\lambda_{q}^{L}$ is the overload coefficient pertaining to a lower-bound analysis, and $\overline{q}_{n}$ is the prescribed load.

As stated earlier, geotechnical structures remain stable when the applied load is no greater than the lower-bound solution. This means in a lower-bound analysis, the objective is to seek the maximum failure load. After having explicitly expressed the four conditions in nodal stress variables, a lower-bound analysis of slope stability is transformed to a linear programming model, which gives:

$$\begin{gathered} \mathop {{\text{max}}}\limits_{{}} \;\;\lambda_{q}^{L} \hfill \\ s.t.\;\;\left\{ \begin{gathered} A_{1} X = B_{1} \hfill \\ A_{2} X = 0 \hfill \\ A_{3} X = B_{3} \hfill \\ A_{4} X \le B_{4} \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered}$$

(22)

in which $X = \left[ {\sigma_{x1} \;\;\sigma_{y1} \;\;\tau_{xy1} \;\;\sigma_{x2} \;\;\sigma_{y2} \;\;\tau_{xy2} \;\; \cdots \;\;\sigma_{xnp} \;\;\sigma_{ynp} \;\;\tau_{xynp} } \right]^{T}$ is the vector of unknown stress components for a total of np nodes, $A_{1} ,\;B_{1} ,\;A_{2} ,\;A_{3} ,\;B_{3} ,\;A_{4} ,\;B_{4}$ are matrices of constraint coefficients that are assembled from $A_{1}^{e} ,\;B_{1}^{e} ,\;A_{2}^{d} ,\;A_{3}^{b} ,\;B_{3}^{b} ,\;A_{4}^{i} ,\;B_{4}^{i}$, respectively. Specific expressions can be found in Appendix B.

Again, the above linear programming model is suited to a pseudo-static analysis of slope stability or pseudo-dynamic analysis at a specific time instant. When considering a time-dependent dynamic earthquake (acceleration), the continuous time is discretized to time increments, and in this case, acceleration time-history is accordingly discretized. Based on various acceleration values at discretized time instants, corresponding $\lambda_{q}^{L} (t)$ results are yielded. The optimal pseudo-dynamic lower-bound solution is then sought from the following modified mathematical programming model.

$$\begin{gathered} \mathop {\min }\limits_{{t,\;t \in \left[ {t_{start} ,t_{end} } \right]}} \;\;\mathop {{\text{max}}}\limits_{X} \;\;\lambda_{q}^{L} (t) \hfill \\ \;\;\;s.t.\;\;\;\;\;\;\left\{ \begin{gathered} A_{1} X = B_{1} \hfill \\ A_{2} X = 0 \hfill \\ A_{3} X = B_{3} \hfill \\ A_{4} X \le B_{4} \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered}$$

(23)

It is worthwhile pointing out that matrix $B_{1}$ is time-dependent, due to the consideration of pseudo-dynamic seismic forces as body forces. In order to solve the model, Eq. (23), the interior-point algorithm implemented into MATLAB is also adopted, to calculate optimal lower-bound solutions of seismic slope stability.

In FEUB and FELB modelling, some assumptions are made for ease of simplification. It mainly includes: rigid failure block without considering volumetric strain, small deformation which is required to make virtual work principle valid, perfectly elastic–plastic soils, and Drucker’s postulation. Meanwhile, an associated flow rule is also assumed for soils used in this study.

3 Finite-element limit-analysis of seismic slope stability

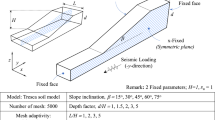
3.1 Slope model containing dual weak interlayers

It is well known that unexpected uncertainties exist below ground, such as weak interlayers. In reality, a weak interlayer in soil strata may not be infinite in length and have negligible effects on slope stability when it is far away from sloping surface. In such case, a proper manner to account for the dimension and position of weak interlayers is imperative. For the case of a soil slope, H denotes its height, and α for slope angle, as shown in Fig. 3. Dual weak interlayers are mainly considered herein, and a detailed slope model including the dimension and position of each weak interlayer is illustrated in Fig. 3. For ease of distinction, the parameters specific to upper and lower weak interlayer are additionally denoted with subscript u and l, respectively. For example, the Mohr–Coulomb strength parameters and unit weight are represented by c_i, φ_i and γ_i (i = u, l). A total of 7 parameters are used to describe the position and dimension of upper and lower weak interlayers. Specifically, a projected horizontal length of l_u1 of upper weak interlayer is positioned at a projected horizontal distance of l_u2 measured from the left terminal of upper weak interlayer to the intersection point on sloping boundary. Such intersection point has a vertical distance of D_u from the slope toe. As for the lower weak interlayer, its left side is extended to the left boundary of the model and its length counts from x = 0 plane with a projected horizontal length of l_l1. D_l denotes the vertical distance of the intersection point between lower weak interlayer and x = 0 plane to slope toe. Hereof, some parameters are normalized by slope height H, i.e., η_u1 = l_u1/ H, η_u2 = l_u2/ H, and η_l1 = l_l1/ H. Meanwhile, the upper (lower) weak interlayer is inclined at an angle of β_u (β_l) with respect to horizontal plane.

Fig. 3

Sketch of the slope model and typical mesh containing dual soft bands

3.2 Upper-bound and lower-bound solutions of seismic slope stability

The presence of weak interlayers complicates the problem of slope stability, particularly in conventional limit analysis, owing to the difficulties to construct KAVF and SASF. A pioneering work is carried out in this study to investigate the seismic stability of a soil slope containing dual weak interlayers, using FEUB and FELB analyses. Such analyses well combine the merits of finite element method and limit-analysis theorems, becoming powerful to tackle seismic slope stability issues under weak interlayers. Since FEM is adopted to construct KAVF and SASF, a typical FE mesh model with corresponding model parameters is presented in Fig. 3 as an example. Meanwhile, velocity and stress boundary conditions must be satisfied in upper- and lower-bound analyses, respectively. For instance, zero velocity conditions in normal and tangential directions of side and bottom boundaries are prescribed in an upper-bound analysis, $v_{n} = u_{s} = 0$. Apart from non-zero normal stress boundary for the case of surcharge loading imposed on slope crest surface, $\lambda_{q} (t)\;\overline{q}_{n}$, zero normal and shear stresses exist on other free boundaries in a lower-bound analysis.

After having generated the mesh, detailed information of nodes and elements is obtained and then used to form the linear programming model. Thereof, the overload coefficient, $\lambda_{q}^{U}$ or $\lambda_{q}^{L}$, is taken as the objective function in upper- or lower-bound analysis. In general, FoS is more commonly used because it tends to provide a more intuitional estimate for slope stability. Therefore, the seismic stability of a soil slope containing weak interlayers is to be evaluated by FoS. Determination of FoS is based on the strength reduction technique, and iterative algorithm is therefore necessitated. The main principle for FoS calculation herein is to compare the optimized overload coefficient computed from the mobilized soil strength parameters with the prescribed value $\overline{\lambda }_{q}$. Based on the definition of $\overline{\lambda }_{q}$(ratio of prescribed surcharge to $\overline{q}_{n}$), it has two specific values: $\overline{\lambda }_{q} = 0$ at the absence of surface surcharge and $\overline{\lambda }_{q} = 1$ in the presence of surcharge. Accordingly, $\lambda_{q}^{U}$ and $\lambda_{q}^{L}$ from upper- and lower-bound analysis should be calculated first, prior to the determination of FoS.

A detailed procedure for the assessment of modified pseudo-dynamic FoS is shown in Fig. 4 with a flow chart and elaborated as below. Firstly, read MC strength parameters, soil cohesion and friction angle in each soil layer, and let the strength reduction factor, SRF, equal 1.0. Secondly, compute mobilized strength parameters, and read other data information including geometric and load parameters such as soil self-weight, traction force $\overline{q}_{n}$, and time-dependent seismic force $\overline{q}^{e} (t)$. Thirdly, establish upper- and lower-bound linear programming models, and then apply the interior-point algorithm to calculations of $\lambda_{q}^{U} (t)$ and $\lambda_{q}^{L} (t)$ at a specific time instant t. Next, repeat the above process to calculate all values of $\lambda_{q}^{U} (t)$ and $\lambda_{q}^{L} (t)$ during the period of an earthquake, and select the minimal value as the optimal solution, $\lambda_{q,opt}^{U}$ and $\lambda_{q,opt}^{L}$. If $\lambda_{q,opt}^{U}$ ($\lambda_{q,opt}^{L}$) is equivalent to $\overline{\lambda }_{q}$, the upper-bound (lower-bound) solution of FoS, $FoS^{U}$ ($FoS^{L}$), is eventually calculated; otherwise, repeat from the second step until the equivalent condition is satisfied, by increasing or decreasing SRF.

Fig. 4

A flow chart showing the procedure of FEUB and FELB analysis for seismic slope stability

In the majority of existing studies, the procedure for seismic slope stability analysis terminates after having obtained $FoS^{U}$ or $FoS^{L}$, in either upper- or lower-bound analysis. Little research is found to provide both upper- and lower-bound solutions, particularly when considering dynamic earthquakes and weak interlayers. Resorting to the proposed procedure of this study, the true solution of failure load, for example true FoS of seismic slope stability, can be estimated. Its true value is theoretically limited within the range of lower- and upper-bound solutions. Ideally, true solution can be sought when the lower-bound solution equals the upper-bound, and this is merely feasible for extremely simple problems. For the case of complicated issues such as in the presence of weak interlayers, narrowing the gap between upper- and lower-bound solutions is of much interest for researchers, so as to better estimate seismic slope stability.

4 Comparison and discussion

4.1 Comparison

Validation of the proposed procedure is divided to two parts: comparison with existing literature for slope stability under a single weak interlayer, and comparison with numerical results for seismic slope stability under dual weak interlayers. Referred to Zolfaghari et al. [33], the same case example containing complex layering is selected for comparison, with identical slope geometry and soil properties. Apart from constant soil unit weight (19 kN/m³) in each layer, the MC strength parameters vary in different layers. Effective soil cohesion values are 15, 17, 5 and 35 kPa, and effective friction angles are 20, 21, 10 and 28 degrees, from layer 1 to 4. Layer 3 herein can be regarded as a weak interlayer which is characterized by much lower MC strength parameters in contrast to neighboring soils. FEUB and FELB modelling as introduced earlier are used to estimate the stability of layering soils, without considering seismic forces. It can be seen as a special case of the pseudo-dynamic analysis of seismic slope stability considering a weak interlayer, with k_h = k_v = 0.

Based on the preceding analyses, it yields an upper-bound solution of 1.123 and a lower-bound solution of 1.094 for FoS. Some researchers performed limit equilibrium analysis (Morgenstern-Price) to calculate FoS with different types of optimization techniques. Specifically, a minimum FoS of 1.24 was obtained using the simple genetic algorithm (SGA) with a non-circular failure surface [33]. In Cheng et al. [5], FoS = 1.144 was optimized from genetic algorithm (GA), 1.110 from particle swarm optimization (PSO), 1.139 from modified harmony search (MHS). In Gandomi et al. [7], the best FoS value was optimized from PSO (1.115), cuckoo search (CS, 1.064), and levy flight krill herd (LKH, 1.058). Theoretically, the true FoS is well within the range of [1.094, 1.123], based on the upper- and lower-bound theorems. On the one hand, one can note that the FoS calculated from FELB and FLUB agrees well with the limit equilibrium solutions from cited references. This to some extent validates the correctness of the proposed procedure for slope stability analysis containing a weak interlayer, with minor discrepancies between FoS results. On the other hand, it is proved that limit equilibrium solutions are neither upper bounds nor lower bounds, and some results are either greater than the upper bound or lower than the lower bound. Interestingly, the development of advanced optimization techniques tends to yield a small FoS value, from 2005 to 2015. It demonstrates that the accuracy of limit equilibrium results is highly associated with optimization algorithms, which in turn may raise some concerns on the reliability of limit equilibrium solutions.

Apart from FoS, the finite-element upper-bound analysis is capable of providing the kinematically admissible velocity field at limit state by post-processing. As for the case example in previous comparison, the velocity field is illustrated in Fig. 5, which can also be used to characterize the critical failure surface. For ease of distinction, the failure surface in Gandomi et al. [7] is selected only for comparison, with the critical failure surface optimized from the limit equilibrium method. It is found that the critical failure surface from two approaches is similar in shape, although the critical failure block simulated from LKH is a little smaller than that obtained from this study. Note that, in the presence of a soft band, the failure surface gradually develops downwards and then penetrates into the soft band. Afterwards, the failure mass tends to slide along the bottom of the soft band, which is observed from both the velocity field and critical failure surface. This is sensible because the soft band provides least resistance to prevent slope failure, showing a worst condition for slope stability.

Fig. 5

Velocity field from FEUB and critical failure surface from FEUB and limit equilibrium

In the presence of earthquakes, seismic forces can be considered in different manner. Pseudo-static and modified pseudo-dynamic solutions of FoS are presented in Fig. 6, which are calculated from FEUB, FELB and FEM and used for comparison herein. The default parameters of this study correspond to: H = 10 m, α = 40°, D_u = 0 m, β_u = 10°, η_u1 = 1, η_u2 = 0.5, D_l = 1 m, β_l = 0°, η_l1 = 3.19; γ = γ_u = γ_l = 18 kN/m³, c = 30 kPa, φ = 20°, c_u = c_l = 10 kPa; φ_u = φ_l; k_h = 0.1; k_v = 0.5k_h, H/TVs = 0.2, Vp = 1.87Vs, ξ = 10%. Undoubtedly, seismic slope stability gradually weakens with the increase in k_h, due to increased seismic forces to destabilize soil slopes. In terms of pseudo-static FoS, it is worthwhile highlighting that FEM results are well within the small range of upper and lower bounds, which in turn validates the applicability of the FEUB and FELB procedure for pseudo-static analysis of seismic slope stability. This phenomenon can be observed for both φ_u = 10° and φ_u = 15°. It is substantiated that larger soil friction angle is favorable for seismic slope stability, owing to higher soil resistance provided to prevent slope failure. Interestingly, modified pseudo-dynamic solutions are much less than the pseudo-static, and this is more pronounced at larger k_h. This is attributed to the fact that at limit state the magnitude of seismic acceleration and forces is larger from the modified pseudo-dynamic approach than that from the pseudo-static, based on above parameters. In such case, the use of pseudo-static approach over-estimates seismic slope stability, which is not conservative in slope design, especially in earthquake-stricken regions with high intensity.

Fig. 6

Slope safety factor against different earthquake inputs and research methodologies

In FEUB modelling, it is straightforward to obtain the velocity field and failure surface at limit state, which aids to reveal the slope failure mechanism in the presence of weak interlayers. After having optimized FoS, velocity fields specific to different scenarios are plotted through post-processing and illustrated in Fig. 7. At the absence of earthquakes, k_h = 0, the results of FoS and velocity field are not influenced by pseudo-static (P-s) or modified pseudo-dynamic (MP-d) approach. It is found that the velocity field (black arrow) obtained based on FEUB agrees well with the deformation contour from FEM modelling; Meanwhile, the critical failure surface at φ = 10° is also consistent with the plastic shear strain band, which further verifies the validity of the FEUB procedure. Velocity magnitude around slope toe is relatively large, in contrast to other parts, which is also demonstrated by red deformation contour from FEM. It is concluded that a rotational-translational failure mechanism is induced in the presence of weak interlayers, i.e., a translational mechanism around the lower weak interlayer and a rotational one far away from the weak interlayer. When pseudo-static acceleration is increased from 0 to 0.2 g, the failure mechanisms are similar but a larger failure region is observed at stronger earthquakes. This is sensible because more driving forces coming from pseudo-static forces are exerted on slope model to make such slope fail. The velocity field and critical failure surface are again in good agreement with FEM results at 0.2 g. When considering earthquake inputs with modified pseudo-dynamic approach, the earthquake magnitude would influence the formation of failure mechanism. Specifically, with an increase in k_h from 0 to 0.2, the failure region below upper weak interlayer gradually disappears, and the failure surface changes from crossing to following the upper weak interlayer. k_h = 0.1 is an intermediate case where the velocity below upper weak interlayer is much less than the above. Meanwhile, the failure width on slope crest surface gradually increases with k_h. Overall, the failure region at limit state is ultimately determined by mobilizing the soils to reach a minimum FoS.

Fig. 7

Effects of earthquake inputs on slope failure mechanisms at limit state

4.2 Discussion

Pseudo-static and modified pseudo-dynamic approaches are separately used to estimate seismic slope stability in this study. Effects of two seismic inputs on FoS are discussed here, and P-s and MP-d solutions of FoS are shown in Fig. 8, with the above default parameters and φ_u = 10°. In order to investigate pseudo-dynamic effects, non-dimensional H/TVs is adopted. Undoubtedly, P-s FoS solutions remain constant irrespective of H/TVs ratios, which gives 1.117 and 1.17 from FELB and FEUB analyses, respectively. It is as expected that MP-d solutions of FoS vary nonlinearly with H/TVs. An increase of H/TVs from 0.03 to 0.25 leads to a significant reduction in FoS, giving a minimal lower- and upper-bound solution of 0.673 and 0.707, respectively. Such minimal solution corresponds to the worst case for seismic slope stability, resulting from the resonance effect when earthquake frequency equals the first natural frequency of soils relating to shear waves. Afterwards, FoS is rocketed to 1.273 and 1.333 at H/TVs = 0.345. When H/TVs ratio continues to increase, FoS value experiences a downward and upward trend regularly. It is worth pointing out that H/TVs = 0.4675 corresponds to the case where earthquake frequency equals the first natural frequency of soils relating to primary waves. It is therefore inferred that minimum FoS solutions can be obtained under resonance conditions where horizontal or vertical accelerations are maximally amplified. H/TVs ratios varying from 0.03 to 0.8 are able to cover quite a large range of earthquake signal (frequency range of 0.3–8 Hz when Vs = 100 m/s), and hence such a range would suffice to consider its effects on seismic slope stability. In contrast to the extremely simplified P-s approach, the MP-d approach carries more dynamic information including frequency, wave velocities, soil damping, temporal and spatial variables. The corresponding pseudo-dynamic solutions are therefore likely to be more reliable. Based on the results of Fig. 8, pseudo-static solutions due to the loss of detailed dynamic information of earthquakes are either under-estimated or over-estimated in different cases. It is concluded that the accuracy of seismic slope stability solution is significantly related to the way to consider earthquake inputs, and the MP-d approach is preferred to the simple pseudo-static.

Fig. 8

Comparison of slope safety factor against H/TVs from different approaches

Different from existing studies where either upper- or lower-bound solution is yielded only, this study is capable of estimating the true solution of seismic slope stability. For the previous case, the true FoS is theoretically within the range of FELB and FEUB FoS curves, as shown in the shadow area of Fig. 8. The narrower the gap between upper and lower bounds, the closer to the true solution. It is calculated that the discrepancy ranges from 4.0 to 5.0% for the MP-d analysis, and it gives a constant difference of 4.5% in the P-s analysis. Relatively, the above difference is satisfactory for slope stability analysis, particularly in the presence of earthquakes and weak interlayers. It also indicates that the finite-element limit-analysis method aids to better estimate the seismic stability of a soil slope containing dual weak interlayers. This is the unrivalled advantage of this method over other approaches. Meanwhile, FEM modelling in Abaqus is also used to calculate FoS, using P-s approach for simplicity. FoS = 1.154 is simulated from FEM, which is 1.4% less than the P-s upper-bound solution, demonstrating the validity of the FEUB analysis.

Velocity fields against different H/TVs ratios are presented in Fig. 9, from P-s and MP-d analyses. In the P-s analysis, the critical failure surface well matches the plastic shear strain band simulated from FEM modelling. It again verifies the correctness of the FEUB modelling in P-s slope stability analysis and the rationality of a rotational-translational failure mechanism induced in the presence of weak interlayers. Critical failure surface crosses the finite upper weak interlayer and then develops downwards to follow the bottom of the lower weak interlayer. In such case, soils close to lower weak interlayer demonstrate translational movement, and rotational movement for other soils. The static case also proves the applicability of a rotational-translational mechanism to slope stability analysis considering a weak interlayer as assumed in Huang et al. [11]. Figure 9 demonstrates that H/TVs ratio has an obvious effect on the critical failure surface. It is noted that at H/TVs = 0.03 the failure mechanism is quite close to the pseudo-static one, apart from similar FoS solutions in Fig. 8. This makes sense because such case corresponds to a very slow earthquake disturbance, demonstrating an insignificant dynamic earthquake and hence resembling the pseudo-static case. For a general case, e.g., H/TVs = 0.2, the failure mechanism (failure surface) is determined by the combined effects of horizontal and vertical seismic accelerations. When H/TVs is increased to 0.25, the failure surface gradually changes to develop along the upper weak interlayer with a long failure width on slope crest. This is attributed to the fact that the horizontal acceleration dominates in the determination of minimal FoS. Comparatively, a deep-seated failure surface is developed to the bottom of lower weak interlayer at H/TVs = 0.4675, because in this case the vertical acceleration is maximally amplified and hence dominates the formation of failure mechanism. For the case of H/TVs = 0.75 where earthquake frequency equals the second natural frequency of soils relating to shear waves, the resonance effect attenuates exponentially with less amplification in horizontal seismic forces. Part of soils below upper weak interlayer are also mobilized to reach critical state under the combined effects of horizontal and vertical accelerations, although the critical velocity field is much less than the above.

Fig. 9

Velocity field and failure surface at limit state under different scenarios

Finite-element limit-analysis method combines the characteristics of FE modelling and limit analysis, and note that in FEM the mesh does have some effects on the accuracy of results. In an effort to discuss the mesh effect, different mesh sizes including Mesh 1 (816 elements), Mesh 2 (1616 elements), Mesh 3 (2460 elements) and Mesh 4 (3248 elements) are considered herein, as shown in Fig. 10. Employing the FEUB and FELB procedures in the preceding section, the upper and lower bound solutions are listed in Table 1 for comparison, considering P-s and MP-d seismic effects. Manifestly, the use of very coarse mesh (Mesh 1) tends to overestimate upper bound results but underestimate lower ones. When mesh elements increase, the difference between upper (lower) bound solutions obtained from Mesh 2, 3, 4 gradually decreases, and it is found that the results from Mesh 3 is very close to those of Mesh 4. Therefore, the use of a fine mesh tends to seek a more accurate result. It is also worthwhile pointing out that too many mesh elements would require more computational efforts.

Fig. 10

Four types of mesh with different mesh elements in finite-element limit analysis

Table 1 Mesh effects on accuracy of upper and lower bound seismic solutions

Another parameter that affects the accuracy of numerical results in FEUB and FELB calculations is time increment chosen in an optimization process. Provided that φ_u = φ_l = 15°, effects of time increment ∆t on MP-d upper and lower bound solutions are investigated, and corresponding results are shown in Table 2 against different H/TVs and k_h. It is found that the selection of T/300 to T/10 has certain effects on the accuracy of MP-d results, especially under large time increment, but negligible effects at small time increment. Overall, the result gradually converges to a specific value with the decrement of ∆t. Nonetheless, it would consume more computational time when choosing a much smaller ∆t. In order to balance the results’ accuracy and computational efficiency, T/30 as selected in this study is proved to be appropriate.

Table 2 Effects of time increment on accuracy of MP-d upper and lower bound seismic solutions

5 MP-d FEUB and FELB solutions

Figure 11 portrays the relationship between MP-d FoS versus β_u, η_u2 and k_h, based on the above default parameters and φ_u =  φ_l = 10°. It is again substantiated that an increment of k_h leads to a significant reduction in FoS, owing to increased driving forces. At the absence of earthquakes, FoS at η_u2 = 0 gradually decreases when the upper weak interlayer inclination is increased from 0 to a specific angle, and afterwards FoS continues to go up. However, a marginal decrement in FoS is observed at η_u2 = 0.5. When k_h value is increased to 0.1 or 0.2, the downward trend at η_u2 = 0.5 becomes gradually obvious, and the overall change pattern of FoS profile is analogous to k_h = 0, with the increase in angle β_u. Note that the upper- and lower-bound FoS profiles are similar, with less than 5% difference between the two. Some velocity fields at limit state are plotted to better interpret the upper-bound results, as illustrated in Fig. 12 where k_h = 0.1. For a horizontal upper weak interlayer with η_u2 varying from 0 to 0.5, more soils are mobilized to reach the limit state, and the critical failure surface is therefore likely to be developed to the lower weak interlayer. Upper weak interlayer is fully covered in the failure block. An increase of its inclination would reduce the internal energy dissipation rates because the velocity field in upper soils tends to decrease, thereby yielding a decreasing FoS. At a fixed η_u2 value (e.g. 0.5), the failure mechanism is evolved from a deep-seated failure to a localized failure on sloping surface, when β_u steepens from 0° to 20°. Due to less internal dissipation rates provided by weak interlayers, lower MP-d FoS solutions are accordingly induced.

Fig. 11

Upper- and lower-bound solutions of MP-d slope safety factor against β_u, η_u2 and k_h

Fig. 12

Critical velocity field and failure surface against η_u2 and β_u

The combined effects of η_u1 and β_l on seismic slope stability are presented in Fig. 13 considering φ_u = φ_l = 15°. Overall, MP-d FoS solutions experience a downward trend with an increase of η_u1. Note that the FoS profile can be categorized to three different sections: a gradual (at β_l = -5°) or minor (non-negative β_l) decrease at small η_u1, a significant drop in the middle range of η_u1, and lastly a gradual convergence section. In the first section, the failure surface is developed to lower weak interlayer, and upper weak interlayer is fully buried. This is why a small increase in η_u1 has minor effects on FoS. The obvious reduction of FoS may be attributed to a transition mechanism from a deep-seated failure to a shallow failure, i.e., the failure surface following the lower weak interlayer gradually moves upwards to follow upper weak interlayer only. Afterwards, the FoS is directly affected by the length of upper weak interlayer and not associated with the lower one, thereby yielding a descending FoS and enlarged failure area, with less internal dissipation rates produced along lengthened upper weak interlayer. It is found that FoS curves gradually converge with increasing η_u1. It can be reasonably inferred that FoS would eventually remain unchanged if η_u1 keeps increasing, regardless of β_l. This is because the critical failure mechanism would not be infinitely affected by the length of upper weak interlayer. For the case of no upper weak interlayer, η_u1 = 0, it is noted that FoS at β_l = − 5° is much greater than that for non-negative β_l. This can be well interpreted by the failure mechanism as shown in Fig. 14a and b where a large portion of soils near lower weak interlayer produces negative external work rates by gravity for the former case. For non-negative β_l, gravity-induced work rates are almost positive with negligible negative values around or ahead of slope toe, in such active failure. The failure mechanism in Fig. 14c proves that at small η_u1 the overall failure region is similar as that without an upper weak interlayer. When η_u1 continues to increase, the failure block is gradually to be truncated by the upper weak interlayer, and the lower weak interlayer’s effect gradually disappears when η_u1 exceeds a specific value, as illustrated in Fig. 14d and e. As for the failure mechanism in Fig. 14f where a portion of soils are mobilized between two weak interlayers with a small velocity field, this shows a transition case and indicates that FoS would continue to decrease until a lowest value which is completely not affected by the lower weak interlayer and η_u1.

Fig. 13

Upper- and lower-bound solutions of MP-d slope safety factor against η_u1 and β_l

Fig. 14

Critical velocity field and failure surface against η_u1 and β_l

As for the position of upper and lower weak interlayers, a total of 7 parameters are necessitated, and 4 parameters’ effects on seismic slope stability are discussed above. For completeness the remaining 3 parameters including η_l1, D_u and D_l, are investigated herein, and their effects on slope safety factor are portrayed in Fig. 15 where above default parameters and φ_u = φ_l = 15° are considered. For the case of D_u = 2 m and D_l = 1 m at very small η_l1, the outcome of FoS only has a minor change, because the failure mechanism does not develop to the lower weak interlayer (Fig. 16a). It is observed that slope safety factor undergoes a significant drop at relative small η_l1, for the case of D_u = 4 m, D_l = 1 m and D_u = 2 m, D_l = 0. This is stemmed from the fact that when the critical failure surface could reach the lower weak interlayer, an increase in the length of lower weak interlayer is likely to induce a larger failure block (Fig. 16b), producing less soil resistance and hence lower safety factor, in contrast to smaller η_l1. However, such η_l1 effect is not infinite and after it exceeds a specific value, the failure mechanism would not change at limit state (Fig. 16c). In such case, additional increase in η_l1 has no influence on safety factor which is therefore converged to a constant. Note that at fixed η_l1 and D_u, a much less FoS is yielded when the lower weak interlayer shifts 1 m upwards, apart from at very small η_l1 where a localized failure happens only. This is sensible because: (1) at small η_l1 the entire lower weak interlayer is fully mobilized and the upper weak interlayer may be partially crossed to reach the limit state, and an increase in η_l1 means an expanded failure region with less soil resistance stemming from weak interlayers; and (2) in contrast to that at D_l = 1 m, more resistance is produced by parent soil due to increased velocity discontinuities, for the latter case, which can be well interpreted from the failure mechanism in Fig. 16d. In contrast, when the upper weak interlayer shifts 2 m upwards, FoS solutions are manifestly raised, and this is particularly pronounced at small η_l1. Since the upper weak interlayer exists close to slope crest surface, a toe or below-the-toe failure is more likely to be induced at limit state, thereby having more soil resistance from parent soil and a larger failure area (Fig. 16e). For ease of comparison, a lower weak interlayer is considered only and the results are proved to be the highest, in contrast to above cases. This is because less internal rates of work are produced in upper weak interlayer, even if the overall failure region is the same. This also demonstrates that existence of additional weak interlayers above is not favorable for slope stability. The change pattern of FoS is similar as above, and the failure mechanism is highly associated with the length of lower weak interlayer (Fig. 16f).

Fig. 15

Upper- and lower-bound solutions of MP-d slope safety factor against ηl1, Dl and Du

Fig. 16

Critical velocity field and failure surface against η_l1, D_l and D_u

6 Conclusions

This study proposed a finite-element limit-analysis procedure for the assessment of seismic slope stability with considerations of dual weak interlayers. Modified pseudo-dynamic approach is principally adopted to represent horizontal and vertical accelerations, apart from the pseudo-static. In the presence of weak interlayers within soils, the scientific challenge lies in the construction of a kinematically admissible velocity field and a statically allowable stress field, within the framework of plasticity theory. In an effort to tackle this issue, finite element method is used to discretize the whole domain of interest into infinitesimal elements. Velocity and stress fields are therefore generated by following corresponding conditions. Within the discretized velocity field and stress field, complicated pseudo-dynamic forces are readily considered in work rate calculations (upper-bound analysis) and stress equilibrium equations (lower-bound analysis). Combining limit analysis theorems with finite element method, seismic stability analysis of soil slopes in the presence of dual weak interlayers is transformed to linear programming models. Interior-point algorithm is implemented into MATLAB to optimize the upper- and lower-bound formulations. P-s and MP-d solutions of FoS are sought after optimization. It is worthwhile highlighting that both upper- and lower-bound solutions can be calculated in this study, aiding to better estimate the true solution of seismic slope stability, which is limited to the range of lower and upper bounds. This is the intrinsic advantage of the proposed procedure over other approaches including FEM and limit equilibrium. Therefore, FoS solutions obtained herein are more meaningful, providing a reliable guidance for the design of soil slopes containing dual weak interlayers at ultimate bearing capacity state. Some key findings are summarized as.

• (1) MP-d approach tends to yield a more reliable solution for seismic slope stability, because more detailed information such as shear and primary wave properties and soil damping is considered. In contrast to the pseudo-static, a smaller FoS tends to be computed from a MP-d analysis, due to amplified seismic forces. It indicates that the use of P-s approach may yield unconservative solutions, and hence is unsafe for slope design.

• (2) In the presence of dual weak interlayers, FoS is complicatedly influenced by the combined effects of two weak interlayers. Overall, increase in η_u1, β_l, η_l1 and decrease in D_u, D_l lead to a reduction of FoS, to varying extent. The key reason lies in the reduced soil resistance provided by weak interlayers, in contrast to patent soil, demonstrating that the presence of weak interlayers is unfavorable for slope stability which is also highly associated with the position of dimension of weak interlayers.

• (3) Velocity fields at limit state provides a sound avenue to reveal the failure mechanism of slope instability under the effects of weak interlayers and earthquakes. The results demonstrate a rotational-translational failure mechanism in the presence of weak interlayers. Meanwhile, the critical velocity field can also be used to better interpret upper-bound solutions.

• (4) In both P-s and MP-d analyses, FEUB and FELB modelling are performed for seismic slope stability analysis, aiming to better estimate the true solution. Overall, the results show around 5% difference between upper- and lower-bound solutions, demonstrating a sound estimate of true FoS. This is the core advantage of the proposed procedure over other approaches, and hence is recommended to be applied to other geotechnical stability problems in future.

Appendices

Appendix A: Finite-element upper-bound analysis

$$A_{11}^{e} = \frac{1}{{2A^{e} }}\left[ {\begin{array}{*{20}c} {b_{1}^{e} } & 0 & {b_{2}^{e} } & 0 & {b_{3}^{e} } & 0 \\ 0 & {c_{1}^{e} } & 0 & {c_{2}^{e} } & 0 & {c_{3}^{e} } \\ {c_{1}^{e} } & {b_{1}^{e} } & {c_{2}^{e} } & {b_{2}^{e} } & {c_{3}^{e} } & {b_{3}^{e} } \\ \end{array} } \right]$$

(A1)

$$A_{12}^{e} = \left[ {\begin{array}{*{20}c} {M_{1}^{{}} } & {M_{2}^{{}} } & \cdots & {M_{k}^{{}} } & \cdots & {M_{p}^{{}} } \\ {N_{1}^{{}} } & {N_{2}^{{}} } & \cdots & {N_{k}^{{}} } & \cdots & {N_{p}^{{}} } \\ {R_{1}^{{}} } & {R_{2}^{{}} } & \cdots & {R_{k}^{{}} } & \cdots & {R_{p}^{{}} } \\ \end{array} } \right]$$

(A2)

$$A_{23}^{d} = \left[ {\begin{array}{*{20}c} {T_{1}^{d} } & 0 \\ 0 & {T_{1}^{d} } \\ \end{array} } \right],\;\;T_{1}^{d} = \left[ {\begin{array}{*{20}c} {\sin \theta^{d} } & { - \cos \theta^{d} } & { - \sin \theta^{d} } & {\cos \theta^{d} } \\ { - \cos \theta^{d} } & { - \sin \theta^{d} } & {\cos \theta^{d} } & {\sin \theta^{d} } \\ \end{array} } \right]$$

(A3)

$$A_{24}^{d} = \left[ {\begin{array}{*{20}c} {T_{2}^{d} } & 0 \\ 0 & {T_{2}^{d} } \\ \end{array} } \right],\;\;T_{2}^{d} = \left[ {\begin{array}{*{20}c} {\tan \varphi } & {\tan \varphi } \\ 1 & { - 1} \\ \end{array} } \right]$$

(A4)

$$A_{3}^{b} = \left[ {\begin{array}{*{20}c} {T_{3}^{b} } & 0 \\ 0 & {T_{3}^{b} } \\ \end{array} } \right],\;\;T_{3}^{b} = \left[ {\begin{array}{*{20}c} {\cos \theta^{b} } & {\sin \theta^{b} } \\ { - \sin \theta^{b} } & {\cos \theta^{b} } \\ \end{array} } \right]$$

(A5)

$$B_{3}^{b} = \left[ {\begin{array}{*{20}c} {\overline{u}_{s1}^{b} } & {\overline{v}_{n1}^{b} } \\ \end{array} \;\;\;\;\begin{array}{*{20}c} {\overline{u}_{s2}^{b} } & {\overline{v}_{n2}^{b} } \\ \end{array} } \right]^{T}$$

(A6)

where $A^{e}$ is the area of a random element e (Fig. 1a), $b_{1}^{e} = y_{2}^{e} - y_{3}^{e}$, $b_{2}^{e} = y_{3}^{e} - y_{1}^{e}$, $b_{3}^{e} = y_{1}^{e} - y_{2}^{e}$, $c_{1}^{e} = - x_{2}^{e} + x_{3}^{e}$,$c_{2}^{e} = - x_{3}^{e} + x_{1}^{e}$, $c_{3}^{e} = - x_{1}^{e} + x_{2}^{e}$, with ($x_{1}^{e}$, $y_{1}^{e}$), ($x_{2}^{e}$, $y_{2}^{e}$), and ($x_{3}^{e}$, $y_{3}^{e}$) being the coordinates of three nodes in element e. For an external linearization of the MC failure criterion with p planes, $M_{k}^{{}} = \cos (2k\pi /p) + \sin \varphi$,$N_{k}^{{}} = - \cos (2k\pi /p) + \sin \varphi$,$R_{k}^{{}} = 2\sin (2k\pi /p)$, $k = 1,\;2, \cdots ,\;p$. $\theta^{d}$ is the angle of velocity discontinuity (e.g., edge d) inclined to x-axis as shown in Fig. 1b. $\theta^{b}$ is the angle of a random boundary (e.g., boundary b) with respect to x-axis as shown in Fig. 1c. $\overline{u}_{si}^{b}$ and $\overline{v}_{ni}^{b}$ denote the prescribed tangential and normal nodal velocity at node i (i = 1, 2), respectively.

$$C_{i1}^{e} = 2A^{e} c\cos \varphi [\underbrace {{\begin{array}{*{20}c} 1 & 1 & \cdots & 1 \\ \end{array} }}_{p}]$$

(A7)

$$C_{i2}^{d} = \frac{1}{2}cl^{d} [\begin{array}{*{20}c} 1 & 1 & 1 & 1 \\ \end{array} ]$$

(A8)

$$C_{e1}^{e} = \frac{{A^{e} }}{3}\left[ {\begin{array}{*{20}c} 0 & {\begin{array}{*{20}c} {\begin{array}{*{20}c} \gamma & 0 \\ \end{array} } & \gamma & 0 & \gamma \\ \end{array} } \\ \end{array} } \right]$$

(A9)

$$C_{e2}^{q} = \frac{{l^{q} }}{2}\left[ {\begin{array}{*{20}c} 0 & {\overline{q}_{n} } & 0 & {\overline{q}_{n} } \\ \end{array} } \right]$$

(A10)

$$C_{e3}^{e} = \frac{{A^{e} \cdot \gamma }}{3}\left[ {\begin{array}{*{20}c} {k_{h} (t,y)} & {\begin{array}{*{20}c} {\begin{array}{*{20}c} {k_{v} (t,y)} & {k_{h} (t,y)} \\ \end{array} } & {k_{v} (t,y)} & {k_{h} (t,y)} & {k_{v} (t,y)} \\ \end{array} } \\ \end{array} } \right]$$

(A11)

where $l^{d}$ denotes the length of a velocity discontinuity (e.g., d), $l^{q}$ is the length of an edge (e.g., q) where traction force $\overline{q}_{n}$ acts.

Appendix B: Finite-element lower-bound analysis

$$A_{1}^{e} = \frac{1}{{2A^{e} }}\left[ {\begin{array}{*{20}c} {b_{1} } & 0 & {c_{1} } & {b_{2} } & 0 & {c_{2} } & {b_{3} } & 0 & {c_{3} } \\ 0 & {c_{1} } & {b_{1} } & 0 & {c_{2} } & {b_{2} } & 0 & {c_{3} } & {b_{3} } \\ \end{array} } \right]$$

(B1)

$$B_{1}^{e} = \left[ {\begin{array}{*{20}c} {X_{x}^{e} } & {X_{y}^{e} } \\ \end{array} } \right]^{T}$$

(B2)

$$A_{2}^{d} = \left[ {\begin{array}{*{20}c} {T^{d} } & { - T^{d} } & 0 & 0 \\ 0 & 0 & {T^{d} } & { - T^{d} } \\ \end{array} } \right],\;\;\;T^{d} = \left[ {\begin{array}{*{20}c} {\sin {}^{2}\theta^{d} } & {\cos {}^{2}\theta^{d} } & { - \sin 2\theta^{d} } \\ { - \frac{1}{2}\sin 2\theta^{d} } & {\frac{1}{2}\sin 2\theta^{d} } & {\cos 2\theta^{d} } \\ \end{array} } \right]$$

(B3)

$$A_{3}^{b} = \left[ {\begin{array}{*{20}c} {T^{b} } & 0 \\ 0 & {T^{b} } \\ \end{array} } \right],\;\;\;T^{b} = \left[ {\begin{array}{*{20}c} {\sin {}^{2}\theta^{b} } & {\cos {}^{2}\theta^{b} } & { - \sin 2\theta^{b} } \\ { - \frac{1}{2}\sin 2\theta^{b} } & {\frac{1}{2}\sin 2\theta^{b} } & {\cos 2\theta^{b} } \\ \end{array} } \right]$$

(B4)

$$B_{3}^{b} = \left[ {\begin{array}{*{20}c} {q_{n1}^{b} } & {t_{s1}^{b} } & {q_{n2}^{b} } & {t_{s2}^{b} } \\ \end{array} } \right]^{T}$$

(B5)

$$A_{4}^{i} = \left[ {\begin{array}{*{20}c} {m_{1} } & {m_{2} } & \cdots & {m_{k} } & \cdots & {m_{p} } \\ {n_{1} } & {n_{2} } & \cdots & {n_{k} } & \cdots & {n_{p} } \\ {r_{1} } & {r_{2} } & \cdots & {r_{k} } & \cdots & {r_{p} } \\ \end{array} } \right]^{T}$$

(B6)

$$B_{4}^{i} = 2c\cos \varphi \cos (\pi /p)[\underbrace {{\begin{array}{*{20}c} 1 & 1 & \cdots & 1 \\ \end{array} }}_{p}]^{T}$$

(B7)

where $A^{e}$ is the area of a random element e (Fig. 2a), $b_{1}^{e} = y_{2}^{e} - y_{3}^{e}$, $b_{2}^{e} = y_{3}^{e} - y_{1}^{e}$, $b_{3}^{e} = y_{1}^{e} - y_{2}^{e}$, $c_{1}^{e} = - x_{2}^{e} + x_{3}^{e}$,$c_{2}^{e} = - x_{3}^{e} + x_{1}^{e}$, $c_{3}^{e} = - x_{1}^{e} + x_{2}^{e}$, with ($x_{1}^{e}$, $y_{1}^{e}$), ($x_{2}^{e}$, $y_{2}^{e}$), and ($x_{3}^{e}$, $y_{3}^{e}$) being the coordinates of three nodes in element e. $X_{x}^{e} ,\;X_{y}^{e}$ are body stress components in x- and y-direction. $\theta^{d}$ is the angle of interface d with respect to x-axis (Fig. 2b). $\theta^{b}$ is the angle of edge b inclined to x-axis (Fig. 2c). $q_{n1}^{b} ,\;t_{s1}^{b}$ ($q_{n2}^{b} ,\;t_{s2}^{b}$) represent nodal normal and shear stresses at the node 1 (node 2) of edge b. For an internal linearization of the Mohr-Coulomb criterion with p planes, $m_{k} = \cos (2k\pi /p) + \sin \varphi \cos (\pi /p)$,$n_{k} = - \cos (2k\pi /p) + \sin \varphi \cos (\pi /p)$, $r_{k} = 2\sin (2k\pi /p)$,$(k = 1,2, \cdots ,p)$.