A Manifold Learning Approach for Integrated Computational Materials Engineering

Abstract

Image-based simulation is becoming an appealing technique to homogenize properties of real microstructures of heterogeneous materials. However fast computation techniques are needed to take decisions in a limited time-scale. Techniques based on standard computational homogenization are seriously compromised by the real-time constraint. The combination of model reduction techniques and high performance computing contribute to alleviate such a constraint but the amount of computation remains excessive in many cases. In this paper we consider an alternative route that makes use of techniques traditionally considered for machine learning purposes in order to extract the manifold in which data and fields can be interpolated accurately and in real-time and with minimum amount of online computation. Locallly Linear Embedding is considered in this work for the real-time thermal homogenization of heterogeneous microstructures.

Appendix: On Computational Homogenization

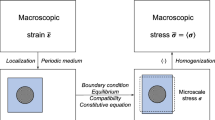
In this section the simplest procedure related to computational homogenization is revisited. Due to the microscopic heterogeneity, the macroscopic thermal modeling needs a homogenized thermal conductivity which depends on the microscopic details. To compute this homogenized thermal conductivity an appropriate RVE is considered at position ${\mathbf {X}} \in \varOmega$, $\omega ({\mathbf {X}})$ [20, 21, 31] in which the microstructure is perfectly defined at this scale.

In the linear case the local microscopic conductivity ${\mathbf {k}}({\mathbf {x}})$ is known at each point ${\mathbf {x}}$ in the microscopic domain $\omega ({\mathbf {X}})$.

We can define the macroscopic temperature gradient at position ${\mathbf {X}}$, ${\mathbf {G}} ({\mathbf {X}})$, from:

$${\mathbf {G}} ({\mathbf {X}}) \ = \ \langle {\mathbf {g}} \rangle \ = \ \frac{1}{| \omega ({\mathbf {X}})|} \int _{\omega ({\mathbf {X}})} {\mathbf {g}}({\mathbf {x}}) \ d{\mathbf {x}}$$

(11)

where the temperature gradient writes ${\mathbf {g}} ({\mathbf {x}}) = \nabla T({\mathbf {x}})$.

We also assume the existence of a localization tensor ${\mathbf {L}}({\mathbf {x}}, {\mathbf {X}})$ such that

$${\mathbf {g}} ({\mathbf {x}}) = {\mathbf {L}}({\mathbf {x}}, {\mathbf {X}}) \cdot {\mathbf {G}} ({\mathbf {X}})$$

(12)

The microscopic heat flux ${\mathbf {q}}$ writes according to Fourier’s law

$${\mathbf {q}}({\mathbf {x}}) \ = \ - {\mathbf {k}}({\mathbf {x}}) \cdot {\mathbf {g}}({\mathbf {x}})$$

(13)

and its macroscopic counterpart ${\mathbf {Q}}({\mathbf {X}})$ reads:

$${\mathbf {Q}}({\mathbf {X}}) \ = \ \langle {\mathbf {q}}({\mathbf {x}}) \rangle \ = \ - \langle {\mathbf {k}}({\mathbf {x}}) \cdot {\mathbf {g}} ({\mathbf {x}}) \rangle \ = \ - \langle {\mathbf {k}}({\mathbf {x}}) \cdot {\mathbf {L}}({\mathbf {x}}, {\mathbf {X}}) \rangle \cdot {\mathbf {G}}({\mathbf {X}})$$

(14)

from which the homogenized thermal conductivity can be defined from

$${\mathbf {K}}({\mathbf {X}}) \ = \ \langle {\mathbf {k}}({\mathbf {x}}) \cdot {\mathbf {L}}({\mathbf {x}}, {\mathbf {X}}) \rangle$$

(15)

Since ${\mathbf {k}}({\mathbf {x}})$ is perfectly known everywhere in the representative volume element $\omega ({\mathbf {X}})$, the definition of the homogenized thermal conductivity tensor only requires the computation of the localization tensor ${\mathbf {L}}({\mathbf {x}}, {\mathbf {X}})$. Several approaches are proposed in the literature to define this tensor, according to the choice of boundary conditions. The objective here is not to discuss this choice. The interested reader can find some details in [14, 19, 20, 39]. For the sake of simplicity, we use essential boundary conditions on $\partial \omega ({\mathbf {X}})$ corresponding to the assumption of uniform temperature gradient on the RVE $\omega ({\mathbf {X}})$. We consider the general 3D case that involves the solution of the three boundary-value problems related to the steady state heat transfer model in the microscopic domain $\omega ({\mathbf {X}})$ for three different boundary conditions on $\partial \omega ({\mathbf {X}})$:

$$\left\{ \begin{array}{l} \nabla \cdot \left( {\mathbf {k}}({\mathbf {x}}) \cdot \nabla \varTheta ^1 ({\mathbf {x}})\right) \ = \ 0 \\ \varTheta ^1 ({\mathbf {x}} \in \partial \omega ({\mathbf {X}})) = x \end{array}\right.,$$

(16)

$$\left\{ \begin{array}{l} \nabla \cdot \left( {\mathbf {k}}({\mathbf {x}}) \cdot \nabla \varTheta ^2 ({\mathbf {x}})\right) \ = \ 0 \\ \varTheta ^2 ({\mathbf {x}} \in \partial \omega ({\mathbf {X}})) = y \end{array}\right.,$$

(17)

and

$$\left\{ \begin{array}{l} \nabla \cdot \left( {\mathbf {k}}({\mathbf {x}}) \cdot \nabla \varTheta ^3 ({\mathbf {x}})\right) \ = \ 0 \\ \varTheta ^3 ({\mathbf {x}} \in \partial \omega ({\mathbf {X}})) = z \end{array}\right.$$

(18)

It is easy to prove that these three solutions verify

$$\left\{ \begin{array}{l} {\mathbf {G}}^1 \ = \ \langle \nabla \varTheta ^1({\mathbf {x}}) \rangle \ = \ (1,0,0)^T \\ {\mathbf {G}}^2 \ = \ \langle \nabla \varTheta ^2({\mathbf {x}}) \rangle \ = \ (0,1,0)^T \\ {\mathbf {G}}^3 \ = \ \langle \nabla \varTheta ^3({\mathbf {x}}) \rangle \ = \ (0,0,1)^T \end{array}\right.$$

(19)

where $(\cdot )^T$ denotes the transpose. Thus, the localization tensor results finally:

$${\mathbf {L}}({\mathbf {x}}, {\mathbf {X}}) \ = \ \left( \nabla \varTheta ^1({\mathbf {x}}) \ \ \ \nabla \varTheta ^2({\mathbf {x}}) \ \ \ \nabla \varTheta ^3({\mathbf {x}}) \right)$$

(20)

The resulting non-concurrent homogenization procedure is illustrated in Fig. 9. As soon as tensor ${\mathbf {L}} ({\mathbf {x}}, {\mathbf {X}})$ is known at each position ${\mathbf {x}}$, the constitutive law relating the macroscopic temperature gradient and the macroscopic heat flux becomes fully defined.

Fig. 9

Homogenization procedure of linear heterogeneous models