Stiff-PDEs and Physics-Informed Neural Networks

Abstract

In recent years, physics-informed neural networks (PINN) have been used to solve stiff-PDEs mostly in the 1D and 2D spatial domain. PINNs still experience issues solving 3D problems, especially, problems with conflicting boundary conditions at adjacent edges and corners. These problems have discontinuous solutions at edges and corners that are difficult to learn for neural networks with a continuous activation function. In this review paper, we have investigated various PINN frameworks that are designed to solve stiff-PDEs. We took two heat conduction problems (2D and 3D) with a discontinuous solution at corners as test cases. We investigated these problems with a number of PINN frameworks, discussed and analysed the results against the FEM solution. It appears that PINNs provide a more general platform for parameterisation compared to conventional solvers. Thus, we have investigated the 2D heat conduction problem with parametric conductivity and geometry separately. We also discuss the challenges associated with PINNs and identify areas for further investigation.

1 Introduction

For a variety of problems, conventional numerical techniques for solving partial differential equations (PDEs) remain difficult. The mesh generation is complicated, noisy experimental data can’t be integrated with the existing algorithms and high-dimensional parametric PDEs often can’t be solved. Ill-posed inverse problems are prohibitively expensive and require complicated algorithms. In an effort to address these issues, the development of powerful computers and machine learning libraries has taken research in physics-informed machine learning to new heights.

Recently, physics-informed neural networks (PINNs) have gained popularity due to the novel approach for solving forward [1,2,3,4] and inverse problems [5,6,7] involving PDEs using neural networks (NNs). Unlike conventional numerical techniques for solving PDEs, PINNs are non-data-driven meshless models that satisfy the prescribed initial (IC) and boundary conditions (BC) as well as the governing PDE. The differential terms in the PDE are approximated using automatic differentiation.

Although, NNs have been present in literature for a long time, it was only in the last decade that they started gaining immense popularity due to the recent advancement in automatic differentiation and the availability of open-source machine learning libraries such as PyTorch and TensorFlow. It is automatic differentiation [8] producing highly accurate derivatives that enhances the accuracy of PINNs even with sparse data points in the spatio-temporal domain.

The numerical solution of ordinary differential equations (ODEs) and PDEs using NNs [9,10,11,12,13,14,15] has been a key area of interest for researchers. This is because the NNs behave like meshless solvers and can be scaled to higher dimensions without the need of additional algorithms.

In this review, we have investigated stiff-PDEs [16], specifically those with a discontinuous solution, such as conflicting BCs at adjacent edges or faces. The reason for this focus is due to the significant challenge posed by solving such problems with PINNs because it is not possible to fit a smooth curve such as a NN on these discontinuities.

The baseline PINN, a generalised NN framework, was proposed by Raissi et al. [17] for solving forward and inverse problems involving PDEs. The baseline PINN takes in the independent variables as the input and gives out the dependent variables as the output, and, depending on the type of problem we construct, the loss function. The baseline PINN accurately predicted the solution of forward problems such as the 1D Burgers equation, 1D Schrodinger equation, 1D Allen–Cahn equation and inverse problems such as recovering the 2D Navier–Stokes equation from the finite element generated flow past a cylinder simulation.

The baseline PINN has several limitations such as scalability to higher dimensions, imbalanced magnitude of individual loss terms in the multiple task loss function, gradient explosion etc. A brief description of these issues has been given in this section and are explored further in the subsequent section.

The baseline PINN can be scaled to higher dimensions by modifying the architecture of the NN. A general approach is to deploy more activated neurons ($\sim 500$) with very few hidden layers ($\sim 4$). This approach helps in fitting complex local variations in the solution. Wang et al. [18] proposed a fully connected NN (FCNN) with two transformer networks [19,20,21], which projects the input variables to a high-dimensional feature space. Sirignano and Spiliopoulos [22] proposed a deep Galerkin method (DGM) architecture influenced by the LSTM architecture [23]. Both these architectures attempt to encapsulate the complex local variations in the solution by using more complex NN architectures.

Spectral bias [24] is a learning bias of deep NNs (DNNs) towards low-frequency functions, which causes convergence issues during training. Novel architectures such as Fourier networks [25], Modified Fourier networks [26, 27], Sinusoidal Representation networks, SiReNs [28] were proposed to remove the spectral bias from computer vision problems.

Imbalanced loss terms appear when the magnitude of a loss term is significantly larger than other loss terms, resulting in early convergence of other loss terms in the multitask loss function. A predominant approach is to multiply a parameter $\lambda$ to each loss term to balance out the contribution of each term to the overall loss [29]. Several frameworks such as self-adaptive PINNs [30] and the self-adaptive weight PINN [31]; algorithms such as learning rate annealing [18] and neural tangent kernel [32] were proposed to balance out the contribution of each term to the overall loss by introducing adaptive coefficients for each loss term.

Gradient explosion [33, 34] is a known issue while training NNs. The baseline PINN uses L-BFGS [35], a second order optimiser, which exhibits exploding gradients when it encounters sharp gradients [36].

Most of the PINN frameworks are readily available as open-source libraries. Libraries such as DeepXDE [37], SciANN [38], TensorDiffEq [39] and NeuralPDE [40] are easy to implement and can be used to solve simple problems in the 1D and 2D spatial domain. NVIDIA Modulus (formerly NVIDIA SimNet) [26, 27] is an advanced open-source library providing access to different PINN frameworks. NVIDIA Modulus has successfully simulated physical systems such as laminar flow over a field programmable gate arrays (FPGA) heatsink, turbulent flow over a simple 3D heatsink with parameterised fin dimensions, conjugate heat transfer over NVIDIA’s NVSwitch heat sink using transfer learning.

This review paper has been divided into five major sections. Section 1 comprises a comprehensive literature review of PINNs. Section 2 discusses the functioning of a baseline PINN [17] and some advanced tools that enhance the performance of PINNs. Section 3 discusses different PINN frameworks that are available in DeepXDE [37] and NVIDIA Modulus [26]. Sections 4 and 5 discuss the solution of 2D and 3D heat conduction test case using various PINN frameworks. Section 6 discusses the results of a series of parametric PDEs. In Sect. 7, we discuss challenges related to implementing PINNs for stiff-PDEs.

We took two heat conduction problems (2D and 3D) with a discontinuous solution at corner points as test cases. In Sects. 4 and 5, we investigated these problems with a number of PINN frameworks from Table 1 and compared the results with the FEM solution. PINNs are also known for solving parametric PDEs [41,42,43,44]. In Sect. 6, we investigated the 2D test case with parameterised conductivity and geometry.

For the forward problems, we used the baseline PINN, DeepXDE’s baseline PINN, NVIDIA Modulus’s baseline PINN, Fourier network, Modified Fourier network, SiReNs and DGM architecture. Whereas for the parametric PDE, we have only used the DeepXDE’s baseline PINN, Modified Fourier network and DGM architecture.

2 How PINNs Work

PINNs are DNNs that obey the physical constraints, such as, the BCs, the ICs and the governing PDE.

PINNs are fundamentally different from conventional PDE solvers such as finite difference or finite elements, in terms of the how the system of equations are represented. In the case of PINNs, the number of equations or the data points are more than the number of unknowns or the network parameters, resulting in a regression problem. On the other hand, the conventional PDE solvers, such as FEM, often solves the system of equations with the number of equations and unknowns being equal.

This section discusses the theoretical aspects of PINNs. Section 2.1 discusses the functioning of NNs. Section 2.2 discusses how the physics knowledge is embedded into the NN. Section 3 discusses the various PINN frameworks, that can solve stiff-PDEs. Finally, Sect. 2.3 discuss various tools that can help in speeding the convergence and improving the accuracy of PINNs.

2.1 Neural Networks for Regression

NNs are nonlinear and non-convex regression frameworks with exceptional predictive capability, widely known as universal approximators of continuous functions [45, 46]. They are known for their ability to learn and generalise very complicated information [47]. This section discusses the evolution of NNs.

One of the simplest regression models is the linear regression. In the case of linear regression, the hypothesis or the trial function is the linear combination of weights and features. Let us assume a dataset with n samples consisting of m features with a bias term ${\varvec{X}} = \left\{ 1,\,{{\varvec{x}}}_{1},\,{{\varvec{x}}}_{2},\,{{\varvec{x}}}_{3},\ldots ,{{\varvec{x}}}_{m}\right\}$ and one label ${\varvec{y}}$. The linear regression hypothesis for the dataset can be written as follows

$${\hat{{\varvec{y}}}}=w_{0}+w_{1}{\varvec{x}}_{1}+w_{2}{\varvec{x}}_{2} +\cdots +w_{m}{\varvec{x}}_{m}={\varvec{W}}^{T}{\varvec{X}},$$

(1)

where the trainable weights ${\varvec{W}}=\left\{ w_{0},\,w_{1},\,w_{2},\ldots ,w_{m}\right\}$ are tweaked such that the mean squared error (MSE) or any loss metric of the ground truth ${\varvec{y}}$ against the predicted output ${\hat{{\varvec{y}}}}$ is minimised.

In principle, we can introduce a hypothesis with a linear combination of weights with nonlinear features too. The main drawback of linear regression is underfitting because it essentially fits a linear equation onto the data points [48, 49].

A simple technique to prevent underfitting is to pass the output of linear regression hypothesis (Eq. 1) to specifically chosen nonlinear function, often referred to as the activation function $\left( \sigma \right)$ [50]. These activation functions, for example, sigmoid, hyperbolic tangent, softmax are continuous and sometimes are infinitely differentiable in the domain of real numbers. The resulting hypothesis (Eq. 2) is referred to as an artificial neuron (Fig. 1) [51]. It transforms the linear regression hypothesis into a nonlinear feature space.

$${\hat{{\varvec{y}}}}=\sigma \left( w_{0}+w_{1}{\varvec{x}}_{1}+w_{2}{\varvec{x}}_{2}+\cdots \right) =\sigma \left( {\varvec{W}}^{T}{\varvec{X}}\right) .$$

(2)

Fig. 1

Schematic diagram of an artificial neuron. Here, ${\varvec{X}}=\left\{ 1,\,x_{1},\,x_{2},\ldots ,x_{m}\right\}$ is the input dataset, ${\varvec{W}}=\left\{ w_{0},\,w_{1},\,w_{2},\ldots ,w_{m}\right\}$ is the vector of trainable weights/parameters, $\sigma$ is the activation function and ${\hat{y}}$ is the predicted output

The artificial neuron is the building block of a NN. DNNs have multiple hidden-layers, each hidden-layer consisting of multiple artificial neurons thus increasing the predictive capability even further. Each hidden layer transforms the feature space into a more complex feature space [52]. It is an open question in interpretable machine learning to explain mathematically, how these nonlinear transformations influence the output [53]. Figure 2 shows the schematic diagram of a FCNN with two hidden layers.

Fig. 2

Schematic diagram of a fully connected neural network (FCNN) with two hidden layers. Here, ${\varvec{X}}=\left\{ 1,\,x_{1},\,x_{2},\ldots ,x_{m}\right\}$ is the input dataset, $\left\{ w^{(1)},\,w^{(2)},\,w^{(3)}\right\}$ is the vector of trainable weights/parameters for each layer, $\left\{ a^{(2)},\,a^{(3)}\right\}$ is the vector of activated layers and ${\hat{y}}$ is the predicted output

In Fig. 2, there are four layers, one input layer, two hidden layers and one output layer. Both the hidden layers consist of three artificial neurons, also known as the activated neurons or simply the nodes. In a FCNN, each node has its own set of weights or parameters.

Let us define some notation, $a_{i}^{\left( k\right) }$ is the ith activated neuron in the kth layer. $w^{k}$ is the weight matrix controlling the nonlinear mapping between kth layer and $\left( k+1\right)$th layer. If the network has $s_{k}$ activated neurons in kth layer and $s_{\left( k+1\right) }$ activated neurons in $\left( k+1\right)$th layer then $w^{k}$ will be of dimension $s_{\left( k+1\right) }\,\times \,s_{k}$.

2.1.1 Forward Pass

The first step in training of a NN is to forward pass the inputs ${\varvec{X}}$ to obtain the predicted output ${\varvec{{\hat{y}}}}$. Let $a_{i}^{\left( k\right) }=\sigma \left( z_{i}^{\left( k\right) }\right)$ such that ${\varvec{z}}$ is the term without the activation. Now, the forward pass for the FCNN in Fig. 2 can be written as follows:

$$\begin{aligned} {\varvec{z}}^{\left( 2\right) }&={\varvec{w}}^{\left( 1\right) }{\varvec{X}}, \\ {\varvec{a}}^{\left( 2\right) }&=\sigma \left( {\varvec{z}}^{\left( 2\right) }\right) , \\ {\varvec{z}}^{\left( 3\right) }&={\varvec{w}}^{\left( 2\right) }{\varvec{a}}^{\left( 2\right) }, \\ {\varvec{a}}^{\left( 3\right) }&=\sigma \left( {\varvec{z}}^{\left( 3\right) }\right) , \\ {\hat{{\varvec{y}}}}&={\varvec{w}}^{\left( 3\right) }{\varvec{a}}^{\left( 3\right) }. \end{aligned}$$

(3)

In regression problems, the last layer is not activated because we want unbounded values. The hypothesis of a FCNN with two hidden layers can be written as follows:

$${\hat{{\varvec{y}}}}={\varvec{w}}^{\left( 3\right) }\sigma \left( {\varvec{w}}^{\left( 2\right) } \sigma \left( {\varvec{w}}^{\left( 1\right) }{\varvec{X}}\right) \right) .$$

(4)

2.1.2 Backpropagation and Automatic Gradient

Once we have obtained the predicted output ${\hat{{\varvec{y}}}}$ from the forward pass, we can calculate the difference from the ground truth ${\varvec{y}}$ using some loss metric [54]. In general, for a regression problem, the MSE (Eq. 5) is used as a loss metric.

$$J= \frac{1}{2n}\sum _{i=1}^{n}\left|y_{i}-{\hat{y}}_{i}\right|^{2}.$$

(5)

Now, the loss J is sent to the optimisers. Optimisers are algorithms that minimise the loss by updating the weights or parameters of the NN. There are many optimisers that are available in open-source libraries such as PyTorch and TensorFlow [55]. On the basis of order of the derivatives of the loss with respect to the weights, the optimisers can be divided mainly into two categories: first order and second order optimisers [56].

The first-order optimisers utilise the gradient of the loss with respect to weights of the NN. Similarly, second-order optimisers utilise the gradient as well as the Hessian of the loss with respect to the weights of the NN. Gradient-descent [57] and Adam [58] are the most popular first-order optimisers. Whereas, L-BFGS [35] is the only second-order optimiser that is still actively used in machine learning.

Now that the optimisers require derivatives, we need to compute the derivatives efficiently and accurately. There are three main techniques that have been successfully used in machine learning: numerical [59], symbolic [60] and automatic differentiations [8]. After the release of TensorFlow 1.0 in 2015, static computational graphs was the standard data structure for representing NNs, which was later substituted with dynamic computational graphs in PyTorch [61, 62]. These libraries use forward-mode or reverse-mode automatic differentiation to compute the derivatives within a computational graph [63]. The automatic differentiation computes the derivative of the loss with respect to weights using the chain rule [64] in differential calculus with a hard-coded expression for the derivative of simple functions [65].

Let us say that we are using the gradient-descent method (Eq. 6) for optimising the weight/parameters.

$${\varvec{w}}^{\left( k\right) }:={\varvec{w}}^{\left( k\right) } -\alpha \frac{\partial J}{\partial {\varvec{w}}^{\left( k\right) }},$$

(6)

where k is the kth layer and $\alpha$ is a constant often referred to as the learning rate, a hyperparameter. It tells the optimiser the amount of perturbation the weights should attain in each epoch [66]. An epoch is a complete cycle of forward pass and backpropagation on the whole dataset.

The gradient of the loss J with respect to the weights in each layer can be computed using the chain rule as follows:

$$\begin{aligned} \frac{\partial J}{\partial {\varvec{w}}^{(3)}}&=\frac{\partial J}{\partial {\hat{{\varvec{y}}}}} \frac{\partial {\hat{{\varvec{y}}}}}{\partial {\varvec{w}}^{(3)}}, \\ \frac{\partial J}{\partial {\varvec{w}}^{(2)}}&=\frac{\partial J}{\partial {\hat{{\varvec{y}}}}} \frac{\partial {\hat{{\varvec{y}}}}}{\partial {\varvec{a}}^{(3)}}\frac{\partial {\varvec{a}}^{(3)}}{\partial {\varvec{z}}^{(3)}}\frac{\partial {\varvec{z}}^{(3)}}{\partial {\varvec{w}}^{(2)}}, \\ \frac{\partial J}{\partial {\varvec{w}}^{(1)}}&=\frac{\partial J}{\partial {\hat{{\varvec{y}}}}} \frac{\partial {\hat{{\varvec{y}}}}}{\partial {\varvec{a}}^{(3)}}\frac{\partial {\varvec{a}}^{(3)}}{\partial {\varvec{z}}^{(3)}}\frac{\partial {\varvec{z}}^{(3)}}{\partial {\varvec{a}}^{(2)}} \frac{\partial {\varvec{a}}^{(2)}}{\partial {\varvec{z}}^{(2)}}\frac{\partial {\varvec{z}}^{(2)}}{\partial {\varvec{w}}^{(1)}}. \end{aligned}$$

(7)

The analytical expression of the basic differential terms are hard-coded in machine learning libraries. The derivative of loss with respect to the weights is decomposed into these hard-coded basic differential terms using the chain rule. Once, these derivatives are calculated we plug them into Eq. 6 to update the weights/parameters. The process is repeated for a number of epochs until the loss J goes below some predefined tolerance.

2.2 Building a PINN

PINNs are supervised machine learning models that obey the prescribed BCs and the governing PDE. In PINNs, the inputs are the independent variables and the outputs are the dependent variables or the solution of the governing PDE.

As an example, for a 3D time-dependent heat conduction PDE, the number of inputs would be four, i.e., the x, y and z coordinates and the time t. Similarly, the number of outputs would be one, i.e. the temperature u.

2.2.1 Defining a Well-Posed PDE

Consider a well-posed PDE problem as follows:

$$\begin{aligned}&{\varvec{u}}_{t}+{\mathcal {N}}_{x}\left[ {\varvec{u}}\right] =0, \quad {\varvec{x}}\,\in \,{\varvec{\Omega }},\quad t\,\in \,\left[ 0,T\right] , \\&{\varvec{u}}\left( {\varvec{x}},0\right) =h\left( {\varvec{x}}\right) , \quad {\varvec{x}}\,\in \,{\varvec{\Omega }}, \\&{\varvec{u}}\left( {\varvec{x}},t\right) =g\left( {\varvec{x}},t\right) , \quad {\varvec{x}}\,\in \,\partial {\varvec{\Omega }},\quad t\,\in \,\left[ 0,T\right] , \end{aligned}$$

(8)

where ${\mathcal {N}}_{x}\left[ {\varvec{u}}\right]$ is a differential operator, ${\varvec{x}}$ and t are the independent variables of the PDE, ${\varvec{\Omega }}$ and $\partial {\varvec{\Omega }}$ denotes the spatial domain and the boundary of the problem, $h\left( {\varvec{x}}\right)$ denotes the prescribed BC which is the solution to the PDE at all spatial points $\left( {\varvec{\Omega }}\right)$ at the initial time $\left( t=0\right)$, $g\left( {\varvec{x}},t\right)$ is the prescribed BC at the boundary of the domain $\left( \partial {\varvec{\Omega }}\right)$.

2.2.2 Discrete Loss Function

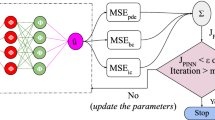
PINNs have a multitask loss function with at least two components, the BC and the PDE losses (Eq. 9). The multitask loss function ensures that the inputs to the PINN satisfy a well-posed PDE problem.

The IC and BC losses are simply the MSE and the PDE loss is the residual of the governing PDE at randomly chosen collocation points. The total loss (Eq. 9) and the individual loss terms (Eq. 10) are as follows:

$$\begin{aligned} {\mathcal {L}}&=\lambda _{PDE}{\mathcal {L}}_{PDE}+\lambda _{BC}{\mathcal {L}}_{BC} +\lambda _{IC}{\mathcal {L}}_{IC}, \end{aligned}$$

(9)

$$\begin{aligned} {\mathcal {L}}_{PDE}&=\frac{1}{N_{r}}\sum _{i=1}^{N_{r}}\left|{\hat{u}}_{t} \left( {\varvec{x}}_{i},t_{i}\right) +{\mathcal {N}}_{x}\left[ {\hat{u}}\left( {\varvec{x}}_{i},t_{i}\right) \right] \right|^{2}, \\ {\mathcal {L}}_{BC}&=\frac{1}{N_{b}}\sum _{i=1}^{N_{b}}\left|{\hat{u}} \left( {\varvec{x}}_{i},t_{i}\right) -g\left( {\varvec{x}}_{i},t_{i}\right) \right|^{2}, \\ {\mathcal {L}}_{IC}&=\frac{1}{N_{0}}\sum _{i=1}^{N_{0}}\left|{\hat{u}}\left( {\varvec{x}}_{i},0\right) -h\left( {\varvec{x}}_{i},0\right) \right|^{2}, \end{aligned}$$

(10)

where $N_{r}$, $N_{b}$ and $N_{0}$ are the number of data points that are sampled to satisfy the PDE loss, the BC loss and the IC loss. The coefficients $\lambda _{PDE}$, $\lambda _{BC}$ and $\lambda _{IC}$ in Eq. 9, help in achieving convergence and better accuracy, and are an active field of research. These weight coefficients can be scalar quantities [29] as well as vectors to apply weights to every single sample in the training dataset based on the pointwise error [27].

We can calculate the residual of the governing equation using automatic differentiation similar to Eq. 4. Figure 3, shows a schematic diagram of a baseline PINN with two hidden layers for a 2D spatio-temporal domain.

A PINN framework, referred to as sparse-regulated PINNs, uses the experimental or the simulation data to provide ground truth at sparse locations in the spatio-temporal domain [67, 68]. The addition of sparse ground truth helps the NN to accurately predict complex local variations in the solution. This introduces one more loss term called the reconstruction loss (Eq. 11), because it points the optimiser towards the true solution.

$${\mathcal {L}}_{reconstruct}=\frac{1}{N_{d}}\sum _{i=1}^{N_{d}}\left|{\hat{u}}\left( {\varvec{x}}_{i},t_{i}\right) -u_{i}^{true}\right|^{2},$$

(11)

where $N_d$ is the number of true solutions being provided. Bajaj et al. [69] showed that the reconstruction loss is not very helpful in preventing overfitting. Instead, NVIDIA Modulus uses the Adam optimiser with exponential decay of the learning rate $\alpha$, so that as we go closer to the minima of the loss, the weights do not attain large perturbations [58].

2.2.3 Integral Formulation of Loss

NVIDIA Modulus uses a slightly different version of the loss function [27, 70]. They define continuous/integral losses for the BC and PDE loss as follows:

$$\begin{aligned} {\mathcal {L}}_{PDE}&=\int _{{\varvec{\Omega }}}\left( {\hat{u}}_{t}\left( {\varvec{x}}_{i},t_{i}\right) +{\mathcal {N}}_{x}\left[ {\hat{u}}\left( {\varvec{x}}_{i},t_{i}\right) \right] \right) ^{2}d{\varvec{\Omega }}, \\ {\mathcal {L}}_{BC}&=\int _{\partial {\varvec{\Omega }}}\left( {\hat{u}}\left( {\varvec{x}}_{i},t_{i}\right) -g\left( {\varvec{x}}_{i},t_{i}\right) \right) ^{2}d\left( \partial {\varvec{\Omega }}\right) . \end{aligned}$$

(12)

Instead of approximating these integrals using deterministic numerical integration techniques, NVIDIA Modulus uses the Monte Carlo integration, a non-deterministic integration technique [71, 72], resulting in Eq. 13. This helps in keeping a specific loss term proportional to its length/area/volume. For example, it doesn’t allow a specific BC applied over a relatively larger area to dominate other BCs.

$$\begin{aligned} {\mathcal {L}}_{PDE}=\frac{1}{N_{r}}\sum _{i=1}^{N_{r}}\left|{\hat{u}}_{t} \left( {\varvec{x}}_{i},t_{i}\right) +{\mathcal {N}}_{x}\left[ {\hat{u}}\left( {\varvec{x}}_{i}, t_{i}\right) \right] \right|^{2}\int _{{\varvec{\Omega }}}d{\varvec{\Omega }}, \\ {\mathcal {L}}_{BC}=\frac{1}{N_{b}}\sum _{i=1}^{N_{b}}\left|{\hat{u}} \left( {\varvec{x}}_{i},t_{i}\right) -g\left( {\varvec{x}}_{i},t_{i}\right) \right|^{2} \int _{\partial {\varvec{\Omega }}}d\left( \partial {\varvec{\Omega }}\right) . \end{aligned}$$

(13)

Fig. 3

Schematic diagram of a physics-informed neural network (PINN) with two hidden layers for a 2D spatio-temporal domain. Here, the inputs are $\left\{ x,\,y,\,t\right\}$, $\left\{ w^{(1)},\,w^{(2)},\,w^{(3)}\right\}$ is the vector of trainable weights/parameters for each layer, $\left\{ a^{(2)},\,a^{(3)}\right\}$ is the vector of activated neurons for each layers and ${\hat{y}}$ is the predicted output

2.2.4 Exact BC Imposition

The output of the PINN can be hard constrained to exactly satisfy the BCs [73]. A function is manually constructed to transform the network outputs to exactly satisfy the BCs. Generally, hard constrained BCs work with simple geometry, constant individual Dirichlet BCs without conflicting each other. This approach does not work well with stiff-PDEs [74]. In Sect. 4.4, we have discusssed the difficulties with exact imposition of BCs in stiff-PDEs with a discontinuous solution.

2.2.5 Overfitted vs. Generalised Solution

The baseline PINN gained its popularity due to the notion that it can solve PDEs with sparse sampling in the spatio-temporal domain. Later on it was realised that, in the case of stiff-PDEs one must sample enough data points to capture the local variations in the solution.

Theoretically, one can obtain an overfitted model as well as a generalised model depending on the number of data points in the training dataset. An overfitted model exhibits low training loss but high validation and testing loss whereas a generalised model exhibits low training, validation and testing error. Thus overfitted model can only be used for inferring the solution from the training dataset, i.e., any data point of interest should be included in the training dataset. On the other hand, a generalised model can be obtained by sampling a significantly greater number of data points in the spatio-temporal domain. The solution can be predicted at new spatio-temporal locations within the domain.

The overfitted or generalised model is a qualitative aspect that depends on human judgement. In the case of stiff-PDEs, the overfitted model may converge with a considerable amount of pointwise error. Thus, it is important to sample more points around the boundary or the problematic region. In this paper, to be on the safer side, we have aimed for a generalised solution, i.e., we sampled a large number of points. Specific details can be found in Sect. 4.5.

2.2.6 Parametric PINNs

PINNs can predict the variation in the solution for a range of parameters such as density, geometry, conductivity etc. by introducing them as features in the training data set, compared to conventional numerical solvers where each parameter needs a separate simulation and may require complex algorithms. The idea is to add the parameter as another feature into the training data set such that each parameter has its own set of sampled points in the spatio-temporal domain. In other words, if there are n parameters for a 2D steady-state problem, than the training data set contains $n+2$ features.

2.3 Additional Tools

In this section, we have discussed tools that enhance the accuracy and efficiency of PINNs. Outside the scope of this paper are tools such as gradient enhanced training [75], learning rate annealing [18], neural tangent kernel [32], integral continuity planes [27]. The gradient enhanced training does not always improve the results compared to the baseline PINN. They may even adversely affect the training convergence and accuracy [76]. The learning rate annealing and neural tangent kernel deals with imbalanced losses where there is a significant difference between the magnitude of individual losses, which is not applicable to our test cases. The integral continuity planes are only applicable to problems involving fluid flow, where the mass flow rate or the volumetric flow rate is applied as an additional constraint, if known. This is particularly useful in the case of channel flow.

2.3.1 Adaptive Activation

An activation function transforms a feature space into a more complex feature space with the help of nonlinear functions. Without the activation function, the NN is just a sophisticated linear model with no performance improvement over linear regression. Jagtap et al. [77] proposed a DNN framework with trainable nonlinear transformations to improve the convergence as well as the accuracy of the NNs. They introduced an additional hyperparameter A in the nonlinear transformation of the hidden layers as follows:

$${\varvec{a}}^{(k)} \left( {\varvec{a}}^{(k-1)}; \theta , A \right) = \sigma \left( A {\varvec{z}}^{(k)} \left( {\varvec{a}}^{(k-1)}\right) \right) ,$$

(14)

where ${\varvec{a}}^{(k)}$ is the nonlinear transformation at layer k, which is a function of ${\varvec{a}}^{(k-1)}$, the output of the hidden layer $\left( k-1\right)$, the weights and biases is denoted by $\theta$, A is a trainable parameter and ${\varvec{z}}^{(k)}$ is the linear transformation at layer k. As A is a trainable parameter, it gets updated in each epoch based on the total loss ${\mathcal {L}}$. Thus the activation function ${\varvec{a}}$ adapts itself to minimise the total loss ${\mathcal {L}}$.

2.3.2 Signed Distance Function

While there have been several efforts to solve stiff-PDEs with discontinuity inside the spatial domain, so far, there is only one viable technique to solve stiff-PDEs with conflicting BCs at the adjacent edges and corners. The difficulty lies in the fact that the activation functions are smooth, i.e., they are differentiable and can’t capture discontinuous BCs. Thus, currently the only way to alleviate the issue is to exclude the points with a discontinuity from the training data set.

In DeepXDE, these corner points are excluded by default, as the normal vector at those corners are not defined, or in other words the derivative at those points are not defined, so any BC that includes a derivative for example, a Neumann BC is not defined at the corners.

NVIDIA Modulus and several other literature takes this one step further by using signed distance function (SDF) weights [74, 78, 79]. SDF weights are used to assign minuscule weights around the region with conflicting BCs. This way a region with a discontinuous solution gets a lower priority compared to the regions where the solution is smooth. The application of SDF weights on complex geometry is an active field of research.

2.3.3 Importance Sampling

Nabian et al. [70] proposed a sampling strategy for efficient training of PINNs based on an approximation method called importance sampling [80], which is often used in reinforcement learning for approximating the expected reward based on the older policy [81, 82]. In optimisation, the optimal parameters ${\varvec {\theta}} ^{*}$ is defined such that

$$\begin{aligned} {\varvec {\theta}} ^{*}&= \underset{{ {\varvec{\theta }} }}{{\text {argmin}}} \ {\mathbb {E}}_{f} \left[ {\mathcal {L}} ({\varvec {\theta}}) \right] \\&\approx \underset{{ {\varvec {\theta}} }}{{\text {argmin}}} \ \frac{1}{N} \sum _{j=1}^{N} {\mathcal {L}} ({\varvec {\theta}}; {\mathbf {x}}_{j} ), \quad {\mathbf {x}}_{j} \sim {f}({\mathbf {x}}), \end{aligned}$$

(15)

where ${\mathbb {E}}_{f} \left[ {\mathcal {L}} ({\varvec {\theta}})\right]$ is the expected value of the total loss ${\mathcal {L}}$, when the collocation points are sampled from f the sampling distribution in the physical domain ${\mathbf {x}}_{j} \in {\varvec{\Omega }}$.

Typically, we use a uniform distribution for sampling the collocation points. In importance sampling, the collocation points are drawn from an alternative sampling distribution $q\left( x \right)$, and the NN parameters are approximated as per Eq. 16 instead of Eqs. 5 and 6.

$${\varvec {\theta}} ^{*} \approx \underset{{ {\varvec {\theta}} }}{{\text {argmin}}} \ \frac{1}{N} \sum _{j=1}^{N} \frac{f({\mathbf {x}}_{j})}{q({\mathbf {x}}_{j})} {\mathcal {L}} ({\varvec {\theta}}; {\mathbf {x}}_{j} ), \quad {\mathbf {x}}_{j} \sim q({\mathbf {x}}).$$

(16)

Sampling the collocation points in each epoch according to $q\left( x \right)$ (Eq. 17), i.e. a distribution proportional to the loss function ${\mathcal {L}}$ improves the efficiency of PINNs without introducing a hyperparameter.

$$q_{j}^{(i)} \approx \frac{{\mathcal {L}}_{j}^{(i)}}{\sum _{j=1}^{N} {\mathcal {L}}_{j}^{(i)}}, \quad \forall j \in {1,\ldots ,N},$$

(17)

where ${\mathcal {L}}_{j}^{(i)}$ is the total loss of the jth sample in the training dataset in ith epoch. Areas with higher $q^{(i)}$ are sampled more frequently in the ith epoch.

2.3.4 Low-Discrepancy Spatio-temporal Sampling

The collocation points may be sampled according to a uniform distribution, or using the Latin hypercube sampling [83] approach. Alternatively, one can choose low-discrepancy sequence generators such as the quasi-random sampling [84, 85], the Halton sequence [86, 87] the Sobol sequence [88, 89] which is used by DeepXDE’s baseline PINN and Hammersley sets [90, 91].

3 Modified Baseline PINNs

Numerous modified frameworks of the baseline PINN have been proposed so far. We have specifically chosen PINN frameworks that not only scale to higher dimensions but can also deal with discontinuous BCs.

3.1 DeepXDE

DeepXDE [37] is a popular Python based physics-informed machine learning library for solving forward and inverse problems involving PDEs. DeepXDE features its own version of the baseline PINN, that not only improves the accuracy, but helps in faster convergence as discussed in Sect. 2.3.2.

Other than baseline PINNs, DeepXDE can also solve forward and inverse integro-differential equations, (IDEs) [92], fractional PDEs, (fPDEs) [92], stochastic PDEs, (sPDEs) [93], topology optimization with hard constraints, (hPINN) [7], PINN with multi-scale Fourier features [94] and multifidelity NN, (MFNN) [95, 96].

DeepXDE also features NNs for nonlinear operator learning such as DeepONet [97], POD-DeepONet [98], MIONet [99], DeepM&Mnet [100, 101] and multifidelity DeepONet [102].

It supports tensor libraries such as TensorFlow, PyTorch, JAX, and PaddlePaddle. There are two notable features in DeepXDE. The first one is that it chooses the model with least training loss. The second one is that it does not include those corner points no matter what the problem is, with the justification that normal vectors are not defined at those corners to be able to apply the Neumann BCs.

3.2 NVIDIA Modulus

NVIDIA Modulus 22.03, formerly NVIDIA SimNet, is an advanced physics-informed machine learning package. It redefines the loss function (Sect. 2.2.3), it also uses SDF weights to avoid problematic edges and corners (Sect. 2.3.2). The SDF weights result in increased convergence speed and improved accuracy.

NVIDIA Modulus employs the SDF weights on the collocation points (they refer to these as interior points) and the boundary points separately. We have discussed the variation of SDF weights in the spatial domain in Sects. 4 and 5.

NVIDIA Modulus features forward models such as Fourier networks [25], Modified Fourier networks [26, 27], Sinusoidal Representation networks, SiReNs [28], Highway Fourier network [103], multi-scale Fourier feature network [94], spatial–temporal Fourier Feature network [97], DGM architecture [22] and multiplicative filter network [27].

NVIDIA Modulus also features NNs for nonlinear operator learning such as Fourier neural operator, (FNO) [103], adaptive FNO, (AFNO) [104], physics-informed neural operator, (PINO) [105], DeepONet [97], Pix2Pix net [106, 107] and super-resolution net [108].

3.2.1 Fourier Network

Spectral bias is a learning bias of DNNs towards low-frequency functions, i.e., functions that vary globally rather than locally. It ignores the high-frequency functions, such as sharp variation in the solution of the PDE. This can adversely affect the training convergence as well as the accuracy.

One approach to alleviate this issue is to perform input encoding, for example, a transformer [109], to transform the inputs to a higher-dimensional feature space with the help of high-frequency functions. In the Fourier network, the input features are encoded into Fourier space using sinusoidal activation functions (Eq. 18).

The trainable input encoding layer is as follows:

$$\phi _{E} = \big [ \sin \left( 2\pi {\mathbf {f}} \times {\mathbf{X }} \right) ; \cos \left( 2\pi {\mathbf {f}} \times {\mathbf{X }} \right) \big ]^{T},$$

(18)

where ${\mathbf {f}} \in {\mathbb {R}}^{n_{f} \times d_{0}}$ is the trainable frequency matrix, $d_{0}$ is the number of features and $n_{f}$ is the number of frequency sets which we can choose and ${\mathbf{X}}$ is the input dataset. These frequencies, similar to network weights, can be sampled from a Gaussian distribution or from a spectral space created from combinations of all entries from a user-defined list of frequencies.

Finally, the encoded inputs are $\phi _{E} x$, which results in a training data with $n_{f}$ number of features, thus, transforming the input features to a higher dimensional feature space. NVIDIA Modulus recommends $n_{f}=10$, however, for our test cases we used $n_{f}=35$, which is computationally expensive, but is reasonable for PDEs with a discontinuous solution.

3.2.2 Modified Fourier Network

In a Fourier network (Sect. 3.2.1), a FCNN is used as the nonlinear mapping between the Fourier features and the model output. The modified Fourier network uses a modified version of the fully-connected network, similar to the one proposed in [18]. The authors were inspired by the neural attention mechanism, which is employed in natural language processing to enhance the hidden states with transformer networks [109].

In Eq. 19, ${\mathbf{U}}$ and ${\mathbf{V}}$ are two transformer layers that help in projecting the Fourier features $\phi _{E}$ to another feature space, and forward passed through the hidden layers (H) using the Hadamard product, similar to its standard fully connected counterpart. The Modified Fourier network takes the following forward propagation rule:

$$\begin{aligned}&{\mathbf{U}} = \sigma \left( {\mathbf{W}} ^{1} \phi _{E} \right) , \quad {\mathbf{V}} = \sigma \left( {\mathbf{W}} ^{2} \phi _{E} \right) , \\&{\mathbf{H}} ^{(1)} = \sigma \left( {\mathbf{W}} ^{z,1}{} {\mathbf{X}} \right) , \\&{\mathbf{Z}} ^{(k)} = \sigma \left( {\mathbf{W}} ^{z,k}{} {\mathbf{H}} ^{z,1} \right) , \quad k = 1,\ldots ,L, \\&{\mathbf{H}} ^{(k+1)} = \sigma \left( 1-{\mathbf{Z}} ^{(k)} \right) \odot {\mathbf{U}} + {\mathbf{Z}} ^{(k)} \odot {\mathbf{V}} , \quad k = 1,\ldots ,L, \\&{\hat{\mathbf{y }}} = {\mathbf{W}} {} {\mathbf{H}} ^{(L+1)}, \end{aligned}$$

(19)

where ${\mathbf{W}} ^{1}$, ${\mathbf{W}} ^{2}$, ${\mathbf{W}} ^{z,k}$ and ${\mathbf{W}}$ are four different sets of weight matrices associated with ${\mathbf{U}}$, ${\mathbf{V}}$, ${\mathbf{H}} ^{(k)}$ and ${\mathbf{H}} ^{(L+1)}$ with $k = 1,\ldots ,L$, where L is the number of hidden layers. Figure 4 shows the structure of a modified Fourier network.

Fig. 4

Structure of modified Fourier network as per Eq. 19

3.2.3 Sinusoidal Representation Networks (SiReNs)

Sitzmann et al. [28] proposed a FCNN which uses the sine trigonometric function as the activation function. This network has some similarities to Fourier networks (Sect. 3.2.1) as both uses a sine activation function, manifesting the same effect as the input encoding for the first layer of the network.

A key component of this network architecture is the weight initialisation scheme. The weights of the NN are sampled from a uniform distribution $W \sim U\left( -\sqrt{\frac{6}{f_{in}}},\sqrt{\frac{6}{f_{in}}}\right)$ where ${f_{in}}$ is the input size to that layer.

The input of each Sine activation has a Gauss-Normal distribution and the output of each Sine activation, a Sine inverse distribution. This preserves the distribution of activations allowing deep architectures to be constructed and trained effectively.

3.2.4 DGM Architecture

The DGM architecture [22] (Eq. 20), consists of several hidden layers, which are referred to as DGM layers, similar to LSTM gates [23], where each layer produces weights based on the last layer, determining how much of the information gets passed to the next layer.

$$\begin{aligned} &{\mathbf{S}} ^{(1)} = \sigma ({\mathbf{W}} ^{1}{\mathbf{X}} ),\\&{\mathbf{Z}} ^{(k)} = \sigma \left( {\mathbf{V}} _{z}^{(k)}{} {\mathbf{X}} + {\mathbf{W}} _{z}^{(k)}{} {\mathbf{S}} ^{(k)}\right) , \quad k = 1,\ldots ,L, \\&{\mathbf{G}} ^{(k)} = \sigma \left( {\mathbf{V}} _{g}^{(k)}{} {\mathbf{X}} + {\mathbf{W}} _{g}^{(k)}{} {\mathbf{S}} ^{(k)}\right) , \quad k = 1,\ldots ,L, \\&{\mathbf{R}} ^{(k)} = \sigma \left( {\mathbf{V}} _{r}^{(k)}{} {\mathbf{X}} + {\mathbf{W}} _{r}^{(k)}{} {\mathbf{S}} ^{(k)}\right) , \quad k = 1,\ldots ,L,\\&{\mathbf{H}} ^{(k)} = \sigma \left( {\mathbf{V}} _{h}^{(k)}{} {\mathbf{X}} + {\mathbf{W}} _{h}^{(k)}({\mathbf{S}} ^{(k)} \odot {\mathbf{R}} ^{(k)})\right) , \quad k = 1,\ldots ,L,\\&{\mathbf{S}} ^{(k+1)} = (1-{\mathbf{G}} ^{(k)}) \odot {\mathbf{H}} ^{(k)} + {\mathbf{Z}} ^{(k)} \odot {\mathbf{S}} ^{(k)}, \quad k = 1,\ldots ,L,\\&{\hat{\mathbf{y }}} = {\mathbf{W}} {} {\mathbf{S}} ^{(L+1)}. \end{aligned}$$

(20)

The DGM architecture consists of multiple nonlinear transformations of the input: ${\mathbf{Z}}$, ${\mathbf{G}}$, ${\mathbf{R}}$ and ${\mathbf{H}}$, that helps with learning complicated functions such as discontinuous functions. Figure 5 shows the structure of DGM architecture and the DGM layers.

A DGM layer includes ${\mathbf{Z}}$, ${\mathbf{G}}$, ${\mathbf{R}}$ and ${\mathbf{H}}$ with their sets of weights ${\mathbf{V}}$ and ${\mathbf{W}}$. Thus, a DGM layer consists of eight weight matrices. Additionally, the DGM architecture consists of two more weight matrices: ${\mathbf{W}} ^{1}$ and ${\mathbf{W}}$.

Fig. 5

Structure of structure of DGM architecture and the DGM layers as per Eq. 20

4 Problem 1: 2D Steady-State Heat Conduction

For Problem 1, we chose a 2D heat conduction problem with conflicting BCs at the corners. We solved the problem with different PINN frameworks and compared with the FEM solution. The 2D heat conduction problem can be stated as follows:

$$\begin{aligned}&u_{xx} + u_{yy} = 0, \quad x\in [-0.5,0.5], \quad y \in [0,1], \\&u(x,0) = u(x,1) = 0, \quad u(-0.5,y) = u(0.5,y) =1. \end{aligned}$$

(21)

We used MATLAB Partial Differential Equation Toolbox [110] to solve the 2D steady-state heat conduction problem (Eq. 21) with quadratic triangles (Fig. 6).

Fig. 6

FEM solution of 2D steady-state heat conduction problem (Eq. 21) using MATLAB Partial Differential Equation Toolbox

We assigned a model number to each of the PINN frameworks (see Table 1). Table 2 summarises the network parameters and relative $L^{2}$ error for various PINN frameworks. Figures 9 and 7 show the solution of 2D steady-state heat conduction problem for different PINN frameworks.

We have not completed a full exploration of the best parameters for each PINN such as the number of hidden layers, the number of neurons in each layers, number of boundary and collocation points to be sampled etc. to use in these models. We started with the default values and retained the results if they were acceptable. We observed early convergence in several models, so we stopped training those models. Unless otherwise specified, the same applies to other upcoming problems. As the PINN reaches maturity we will hopefully come up with the best practices to benchmark different PINN frameworks.

Table 1 Models considered in the numerical study

Table 2 Problem 1: summary of training parameters and relative $L^{2}$ error for different PINN frameworks

Fig. 7

Solution of 2D steady-state heat conduction problem using Model 1. The predicted temperature distribution (on the top) and the absolute pointwise error (on the bottom) is shown at 5k, 10k and 30k epochs respectively. Temperature predicted outside the expected bound, i.e., when $u\notin \left[ 0,1\right]$, is shown using the white and grey colour

Fig. 8

The training loss (top) and the validation loss (bottom) for the 2D steady-state heat conduction problem. The training loss plot shows the BC loss (BC loss), the residual loss (PDE loss) and the sum of both, i.e., the total loss. The validation loss plot shows the mean squared error between the temperature predicted from the training dataset and the FEM solution. The black dot denotes the least validation loss

Fig. 9

PINN predicted solution of 2D steady-state heat conduction problem is shown on the left side. The absolute pointwise error between the FEM solution and PINN predicted solution is shown on the right side. Temperature predicted outside the expected bound (if any), i.e., when $u\notin \left[ 0,1\right]$ is shown using the white and grey colour

4.1 Model 1: Baseline PINN (See Also Table 1)

Firstly, we trained a baseline PINN with 8 hidden layers and 20 neurons in each layer using the L-BFGS optimiser with hyperbolic tangent activation. We used the nodal coordinates from the mesh of FEM solution consisting of 612 boundary points and 5800 collocation points. We observed that the gradient explodes while training with L-BFGS. That is why we switched to the Adam optimiser with default parameters, unless otherwise stated.

Figure 7 shows the predicted temperature distribution and pointwise absolute error at 5k, 10k and 30k epochs. Initially, i.e., around 5k epochs, the pointwise absolute error around the corners is much higher compared to the interior points. If we continue the training past 5k epochs, the optimiser tries to reduce the loss around the corners at the cost of high errors at the interior points, which can be clearly seen in the pointwise absolute error plot at 30k epochs. This is a result of the fact that we did not use a learning rate scheduler [111]. A learning rate scheduler adjusts the learning rate $\alpha$ between epochs during the training which helps convergence.

Figure 8 shows the training and validation losses. We purposely used the predicted temperature distribution from the training dataset against the FEM solution to calculate the validation loss. In the validation loss plot, we can clearly see that the least validation error occurs somewhere between 15k and 20k. However, the total training loss continues to decrease even after 20k epochs resulting in increased validation loss in the interior points as discussed earlier.

The FCNNs are continuous and differentiable functions and can’t predict discontinuities such as the corners with conflicting BCs. Also, it is very challenging to obtain a trained PINN model with minimum validation error because we are not using the ground truth to calculate the training loss.

4.2 Model 2: DeepXDE’s Baseline PINN

We trained a FCNN with 8 hidden layers and 20 neurons in each layer using the Adam optimiser with hyperbolic tangent activation and exponential decay of the learning rate. We used DeepXDE’s default sampling method, i.e., the Sobol sequence to sample 800 boundary points and 2500 collocation points, i.e. only about half the collocation points compared to Model 1.

Although the training loss converged in 5k epochs, we continued to train the model until 30k epochs to demonstrate the benefits of exponential decay of the learning rate. As the training progresses, the amount of perturbation in the weights (as per Eq. 6) decreases. Thus, we don’t see much difference in the predicted temperature distribution after 5k epochs, which was not possible with Model 1.

As discussed in Sect. 2.3.2, DeepXDE does not sample the corner points, so we ignored these points from the FEM solution to compute the relative $L^{2}$ error. Thus we obtain very low relative $L^{2}$ error as most of the error occurs around the corners.

Figure 9a shows the predicted temperature distribution and the pointwise absolute error for the 2D steady-state heat conduction problem.

4.3 Models 3–11: NVIDIA Modulus

We used NVIDIA Modulus to train PINN frameworks from Models 3 to 11. We started with NVIDIA Modulus’s baseline PINN with the integral form of the loss function (Model 3). Then we applied the SDF weights on interior points (Model 4) and on both interior and boundary points (Model 5). We used additional tools such as importance sampling (Model 6) and combined the importance sampling with adaptive activation and quasi-random sampling (Model 7). We also used the Fourier network (Model 8), SiReNs network (Model 9), Modified-Fourier network (Model 10) and DGM architectures (Model 11) with adaptive activation, importance sampling, quasi-random sampling and full SDF weights, i.e., SDF weights on both interior and boundary points with an exception for SiReNs network which does not has an adaptive activation implemented in NVIDIA Modulus 22.03. Furthermore, NVIDIA Modulus 22.03 only implements the Halton sequence to generate a quasi-random sample.

The SDF weights are manually adjusted depending on the problem and is an active field of research. We formulated the SDF weights on boundary points such that the weights on the corner points is zero and increased as we move away from the corner (see Eq. 22). The SDF weights on the interior points depends on the shape of the spatial domain. We used the default SDF weights on collocation/interior points. Figure 10 shows the magnitude of the SDF weights on the boundary and interior points of the square domain for Problem 1. In the case of a full set of SDF weights, it is worth noting that the maximum magnitude of the SDF weights on the interior points is 0.5. So, We are giving 50% less importance to the interior points compared to the boundary points, because we want the optimiser to obtain more information from the BC loss, as it does not converge in the case of Model 1 (as shown in Fig. 8).

$$\begin{aligned}&{\text {Top and bottom boundary: }} y=1.0-2\left|x \right|, \\&{\text {Left and right boundary: }} x=1.0-2\left|y-0.5 \right|. \end{aligned}$$

(22)

Fig. 10

The magnitude of SDF weights on interior and boundary points of a square domain. The SDF weights for Model 4, i.e., with only interior points is shown on the left side. Whereas, the SDF weights with interior and boundary points is shown on the right side (for Models 5 to 11)

In Models 3, 4 and 5, we trained NVIDIA Modulus’s baseline PINN with default values, i.e., with 6 hidden layers and 512 neurons in each layer using the Adam optimiser with exponential decay in the learning rate and SiLU activation (Sigmoid Linear Unit) [112] for 20k epochs. We used 4000 boundary points and 4000 collocation points sampled from a uniform distribution. We used the same number of boundary points and collocation points in models from Models 3 to 11. We obtained a relative $L^{2}$ error of 0.08931, 0.10124, 0.09557 for Models 3, 4 and 5, respectively.

In Model 6, we replaced the uniform sampling with importance sampling to resample the interior points in Model 5. We observed a significant improvement around the corners, resulting in a relative $L^{2}$ error of 0.06448. In the case of Model 7, we used adaptive activation with quasi-random sampling for the initial sampling in each batch and importance sampling for resampling of the interior points. We obtained a relative $L^{2}$ error of 0.06433, not a significant improvement over Model 6.

In Model 8, we trained a Fourier network with 10 Fourier features (see Sect. 3.2.1) using 6 hidden layers and 512 neurons in each layer using the Adam optimiser with SiLU adaptive activation for 20k epochs, with full SDF weights, quasi-random sampling and importance sampling. We used 10, 15, 25 and 35 Fourier features for the input encoding. We observed that the Fourier network is only working for 10 Fourier features and the absolute pointwise error is 0.18741, which is even higher than Model 1. For 15, 25 and 35 Fourier features the predicted temperature distribution were close to 0.5 over the entire domain, i.e., the average of upper and lower bound temperature in the domain.

In Model 9, we trained a SiReNs network (Sect. 3.2.3) with 6 hidden layers and 512 neurons in each layer using the Adam optimiser with Sine activation for 20k epochs, with full SDF weights, quasi-random sampling and importance sampling. The network was continuously experiencing exploding gradients until we reduced the learning rate to (2e−5). Still after 12k epochs the training loss would abruptly increase, leading to prohibitively large absolute pointwise error. Hence, we forced the training to stop around 11k epochs and the relative $L^{2}$ error was found to be 0.12640.

In Model 10, we trained a modified Fourier network (Sect. 3.2.2) with 6 hidden layers and 512 neurons in each layer using the Adam optimiser with SiLU activation for 20k epochs, with full SDF weights, quasi-random sampling and importance sampling. Similar to Model 10, we used 10 Fourier features for the input encoding. The predicted temperature distribution looks similar to Model 8 and the relative $L^{2}$ error was found to be 0.17577.

In Model 11, we trained a DGM architecture (see Sect. 3.2.4), with 6 hidden layers and 512 neurons in each layer using the Adam optimiser with SiLU activation for 20k epochs, with full SDF weights, quasi-random sampling and importance sampling. We obtained a relative $L^{2}$ error of 0.08229.

In Fig. 9, Models 6, 7 and 11 resulted in less than 1% absolute pointwise error at most of the points in the domain. This indicates that the SDF weights and the importance sampling plays an important role in solving stiff-PDEs with a discontinuous solution. In Table 2, Models 3, 5, 6, 7 and 11 resulted in less than 10% relative $L^{2}$ error. Further investigation is required to determine whether the DGM architecture is advantageous compared to the baseline PINNs in higher dimensions.

4.4 Hard Constrained BCs

In this section, we discuss the exact imposition of BCs in PINNs. Hard constrained BCs involves the construction of a continuous and differentiable function through which we pass the output of the NN. Problem 1, involves discontinuous BCs which can’t be exactly satisfied with a continuous and differentiable function. However, it is possible to satisfy the BCs on two opposite walls, here we chose to exactly satisfy the top and bottom walls using the following output transform function.

$$u:=y\left( y-1\right) u.$$

(23)

We trained the Model 2 (see Table 1) with 3500 collocation points and 400 boundary points with Adam for 30k epochs. Figure 11 shows the DeepXDE predicted solution to Problem 1 with the hard constrained BCs at the top and bottom walls. Due to hard constrained BCs at the top and bottom walls, we observe significant errors around the left and right walls resulting in a relative $L^{2}$ error of 0.183119. Thus, it is not recommended to apply hard constraints to the BCs in stiff-PDEs.

Fig. 11

DeepXDE predicted solution of 2D steady-state heat conduction problem (Eq. 21) with hard constrained BCs at the top and bottom walls on the left and the absolute pointwise error between the FEM and PINN predicted solutions is shown on the right side. Temperature predicted outside the expected bound (if any), i.e., when $u\notin \left[ 0,1\right]$ is shown using the white and grey colour

4.5 Overfitted Solution

Fig. 12

Comparison of PINN predicted solution from the training dataset and at new data-points. a The FEM solution of Problem 1 (Eq. 21), b the DeepXDE predicted solution of the same problem from the training dataset, and c the DeepXDE predicted solution of the same problem at new spatio-temporal locations in the domain. Temperature predicted outside the expected bound (if any), i.e., when $u\notin \left[ 0,1\right]$ is shown using the white and grey colour

In this section, we discuss the behaviour of an overfitted PINN model while predicting the solution of the PDE at new spatio-temporal locations in the domain. We trained the Model 2 (see Table 1) with 2500 collocation points and 200 boundary points with Adam for 30k epochs. Figure 12 shows the DeepXDE predicted solution to Problem 1 from both the training dataset and on new spatio-temporal locations within the domain. Given that the trained model’s accuracy during the validation is low, we will categorise the model as an overfitted model. The validation loss can be decreased by adding more points in the training data set, for instance, NVIDIA Modulus samples different points for the training in each epoch. Intuitively, the overfitted model is computationally cheaper than a generalised model as it requires very few collocation points, which is evident with this example.

5 Problem 2: 3D Steady-State Heat Conduction

The next problem we address is a 3D steady-state heat conduction problem with conflicting BCs at the edges and the corners. We solved the problem with different PINN frameworks and compared the results to the FEM solution. The 3D heat conduction problem is described as follows:

$$\begin{aligned} & u_{xx} + u_{yy} + u_{zz} = 0, \quad x\in [-0.5,0.5], \quad y\in [-0.5,0.5], \quad z \in [0,1], \\ & u \left( x,y,0 \right) = u(x,y,1) = u(0.5,y,z) = 0, \\ & u(-0.5,y,z) = u(x,-0.5,z) = u(x,0.5,z) = 1. \end{aligned}$$

(24)

We used MATLAB Partial Differential Equation Toolbox [110] to solve the 3D steady-state heat conduction problem (Eq. 24) with quadratic triangles (Fig. 13).

Fig. 13

FEM solution for the 3D steady-state heat conduction problem (Eq. 24) using MATLAB Partial Differential Equation Toolbox

We again used the same PINN models (see Table 1) to solve the 3D steady-state heat conduction problem. We did not use the full SDF weights because the boundary walls are planes instead of lines in 2D. This is where we potentially require an algorithm, instead of manually constructing the SDF weights for the boundary points. Therefore, for this problem, we refer to the SDF weights on interior points as the full SDF weights and we exclude Model 4. Table 3 summarises the network parameters and relative $L^{2}$ error for various PINN frameworks. Figure 14 shows the solution of the 3D steady-state heat conduction problem for different PINN frameworks.

Table 3 Problem 2: summary of training parameters and relative $L^{2}$ error for different PINN frameworks

Fig. 14

PINN predicted solution of 3D steady-state heat conduction problem is shown on the left side. The absolute pointwise error between the FEM solution and PINN predicted solution is shown on the right side. Temperature predicted outside the expected bound (if any), i.e., when $u\notin \left[ 0,1\right]$ is shown using the white and grey colour

In Problem 1 (Sect. 4), the discontinuities occurred at the corners of the square domain, which affected only a few training points. Whereas, in Problem 2, the discontinuities affected not only the vertices but also the edges. We can sample a large number of points along these edges. Thus, Problem 2 is more suitable for testing the robustness of different PINN frameworks.

In Problem 2, all the models had the same number of layers, nodes per layer and the learning rate as in Problem 1. However, we increased the number of boundary points and collocation/ interior points in Models 1 and 2.

In Model 1, we observed that the interior points had significant absolute pointwise error, meaning the PDE loss didn’t converge. We obtained a relative $L^{2}$ error of 0.23778. In Model 2, the DeepXDE network didn’t sample the points at the edges and vertices (see Sect. 2.3.2). We obtained a relative $L^{2}$ error of 3.15547.

In the case of models trained within NVIDIA Modulus, the SDF weights on the interior nodes from Problem 1 was extended to three dimension such that interior points close to the boundary were assigned negligible weights. As we move away from the boundary, the SDF weights on the interior points increases until it reaches close to 0.5 around the centroid of the cubical domain (see Fig. 15).

Fig. 15

The magnitude of SDF weights on interior points of the cubical domain of Problem 2

NVIDIA Modulus’s baseline PINN (Model 3) predicts better temperature distribution compared to Models 1 and 2 with a relative $L^{2}$ error of 0.12031. The addition of SDF weights on the interior points (Model 5) dramatically reduces the relative $L^{2}$ error to 0.07455.

To obtain accurate results, the nodal coordinates or the training data needs special treatment either by transforming the coordinates to higher dimensions using the Fourier network or by adding more transformer layers using the DGM architecture or both using the modified Fourier network. From Table 3, it is clear that the baseline PINN without SDF weights is not suitable for solving stiff-PDEs with discontinuities in 3D.

In summary, Models 5, 6, 7, 8, 10 and 11 resulted in less than 10% relative $L^{2}$ error and less than 5% absolute pointwise error at most of the points in the domain. It is worth mentioning that the SiReNs network (Model 9) experiences difficulty while minimising the loss, resulting in a constant temperature over the entire domain with a relative $L^{2}$ error of 0.56448 (see Fig. 14).

A summary of the total training time (s) and training time (s) per epoch in Problems 1 and 2 for each model is presented in Table 4. The training time does not include the time taken in pre-processing of the data and initialisation of the NN. In Models 1 and 2, the number of data points were different in Problems 1 and 2, which influences the training time. Thus, we could not draw a concrete conclusion. In Models 3–10, even though the number of data points were same there was no noticeable increase in the training time per epoch. However, in Model 11, the training time per epoch was almost 3 times for Problem 2, a 3D problem, compared to Problem 1, a 2D problem. This is because one DGM layers contains eight weight matrices and introducing one more feature into the training dataset increases the number of operations exponentially.

Table 4 Summary of the total training time (s) and training time (s) per epoch in Problems 1 and 2 for each model

6 Parametric Heat Conduction Problem

As discussed in Sect. 2.2.6, PINNs can be parameterised by adding the parameter of interest as another feature in the training dataset. We solved two parametric 2D steady-state heat conduction problems with parameterised conductivity and parameterised geometry (see Table 5).

Table 5 Summary of parametric heat conduction problems

6.1 Problem 3: Parameterised Conductivity

We formulated the 2D steady-state heat conduction problem such that the conductivity $\kappa$ is varying from 0 to 1 in Eq. 25.

$$\begin{aligned}&u_{xx} + \kappa \,u_{yy} = 0, \quad x\in [-0.5,0.5], \quad y \in [0,1], \quad \kappa \in [0,1], \\&u(x,0) = u(x,1) = 0, \quad u(-0.5,y) = u(0.5,y) =1. \end{aligned}$$

(25)

We trained Problem 3, with various models from Table 1 and observed that the predicted temperature distribution was fairly accurate except for Model 1 because we did not use a learning rate scheduler (see Sect. 4.1). The absolute pointwise error is less than 5% on the interior points with some errors around the corners, similar to Problems 1 and 2. Figure 16 shows the solution to Problem 3 using Model 2. Model 2 predicted a reasonably accurate temperature distribution in just 523 s. Model 3 to 11 took 2–3 times the time to train the model with very little improvement.

Fig. 16

Solution to Problem 3 using Model 2. The predicted temperature distribution (on the top) and the absolute pointwise error (on the bottom) for different values of $\kappa$ (see Eq. 25). Temperature predicted outside the expected bound, i.e., when $u\notin \left[ 0,1\right]$, is shown in white and grey colour

6.2 Problem 4: Parameterised Geometry

Similar to conductivity the geometry can also be parameterised. We used the y-dimension of the 2D steady-state heat conduction problem as the parameter (Eq. 26).

$$\begin{aligned} & u_{xx} + u_{yy} = 0, \quad x\in [-0.5,0.5], \quad y \in [0,L], \quad L \in [1,10], \\ & u(x,0) = u(x,L) = 0, \quad u(-0.5,y) = u(0.5,y) =1 . \end{aligned}$$

(26)

Implementing the parametric geometry is not straightforward, care should be taken that for each geometry parameter the sampled points along the geometry parameter is within the spatio-temporal domain. For example, as per Eq. 26, $y \in \left[ 0,L \right]$ and $L \in [1,10]$, i.e., $y \le L$ for each sample in the training dataset.

Figure 17 shows the boundary points sampling of Problem 4 to illustrate the implementation of parametric geometry. Here, x and y axes shows the 2D spatial domain for each geometry parameter along the L axis. As discussed earlier, for $y \le L$, this results in moving the upper boundary on the y axis as L increases.

Fig. 17

The boundary points sampling of the parameterised geometry in Problem 4

We observed that none of the models could predict a temperature distribution that visually looks similar to the FEM solution. Some of the models such as Models 1, 3, 4, 5, 6 and 7 could not converge the loss. Whereas, Models 10 and 11 resulted in gradient explosion. We think that none of the PINN frameworks in Table 1 does have enough features and parameters to predict multiple discontinuous temperature distribution around the moving upper boundary. We need more sophisticated PINN frameworks to solve these types of problems.

Thus, we decreased the range of the parameter L until we could predict a temperature distribution that visually resembles the FEM solution. The parameter’s range was eventually narrowed to 1.05, i.e. $L\, \in \left[ 1, 1.05 \right]$.

We trained Models 7, 10 and 11 with the redefined L parameter. For Models 10 and 11, we have also shown the predicted temperature distribution without the SDF weights to highlight how important they are while solving problems with discontinuities. Figure 18 shows the predicted temperature distribution for the redefined problem with Models 7, 10 and 11 with and without the SDF weights.

Fig. 18

Solution of 2D steady-state heat conduction problem with parameterised upper boundary. Each plot shows the predicted temperature distribution for a specific value of parameter $L \in \left[ 1,1.05\right]$. Temperature predicted outside the expected bound, i.e., when $u\notin \left[ 0,1\right]$, is shown using white and grey colour

In Model 7, the predicted temperature distribution around the left and right boundary does not change with the moving upper boundary, especially, around the upper-left and upper-right corners of the square domain. In Model 10 without the SDF weights, the predicted temperature distribution does not visually resemble the FEM solution. Whereas, when we use the SDF weights, the predicted temperature distribution improves dramatically.

In Model 11, the predicted temperature distribution without the SDF weights was much better than any other Model without the SDF weights. Also, Model 11 with SDF weights predicts better temperature distribution compared to Models 7 and 10 with SDF weights.

7 Conclusion

In this paper, we have reviewed application of PINNs to stiff-PDEs, specifically for simple steady-state heat conduction problems with discontinuous BCs at the corners. We defined a list of PINN frameworks in Table 1 which included the baseline PINN and models from open-source libraries such as DeepXDE and NVIDIA Modulus.

We started with a 2D steady-state heat conduction problem (Problem 1). We observed that both the baseline PINN and DGM architecture predicted temperature distribution with 5–10% absolute pointwise error in the corner regions for most models. The results are summarised in Table 2.

Next, we solved Problem 1 with hard constrained BCs. We showed that we can’t satisfy all the BCs exactly when they conflict with each other. Problem 1 contains discontinuous BCs, which can’t be satisfied exactly with a differentiable function such as a NN. Thus, we do not recommend applying hard constrained BCs on a stiff-PDE.

We also demonstrated the inability of an overfitted PINN to predict the temperature distribution at new spatio-temporal locations. However, an overfitted PINN proves to be computationally cheap when the solution is to be inferred on the training dataset only.

We then solved a 3D steady-state heat conduction problem (Problem 2), an equivalent of Problem 1 in 3D space. This is where modified PINN frameworks such as Fourier network, Modified Fourier network, DGM architecture proves to be more accurate than the baseline PINN frameworks (Models 1–7) in terms of the relative $L^{2}$ error. Furthermore, the SDF weights significantly improved the accuracy. This is primarily because the modified PINN frameworks are inherently evolutional over the baseline PINN. The Fourier network addresses the spectral bias in the baseline PINNs, the DGM architecture is useful for solving problems in higher dimensions and the Modified Fourier network is a combination of both.

Then we solved Problem 1 with parametric conductivity (Problem 3) using DeepXDE’s baseline PINN. DeepXDE’s baseline PINN accurately predicted the temperature distribution while using fewer resources compared to Models 3–11.

We also solved Problem 1 with parametric geometry by extending the y-dimension (Problem 4). We observed that solving stiff-PDEs with parametric geometry can be very challenging for PINNs. Even robust PINN frameworks such as the Modified Fourier Network resulted in exploding gradients. In Problem 4, we also showed that the predicted temperature distribution with SDF weights significantly outperforms those without the SDF weights. Table 5 summarises the network parameters and the accuracy (relative $L^{2}$ error) of various models for Problems 3 and 4.

Among the PINN frameworks (see Sect. 1), baseline PINNs are not useful in the case of 3D problems. On the other hand, PINN frameworks such as Modified Fourier network and DGM architecture are robust even on 3D problems. The SiReNs network is very unstable and often results in exploding gradients even with exponential decay of the learning rate. The SiReNs network fails to predict the temperature distribution in Problem 2 even with a reduced learning rate. A summary of the best models for each problem is shown in Table 6.

Table 6 Summary of models with least relative $L^{2}$ error

In Table 6, Models 7 and 11 can be categorised as the best performing models in general for the four problems we considered. Model 10 also works in most of the cases. Model 7 is computationally cheaper than Model 11 (see Table 4). However, Model 11 seems to work without SDF weights in Problem 4 which is an advantage for solving more complicated problems.

Among the additional tools (see Sect. 2.3), the SDF weights are an important asset for solving problems with discontinuous BCs. The importance sampling is a loss dependent resampling strategy of the collocation points. It samples points proportional to the absolute pointwise error, which is particularly useful in stiff-PDEs where we need more points to capture the sharp gradients. The adaptive activation and quasi-random sampling improves the convergence and the accuracy respectively.

We also tried to solve 2D steady-state heat conduction problem with a temperature dependent conductivity along the y-direction. However, we could not converge the training loss with any of the models in Table 1. We were also interested in solving Problem 1 with parametric prescribed BCs, but it seems, currently, this is not possible with any PINN framework.

The development of FEM took us almost five decades. In contrast, PINNs are evolving rather quickly. As of now, PINNs are able to solve simple discontinuous problems in 2D and 3D without any problem-specific tuning and transfer learning. The same framework can be used to solve the parametric PDEs which is difficult to achieve with conventional PDE solvers. We believe that in 2–3 years, we will see PINNs solving complex benchmark problems.

There is a need to automate the SDF for problems with discontinuous solutions. Also, there is a lack of benchmarking in PINNs. We can not use the same parameters for all the Models in Table 1. To compare different PINN frameworks, an improvement to this field would be for the research community to collectively agree upon a standard set of benchmarks.