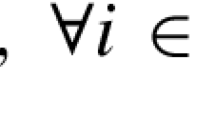Solving quadratic programs to high precision using scaled iterative refinement

Abstract

Quadratic optimization problems (QPs) are ubiquitous, and solution algorithms have matured to a reliable technology. However, the precision of solutions is usually limited due to the underlying floating-point operations. This may cause inconveniences when solutions are used for rigorous reasoning. We contribute on three levels to overcome this issue. First, we present a novel refinement algorithm to solve QPs to arbitrary precision. It iteratively solves refined QPs, assuming a floating-point QP solver oracle. We prove linear convergence of residuals and primal errors. Second, we provide an efficient implementation, based on SoPlex and qpOASES that is publicly available in source code. Third, we give precise reference solutions for the Maros and Mészáros benchmark library.

1 Introduction

Quadratic optimization problems (QPs) are optimization problems with a quadratic objective function and linear constraints. They are of interest directly, e.g., in portfolio optimization or support vector machines [1]. They also occur as subproblems in sequential quadratic programming, mixed-integer quadratic programming, and nonlinear model predictive control. Efficient algorithms are usually of active set, interior point, or parametric type. Examples of QP solvers are BQPD [5], CPLEX [2], Gurobi [15], qp_solve [12], qpOASES [4], and QPOPT [7]. These QP solvers have matured to reliable tools and can solve convex problems with many thousands, sometimes millions of variables. However, they calculate and check the solution of a QP in floating-point arithmetic. Thus, the claimed precision may be violated and in extreme cases optimal solutions might not be found. This may cause inconveniences, especially when solutions are used for rigorous reasoning.

One possible approach is the application of interval arithmetic. It allows to include uncertainties as lower and upper bounds on the modeling level, see [16] for a survey for the case of linear optimization. As a drawback, all internal calculations have to be performed with interval arithmetic. Standard solvers can not be used any more and their conversion to interval arithmetic becomes non-trivial when division by intervals containing zero is encountered. In any case, computation times increase and solutions may be very conservative.

We are aware of only one advanced algorithm that solves QPs exactly over the rational numbers. It is designed to tackle problems from computational geometry with a small number of constraints or variables [6]. Based on the classical QP simplex method [23], it replaces critical calculations inside the QP solver by their rational counterparts. Heuristic decisions that do not affect the correctness of the algorithm are performed in fast floating-point arithmetic.

In this paper we propose a novel algorithm that can use efficient floating-point QP solvers as a black box. Our method is inspired by iterative refinement, a standard procedure to improve the accuracy of an approximate solution for a system of linear equalities [22]: The residual of the approximate solution is calculated, the linear system is solved again with the residual as a right-hand side, and the new solution is used to refine the old solution, thus improving its accuracy. A generalization of this idea to the solution of optimization problems needs to address several difficulties: most importantly, the presence of inequality constraints; the handling of optimality conditions; and the numerical accuracy of floating-point solvers in practice.

For linear programs (LPs) this has first been developed in [9, 10]. The approach refines primal-dual solutions of the Karush–Kuhn–Tucker (KKT) conditions and utilizes scaling and calculations in rational arithmetic. We generalize this method further and discuss the specific issues due to the presence of a quadratic objective function. The fact that the approach carries over from LP to QP was remarked in [8]. Here we provide the details, provide a general lemma showing how the residuals bound the primal and dual iterates, and analyze the computational behavior of the algorithm based on an efficient implementation that is made publicly available in source code and can be used freely for research purposes.

The idea to refine QP solutions has been explored before. In [18] a reference QP is solved in floating-point precision by an active-set method and its basis matrix factorization is used to set up and solve a transformed QP. The error introduced by this matrix approximation is then corrected by an iterative refinement procedure. This leads to a sequence of QPs with differing right-hand side vectors that compute refinement steps converging to a solution of the original QP in floating-point precision. The main purpose here is to speed up the QP solution process by avoiding to factorize the basis matrix of the QP.

Other methods use iterative refinement to deal with errors introduced by the implicit treatment of the constraints. In [20] one part of the constraints of a nonlinear programming problem is treated implicitly inside a sequential quadratic programming scheme. The nullspace of these equations is only approximated and the refinement equation for the error is included into the QPs to stabilize the inexact newton scheme. In [13] a QP is solved by a conjugate gradient algorithm implicitly treating all constraints. In order to cope with numerical inaccuracies in the projection of the iterates onto the feasible set, different iterative refinement extensions to the algorithm are proposed. These approaches use iterative refinement on a lower level inside of a dedicated algorithm. In contrast, the iterative refinement scheme is designed to employ any floating-point QP algorithm as a black-box subroutine.

The paper is organized as follows. In Sect. 2 we define and discuss QPs and their refined and scaled counterparts. We give one illustrating and motivating example for scaling and refinement. In Sect. 3 we formulate an algorithm and prove its convergence properties. In Sect. 4 we consider performance issues and describe how our implementation based on SoPlex and qpOASES can be used to calculate solutions for QPs with arbitrary precision. In Sect. 5 we discuss run times and provide solutions for the Maros and Mészáros benchmark library [19]. We conclude in Sect. 6 with a discussion of the results and give directions for future research and applications of the algorithm.

In the following we will use $\Vert \cdot \Vert$ for the maximum norm $\Vert \cdot \Vert _\infty$. The maximal entry of a vector $\max _i\{v_i\}$ is written as $\max \{v\}$. Inequalities $a\le b$ for $a,b\in {\mathbb {Q}}^n$ hold componentwise. $\mathbb {Q}_+$ denotes the set of positive rationals.

2 Refinement and scaling of quadratic programs

In this section we collect some basic definitions and results that will be of use later on. We consider convex optimization problems of the following form.

Definition 1

(Convex QP with Rational Data) Let a symmetric matrix $Q \in \mathbb {Q}^{n\times n}$, a matrix $A \in \mathbb {Q}^{m\times n}$, and vectors $c \in \mathbb {Q}^n, b \in \mathbb {Q}^m, l \in \mathbb {Q}^n$ be given. We consider the quadratic optimization problem (QP)

assuming that (P) is feasible and bounded, and Q is positive semi-definite on the feasible set.

A point $x^* \in \mathbb {Q}^n$ is a global optimum of (P) if and only if it satisfies the Karush–Kuhn–Tucker (KKT) conditions [3], i.e., if multipliers $y^* \in \mathbb {Q}^m$ exist such that

$$\begin{aligned} A x^*= & {} b \end{aligned}$$

(1a)

$$\begin{aligned} x^*\ge & {} l \end{aligned}$$

(1b)

$$\begin{aligned} A^Ty^*\le & {} Qx^* + c \end{aligned}$$

(1c)

$$\begin{aligned} (Qx^* + c - A^Ty^*)^T(x^*-l)= & {} 0. \end{aligned}$$

(1d)

The pair $(x^*,y^*)$ is then called KKT pair of (P). Primal feasibility is given by (1a) and (1b), dual feasibility by (1c), and complementary slackness by (1d). Refinement of this system of linear (in-)equalities is equivalent to the refinement of (P).

Definition 2

(Refined QP) Let the QP (P), scaling factors $\varDelta _P,\varDelta _D \in \mathbb {Q}_+$ and vectors $x^* \in \mathbb {Q}^n,y^* \in \mathbb {Q}^m$ be given. We define the refined QP as

where $\hat{c}=Qx^*+c-A^Ty^*$, $\hat{b}=b-Ax^*$, and $\hat{l}=l-x^*$.

The following theorem is the basis for our theoretical and algorithmic work. It is a generalization of iterative refinement for LP and was formulated and proven in [8, Theorem 5.2]. Again, primal feasibility refers to (1a) and (1b), dual feasibility to (1c), and complementary slackness to (1d).

Theorem 3

(QP Refinement) Let the QP (P), scaling factors $\varDelta _P,\varDelta _D \in \mathbb {Q}_+$, vectors $x^* \in \mathbb {Q}^n,y^* \in \mathbb {Q}^m$, and the refined QP ($P^{\varDelta }$) be given. Then for any $\hat{x} \in \mathbb {R}^n$, $\hat{y} \in \mathbb {R}^m$ and tolerances $\epsilon _P,\epsilon _D,\epsilon _S \ge 0$:

• 1. $\hat{x}$ is primal feasible for ($P^{\varDelta }$) within an absolute tolerance $\epsilon _P$ if and only if $x^* + \frac{\hat{x}}{\varDelta _P}$ is primal feasible for (P) within $\epsilon _P/\varDelta _P$.

• 2. $\hat{y}$ is dual feasible for ($P^{\varDelta }$) within an absolute tolerance $\epsilon _D$ if and only if $y^* + \frac{\hat{y}}{\varDelta _D}$ is dual feasible for (P) within $\epsilon _D/\varDelta _D$.

• 3. $\hat{x}$, $\hat{y}$ satisfy complementary slackness for ($P^{\varDelta }$) within an absolute tolerance $\epsilon _S$ if and only if $y^* + \frac{\hat{y}}{\varDelta _D}$, $x^* + \frac{\hat{x}}{\varDelta _P}$ satisfy complementary slackness for (P) within $\epsilon _S/(\varDelta _P\varDelta _D)$.

For illustration, consider the following example.

Example 4

(QP Refinement) Consider the QP with two variables

$$\begin{aligned} \begin{array}{c} \displaystyle \min _{x} {\frac{1}{2} (x_1^2 + x_2^2) + x_1 + (1+10^{-6})x_2} \\ \text {s.t. } x_1 + x_2 = 10^{-6} \\ x_1,x_2 \ge 0. \\ \end{array} \end{aligned}$$

An approximate solution to a tolerance of $10^{-6}$ is $x^*_1=x^*_2=0$ with dual multiplier $y^*=1$. This solution is slightly primal and dual infeasible, but the solver can not recognize this on this scale. The situation is depicted in Fig. 1 on the left.

Fig. 1

Illustration of nominal QP (left) and of refined QP (right) for Example 4. The scaled (and shifted) QP ($P^{\varDelta }$) acts as a shift and zoom for (P), allowing to correct the solution $x^*$ (orange dot) from (0, 0) to $(10^{-6},0)$

The point $x^*$ seems to be the optimal solution satisfying the equality constraint and the brown circle representing the level curve of the objective function indicates the optimality. The corresponding violations are $\hat{l}=(0,0)^T$, $\hat{b}=10^{-6}$, and $\hat{c}=(0,10^{-6})^T$. The refined QP is

$$\begin{aligned} \begin{array}{c} \displaystyle \min _{x} {\frac{1}{2} (x_1^2 + x_2^2) + x_2} \\ \text {s.t. } x_1 + x_2 = 1 \\ x_1,x_2 \ge 0 \\ \end{array} \end{aligned}$$

with scaling factors $\varDelta _P=\varDelta _D=10^6$. The optimal solution to this problem is $\hat{x}_1=1,\hat{x}_2=0$ with multiplier $\hat{y}=1$. This situation is depicted in Fig. 1 on the right. The initial point $x^*$ is obviously not the optimal solution and the solution to the refined problem is $\hat{x}$. The refined solution is $x^*+\hat{x}/\varDelta _P=(10^{-6},0)^T$ and $y^*+\hat{y}/\varDelta _D=1+10^{-6}$. These values are primal and dual feasible in the original problem.

Note that we restrict the presentation to QPs with rational data because this parallels the implementation on which the computational study in Sect. 5 is based. However, the method is applicable to QPs over any field that is dense in $\mathbb {R}$ and contains the floating-point numbers returned by the QP solver. In practice, it is merely required that we can perform exact arithmetic over the field and that numbers from the field can be rounded to a floating-point approximation with small error. This certainly holds for $\mathbb {Q}$, for which software support is provided by several libraries.

The increased arithmetic cost of rational arithmetic stems from storing arbitrarily large integer numerators and denominators and reducing them to be co-prime by regularly computing their greatest common divisor. Floating-point numbers such as standard double-precision numbers specified by the IEEE Microcomputer Standards Committee [17] are rational numbers usually stored in binary representation

$$\begin{aligned} \pm 1.q_1q_2q_3\ldots q_{52} \cdot 2^{e} \end{aligned}$$

with $q_i\in \{0,1\}$ and $e\in \{-1022, -1021, \ldots , 1023\}$, plus special bit patterns for zero, plus and minus infinity, and the result of undefined arithmetic operations (“not-a-number”). This gives 15 to 17 significant decimal digits to which each rational number can be rounded. Specifically, we will round the rational data of the QPs P and ($P^{\varDelta }$) defined above in order to pass their floating-point versions $\tilde{P}$ and $\tilde{P}^{\varDelta }$, respectively, to the underlying QP solver. Conversely, each floating-point number is a rational number, so no precision is lost when using solutions from the QP solver for a correction step as in Theorem 3. For further details on rational and floating-point arithmetic we refer to [11, 14].

3 The iterative refinement algorithm for quadratic programming

To solve quadratic programs to arbitrary, a priori specified precision, we apply the refinement idea from the previous section iteratively as detailed in Algorithm 1. Algorithm 1 expects QP data (Q, A, c, b, l) in rational precision, primal and dual termination tolerances ($\epsilon _P,\epsilon _D$), complementary slack termination tolerance ($\epsilon _S$), scaling limit $\alpha > 1$ and iteration limit $k_{max}$. First the rounded QP ($\tilde{P}$) is solved with a floating-point QP solver oracle which returns optimal primal and dual solution vectors (Line 2). In Line 3 the main loop begins. The primal violations for constraints ($\hat{b}$, Line 4) and for bounds ($\hat{l}$, Line 5) are calculated. The maximal primal violation is saved as $\delta _P$ in Line 6. The reduced cost vector $\hat{c}$ and its maximal violation $\delta _D$ are calculated in Lines  7–8. In Line 9 the scaling factor $\varDelta _k$ is chosen as the maximum of $\alpha \varDelta _{k-1}$ and the inverses of the violations $\delta _P$ and $\delta _D$. The complementary slack violation $\delta _S$ is calculated in Line 10. If the primal, dual and complementary slack violations are already below the specified tolerances the loop is stopped (Lines 11–12) and the optimal solution is returned (Line 17). Else (Line 13) the refined, scaled, and rounded QP ($\tilde{P}^{\varDelta _k}$) is solved with the floating-point QP oracle in Line 14. We save the floating-point optimal primal and dual solution vectors (Line 15). We scale and add them to the current iterate ($x_k,y_k$) to obtain ($x_{k+1},y_{k+1}$), Line 16.

Note that all calculations except the expensive solves of the QPs are done in rational precision. Algorithm 1 uses only one scaling factor $\varDelta _k$ for primal and dual infeasibility to avoid the scaling of the quadratic term of the objective. Keeping this matrix and the constraint matrix A fixed gives QP solvers the possibility to reuse the internal factorization of the basis system between refinements, as the transformation does not change the basis. Hence one can perform hotstarts with the underlying QP solver which is crucial for the practical performance of the algorithm. This comes at the cost of only scaling either primal or dual infeasibilities as required, especially if they differ a lot, possibly slowing convergence.

To investigate the performance of the algorithm we make, in analogy with the LP case [10, Ass. 1], the following assumption.

Assumption 5

(QP Solver Accuracy) We assume that there exists $\epsilon \in [0,1)$ and $\sigma \ge 0$ such that the QP solver oracle returns for all rounded QPs ($\tilde{P}^{\varDelta _k}$) solutions $(\bar{x},\bar{y})$ that satisfy

$$\begin{aligned} \Vert A \bar{x} - \varDelta _k\hat{b}\Vert\le & {} \epsilon \\ \bar{x}\ge & {} \varDelta _k\hat{l} - \mathbb {1} \epsilon \\ Q\bar{x} + \varDelta _k\hat{c}\ge & {} A^T\bar{y} - \mathbb {1} \epsilon \\ |(Q\bar{x} + \varDelta _k\hat{c} - A^T\bar{y})^T(\bar{x}-\varDelta _k\hat{l})|\le & {} \sigma \\ \end{aligned}$$

with respect to the rational input data of QPs ($P^{\varDelta _k}$).

Note that this $\epsilon$ corresponds to a termination tolerance passed to a floating-point solver, while the algorithm uses overall termination tolerances $\epsilon _P$ and $\epsilon _D$ and a scaling limit $\alpha > 1$ per iteration. We denote $\tilde{\epsilon }=\max \{1/\alpha ,\epsilon \}$.

Lemma 6

(Termination and Residual Convergence) Algorithm 1 applied to a primal and dual feasible QP (P) and using a QP solver that satisfies Assumption 5 will terminate in at most

$$\begin{aligned} k_{max} = \max \left\{ \;\log (\epsilon _P)/\log (\tilde{\epsilon }),\;\log (\epsilon _D)/\log (\tilde{\epsilon }),\;\log (\epsilon _S/\sigma )/(2\log (\tilde{\epsilon }))+1\;\right\} \end{aligned}$$

(2)

iterations. Furthermore, after each iteration $k=1,2,\ldots$ the primal-dual iterate ($x_k,y_k$) and the scaling factor $\varDelta _k$ satisfy

$$\begin{aligned} \varDelta _k\ge & {} 1/\tilde{\epsilon }^{k} \end{aligned}$$

(3a)

$$\begin{aligned} \Vert A x_k - b\Vert\le & {} \tilde{\epsilon }^{k} \end{aligned}$$

(3b)

$$\begin{aligned} x_k - l\ge & {} - \mathbb {1} \tilde{\epsilon }^{k} \end{aligned}$$

(3c)

$$\begin{aligned} Qx_k + c - A^Ty_k\ge & {} - \mathbb {1} \tilde{\epsilon }^{k} \end{aligned}$$

(3d)

$$\begin{aligned} |(Qx_k + c - A^Ty_k)^T(x_k-l)|\le & {} \sigma \tilde{\epsilon }^{2(k-1)}. \end{aligned}$$

(3e)

Proof

We prove (3) by induction over k, starting with $k=1$. As $\tilde{\epsilon } \ge \epsilon$, the claims (3b–3e) follow directly from Assumption 5. Using Lines 6, 4–5, and Assumption 5 we obtain

$$\begin{aligned} \delta _P = \max \left\{ 0,\Vert \hat{b}\Vert ,\max \{\hat{l}\}\right\} = \max \{0,\Vert Ax_1 - b \Vert , \max \{l - x_1\} \} \le \epsilon \end{aligned}$$

and with Lines 8,7 and Assumption 5

$$\begin{aligned} \delta _D = \max \left\{ 0,\max \{ -\hat{c}\}\right\} = \max \left\{ 0,\max \{Qx_1+c-A^Ty_1\}\right\} \le \epsilon . \end{aligned}$$

Thus from Line 9 we have

$$\begin{aligned} \varDelta _1 = \min \left\{ \delta _P^{-1},\delta _D^{-1},\alpha \varDelta _{0}\right\} \ge \min \left\{ \epsilon ^{-1},\epsilon ^{-1},\alpha \right\} \ge \tilde{\epsilon }^{-1} \end{aligned}$$

and hence claim (3a) for the first iteration.

Assuming (3) holds for k we know that $\delta _{P,k},\delta _{D,k} \le \tilde{\epsilon }^k$ and $\varDelta _k \ge 1/\tilde{\epsilon }^{k}$. With the scaling factor $\varDelta _{k}$ using $x^*=x_k$ and $y^*=y_k$ we scale the QP (P) as in Theorem 3 and hand it to the QP solver. By Theorem 3 this scaled QP is still primal and dual feasible and by Assumption 5 the solver hands back a solution $(\hat{x},\hat{y})$ with tolerance $\epsilon \le \tilde{\epsilon }$. Therefore using Theorem 3 again the next refined iterate ($x_{k+1},y_{k+1}$) has a tolerance in QP (P) of $\tilde{\epsilon }/\varDelta _{k} \le \tilde{\epsilon }^{k+1}$, which proves (3b–3d).

With the same argument the solution $(\hat{x},\hat{y})$ violates complementary slackness by $\sigma$ in the scaled QP (Assumption 5) and the refined iterate ($x_{k+1},y_{k+1}$) violates complementary slackness in QP (P) by $\sigma /\varDelta _{k}^2\le \sigma \tilde{\epsilon }^{2k}$ proving (3e).

We have now $\delta _{P,k+1},\delta _{D,k+1} \le \tilde{\epsilon }^{k+1}$. Also it holds that $\alpha \varDelta _k \ge \alpha /\tilde{\epsilon }^{k}\ge 1/\tilde{\epsilon }^{k+1}$. Line 9 of Algorithm 1 gives

$$\begin{aligned} \varDelta _{k+1} \ge 1/\tilde{\epsilon }^{k+1}, \end{aligned}$$

proving (3a).

Then (2) follows by assuming the slowest convergence rate of the primal, dual and complementary violations and by comparing this with the termination condition in Line 11 of Algorithm 1

$$\begin{aligned} \tilde{\epsilon }^k \le \epsilon _P,\;\tilde{\epsilon }^k \le \epsilon _D, \sigma \tilde{\epsilon }^{2(k-1)}\le \epsilon _S. \end{aligned}$$

This is equivalent to (2). $\square$

The results show that even though we did not use the violation of the complementary slackness to choose the scaling factor in Algorithm 1, the complementary slackness violation is bounded by the square of $\tilde{\epsilon }$.

Remark 7

(Nonconvex QPs) Algorithm 1 can also be used to calculate high precision KKT pairs of nonconvex QPs. If the black box QP solver hands back local solutions of the quality specified in Assumption 5 Lemma 6 holds as well for nonconvex QPs then Algorithm 1 returns a high precision local solution.

However, assuming strict convexity, an even stronger result holds. Inspired by the result for the equality-constrained QP [3, Proposition 2.12] we investigate how this right-hand side convergence of the KKT conditions is related to the primal-dual solution.

Lemma 8

(Primal and Dual Solution Accuracy) Let QP (P) be given and be strictly convex, the minimal and maximal eigenvalues of Q be $\lambda _{\min }(Q)$ and $\lambda _{\max }(Q)$, respectively, and the minimal nonzero singular value of A be $\sigma _{\min }(A)$. Let the KKT conditions (1) hold for $(x^*,y^*,z^*)$, i.e.,

$$\begin{aligned} A x^*= & {} b \end{aligned}$$

(4a)

$$\begin{aligned} A^Ty^* +z^*= & {} Qx^* + c \end{aligned}$$

(4b)

$$\begin{aligned} z^{*T}(x^*-l)= & {} 0 \end{aligned}$$

(4c)

$$\begin{aligned} x^*\ge & {} l \end{aligned}$$

(4d)

$$\begin{aligned} z^*\ge & {} 0 \end{aligned}$$

(4e)

and the perturbed KKT conditions for perturbations $e \in \mathbb {Q}^m,\,g,f,h \in \mathbb {Q}^n,$ and $i \in \mathbb {Q}$ hold for (x, y, z), i.e.,

$$\begin{aligned} A x= & {} b + e \end{aligned}$$

(5a)

$$\begin{aligned} A^Ty +z= & {} Qx + c + g \end{aligned}$$

(5b)

$$\begin{aligned} z^T(x-l)= & {} i \end{aligned}$$

(5c)

$$\begin{aligned} x\ge & {} l + f \end{aligned}$$

(5d)

$$\begin{aligned} z\ge & {} h. \end{aligned}$$

(5e)

Denote

$$\begin{aligned} a:= & {} \frac{ \lambda _{\max }(Q) \Vert e\Vert _2}{2\sigma _{\min }(A)} +\lambda _{\max }(Q) \lambda _{\min }(Q)\Vert g\Vert _2/2 \\ d:= & {} \lambda _{\max }(Q)\Vert i- h^T(x^*-l) -z^{*T}f\Vert _2. \end{aligned}$$

Then

$$\begin{aligned} \Vert A^T(y-y^*) + (z-z^*)\Vert _2 \le a +\sqrt{ a^2 + d } \end{aligned}$$

(6)

and

$$\begin{aligned} \Vert x-x^*\Vert _2 \le \lambda _{\min }(Q) ( a +\sqrt{ a^2 + d } ) + \lambda _{\min }(Q)\Vert g\Vert _2 . \end{aligned}$$

(7)

Proof

By (4a) and (5a) we have that $A(x-x^*)=e$ and taking the Moore-Penrose pseudoinverse $A^{+}$ of A we define $\delta =A^{+}e$ with $A\delta =e$ and $\Vert \delta \Vert _2\le \sigma _{\min }(A)^{-1}\Vert e\Vert _2$. Using this we can start to derive the dual bound by taking the difference of (4b) and (5b)

$$\begin{aligned} A^T(y-y^*) + (z-z^*) = Q(x-x^*) + g. \end{aligned}$$

(8)

Multiplying from the left with $Q^{-1}(A^T(y-y^*) + (z-z^*))$ transposed gives

$$\begin{aligned}&\Vert A^T(y-y^*) + (z-z^*)\Vert ^2_{Q^{-1}} = (A^T(y-y^*) + (z-z^*))^T ((x-x^*) + Q^{-1} g) \nonumber \\&\quad = (A^T(y-y^*) + (z-z^*))^T Q^{-1} g + (y-y^*)^T\underbrace{A(x-x^*)}_{A\delta } + (z-z^*)^T(x-x^*) \nonumber \\&\quad \quad = (A^T(y-y^*) + (z-z^*))^T (Q^{-1} g + \delta ) + (z-z^*)^T(x-x^*-\delta ). \end{aligned}$$

(9)

The second term of (9) can be expressed as

$$\begin{aligned}&(z-z^*)^T(x-l-(x^*-l)-\delta )=\underbrace{z^T(x-l)}_i+\underbrace{z^{*T}(x^*-l)}_0 -\underbrace{z^T(x^*-l)}_{\ge h^T(x^*-l)}-\underbrace{z^{*T}(x-l)}_{\ge z^{*T}f} \\&\quad (z-z^*)^T(x-l-(x^*-l)-\delta ) \le i - h^T(x^*-l) -z^{*T}f. \end{aligned}$$

With this and (9) we bound from above the term $\Vert A^T(y-y^*) + (z-z^*)\Vert ^2_{Q^{-1}}=*$ giving the inequality

$$\begin{aligned} * \le (A^T(y-y^*) + (z-z^*))^T (Q^{-1} g + \delta ) + i- h^T(x^*-l) -z^{*T}f. \end{aligned}$$

Taking the norm on the right and reordering terms gives

$$\begin{aligned}&\Vert Q\Vert _2^{-1}\Vert A^T(y-y^*) + (z-z^*)\Vert _2^2 \le \Vert A^T(y-y^*) + (z-z^*)\Vert _2 \Vert Q^{-1} g + \delta \Vert _2 \\&\quad + \Vert i- h^T(x^*-l) -z^{*T}f\Vert _2. \end{aligned}$$

This is a quadratic expression in $\Vert A^T(y-y^*) + (z-z^*)\Vert _2=m$

$$\begin{aligned} m^2 - m \Vert Q^{-1} g + \delta \Vert _2 \Vert Q\Vert _2 - \Vert i- h^T(x^*-l) -z^{*T}f\Vert _2 \Vert Q\Vert _2 \le 0. \end{aligned}$$

It has two roots, but only one is greater than zero and bounds $\Vert A^T(y-y^*) + (z-z^*)\Vert _2(=m)$ from above

$$\begin{aligned} \begin{array}{rl} m \le &{} \Vert Q^{-1} g + \delta \Vert _2 \Vert Q\Vert _2/2 \\ &{}+\, \sqrt{ (\Vert Q^{-1} g + \delta \Vert _2\Vert Q\Vert _2)^2/4 + \Vert i- h^T(x^*-l) -z^{*T}f\Vert _2\Vert Q\Vert _2 }. \end{array} \end{aligned}$$

(10)

This can be expressed as

$$\begin{aligned} \Vert A^T(y-y^*) + (z-z^*)\Vert _2 \le a +\sqrt{ a^2 + d } \end{aligned}$$

(11)

where a and d are defined as above. This proves (6). To prove the primal bound we multiply equation (8) from the left with $Q^{-1}$

$$\begin{aligned} (x-x^*) = Q^{-1}(A^T(y-y^*)+(z-z^*)-g). \end{aligned}$$

Taking norms gives the inequality

$$\begin{aligned} \Vert x-x^*\Vert _2 \le \Vert Q^{-1}\Vert _2 \Vert A^T(y-y^*)+(z-z^*)\Vert _2 + \Vert Q^{-1}g\Vert _2. \end{aligned}$$

(12)

Combining the dual bound (11) and (12) we get the final primal bound

$$\begin{aligned} \Vert x-x^*\Vert _2 \le \lambda _{\min }(Q) ( a +\sqrt{ a^2 + d } ) + \lambda _{\min }(Q) \Vert g\Vert _2 \end{aligned}$$

which proves (7). $\square$

Note that $\lambda _{\max }(Q) \lambda _{\min }(Q)$ is the condition number of Q. The above assumption and lemmas can be summarized to a statement about the convergence of the algorithm for a strictly convex QP.

Theorem 9

(Rate of Convergence) Algorithm 1 with corresponding input and using a QP solver satisfying Assumption 5 solving the QP (P) that is also strictly convex has a linear rate of convergence with a factor of $\tilde{\epsilon }^{1/2}$ for the primal iterates, i.e.

$$\begin{aligned} \Vert x_k-x^*\Vert \le \tilde{\epsilon }^{1/2} \Vert x_{k-1}-x^*\Vert , \end{aligned}$$

with $x^*$ being the unique solution of (P).

Proof

By Assumption 5 and Lemma 6 we know that the right-hand side errors of the KKT conditions are bounded by

$$\begin{aligned} \Vert e\Vert \le \tilde{\epsilon }^{k},\,\Vert g\Vert \le \tilde{\epsilon }^{k},\,\Vert f\Vert \le \tilde{\epsilon }^{k},\,\Vert i\Vert \le \sigma \tilde{\epsilon }^{2(k-1)}, \Vert h\Vert = 0. \end{aligned}$$

Here we set the violations h of the inequality KKT multipliers z to zero and count them as additional dual violations g for simplicity. Also note that in Lemma 8 the bound is just depending on the norm of the right-hand side violation vectors, two different violation vectors with the same norm give the same bound. Therefore we just consider the norms. Combining the above with Lemma 8 we get

$$\begin{aligned} \Vert x_k-x^*\Vert \le c_1 \tilde{\epsilon }^{k} + \sqrt{c_2\tilde{\epsilon }^{k}+c_3\tilde{\epsilon }^{2k}} \end{aligned}$$

for the primal iterate in iteration k with constants

$$\begin{aligned} c_1= & {} \lambda _{\min }(Q) \lambda _{\max }(Q) \left( \frac{1}{\lambda _{\max }(Q)} + \frac{\lambda _{\min }(Q)}{2} + \frac{1}{2\sigma _{\min }(A)}\right) \\ c_2= & {} \lambda _{\max }(Q) \Vert z^* \Vert \\ c_3= & {} (c_1-\lambda _{min}(Q))^2 + \lambda _{\max }(Q)\sigma /\tilde{\epsilon }^2. \\ \end{aligned}$$

Looking at the quotient

$$\begin{aligned} \frac{\Vert x_k-x^*\Vert }{\Vert x_{k-1}-x^*\Vert } \le \frac{c_1 \tilde{\epsilon }^{k} + \sqrt{c_2\tilde{\epsilon }^{k}+c_3\tilde{\epsilon }^{2k}}}{c_1 \tilde{\epsilon }^{k-1} + \sqrt{c_2\tilde{\epsilon }^{k-1}+c_3\tilde{\epsilon }^{2(k-1)}}} \end{aligned}$$

and seeing that

$$\begin{aligned} \frac{\Vert x_k-x^*\Vert }{\Vert x_{k-1}-x^*\Vert } \le \frac{\tilde{\epsilon }^{k/2}(c_1 \tilde{\epsilon }^{k/2} + \sqrt{c_2+c_3\tilde{\epsilon }^{k}})}{\tilde{\epsilon }^{(k-1)/2}(c_1 \tilde{\epsilon }^{(k-1)/2} + \sqrt{c_2+c_3\tilde{\epsilon }^{k-1}})}=\tilde{\epsilon }^{1/2}\gamma _k \end{aligned}$$

with $\gamma _k \le 1$ proves the result. $\square$

This theoretical investigation shows us two things. First, we have linear residual convergence with a rate of $\tilde{\epsilon }$. In contrast to usual convergence results our algorithm achieves this rate in practice by the use of rational computations if the floating-point solver delivers solutions of the quality specified in Assumption 5. This is also checked by the rational residual calculation in our algorithm in every iteration. Second, this residual convergence implies primal iterate convergence with a linear rate of $\tilde{\epsilon }^{1/2}$ for strictly convex QPs.

4 Implementation

Following previous work [10] on the LP case we implemented Algorithm 1 in the same framework within the SoPlex solver [24], version 2.2.1.2, using the GNU multiple precision library (GMP) [14] for rational computations, version 6.1.0. Note that SoPlex is not used to solve LPs but provides support functionalities. These are functionalities to read and write mps files (extended to qps files) and to save the corresponding QP problems in rational and floating-point precision. Additionally SoPlex provides rational and floating-point calculations with operator overloading reducing implementation complexity (based on GMP). As underlying QP solver we use the active-set solver qpOASES [4] version 3.2. This version of qpOASES was originally designed for small to medium QPs (up to 1000 variables and constraints). Furthermore, we implemented an interface to a pre-release version of qpOASES 4.0, which can handle larger, sparse QPs of a size up to 40,000 variables and constraints. Compared to the matured qpOASES 3.2, this version is not yet capable of hotstarts and in some cases is less robust. Nevertheless, it allows us to study the viability of iterative refinement on larger QPs. The source code of our implementation is available for download in a public repository [21].

In order to treat general QPs with inequalities, our implementation recovers the form (P) by adding one slack variable per inequality constraint. Note that not only lower, but also upper bounds on the variables need to be considered. However, this is a straightforward modification to our algorithm and realized in the implementation.

One advantage of using the active-set QP solver qpOASES is the returned basis information. We use the basis in three aspects: first, to calculate dual and complementary slack violations; second, to explicitly set nonbasic variables to their lower bounds after the refinement step in Line 16 of Algorithm 1; and third, to compute a rational solution defined by the corresponding system of linear equations. This is solved by a standard LU factorization in rational arithmetic. If the resulting primal-dual solution is verified to be primal and dual feasible, the algorithm can terminate early with an exact optimal basic solution.

Since the LU factorization can be computationally expensive, we only perform this step if we believe the basis to be optimal. When the QP solver returns the same basis as “optimal” for several iterations this can be used as a heuristic indicator that the basis might be truly optimal, even if the iteratively corrected numerical solution is not yet exact. Hence, the number of consecutive iterations with the same basis is used to trigger a rational basis system solve. This can be controlled by a threshold parameter called “ratfac minstalls”, see Table 1.

If the floating-point solver fails to compute an approximately optimal solution, we decrease the scaling factor by two orders of magnitude and try to solve the resulting QP again. The scaling factor is reduced either until the maximum number of backstepping rounds is reached or until the next backstepping round would result in a scaling factor lower than in the last refinement iteration ($k-1$).

The default parameter set (s1) of our implementation is given in Table 1. The other four parameter sets (s2–s5) are used for our numerical experiments to derive either exact or inexact solutions.

Table 1 IQPR parameters

We exploit the different features of the two qpOASES versions. Version 3.2 has hotstart capabilities that allow reusing the internal basis system factorization of the preceding optimal basis. Therefore we start in the old optimal basis and build on the progress made in the previous iterations instead of solving the QP from scratch at every iteration. Additionally we increase the termination tolerance and relax other parameters that ensure a reliable solve. This speeds up the solving process and is possible because the inaccuracies, introduced by the floating-point solution, are detected anyway and handed back to the QP solver in the next iteration for correction. If the QP solver fails we simply change to reliable settings and resolve the same QP from the same starting basis before downscaling. Hence, in Algorithm 1 each ‘solve’ statement means: try fast settings first and if this fails switch to slow and reliable settings of qpOASES 3.2. These two sets of options are given in Table 2. In this Table we only state the options chosen differently from the standard qpOASES settings sets (MPC, Reliable) which are given in the “Appendix” in Table 5.

For the pre-release version 4.0 we use default settings and no resolves. We either factorize after each iteration or not at all (see Table 1).

Table 2 qpOASES options in Version 3.2

5 Numerical results

For the numerical experiments the standard testset of Maros and Mészáros [19] was used. It contains 138 convex QPs that feature between two and about 90,000 variables. The number of constraints varies from one to about 180,000 and the number of nonzeros ranges between two and about 550,000. The computations were performed on a cluster of 64-bit Intel XeonE5-2660 (v3) CPUs at 2.6 GHz with 25 MB L3 cache and 125 GB main memory.

We conduct two different experiments. The goal of the first experiment is to solve as many QPs from the testset as precisely as possible in order to analyze the iterative refinement procedure computationally and to provide exact reference solutions for future research on QP solvers. In the second experiment we want to compare qpOASES (version 3.2, no QP refinement, one solve, default settings) to low accuracy refinement (low tolerance of 1e−10 in Algorithm 1, using also qpOASES 3.2). This allows us to investigate whether refinement could also be beneficial in cases that do not require extremely high accuracy, but a strictly guaranteed solution tolerance in shortest possible runtime.

Experiment 1

We use the three different parameter sets (s2–s4) given in Table 1 to calculate exact solutions. The first set (s2) contains a primal and dual termination tolerance of 1e−100, enables rational factorization in every iteration, and allows for 50 refinements and 10 backsteppings using a dense QP formulation with qpOASES version 3.2. In contrast the other two sets (s3, s4) with qpOASES version 4.0 use a sparse QP formulation, either with factorization in every iteration or without factorization. For this experiment, a time limit of three hours is imposed per instance and solver.

Table 3 states for each setting the number of instances which were solved exactly, for which tolerance 1e−100 was reached, for which only low tolerance solutions were produced, and the number of instances which did not return from the cluster due to memory limitations. In total these three strategies could solve 91 out of the 138 QPs in the testset exactly and 39 instances within tolerance 1e−100. For eight instances no high-precision solution was computed. These “virtual best” results stated in the fifth column consider for each QP the result of the individual parameter sets that resulted in the smallest violation. It should be emphasized that for each of the three parameter sets there exists at least one instance for which it produced the most accurate solution.

The last column reports the average number of nonzeros of the QPs in the three “virtual best” categories. This suggests that for problems with fewer nonzeros a higher accuracy was reached. In the third and fourth column one problem did not return (BOYD1 with over 90000 variables). For the parameter set s4 without rational factorization we see that one QP is solved exactly while for all others the algorithm terminates with violations greater zero.

Table 3 Results for the three exact parameter sets (s2–s4) over all 138 QPs in the testset: number of instances according to terminal solution accuracy for each setting, for the virtual best setting, and the average number of nonzeros over the instances in the “best” categories

In order to solve the 197 ($=33+45+118$) QPs to high precision the algorithm needed on average 8.84 refinements. This confirms the linear convergence because we bounded the increase of the scaling factor in each iteration by $\alpha$ = 10e$+$12 and terminate after reaching a tolerance of 1e−100. If qpOASES would consistently return solutions with an accuracy of 1e−12 we would expect the algorithm to need 9 iterations ($100/12 \approx 8.33\ldots$ rounded up). We see that qpOASES usually delivers solutions of a tolerance below 1e−12.

Detailed results can be found in the “Appendix” in Tables 6, 7, and 8. The column “Status” reports “optimal” if a solution of tolerance below 1e−100 is computed. Otherwise, if the tolerance is not reached the status is declared “fail”. If the objective value found differs from the value in literature [19] by more than 1e−7, then the status is reported as “inconsistent”.¹ If we exceed the timelimit, then the status is “timeout”. The status “error” is an internal algorithmic error, e.g., the QP solver fails to solve one of the QPs in the sequence and hence the algorithm stops. If the maximum number of algorithm iterations is reached (e.g., because the solutions calculated by the QP solver violate Assumption 5) the status is “abort” and results in “NaN” (not a number) in the other columns. The column “Iterations” counts all QP solver iterations (active set changes) summed over all algorithm iterations. The algorithm iterations are the number of refinements (plus one) given in the “Refinement” column. The QP solver iterations were only counted for the parameter set s2 and hence are zero for the other two settings.

If an exact solution is found qpOASES usually returns the optimal basis in the first three refinement iterations. The optimal basis was found in the first iteration (without refinement) for 55 instances when using parameter set s2, with set s3 and s4 this where 74 and one instances. Subsequently, the corresponding basis system is solved exactly by a rational LU factorization.² For six problems we found that the objective values given in [19] differ from our results by more than 1e−7: GOULDQP2, HS268, S268, HUESTIS, HUES-MOD, and LISWET8. This might be due to the use of a floating-point QP solver with termination tolerance about 1e−7 when originally computing the values reported. The precise objective value can be found in the online material associated with this paper.

Experiment 2

In the following the iterative refinement algorithm is set to a termination tolerance $10^{-10}$ and the rational factorization of the basis system is disabled. The refinement limit is set to 10 and the backstepping limit is set to one (parameter set s5). We compare this implementation to qpOASES 3.2 with the three predefined qpOASES settings (MPC, Default, Reliable) that include termination tolerances of 2.2210e−7, 1.1105e−9, and 1.1105e−9, respectively. For these fast solves we select only part of the testset, including the 73 problems that have no more than 1,000 variables and constraints. This corresponds to the problem size for which qpOASES 3.2 was originally designed. In order to allow for a meaningful comparison of runtimes, the evaluation only considers QPs which were solved by all three qpOASES 3.2 settings and by refinement to “optimality”, where optimality was certified by qpOASES 3.2 (with its internal floating-point checks) or rational checks in our algorithm, respectively. For this experiment, a time limit of one hour is imposed per instance and solver.

Table 4 Performance comparison for inexact solves (runtimes are in seconds)

An overview of the performance results is given in Table 4. We report runtime, QP solver iterations, and the final tolerance reached, each time as arithmetic and shifted geometric mean. To facilitate a more detailed analysis, we consider the series of subsets “$> t$” of instances, for which at least one algorithm took more than t seconds. Equivalently, we exclude the QPs for which all settings took at most 0.01 s, 0.1 s, 1 s, and 10 s. Defining the exclusion by all instead of one method only avoids a biased definition of these sets of increasing difficulty.

The results show that in no case is the mean runtime of the refinement algorithm larger than the runtime of qpOASES with reliable setting. At the same time, the accuracy reached is always significantly higher. Compared to qpOASES Default, which results in an even lower level of precision, refinement is faster in arithmetic and slightly slower in shifted geometric mean. The QP solver iterations of the refinement are comparable to the MPC setting. When looking at the different subsets we see that for QPs with larger runtime the refinement approach performs relatively better (smaller runtime, iterations and lower tolerance) than the three qpOASES 3.2 standard settings. The refinement guarantees the tolerance of 1e−10 if it does not fail. To achieve this tolerance, for 9 QPs two refinements were necessary, for 21 QPs only one refinement was necessary, and for 35 instances no refinement was necessary at all. The rational computation overhead stated in brackets after the runtime and is well below 2%. The details are shown in Table 9 in the “Appendix”. Also note that due to exclusion of fails (which mainly occur with the qpOASES MPC settings) the summarized results have a slight bias towards qpOASES.

6 Conclusion

We presented a novel refinement algorithm and proved linear convergence of residuals and errors. Notably, this theoretical convergence result also carries over to our implementation due to the use of exact rational calculations. We provided high-precision solutions for most of the QPs in the Maros and Mészáros testset, correcting inaccuracies in optimal solution values reported in the literature. This is beneficial for future research on QP solvers that are evaluated on this testset.

In a second experiment we saw that iterative refinement provides proven tolerance solutions with smaller or equal computation times compared to qpOASES with “Reliable” solver settings. It can therefore be used as a tool to increase the reliability and speed of standard floating-point QP solvers. The related approach in [18] is designed to speed up QP solutions without extended-precision or rational arithmetic. One could think of combining the two approaches, only using extended precision when necessary, e.g., when convergence stalls.

If optimal solutions are needed for rigorous reasoning or to make decisions in the real world the algorithm presented is useful because it is able to fully ensure a specified tolerance. This tolerance then can be adapted to the necessity of the application at hand. At the same time this comes with little overhead in rational computation time, which is important for practical applications.

Regarding algorithmic research and solver development, our framework also provides the possibility to compare different floating-point QP solvers by looking at the number of refinements needed with each solver to detect optimal bases or solutions of a specified tolerance as a measure for solver accuracy. Solver robustness can be checked precisely because violations are computed in rational precision. In the future, it would be valuable to extend the implementation to handle cases of unbounded or infeasible QPs and to experiment with more general variable transformations that apply, e.g., a different scaling factor for each variable. As a final remark, we hope that the idea of checking numerical results of floating-point algorithms in exact or safe arithmetic will become a future trend when applying or analyzing numerical algorithms.

Appendix

The following tables contain a list of detailed parameter settings for the QP solver qpOASES and instancewise results for the different experiments described in Sect. 5.

1.1 Detailed QP solver options

See Table 5.

Table 5 Standard parameter values for different qpOASES 3.2 settings (EPS = 2.221e−16)

1.2 Detailed results

See Tables 6, 7, 8 and 9.

Table 6 Detailed results for exact solve of large QP set with parameter set s2

Table 7 Detailed results for exact solve of large QP set with parameter set s3

Table 8 Detailed results for exact solve of large QP set with parameter set s4

Table 9 Detailed results for inexact and fast solves of medium QP set with parameter set s5 and the three standard qpOASES option sets