Dynamics of a micro-cantilever for capacitive energy harvesting considering nonlinear inertia and curvature

Abstract

In this paper, the nonlinear dynamics of a cantilever-based capacitive energy harvesting device with out-of-plane gap closing scheme is investigated under large deformations. The frequency response of the micro-cantilever in these devices exhibits a softening behavior when subjected to large deformations, which can be exploited to increase the operational bandwidth of the device. However, linear beam theories fail to accurately predict the dynamic response of the system due to the nonlinearities induced by these large deformations, which demonstrates the importance of using nonlinear beam theories in design of such systems. Therefore, in this work, the micro-cantilever is modeled continuously based on a nonlinear Euler–Bernoulli beam theory which takes the curvature and inertia nonlinearities into account. The governing electric equation of the device is obtained by employing the Kirchhoff’s voltage law in the equivalent electric circuit of the system, which is coupled with the mechanical domain. The coupled nonlinear electro-mechanical equations of the device are discretized using Galerkin technique and are integrated numerically over time. The static and dynamic pull-in instability of the micro-cantilever is studied, and the performance of the device subjected to ambient vibrations is evaluated and analyzed by obtaining the frequency response of the system. In order to harvest the maximum energy in the bi-stable regions of the frequency response, a hoping voltage is introduced to force the system to settle to the steady-state response that has a larger oscillation amplitude.

Appendix

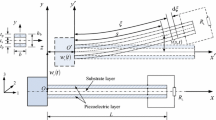
In this section, a nonlinear Euler–Bernoulli beam model is derived based on Newtonian dynamics for a micro-cantilever in a capacitive energy harvesting device under base excitation. Figure 

Fig. 18

(a) Schematic of the micro-cantilever in undeformed and deformed configuration (b) the centerline of an element on the micro-cantilever before and after deformation

18(a) shows a schematic of the capacitive micro-cantilever before and after deformation. The micro-cantilever has a length of L, width of b, and thickness of h, Young’s modulus of E, and mass density of ρ. Figure 18(b) demonstrates the centerline of an element on this micro-cantilever before and after deformation. As shown in this figure, the element undergoes both axial and vertical displacements, which are denoted by u and w, respectively.

To obtain the motion equation of the beam, the free body diagram of the beam element after deformation is considered. As shown in Fig. 

Fig. 19

Free body diagram of an element on the micro-cantilever

19, the beam element is subjected to different loads at its cross sections including axial force, N, shear force, V, and bending moment, M. The variation of these forces is assumed to be small along the element length, dx, which are approximated using Taylor expansion series up to the first order of dx. In addition, the element of the micro-cantilever is under electrostatic pressure, F_E.

Using this free body diagram, three equilibrium equations can be written as follow:

• 1. Newton’s second law of motion in horizontal direction:

  $$\begin{aligned} & \left( {N + \frac{\partial N}{{\partial x}}{\text{d}}x} \right)\cos \left( {\theta + \frac{\partial \theta }{{\partial x}}{\text{d}}x} \right) - N\cos \theta + V\sin \theta - \left( {V + \frac{\partial V}{{\partial x}}{\text{d}}x} \right)\sin \left( {\theta + \frac{\partial \theta }{{\partial x}}{\text{d}}x} \right) \\ & \quad = \rho A{\text{d}}x\frac{{\partial^{2} u}}{{\partial t^{2} }} \\ \end{aligned}$$

  (24)

• 2. Newton’s second law in vertical direction gives:

  $$\begin{aligned} & V\cos \theta - \left( {V + \frac{\partial V}{{\partial x}}{\text{d}}x} \right)\cos \left( {\theta + \frac{\partial \theta }{{\partial x}}{\text{d}}x} \right) - N\sin \theta + \left( {N + \frac{\partial N}{{\partial x}}{\text{d}}x} \right)\sin \left( {\theta + \frac{\partial \theta }{{\partial x}}{\text{d}}x} \right) - F_{{\text{E}}} \\ & \quad = \rho Adx\frac{{\partial^{2} w}}{{\partial t^{2} }} \\ \end{aligned}$$

  (25)

• 3. Moment equilibrium along y-axis:

  $$M + \frac{\partial M}{{\partial x}}{\text{d}}x - M + V{\text{d}}x = J{\text{d}}x\frac{{\partial^{2} \theta }}{{\partial t^{2} }}$$

  (26)

  where J is the rotary inertia given by:

  $$J = \int_{A} {\rho z^{2} {\text{d}}A}$$

  (27)

Further simplifying Eq. (26) yields:

$$\frac{\partial M}{{\partial x}} + V = J\frac{{\partial^{2} \theta }}{{\partial t^{2} }}$$

(28)

To simplify Eqs. (24) and (25), the following triangular expansions are used:

$$\cos \left( {\theta + \frac{\partial \theta }{{\partial x}}{\text{d}}x} \right) = \cos \theta \cos \left( {\frac{\partial \theta }{{\partial x}}{\text{d}}x} \right) - \sin \theta \sin \left( {\frac{\partial \theta }{{\partial x}}{\text{d}}x} \right) \approx \cos \theta - \frac{\partial \theta }{{\partial x}}{\text{d}}x\sin \theta$$

(29)

$$\sin \left( {\theta + \frac{\partial \theta }{{\partial x}}{\text{d}}x} \right) = \sin \theta \cos \left( {\frac{\partial \theta }{{\partial x}}{\text{d}}x} \right) + \cos \theta \sin \left( {\frac{\partial \theta }{{\partial x}}{\text{d}}x} \right) \approx \sin \theta + \frac{\partial \theta }{{\partial x}}{\text{d}}x\cos \theta$$

(30)

Therefore, Eq. (24) reduces to:

$$\begin{aligned} & N\cos \theta - N\frac{\partial \theta }{{\partial x}}{\text{d}}x\sin \theta + \frac{\partial N}{{\partial x}}{\text{d}}x\cos \theta - \frac{\partial N}{{\partial x}}\frac{\partial \theta }{{\partial x}}\left( {{\text{d}}x} \right)^{2} \sin \theta - N\cos \theta + V\sin \theta \\ & \quad - V\sin \theta - V\frac{\partial \theta }{{\partial x}}{\text{d}}x\cos \theta - \frac{\partial V}{{\partial x}}{\text{d}}x\sin \theta - \frac{\partial V}{{\partial x}}\frac{\partial \theta }{{\partial x}}\left( {{\text{d}}x} \right)^{2} \cos \theta = \rho A{\text{d}}x\frac{{\partial^{2} u}}{{\partial t^{2} }} \\ \end{aligned}$$

(31)

Neglecting higher-order differential terms, Eq. (31) is further simplified as:

$$\frac{\partial }{\partial x}\left( {N\cos \theta - V\sin \theta } \right) = \rho A\frac{{\partial^{2} u}}{{\partial t^{2} }}$$

(32)

With a similar approach, Eq. (25) reduces to:

$$\frac{\partial }{\partial x}\left( {N\sin \theta + V\cos \theta } \right) = F_{E} + \rho A\frac{{\partial^{2} w}}{{\partial t^{2} }}$$

(33)

Integrating Eq. (32) over the length of the beam results in:

$$N\cos \theta - V\sin \theta = \int_{0}^{x} {\rho A\frac{{\partial^{2} u}}{{\partial t^{2} }}{\text{d}}x} + C_{1}$$

(34)

where C₁ is the integration constant. There is no external axial force applied to the micro-cantilever at its free end (x = L). Applying this boundary condition to Eq. (34) yields:

$$C_{1} = - \int_{0}^{L} {\rho A\frac{{\partial^{2} u}}{{\partial t^{2} }}{\text{d}}x}$$

(35)

Therefore, by substituting Eq. (35) into Eq. (34), an expression for the axial force within the micro-cantilever is obtained as follows:

$$N = \frac{{\int_{L}^{x} {\rho A\frac{{\partial^{2} u}}{{\partial t^{2} }}{\text{d}}x} + V\sin \theta }}{\cos \theta }$$

(36)

According to Fig. 18b, the position of point P after deformation can be written as:

$$\tilde{x} = x + u$$

(37)

$$\tilde{z} = w$$

(38)

The variation of these positions can be expressed as:

$${\text{d}}\tilde{x} = {\text{d}}x + \frac{\partial u}{{\partial x}}{\text{d}}x$$

(39)

$${\text{d}}\tilde{z} = \frac{\partial w}{{\partial x}}{\text{d}}x$$

(40)

Therefore, the final length of the beam element after deformation can be obtained:

$${\text{d}}s = {\text{d}}x\sqrt {\left[ {1 + \left( {\frac{\partial u}{{\partial x}}} \right)^{2} } \right] + \left( {\frac{\partial w}{{\partial x}}} \right)^{2} }$$

(41)

Having the length of the element before and after deformation, the axial strain is obtained as follows:

$$\varepsilon = \frac{{{\text{d}}s - {\text{d}}x}}{{{\text{d}}x}} = \sqrt {\left[ {1 + \left( {\frac{\partial u}{{\partial x}}} \right)} \right]^{2} + \left( {\frac{\partial w}{{\partial x}}} \right)^{2} } - 1$$

(42)

A cantilever with no axial force applied to its free end is treated as an inextensional beam, which means the axial strain is neglected [36]. Applying the inextensionality condition to Eq. (42) results in:

$$\frac{\partial u}{{\partial x}} = \sqrt {1 - \left( {\frac{\partial w}{{\partial x}}} \right)^{2} } - 1$$

(43)

By integrating Eq. (43) over the length of the beam, the axial deflection is obtained in terms of the transverse deflection as:

$$u = \int_{0}^{x} {\left( {\sqrt {1 - \left( {\frac{\partial w}{{\partial x}}} \right)^{2} } - 1} \right){\text{d}}x}$$

(44)

By substituting Eq. (44) into Eq. (36), the expression for the axial force reduces to:

$$N = \frac{{\int_{L}^{x} {\rho A\frac{{\partial^{2} }}{{\partial t^{2} }}\left[ {\int_{0}^{x} {\left( {\sqrt {1 - \left( {\frac{\partial w}{{\partial x}}} \right)^{2} } - 1} \right){\text{d}}x} } \right]{\text{d}}x} + V\sin \theta }}{\cos \theta }$$

(45)

By using Eq. (45), the axial displacement can be omitted from Eq. (33) as follows:

$$\frac{\partial }{\partial x}\left( {\tan \theta \int_{L}^{x} {\rho A\frac{{\partial^{2} }}{{\partial t^{2} }}\left[ {\int_{0}^{x} {\left( {\sqrt {1 - \left( {\frac{\partial w}{{\partial x}}} \right)^{2} } - 1} \right){\text{d}}x} } \right]{\text{d}}x} + \frac{V}{\cos \theta }} \right) = F_{{\text{E}}} + \rho A\frac{{\partial^{2} w}}{{\partial t^{2} }}$$

(46)

The following geometric relations can be written based on Fig. 18(b):

$$\sin \theta = \frac{{{\text{d}}\tilde{z}}}{{{\text{d}}s}}$$

(47)

$$\cos \theta = \frac{{{\text{d}}\tilde{x}}}{{{\text{d}}s}}$$

(48)

Due to the inextensionality condition, the length of the beam element remains unchanged before and after the deformation. Therefore, by making use Eqs. (39) and (40) along with Eq. (43), the expressions in Eqs. (47) and (48) take the following form:

$$\sin \theta = \frac{{{\text{d}}\tilde{z}}}{{{\text{d}}x}} = \frac{\partial w}{{\partial x}}$$

(49)

$$\cos \theta = \frac{{{\text{d}}\tilde{x}}}{{{\text{d}}x}} = 1 + \left( {\frac{\partial u}{{\partial x}}} \right)^{2} = \sqrt {1 - \left( {\frac{\partial w}{{\partial x}}} \right)^{2} }$$

(50)

Therefore:

$$\tan \theta = \frac{{{\raise0.7ex\hbox{${\partial w}$} \!\mathord{\left/ {\vphantom {{\partial w} {\partial x}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\partial x}$}}}}{{\sqrt {1 - \left( {{\raise0.7ex\hbox{${\partial w}$} \!\mathord{\left/ {\vphantom {{\partial w} {\partial x}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\partial x}$}}} \right)^{2} } }}$$

(51)

The bending moment at the cross section of the beam can expressed in terms of axial stress, σ, as follows:

$$M = \int\limits_{A} {\sigma z{\text{d}}A}$$

(52)

Considering the inextensionality condition, the strain in the direction can be obtained as [36]:

$$\varepsilon_{x} = z\frac{\partial \theta }{{\partial x}}$$

(53)

Therefore, by having the axial strain, the axial stress is obtained using the Hooke’s law for linear isotropic elastic materials as [36]:

$$\sigma_{x} = E\varepsilon_{x} = Ez\frac{\partial \theta }{{\partial x}}$$

(54)

Substituting Eq. (54) into Eq. (52), the expression for bending moment takes the following form:

$$M = EI\frac{\partial \theta }{{\partial x}}$$

(55)

where I is the moment of inertia of the micro-cantilever cross section with respect to x axis:

$$I = \int\limits_{A} {z^{2} {\text{d}}A}$$

(56)

Therefore, the following expression is obtained for shear force by inserting Eq. (55) into Eq. (28):

$$V = - EI\frac{{\partial^{2} \theta }}{{\partial x^{2} }} + J\frac{{\partial^{3} \theta }}{{\partial x\partial t^{2} }}$$

(57)

Substituting Eq. (51) along with Eq. (57) into Eq. (46), the governing equation of the motion in terms of transverse deflection and rotation angle is obtained as:

$$\begin{aligned} & \frac{\partial }{\partial x}\left( {\frac{{{\raise0.7ex\hbox{${\partial w}$} \!\mathord{\left/ {\vphantom {{\partial w} {\partial x}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\partial x}$}}}}{{\sqrt {1 - \left( {{\raise0.7ex\hbox{${\partial w}$} \!\mathord{\left/ {\vphantom {{\partial w} {\partial x}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\partial x}$}}} \right)^{2} } }}\int_{L}^{x} {\rho A\frac{{\partial^{2} }}{{\partial t^{2} }}\left[ {\int_{0}^{x} {\left( {\sqrt {1 - \left( {\frac{\partial w}{{\partial x}}} \right)^{2} } - 1} \right){\text{d}}x} } \right]{\text{d}}x} } \right) \\ & \quad + \frac{\partial }{\partial x}\left( {\frac{{ - EI\frac{{\partial^{2} \theta }}{{\partial x^{2} }} + J\frac{{\partial^{3} \theta }}{{\partial x\partial t^{2} }}}}{\cos \theta }} \right) = F_{{\text{E}}} + \rho A\frac{{\partial^{2} w}}{{\partial t^{2} }} \\ \end{aligned}$$

(58)

By relating the rotation angle and the transverse deflection, the motion equation in Eq. (58) can be expressed only in terms of the transverse deflection. From Eq. (49), one can obtain:

$$\theta = \sin^{ - 1} \left( {\frac{\partial w}{{\partial x}}} \right)$$

(59)

Therefore:

$$\begin{aligned} \frac{{\partial^{4} \theta }}{{\partial x^{2} \partial t^{2} }} & = \frac{{{\raise0.7ex\hbox{${\partial^{4} w}$} \!\mathord{\left/ {\vphantom {{\partial^{4} w} {\partial x^{2} \partial t^{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\partial x^{2} \partial t^{2} }$}}}}{{\sqrt {1 - \left( {{\raise0.7ex\hbox{${\partial w}$} \!\mathord{\left/ {\vphantom {{\partial w} {\partial x}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\partial x}$}}} \right)^{2} } }} + \frac{{\left( {{\raise0.7ex\hbox{${\partial^{3} w}$} \!\mathord{\left/ {\vphantom {{\partial^{3} w} {\partial x\partial t^{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\partial x\partial t^{2} }$}}} \right)\left( {{\raise0.7ex\hbox{${\partial w}$} \!\mathord{\left/ {\vphantom {{\partial w} {\partial x}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\partial x}$}}} \right)\left( {{\raise0.7ex\hbox{${\partial^{2} w}$} \!\mathord{\left/ {\vphantom {{\partial^{2} w} {\partial x^{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\partial x^{2} }$}}} \right)}}{{\left[ {1 - \left( {{\raise0.7ex\hbox{${\partial w}$} \!\mathord{\left/ {\vphantom {{\partial w} {\partial x}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\partial x}$}}} \right)^{2} } \right]^{{{\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} }} \\ & \quad + \frac{{2\left( {{\raise0.7ex\hbox{${\partial^{3} w}$} \!\mathord{\left/ {\vphantom {{\partial^{3} w} {\partial x^{2} \partial t}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\partial x^{2} \partial t}$}}} \right)\left( {{\raise0.7ex\hbox{${\partial w}$} \!\mathord{\left/ {\vphantom {{\partial w} {\partial x}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\partial x}$}}} \right)\left( {{\raise0.7ex\hbox{${\partial^{2} w}$} \!\mathord{\left/ {\vphantom {{\partial^{2} w} {\partial x\partial t}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\partial x\partial t}$}}} \right)}}{{\left[ {1 - \left( {{\raise0.7ex\hbox{${\partial w}$} \!\mathord{\left/ {\vphantom {{\partial w} {\partial x}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\partial x}$}}} \right)^{2} } \right]^{{{\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} }} + \frac{{3\left( {{\raise0.7ex\hbox{${\partial^{2} w}$} \!\mathord{\left/ {\vphantom {{\partial^{2} w} {\partial x^{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\partial x^{2} }$}}} \right)\left( {{\raise0.7ex\hbox{${\partial w}$} \!\mathord{\left/ {\vphantom {{\partial w} {\partial x}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\partial x}$}}} \right)^{2} \left( {{\raise0.7ex\hbox{${\partial^{2} w}$} \!\mathord{\left/ {\vphantom {{\partial^{2} w} {\partial x\partial t}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\partial x\partial t}$}}} \right)^{2} }}{{\left[ {1 - \left( {{\raise0.7ex\hbox{${\partial w}$} \!\mathord{\left/ {\vphantom {{\partial w} {\partial x}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\partial x}$}}} \right)^{2} } \right]^{{{\raise0.7ex\hbox{$5$} \!\mathord{\left/ {\vphantom {5 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} }} \\ & \quad + \frac{{\left( {{\raise0.7ex\hbox{${\partial^{2} w}$} \!\mathord{\left/ {\vphantom {{\partial^{2} w} {\partial x^{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\partial x^{2} }$}}} \right)\left( {{\raise0.7ex\hbox{${\partial^{2} w}$} \!\mathord{\left/ {\vphantom {{\partial^{2} w} {\partial x\partial t}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\partial x\partial t}$}}} \right)^{2} }}{{\left[ {1 - \left( {{\raise0.7ex\hbox{${\partial w}$} \!\mathord{\left/ {\vphantom {{\partial w} {\partial x}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\partial x}$}}} \right)^{2} } \right]^{{{\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} }} \\ \end{aligned}$$

(60)

The following parameters are considered for simplicity:

$$a = \frac{\partial w}{{\partial x}}, \, b = \frac{{\partial^{4} w}}{{\partial x^{2} \partial t^{2} }}, \, c = \frac{{\partial^{3} w}}{{\partial x\partial t^{2} }}, \, d = \frac{{\partial^{2} w}}{{\partial x^{2} }}, \, e = \frac{{\partial^{2} w}}{\partial x\partial t}, \, f = \frac{{\partial^{3} w}}{{\partial x^{2} \partial t}}$$

(61)

Therefore, Eq. (60) can be written as:

$$\frac{{\partial^{4} \theta }}{{\partial x^{2} \partial t^{2} }} = \frac{b}{{\sqrt {1 - a^{2} } }} + \frac{acd}{{\left( {1 - a^{2} } \right)^{{{\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} }} + \frac{2aef}{{\left( {1 - a^{2} } \right)^{{{\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} }} + \frac{{3a^{2} de^{2} }}{{\left( {1 - a^{2} } \right)^{{{\raise0.7ex\hbox{$5$} \!\mathord{\left/ {\vphantom {5 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} }} + \frac{{de^{2} }}{{\left( {1 - a^{2} } \right)^{{{\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} }}$$

(62)

Using the following expansion series:

$$\left( {1 + x} \right)^{r} = 1 - rx + \frac{{r\left( {r - 1} \right)}}{2!}x^{2} + \cdots$$

(63)

and considering only the first two terms, Eq. (62) is approximated as follows:

$$\frac{{\partial^{4} \theta }}{{\partial x^{2} \partial t^{2} }} \approx b\left( {1 + \frac{{a^{2} }}{2}} \right) + acd\left( {1 + \frac{{3a^{2} }}{2}} \right) + 2aef\left( {1 + \frac{{3a^{2} }}{2}} \right) + 3a^{2} de^{2} \left( {1 + \frac{{5a^{2} }}{2}} \right) + de^{2} \left( {1 + \frac{{3a^{2} }}{2}} \right)$$

(64)

Since the rotary inertia is small, the nonlinear terms can be neglected in Eq. (64). Therefore:

$$\frac{{\partial^{4} \theta }}{{\partial x^{2} \partial t^{2} }} \approx \frac{{\partial^{4} w}}{{\partial x^{2} \partial t^{2} }}$$

(65)

On the other hand, from Eq. (59):

$$\frac{{\partial^{2} \theta }}{{\partial x^{2} }} = \frac{{{\raise0.7ex\hbox{${\partial^{3} w}$} \!\mathord{\left/ {\vphantom {{\partial^{3} w} {\partial x^{3} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\partial x^{3} }$}}}}{{\sqrt {1 - \left( {{\raise0.7ex\hbox{${\partial w}$} \!\mathord{\left/ {\vphantom {{\partial w} {\partial x}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\partial x}$}}} \right)^{2} } }} + \frac{{\left( {{\raise0.7ex\hbox{${\partial^{2} w}$} \!\mathord{\left/ {\vphantom {{\partial^{2} w} {\partial x^{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\partial x^{2} }$}}} \right)^{2} \left( {{\raise0.7ex\hbox{${\partial w}$} \!\mathord{\left/ {\vphantom {{\partial w} {\partial x}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\partial x}$}}} \right)}}{{\left[ {1 - \left( {{\raise0.7ex\hbox{${\partial w}$} \!\mathord{\left/ {\vphantom {{\partial w} {\partial x}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\partial x}$}}} \right)^{2} } \right]^{{{\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} }}$$

(66)

For simplicity, the following parameters are introduced:

$$a = \frac{\partial w}{{\partial x}}, \, b = \frac{{\partial^{2} w}}{{\partial x^{2} }}, \, c = \frac{{\partial^{3} w}}{{\partial x^{3} }}$$

(67)

Therefore, Eq. (66) takes the following form:

$$\frac{1}{\cos \theta }\frac{{\partial^{2} \theta }}{{\partial x^{2} }} = \frac{c}{{1 - a^{2} }} + \frac{{ab^{2} }}{{\left( {1 - a^{2} } \right)^{2} }} = \frac{{c - a^{2} c + ab^{2} }}{{\left( {1 - a^{2} } \right)^{2} }}$$

(68)

Using the expansion series given in Eq. (63) within Eq. (68) and keeping the nonlinear terms up to the third-order yield:

$$\frac{1}{\cos \theta }\frac{{\partial^{2} \theta }}{{\partial x^{2} }} \approx \frac{{\partial^{3} w}}{{\partial x^{3} }} + \left( {\frac{\partial w}{{\partial x}}} \right)^{2} \frac{{\partial^{3} w}}{{\partial x^{3} }} + \frac{\partial w}{{\partial x}}\left( {\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right)^{2}$$

(69)

Additionally, the following terms can be approximated using the same expansion series:

$$\frac{{{\raise0.7ex\hbox{${\partial w}$} \!\mathord{\left/ {\vphantom {{\partial w} {\partial x}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\partial x}$}}}}{{\sqrt {1 - \left( {{\raise0.7ex\hbox{${\partial w}$} \!\mathord{\left/ {\vphantom {{\partial w} {\partial x}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\partial x}$}}} \right)^{2} } }} = \frac{\partial w}{{\partial x}}\left[ {1 + \frac{1}{2}\left( {\frac{\partial w}{{\partial x}}} \right)^{2} + \cdots } \right] \approx \frac{\partial w}{{\partial x}}$$

(70)

$$\sqrt {1 - \left( {\frac{\partial w}{{\partial x}}} \right)^{2} } = 1 - \frac{1}{2}\left( {\frac{\partial w}{{\partial x}}} \right)^{2} + \cdots \approx 1 - \frac{1}{2}\left( {\frac{\partial w}{{\partial x}}} \right)^{2}$$

(71)

Finally, by substituting Eqs. (65), (69), (70), and (71) into Eq. (58), the nonlinear equation of motion for the micro-cantilever is obtained only in terms of the transverse deflection as:

$$\begin{aligned} & \rho A\frac{{\partial^{2} w}}{{\partial t^{2} }} + EI\frac{{\partial^{4} w}}{{\partial x^{4} }} + EI\left( {\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right)^{3} + 4EI\frac{\partial w}{{\partial x}}\frac{{\partial^{2} w}}{{\partial x^{2} }}\frac{{\partial^{3} w}}{{\partial x^{3} }} + EI\frac{{\partial^{4} w}}{{\partial x^{4} }}\left( {\frac{\partial w}{{\partial x}}} \right)^{2} - J\frac{{\partial^{4} \theta }}{{\partial x^{2} \partial t^{2} }} \\ & \quad + \frac{\partial }{\partial x}\left\{ {\frac{\partial w}{{\partial x}}\int_{x}^{L} {\rho A\int_{0}^{x} {\left[ {\left( {\frac{{\partial^{2} w}}{\partial x\partial t}} \right)^{2} + \frac{\partial w}{{\partial x}}\frac{{\partial^{3} w}}{{\partial x\partial t^{2} }}} \right]{\text{d}}x} {\text{d}}x} } \right\} = F_{{\text{E}}} \\ \end{aligned}$$

(72)

For a micro-cantilever subjected to base excitation, the total deflection can be written as:

$$w\left( {x,t} \right) = \hat{w}\left( {x,t} \right) + w_{{\text{b}}} \left( t \right)$$

(73)

where $\hat{w}\left( {x,t} \right)$ is the transverse deflection of the beam with respect to its base, and w_b(t) is the base excitation. Substituting the expression in Eq. (73) (72) into Eq. (72), rearranging the terms yields, and removing the hat notation for brevity, we obtain:

$$\begin{aligned} & \rho A\frac{{\partial^{2} w}}{{\partial t^{2} }} + EI\frac{\partial }{\partial x}\left[ {\frac{{\partial^{3} w}}{{\partial x^{3} }} + \frac{\partial w}{{\partial x}}\left( {\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right)^{2} + \frac{{\partial^{3} w}}{{\partial x^{3} }}\left( {\frac{\partial w}{{\partial x}}} \right)^{2} } \right] - J\frac{{\partial^{4} w}}{{\partial x^{2} \partial t^{2} }} \\ & \quad - \frac{1}{2}\frac{\partial }{\partial x}\left\{ {\frac{\partial w}{{\partial x}}\int_{L}^{x} {\rho A\frac{{\partial^{2} }}{{\partial t^{2} }}\left[ {\int_{0}^{x} {\left( {\frac{\partial w}{{\partial x}}} \right)^{2} {\text{d}}x} } \right]{\text{d}}x} } \right\} = F_{E} - \rho A\frac{{\partial^{2} w_{{\text{b}}} }}{{\partial t^{2} }} \\ \end{aligned}$$

(74)