Characterizing water-on-deck propagation with a nonlinear advection-diffusion equation

Abstract

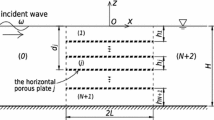
Shipping water events (SWE) occur when incident waves flood and propagate over the deck of maritime structures, usually during extreme wave climate. SWE can cause structural damage, unexpected overloading, human losses or even spills of products that are harmful to the environment. Therefore, the estimation of variables that help to predict the evolution of these events is highly helpful to lessen catastrophic consequences. In this regard, this work proposes a model-based approach to describe the spatiotemporal evolution of SWE on a fixed structure with a horizontal propagation domain. The approach is based on a model expressed as an advection-difussion equation with space-dependent nonlinear coefficients. To explore the suitability of the model, for characterizing the SWE evolution, its numerical response is compared with elevation data of SWE generated in a channel by incident regular wave trains. For the comparison, the model coefficients were estimated from an experimental data set with the use of an adaptive observer. The results of the comparison show that the response of the model allows to represent the physics of the analyzed SWE in an acceptable way. The advantage of using an adaptive observer for the estimation is that it can be used in further applications where the actual values of varying coefficients could be required in a reasonable computational time.

A Appendix A: Stability and robustness analysis of the used adaptive observer

1.1 A.1 Stability and convergence analysis

Following the same steps as provided in [31], in first place take the system (10):

$$\begin{aligned} \begin{array}{rcl} \dot{{\hat{\eta }}}&{}=&{}L{\hat{\eta }}+\phi (\eta ){{\hat{\theta }}}+(K+\varvec{\Upsilon }\Gamma \varvec{\Upsilon }^T\Sigma )(\eta -{{\hat{\eta }}}) \\ {{\dot{\varvec{\Upsilon }}}}&{}=&{}(L-K)\varvec{\Upsilon }+\phi (\eta )\\ \dot{{{\hat{\theta }}}}&{}=&{}\Gamma \varvec{\Upsilon }^T\Sigma (\eta -{{\hat{\eta }}}), \end{array} \end{aligned}$$

(13)

Define the observation and parametric errors ${{\tilde{\eta }}}={{\hat{\eta }}}-\eta$, ${{\tilde{\theta }}}={{\hat{\theta }}}-\theta$. Assuming that the actual parameters $\theta$ are constant, then:

$$\begin{aligned} \dot{{\tilde{\eta }}}=(L-K){{\tilde{\eta }}}+\phi {\tilde{\theta }}+\varvec{\Upsilon }\dot{{{\tilde{\theta }}}} \end{aligned}$$

(14)

Taking $\chi ={{\tilde{\eta }}}-\varvec{\Upsilon }{{\tilde{\theta }}}$, its derivative is

$$\begin{aligned} {{\dot{\chi }}}=(L-K)\chi +((L-K)\varvec{\Upsilon }+\phi -{{\dot{\varvec{\Upsilon }}}}){{\tilde{\theta }}} \end{aligned}$$

(15)

From (10), it is obtained that ${{\dot{\chi }}}=(L-K)\chi$. Therefore, if in the design $\Re \{\lambda \{(L-K)\}\}<0$, then $\lim _{t\rightarrow \infty }\chi =0\Rightarrow \lim _{t\rightarrow \infty }{\tilde{\eta }}=\varvec{\Upsilon }{{\tilde{\theta }}}$.

The dynamics of $\varvec{\Upsilon }$ indicate that, if $\phi$ is bounded, then $\varvec{\Upsilon }$ is bounded. Then, from the adaptation law for ${{\hat{\theta }}}$, we obtain:

$$\begin{aligned} \dot{{{\tilde{\theta }}}}= & {} \Gamma \varvec{\Upsilon }^T\Sigma (\eta -{{\hat{\eta }}})\\ \nonumber= & {} -\Gamma \varvec{\Upsilon }^T\Sigma \varvec{\Upsilon }{{\tilde{\theta }}}-\Gamma \varvec{\Upsilon }^T\Sigma \chi \end{aligned}$$

(16)

Therefore, if $\varvec{\Upsilon }$ is bounded, then $\Gamma \varvec{\Upsilon }^T\Sigma \varvec{\Upsilon }$ is bounded. If the persistent excitation condition

$$\begin{aligned} \int _t^{t+T}\varvec{\Upsilon }^T(\tau )\Sigma \varvec{\Upsilon }(\tau )d\tau >\delta I \end{aligned}$$

is fulfilled, then ${{\tilde{\theta }}}=0$ is exponentially stable. Given the previous reasons, then $\chi$ converges to zero, leading exponentially ${{\tilde{\eta }}}$ to zero as well.

1.2 A.2 Robustness analysis of the observer

Following the same procedure as in [31], now consider that the system to be identified is subject to bounded additive uncertainties in the state equation $\xi =\xi (t)$, in the parameters dynamics $\delta _t\theta =\delta _t\theta (t)$ and measurement noise $\nu =\nu (t)$:

$$\begin{aligned} {{\dot{\eta }}}= & {} \phi _A(\eta )\theta _A+\phi _B(\eta )\theta _B+\xi ,\end{aligned}$$

(17)

$$\begin{aligned} {{\dot{\theta }}}= & {} \delta _t\theta \end{aligned}$$

(18)

$$\begin{aligned} \eta _m= \eta +\nu , \end{aligned}$$

(19)

where $\eta _m$ is the measured state. Defining once again $\chi ={{\tilde{\eta }}}-\varvec{\Upsilon }{{\tilde{\theta }}}$, the error dynamics of the state observation and parameter adaptation are

$$\begin{aligned} {{\dot{\chi }}} = & (L-K)\chi +K\nu +\varvec{\Upsilon }\delta _t\theta -\xi ,\nonumber \\ \dot{{{\tilde{\theta }}}}= & {} -\Gamma \varvec{\Upsilon }^T\Sigma \varvec{\Upsilon }{{\tilde{\theta }}}-\Gamma \varvec{\Upsilon }^T\Sigma \chi -\Gamma \varvec{\Upsilon }^T\Sigma \xi +\Gamma \varvec{\Upsilon }^T\Sigma \nu -\delta _t\theta . \end{aligned}$$

It is clear that $\chi$ remains bounded if $\xi$, $\delta _t\theta$ and $\nu$ remain bounded, and therefore ${{\tilde{\theta }}}$ remains bounded. If those are independent on $\phi$ and with zero mean, that is ${\mathcal {E}}\{\xi \}=0$, ${\mathcal {E}}\{\delta _t\theta \}=0$, ${\mathcal {E}}\{\nu \}=0$, where ${\mathcal {E}}$ is the mathematical expectation operator, then as previously shown, $\lim _{t\rightarrow \infty }{\mathcal {E}}\{\chi \}=0$ and $\lim _{t\rightarrow \infty }{\mathcal {E}}\{{{\tilde{\theta }}}\}=0$. Therefore, $\lim _{t\rightarrow \infty }{\mathcal {E}}\{{{\tilde{\eta }}}\}=0$ exponentially.