1 Introduction

Offshore floating wind turbines (OFWTs) are becoming one of the most interesting options in the renewable energy landscape. In fact, on the one hand, they enable a considerable increase in the world wind power potential, and on the other hand, offshore installations are often characterized by higher capacity factors than fixed ones (IEA 2019; Ramirez et al. 2020; RSE 2020). Beyond sea depths of 50 m, the investment in bottom-fixed structures (piling foundation) becomes inconvenient, and this justifies a progressive transition to the use of floating platforms (IRENA 2016; Matthew Hannon et al. 2019; Equinor 2020). As today the concept of visual pollution is very important, combined with the high wind resource availability in open sea, the study of the productivity of OFWT becomes very interesting. However, OFWTs also face various technological challenges (Jiang et al. 2013; Kaldellis and Zafirakis 2011; Butterfield et al. 2007), linked in particular to the construction of economic platforms that guarantee stability to the wind turbine (WT) (Ghigo et al. 2020; Moné et al. 2017; Akay et al. 2013a; Jiang et al. 2015) and moorings that can effectively limit the platform motion.

An OFWT consists of a wind turbine mounted on a floating platform; the moorings have the task of keeping the OFWT, subjected to the action of waves and wind, as still as possible. Waves and wind set the system in motion. To predict its aerodynamic behavior, researchers have developed several analysis tools to simulate the interaction between the wind profile and the wind turbine and study its effects on the overall system. Existing models are based on different theories, among which the most commonly used is the Blade Element Momentum (BEM) theory with its corrections (Ning et al. 2015). There are several models based on this theory, including OrcaFlex (Orcina 2020), developed by orcina, and FAST (Jonkman and Jonkman 2016; NREL 2020), developed by NREL; the latter was also successfully validated with experimental data (Driscoll et al. 2016). Another very common theory is the Free Vortex Method (FVM), also used by many mathematical models including QBlade (Qblade 2020; Marten and Wendler 2013a, b), developed by Technical University of Berlin, and WInDS (Sebastian and Lackner 2011, 2012a, b; Akay et al. 2013b), developed by Sebastian and Lackner. Nevertheless, the most accurate method to simulate full physical flow behaviors of a complex flow field around a wind turbine blade is to use a CFD model, as the one described in Benjanirat (2006).

Fig. 1
figure 1

OFWT fixed reference axis Oxyz

Full size image

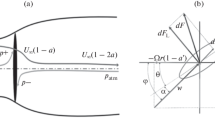
The main motions of the system, depicted in Fig. 1, are a translation along the x-axis (surge motion) and a rotation around the y-axis (pitch motion). The former is a simple translation until an offset is reached, but its influence on the extracted power is limited (Wen et al. 2017; Tran and Kim 2016; Yasar et al. 2011; Micallef and Sant 2015). The latter is the most important DoF, as its movement strongly affects productivity (Wen et al. 2018; Tran and Kim 2015; Barakos and Leble 2017; Lei et al. 2017).

Previous pitch motion studies on the NREL 5-MW were done by Wen et al. (Wen et al. 2018) (who used the FVM), Tran and Kim (Tran and Kim 2015) (who compared different BEM theories and CFD), while Leble and Barakos (Barakos and Leble 2017) have studied a 10 MW DTU wind turbine and Zhou et al. (Lei et al. 2017) have studied a vertical axis wind turbine. All of them suggest a general slight average power increase for offshore floating wind turbines with respect to fixed ones.

However, other studies (van der Veen et al. 2012; Fleming et al. 2019; Abbas and Wright 2022) focalized on how to mitigate the platform pitching and the related structural loads, considering pitch motion as a undesired phenomenon. For this reason, it is interesting to evaluate the contribution of pitching motion on the extracted power, since previous studies were limited to the variability of aerodynamic power. The novelty of this study is the introduction of the transition from aerodynamic power to electric power through a control logic to analyze the effect of pitching motion on the real generated power. Considering the generator power, it is indeed necessary following a control law which can even cause relevant differences between the aerodynamic and electric power. To the extent of our knowledge, there are no articles that study clearly how much the movements of an OFWT can affect its real productivity compared to a traditional onshore or bottom-fixed case.

In this article, an in-house model (Caradonna et al. 2021) developed in Matlab/Simulink (Mathworks 2020a, b) is used. The model, available online as a beta-release called MOST (MOREnergyLab 2022), is based on the BEM theory and has been compared with FAST obtaining satisfactory results, with an average RMSE on position and output power lower than 2% (Caradonna et al. 2021). The choice to use MOST instead of FAST is given by a greater flexibility of the former, which allows the user to set a forced pitch movement. As reported in Tran and Kim (2015), for small pitching motion amplitudes, the BEM theory shows a good agreement with respect to the most accurate but highly computing demanding CFD theory. Our model can be considered a wind-to-power model including all the components of an OFWT (floating platform and hydrodynamics, wind turbine and aerodynamics, electric generator). Thus, a model of the electric generator and its control law is included. Furthermore, the control law involves some feedbacks, which also impact on the aerodynamic power. The study hereby aims to identify the differences between fixed and floating offshore installations and to obtain reliable results for the power variation related to OFWT oscillations. From the resulting observations, cause–effect relationships could be identified to support the phase of design of OFWT, trying to limit harmful effects.

The paper is organized as follows. Section 2 analyses the mathematical model used in this work: in Sect. 2.1, the aerodynamic model (BEM theory) and the control model are presented; in Sect. 2.2, the imposed pitch motions and their presumed influence on power are exposed. Section 3 describes and analyzes the average generated power trend obtained from the different tests carried out, for various combinations of winds and pitch oscillations. Finally, Sect. 4 sets out conclusions and future work.

2 Methodology

In this work, the OFWT mathematical model presented in Caradonna et al. (2021) is used. For the application hereby presented, a regular sinusoidal motion has been imposed on the pitch of the entire structure, with the remaining 5 DoFs fixed at 0. Therefore, the only model block involved in the simulation is that of the wind turbine, which oscillates according to the imposed motion. The theoretical NREL offshore 5-MW baseline wind turbine (Jonkman et al. 2009) is used, in which tower, nacelle and blades are modeled as rigid bodies.

The turbine model is composed of the aerodynamic model and control model that interacting with each other.

The steady Blade Element Momentum (BEM), developed by Glauert (H. 1935) in 1935, is used for calculating the loads acting on the wind turbine rotor for any set of wind speed, rotor speed, pitch angle and turbine orientation (Manwell et al. 2009; Eliassen 2015; Rommel et al. 2020).

Once the rotor torque has been calculated, the torque on the generator, on which the control is applied, is obtained through the generator gearbox ratio. The control logic has the purpose of optimizing the power extraction in situations of low wind, while limiting the loads in correspondence of strong wind, through the control on the blade pitch; in these conditions, the rated power is delivered.

The BEM theory and the control logic on the generator are presented in Sect. 2.1. Then, some theoretical considerations on the expected results, the motion imposed on the pitch and the wind speeds used in the numerical tests are introduced in Sect. 2.2.

2.1 Numerical model

The mathematical model used is the one of the wind turbine, since the pitch movements of the platform are imposed externally. The model is made of two set of equations: in the former the aerodynamic loads are calculated, while in the latter the generator controls are applied.

2.1.1 Aerodynamic model

The Blade element momentum theory (BEM) is the union of momentum theory and blade element model theory, that are then combined in a iteration algorithm.

The first theory is the moment balance on the rotor disk (momentum theory) that is considered frictionless while the flow is considered stationary. The rotor disk removes kinematic energy from the wind, making the streamlines diverge. The second theory (blade element model theory), consist of dividing the blades in 2D small element (airfoil) defined by nodes position along the blades, to evaluate the interaction between the fluid and the blades independently for each section.

The BEM theory is widely used to calculate the wind velocity and then the loads acting on the blades. To overcome the limitations of this approach, three important corrections are made Ning et al. (2015):

  • Prandtl’s tip-loss, to consider that the airflow is not parallel to the blade profile near the tip of the blades.

  • Glauert correction which is an empirical correlation between the thrust and the axial induction factor.

  • Skewed wake, to consider that the deflection of the wind direction respect the rotor disk affects the induction factor.

2.1.2 Control model

The control logic of the NREL 5-MW wind turbine is composed of two independent control systems:

  • A generator-torque controller, which links the torque and the speed of the generator, is designed to maximize the power extraction below the nominal point and to limit it beyond it.

  • A full-span rotor-collective blade-pitch controller, is designed to regulate the generator speed above the nominal point.

The nominal or rated point is defined as the reference operation point for the maximum continuous power conversion, towards which the control system tends. It is summarized in Table 1.

Table 1 Rated operation point for the wind turbine
Full size table

The generator-torque control law is divided in three main regions and two transition regions in-between. Before analyzing the control law, it is important to note that, while the torque originated by wind acts as an accelerating load, the generator torque, converting mechanical energy to electrical energy, acts as a braking load: the difference between the two torques generates an acceleration/deceleration of the rotor speed.

The control law is described in the next lines and represented in Fig. 2: the generator torque is presented as a tabulated function of the filtered generator speed, incorporating five control regions: 1, 1\(^1_2\), 2, 2\(^1_2\), and 3.

Fig. 2
figure 2

Control law on generator torque

Full size image

Region 1 is a control region before cut-in wind speed, where the generator is detached from the rotor so as to allow the wind to accelerate the rotor for start-up. In this region, the generator torque is zero and no power is extracted from the wind.

Region 1\( \frac{1}{2} \) is the start-up region, a linear transition between Region 1 and Region 2. This region is used to place a lower limit on the generator speed to limit the wind turbine operational speed range and is defined in the region of generator speed between 670 rpm and 30% above this value (or 871 rpm).

Region 2 is a control region for optimizing power capture. Here, to maintain the tip speed ratio constant at its optimal value, the generator torque is proportional to the square of the filtered generator speed \( T_\mathrm{gen} = k_\mathrm{opt} \, \Omega _\mathrm{gen}^2 \).

Region 2\( \frac{1}{2} \) is a linear transition between Region 2 and Region 3 with a torque slope corresponding to the slope of an induction machine (10% in our case). This region is typically needed to limit tip speed (and hence noise emissions) at rated power. The boundaries of this region are the optimum power extraction curve of Region 2 and the constant curve power of Region 3, intersected at 99% of the rated generator speed, or 1162 rpm (Jonkman et al. 2009).

Region 3 is the constant power region, where the generator torque is inversely proportional to the filtered generator speed. Therefore, by increasing the generator speed beyond the rated value \(\Omega _\mathrm{gen,rated}\) = 1173 rpm, the torque will drop below the rated value \(T_\mathrm{gen,rated}\) = 43,093 Nm.

There is, however, a conditional statement (green curve in Fig. 2) on the generator-torque controller so that the torque would follow the constant curve power (as if it was in Region 3)—regardless of the generator speed—whenever the previous blade–pitch–angle command was 1 deg or greater (Jonkman et al. 2009). Since the blade–pitch–angle control intervenes when the generator speed is greater than the nominal value, bringing it back below this value, there is a transient in which the generator speed is already below the nominal value, while the blade–pitch–angle has not yet returned to zero. In this situation, the constant curve power is followed to optimize the extracted power. This results in improved output power quality (fewer dips below rated) and quantity (tests show a 5% increase of the extracted power) at the expense of short-term overloading of the generator and the gearbox: for this reason, the torque is saturated to a maximum of 10% above rated, or 47,403 Nm, to avoid this excessive overloading. Finally, a torque rate limit of 15,000 Nm/s has been imposed.

In Region 3, where the generator speed is above the rated value, the blade–pitch control system is active: the full-span rotor-collective blade–pitch–angle regulates the generator speed to maintain it at its rated value through a proportional-integral control (PI), using variable gains (Caradonna et al. 2021; Namik and Stol 2010).

The parameters used in the control logic are specified in Jonkman et al. (2009).

2.2 Pitch motion influence on power

Since the pitch is the degree of freedom that most affects the power produced by the turbine, a regular sinusoidal oscillation has been set at different amplitudes and frequencies, and with different offsets, to obtain the average power extracted and compare it with the results obtained with a fixed turbine, with the same wind speed. In this regard, a constant wind profile along the entire turbine profile was considered. Finally, the wind direction is along the x-axis of the turbine, so it is perpendicular to the pitch axis (turbine y-axis).

2.2.1 Pitch motion and wind profile: theoretical considerations

In the tests carried out, a steady wind profile was assumed: in this way, the wind speed \(V_\mathrm{wind}\) is homogeneous both spatially and temporally. This choice has been made to underline the effect of the pitch motion on the relative wind speed and so on the power, without any other more realistic factor (like the turbulence) that could complicate a first analysis of this phenomenon. The movement imposed on the pitch is a regular sinusoidal oscillation:

$$\begin{aligned} \theta = A\sin (\omega t) + \theta _0, \end{aligned}$$
(1)

where A is the pitch amplitude, \(\omega = 2\pi f\), with f being the pitch frequency, and \(\theta _0\) is the pitch offset.

The consequence of a pitch oscillation is a displacement of the nacelle, which is at a height H with respect to the SWL and has a speed in the wind direction:

$$\begin{aligned} V_\mathrm{nac} = H\omega A\cos (\omega t). \end{aligned}$$
(2)

The relative wind speed with respect to the nacelle \(V_0\) is, thus,

$$\begin{aligned} V_0 = V_\mathrm{wind} - V_\mathrm{nac} = V_\mathrm{wind} - H\omega A\cos (\omega t). \end{aligned}$$
(3)
Fig. 3
figure 3

\(V_\mathrm{wind}\) and \(V_\mathrm{nac}\) contribution on \(V_0\)

Full size image

The oscillation of the pitch, therefore, causes an oscillation \(V_\mathrm{nac}\) of the speed \(V_0\) around the offset \(V_\mathrm{wind}\) (Fig. 3). The oscillation is more severe the greater the pitch amplitude A or frequency f. As for the offset \(\theta _0\), it does not affect \(V_0\) but the angle of attack of the wind with respect to the blade. The equation that links the aerodynamic power to the wind speed relative to the nacelle is (Wen et al. 2018; Barakos and Leble 2017)

$$\begin{aligned}&P_\mathrm{aer} = \frac{1}{2}\rho \pi R^2 (V_\mathrm{wind} - H\omega A\cos (\omega t))^3\cdot \nonumber \\&\quad \quad \quad \cdot \bigg [1+\frac{3}{4}\bigg (\frac{A \omega R \cos (\omega t)}{V_\mathrm{wind} - H\omega A\cos (\omega t)}\bigg )^2\bigg ], \end{aligned}$$
(4)

in which R is the rotor radius. The previous equation highlights that the aerodynamic power is directly proportional to the cube of the relative wind speed \(V_0\):

$$\begin{aligned} P_\mathrm{aer} \propto V_0^3. \end{aligned}$$
(5)

In the fixed case, \(V_0\) = \(V_\mathrm{wind}\); while in the case of pitching, \(V_0\) oscillates around \(V_\mathrm{wind}\), which is thus the average value. However, the average of the aerodynamic power in the case of pitching will be higher than the fixed value, as the average of the cube of a cosine wave around an offset is greater than the average of the cube of the offset. The aerodynamic power expresses the potentially extractable power for a given value of \(V_0\). However, the real exploitable power depends on the size of the generator: the generated power saturates at the nominal value; furthermore, the controls modify the general performance of the power extracted with respect to aerodynamic power. An accurate analysis is, therefore, necessary to derive the turbine performance for various combinations of wind speed and pitch oscillations.

2.2.2 Pitch motion and wind profile: numerical experiments

This section presents the settings of the numerical experiments that were developed to derive the turbine performance with various combinations of wind speed and pitch oscillations (Table 2).

Table 2 Wind and pitch data for tests
Full size table
Fig. 4
figure 4

Block diagram of the four different powers analyzed: Aerodynamic power \(P_\mathrm{aer}\), open \(P_\mathrm{gen-open}\) and closed \(P_\mathrm{gen-closed}\) loop Generator power, fixed Generator power \(P_\mathrm{gen-fix}\)

Full size image

For the choice of wind speeds, the range between 3 m/s (cut-in value of the wind turbine) and 25 m/s (cut-off value of the wind turbine) was considered. It was decided to use a minimum speed of 5 m/s, given that for lower speeds the contribution of \(V_ {nac}\) is predominant compared to \(V_\mathrm{wind}\); in addition, it would be implausible to observe in real conditions great pitch fluctuations considered with such low wind speed. The maximum speed considered is 15 m/s, as above this value the extracted power is constant at the nominal value regardless of the imposed pitch oscillation. The discretization between the minimum and maximum values is with a 0.5 m/s step, with the exception of the neighborhood of the nominal value, where the grid is refined to 0.1 m/s (to have more data in an operational area where the performances of the wind turbine are particularly interesting).

As for the pitch, three parameters affect its oscillation:

  • Amplitude: it ranges from 0 (fixed case) to 2.5 deg which is considered a relatively high amplitude in reference to experimental evidence. The step chosen is 0.25 deg.

  • Frequency: it ranges from 0.05 to 0.2 Hz with a step of 0.025 Hz. It should be noted that the frequencies chosen fall in the range of typical sea states, which have peak spectral periods in the range of 5–20 s (Buhl and Jonkman 2007; Raach et al. 2014; Tran and Kim 2015) corresponding to frequencies in the chosen range.

  • Offset: generally the offset is positive. According to the offshore standards (DNV GL 2015), the following values have been considered: − 5, − 3, 0, 3, 5 deg.

3 Results and discussion

The correlation between the aerodynamic and generator power and the pitch oscillation of an OFWT was explored through the wind turbine model presented in Sect. 2.1 and the set of experimental tests described in Sect. 2.2.2. In the following paragraphs, some representative outcomes of the performed study are provided.

Figure 4 illustrates four different types of power which will be analyzed:

Fig. 5
figure 5

Different powers’ comparison (\(P_\mathrm{aer}\), \(P_\mathrm{gen-open}\), \(P_\mathrm{gen-closed}\) and \(P_\mathrm{gen-fix}\) ) at two different wind speeds ((a) \(V_\mathrm{wind}\) = 8 m/s and (b) \(V_\mathrm{wind}\) = 11 m/s) with Pitch A = 1.5 deg, f = 0.1 Hz and \(\theta _0\) = 0 deg

Full size image
Fig. 6
figure 6

Power increase/decrease vs. fixed case at different pitch amplitudes, with f = 0.05 Hz and \(\theta _0\) = 0 deg

Full size image

  • The aerodynamic power (AeroPower open, or \(P_\mathrm{aer}\)), given by multiplying the rotor speed (set constant) by the rotor torque obtained with that speed through the BEM Theory (set 9.16 rpm and 12 rpm, respectively, for wind speed of 8 m/s and 11 m/s: this is the correspondence between rotor speed and wind speed in steady-state conditions);

  • The open-loop generator power (GenPower open), or \(P_\mathrm{gen-open}\), is obtained by applying the generator control logic and imposing a constant rotor speed as input of the BEM Theory (set 9.16 rpm and 12 rpm, respectively, for wind speed of 8 m/s and 11 m/s), multiplying the rotor speed (set constant) by the generator torque obtained as output of the control logic;

  • The closed loop generator power (GenPower closed, or \(P_\mathrm{gen-closed}\)), which is obtained by including the feedback of rotor speed in the BEM Theory; it represents the real generator power, as the product between generator speed and generator torque, both outputs of the control logic.

  • The generator power in the fixed case (\(P_\mathrm{gen-fix}\)), which represents a zero pitch oscillation and is used as a reference case.

Figure 5 represents the comparison among the time evolution of these four significant powers at the two different wind speeds.

Fig. 7
figure 7

Curve power fixed vs. offshore with A = 2 deg, f = 0.1 Hz and \(\theta _0\) = 0 deg

Full size image

For both \(V_\mathrm{wind}= 8\) m/s (Fig. 5a) and \(V_\mathrm{wind}= 11\) m/s (Fig. 5b), the aerodynamic power has a higher average value than the extracted power in the fixed case. However, the introduction of the control logic and the consequent saturation of the power at the nominal value, combined with the feedback of rotor speed, modifies the results. In fact, the pitch oscillation produces an increase in average power for low wind speeds (Fig. 5a), while causes a decrease in average power for wind speeds near (Fig. 5b) or above the nominal value (\(V_\mathrm{nom}\) = 11.4 m/s), when generator power reaches saturation. Finally, the difference between generator power with open-loop and closed-loop is very small: this demonstrates that what especially affects the difference between aerodynamic power and generator power is the control logic used to extract the power. The time shift between aerodynamic power and generator power is due to the PI control on the blade pitch, which implies a delay in the feedback.

Since the closed loop generator power (GenPower closed) represents the real generator power, the results related to this type of power will be analyzed from here on.

Figure 6 represents the average power increase or decrease of the analyzed OFWT with respect to the fixed case as a function of wind speed for different pitch amplitudes. The presented case is the one with offset equal to 0 deg and frequency equal to 0.05 Hz. The chart shows that in Region 1\( \frac{1}{2} \) there is a high sensitivity of power to the wind speed variation, with higher average power increase at higher pitch amplitudes. Moving on to Region 2 there is an area in which the increase in power compared to the fixed case is almost constant as the wind speed varies. Passing through Region 2\( \frac{1}{2} \), on the other hand, there is a generalized decrease in the average power produced, up to the minimum reached in correspondence to the border with Region 3; troughs are more pronounced at higher pitch amplitudes. In Region 3, the power increases until it reaches the value of the fixed case.

The trend visible in Region 1\( \frac{1}{2} \) is motivated by observing that this is a torque control transition region used to reach the optimization curve: thus the extracted power is more sensitive to changes in rotor speed caused by changes in relative wind speed. The pitch oscillations cause a speed to the nacelle that adds to that of wind to form the relative speed \(V_0\) (Eq. 3). By decreasing the wind speed while maintaining the same pitch oscillation, the latter will have a greater contribution on \(V_0\). As Region 1\( \frac{1}{2} \) is very sensitive to the variation of \(V_0\), the same oscillation will have a greater beneficial effect at low wind speeds. By further increasing the speed we reach Region 2, where the optimal power is extracted for any wind speed: for this reason the variation of the power increase/decrease is minimal as the wind speed changes. Finally, observing the behavior in Region 2\( \frac{1}{2} \) and in Region 3 it can be seen that beyond a certain wind speed value, pitch oscillations have a negative effect in terms of average power output.

Overall, from the curves in Fig. 6, it can be concluded that by increasing the amplitude, beneficial effects are observed at low wind speeds (where the speed induced on the nacelle by the pitch oscillation gives a higher percentage contribution on \(V_0\)), while at wind speeds near or above the nominal value there is a decrease in the produced power.

The observed trend may be better understood by analyzing Fig. 7, where the curve power of an fixed case is compared with the curve power of a pitching case. From Region 1 to Region 2 the average power generated in the pitching case is higher than in the fixed case, however the difference gradually tapers off as wind speed increases. In Region 2\( \frac{1}{2} \) and in the first part of Region 3, the average power generated in the pitching case is lower than that generated in the fixed case. Finally, at high wind speeds, both curves are constant at the nominal power value. The large difference between the curves around the nominal value of the wind speed (\(V_\mathrm{nom}\) = 11.4 m/s) is due to the saturation value caused by the control on the generator.

In Region 2\( \frac{1}{2} \) and in the first part of Region 3, as \(V_0\) is oscillating due to the pitch oscillations (Eq. 3), there may be areas where \(V_0\) is higher than 11.4 m/s, resulting in power saturation, at 5 MW, and areas where \(V_0<\) 11.4 m/s. This may lead to an extracted power lower than the nominal value, resulting in a global average power lower than 5 MW. For example, Fig. 8 represents the time course of an fixed case compared with a pitching case with a wind speed \(V_\mathrm{wind}\) of 12 m/s (therefore, higher than 11.4 m/s, Region 3) which, in the fixed case, would bring an extracted power constant at 5 MW. In the pitching case, due to the oscillations of the pitch, there will be an oscillation of \(V_0\) around the value of \(V_\mathrm{wind}\), which will bring the power to have minimums (in correspondence of \(V_0\) minimums, lower than 11.4 m/s) which will lead to obtaining an average extracted power of less than 5 MW. This explains why in Region 3 there is a decrease in the extracted power the greater the higher the oscillation value.

Fig. 8
figure 8

Extracted power fixed vs. offshore pitching with wind speed \(V_\mathrm{wind}\) = 12 m/s and Relative wind speed on structure \(V_0\) vs. nominal value of \(V_0\). Pitch A = 2 deg, f = 0.1 Hz and \(\theta _0\) = 0 deg

Full size image

This effect actually starts to act already in the Region 2\( \frac{1}{2} \), causing the saturation of the power maximums (corresponding to the maximums of \(V_0\)). Combining the previous considerations with the fact that the Control Region 2\( \frac{1}{2} \) is very sensitive to changes in \(V_0\), it is easy to understand how in the graph in Fig. 6 there is the crossing of 0 in this region. By carrying out a test with wind speed \(V_\mathrm{wind}\) of 10.8 m/s (therefore, located in Region 2\( \frac{1}{2} \)), for A = 1.5 deg there is, according to the green curve in Fig. 6, an increase in power compared to the fixed case: in fact, at the value \(V_\mathrm{wind}\) = 10.8 m/s, the green curve has not yet crossed the abscissa axis.

The explanation of this can be found in Fig. 9: at this wind speed, with this oscillation, the saturation of the maximum power occurs for short lengths, therefore, the beneficial aspect of the pitch oscillation still prevails. All other parameters being equal, by slightly increasing the wind speed, the oscillation amplitude or frequency, the saturated power section will increase until the average power generated will be lower than the value obtained in the fixed case.

Fig. 9
figure 9

Extracted power fixed vs. offshore pitching with wind speed \(V_\mathrm{wind}\) = 10.8 m/s and relative wind speed on structure \(V_0\) vs. nominal value of \(V_0\). Pitch A = 2 deg, f = 0.1 Hz and \(\theta _0\) = 0 deg

Full size image

Figure 10 presents how the extracted power in pitching case varies with respect to the fixed case for different values of wind speed and pitching frequency.

Fig. 10
figure 10

Power increase/decrease vs. fixed case at different pitch frequencies, with A = 1.5 deg and \(\theta _0\) = 0 deg

Full size image
Fig. 11
figure 11

Power increase/decrease vs. fixed case at different Pitch offsets, with A = 1.5 deg and f = 0.05 Hz

Full size image

The trend presented is similar to that shown in Fig. 6: for low wind speeds (Region 1\( \frac{1}{2} \)) the power extracted is very sensitive to the wind speed variation itself. In Region 2, the extracted power slightly varies as the wind speed varies. Finally, passing through Region 2\( \frac{1}{2} \), there is a decrease in the average power produced, up to the minimum reached in correspondence with border with Region 3, where the power increases until it reaches the value of the reference fixed case.

It can be observed that the changes in pitch oscillation frequency have similar effects to the changes in amplitude. Furthermore, for low wind speeds, increasing the pitch oscillation frequency causes much greater increases in average power than increasing the pitch oscillation amplitude.

Finally, Fig. 11 presents the variation of the extracted power in the pitching case at different values of pitch offset, with fixed amplitude and frequency. The behavior of the extracted power with respect to the wind speed is similar to that shown in Figs. 6 and 10. By varying the pitch offset, it can be seen that the maximum extracted power is obtained for \(\theta _0\) = 0 deg, while moving away from it, there is a power decrease that only depends on the absolute value of the pitch oscillation offset (i.e., all other conditions being equal, the same power is obtained by having an oscillating pitch with \(\theta _0\) = +/− 3 deg).

The observed average power reduction is attributable to the variation of the angle of attack: the configuration with \(\theta _0\) = 0 deg is the one that guarantees maximum power extraction. However, there is a limited difference in the extracted power with different offsets, especially if compared with the results obtained by varying pitch oscillation amplitude or frequency: this means that the preponderant contribution to the increase/decrease in power is given by \(V_\mathrm{nac}\) rather than by the average tower inclination.

From the results presented, it can be stated that the power production of an offshore wind turbine is very sensitive to the pitch motion. In particular, the pitch motion parameters that seem to have higher influence are the oscillation frequency and amplitude. In addition, the increase in power becomes greater the more the contribution of the pitch oscillation becomes relevant with respect to the wind speed. By coupling wind speeds near or above the nominal value with important pitch oscillations and offset there is a decrease in the extracted power; this decrease could be seen also for low wind speeds with minimal pitch oscillations and offset, but with values lower than those analyzed. For example, in real conditions the pitch parameters compatible with \(V_\mathrm{wind}\) = 8.5 m/s would be A = 0.5 deg, f = 0.01 Hz and \(\phi _0\) = 2.5 deg (Caradonna et al. 2021), with an average extracted power lower than the fixed case. This correspondence between wind and pitch oscillations is generally proven, as the greatest contribution to the My moment on the OFWT is given by the moment of transport of the rotor thrust to the base.

Finally, since the structure motion modifies the relative wind speed that impacts on the blades, the effect of the frequency and the amplitude on \(V_0\) is similar. This leads to an increase in aerodynamic power, with results similar to those described by Wen et al. (Wen et al. 2018) and Tran and Kim (Tran and Kim 2015). However, in addition to the previous works, the control logic of the generator is taken into account, leading to more realistic results. The control logic in some conditions limits the beneficial effects of the structure motion, resulting in an average power decrease with respect to the fixed case: this is mainly related to the power saturation imposed by the generator control.

4 Conclusion

In this study, the power performance of the NREL 5-MW baseline wind turbine installed on a floating platform is investigated with the BEM Theory. A comparison between the fixed case and different pitching cases is conducted: the influences of the platform pitching amplitude, frequency and offset on the electrical extracted power are analyzed at various wind speeds.

In general, it has been noted that pitch oscillation leads to an increase in aerodynamic power, due to the fact that the relative wind speed with respect to the structure \(V_0\) has a cosinusoidal trend around the absolute wind speed \(V_\mathrm{wind}\): since there is a cubic relationship between the relative wind speed \(V_0\) and the aerodynamic power \(P_\mathrm{aer}\), the increase in power in the forward pitching motion is more relevant than the decrease in power in the backward pitching motion.

However, the passage from the extractable power (\(P_\mathrm{aer}\)) to the actually extracted power (\(P_\mathrm{gen}\)) depends on the size of the generator and its control logic. For low wind speeds, the influence of pitch oscillation is not such as to bring \(V_0\) beyond the nominal point, where the control intervenes to keep the power at nominal value. For wind speeds around the nominal value, the pitch oscillations may impose an oscillation of \(V_0\) across this value: in these conditions, there would be time intervals in which the generated power is saturated at the nominal value (\(V_0 > V_\mathrm{nom}\)) and time intervals where the power is lower than the nominal value (\(V_0 < V_\mathrm{nom}\)). By analyzing a single period of pitch oscillation T, which corresponds to a period of oscillation of \(V_0\), we can identify a time interval t in which \(V_0 > V_\mathrm{nom}\), and the remaining interval \(T-t\) in which \(V_0 < V_\mathrm{nom}\). Let us define \(\tau ^+ = \frac{t}{T}\) and \(\tau ^- = \frac{T-t}{T}\). Starting from \(\tau ^-=1\) and \(\tau ^+=0\), by increasing \(\tau ^+\), the beneficial contribution to the power is gradually reduced, up to a condition (a certain value \(\tau ^*\) of \(\tau ^+\), different for each combination of wind speed and pitch oscillation) beyond which the effect of pitch oscillation is harmful for the extracted electrical power. This is motivated by the fact that, for wind speeds near or above the nominal value, in the fixed case an average electrical power close to or equal to the nominal value would be obtained. By introducing oscillations to the pitch, and therefore, to \(V_0\), the power trend obtained is characterized mostly by the minimums, since the maximums are saturated at the nominal value: this implies that the average power extracted is lower than the value obtained in the fixed case. Finally, when the absolute wind speed \(V_\mathrm{wind}\) is sufficiently higher than the nominal value, so that the minimums of \(V_0\) caused by the pitch oscillation are still higher than \(V_\mathrm{nom}\) (when \(\tau ^+=1\)), the extracted power equals the nominal value anyway. Ultimately, based on the values of \(\tau ^+\), \(\tau ^-\) and \(\tau ^*\), we can say that:

  • If \(0\le \tau ^+<\tau ^*\), the average extracted power in a pitching case is higher that the value obtained in the fixed case.

  • If \(\tau ^*<\tau ^+<1\), the average extracted power in a pitching case is lower that the value obtained in the fixed case.

  • If \(\tau ^+=\tau ^*\) or \(\tau ^+=1\), the average extracted power in a pitching case and in the fixed case are equal (when \(\tau ^+=1\), equal to the nominal value).

From this study, it was found that what causes power variation of a pitching wind turbine with respect to a fixed one is the change of \(V_0\) components (\(V_\mathrm{wind}\) and \(V_\mathrm{nac}\) in Eq. 3), as already observed in Wen et al. (2017, 2018). Moreover, the variation of its values is mainly due to the variation of \(V_\mathrm{nac}\), therefore, from the variation of the pitch amplitude or frequency, rather than from the variation of the angle between the structure and the \(V_\mathrm{wind}\) direction. Compared to the previous works (Wen et al. 2018; Tran and Kim 2015), the real generator power was analyzed, instead of the theoretical aerodynamic power; the introduction of the generator led to the insertion of a control logic which implied different but more realistic results.

In this article, a specific control logic has been used, which led to results that could be different using other types of control logic. However, it is clear that what causes the decrease of average power extracted with respect to the value obtained in the fixed case is the saturation imposed on it for wind speeds near or above \(V_\mathrm{nom}\). This is a characteristic of the generator size, not of the chosen control logic. In fact, whatever is the \(V_{0}\) caused by wind and pitching, the generator can produce at most its electrical nominal power, given by its size.

Future work should especially focus on the effects of the described and other relevant phenomena on OFWTs operating in real sea environment and wind conditions, to understand how their power output may be influenced by the overall structure motion. To do so, a numerical simulation campaign should be carried out while taking into account:

  • The real motion that irregular waves cause on OFWT structures.

  • The wind turbulences.

  • All the 6 DoFs of the OFWT structure, to especially take into account the direction of waves, which is not necessarily the same as wind.

  • The influence of mooring systems on the floating structure motion, which may be significant.

To study the real impact of OFWT motion on their net energy production, the outcomes hereby presented should be accurately weighted on the occurrences of the different real sea states and wind speed profiles: it is in fact necessary to evaluate the amplitude and frequency of pitch oscillations deriving from the combination of different waves and winds. In particular, it is necessary to check the compatibility of weak winds with those pitch oscillation values that cause large increase in power. For this reason, those tests characterized by low wind speeds and high pitch oscillation amplitude and frequency, which could theoretically cause a substantial increase in power, were not considered, since they would have been extremely unrealistic and dangerous for the turbine structure.