Neuroadaptive control of information-poor servomechanisms with smooth and nonsmooth uncertainties

Abstract

For motion control of uncertain servomechanisms, nonlinear dynamics including smooth and nonsmooth types, external disturbances, signal measurement noises, asymmetric input saturation, and so on seriously hinder the further development of high-performance closed-loop control algorithms. However, already existing control strategies cannot address the above-mentioned issues at the same time. It greatly increases the difficulty of controller design especially when some states are not measurable. Inspired by above motivations, this paper exploits neural networks to deal with nonlinear dynamics including discontinuous types, and combines extended state observers to estimate disturbances and unmeasurable states for uncertain nonlinear servomechanisms. Meanwhile, the desired-command-based model compensation approach is integrated into the controller design. It is worth noting that the neural network weights are updated by the combination of the estimation error and tracking error to acquire better approximation accuracy. According to above technologies, a novel extended-state-observer-based neural network adaptive motion control algorithm will be synthesized. The bounded stability of the whole closed-loop system is proved strictly. In addition, the comparisons of the application results on an electro-hydraulic servo system verify the availability and superiority of the developed control algorithm.

Introduction

Servo mechanical systems, such as servo motor systems [1,2,3,4], hydraulic servo systems [5,6,7,8], and aerocrafts [9, 10], play an important role in industry and engineering applications, including processing, manufacturing, production, and so on. And they are often affected by unknown nonlinear dynamics, including continuous and discontinuous types, external disturbances, signal measurement noises, input saturation, and other factors. In addition, some signals in the system cannot be measured, because they are not equipped with corresponding sensors. Above-mentioned factors will seriously affect the motion accuracy of servo mechanical systems, leading it difficult to synthesize high-performance closed-loop controllers.

During the past few decades, the motion control for uncertain nonlinear servo systems has mainly revolved around overcoming the modeling uncertainties therein. It is worth noting that a large number of leading control algorithms have been presented along with the development of control theory. Examples like adaptive robust control (ARC) [11], integral robust control (IRC) [12, 13], sliding mode control (SMC) [14, 15], disturbance-observer-based control [1, 2, 9, 16,17,18], neural network (NN)-based control [19,20,21,22,23,24], and so on. In [25], the authors have presented an integral retarded controller for velocity control of a direct current motor servo system. However, only a part of modeling uncertainties has been dealt with. In [26], for a servo motor actuated gantry system, the authors have developed a friction-compensation-based adaptive SMC control algorithm which utilizes the adaptive control technique to handle uncertain parameters that lie linearly in the system and employs the SMC to deal with external disturbances. However, the final control input contains a discontinuous term, which may cause severe chattering for the actual system. To handle large disturbances existing in a pneumatic servo system, Yuanqing Xia et al. have employed an extended state observer (ESO) to acquire the estimate of lumped nonlinearities and thus compensate for the total disturbances feedforwardly [27]. Furthermore, Daehee Won et al. have developed an output feedback integral sliding mode controller by incorporating a high gain observer to acquire the estimate of the unmeasured velocity as well as load pressure [16]. However, unknown nonlinear dynamics have not been considered in [16]. By taking advantage of the good approximation performance of NN for unknown functions, the authors in [7] and [23] have synthesized an adaptive NN (ANN) control algorithm to treat largely uncertain nonlinear dynamics existing in hydraulic cylinder actuated active suspension systems. Furthermore, by exploiting NNs to approximate unknown nonlinear functions and dead zone, the authors in [24] have proposed a ANN control strategy for a family of servo mechanisms. To simultaneously cope with unknown nonlinear dynamic uncertainties and exogenous disturbances, some control strategies which combine neural network with robust control methods have been proposed. In [21], a NN-based ARC control algorithm has been synthesized for a linear motor driven stage to obtain high-accuracy tracking effect and reject external disturbances. In [28], the authors have presented a recurrent NN-based SMC control structure for nonlinear systems to compensate for unknown nonlinear dynamics and suppress external disturbances. Moreover, a NN-based IRC control algorithm has been proposed by Jing Na et al. for uncertain servomechanisms. Nevertheless, the control strategies mentioned above exist certain conservatism when the considered system is faced with large external disturbances. Furthermore, influenced by external disturbances, the actual control input added to the system may be saturated due to the limitation of electrical hardware. Some control algorithms with saturation compensation [11, 15, 29,30,31] have been developed for this working condition.

After careful analysis of the existing studies, it is known that scholars mainly deal with the continuous nonlinear dynamic uncertainties via NN, but pay little attention to the existence of discontinuous nonlinear dynamics in the system. As for servomechanisms, there prominently exist various discontinuous nonlinear dynamics, such as discontinuous nonlinear friction, discontinuous hydraulic fluid leakage, and so on. In addition, for feedback control, the measurement values of state feedback information are often needed, but they are usually not measurable for actual systems due to economic, structural, and other factors. As for speed feedback and acceleration feedback in the actual servo mechanical systems, these information are often not obtained by adding corresponding sensors, but by position information via filters. However, the dynamics of these filters are often not included in the closed-loop stability proof of the system, resulting in great conservatism in implementing the final controller. In addition, using the measured value of the signals directly when designing the controller causes a large amount of noises to be mixed, which may lead to unsatisfactory control effects. It is worth noting that most of the existing controllers still use the traditional backstepping method, which will lead to the issue of “explosion of complexity (EC)”. By analyzing and summarizing the above studies, it can be found that unknown nonlinear dynamics in the system, especially the types of discontinuities, external interference, measurement noises, and input saturation, and so on, cannot simultaneously be handled under the condition that only some state signals can be measured. And it will also be affected by EC when designing the controller. The above factors bring great challenges to the design of the controller.

Stimulated by above analysis, we will propose a novel control algorithm to deal with the issues. Specially, the proposed control algorithm will employ NN adaptive control [32] to simultaneously estimate the continuous and discontinuous nonlinear dynamics that present in the system. And ESOs [33] will be exploited to estimate unmeasured states, mismatched, and matched exogenous disturbances in the system. By incorporating the desired-command-based technology into NN adaptive control, observer and controller to minimize the influence of signal measurement noises. More importantly, the effect of EC will be eliminated via the command-filtered backstepping technique. And the saturation compensation technology will be utilized to deal with the input saturation effect suffered by the system.

In summary, the proposed control algorithm has the following innovations:

• The proposed control algorithm can simultaneously handle smooth and nonsmooth nonlinear dynamics, matched and mismatched exogenous disturbances, measurement signal noises, and input saturation.

• The better neural network adaptive performance can be acquired, since the weight adaption laws are driven by the composite errors comprised of state prediction errors and system tracking errors.

• The proposed control algorithm can be adapted in the working condition with unmeasurable information, which means that it has strong adaptability to working conditions.

• The integrated control algorithm can not only eliminate the effects of “explosion of complexity”, but also avoid the influence of filtering error.

For simplification, some notations are presented as follows:

i	1, 2, 3
j	2, 3
b	1, 2
$\hat{ \bullet }$	the estimate of $\bullet$
$\tilde{ \bullet } = \bullet - \hat{ \bullet }$	the estimation error of $\bullet$

Problem statement

A family of third-order uncertain nonlinear servomechanisms in the following state-space form is considered as

$$ \begin{aligned} \dot{\chi }_{1} &= \chi_{2} \\ \dot{\chi }_{2} &= \chi_{3} + \xi_{2} (\overline{\chi }_{2} ) + \varepsilon_{2} (t) \\ \dot{\chi }_{3}& = u(\nu ) + \xi_{3} (\overline{\chi }_{3} ) + \psi_{3} (\chi_{3} ) + \varepsilon_{3} (t) \\ y_{o}& = \chi_{1} . \\ \end{aligned} $$

(1)

Here, χ_i means the system state variable; $\xi_{j} (\overline{\chi }_{j} )$ denotes the unknown nonlinear dynamic with respect to $\overline{\chi }_{j}$ = [χ₁, …, χ_j]^T; $\psi_{3} (\chi_{3} )$ means the unknown nonlinear dynamic with respect to χ₃; ε_j(t) represents the lumped time-varying external disturbance; y_o stands for the system output; and the input saturation nonlinearity u $(\nu )$ can be described by

$$ u(\nu ) = {\text{sat}} (\nu ) = \left\{ \begin{aligned} & \overline{u},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \nu \ge \overline{u} \hfill \\ & \nu ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \underline {u} < \nu < \hfill \\ & \underline {u} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \nu \le \underline {u} \hfill \\ \end{aligned} \right.\overline{u}, $$

(2)

where $\nu$ indicates the control input; moreover, $\overline{u}$ > 0 and $\underline {u}$ < 0 denote known bounds for u $(\nu )$.

Control Goal: To construct a bounded input $\nu$ with only partial state measurements, so that the y_o = χ₁ can follow any desired command χ_1d(t) ∈ Ϲ¹ closely in spite of various modeling uncertainties and input saturation nonlinearity.

Before synthesizing the control scheme to acquire the above-mentioned control objective, we firstly make the following several assumptions.

Assumption 1

The desired command χ_1d(t) belongs to C². The system signals χ₁ and χ₃ are measurable, while the system signal χ₂ is immeasurable. The unknown nonlinear function $\xi_{j} (\overline{\chi }_{j} )$ belongs to C¹. Specially, the unknown nonlinear function ψ₃(χ₃) is bounded and continuous except at χ₃ = c_c where it exhibits a finite jump and is always continuous from the right, in which c_c means a constant.

Assumption 2

There exist some positive constants ε_2m and ε_3m, such that exogenous disturbances ε₂(t) and ε₃(t) fulfill

$$ \left| {\varepsilon_{2} (t)} \right| \le \varepsilon_{2m} ,\left| {\varepsilon_{3} (t)} \right| \le \varepsilon_{3m} . $$

(3)

Lemma 1

Denote a command filter as follows [31]:

$$ \begin{aligned} & \dot{x}_{1} = w_{c} x_{2} \hfill \\ & \dot{x}_{2} = - 2w_{f} w_{c} x_{2} - w_{c} (x_{1} - x_{r} ). \hfill \\ \end{aligned} $$

(4)

If the input variable x_r fulfills |$\dot{x}_{r} (0)$|≤ x_r1 and |$\ddot{x}_{r} (0)$|≤ x_r2 for any time t ≥ 0 with x_r1 and x_r2 being some positive constants, and meanwhile, x₁(0) = x_r(0), x₂(0) = 0, hence there exist positive constants ω_c, ε_c, and 0 < ω_f < 1, so that |x₁–x_r|≤ ε_c.

Remark 1

For a large number of practical applications, typical examples like hydraulic/motor servo systems [1, 2, 6, 18, 34], they can always be modeled or transformed as (1). Furthermore, some discontinuous nonlinear dynamics, such as discontinuous friction and discontinuous leakage, which are not ignored have yet been considered in (1). In addition, it can be found from (1) that mismatched modeling uncertainties including $\xi_{2} (\overline{\chi }_{2} )$ and ε₂(t), matched modeling uncertainties including $\xi_{3} (\overline{\chi }_{3} )$ and ε₃(t), and input saturation nonlinearity are simultaneously taken into account.

Command-filter-based neural network controller with partial state feedback

Neural network approximation

According to the powerful universal approximation characteristic of NN, for any C¹ nonlinear function F₁(x), there exist ideal weights W_* ∈ ℝ^L with L being the number of RBFNN nodes, so that [32]

$$ F_{1} (x) = W_{ * }^{T} \eta_{ * } (x) + \sigma (x), $$

(5)

where x means the input vector, σ(x) indicates the approximation error, and $\eta_{ * } (x)$ = [$\eta_{ * 1} (x)$,$\eta_{ * 2} (x)$, …,$\eta_{ * L} (x)$]^T with the function $\eta_{ * l} (x)$, l = 1, 2, …, L, usually being chosen as the Gaussian RBF [32]

$$ \eta_{ * l} (x) = e^{{ - {{\left\| {x - c_{l} } \right\|^{2} } \mathord{\left/ {\vphantom {{\left\| {x - c_{l} } \right\|^{2} } {2w_{l}^{2} }}} \right. \kern-\nulldelimiterspace} {2w_{l}^{2} }}}} , $$

(6)

in which c_l and w_l are center vectors and widths of the RBF, respectively.

Noting (5), the function F₁(x) is able to be approximated by

$$ \hat{F}_{1} (x) = \hat{W}_{ * }^{T} \eta_{ * } (x). $$

(7)

Furthermore, for any continuously nonlinear function F₂(x) except at x = c_c where it exhibits a jump and is also continuous from the right, there exist ideal weights G_* ∈ ℝ^M with M being the number of NN nodes, so that

$$ F_{2} (x) = G_{*}^{T} \psi_{*} (x) + \mu_{c} (x), $$

(8)

where μ_c(x) indicates the approximation error; and $\psi_{ * } (x)$ = [$\psi_{ * 1} (x)$,$\psi_{ * 2} (x)$, …,$\psi_{ * M} (x)$]^T with the sigmoid jump function $\psi_{ * m} (x)$, m = 0, 1, …, M, usually being chosen as follows [35]:

$$ \psi_{ * m} (x) = \left\{ {\begin{array}{ll} {\left( {1 - e^{ - x} } \right)^{m} } & {{\text{if}}{\kern 1pt} x \ge 0} \\ 0 & {{\text{otherwise}}} \\ \end{array} } \right..$$

(9)

Based on (8), F₂(x) can be estimated by

$$ \hat{F}_{2} (x) = \hat{G}_{*}^{T} \psi_{*} (x) $$

(10)

NN-based ESOs design

Noting the considered system in (1), we can reorganize the expression $\xi_{3} (\overline{\chi }_{3} )$ as

$$ \xi_{3} (\overline{\chi }_{3} ) \,=\, \varphi_{3} (\overline{\chi }_{2} ,\dot{\chi }_{2} ) + \varepsilon_{4} (t), $$

(11)

where $\varphi_{3} (\overline{\chi }_{2} ,\dot{\chi }_{2} )$ indicates a nonlinear function with respect to $\overline{\chi }_{2}$ and $\dot{\chi }_{2}$, and ε₄(t) represents the lumped time-varying external disturbance.

Based on (1) and (11), the nonlinear system (1) can be reorganized as

$$ \begin{aligned} \dot{\chi }_{1} & = \chi_{2} \\ \dot{\chi }_{2} &= \chi_{3} + \xi_{2} (\overline{\chi }_{2d} ) + \tilde{N}_{2} + \varepsilon_{2} (t) \\ \dot{\chi }_{3}& = u(\nu ) + \varphi_{3} (\overline{\chi }_{3d} ) + \tilde{N}_{3} + \varepsilon_{4} (t) + \psi_{3} (\chi_{3} ) + \varepsilon_{3} (t), \\ \end{aligned} $$

(12)

where $\overline{\chi }_{2d} =$ $\left[ {\chi_{1d} ,\dot{\chi }_{1d} } \right]^{T}$ and $\overline{\chi }_{3d} =$ $\left[ {\chi_{1d} ,\dot{\chi }_{1d} ,\ddot{\chi }_{1d} } \right]^{T}$ are vectors with respect to desired commands. In addition, $\tilde{N}_{2}$ and $\tilde{N}_{3}$ are expressed as

$$ \tilde{N}_{2} \triangleq \xi_{2} (\overline{\chi }_{2} ) - \xi_{2} (\overline{\chi }_{2d} ),\tilde{N}_{3} \triangleq \varphi_{3} (\overline{\chi }_{2} ,\dot{\chi }_{2} ) - \varphi_{3} (\overline{\chi }_{3d} ). $$

(13)

Depending on (5), (8), (12), and (13), the system (1) can be equivalent to the form as below

$$ \begin{gathered} \dot{\chi }_{1} = \chi _{2} \hfill \\ \dot{\chi }_{2} = \chi _{3} + W_{2}^{T} \eta _{2} (\bar{\chi }_{{2d}} ) + \sigma _{2} (\bar{\chi }_{{2d}} ) + \tilde{N}_{2} + \varepsilon _{2} (t) \hfill \\ \dot{\chi }_{3} = u(\nu ) + W_{3}^{T} \eta _{3} (\bar{\chi }_{{3d}} ) + \sigma _{3} (\bar{\chi }_{{3d}} ) + \tilde{N}_{3} + \varepsilon _{4} (t)\\ \quad \quad \quad +\, G^{T} \psi _{p} (\chi _{3} ) + \mu (\chi _{3} ) + \varepsilon _{3} (t), \hfill \\ \end{gathered} $$

(14)

where $\eta_{2} (\overline{\chi }_{2d} )$ and $\eta_{3} (\overline{\chi }_{3d} )$ are Gaussian RBFs whose expressions are similar to (6); ψ_p(χ₃) indicates the sigmoid jump function whose expression is similar to (9); in addition,$\sigma_{2} (\overline{\chi }_{2d} )$, $\sigma_{3} (\overline{\chi }_{3d} )$ and $\mu (\chi_{3} )$ represent different approximation errors.

First, let us introduce two variables χ_D2(t) = $\sigma_{2} (\overline{\chi }_{2d} )$ + ε₂(t) and χ_D3(t) = $\sigma_{3} (\overline{\chi }_{3d} )$ + ε₃(t) + ε₄(t) as extended states; thus, the state-space expression (14) can be converted into the following form:

$$ \begin{gathered} \left\{ \begin{gathered} \dot{\chi }_{1} = \chi _{2} \hfill \\ \dot{\chi }_{2} = \chi _{3} + W_{2}^{T} \eta _{2} (\bar{\chi }_{{2d}} ) + \chi _{{D2}} + \tilde{N}_{2} \hfill \\ \dot{\chi }_{{D2}} = \alpha _{1} (t) \hfill \\ \end{gathered} \right. \\ \left\{ \begin{gathered} \dot{\chi }_{3} = u(\nu ) + W_{3}^{T} \eta _{3} (\bar{\chi }_{{3d}} ) + \tilde{N}_{3} \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} + G^{T} \psi _{p} (\chi _{3} ) + \mu (\chi _{3} ) + \chi _{{D3}} . \hfill \\ \dot{\chi }_{{D3}} = \alpha _{2} (t) \hfill \\ \end{gathered} \right. \\ \end{gathered} $$

(15)

Thus, the NN-based ESOs for (15) can be synthesized as

$$ \begin{aligned}& \left\{ \begin{aligned} &\dot{\hat{\chi }}_{1} = \hat{\chi }_{2} + \gamma_{1} \omega_{o1} \left( {\chi_{1} - \hat{\chi }_{1} } \right) \hfill \\ & \dot{\hat{\chi }}_{2} = \chi_{3} + \hat{W}_{2}^{T} \eta_{2} (\overline{\chi }_{2d} ) + \hat{\chi }_{D2} + \gamma_{2} \omega_{o1}^{2} \left( {\chi_{1} - \hat{\chi }_{1} } \right) \hfill \\ & \dot{\hat{\chi }}_{D2} = \gamma_{3} \omega_{o1}^{3} \left( {\chi_{1} - \hat{\chi }_{1} } \right) \hfill \\ \end{aligned} \right. \\ &\left\{ \begin{aligned} & \dot{\hat{\chi }}_{3} = u(\nu ) + \hat{W}_{3}^{T} \eta_{3} (\overline{\chi }_{3d} ) + \hat{G}^{T} \psi_{p} (\chi_{3} ) \hfill \\ & {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} + \hat{\chi }_{D3} + r_{1} \omega_{o2} \left( {\chi_{3} - \hat{\chi }_{3} } \right) \hfill \\ & \dot{\hat{\chi }}_{D3} = r_{2} \omega_{o2}^{2} \left( {\chi_{3} - \hat{\chi }_{3} } \right) \hfill \\ \end{aligned} \right., \\ \end{aligned} $$

(16)

where the adjustable gains ω_o1 > 0 and ω_o2 > 0 can be seen as the bandwidths of the designed observers; design parameters γ_i and r_b need to be chosen to guarantee that the characteristic polynomials γ₁s² + γ₂s + γ₃ and r₁s + r₂ of the following matrices C_o and R_o are Hurwitz, respectively. It is worth noted from [36] that γ_i and r_b can be parameterized as γ₁ = 3, γ₂ = 3, γ₃ = 1 and r₁ = 2, r₂ = 1, respectively.

Upon (15) and (16), the estimation error dynamics of the constructed observers are arranged as

$$ \begin{gathered} \left\{ \begin{gathered} \dot{\tilde{\chi }}_{1} = - \gamma _{1} \omega _{{o1}} \tilde{\chi }_{1} + \tilde{\chi }_{2} \hfill \\ \dot{\tilde{\chi }}_{2} = - \gamma _{2} \omega _{{o1}}^{2} \tilde{\chi }_{1} + \tilde{\chi }_{{D2}} + \tilde{W}_{2}^{T} \eta _{2} (\bar{\chi }_{{2d}} ) + \tilde{N}_{2} \hfill \\ \dot{\tilde{\chi }}_{{D2}} = - \gamma _{3} \omega _{{o1}}^{3} \tilde{\chi }_{1} + \alpha _{1} (t) \hfill \\ \end{gathered} \right. \\ \left\{ \begin{gathered} \dot{\tilde{\chi }}_{3} = - r_{1} \omega _{{o2}} \tilde{\chi }_{3} + \tilde{\chi }_{{D3}} + \tilde{W}_{3}^{T} \eta _{3} (\bar{\chi }_{{3d}} ) \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} + \tilde{N}_{3} + \tilde{G}^{T} \psi _{p} (\chi _{3} ) + \mu (\chi _{3} ) \hfill \\ \dot{\tilde{\chi }}_{{D3}} = - r_{2} \omega _{{o2}}^{2} \tilde{\chi }_{3} + \alpha _{2} (t) \hfill \\ \end{gathered} \right.. \\ \end{gathered} $$

(17)

For facilitating the subsequent theoretical analysis, a set of state vectors ζ = [ζ₁, ζ₂, ζ₃]^T = [$\tilde{\chi }_{1}$,${{\tilde{\chi }_{2} } \mathord{\left/ {\vphantom {{\tilde{\chi }_{2} } {\omega_{o1} }}} \right. \kern-\nulldelimiterspace} {\omega_{o1} }}$,${{\tilde{\chi }_{D2} } \mathord{\left/ {\vphantom {{\tilde{\chi }_{D2} } {\omega_{o1}^{2} }}} \right. \kern-\nulldelimiterspace} {\omega_{o1}^{2} }}$]^T and δ = [δ₁, δ₂]^T = [$\tilde{\chi }_{3}$,${{\tilde{\chi }_{D3} } \mathord{\left/ {\vphantom {{\tilde{\chi }_{D3} } {\omega_{o2} }}} \right. \kern-\nulldelimiterspace} {\omega_{o2} }}$]^T are introduced. Hence, (17) can be rearranged as

$$ \dot{\zeta } = \omega_{o1} C_{o} \zeta + H_{1} \frac{{\tilde{W}_{2}^{T} \eta_{2} (\overline{\chi }_{2d} ) + \tilde{N}_{2} }}{{\omega_{o1} }} + H_{2} \frac{{\alpha_{1} (t)}}{{\omega_{o1}^{2} }} $$

(18)

$$ \begin{gathered} \dot{\delta } = \omega_{o2} R_{o} \delta + S_{1} \left[ {\tilde{W}_{3}^{T} \eta_{3} (\overline{\chi }_{3d} ) + \tilde{N}_{3} } \right] \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} + S_{1} \left[ {\tilde{G}^{T} \psi_{p} (\chi_{3} ) + \mu (\chi_{3} )} \right] + S_{2} \frac{{\alpha_{2} (t)}}{{\omega_{o2} }}, \hfill \\ \end{gathered} $$

(19)

in which

$$ C_{o} = \left[ {\begin{array}{*{20}c} { - \gamma_{1} } & 1 & 0 \\ { - \gamma_{2} } & 0 & 1 \\ { - \gamma_{3} } & 0 & 0 \\ \end{array} } \right],{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} H_{1} = \left[ {\begin{array}{*{20}c} 0 \\ 1 \\ 0 \\ \end{array} } \right],{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} H_{2} = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ 1 \\ \end{array} } \right] $$

(20)

$$ R_{o} = \left[ {\begin{array}{*{20}c} { - r_{1} } & 1 \\ { - r_{2} } & 0 \\ \end{array} } \right],{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} S_{1} = \left[ {\begin{array}{*{20}c} 1 \\ 0 \\ \end{array} } \right],{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} S_{2} = \left[ {\begin{array}{*{20}c} 0 \\ 1 \\ \end{array} } \right]. $$

(21)

As the matrices C_o and R_o are Hurwitz, there must exist positive definite matrices E_o and Y_o, such that $C_{o}^{T} E_{o}$ + E_oC_o = –I and $R_{o}^{T} Y_{o}$ + Y_oR_o = –I always hold [37]. Furthermore, according to aforementioned parameterized values γ_i and r_b, E_o and Y_o can be, respectively, calculated as

$$ E_{o} = \left[ {\begin{array}{*{20}c} 1 & { - \frac{1}{2}} & { - 1} \\ { - \frac{1}{2}} & 1 & { - \frac{1}{2}} \\ { - 1} & { - \frac{1}{2}} & 4 \\ \end{array} } \right],Y_{o} = \left[ {\begin{array}{*{20}c} \frac{1}{2} & { - \frac{1}{2}} \\ { - \frac{1}{2}} & \frac{3}{2} \\ \end{array} } \right]. $$

(22)

Furthermore, the theoretical analysis for the stability of the constructed NN-based ESOs which is included in that of the whole closed-loop system will be provided in Appendix A.

Command filtered model compensation controller with partial state feedback

To synthesize the subsequent control scheme, we define a set of tracking error variables z_i and error compensation signals e_i as follows:

$$ \begin{aligned} z_{1} = \chi_{1} - \chi_{1d} ,e_{1} = z_{1} - \phi_{1} \hfill \\ z_{2} = \chi_{2} - v_{1} ,e_{2} = z_{2} - \phi_{2} \hfill \\ z_{3} = \chi_{3} - v_{2,c} ,e_{3} = z_{3} - \phi_{3} , \hfill \\ \end{aligned} $$

(23)

where v₁ and v₂ indicate virtual control functions; v_2,c denotes the filtered signal of v₂ via the presented command filter in (4). In addition, a set of compensating signals ϕ_i is introduced as follows:

$$ \begin{gathered} \dot{\phi }_{1} = - k_{1} \phi_{1} + \phi_{2} \hfill \\ \dot{\phi }_{2} = - k_{2} \phi_{2} + \phi_{3} + (v_{2,c} - v_{2} ) \hfill \\ \dot{\phi }_{3} = - k_{3} \phi_{3} + \Delta u, \hfill \\ \end{gathered} $$

(24)

where k_i indicates positive feedback gains and Δu = u $(\nu )$–$\nu$.

Step 1:

Upon (1), (11), and (12), the time derivative of e₁ is produced as

$$ \begin{gathered} \dot{e}_{1} = e_{2} + \phi_{2} + v_{1} - \dot{\chi }_{1d} - ( - k_{1} \phi_{1} + \phi_{2} ) \\ = e_{2} + v_{1} - \dot{\chi }_{1d} + k_{1} \phi_{1} . \\ \end{gathered} $$

(25)

Thus, the virtual control function v₁ is synthesized as

$$ v_{1} = - k_{1} z_{1} + \dot{\chi }_{1d} . $$

(26)

After substituting (26) into (25), we have

$$ \dot{e}_{1} = - k_{1} e_{1} + e_{2} . $$

(27)

Step 2:

Noting (14), (23), and (24), we can get the time derivative of e₂ as

$$ \begin{aligned} \dot{e}_{2} & = \dot{\chi }_{2} - \dot{v}_{1} - \dot{\phi }_{2} \hfill \\ &= \chi _{3} + W_{2}^{T} \eta _{2} (\bar{\chi }_{{2d}} ) + \chi _{{D2}} + \tilde{N}_{2} \hfill \\ &\quad\quad - \left( { - k_{1} \dot{z}_{1} + \ddot{\chi }_{{1d}} } \right) + k_{2} \phi _{2} - \phi _{3} - (v_{{2,c}} - v_{2} ). \hfill \\ \end{aligned} $$

(28)

As

$$ \begin{aligned} \dot{z}_{1}& = \dot{e}_{1} + \dot{\phi }_{1} \\& = - k_{1} e_{1} + e_{2} - k_{1} \phi_{1} + \phi_{2} . \\ \end{aligned} $$

(29)

We can achieve

$$ \begin{aligned} \dot{e}_{2} & =\, e_{3} + v_{2} + k_{2} \phi_{2} + W_{2}^{T} \eta_{2} (\overline{\chi }_{2d} ) + \chi_{D2} \\ & \quad\, + \tilde{N}_{2} + k_{1} \left( { - k_{1} e_{1} + e_{2} - k_{1} \phi_{1} + \phi_{2} } \right) - \ddot{\chi }_{1d} . \\ \end{aligned} $$

(30)

Therefore, we can construct the virtual control function v₂ as

$$ v_{2} = - k_{2} \left( {\hat{\chi }_{2} - v_{1} } \right) - \hat{W}_{2}^{T} \eta_{2} (\overline{\chi }_{2d} ) - \hat{\chi }_{D2} + \ddot{\chi }_{1d} - e_{1} . $$

(31)

After substituting (31) into (30), one has

$$ \begin{aligned} \dot{e}_{2} &= e_{3} - k_{2} e_{2} - e_{1} + k_{2} \tilde{\chi }_{2} + \tilde{W}_{2}^{T} \eta _{2} (\bar{\chi }_{{2d}} ) \hfill \\ &\quad + \tilde{\chi }_{{D2}} + \tilde{N}_{2} - k_{1}^{2} e_{1} + k_{1} e_{2} - k_{1}^{2} \phi _{1} + k_{1} \phi _{2} . \hfill \\ \end{aligned} $$

(32)

Step 3:

Based on (14), (23), and (24), we are able to acquire the time derivative of e₃ as

$$ \begin{aligned} \dot{e}_{3} &= \dot{\chi }_{3} - \dot{v}_{2,c} - \dot{\phi }_{3} \\ &= u(\nu ) + W_{3}^{T} \eta_{3} (\overline{\chi }_{3d} ) + \tilde{N}_{3} + G^{T} \psi_{p} (\chi_{3} ) \\ &\quad \, + \mu (\chi_{3} ) + \chi_{D3} - \dot{v}_{2,c} - \left( { - k_{3} \phi_{3} + \Delta u} \right) \\ &= \nu + k_{3} \phi_{3} + W_{3}^{T} \eta_{3} (\overline{\chi }_{3d} ) + \tilde{N}_{3} \\ &\quad\, + G^{T} \psi_{p} (\chi_{3} ) + \mu (\chi_{3} ) + \chi_{D3} - \dot{v}_{2,c} . \\ \end{aligned} $$

(33)

Noting (33), the resulting control law $\nu$ can be synthesized by

$$ \begin{aligned} \nu &= - k_{3} (\chi_{3} - v_{2,c} ) - \hat{W}_{3}^{T} \eta_{3} (\overline{\chi }_{3d} ) \\ &\quad \, - \hat{G}^{T} \psi_{p} (\chi_{3} ) - \hat{\chi }_{D3} + \dot{v}_{2,c} - e_{2} . \\ \end{aligned} $$

(34)

After substituting (34) into (33), one gets

$$ \begin{aligned} \dot{e}_{3} &= - k_{3} e_{3} - e_{2} + \tilde{W}_{3}^{T} \eta_{3} (\overline{\chi }_{3d} ) \\ &\quad\, + \tilde{N}_{3} + \tilde{G}^{T} \psi (\chi_{3} ) + \mu (\chi_{3} ) + \tilde{\chi }_{D3} . \\ \end{aligned} $$

(35)

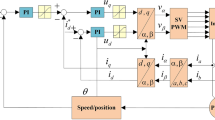
The framework of the developed controller is shown in Fig. 1.

Fig. 1

The framework of the developed control scheme

Main results

Theorem 1

With the NNs’ weights online updated by

$$ \begin{aligned} & \dot{\hat{W}}_{2} = {\text{Proj}} \left\{ {\Upsilon_{2} \left[ {\eta_{2} (\overline{\chi }_{2d} )\left( {\hat{\chi }_{2} - v_{1} - \phi_{2} - \frac{1}{{2\omega_{o1} }}\zeta_{1} } \right) - \rho_{2} \hat{W}_{2} } \right]} \right\} \hfill \\ &\dot{\hat{W}}_{3} = {\text{Proj}} \left\{ {\Upsilon_{3} \left[ {\eta_{3} (\overline{\chi }_{3d} )\left( {e_{3} + \frac{1}{2}\delta_{1} } \right) - \rho_{3} \hat{W}_{3} } \right]} \right\} \hfill \\ & \dot{\hat{G}} = {\text{Proj}} \left\{ {\Gamma \left[ {\psi_{p} (\chi_{3} )\left( {e_{3} + \frac{1}{2}\delta_{1} } \right) - \rho_{G} \hat{G}} \right]} \right\}, \hfill \\ \end{aligned} $$

(36)

in which Proj(•) indicates a smooth projection operator; ϒ₂, ϒ₃, and Г mean positive definite and symmetric adjustable gain matrices; moreover, ρ₂, ρ₃, and ρ_G indicate adjustable positive gains. By choosing design parameters w_c, w_f for the introduced command filter and other positive gains including ω_o1, ω_o2, k_i felicitously, thus the integrated control algorithm can make sure that all signals in the closed-loop servomechanism (1) with largely unknown mismatched, matched modeling uncertainties and input saturation nonlinearity are bounded.

Proof

See Appendix A.

Remark 2

Notably, the developed control strategy can compensate for largely uncertain nonlinear dynamics and external disturbances with only partial state measurements. Specially, discontinuous nonlinear dynamics are also handled. And a command filter is introduced to remove the effect of EC. Moreover, by introducing a series of compensation functions, not only the input saturation effect is compensated, but also the filtering error is eliminated [38, 39]. Furthermore, measurement noises are suppressed by introducing the desired compensation technique.

Application verification

To check the performance of the above-mentioned control strategy in different aspects, we will carry out numerical simulations for a typical verification platform, i.e., a double-rod electric-hydraulic position servomechanism [8]. Moreover, random measurement noises are added.

By introducing a set of state variables χ₁ = y_L, χ₂ $= \dot{y}_{L}$, and χ₃ = A_JP_L/J, the nonlinear model of the double-rod hydraulic position servomechanism in [8] can be written as

$$ \begin{aligned} & \dot{\chi }_{1} = \chi_{2} \\ & \dot{\chi }_{2} = \chi_{3} + \xi_{2} (\overline{\chi }_{2} ) + \varepsilon_{2} (t) \\ & \dot{\chi }_{3} = U(\nu ) + \xi_{3} (\overline{\chi }_{3} ) + \psi_{3} (\chi_{3} ) + \varepsilon_{3} (t), \\ \end{aligned} $$

(37)

where U(ν) = g_mu(ν) with g_m being g_m = 4A_Jβ_oek_tk_v/(JV_t).

Specially, the definitions of the system variables are presented as follows.

J	The load mass
yL	The displacement of the load
Vt	The total volume of the hydraulic chambers
AJ	The active area of the piston rod
Ps	The oil supply pressure
Pr	The oil return pressure
PL	The load pressure
βoe	The effective bulk modulus of oil
kv	The gain of the employed servo valve
kt	The discharge coefficient

It is worth noted from (37) that an additional variable $U(\nu )$ is employed, which means that the actual control input $\nu$ can be calculated once $U(\nu )$ is synthesized out. Moreover, the central physical values of the system parameters for the employed hydraulic servomechanism are collected in Table 1.

Table 1 The central physical values for the hydraulic servomechanism

To indicate the high-performance tracking effect of the developed algorithm, the following controllers are set for comparison in two working conditions.

• (1) C1: This is the integrated control scheme in this paper, i.e., the NN controller with disturbance and nonlinear dynamics compensation via partial state information feedback. To make it clear, the design parameters of this controller are presented in Table 2.

• (2) C2: This is the controller which is same as the aforementioned C1 control scheme but without external disturbance compensation. The objective of setting such a controller is to test the disturbance compensation performance of the developed C1 controller.

• (3) C3: This is the controller which is same as the aforementioned C1 control algorithm but without NN adaptive and disturbance compensation.

• (4) C4: This is the integral robust controller whose control scheme is integrated as follows:

  $$ \begin{aligned} & z_{1} = \chi_{1} - \chi_{1d} ,z_{2} = \chi_{2} - v_{1} , \\ & z_{3} = \chi_{3} - v_{2} ,v_{1} \triangleq - k_{1} z_{1} + \dot{\chi }_{1d} , \\ & v_{2} = \dot{v}_{1} - k_{2} z_{2} - k_{r} z_{2} \\ &\quad\quad - \int_{0}^{t} {[k_{r} k_{2} z_{2} + \beta_{r2} {\text{sign}}(z_{2} )d} \tau , \\ & u = {{[ - k_{3} z_{3} + \dot{v}_{2} - \beta_{r3} {\text{sign}}(z_{3} )]} \mathord{\left/ {\vphantom {{[ - k_{3} z_{3} + \dot{v}_{2} - \beta_{r3} {\text{sign}}(z_{3} )]} {g_{m} }}} \right. \kern-\nulldelimiterspace} {g_{m} }}. \\ \end{aligned} $$

  (38)

Table 2 The design parameters of the C1 controller

The gains of this controller are presented as k_r = 80, β_r2 = 80, and β_r3 = 80, respectively.

• (5) C5: This is the distinguished proportional integral controller with its proportional gain and integral gain being 1500 and 600, respectively.

For fair comparison, all corresponding design parameters of C2, C3, and C4 controllers are chosen as same as that of the C1 controller.

Working condition 1: normal motion

To indicate the high-performance tracking effects of the synthesized C1 controller, we employ the desired motion trajectory χ_1d(t) = 38sin(πt)mm which is displayed in Fig. 2. Moreover, we can see from Fig. 2 that the output χ₁ under the C1 controller can track χ_1d closely. Furthermore, the tracking errors of the employed five controllers are shown in Fig. 3. From them, we can easily find that the synthesized C1 controller in this paper expresses best tracking performance than the other three controllers in terms of transient and steady-state performance. Moreover, the high tracking performance of C1 can be indicated via the presented performance indices in Figs. 4 and 5. It is noted that the reason why the C1 controller exhibits such excellent control performance is due to its model compensations for nonlinear dynamics and disturbances. In detail, the availability of the developed adaptive NN-based nonlinear dynamics compensation can be verified by comparing the tracking errors of C2 and C3. Furthermore, the validity of the developed ESO-based disturbance compensation performance can be proved by comparing the tracking errors of C1 and C2. Specially, the good state estimation performance and disturbance estimation performance from Figs. 6 and 7 illustrate the effectiveness of the developed ESOs. In addition, the estimation performance of nonlinear functions with the C1 controller in Fig. 8, who is regular and bounded, shows that the developed NN adaptive control has good function approximation performance. The effectiveness of combining nonlinear dynamics and disturbance compensation can be illustrated by comparing the tracking errors of C1 and C3. From Fig. 9, we can make out that the actual control input is always within the preset ranges and presents corresponding rules, even in the case of input saturation.

Fig. 2

The tracking performance of C1

Fig. 3

Tracking errors of the contradistinctive controllers

Fig. 4

Performance indices of C1, C4, and C5 controllers during last one cycle

Fig. 5

Performance indices of C2 and C3 controllers during last one cycle

Fig. 6

State estimation performance with the proposed observer in C1

Fig. 7

Disturbances’ estimation performance with the C1 controller

Fig. 8

Estimation performance of nonlinear functions with the C1 controller

Fig. 9

Control input u with its upper and lower bounds of the C1 controller

Working condition 2: high-frequency motion

To further indicate the high-performance tracking effects of the synthesized C1 controller, we employ the desired motion trajectory χ_1d(t) = 10sin(6πt)mm which is displayed in Fig. 10. Moreover, we can see from Fig. 10 that the output χ₁ under the C1 controller can track χ_1d closely. Furthermore, the tracking errors and performance indices of the employed five controllers are shown from Figs. 11, 12, 13. All results indicate the high tracking performance of C1. In addition, from Fig. 14, we can make out that the actual control input is always within the preset ranges and presents corresponding rules, even in the case of input saturation.

Fig. 10

The tracking performance of C1

Fig. 11

Tracking errors of the contradistinctive controllers

Fig. 12

Performance indices of C1 and C5 controllers during last 1 s

Fig. 13

Performance indices of C2, C3, and C4 controllers during last 1 s

Fig. 14

Control input u with its upper and lower bounds of the C1

Conclusion

In this article, a ESO-based NN adaptive motion control strategy has been proposed for a family of servomechanisms with input saturation, which can be adapted to the working condition where some state information can be measured. By comparing several controllers, the compensation performances for disturbance, nonlinear dynamics, and input saturation have been verified. Especially, the estimation-error-and-tracking-error-based NN adaptive control has good approximation ability to function uncertainties including the nonsmooth unknown nonlinear dynamics. In addition, even when the system is saturated, the actual control input still does not exceed the preset limits. Moreover, the system shows high-performance tracking effects with the joint action of ESO and NN. Finally, strict theoretical proof has been presented to ensure the stability of the synthesized closed-loop controller.

Appendix A

Proof of Theorem 1

Consider a non-negative Lyapunov function candidate V_L which consists of state estimation errors, disturbance estimation errors, NNs weights approximate errors, tracking errors, and compensating signals as follows:

$$ \begin{aligned} V_{L} &= \frac{1}{2}e_{1}^{2} + \frac{1}{2}e_{2}^{2} + \frac{1}{2}e_{3}^{2} + \frac{1}{2}\phi_{1}^{2} + \frac{1}{2}\phi_{2}^{2} + \frac{1}{2}\phi_{3}^{2} + \frac{1}{2}\zeta^{T} E_{o} \zeta \\ &\quad\, + \frac{1}{2}\delta^{T} Y_{o} \delta + \frac{1}{2}\tilde{W}_{2}^{T} \Upsilon_{2}^{ - 1} \tilde{W}_{2} + \frac{1}{2}\tilde{W}_{3}^{T} \Upsilon_{3}^{ - 1} \tilde{W}_{3}\\ &\quad + \frac{1}{2}\tilde{G}^{T} \Gamma^{ - 1} \tilde{G}. \\ \end{aligned} $$

(A.1)

After differentiating both sides of (A.1) with time and substituting (18), (19), (24), (27), (32), (35) into it, one obtains

$$ \begin{aligned} \dot{V}_{L}& = e_{1} \left( { - k_{1} e_{1} + e_{2} } \right) + e_{2} \left[ {e_{3} - k_{2} e_{2} + k_{2} \tilde{\chi }_{2} + \tilde{W}_{2}^{T} \eta_{2} (\overline{\chi }_{2d} )} \right] \hfill \\ &\quad + e_{2} \left( { - e_{1} + \tilde{\chi }_{D2} + \tilde{N}_{2} - k_{1}^{2} e_{1} + k_{1} e_{2} - k_{1}^{2} \phi_{1} + k_{1} \phi_{2} } \right) \hfill \\ &\quad + e_{3} \left[ { - k_{3} e_{3} + \tilde{W}_{3}^{T} \eta_{3} (\overline{\chi }_{3d} ) + \tilde{N}_{3} + \tilde{G}^{T} \psi (\chi_{3} ) + \mu (\chi_{3} ) + \tilde{\chi }_{D3} } \right] \hfill \\ &\quad - e_{2} e_{3} + \phi_{1} ( - k_{1} \phi_{1} + \phi_{2} ) + \phi_{2} \left[ { - k_{2} \phi_{2} + \phi_{3} + (v_{2,c} - v_{2} )} \right] \hfill \\ &\quad - \frac{1}{2}\omega_{o1} \left\| \zeta \right\|^{2} + \zeta^{T} E_{o} \left[ {H_{1} \frac{{\tilde{W}_{2}^{T} \eta_{2} (\overline{\chi }_{2d} ) + \tilde{N}_{2} }}{{\omega_{o1} }} + H_{2} \frac{{\alpha_{1} (t)}}{{\omega_{o1}^{2} }}} \right] \hfill \\ &\quad\, + \phi_{3} ( - k_{3} \phi_{3} + \Delta u) - \frac{1}{2}\omega_{o2} \left\| \delta \right\|^{2} + \delta^{T} Y_{o} S_{1} \left[ {\tilde{W}_{3}^{T} \eta_{3} (\overline{\chi }_{3d} ) + \tilde{N}_{3} } \right] \hfill \\ &\quad\, + \delta^{T} Y_{o} S_{1} \left[ {\tilde{G}^{T} \psi_{p} (\chi_{3} ) + \mu (\chi_{3} )} \right] + \delta^{T} Y_{o} S_{2} \frac{{\alpha_{2} (t)}}{{\omega_{o2} }} \hfill \\ &\quad\, - \tilde{W}_{2}^{T} \Upsilon_{2}^{ - 1} \dot{\hat{W}}_{2} - \tilde{W}_{3}^{T} \Upsilon_{3}^{ - 1} \dot{\hat{W}}_{3} - \tilde{G}^{T} \Gamma^{ - 1} \dot{\hat{G}}. \hfill \\ \end{aligned} $$

(A.2)

Moreover, we can reorganize (A.2) as

$$ \begin{aligned} \dot{V}_{L} &= - k_{1} e_{1}^{2} - \left( {k_{2} - k_{1} } \right)e_{2}^{2} - k_{3} e_{3}^{2} - k_{1}^{2} e_{1} e_{2} \hfill \\ &\quad\,+ k_{2} e_{2} \tilde{\chi }_{2} + e_{2} \tilde{\chi }_{D2} + e_{2} \tilde{N}_{2} + e_{3} \tilde{N}_{3} + \mu (\chi_{3} )e_{3} + e_{3} \tilde{\chi }_{D3} \hfill \\ &\quad\,- k_{1}^{2} e_{2} \phi_{1} + k_{1} e_{2} \phi_{2} - k_{1} \phi_{1}^{2} + \phi_{1} \phi_{2} - k_{2} \phi_{2}^{2} + \phi_{2} \phi_{3} \hfill \\ &\quad\, + \phi_{2} (v_{2,c} - v_{2} ) - k_{3} \phi_{3}^{2} + \phi_{3} \Delta u - \frac{1}{2}\omega_{o1} \left\| \zeta \right\|^{2} + \frac{1}{{\omega_{o1} }}\zeta^{T} E_{o} H_{1} \tilde{N}_{2} \hfill \\ &\quad\, + \zeta^{T} E_{o} H_{2} \frac{{\alpha_{1} (t)}}{{\omega_{o1}^{2} }} - \frac{1}{2}\omega_{o2} \left\| \delta \right\|^{2} + \delta^{T} Y_{o} S_{1} \tilde{N}_{3} + \delta^{T} Y_{o} S_{1} \mu (\chi_{3} ) \hfill \\ &\quad\, + \delta^{T} Y_{o} S_{2} \frac{{\alpha_{2} (t)}}{{\omega_{o2} }} + \tilde{W}_{2}^{T} \eta_{2} (\overline{\chi }_{2d} )e_{2} + \frac{1}{{\omega_{o1} }}\tilde{W}_{2}^{T} \eta_{2} (\overline{\chi }_{2d} )\zeta^{T} E_{o} H_{1} \hfill \\ &\quad\,- \tilde{W}_{2}^{T} \Upsilon_{2}^{ - 1} \dot{\hat{W}}_{2} + \tilde{W}_{3}^{T} \eta_{3} (\overline{\chi }_{3d} )e_{3} + \tilde{W}_{3}^{T} \eta_{3} (\overline{\chi }_{3d} )\delta^{T} Y_{o} S_{1} \hfill \\ &\quad\, - \tilde{W}_{3}^{T} \Upsilon_{3}^{ - 1} \dot{\hat{W}}_{3} + \tilde{G}^{T} \psi (\chi_{3} )e_{3} + \tilde{G}^{T} \psi_{p} (\chi_{3} )\delta^{T} Y_{o} S_{1} - \tilde{G}^{T} \Gamma^{ - 1} \dot{\hat{G}}. \hfill \\ \end{aligned} $$

(A.3)

Noting the definitions of ζ and δ as well as (20), (21), (22), we have

$$ \zeta^{T} E_{o} H_{1} = - \frac{1}{2}\zeta_{1} + \zeta_{2} - \frac{1}{2}\zeta_{3} ,\delta^{T} Y_{o} S_{1} = \frac{1}{2}\delta_{1} - \frac{1}{2}\delta_{2} . $$

(A.4)

Based on (36) and (A.4), we can get the upper bound of (A.3) as

$$ \begin{aligned} & \dot{V}_{L} \le - k_{1} e_{1}^{2} - \left( {k_{2} - k_{1} } \right)e_{2}^{2} - k_{3} e_{3}^{2} - k_{1}^{2} e_{1} e_{2} \hfill \\ &\quad\,+ k_{2} e_{2} \tilde{\chi }_{2} + e_{2} \tilde{\chi }_{D2} + e_{2} \tilde{N}_{2} + e_{3} \tilde{N}_{3} + \mu (\chi_{3} )e_{3} + e_{3} \tilde{\chi }_{D3} \hfill \\ &\quad\, - k_{1}^{2} e_{2} \phi_{1} + k_{1} e_{2} \phi_{2} - k_{1} \phi_{1}^{2} + \phi_{1} \phi_{2} - k_{2} \phi_{2}^{2} + \phi_{2} \phi_{3} + \rho_{G} \tilde{G}^{T} \hat{G} \hfill \\ &\quad\, + \phi_{2} (v_{2,c} - v_{2} ) - k_{3} \phi_{3}^{2} + \phi_{3} \Delta u - \frac{1}{2}\omega_{o1} \left\| \zeta \right\|^{2} + \frac{1}{{\omega_{o1} }}\zeta^{T} E_{o} H_{1} \tilde{N}_{2} \hfill \\ &\quad\, + \zeta^{T} E_{o} H_{2} \frac{{\alpha_{1} (t)}}{{\omega_{o1}^{2} }} - \frac{1}{2}\omega_{o2} \left\| \delta \right\|^{2} + \delta^{T} Y_{o} S_{1} \tilde{N}_{3} + \delta^{T} Y_{o} S_{1} \mu (\chi_{3} ) + \hfill \\ & \delta^{T} Y_{o} S_{2} \frac{{\alpha_{2} (t)}}{{\omega_{o2} }} + \tilde{W}_{2}^{T} \eta_{2} (\overline{\chi }_{2d} )\tilde{\chi }_{2} + \rho_{2} \tilde{W}_{2}^{T} \hat{W}_{2} - \frac{1}{2}\tilde{W}_{3}^{T} \eta_{3} (\overline{\chi }_{3d} )\delta_{2} \hfill \\ &\quad\,+ \frac{1}{{\omega_{o1} }}\tilde{W}_{2}^{T} \eta_{2} (\overline{\chi }_{2d} )\left( {\zeta_{2} - \frac{1}{2}\zeta_{3} } \right) + \rho_{3} \tilde{W}_{3}^{T} \hat{W}_{3} - \frac{1}{2}\tilde{G}^{T} \psi_{p} (\chi_{3} )\delta_{2} . \hfill \\ \end{aligned} $$

(A.5)

Depending on Young’s inequality, one yields

$$ \begin{aligned} &\tilde{W}_{2}^{T} \hat{W}_{2} = - \left\| {\tilde{W}_{2} } \right\|^{2} + \tilde{W}_{2}^{T} W_{2} \le - \frac{1}{2}\left\| {\tilde{W}_{2} } \right\|^{2} + \frac{1}{2}\left\| {W_{2} } \right\|^{2} \hfill \\ & \tilde{W}_{3}^{T} \hat{W}_{3} = - \left\| {\tilde{W}_{3} } \right\|^{2} + \tilde{W}_{3}^{T} W_{3} \le - \frac{1}{2}\left\| {\tilde{W}_{3} } \right\|^{2} + \frac{1}{2}\left\| {W_{3} } \right\|^{2} \hfill \\ & \tilde{G}^{T} \hat{G} = - \left\| {\tilde{G}} \right\|^{2} + \tilde{G}^{T} G \le - \frac{1}{2}\left\| {\tilde{G}} \right\|^{2} + \frac{1}{2}\left\| G \right\|^{2} . \hfill \\ \end{aligned} $$

(A.6)

Moreover, we have

$$ \begin{aligned} & \left| {\tilde{N}_{2} } \right| \le p_{2} \left( {\left| {e_{1} } \right| + \left| {e_{2} } \right| + \left| {\phi_{1} } \right| + \left| {\phi_{2} } \right|} \right) \hfill \\ & \left| {\tilde{N}_{3} } \right| \le p_{3} \left( {\left| {e_{1} } \right| + \left| {e_{2} } \right| + \left| {e_{3} } \right| + \left| {\phi_{1} } \right| + \left| {\phi_{2} } \right| + \left| {\phi_{3} } \right| + \varepsilon_{N3} } \right) \hfill \\ & \left| {\mu (\chi_{3} )} \right| \le \mu_{M} ,\left| {v_{2,c} - v_{2} } \right| \le \varepsilon_{f} ,\left| {\Delta u} \right| \le \varepsilon_{s} \hfill \\ & \left| {\alpha_{1} (t)} \right| \le \alpha_{1M} ,\left| {\alpha_{2} (t)} \right| \le \alpha_{2M} , \hfill \\ \end{aligned} $$

(A.7)

where p₂, p₃, ε_N3, μ_M, ε_f, ε_s, α_1M, and α_2M indicate some positive constants.

Based on (A.6) and (A.7), we can rearrange (A.5) as

$$ \begin{aligned} & \dot{V}_{L} \le - k_{1} e_{1}^{2} - \left( {k_{2} - k_{1} - p_{2} } \right)e_{2}^{2} - \left( {k_{3} - p_{3} } \right)e_{3}^{2} - k_{1} \phi_{1}^{2} - k_{2} \phi_{2}^{2} \hfill \\ &\quad\, - k_{3} \phi_{3}^{2} + \left| {\phi_{1} } \right|\left| {\phi_{2} } \right| + \left| {\phi_{2} } \right|\left| {\phi_{3} } \right| + \varepsilon_{f} \left| {\phi_{2} } \right| + \varepsilon_{s} \left| {\phi_{3} } \right| + p_{3} \left| {e_{1} } \right|\left| {e_{3} } \right| \hfill \\ &\quad\, + p_{2} \left| {e_{2} } \right|\left( {\left| {\phi_{1} } \right| + \left| {\phi_{2} } \right|} \right) + p_{3} \left| {e_{3} } \right|\left( {\left| {\phi_{1} } \right| + \left| {\phi_{2} } \right| + \left| {\phi_{3} } \right| + \varepsilon_{N3} } \right) \hfill \\ &\quad\, + \left( {k_{1}^{2} + p_{2} } \right)\left| {e_{1} } \right|\left| {e_{2} } \right| + p_{3} \left| {e_{2} } \right|\left| {e_{3} } \right| + k_{2} \left| {e_{2} } \right|\left| {\tilde{\chi }_{2} } \right| + \left| {e_{2} } \right|\left| {\tilde{\chi }_{D2} } \right| \hfill \\ &\quad\, + \mu_{M} \left| {e_{3} } \right| + \left| {e_{3} } \right|\left| {\tilde{\chi }_{D3} } \right| - \frac{1}{2}\omega_{o1} \left\| \zeta \right\|^{2} + \frac{{p_{2} }}{{\omega_{o1} }}\left\| \zeta \right\|\left\| {E_{o} H_{1} } \right\|\left( {\left| {e_{1} } \right| + \left| {e_{2} } \right|} \right) \hfill \\ &\quad\, + \frac{{p_{2} }}{{\omega_{o1} }}\left\| \zeta \right\|\left\| {E_{o} H_{1} } \right\|\left( {\left| {\phi_{1} } \right| + \left| {\phi_{2} } \right|} \right) + \left\| \zeta \right\|\left\| {E_{o} H_{2} } \right\|\frac{{\alpha_{1M} }}{{\omega_{o1}^{2} }} - \frac{1}{2}\omega_{o2} \left\| \delta \right\|^{2} \hfill \\ &\quad\, + p_{3} \left\| \delta \right\|\left\| {Y_{o} S_{1} } \right\|\left( {\left| {e_{1} } \right| + \left| {e_{2} } \right| + \left| {e_{3} } \right| + \left| {\phi_{1} } \right| + \left| {\phi_{2} } \right| + \left| {\phi_{3} } \right| + \varepsilon_{N3} } \right) \hfill \\ &\quad\, + \mu_{M} \left\| \delta \right\|\left\| {Y_{o} S_{1} } \right\| + \left\| \delta \right\|\left\| {Y_{o} S_{2} } \right\|\frac{{\alpha_{2M} }}{{\omega_{o2} }} + \left\| {\tilde{W}_{2} } \right\|\left\| {\eta_{2} (\overline{\chi }_{2d} )} \right\|\left| {\tilde{\chi }_{2} } \right| \hfill \\ &\quad\, + \frac{3}{{2\omega_{o1} }}\left\| {\tilde{W}_{2} } \right\|\left\| {\eta_{2} (\overline{\chi }_{2d} )} \right\|\left\| \zeta \right\| + \frac{1}{2}\left\| {\tilde{W}_{3} } \right\|\left\| {\eta_{3} (\overline{\chi }_{3d} )} \right\|\left\| \delta \right\| \hfill \\ &\quad\, - \frac{1}{2}\rho_{2} \left\| {\tilde{W}_{2} } \right\|^{2} - \frac{1}{2}\rho_{3} \left\| {\tilde{W}_{3} } \right\|^{2} + \frac{1}{2}\left\| {\tilde{G}} \right\|\left\| {\psi (\chi_{3} )} \right\|\left\| \delta \right\| \hfill \\ &\quad\,- \frac{1}{2}\rho_{G} \left\| {\tilde{G}} \right\|^{2} + \frac{1}{2}\rho_{2} \left\| {W_{2} } \right\|^{2} + \frac{1}{2}\rho_{3} \left\| {W_{3} } \right\|^{2} + \frac{1}{2}\rho_{G} \left\| G \right\|^{2} . \hfill \\ \end{aligned} $$

(A.8)

Applying on Young’s inequality, thus one gets

$$ \begin{aligned} \dot{V}_{L} &\le - k_{e1} e_{1}^{2} - k_{e2} e_{2}^{2} - k_{e3} e_{3}^{2} - k_{\phi 1} \phi_{1}^{2} - k_{\phi 2} \phi_{2}^{2} \\ &\quad\,- k_{\phi 3} \phi_{3}^{2} - k_{\zeta } \left\| \zeta \right\|^{2} - k_{\delta } \left\| \delta \right\|^{2} - k_{{\tilde{W}_{2} }} \left\| {\tilde{W}_{2} } \right\|^{2} \\ &\quad\,- k_{{\tilde{W}_{3} }} \left\| {\tilde{W}_{3} } \right\|^{2} - k_{{\tilde{G}}} \left\| {\tilde{G}} \right\|^{2} + \varepsilon_{L} , \\ \end{aligned} $$

(A.9)

where

$$ \begin{aligned} k_{e1} & = k_{1} - q_{1} - \frac{1}{2}p_{3} - \frac{{p_{2}^{2} }}{2} - \frac{{p_{3}^{2} }}{2}, \\ k_{e2} &= k_{2} - k_{1} - 2p_{2} - \frac{1}{2}(p_{3} + p_{2}^{2} + p_{3}^{2} ) \\ &\quad\,- \frac{{\left( {k_{1}^{2} + p_{2} } \right)^{2} }}{{q_{1} }} - \frac{{k_{2}^{2} }}{{q_{2} }} - q_{3} - q_{4} , \\ k_{e3} &= k_{3} - \frac{7}{2}p_{3} - \frac{{p_{3}^{2} }}{2} - \frac{1}{2}, \\ k_{\phi 1} & = k_{1} - \frac{1}{2} - \frac{1}{2}p_{2} - \frac{1}{2}p_{3} - \frac{{p_{2}^{2} }}{2} - \frac{{p_{3}^{2} }}{2}, \\ k_{\phi 2} & = k_{2} - \frac{3}{2} - \frac{1}{2}p_{2} - \frac{1}{2}p_{3} - \frac{{p_{2}^{2} }}{2} - \frac{{p_{3}^{2} }}{2}, \\ k_{\phi 3} & = k_{3} - 1 - \frac{1}{2}p_{3} - \frac{{p_{3}^{2} }}{2}, \\ k_{\zeta } &= \frac{1}{2}\omega_{o1} - q_{2} \omega_{o1}^{2} - \frac{{2\left\| {E_{o} H_{1} } \right\|^{2} }}{{\omega_{o1}^{2} }} - \frac{{\omega_{o1}^{4} }}{{q_{3} }} \\ &\quad\,- \frac{{\left\| {E_{o} H_{2} } \right\|^{2} }}{{2\omega_{o1}^{4} }} - q_{5} - \frac{1}{2} \\ \end{aligned} $$

$$ \begin{aligned} k_{\delta } &= \frac{1}{2}\omega_{o2} - \frac{{\omega_{o2}^{2} }}{{q_{4} }} - 4\left\| {Y_{o} S_{1} } \right\|^{2} - \frac{1}{{2\omega_{o2}^{2} }}\left\| {Y_{o} S_{2} } \right\|^{2} - 1, \\ k_{{\tilde{W}_{2} }} &= \frac{1}{2}\rho_{2} - \frac{{\omega_{o1}^{2} \eta_{2M}^{2} }}{{q_{5} }} - \frac{{9\eta_{2M}^{2} }}{{8\omega_{o1}^{2} }},k_{{\tilde{W}_{3} }} = \frac{1}{2}\rho_{3} - \frac{{\eta_{3M}^{2} }}{8}, \\ k_{{\tilde{G}}} &= \frac{1}{2}\rho_{G} - \frac{{\psi_{M}^{2} }}{8}, \\ \varepsilon_{L} &= \frac{1}{2}\rho_{2} \left\| {W_{2} } \right\|^{2} + \frac{1}{2}\rho_{3} \left\| {W_{3} } \right\|^{2} + \frac{1}{2}\rho_{G} \left\| G \right\|^{2} \\ &\quad \, + \alpha_{1M}^{2} + \frac{1}{2}\mu_{M}^{2} + \frac{1}{2}\varepsilon_{f}^{2} + \frac{1}{2}\varepsilon_{s}^{2} + \varepsilon_{N3}^{2} p_{3}^{2} , \\ \end{aligned} $$

(A.10)

in which q₁, q₂, q₃, q₄, η_2M, η_3M, and ψ_M indicate some positive constants. Specially, η_2M, η_3M, and ψ_M denote the upper bounds of $\eta_{2} (\overline{\chi }_{2d} )$, $\eta_{3} (\overline{\chi }_{3d} )$, and ψ(χ₃), respectively.

From (A.9), we have

$$ \dot{V}_{L} \le - \rho_{L} V_{L} + \varepsilon_{L} , $$

(A.11)

where ρ_L = 2 min{k_e1, k_e2, k_e3, k_ϕ1, k_ϕ2, k_ϕ3, k_ζ/λ_max(E_o), k_δ/λ_max(Y_o),${{k_{{\tilde{W}_{2} }} } \mathord{\left/ {\vphantom {{k_{{\tilde{W}_{2} }} } {\lambda_{\max } (\Upsilon_{2}^{ - 1} )}}} \right. \kern-\nulldelimiterspace} {\lambda_{\max } (\Upsilon_{2}^{ - 1} )}}$,${{k_{{\tilde{W}_{3} }} } \mathord{\left/ {\vphantom {{k_{{\tilde{W}_{3} }} } {\lambda_{\max } (\Upsilon_{3}^{ - 1} )}}} \right. \kern-\nulldelimiterspace} {\lambda_{\max } (\Upsilon_{3}^{ - 1} )}}$,${k_{{\tilde{G}}} } \mathord{\left/ {\vphantom {{k_{{\tilde{G}}} } {\lambda_{\max } (\Gamma^{ - 1} )}}} \right. \kern-\nulldelimiterspace}\break {\lambda_{\max } (\Gamma^{ - 1} )}$} indicates a positive constant.

Furthermore, we have

$$ V_{L} (t) \le V_{L} (0)e^{{ - \rho_{L} t}} + \frac{{\varepsilon_{L} }}{{\rho_{L} }}\left( {1 - e^{{ - \rho_{L} t}} } \right). $$

(A.12)

Noting the expressions in (A.1) and (A.12), we can infer that all system signals in the considered closed-loop servomechanism always stay bounded [40]. Consequently, all the results in Theorem 1 have been completely proved.