Caputo Fractal Fractional Order Derivative of Soil Pollution Model Due to Industrial and Agrochemical

Abstract

This paper narrates a non-linear and non-local Caputo fractal fractional operator of eco epidemic model with the advance of soil pollution considered in five compartments. The qualitative analysis of solutions such as existence and uniqueness of the model is carried out by using the standard condition of Schauder’s fixed point theorem and Banach Contraction principle. The local and global stability are characterized with the help of basic reproduction number. The Ulam-Hyer stability is analyzed for the small perturbation. The Power law kernel is used to get a reliable result for the soil pollution model. Analytical solution studied by means of Modified Euler method. Numerical simulation of Euler scheme algorithm is performed to show the effects of various fractional orders $(0.5<\eta <1)$ and validating the theoretical parameter values of real time data by the support of MATLAB.

Introduction

Environmental pollution is a world’s greatest problem facing humanity and leading environmental issues of mortality and mobility. In this regard, soil is a natural resource which contains organic material, water, air and weathered. It is an important aspect for living organism in the form of agricultural soil. The main global issue is a contamination of soil occurs due to pesticides, fertilizers, compost, substandard manure, anthropogenic activities and industrial activities. In addition to this the immeasurable quantities of human-made unwanted products, sludge and new waste treatment plants. Also, the treacherous polluted water leading or causing to soil pollution.

The pollution is due to agricultural run-off and heavy metals that has been studied by various authors [14, 18, 25, 44, 45]. Nazzal et al. [31] reported the case study in Punjab where there is a huge amount of agrochemicals like fertilizers, pesticides, fungicides, weedicides are used in agricultural soil which are ultimately increase the heavy metals in the agricultural land. Zhao et al. find that roadsides activities like vehicular emissions, tyre abrasions etc. leads to damage the agricultural soil in Jalandhar [50]. In Tamil Nadu, the area under slow permeable soil in around 7,54,631 ha (7.5% of TGA). The Bengal delta is one of the most arsenic polluted areas in the world. Concentrations of arsenic in groundwater are elevated by geogenic sources from aquifer sediments. The main arsenic in the soils is reported in Bangladesh and India. In Tamil Nadu, Industrial effluents and municipal waste water are usually contained high amount of heavy metals such as As, Cd, Cr, Cu, Fe, Hg, Mn, Ni, Pb and Zn Arora et al. [7]. Continuous usage of these metals in agricultural soil may cause serious results in metal accumulation in surface soil which has been studied by Gupta et al. [15]. Some heavy metals are useful for plants (Zn, Cu, Fe, Mn, Mo and Co) and animals (Cr, Ni and Sn) growth. The common hazards heavy metals for plant growth and animals are As, Cd, Hg and Pb reported by Greenland and Hayes [14]. The huge amount of health issues related to the environment poisoning is due to the usage of Cd and Hg. There is increase amount of Pb in the infant blood may cause major issues. Krosshaven et al. [22] have investigated that an anthropogenic pollution of heavy metals and their phytotoxicities.

Mathematical model is a major tool to investigate many physical, biological and ecological problems. Eco-epidemiology is a study of disease that move from one source to another source by the transmission which includes air droplet, water, physical contact, industrial effluents and man made mistakes. Differential, difference equation and statistical estimation are used to study these transmission diseases [28, 30]. In the recent years many authors are proved that these ecological transmission diseases have studied through Fractional calculus. It is a dominant tool to get the accurate value of many physical problems. Study of eco-epidemic models maintain high memory which are connected to non Markovian dynamics [1, 3]. Nevertheless, most of the biological and ecological models are taken in classical methods of nonlinear differential equation. There are many investigations done in comparative study of ordinary differential and fractional differential equations. Fractional calculus won the role by the usage of high maintains memory capacitor and their hereditary property. Many researches embarked to study the power law kernel, Mittag Leffer kernel and exponential kernel including RL (Riemann-Lioville) and Caputo operator sense [4, 5, 7, 47, 48]. There exists a nonconforming derivative kind known as fractal dimension, in fractional order differential equation which helps to study the possible physical problems for a general physical law. Fractal dimension is applied in well-known Fourier’s law, Darcy’s law, Fricks law and many real world applications such as aquifer, porous media, turbulence etc. Fractal dimension is the self-similar singularities since it may have used to study the Electrochemical process, diagnostic imagining, physical, neuroscience, image analysis, physiology, acoustic and Riemann zeta zeros [13, 36].

Atangana Abdon, introduce a new derivative of fractal objects that are very efficient, non-local and memory resistor to solve many real world fractal operators. The fractal fractional operator is the sub diffusion and super diffusion problem in complex media of heterogeneous self-similar aquifer [1, 42]. Followed by many authors [21, 23, 39] show their idea to improve characteristics of factor dimensions, for example in [10] the authors established a fractional model used in thermal analysis of GO-Na Alg-Gr hybrid nano fluid flow in shape effects by considering its channel and Power law kernel is used to define the fractional equation. In [3], the authors developed to analyze the complex dynamics of multi strain TB model in the sense of Atangana Baleanue fractal fractional order and the nonlinear dynamics chaotic behaviors are proposed. The nonlinear fractional order model for various real phenomena of magneto dynamics and environmental flow process therein [32] and partial differential equation of fractional order model in the caputo sense is given in [33]. In [8], the author analyzed fractal fractional order of HIV-AIDS model in the sense of Caputo Fabrizio. The numerical scheme on Newton polynomial of fractal fractional model Q-Fever described through Atangana Baleanu (Mittag Leffler kernel) in [19, 20]. The inverse source problem investigated for diffusion equation in a time–space fractional sense therein [34]. In [35], the author proposed the numerical algorithm for the van der pol damping model in terms of reproductive kernel and AB fractional methodology. Adnan et al. [4], read up on a Atangana Baleanu Caputo fractal fractional order nonlinear SIQR pandemic model of COVID 19 disease. Here, the non-integer and fractal dimension taken in between 0 and 1. Followed by many authors examined the nature of fractal fractional order model in pandemic disease COVID 19 model [19, 43]. In author [37, 38], incorporate vaccination for COVID 19 people, in this regard vaccinated people is not totally protected and viable to infection after vaccination offered. Also, some elementary restriction for epidemic SIR model is Confiscated. The Caputo-Fabrizio fractional derivative model for hearing loss in children caused by the mumps virus [17] and a wavelet based numerical scheme for SEIR model of measles by using Genocchi polynomials is investigated [40]. The generalization of fractional derivatives of electrical circuits in the sense of Caputo-Fabrizio is also presented in [6].

It is important to scrutinize the qualitative and quantitative analysis of dynamical behavior of the model. Qualitative analysis means equilibrium, existence and uniqueness of various form of stability. In this review the different form of stability is included in many literatures as in the sense of Lyapunov, exponential, Asymptotic etc. Most important style of stability is inspected by Ulam in 1940 [41] named as Ulam stability. Later on, Hyer answered the question raised by Ulam in the context about the functional behavior of the stability in the Banach space [13]. Ulam-Hyer stability is indispensable in the point of numerical and optimization since it is viaduct between numerical and exact solutions. In [16], Khan et al. investigated advection reaction diffusion fractional order system via Ulam stability and he also studied the Ulam- Hyer stability of the co infection HIV-TB model through fractional AB derivative. Consecutively many researches [49] built numerous fractional order mathematical models and analyzed the dynamical behavior using Ulam stability. Finding the numerical solution of differential equation is the important aspects, for example [32] Shabir Ahmad et al. studied the COVID 19 mathematical model of fractional order using Modified Euler method. Tian wei Zhang, Yongkin Li [46] developed the Mittag Leffler Euler differences for Caputo fractional order system and established the implicit form of fractional differential equations by using constant variation method. The explicit formulae for the analytic solution of peak time epidemic model was therein [26]. In [27], Simplicity reaction diffusion model is offered to explore the spatio temporal development of indoor aerosols containing respiratory COVID 19. The main aim of this document is to propose a mathematical model of fractal fractional soil pollution in the sense of caputo and power law kernel. The upcoming research work is organized as follow: In Sect. 1, we give brief introduction about fractal fractional order. In Sect. 2, we study the general description of model framework and mathematical model of soil pollution due to industrial and agricultural disposal. Section 3 recollects the basic definitions of Caputo and Riemann Liouvilles derivatives and integrals. In Sect. 4, we examine the feasibility, uniqueness and existence and boundedness of the model. Section 5 describes the local, global stability of pollution free equilibrium. Section 6 devotes the numerical approximate solution of the given model using Euler method. In Sect. 7, we present the numerical simulation and discussion for the case study of Ranipet taluk, Vellore District, Tamil Nadu for various samples in two zone (near industrial area and agricultural land) using MATLAB.

Description of Caputo Fractal Fractional Order Model

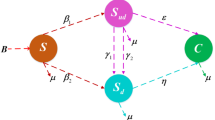
The dynamical soil pollution model consists of five compartments at any time instant of the real valued fractal fractional order namely, Susceptible soil area S(t), Industrial pollution I(t), Agricultural pollution A(t), Action taken by applying necessary remedies to the soil R(t) and return to normal state of healthy soil H(t). Soils are polluted by the anthrophonic activities, agricultural chemicals or improper waste disposal. It is important to take necessary action and apply the desirable remedies to the polluted soil by soil washing, thermal desorption and bioremediation. This remediation processes may produce healthy soil. In this, some of the soil particles washed or loosened their nature and allows the effect of soil erosion. From the above assumption, the transmission of soil pollution under treatment measures is shown in the compartment Fig. 1.

Fig. 1

Schematic diagram for SIARH model

The mathematical representation of Caputo fractal fractional order model is presented as follows,

$${}_{0}{}^{CFF}{D}^{\eta ,\gamma }\left(S\left(t\right)\right)=\alpha -\frac{{\beta }_{1}I\left(t\right)S\left(t\right)+{\beta }_{2}A(t)S(t)}{N}-\mu S\left(t\right)$$

$${}_{0}{}^{CFF}{D}^{\eta ,\gamma }(I(t))=\frac{{\beta }_{1}I(t)S\left(t\right)}{N}-{\vartheta }_{1}I\left(t\right)-{\varepsilon }_{1}I(t)-\mu I(t)$$

$${}_{0}{}^{CFF}{D}^{\eta ,\gamma }(A(t))=\frac{{\beta }_{2}A(t)S\left(t\right)}{N}-{\vartheta }_{2}A\left(t\right)-{\varepsilon }_{2}A(t)-\mu A(t)$$

$${}_{0}{}^{CFF}{D}^{\eta ,\gamma }\left(R\left(t\right)\right)={\vartheta }_{1}I\left(t\right)+{\vartheta }_{2}A\left(t\right)-aR\left(t\right)-\mu R\left(t\right)$$

$${}_{0}{}^{CFF}{D}^{\eta ,\gamma }(H(t))=aR\left(t\right)-\mu H(t)$$

(2.1)

the above model subject to the initial conditions $S\left(0\right)={S}^{0}\ge 0, I\left(0\right)={I}^{0}\ge 0, A\left(0\right)={A}^{0}\ge 0,R\left(0\right)={R}^{0}\ge 0, H\left(0\right)={H}^{0}\ge 0$. We take the function S, I, A, R, H and their derivatives are continuous at $t\ge 0.$

The descriptions of the parameters are represented as follows:

$\alpha$—The per capita fertility rate of soil,

${\beta }_{1}$—Pollution transmission rate due to industrial disposal.

${\beta }_{2}$—Pollution transmission rate due to Agricultural disposal.

${\vartheta }_{1}$—Action taken rate for the polluted soil due to industrial stress.

${\vartheta }_{2}$– Action taken rate for the polluted soil due to agricultural runoff.

${\varepsilon }_{1}$—Expiring rate due to heavy metals released by industries.

${\varepsilon }_{2}$—Expiring rate due to heavy metals used in agricultural cultivation.

$\mu$—Natural demise rate of different compartment.

a—Bring back the nature of vigorous soil.

Preliminaries of Fractal Fractional Derivatives

Definition

3.1: [1] Let u(t) be a continuous and fractional derivative on (m, n). Let $0\le \eta , \gamma <1$ where $\eta$ is a fractional order and $\gamma$ is fractional dimension then the fractal fraction in the sense of Caputo having power law type kernel is defined as,

$${}_{0}{}^{FFP}{D}^{\eta ,\gamma }(u(t))=\frac{1}{\Gamma \left(m-\eta \right)}\int_{0}^{t}{\frac{{d}^{\eta }}{d{\phi }^{\gamma }}\left(t-\phi \right)}^{m-\eta -1}\left(u\left(\phi \right)\right)d\phi $$

(3.2)

where $m-1<\eta ,\gamma \le m\in N$ and $\frac{{d}^{\eta }}{d{\phi }^{\gamma }}u\left(\phi \right)={\mathrm{lim}}_{t\to \phi }\frac{{u}^{\eta }\left(t\right)-{u}^{\eta }(\phi )}{{t}^{\gamma }-{\phi }^{\gamma }}.$

Definition

3.2: [1] Let u(t) be a continuous on (m, n) so integral regarding fractal-fractional concept for u(t) subject to $\eta$ order is.

$${}_{0}{}^{FFP}{D}^{\eta ,\gamma }(u(t))=\frac{\gamma }{\Gamma \left(m-\eta \right)}\int_{0}^{t}{\left(t-\phi \right)}^{m-\eta -1}{\phi }^{\eta -1}\left(u\left(\phi \right)\right)d\phi $$

(3.3)

Qualitative Analysis of the Model

Existence and Uniqueness of the Solution

The existence and uniqueness of the fractional order model devoted by applying integral and initial condition to the model (2.1),

$$S\left(t\right)={S}^{0}+\frac{\gamma }{\Gamma (\eta )}{\int }_{0}^{t}{s}^{\eta -1}{\left(t-s\right)}^{\eta -1}\left[\alpha -\frac{{\beta }_{1}I\left(t\right)S\left(t\right)+{\beta }_{2}A\left(t\right)S\left(t\right)}{N}-\mu S\left(t\right)\right]ds$$

$$I\left(t\right)={I}^{0}+\frac{\gamma }{\Gamma (\eta )}{\int }_{0}^{t}{s}^{\eta -1}{\left(t-s\right)}^{\eta -1}\left[\frac{{\beta }_{1}I\left(t\right)S\left(t\right)}{N}-{\vartheta }_{1}I\left(t\right)-{\varepsilon }_{1}I\left(t\right)-\mu I\left(t\right)\right]ds$$

$$P\left(t\right)={P}^{0}+\frac{\gamma }{\Gamma (\eta )}{\int }_{0}^{t}{s}^{\eta -1}{\left(t-s\right)}^{\eta -1}\left[\frac{{\beta }_{2}A\left(t\right)S\left(t\right)}{N}-{\vartheta }_{2}A\left(t\right)-{\varepsilon }_{2}A\left(t\right)-\mu A\left(t\right)\right]ds$$

(4.1)

$$R\left(t\right)={R}^{0}+\frac{\gamma }{\Gamma (\eta )}{\int }_{0}^{t}{s}^{\eta -1}{\left(t-s\right)}^{\eta -1}\left[{\vartheta }_{1}I\left(t\right)+{\vartheta }_{2}A\left(t\right)-aR\left(t\right)-\mu R\left(t\right)\right]ds$$

$$H\left(t\right)={H}^{0}+\frac{\gamma }{\Gamma (\eta )}{\int }_{0}^{t}{s}^{\eta -1}{\left(t-s\right)}^{\eta -1}\left[aR\left(t\right)-\mu H\left(t\right)\right]ds$$

Rewrite the given system (2.1) as,

$${}_{0}{}^{C}{D}_{t}^{\eta }S\left(t\right)=\gamma {t}^{\gamma -1}A(t,S,T,A,R,H)$$

$${}_{0}{}^{C}{D}_{t}^{\eta }I\left(t\right)=\gamma {t}^{\gamma -1}A(t,S,T,A,R,H)$$

$${}_{0}{}^{C}{D}_{t}^{\eta }A\left(t\right)=\gamma {t}^{\gamma -1}A(t,S,T,A,R,H)$$

(4.2)

$${}_{0}{}^{C}{D}_{t}^{\eta }R\left(t\right)=\gamma {t}^{\gamma -1}A\left(t,S,T,A,R,H\right)$$

$${}_{0}{}^{C}{D}_{t}^{\eta }H(t)=\gamma {t}^{\gamma -1}A(t,S,T,A,R,H)$$

Generalized form of the above system is,

$${}_{0}{}^{C}{D}_{t}^{\eta }J\left(t\right)=\gamma {t}^{\gamma -1}L\left(t,J\left(t\right)\right)$$

(4.3)

$$J\left(0\right)={J}^{0}$$

Applying the fractional integral in (4.3),

$$J\left(t\right)=J\left(0\right)+\frac{\gamma }{\Gamma (\eta )}\int_{0}^{t}{s}^{\eta }{\left(t-s\right)}^{\eta -1}L(s,J(s))\,ds$$

(4.4)

where, $J\left(t\right)=\left\{S\left(t\right),I\left(t\right),A\left(t\right),R\left(t\right),H\left(t\right)\right\}, J\left(0\right)=\left\{S\left(0\right),I\left(0\right),A\left(0\right),R\left(0\right),H\left(0\right)\right\},L\left(s,J\left(s\right)\right) =\{A\left(t,S,I,A,R,H\right), B\left(t,S,I,A,R,H\right), C\left(t,S,I,A,R,H\right), D\left(t,S,I,A,R,H\right), E\left(t,S,I,A,R,H\right)$. Let us define a Banach space $B=C\times C\times C\times C\times C$ and $P=C [0,T]$ under the norm operator, $\Vert J\Vert ={\mathrm{max}}_{t\in [0,T]}|S\left(t\right)+I\left(t\right)+A\left(t\right)+R\left(t\right)+H(t)|$. Consider the nonlinear term satisfies the following assumption,

(A1) For any function $J\in B$, there exists ${f}_{n}>0$ and ${M}_{n}>0$ satisfies the following relation,

$$\left|L\left(t,J\left(t\right)\right)\right|<{f}_{n}\left|J\left(t\right)\right|+{M}_{n}$$

(4.5)

(A2) For each $J, \overline{J }\in B$, there exists a constant ${\phi }_{n}>0$ such that,

$$\left|L\left(t,J\left(t\right)-L\left(t,\stackrel{-}{J\left(t\right)}\right)\right)\right|<{\phi }_{n}|J\left(t\right)-\stackrel{-}{J(t)}|$$

(4.6)

Feasibility of the System

Theorem

4.1: The region $\Delta =\left\{S\left(t\right), I\left(t\right),A\left(t\right),R\left(t\right),H\left(t\right)\in {R}_{+}^{5}:0\le E\left(t\right)\le \frac{\alpha }{\mu +{b}_{1}+{b}_{2}}\right\}$ is bounded and feasible for the model (2.1).

Proof

Let $E\left(t\right)=S\left(t\right)+I\left(t\right)+A\left(t\right)+R\left(t\right)+H(t)$, take factional derivative we have,

$$\begin{aligned}{}_{0}{}^{CFF}{D}^{\eta ,\gamma }\left(E\left(t\right)\right)&={}_{0}{}^{CFF}{D}^{\eta ,\gamma }\left(S\left(t\right)\right)+{}_{0}{}^{CFF}{D}^{\eta ,\gamma }\left(I\left(t\right)\right)+{}_{0}{}^{CFF}{D}^{\eta ,\gamma }\left(A\left(t\right)\right)\\ &\quad +{}_{0}{}^{CFF}{D}^{\eta ,\gamma }\left(R\left(t\right)\right)+{}_{0}{}^{CFF}{D}^{\eta ,\gamma }\left(H\left(t\right)\right)\end{aligned}$$

$$=\alpha -\frac{{\beta }_{1}I\left(t\right)S\left(t\right)+{\beta }_{2}A\left(t\right)S\left(t\right)}{N}-\mu S\left(t\right)+\frac{{\beta }_{1}I\left(t\right)S\left(t\right)}{N}-{\vartheta }_{1}I\left(t\right)-{\varepsilon }_{1}I\left(t\right)-\mu I\left(t\right)+\frac{{\beta }_{2}A\left(t\right)S\left(t\right)}{N}-{\vartheta }_{2}A\left(t\right)-{\varepsilon }_{2}A\left(t\right)-\mu A\left(t\right)+{\vartheta }_{1}I\left(t\right)+{\vartheta }_{2}A\left(t\right)-aR\left(t\right)-\mu R\left(t\right)+aR\left(t\right)-\mu H(t)$$

$$\le \alpha -(\mu +{b}_{1}+{b}_{2})(E(t))$$

$${}_{0}{}^{CFF}{D}^{\eta ,\gamma }\left(E\left(t\right)\right)+\left(\mu +{b}_{1}+{b}_{2}\right)E\left(t\right)\le \alpha $$

$$E\left(t\right)\le \frac{\alpha }{\mu +{b}_{1}+{b}_{2}}+c{e}^{-(\mu +{b}_{1}+{b}_{2})}$$

(4.7)

where c is the constants of integration, when t approaches to infinity we have

$$E\left(t\right)\le \frac{\alpha }{\mu +{b}_{1}+{b}_{2}}$$

Hence the feasible and bounded region for the model (2.1) is $\Delta =\left\{S\left(t\right), I\left(t\right),A\left(t\right),R\left(t\right),H\left(t\right)\in {R}_{+}^{5}:0\le E\left(t\right)\le \frac{\alpha }{\mu +{b}_{1}+{b}_{2}}\right\}.$

If $S\left(t\right),I\left(t\right),A\left(t\right),R\left(t\right) and H(t)$ are non-negative and bounded then there exist some positive constants ${\Delta }_{1},{\Delta }_{2},{\Delta }_{3},{\Delta }_{4},{\Delta }_{5}$ such that $\left|\left|S\left(t\right)\right|\right|\le {\Delta }_{1}, \left|\left|I\left(t\right)\right|\right|\le {\Delta }_{2}, \left|\left|A\left(t\right)\right|\right|\le {\Delta }_{3}, \left|\left|R\left(t\right)\right|\right|\le {\Delta }_{4},\left|\left|H\left(t\right)\right|\right|\le {\Delta }_{5}.$

Theorem

4.2: If the assumption holds with the mapping $L:\left[0,T\right]\times B\to R$, then there exists atleast one solution holds for model (2.1).

Proof

If L is continuous, then N is also continuous. Now, to prove N is completely continuous.

Let $H=\{J\in B:\Vert J\Vert <R\}$. For each $J\in B$,

$$\Vert N(S(t))\Vert ={\mathrm{max}}_{t\in [0,T]}\left|S\left(0\right)+\frac{\gamma }{\Gamma \left(\eta \right)}\int_{0}{t}{s}^{\eta -1}{\left(t-s\right)}^{\eta -1}L\left(s,S\left(s\right)\right)\,ds\right|$$

$$\le S\left(0\right)+{\mathrm{max}}_{t\in [0.T]}\frac{\gamma }{\Gamma (\eta )}\int_{0}^{t}{s}^{\eta -1}{\left(t-s\right)}^{\eta -1}\left|L\left(s,S\left(s\right)\right)\right|\,ds$$

$$\le S\left(0\right)+\frac{\gamma {T}^{\eta +\gamma -1}}{\Gamma \left(\eta \right)}\left({f}_{n}\left|J\left(t\right)\right|+{M}_{n}\right)\overline{\Phi }\left(\eta ,\gamma \right)\le\Delta $$

$\overline{\Phi }\left(\eta ,\gamma \right)$ is the beta function. Therefore, N is uniformly bounded. Now, to prove N is equicontinuity. Let us consider ${t}_{1}<{t}_{2}\le T.$

$$\begin{aligned}\left|N\left(J\left({t}_{2}\right)\right)-N(J\left({t}_{1}\right))\right| &=\left|\frac{\gamma }{\Gamma \left(\eta \right)} \int_{0}{{t}_{2}}{s}^{\eta -1}{\left({t}_{2}-1\right)}^{\eta -1}L\left(s,J\left(s\right)\right)\, ds\right.\nonumber\\&\quad\left. -\frac{\gamma }{\Gamma \left(\eta \right)} \int_{0}{{t}_{1}}{s}^{\eta -1}{\left({t}_{1}-1\right)}^{\eta -1}L\left(s,J\left(s\right)\right)\,ds\right|\end{aligned}$$

$$\le \frac{\gamma }{\Gamma \left(\eta \right)}({f}_{n}\left|J\left(t\right)\right|+{M}_{n})\overline{\Phi }\left(\eta ,\gamma \right)({t}_{2}^{\eta +\gamma -1}-{t}_{1}^{\eta +\gamma -1})$$

When ${t}_{1}\to {t}_{2}$ then $\left|N\left(J\left({t}_{2}\right)\right)-N(J\left({t}_{1}\right))\right|\to 0.$ Therefore from Arzela-Ascoli theorem N is completely continuous. Hence the model (2.1) provides atleast one solution by using “Schauder’s fixed point theorem.

Theorem

4.3: If the assumption (A2) holds true for some $\rho <1$ then the model (2.1) has atmost one solution, where $\rho =\frac{\gamma }{\Gamma \left(\eta \right)}{T}^{\eta +\gamma -1}H\left(\eta ,\gamma \right).$

Proof

Assume for any $J,\overline{J }\in B$,

$$ \begin{aligned}\left|\left|N\left(J\right)-N\left(\overline{J }\right)\right|\right| &=\left|\left|J\left(0\right)+\frac{\gamma }{\Gamma \left(\eta \right)}\int_{0}{t}{s}^{\eta -1}{\left(t-s\right)}^{\eta -1}L\left(s,J\left(s\right)\right)ds-\stackrel{-}{J\left(0\right)}\right.\right.\\& \quad \left.\left. +\frac{\gamma }{\Gamma \left(\eta \right)}\int_{0}{t}{s}^{\eta -1}{\left(t-s\right)}^{\eta -1}L\left(s,\stackrel{-}{J\left(s\right)}\right)ds\right|\right|\end{aligned}$$

$$\le {\mathrm{max}}_{t\in [0,T]}\left|\frac{\gamma }{\Gamma \left(\eta \right)}\int_{0}{t}{s}^{\eta -1}{\left(t-s\right)}^{\eta -1}\left[L\left(s,J\left(s\right)\right)-L\left(s,\overline{J }\left(s\right)\right)\right]\,ds\right|$$

$$\le \left[\frac{\gamma }{\Gamma \left(\eta \right)}{T}^{\eta +\gamma -1}\overline{\Phi }\left(\eta ,\gamma \right)\right]\Vert J-\overline{J }\Vert \le \rho \left|\left|J-\overline{J }\right|\right| \le \left|\left|J-\overline{J }\right|\right| for \rho <1.$$

Thus, the operator N satisfies the contraction condition. The given model (2.1) has unique solution by using the Banach contraction principle.

Equilibrium and Stability Analysis

Ulam- Hyer Stability

Definition

5.1: The model (2.1) is Ulam-Hyer stable if there exists ${N}_{\eta ,\gamma }\ge 0$ such that for any r > 0 and for any $J\in (\left[0,T\right],R)$ satisfies the condition $\left|{}_{0}{}^{CFF}{D}^{\eta ,\gamma }J\left(t\right)-L\left(t,J\left(t\right)\right)\right|<r, t\in \left[0,T\right]$ and there exist a unique solution $\omega \in (\left[0,T\right],R)$ such that $\left|J\left(t\right)-\omega \left(t\right)\right|\le {N}_{\eta ,\gamma }r , t\in \left[0,T\right].$

Now for the small perturbation $\phi \in C[0,T]$ satisfies the following condition.

$\left|\Phi \left(t\right)\right|\le r$, for $r>0.$

$${}_{0}{}^{CFF}{D}^{\eta ,\gamma }J\left(t\right)=L\left(t,J\left(t\right)\right)+\Phi \left(t\right).$$

Lemma

5.1: Assumption (A3) and (A4) holds true and $\rho <1$ then the solution of the model (2.1) is Ulam-Hyer stable.

Proof

There exist any unique solution $\omega \in B$ and for any solution $J\in B$ we have,

$$\begin{aligned}{} \left|J\left(t\right)-\omega \left(t\right)\right| & =\left|J\left(t\right)-\left[\omega \left(0\right)+\frac{\gamma }{\Gamma \left(\eta \right)}\int_{0}{t}{s}^{\gamma -1}{\left(t-s\right)}^{s-1}L\left(s,J\left(s\right)\right)ds\right]\right| \\ & \le \left|J\left(t\right)-(J\left(0\right)+\frac{\gamma }{\Gamma \left(\eta \right)}\int_{0}{t}{s}^{\eta -1}{\left(t-s\right)}^{\eta -1 }L\left(s,J\left(s\right)\right)ds) \right|\\ &\qquad +\left|J\left(0\right)+\frac{\gamma }{\Gamma \left(\eta \right)}\int_{0}{t}{s}^{\eta -1}{\left(t- s\right)}^{\eta -1 }L\left(s,J\left(s\right)\right)ds\right| \\ &\qquad -\left|\omega (0)+\frac{\gamma }{\Gamma \left(\eta \right)}\int_{0}{t}{s}^{\eta -1}{\left(t-s\right)}^{\eta -1 }L\left(s,J\left(s\right)\right)ds\right| \\ & \le {\eta }_{\eta ,\gamma }^{*}r+\left(\frac{\gamma }{\Gamma \left(\eta \right)}{T}^{\eta +\gamma -1}\overline{\Phi }\left(\eta ,\gamma \right)\right){L}_{n}\left|J\left(t\right)-\omega \left(t\right)\right| \\ & \le {\eta }_{\eta ,\gamma }^{*}r+\rho \left|J\left(t\right)-\omega \left(t\right)\right| \\ & \Vert J-\omega \Vert \le {N}_{\eta ,\gamma }r\end{aligned}$$

where ${N}_{\eta ,\gamma }=\frac{{\eta }^{*}}{1-\rho }$

Basic Reproduction Number ${(\mathfrak{R}}_{0})$

The next generation matrix is used to find the basic reproduction number $({\mathfrak{R}}_{0})$ of the model (2.1),

Consider, ${}_{0}{}^{CFF}{D}^{\eta ,\gamma }E\left(t\right)=F\left(t\right)-V\left(t\right)$,

where, $F\left(t\right)=\left(\begin{array}{ccc}{\beta }_{1}{S}_{1}& 0& 0\\ {\beta }_{2}{S}_{2}& 0& 0\\ 0& 0& 0\end{array}\right)$,

$${V}^{-1}\left(t\right)=\left(\begin{array}{ccc}\frac{1}{{\vartheta }_{1}+\mu +{\varepsilon }_{1}}& 0& 0\\ 0& \frac{1}{{\vartheta }_{2}+\mu +{\varepsilon }_{2}}& 0\\ -\frac{{\vartheta }_{1}}{({\vartheta }_{1}+\mu +{\varepsilon }_{1})({\vartheta }_{2}+\mu +{\varepsilon }_{2})(a+\mu )}& -\frac{{\vartheta }_{2}}{({\vartheta }_{1}+\mu +{\varepsilon }_{1})({\vartheta }_{2}+\mu +{\varepsilon }_{2})(a+\mu )}& \frac{1}{(a+\mu )}\end{array}\right)$$

Then the spectral radius of the matrix of $\rho \left(F{V}^{-1}\right)={\mathfrak{R}}_{0}=\frac{\alpha {\beta }_{1}}{{\vartheta }_{1}+\mu +{\varepsilon }_{1}}$.

Equilibrium Points

There are two equilibrium points exists for the model (2.1). For finding the equilibrium, equating right side of Eq. (2.1) to zero,

$$\alpha -\frac{{\beta }_{1}I\left(t\right)S\left(t\right)+{\beta }_{2}A\left(t\right)S\left(t\right)}{N}-\mu S\left(t\right)=0$$

$$\frac{{\beta }_{1}I(t)S\left(t\right)}{N}-{\vartheta }_{1}I\left(t\right)-{\varepsilon }_{1}I\left(t\right)-\mu I\left(t\right)=0$$

(5.1)

$$\frac{{\beta }_{2}A(t)S\left(t\right)}{N}-{\vartheta }_{2}A\left(t\right)-{\varepsilon }_{2}A\left(t\right)-\mu A\left(t\right)=0$$

$${\vartheta }_{1}I\left(t\right)+{\vartheta }_{2}A\left(t\right)-aR\left(t\right)-\mu R\left(t\right)=0$$

$$aR\left(t\right)-\mu H\left(t\right)=0$$

By solving the above equations, we obtain the two steady states of equilibrium point for the model (2.1),

Pollution free equilibrium: ${S}_{f}(\frac{\alpha }{\mu },\mathrm{0,0},\mathrm{0,0})$

The Model (2.1) has a unique pollution existence equilibrium point in the interior of $\Delta$ that is given by,

$${S}^{*}\left(t\right)=\frac{\alpha }{{\beta }_{1}{I}^{*}\left(t\right)+{\beta }_{2}{A}^{*}\left(t\right)+\mu }; \,\,{R}^{*}=\frac{{\vartheta }_{1}{I}^{*}\left(t\right)+{\vartheta }_{2}{A}^{*}\left(t\right)}{a+\mu };\,\, {H}^{*}\left(t\right)=\frac{a{R}^{*}\left(t\right)}{\mu }.$$

Here, $\left({I}^{*}\left(t\right), {A}^{*}\left(t\right)\right)$ represents the positive interaction point of the following two isocline,

$$f\left({I}^{*}, {A}^{*}\right)={\beta }_{1}{I}^{*}\left(t\right)\left(\frac{\alpha }{{\beta }_{1}{I}^{*}\left(t\right)+{\beta }_{2}{A}^{*}\left(t\right)+\mu }\right)-\left({\vartheta }_{1}+{\varepsilon }_{1}+\mu \right){I}^{*}\left(t\right)=0$$

(5.2)

$$g\left({I}^{*}, {A}^{*}\right)={\beta }_{2}{A}^{*}\left(t\right)\left(\frac{\alpha }{{\beta }_{1}{I}^{*}\left(t\right)+{\beta }_{2}{A}^{*}\left(t\right)+\mu }\right)-\left({\vartheta }_{2}+{\varepsilon }_{2}+\mu \right){A}^{*}\left(t\right)=0$$

(5.3)

Putting ${A}^{*}=0,$ and ${I}^{*}=0$ in Eq. (5.2), (5.3) respectively, then the two isoclines become,

$$f\left({I}^{*},0\right)={\beta }_{1}{I}^{*}\left(t\right)\left(\frac{\alpha }{{\beta }_{1}{I}^{*}\left(t\right)+\mu }\right)-\left({\vartheta }_{1}+{\varepsilon }_{1}+\mu \right){I}^{*}\left(t\right)=0$$

(5.4)

$$g\left(0,{A}^{*}\right)={\beta }_{2}{A}^{*}\left(t\right)\left(\frac{\alpha }{{\beta }_{2}{A}^{*}\left(t\right)+\mu }\right)-\left({\vartheta }_{2}+{\varepsilon }_{2}+\mu \right){A}^{*}\left(t\right)=0$$

(5.5)

Solving the above two equations, we obtain the possible positive equilibrium,

$${I}^{*}\left(t\right)=\frac{\alpha }{{\vartheta }_{1}+{\varepsilon }_{1}+\mu }, {A}^{*}\left(t\right)=\frac{\alpha }{{\vartheta }_{2}+{\varepsilon }_{2}+\mu },$$

Local Stability

Theorem

5.1: If ${\mathfrak{R}}_{0}<1$ and $\frac{\alpha }{\mu }<\frac{{\vartheta }_{2}+{\varepsilon }_{2}+\mu }{{\beta }_{2}}$ then the pollution free equilibrium point ${S}_{f}(\frac{\alpha }{\mu },\mathrm{0,0},\mathrm{0,0})$ of the model (2.1) is locally asymptotically stable.

Proof

To prove the Pollution free equilibrium point (${S}_{f}$) is locally asymptotically stable by considering the Jacobian matrix of the model (2.1)is.

$$J\left(S\right)=\left[\begin{array}{cccc}\frac{\partial {F}_{1}}{\partial S}& \frac{\partial {F}_{1}}{\partial I}& \frac{\partial {F}_{1}}{\partial A}& \frac{\partial {F}_{1}}{\partial R}\\\frac{\partial {F}_{2}}{\partial S}& \frac{\partial {F}_{2}}{\partial I}& \frac{\partial {F}_{2}}{\partial A}&\frac{\partial {F}_{2}}{\partial R}\\ \frac{\partial {F}_{3}}{\partial S}& \frac{\partial {F}_{3}}{\partial I}&\frac{\partial {F}_{3}}{\partial A}& \frac{\partial {F}_{3}}{\partial R}\\ \frac{\partial {F}_{4}}{\partial S}&\frac{\partial {F}_{4}}{\partial I}& \frac{\partial {F}_{4}}{\partial R}& \frac{\partial {F}_{4}}{\partial R}\end{array}\right]$$

$$=\left[\begin{array}{cccc}{\beta }_{1}I+{\beta }_{2}A-\mu & {\beta }_{1}S& {\beta }_{2}S& 0\\ {\beta }_{1}I& {\beta }_{1}S-({\vartheta }_{1}+\mu +{\varepsilon }_{1})& 0& 0\\ {\beta }_{2}A& 0& {\beta }_{2}S-({\vartheta }_{2}+\mu +{\varepsilon }_{2})& 0\\ 0& {\vartheta }_{1}& {\vartheta }_{2}& -(a+\mu )\end{array}\right]$$

(5.2)

$$J({S}_{f})=\left[\begin{array}{cccc}-\mu &\frac{{\beta }_{1}\alpha }{\mu }& \frac{{\beta }_{2}\alpha }{\mu }& 0\\ 0& \frac{{\beta }_{1}\alpha }{\mu }-({\vartheta }_{1}+\mu +{\varepsilon }_{1})&0& 0\\ {\beta }_{2}A& 0& \frac{{\beta }_{2}\alpha }{\mu }-({\vartheta }_{2}+\mu +{\varepsilon }_{2})& 0\\ 0&{\vartheta }_{1}& {\vartheta }_{2}& -(a+\mu )\end{array}\right]$$

Finding the characteristic equation of the above Jacobian matrix and obtain the Eigen values are ${\lambda }_{1}=-\mu , {\lambda }_{3}=-(a+\mu )$, ${\lambda }_{2,4}=\left[\begin{array}{ccc}\frac{{\beta }_{1}\alpha }{\mu }-\left({\vartheta }_{1}+\mu +{\varepsilon }_{1}\right)-\lambda & 0\\0& \frac{{\beta }_{2}\alpha }{\mu }-\left({\vartheta }_{2}+\mu +{\varepsilon }_{2}\right)-\lambda \end{array}\right].$

Solving ${\lambda }_{\mathrm{2,4}}$ we get, ${\lambda }_{2}={\vartheta }_{1}+\mu +{\varepsilon }_{1}({\mathfrak{R}}_{0}-1)$ and ${\lambda }_{4}=\frac{{\beta }_{2}\alpha }{\mu }-\left({\vartheta }_{2}+\mu +{\varepsilon }_{2}\right)$. Hence ${\lambda }_{2}$ and ${\lambda }_{4}$ are negative if ${\mathfrak{R}}_{0}<1\mathrm{ and }\frac{\alpha }{\mu }<\frac{{\vartheta }_{2}+{\varepsilon }_{2}+\mu }{{\beta }_{2}}$ respectively.

Global Stability

In this section, we investigate the global stability of the pollution free equilibrium ${S}_{f}$ for the system (2.1) by constructing pertinent Lyapunov functions. Now, to delineate a mapping $\Phi :{R}_{+}\to {R}_{+}$ given by $\Phi \left(\zeta \left(t\right)\right)=\zeta \left(t\right)-{\zeta }^{*}-{\zeta }^{*}\mathrm{ln}\frac{\zeta }{{\zeta }^{*}} , t\ge 0.$ Here,$\Phi \left(\zeta \left(t\right)\right)$ is a positive function for any $\zeta >0$ and attains its global minimum at 1. Define $L\left(t\right)=\left\{\left(S,I,A,R,H\right)\in {R}^{4}:S>0,I>0,A>0,R>0,H>0\right\}.$

Theorem

5.2: The equilibrium points for the system (2.1) is globally asymptotically stable, if the fraction derivative for the Lyapunov function V(t) of the system (2.1), that is ${}_{0}{}^{CFF}{D}^{\eta ,\gamma }V(t)\le 0.$

Proof

The Lyapunov function based on the above a statement,

$$L\left(t\right)=\left(S-{S}^{*}-{S}^{*}\mathrm{ln}\frac{S}{{S}^{*}}\right)+\left(I-{I}^{*}-{I}^{*}\mathrm{ln}\frac{I}{{I}^{*}}\right)+\left(A-{A}^{*}-{A}^{*}\mathrm{ln}\frac{A}{{A}^{*}}\right)+\left(R-{R}^{*}-{R}^{*}\mathrm{ln}\frac{R}{{R}^{*}}\right)+ (H-{H}^{*}-{H}^{*}\mathrm{ln}\frac{H}{{H}^{*}})$$

Take fractional derivatives of the above Lyapunov equation,

$${}_{0}{}^{CFF}{D}^{\eta ,\gamma }L\left(t\right)=\left(1-\frac{{S}^{*}}{S}\right){}_{0}{}^{CFF}{D}^{\eta ,\gamma }S\left(t\right)+\left(1-\frac{{I}^{*}}{I}\right){}_{0}{}^{CFF}{D}^{\eta ,\gamma }I\left(t\right)+\left(1-\frac{{A}^{*}}{A}\right){}_{0}{}^{CFF}{D}^{\eta ,\gamma }A\left(t\right)+\left(1-\frac{{R}^{*}}{R}\right){}_{0}{}^{CFF}{D}^{\eta ,\gamma }R\left(t\right)+\left(1-\frac{{H}^{*}}{H}\right){}_{0}{}^{CFF}{D}^{\eta ,\gamma }H\left(t\right)$$

$$=\left(1-\frac{{S}^{*}}{S}\right)\left[\alpha -{\beta }_{1}I\left(t\right)S\left(t\right)-{\beta }_{2}A\left(t\right)S\left(t\right)-\mu S\left(t\right)\right]+\left(1-\frac{{I}^{*}}{I}\right)\left[{\beta }_{1}I\left(t\right)S\left(t\right)-{\vartheta }_{1}I\left(t\right)-{\varepsilon }_{1}I\left(t\right)-\mu I\left(t\right)\right]+ \left(1-\frac{{A}^{*}}{A}\right) [{\beta }_{2}A\left(t\right)S\left(t\right)-{\vartheta }_{2}A\left(t\right)-{\varepsilon }_{1}A\left(t\right)-\mu A\left(t\right)]+\left(1-\frac{{R}^{*}}{R}\right)[{\vartheta }_{1}I\left(t\right)+{\vartheta }_{2}A\left(t\right)-aR\left(t\right)-\mu R\left(t\right)]+\left(1-\frac{{H}^{*}}{H}\right)\left[aR\left(t\right)-\mu H\left(t\right)\right]$$

After some simplification we attain,

$${}_{0}{}^{CFF}{D}^{\eta ,\gamma }L\left(t\right)=-\left(\frac{{\left(S-{S}^{*}\right)}^{2}}{S}\left[\mu +{\beta }_{1}{I}^{*}+{\beta }_{2}{A}^{*}\right]\right)-\frac{{\left(R-{R}^{*}\right)}^{2}}{R} [a+\mu ]$$

Hence, we obtain ${}_{0}{}^{CFF}{D}^{\eta ,\gamma }V\left(t\right)\le 0$. Therefore, the equilibrium points are globally asymptotically stable.

Numerical Approximation

The general algorithm for the fractal fractional order model of (2.1) using Euler method. Let us reconsider our model (2.1) as,

$${D}^{\eta ,\gamma }S\left(t\right)=\theta \left(t,S\left(t\right)\right)=\alpha -{\beta }_{1}I\left(t\right)S\left(t\right)-{\beta }_{2}A\left(t\right)S\left(t\right)-\mu S\left(t\right)$$

$${D}^{\eta ,\gamma }I\left(t\right)=\theta \left(t,I\left(t\right)\right)={\beta }_{1}I\left(t\right)S\left(t\right)-{\vartheta }_{1}I\left(t\right)-{\varepsilon }_{1}I\left(t\right)-\mu I\left(t\right)$$

$${D}^{\eta ,\gamma }A\left(t\right)=\theta \left(t,A\left(t\right)\right)={\beta }_{2}A\left(t\right)S\left(t\right)-{\vartheta }_{2}A\left(t\right)-{\varepsilon }_{1}A\left(t\right)-\mu A\left(t\right)$$

$${D}^{\eta ,\gamma }R\left(t\right)=\theta \left(t,R\left(t\right)\right)={\vartheta }_{1}I\left(t\right)+{\vartheta }_{2}A\left(t\right)-aR\left(t\right)-\mu R\left(t\right)$$

$${D}^{\eta ,\gamma }H\left(t\right)=\theta \left(t,H\left(t\right)\right)= aR\left(t\right)-\mu H\left(t\right)$$

(6.1)

The general system of equation for model (2.1) is taken as,

$${D}^{\eta ,\gamma }J\left(t\right)=\theta \left(t,J\left(t\right)\right)$$

(6.2)

$$J\left(0\right)={J}_{0} ,t>0$$

where $J(t)=\{S(t), I(t),A(t),R(t),H(t)\}$. Taking the set of points in the interval [0,tmax] and divide the interval into k subinterval $\left[{t}_{r},{t}_{r+1}\right]$ which is used to generate the points for our iterative procedure. The Equal sub width can be taken as $h=\frac{tmax}{k}$, using the nodes as ${t}_{r}=rh$ for r = 1,2,3…,k. Assume that $J\left(t\right), {D}^{\eta , \gamma }J\left(t\right), {D}^{2\eta , \gamma }J\left(t\right)$ are continuous and differentiable on [0, tmax]. Now, Expanding J(t) using Taylor’s series method,

$$J\left(t\right)=J\left({t}_{0}\right)+{D}^{\eta ,\gamma }J\left(t\right){t}_{0}\frac{{\gamma t}^{\eta }}{\Gamma (\eta +1)}+{D}^{2\eta ,\gamma }J\left(t\right){K}_{1 }\frac{\gamma {t}^{2\eta }}{\Gamma (2\eta +1)}$$

(6.3)

Since h is small, eliminate the higher term. The general equation of the scheme is given by,

$$J\left({t}_{r+1}\right)=J\left({t}_{r}\right)+\theta ({t}_{r},S({t}_{r}))\frac{{\gamma h}^{\eta }}{\Gamma (\eta +1)}$$

(6.4)

Equation (6.4) is the general formula for fractal fractional Euler equation. Now applying the fractional integral to both the sides of Eq. (6.2),

$$J\left({t}_{1}\right)=J\left(0\right)+{I}^{\eta ,\gamma }\left[\theta \left(t,J\left(t\right)\right)\right]({t}_{1})$$

(6.5)

Now applying the modified trapezoidal rule to approximate ${I}^{\eta ,\gamma }\left[{\theta }_{1}\left(t,J\left(t\right)\right)\right]({t}_{1})$ with $h={t}_{1}-{t}_{0}$, then we have,

$$J\left({t}_{1}\right)=J\left(0\right)+\frac{\gamma \eta {h}^{\eta }\left[\theta \left({t}_{0},J\left({t}_{0}\right)\right)\right]}{\Gamma (\eta +2)}+\frac{{\gamma h}^{\eta }\left[\theta \left({t}_{1},J\left({t}_{1}\right)\right)\right]}{\Gamma (\eta +2)}$$

By using the fractional Euler equation to the above equation we obtain,

$$J\left({t}_{1}\right)=J\left(0\right)+\frac{\gamma \eta {h}^{\eta }\left[\theta \left({t}_{0},J\left({t}_{0}\right)\right)\right]}{\Gamma (\eta +2)}+\frac{{\gamma h}^{\eta }\left[\theta \left({t}_{1},J\left({t}_{1}\right)\right)\right]+\gamma {h}^{\eta }[\theta ({t}_{0},J({t}_{0}))]}{\Gamma (\eta +2)}$$

Repeating the same process, we obtain the general formula for (6.2),

$$J\left({t}_{r}\right)=J\left(0\right)+\frac{\gamma {h}^{\eta }}{\Gamma \left(\eta +2\right)}\left({\left(r-1\right)}^{\eta +1}-\left(r-\eta -1\right){r}^{\eta }\right)\theta \left({t}_{0},J\left({t}_{0}\right)\right)+\frac{\gamma {h}^{\eta }}{\Gamma \left(\eta +2\right)}\sum_{i=1}^{r-1}\left({\left(r-i+1\right)}^{\eta +1}-2{\left(r-1\right)}^{\eta +1}+{\left(r-i-1\right)}^{\eta +1}\right))\theta ({t}_{i},J({t}_{i}))+\frac{\gamma {h}^{\eta }}{\Gamma \left(\eta +2\right)}\theta ({t}_{r},J\left({t}_{r-1}\right)+\frac{\gamma {h}^{\eta }}{\Gamma \left(\eta +1 \right)}\theta \left({t}_{r-1},J\left({t}_{r-1}\right)\right) (6.6)$$

Now applying Eq. (6.6) to our model Eq. (2.1),

$$S\left({t}_{r}\right)=S\left(0\right)+\frac{\gamma {h}^{\eta }}{\Gamma \left(\eta +2\right)}\left({\left(r-1\right)}^{\eta +1}-\left(r-\eta -1\right){r}^{\eta }\right){\theta }_{1}\left({t}_{0},S\left({t}_{0}\right)\right)+\frac{\gamma {h}^{\eta }}{\Gamma \left(\eta +2\right)}\sum_{i=1}^{r-1}\left({\left(r-i+1\right)}^{\eta +1}- 2{\left(r-1\right)}^{\eta +1}+{\left(r-i-1\right)}^{\eta +1}\right)){\theta }_{1}({t}_{i},S({t}_{i}))+\frac{\gamma {h}^{\eta }}{\Gamma \left(\eta +2\right)}{\theta }_{1}({t}_{r},S\left({t}_{r-1}\right)+\frac{\gamma {h}^{\eta }}{\Gamma \left(\eta +1 \right)}{\theta }_{1}\left({t}_{r-1},S\left({t}_{r-1}\right)\right)$$

$$I\left({t}_{r}\right)=I\left(0\right)+\frac{\gamma {h}^{\eta }}{\Gamma \left(\eta +2\right)}\left({\left(r-1\right)}^{\eta +1}-\left(r-\eta -1\right){r}^{\eta }\right){\theta }_{2}\left({t}_{0},I\left({t}_{0}\right)\right)+\frac{\gamma {h}^{\eta }}{\Gamma \left(\eta +2\right)}\sum_{i=1}^{r-1}\left({\left(r-i+1\right)}^{\eta +1}- 2{\left(r-1\right)}^{\eta +1}+{\left(r-i-1\right)}^{\eta +1}\right)){\theta }_{2}({t}_{i},I({t}_{i}))+\frac{\gamma {h}^{\eta }}{\Gamma \left(\eta +2\right)}{\theta }_{2}({t}_{r},I\left({t}_{r-1}\right)+\frac{\gamma {h}^{\eta }}{\Gamma \left(\eta +1 \right)}{\theta }_{2}\left({t}_{r-1},I\left({t}_{r-1}\right)\right)$$

$$A\left({t}_{r}\right)=A\left(0\right)+\frac{\gamma {h}^{\eta }}{\Gamma \left(\eta +2\right)}\left({\left(r-1\right)}^{\eta +1}-\left(r-\eta -1\right){r}^{\eta }\right){\theta }_{3}\left({t}_{0},A\left({t}_{0}\right)\right)+\frac{\gamma {h}^{\eta }}{\Gamma \left(\eta +2\right)}\sum_{i=1}^{r-1}\left({\left(r-i+1\right)}^{\eta +1}- 2{\left(r-1\right)}^{\eta +1}+{\left(r-i-1\right)}^{\eta +1}\right)){\theta }_{3}({t}_{i},A({t}_{i}))+\frac{\gamma {h}^{\eta }}{\Gamma \left(\eta +2\right)}{\theta }_{3}({t}_{r},A\left({t}_{r-1}\right)+\frac{\gamma {h}^{\eta }}{\Gamma \left(\eta +1 \right)}{\theta }_{3}\left({t}_{r-1},A\left({t}_{r-1}\right)\right)$$

$$R\left({t}_{r}\right)=R\left(0\right)+\frac{\gamma {h}^{\eta }}{\Gamma \left(\eta +2\right)}\left({\left(r-1\right)}^{\eta +1}-\left(r-\eta -1\right){r}^{\eta }\right){\theta }_{4}\left({t}_{0},R\left({t}_{0}\right)\right)+\frac{\gamma {h}^{\eta }}{\Gamma \left(\eta +2\right)}\sum_{i=1}^{r-1}\left({\left(r-i+1\right)}^{\eta +1}- 2{\left(r-1\right)}^{\eta +1}+{\left(r-i-1\right)}^{\eta +1}\right)){\theta }_{4}({t}_{i},R({t}_{i}))+\frac{\gamma {h}^{\eta }}{\Gamma \left(\eta +2\right)}{\theta }_{4}({t}_{r},R\left({t}_{r-1}\right)+\frac{\gamma {h}^{\eta }}{\Gamma \left(\eta +1 \right)}{\theta }_{4}\left({t}_{r-1},A\left({t}_{r-1}\right)\right)$$

$$\begin{aligned} H({t}_{r})&=H\left(0\right)+\frac{\gamma {h}^{\eta }}{\Gamma (\eta +2)}({(r-1)}^{\eta +1}-(r-\eta -1){r}^{\eta }){\theta }_{5}({t}_{0},H({t}_{0}))\\&\quad +\frac{\gamma {h}^{\eta }}{\Gamma (\eta +2)}\sum_{i=1}^{r-1} ({(r-i+1)}^{\eta +1}- 2{(r-1)}^{\eta +1}+{(r-i-1)}^{\eta +1})){\theta }_{5}({t}_{i},H({t}_{i}))\\ &\quad +\frac{\gamma {h}^{\eta }}{\Gamma (\eta +2)}{\theta }_{5}({t}_{r},H({t}_{r-1})+ \frac{\gamma {h}^{\eta }}{\Gamma (\eta +1)}{\theta }_{5}({t}_{r-1},H({t}_{r-1}))\end{aligned} $$

Graphical Representation and Discussion

In Tamil Nadu, one of the major land pollution areas is Ranipet Taluk, Vellore district. Tamil Nadu agricultural University research center in Vellore take survey of nearly 35,000 ha of agricultural land in the Tanneries belt. It is observed that the land has become either partially or totally unfit for cultivation. Also, there are 170 types of chemicals includes sodium chloride, lime, Sodium Sulphate, Chlorium Sulphate, fat liquor ammonia and Sulphuric acid are used in large quantities. There are 600 Tanneries are located in Vellore district, among 150 Tannaries are in Ranipet taluk. The study area of Pulliyanthangal village (12.9180 degree N, 79.3336 degree E) is located in Ranipe which is 1 km away from industrial area such as ceramic industries, chemical factories, leather and tanning industries. In this study, pulliyanthangal village divided into two areas, one is industrial area and other one is Agricultural land field. Three soil samples were taken from different areas of the village and studied the PH level at three different depth of the surface [2, 24, 29, 33, 34].

Choosing the values $\alpha =0.0643, { \beta }_{1}=0.00038495971, { \beta }_{2}=0.0002775291, {\vartheta }_{1}=0.0895,{\vartheta }_{2}=0.0547, {\varepsilon }_{1}=0.0395, {\varepsilon }_{2}=0.0195, a=0.0234, \mu =0.0002$, fractional order 0.85, fractal dimension 0.2 and the initial values are $(321.5,\mathrm{ 200,100},\mathrm{ 0,0})$, we attain the pollution free equilibrium (321.5,0,0,0,0) and ${\mathfrak{R}}_{0}=0.9509<1$. This show from the theorem (5.1), the pollution free equilibrium is locally asymptotically stable. The numerical scheme of the Euler method algorithm is used to approximate the solution of the model (2.1).

From Fig. 2, we observe the dynamical behavior of model (2.1) which demonstrates the initial values of the susceptible soil start decreasing for applying the necessary remedies to the prohibited polluted area. At certain stage susceptible soil and remediation converges to the same point. Consequently, the fitness of healthy cultivate soil incline while at the same time pollution caused by the industrial (I(t)) and Agricultural (A(t)) after 150 days converges to zero. Figure 3 initiate the density of susceptible soil at different fractional order $\eta =0.6, 0.7, 0.8, \mathrm{0.85,0.9}$ and fractal dimension is 0.2. It shows that the initial value 321.5 the Susceptible soil decreasing and converges to certain values.

Fig. 2

Dynamical behavior of all the compartment at $\eta =0.85, \gamma =0.2$

Fig. 3

Dynamical behavior of Susceptible Soil at various fractional order and fractal dimensions

From Figs. 4 and 5, we observe that pollution caused by agricultural and industrial zone start decreasing at the initial values and converges to zero for different fractional order and fixed fractal dimensions. In Figs. 6 and 7, we identify industrial pollution and agricultural soil pollution at different PH levels. This shows that increasing of PH level cause the increasing of pollution in different zones.

Fig. 4

Dynamical behavior of Pollution due to industrial disposal at various fractal and fractional orders

Fig. 5

Dynamical behavior of Pollution due to Agricultural disposal at various fractal and fractional orders

Fig. 6

Polluted area for different PH level at Sample1 = 8.9; Sample 2 = 8.1; Sample 3 = 7.8

Fig. 7

Polluted area for different PH level at Sample1 = 6.8; Sample 2 = 6.1; Sample 3 = 5.9

Figure 8 intimates the dynamical behavior of action taken at different fractional order and fixed fractal dimensions. It enumerates remediation of soil decline at initial state and converging to some point. In Fig. 9, we observe the increase of vigor soil for different fractional order and fixed fractal dimensions. From the figures, we assure that the fewer fractional orders give the better results contrast with classical integer order.

Fig. 8

Dynamical Behavior of necessary remedies taken at different fractal and fractional order

Fig. 9

Dynamical behavior of Healthy soil after necessary action taken at different fractal and fractional order

Conclusion

In this manuscript, we have analyzed a Caputo-type fractional order SIARH model on soil pollution with control measures. The power law kernel involved in caputo type system explains the memory behavior of the compartments and which are more applicable for ecological control phenomena due to its high degree of freedom than ordinary order different integrals. A comparative study has been visualized for various fractal fractional order of all five compartments. Stability analysis of the proposed model intimate the local and global stability around the pollution free state at ${\mathfrak{R}}_{0}<1$ and pollution existence state as ${\mathfrak{R}}_{0}>1.$

Soil PH is one of the main factors to identify the suitability of the cultivation. The suitable cultivation of the PH level is 6.6–7.0 units. In this view, the study of Ranipet zone 1 (Industrial area), the PH level is high due to the disposal of heavy metals. Also the crop cultivation is non-suitable for the state of PH level. In zone 2 (Agricultural area), the PH level is low due to the usage of high chemical fertilizer and pesticides. These results in insufficiency of PH level can weaken the healthy vegetative growth and disturb the nitrogen consumption of plants, root system etc. Hence, it is necessary to reform the polluted soil at different cause and restricting usage of high hazard materials.

Numerical approximation for the defined model has been derived using Euler’s method. Simulations are graphically exhibited through MATLAB to validate the productivity and conclusion of effective control steps are listed below:

• i. Gradual increase of fractional order results a rapid hike in pollution level of both agricultural and industrial area.

• ii. By efficacious remedial actions applied to the contaminated soil show a deep downturn of both agricultural and industrial pollutants.

• iii. Forceful implementation remedies boost up the nutrient healthy soil fairly.