Skip to main content
SpringerLink
Log in

Modeling of Delayed Thermo Elastic Waves in a Polygonal Ring Reinforced with Graphene Platelets

  • Original Paper
  • Published:
International Journal of Applied and Computational Mathematics Aims and scope Submit manuscript

Abstract

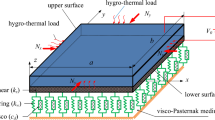
The free vibration analysis of generalized thermo elastic waves in a clamped free polygonal ring incorporated with graphene platelets is addressed in the purview of delayed heat conduction equation. Homogeneous thermo elastic polygonal ring in isotropic plain strain form is considered for controlling equations. The distribution model of Halpin–Tsai is adopted for homogenization. The consistent formulation is derived by the nonlinear surface of the GPLRC ring via Fourier expansion collocation method. Numerical values are discussed for triangular, square, pentagonal and hexagonal GPLRC rings. To verify the analytical model, the field functions are presented in tabular and graphical forms with weight fraction and various patterns of GPLRC. This study may find the applications in design of thermal polygonal GPL ring structures.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23
Fig. 24
Fig. 25

Similar content being viewed by others

Data Availability

Enquiries about data availability should be directed to the authors.

References

  1. Talebitooti, R., Daneshjou, K., Tarkashvand, A.: Incorporating the Havriliak-Negami model in wave propagation through polymeric viscoelastic core in a laminated sandwich cylinder. Thin-Walled Struct. 134, 460–474 (2019)

    Article  Google Scholar 

  2. Shahsavari, H., Talebitooti, R., Kornokar, M.: Analysis of wave propagation through functionally graded porous cylindrical structures considering the transfer matrix method. Thin-Walled Struct. 159, 107212 (2020)

    Article  Google Scholar 

  3. Bakhtiari, M., Tarkashvand, A., Daneshjou, K.: Plane-strain wave propagation of an impulse-excited fluid-filled functionally graded cylinder containing an internally clamped shell. Thin-Walled Struct. 149, 106482 (2020)

    Article  Google Scholar 

  4. Lu, Z.Q., Gu, D.H., Ding, H., Lacarbonara, W., Chen, L.Q.: Nonlinear vibration isolation via a circular ring. Mech. Syst. Signal Process. 136, 106490 (2020)

    Article  Google Scholar 

  5. Draiche, K., Bousahla, A.A., Tounsi, A.S., Alwabli, A., Tounsi, K., Mahmoud, S.R.: Static analysis of laminated reinforced composite plates using a simple first-order shear deformation theory. Comput. Concr. 24, 369–378 (2019)

    Google Scholar 

  6. Vlase, S., Marin, M., Öchsner, A., Scutaru, M.L.: Motion equation for a flexible one-dimensional element used in the dynamical analysis of a multibody system. Contin. Mech. Thermodyn. 31(3), 715–724 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  7. Bhatti, M.M., Marin, M., Zeeshan, A., Ellahi, R., Abdelsalam, S.I.: Swimming of motile gyrotactic microorganisms and nanoparticles in blood flow through anisotropically tapered arteries. Front. Phys. 8, 1–12 (2020)

    Article  Google Scholar 

  8. Lord, H.W., Shulman, Y.: A generalized dynamical theory of thermo elasticity. J. Mech. Phys Solids. 5, 299–309 (1967)

    Article  MATH  Google Scholar 

  9. Catteneo, C.: A form of heat conduction equation which eliminates the paradox of instantaneous propagation. Compt Rend. 247, 431–433 (1948)

    Google Scholar 

  10. Dhaliwal, R.S., Sherief, H.H.: Generalized thermo elasticity for anisotropic media. Q. Appl. Math. 8, 1–8 (1980)

    Article  MATH  Google Scholar 

  11. Ignaczak, J.: A strong discontinuity wave in thermoelasticity with relaxation times. J. Therm. Stresses 8, 25–40 (1985)

    Article  MathSciNet  Google Scholar 

  12. Ignaczak, J.: Decomposition theorem for thermoelasticity with finite wave speeds. J. Therm. Stresses 1, 41–52 (1978)

    Article  Google Scholar 

  13. Sherief, H.H.: Fundamental solution of the generalized thermoelastic problem for short times. J. Therm. Stresses 9(2), 151–164 (1986)

    Article  MathSciNet  Google Scholar 

  14. Sherief, H.H.: State space approach to thermoelasticity with two relaxation times. Int. J. Eng. Sci. 31, 1177–1189 (1993)

    Article  MathSciNet  MATH  Google Scholar 

  15. Sherief, H.H.: A thermo-mechanical shock problem for thermoelasticity with two relaxation times. Int. J. Eng. Sci. 32, 313–325 (1994)

    Article  MATH  Google Scholar 

  16. Varma, K.L.: On the propagation of waves in layered anisotropic media in generalized thermo elasticity. Int. J. Eng. Sci. 40, 2077–2096 (2002)

    Article  Google Scholar 

  17. Jiangong, Y., Bin, W., Cunfu, H.: Circumferential thermoelastic waves in orthotropic cylindrical curved plates without energy dissipation. Ultrosonics 53, 416–423 (2010)

    Article  Google Scholar 

  18. Jiangong, Y., Tonglong, X.: Generalized thermoelastici waves in spherical curved plates without energy dissipation. Acta Mech. 212, 39–50 (2010)

    Article  MATH  Google Scholar 

  19. Ponnusamy, P., Selvamani, R.: Wave propagation in magneto thermo elastic cylindrical panel. Eur. J. Mech. A Solids 39, 76–85 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  20. Ponnusamy, P., Selvamani, R.: Dispersion analysis of a generalized magneto thermo elastic cylindrical panel. J. Therm. Stresses 35, 1119–1142 (2012)

    Article  Google Scholar 

  21. Ebrahimi, F., Jafari, A., Selvamani, R.: Thermal buckling analysis of magneto electro elastic porous FG beam in thermal environment. Adv. Nano Res. 8, 83–94 (2020)

    Google Scholar 

  22. Ebrahimi, F., Karimiasl, M., Selvamani, R.: Bending analysis of magneto-electro piezoelectric nanobeams system under hygro-thermal loading. Adv. Nano Res. 8, 203–214 (2020)

    Google Scholar 

  23. Ebrahimi, F., Kokaba, M., Shaghaghi, G., Selvamani, R.: Dynamic characteristics of hygro-magneto-thermo-electrical nanobeam with non-ideal boundary conditions. Adv. Nano Res. 8, 169–182 (2020)

    Google Scholar 

  24. Ebrahimi, F., Hosseini, H., Selvamani, R.: Thermo-electro-elastic nonlinear stability analysis of viscoelastic double-piezo nanoplates under magnetic field. Struct. Eng. Mech. 73, 565–584 (2020)

    Google Scholar 

  25. Quintanilla, R., Racke, R.: A note on stability in three-phase-lag heat conduction. Int. J. Heat Mass Transf. 51, 24–29 (2008)

    Article  MATH  Google Scholar 

  26. Dreher, M., Quintanilla, R., Racke, R.: Ill posed problems in thermo mechanics. Appl. Math. Lett. 22, 1374–1379 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  27. Abd-Elaziz, E.M., Marin, M., Othman, M.I.A.: On the effect of Thomson and initial stress in a thermo-porous elastic solid under GN electromagnetic theory. Symmetry 11(3), 413 (2019)

    Article  MATH  Google Scholar 

  28. Quintanilla, R.: Some solutions for a family of exact phase phase-lag heat conduction problems. Mech. Res. Commun. 38, 355–360 (2011)

    Article  MATH  Google Scholar 

  29. Song, M., Kitipornchai, S., Yang, J.: Free and forced vibrations of functionally graded polymer composite plates reinforced with graphene nanoplatelets. Compos. Struct. 159, 579–588 (2017)

    Article  Google Scholar 

  30. Feng, C., Kitipornchai, S., Yang, J.: Nonlinear free vibration of functionally graded polymer composite beams reinforced with graphene nanoplatelets (GPLs). Eng. Struct. 140, 110–119 (2017)

    Article  Google Scholar 

  31. Feng, C., Kitipornchai, S., Yang, J.: Nonlinear bending of polymer nanocomposite beams reinforced with non-uniformly distributed graphene platelets (GPLs). Compos. B Eng. 110, 132–140 (2017)

    Article  Google Scholar 

  32. Shen, H.S., Xiang, Y., Lin, F., Hui, D.: Buckling and postbuckling of functionally graded graphene-reinforced composite laminated plates in thermal environments. Compos. B Eng. 119, 67–78 (2017)

    Article  MATH  Google Scholar 

  33. Li, C., Han, Q., Wang, Z.: Analysis of wave propagation in functionally graded piezoelectric composite plates reinforced with graphene platelets. Appl. Math. Model. 81, 487–505 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  34. Yang, J., Chen, D., Kitipornchai, S.: Buckling and free vibration analyses of functionally graded graphene reinforced porous nanocomposite plates based on Chebyshev-Ritz method. Compos. Struct. 193, 281–294 (2018)

    Article  Google Scholar 

  35. Mao, J.J., Zhang, W.: Buckling and post-buckling analyses of functionally graded graphene reinforced piezoelectric plate subjected to electric potential and axial forces. Compos. Struct. 216, 392–405 (2019)

    Article  Google Scholar 

  36. Barati, M.R., Zenkour, A.M.: Vibration analysis of functionally graded graphene platelet reinforced cylindrical shells with different porosity distributions. Mech. Adv. Mater. Struct. 26, 1580–1588 (2018)

    Article  Google Scholar 

  37. Zhao, Z., Feng, C., Wang, Y., Yang, J.: Bending and vibration analysis of functionally graded trapezoidal nanocomposite plates reinforced with graphene nanoplatelets (GPLs). Compos. Struct. 180, 799–808 (2017)

    Article  Google Scholar 

  38. Barati, M.R., Zenkour, A.M.: Post-buckling analysis of refined shear deformable graphene platelet reinforced beams with porosities and geometrical imperfection. Compos. Struct. 181, 194–202 (2017)

    Article  Google Scholar 

  39. Wang, Y., Feng, C., Zhao, Z., Yang, J.: Eigenvalue buckling of functionally graded cylindrical shells reinforced with graphene platelets (GPL). Compos. Struct. 202, 38–46 (2017)

    Article  Google Scholar 

  40. Sahmani, S., Aghdam, M.M., Rabczuk, T.: Nonlinear bending of functionally graded porous micro/nano-beams reinforced with graphene platelets based upon nonlocal strain gradient theory. Compos. Struct. 186, 68–78 (2018)

    Article  Google Scholar 

  41. Sharma, D.K., Thakur, D., Walia, V., Sarkar, N.: Free vibration analysis of a nonlocal thermoelastic hollow cylinder with diffusion. J. Therm. Stresses 43(8), 981–997 (2020)

    Article  Google Scholar 

  42. Lata, P., Singh, S.: Effects of nonlocality and two temperature in a nonlocal thermoelastic solid due to ramp type heat source. Arab. J. Basic Appl. Sci. 27(1), 358–364 (2020)

    Article  Google Scholar 

  43. Sharma, S.R., Chand Mehalwal, J., Sarkar, N., Sharma, D.K.: Vibration analysis of electro-magneto transversely isotropic non-local thermoelastic cylinder with voids material. Eur. J. Mech. A Solids 92, 104455 (2022)

    Article  MathSciNet  MATH  Google Scholar 

  44. Nowinski, J.L.: On the nonlocal theory of wave propagation in elastic plates. ASME J. Appl. Mech. 51(3), 608–613 (1984)

    Article  Google Scholar 

  45. Patnaik, S., Sidhardh, S., Semperlotti, F.: Geometrically nonlinear analysis of nonlocal plates using fractional calculus. Int. J. Mech. Sci. 179(15), 105710 (2020)

    Article  Google Scholar 

Download references

Funding

The authors have not disclosed any funding.

Author information

Authors and Affiliations

  1. Department of Mathematics, Karunya University, Coimbatore, 641 114, Tamil Nadu, India

    R. Selvamani

  2. Department of Applied Mathematics, University of Calcutta, Kolkata, West Bangal, 700009, India

    N. Sarkar

  3. Department of Mechanical Engineering, Imam Khomeini International University, Qazvin, Iran

    Farzad Ebrahami

Authors
  1. R. Selvamani
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. N. Sarkar
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Farzad Ebrahami
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to R. Selvamani.

Ethics declarations

Conflict of interest

The authors have not disclosed any competing interests.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix A

Appendix A

$$ \begin{aligned} a_{n}^{j} & = 2\left\{ {p(p - 1)J_{p} (\alpha_{i} ax) + (\alpha_{i} ax)J_{p + 1} (\alpha_{i} ax)} \right\}\cos 2(\theta - \gamma_{i} )\cos m\theta \\ & \quad - x^{2} \left\{ {(\alpha_{i} a)^{2} + \left[ {\overline{\lambda } + 2\cos^{2} (\theta - \gamma_{i} )} \right] + a_{i} } \right\}J_{p} \left( {\alpha_{i} ax} \right)\cos m\theta \\ & \quad + 2p\left\{ {(p - 1)J_{p} (\alpha_{i} ax) - (\alpha_{i} ax)J_{p + 1} (\alpha_{i} ax)} \right\}\sin m\theta \sin 2(\theta - \gamma_{i} ),\quad j = 1,2 \\ \end{aligned} $$
(A1)
$$ \begin{aligned} a_{n}^{3} & = - 2\left\{ {J_{p + 1} (\alpha_{3} ax)(\alpha_{3} ax) - J_{p} (\alpha_{3} ax)p\,(p - 1)} \right\}\cos m\,\theta \cos 2(\theta - \gamma_{i} ) \\ & \quad - 2\left\{ {J_{p} (\alpha_{3} ax)[(p - 1)p - (\alpha_{3} ax)^{2} ] + J_{p + 1} (\alpha_{3} ax)(\alpha_{3} ax)} \right\}\sin m\,\theta \sin 2(\theta - \gamma_{i} ) \\ \end{aligned} $$
(A2)
$$\begin{aligned} a_{n}^{4} & = 2\left\{ {p\,(p - 1)Y_{p} (\alpha_{4} ax)\cos m\,\theta - (\alpha_{4} ax)Y_{p + 1} (\alpha_{4} ax)\cos m\,\theta } \right\}\cos 2(\theta - \gamma_{i} ) \\ & \quad + 2\left\{ {Y_{p} (\alpha_{4} ax)\,[p(p - 1) - (\alpha_{4} ax)^{2} ]\sin m\,\theta + Y_{p + 1} (\alpha_{4} ax)(\alpha_{4} ax)\sin m\,\theta } \right\}\sin 2(\theta - \gamma_{i} ) \\ \end{aligned} $$
(A3)
$$ \begin{aligned} a_{n}^{j} & = 2\left\{ {p(p - 1)Y_{p} (\alpha_{i} ax) + (\alpha_{i} ax)Y_{p + 1} (\alpha_{i} ax)} \right\}\cos 2(\theta - \gamma_{i} )\cos m\,\theta \\ & \quad - x^{2} \left\{ {(\alpha_{i} a)^{2} + \left[ {\overline{\lambda } + 2\cos^{2} (\theta - \gamma_{i} )} \right] + a_{i} } \right\}Y_{p} \left( {\alpha_{i} ax} \right)\cos m\,\theta \\ & \quad + 2p\left\{ {(p - 1)Y_{p} (\alpha_{i} ax) - (\alpha_{i} ax)Y_{p + 1} (\alpha_{i} ax)} \right\}\sin m\,\theta \sin 2(\theta - \gamma_{i} ),\quad j = 5,6 \\ \end{aligned} $$
(A4)
$$ \begin{aligned} b_{n}^{j} & = 2\left\{ {[p(p - 1) - (\alpha_{i} ax)^{2} ]J_{p} (\alpha_{i} ax) + (\alpha_{i} ax)J_{p + 1} (\alpha_{i} ax)} \right\}\cos m\,\theta \sin 2(\theta - \gamma_{i} ) \\ &\quad + 2p\left\{ {(\alpha_{i} ax)J_{p + 1} (\alpha_{i} ax) - (p - 1)J_{p} (\alpha_{i} ax)} \right\}\sin m\,\theta \cos 2(\theta - \gamma_{i} ),j = 1,2 \\ \end{aligned} $$
(A5)
$$ \begin{aligned} b_{n}^{3} & = - \left\{ {J_{p + 1} (\alpha_{3} ax)(\alpha_{3} a\,x)\cos m\,\theta - \,J_{p} (\alpha_{3} a\,x)(p - 1)\cos m\,\theta } \right\}\sin 2\theta - 2\gamma_{i} \\ & \quad - \left[ {2(\alpha_{3} ax)J_{p + 1} (\alpha_{3} ax)2p\,\,\sin m\,\theta \,\,\cos 2(\theta - \gamma_{i} )}\right.\\ & \quad \left.{ - \,[(\alpha_{3} ax)^{2} - 2p(p - 1)]2p\,\,\sin m\,\theta \,\,\cos 2(\theta - \gamma_{i} )J_{p} (\alpha_{3} ax)} \right] \\ \end{aligned} $$
(A6)
$$ \begin{aligned} b_{n}^{4} & = \left\{ {(p - 1)Y_{p} (\alpha_{4} ax) - (\alpha_{4} ax)Y_{p + 1} (\alpha_{4} ax)} \right\}\cos m\,\theta \,\,\,\sin 2(\theta - \gamma_{i} ) \\ & \quad - \left\{ {2(\alpha_{4} ax)Y_{p + 1} (\alpha_{4} ax) - \,[(\alpha_{4} ax)^{2} - 2p(p - 1)]Y_{p} (\alpha_{4} ax)} \right\}2p\,\,\sin m\,\theta \,\,\,\cos 2(\theta - \gamma_{i} ) \\ \end{aligned} $$
(A7)
$$ \begin{aligned} b_{n}^{j} & = 2\left\{ {[p(p - 1) - (\alpha_{i} ax)^{2} ]Y_{p} (\alpha_{i} ax)\cos m\,\theta + (\alpha_{i} ax)Y_{p + 1} (\alpha_{i} ax)\cos m\,\theta } \right\}\sin 2\theta - 2\gamma_{i} \\ & \quad + 2p\left\{ {\,(\alpha_{i} ax)Y_{p + 1} (\alpha_{i} ax)\sin m\,\theta - (p - 1)Y_{p} (\alpha_{i} ax)\sin m\,\theta } \right\}\cos 2(\theta - \gamma_{i} ),\,j = 5,\,6 \\ \end{aligned} $$
(A8)
$$ c_{n}^{j} = d_{i} \left\{ {p\cos \left( {\overline{n - 1} \theta + \gamma_{i} } \right)J_{p} \left( {\alpha_{i} ax} \right) - \left( {\alpha_{i} ax} \right)J_{p + 1} \left( {\alpha_{i} ax} \right)\cos (\theta - \gamma_{i} )\cos m\,\theta } \right\},\quad j = 1,2 $$
(A9)
$$ c_{n}^{3} = 0.0,\quad c_{n}^{4} = 0.0 $$
(A10)
$$ c_{n}^{j} = d_{i} \left\{ {p\cos \left( {\overline{n - 1} \theta + \gamma_{i} } \right)Y_{p} \left( {\alpha_{i} ax} \right) - \left( {\alpha_{i} ax} \right)Y_{p + 1} \left( {\alpha_{i} ax} \right)\cos (\theta - \gamma_{i} )\cos m\,\theta } \right\},\quad j = 5,6 $$
(A11)

The expressions \(\overline{a}_{n}^{j} ,b_{n}^{j} \& \overline{c}_{n}^{j}\) is got by interchanging \(\cos n\theta\) and \(\sin n\theta\) in the Eqs. (A1)–(A11).

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Selvamani, R., Sarkar, N. & Ebrahami, F. Modeling of Delayed Thermo Elastic Waves in a Polygonal Ring Reinforced with Graphene Platelets. Int. J. Appl. Comput. Math 8, 234 (2022). https://doi.org/10.1007/s40819-022-01435-w

Download citation

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40819-022-01435-w

Keywords

Search

Navigation