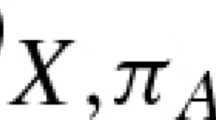Skip to main content
SpringerLink
Log in

Hurwitz class numbers with level and modular correspondences

  • Research
  • Published:
Research in Number Theory Aims and scope Submit manuscript

Abstract

In this paper, we prove Hurwitz–Eichler type formulas for Hurwitz class numbers with each level M when the modular curve \( X_0(M) \) has genus zero. A key idea is to calculate intersection numbers of modular correspondences with the level in two different ways. A generalization of Atkin–Lehner involutions for \( \Gamma _0(M) \) and its subgroup \( \Gamma _0^{(M')}(M) \) is introduced to calculate intersection multiplicities of modular correspondences at cusps.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Data availibility

Data sharing not applicable to this article as no datasets were generated or analysed during the current study

References

  1. Akbas, M., Singerman, D.: The normalizer of \(\Gamma _0(N)\) in \({\rm PSL}(2,{ R})\). Glasgow Math. J. 32(3), 317–327 (1990)

    Article  MathSciNet  MATH  Google Scholar 

  2. Atkin, A.O.L., Lehner, J.: Hecke operators on \(\Gamma _{0}(m)\). Math. Ann. 185, 134–160 (1970)

  3. Bars, F.: The group structure of the normalizer of \(\Gamma _0(N)\) after Atkin-Lehner. Commun. Algebra 36(6), 2160–2170 (2008)

    Article  MATH  Google Scholar 

  4. Bruinier, J.H., Schwagenscheidt, M.: Theta lifts for Lorentzian lattices and coefficients of mock theta functions. Math. Z. (2020)

  5. Cho, B.: Recurrence relations satisfied by the traces of singular Moduli for \(\Gamma _0(N)\). Taiwan. J. Math. 24(5), 1045–1072 (2020)

    Article  MATH  Google Scholar 

  6. Conway, J.H., Norton, S.P.: Monstrous moonshine. Bull. Lond. Math. Soc. 11(3), 308–339 (1979)

    Article  MathSciNet  MATH  Google Scholar 

  7. Diamond, F., Shurman, J.: A First Course in Modular Forms. Graduate Texts in Mathematics, vol. 228. Springer, New York (2005)

    MATH  Google Scholar 

  8. Eichler, M.: On the class of imaginary quadratic fields and the sums of divisors of natural numbers. J. Indian Math. Soc. (N.S.) 19, 153–180 (1956)

    MathSciNet  MATH  Google Scholar 

  9. Gross, B., Kohnen, W., Zagier, D.: Heegner points and derivatives of \(L\)-series. II. Math. Ann. 278(1–4), 497–562 (1987)

    Article  MathSciNet  MATH  Google Scholar 

  10. Lehner, J., Newman, M.: Weierstrass points of \(\Gamma _{0}\,(n)\). Ann. Math. 2(79), 360–368 (1964)

    Article  MATH  Google Scholar 

  11. Ling, J.: Intersection of modular polynomials. Proc. Am. Math. Soc. 137(5), 1543–1549 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  12. Maier, R.S.: On rationally parametrized modular equations. J. Ramanujan Math. Soc. 24, 1–73 (2009)

    MathSciNet  MATH  Google Scholar 

  13. Murakami, Y.: Intersection numbers of modular correspondences for genus zero modular curves. J. Number Theory 209, 167–194 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  14. Sebbar, A.: Torsion-free genus zero congruence subgroups of \( \rm PSL _2(\mathbb{R} ) \). Duke Math. J. 110, 377–396 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  15. Zemel, S.: Normalizers of congruence groups in \({\rm SL}_2(\mathbb{R} )\) and automorphisms of lattices. Int. J. Number Theory 13(5), 1275–1300 (2017)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

I would like to show my greatest appreciation to Professor Takuya Yamauchi for giving many pieces of advice. I am deeply grateful to Dr. Toshiki Matsusaka for giving many comments and pointing out that the 0th Hurwitz class number has a form \( -(p+1)/12 \) when a level is a prime number p. I would like to express my gratitude to Dr. Markus Schwagenscheidt for telling me the relation between my work and theta lift. I would like to thank Dr. Dongxi Ye for telling me that Theorem 1.1 follows from [5, Corollary 2.12 (1)] and Theorem 1.1 for a square N follows from [5, Theorem 2.13 (2)]. I also thank the referees for making many suggestions which definitely help to improve the readability and quality of the paper. The author is supported by JSPS KAKENHI Grant Number JP 20J20308.

Author information

Authors and Affiliations

  1. Mathematical Institute of Tohoku University, 6-3, Aoba, Aramaki, Aoba-ku, Sendai, 980-8578, Japan

    Yuya Murakami

Authors
  1. Yuya Murakami
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yuya Murakami.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Murakami, Y. Hurwitz class numbers with level and modular correspondences. Res. number theory 9, 40 (2023). https://doi.org/10.1007/s40993-023-00443-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40993-023-00443-z

Search

Navigation