Introduction

Nowadays, technological and medical advances have made organ transplantation one of the most successful and popular treatment methods. The first successful kidney transplant surgery was conducted by Joseph Murray in 1954 in the USA (Leppke et al., 2013). Transplantation surgery is regarded to be the only treatment for the end-stage failure of organs such as the liver, lung, and heart, and also the most low-cost way to treat kidney end-stage diseases (Bouwman, Lie, Bomhoff, & Friele, 2013). Based on the statistics, over 40,000 transplants were performed in 2021. However, unfortunately, 17 people die each day waiting for an organ transplant. Figure 1 shows the number of patients on the waiting list and the performed transplantations divided by 4 major transplantable and other organs in 2021 (HRSA 2022).

Fig. 1
figure 1

Patients on the waiting list vs. transplants performed by organ in 2021 (HRSA 2022). *Other includes allograft transplants like face, hands, and abdominal wall

Full size image

According to a definition by Ahmadvand and Pishvaee (2018b), organ transplantation is a procedure in which a healthy organ is harvested from a living or deceased person (a donor) and it is transferred into the body of an individual who has been diagnosed with organ failure (a recipient). The intrinsic fact in this matter is that there is always a greater demand for organs than their supply. Thus, as precious scarce national resources, it is essential to plan strategies and policies to manage organs efficiently through the supply network (Ahmadvand & Pishvaee, 2018a).

The supply chain management (SCM) concept refers to the efficient process of planning, implementing, and controlling supply chain operations (Hernández-Pérez & Ponce-Ortega, 2021; Melo, Nickel, & Saldanha-Da-Gama, 2009; Mohammadnazari, Aghsami, & Rabbani, 2022; Abolfazli et al., 2022). Supply chain network design (SCND) decisions typically entail determining the facilities’ optimal location, allocation, and capacity in order to meet the demand at the lowest possible cost (Jabbarzadeh, Fahimnia, & Seuring, 2014). A well-organized Organ Transplantation Network (OTN) provides efficient and collaborative management of all transplantation activities, including donation, procurement, preservation, transportation, and organ transplants (Ahmadvand & Pishvaee, 2018a). In transplantation networks, the location of facilities plays a crucial role since poor locations can lead to a higher mortality rate (Daskin & Dean, 2005).

There are various types of facilities in an organ transplant network in every country. In a case by Rouhani and Amin (2022), it is described as follows: Organ transplant network is comprised of initial hospitals, Organ Procurement Unit (OPU), and Transplant Center (TC). The brain-dead donors are diagnosed at initial hospitals, as they make up the bulk of donor numbers. All activities associated with the procurement of organs, from identifying the donor to harvesting his/her organs, are done in an OPU. Ultimately, a center where the organs are transplanted to the recipient’s body is called a TC. In this study, the OTN is made up of donor hospitals (H), TCs, recipient zones (Jabbarzadeh et al.; Sy et al., 2021), and shipping agents (Sh.A). The donation operations take place in hospitals. The shipping agents are responsible for transporting blood samples and information of donors from hospitals to TCs, and then bringing back the results to the hospitals. The transplant centers are in charge of registering the recipients and conducting analyses of donors’ blood samples. TCs are where the transplantation operations are carried out.

The organ transplantation process requires subtle management by virtue of its many constraints, such as time and perishability. For instance, Cold Ischemia Time (CIT) is the time period during which an organ is able to survive outside of the body without blood perfusion. It begins after the organ is harvested from a donor body and ends with the implantation of the organ into a recipient body. Each organ has a maximum allowable CIT, and also it is preferable to minimize it in order to optimize the post-transplant outcomes. Furthermore, because deceased donors are kept artificially alive, obviously, this condition cannot be sustained for a long time (Ahmadvand & Pishvaee, 2018b; Uehlinger, 2010).

A successful and on-time transplant cannot always be achieved if there is an availability of organs. There are further problems, namely long transportation time to recipients and medical staff unavailability, that may bring about the waste of time and, finally, shortage of organs (Fuzzati, 2005). Therefore, this increases the significance of determining the location of OTN’s facilities, applying efficient coordination among medical staff, and considering transportation matters. Equity and efficiency are the other substantial issues in the optimization of OTN which are construed to be the two opposing objectives of the allocation process. To clarify, equity is comprised of (1) equal access (avoiding biases based on age, sex, waiting time, etc.) and (2) maximum benefit (considering the length of recipient’s life after transplantation, the recipient’s urgency level, etc.) (Ahmadvand & Pishvaee, 2018b; Benjamin, 1988).

In the healthcare sector, optimal resource allocation and enhancing the quality of public health are crucial and have always been among controversial issues (Asante & Zwi, 2009). Resource allocation requires a great deal of attention in the context of organ transplantation due to the nature of body organs as scarce resources and the sensitivity of organ transplantation surgery for mortality possibilities. As mentioned before, the viability of organs out of the body depends on each type’s maximum allowable CIT. In response to this demand, the cold chain logistics infrastructure has needed a major overhaul, which may eventually be able to accommodate the transportation of organs as well. In this study, the vehicles for transporting the organs are refrigerated ones.

In this study, the locations of the network’s facilities, including hospitals, TCs, and shipping agents, are determined in some recipient zones with uncertainty due to this industry’s dynamic nature. Our novelties in this context are represented as below:

  • We contribute to the literature by designing an OTN with the approach of location-allocation and resource-allocation. The perishable nature of the organs necessitates the employment of transportation methods that guarantee the organs’ requisite temperature restrictions. As a result, the cold chain problem arises. The cold chain logistic is regarded as involving refrigerated vehicles for transporting the organs as a resource, and their capacities are also taken into account. To the best of our knowledge, the combination of organ transplant network design and cold chain vehicle allocation has not been addressed so far.

  • Furthermore, global warming is one of the most critical topics that humanity faces today. As one of the primary contributors to global warming, the fuel consumption of various modes of transportation has prompted us to include carbon neutrality as one of the article’s objectives.

  • One of the important issues in organ transplantation is the successful performance of the surgical process, the failure of which can be manifested in the death of the recipient or an unsuccessful surgery. To this end, in addition to minimizing the total costs, this study aims to minimize the total number of unsatisfied demands that some of which may cause death and others may not. In addition, we have considered a prioritization of unmet demands leading to death over the ones that do not.

  • Most of the papers in this context have studied kidney and liver transplantation as the two most transplanted organs worldwide. Due to the possibility that pulmonary insufficiencies could grow in the future as a result of the COVID-19 outbreak, we felt it vital to include lung transplantation as well.

The rest of this study is structured as follows. In the “Literature Review” section, a literature review of the research is provided. The problem description and research methodology are presented in the “Problem Description and Formulation” section. In the “Solution Approach” section, the solution approach of the previous section is presented. Segment “Numerical Examples” corresponds to test problems and model validation. In the “Case Study Implementation” section, a real case study is implemented. Some sensitivity analyses and their attained managerial insights are provided in sections “Sensitivity Analysis” and “Discussion and Managerial Insights,” respectively. Finally, the conclusion is presented in the “Conclusion” section.

Literature Review

In this section, the research literature is divided into two categories. Studies related to healthcare location-allocation are provided in the first category, and in the second one, a review of healthcare resource allocation is presented. Subsequently, the contributions of this research are clarified.

Healthcare Location-Allocation

Research in this area has presented different models for determining the location-allocation of healthcare facilities. In the work by Zhang, Cao, Liu, and Huang (2016), a multi-objective genetic algorithm is used to achieve Pareto-optimal solutions and trade-offs between conflicting objectives. Shariff, Moin, and Omar (2012) applied a healthcare location-allocation model in Malaysia. The formulation was a capacitated maximal covering location problem aiming for maximization of the population assigned to a facility. A genetic algorithm was developed to solve the large-size problem. Salimian and Mousavi (2022) introduced a novel scenario-based MINLP model to design a transplant network considering climate change. The objectives of this research are maximization of blood-type compatibility and organ quality while minimizing the amount of time it takes to deliver organs following a disruption. A mixed-integer linear programming methodology is proposed by Devi, Patra, and Singh (2022) for the location-allocation of healthcare service networks. The study’s objective is to determine the quickest and most cost-effective ways to transport test samples from different locations to testing laboratories. Aghsami et al. (2023a) presented a location-allocation problem in the blood supply chain using queueing theory in the collection centers in order to minimize expected total costs and maximize donor satisfaction.

Due to controversy and questionability surrounding optimal allocation methods and various policies, organ allocation methods and their associated policies have developed rapidly (Alagoz, Schaefer, & Roberts, 2009). Zahiri, Tavakkoli-Moghaddam, and Pishvaee (2014a) proposed a robust possibilistic programming model for the location-allocation of organ transplantation supply chain in Iran under uncertainty. The objective function of the proposed MILP model was to minimize the total costs. Zahiri, Tavakkoli-Moghaddam, Mohammadi, and Jula (2014b) extended their earlier work by developing a multi-objective location-allocation model for designing an organ transplant transportation network to minimize cost and delivery time, considering uncertainty. Bruni, Conforti, Sicilia, and Trotta (2006) developed a MILP optimization model to find the optimal location of OTN facilities based on equity. This was applied to an Italian case study. The possibilistic programming for liver allocation and transportation with a hybrid interactive fuzzy optimization model was proposed by Kargar, Pishvaee, Jahani, and Sheu (2020). In this study, trade-offs are made between equity and efficiency. Ahmadvand and Pishvaee (2018b) applied a model based on Data Envelopment Analysis (Daskin & Dean) for kidney allocation to evaluate the efficiency of eligible patient-organ allocation pairs as way to prioritize candidates. Rouhani and Amin (2022) developed a multi-objective hierarchical location-allocation model with the goal of minimization of total costs and time, and maximization of geographical equality. Supply and demand uncertainty was taken into account. In a work by Beliën, De Boeck, Colpaert, Devesse, and Van den Bossche (2013), mixed-integer linear programming was used to optimize the location of TCs as one of the most important components of an OTN by minimizing total weighted time as the objective function.

Healthcare Resource Allocation

Almost every society in the world struggles with the availability and efficient allocation of healthcare resources. Healthcare service delivery gaps were investigated by Basu, Jana, Bardhan, and Bandyopadhyay (2017) using pinch analysis, a quantitative tool developed to optimize source-demand allocation networks. Lai, Cheung, and Fu (2018) designed a new mechanism to optimize the allocation of public healthcare resources by utilizing a team-DEA model. Public healthcare was assumed as a public good, and the computations were applied to Chinese healthcare data. Another application of healthcare resource allocation was studied by Ordu, Demir, Tofallis, and Gunal (2021) using the integration of the forecast-simulation-optimization method to find the optimal number of beds and staff in a mid-size English hospital. Keshtkar, Salimifard, and Faghih (2015) worked on optimizing waiting time by considering budget constraints and resource management by evaluating 3 KPIs and making a simulation model. In order to allocate the optimal number of nurses to the shifts, Kiani Nahand, Hamid, Bastan, and Mollajan (2019) proposed a novel multi-objective integer model that incorporates human errors.

In this direction, some papers have investigated uncertainty in their research (Jalilvand, Karimi, Mohammadnazari, Aghsami, & Jolai, 2023). Yin and Büyüktahtakın (2021) developed a multi-stage stochastic epidemic-logistic model to minimize new infections, while equal resource allocation and uncertain disease growth are taken into account. Feng, Wu, and Chen (2017) proposed a multi-objective simulation optimization algorithm for resource allocation in emergency departments by assuming the service time and patient arrival as uncertain parameters. Two objectives, one social and one economic, have been taken into account by Hernández-Pérez and Ponce-Ortega (2021). Minimizing the number of unaccepted patients is a social objective since it improves the likelihood of saving lives while minimizing transportation and healthcare equipment (hospital beds and ICUs) expenses is an economic one. They have taken demand uncertainty into account. Considering the uncertainty of the disease’s spread speed, Eriskin, Karatas, and Zheng (2022) developed a multi-objective location-allocation model that combines strategic, tactical, and operational decisions into a single decision model employing across-scenario robust (ASR).

One of the most important issues in some healthcare subcategories is the matter of temperature. Since some healthcare stuff like vaccines or organs must be frozen to prevent spoilage, the cold chain gains significance in this context. Ashok, Brison, and LeTallec (2017) have investigated cold chain systems’ challenges and solutions like inadequate cold chain capacity, absence of cutting-edge or optimal equipment, and insufficient inspection and maintenance systems for temperature. Another paper studies a cold chain logistics vehicle routing optimization problem considering customer satisfaction and carbon emissions (Fereidouni, Mehdizadeh Somarin, Mohammadnazari, Aghsami, & Jolai, 2022; Qin, Tao, & Li, 2019). In our article, cold chain vehicles are utilized as resources to transport organs from hospitals to TCs, in order to prevent organ wastage as much as possible.

Research Gaps, Motivation, and Contributions

There is a gap in the current literature addressing the integration of designing organ transplantation location-allocation and resource-allocation. To the best of our knowledge, cold chain vehicles have not been considered as resources in this context. Another issue that has not been considered in previous studies is the external cost of carbon emission during transportation. Also, a large number of publications discussing organ transplantation issues have focused on kidney and liver transplants as the two most transplanted organs in the world. Another existing gap is that minimization of unsatisfied demand has not been regarded yet.

Due to the different nature of each organ type, they have various maximum allowable CIT. Therefore, assigning a specific refrigerated vehicle to each organ is essential to ensure it will not perish and lead to organ wastage. With the increasing rise of global warming, it is crucial to pay attention to carbon neutrality and bestow on our environment as much as we are able to. Hence, involving green logistic techniques may reduce these emissions. With the epidemy of COVID-19, many people will suffer from lung diseases in the future, and it is estimated that the demand for lung transplantation will increase. That is our motivation to involve this type of organ in this study, as well as the heart and kidney. Organ transplantation unsatisfied demand requires substantial attention since it directly deals with humans’ lives.

This paper’s multi-period location-allocation model’s goal is to find the optimal locations of hospitals, TCs, and shipping agents under uncertain environments. Furthermore, the optimal interrelationship between these facilities will be obtained in order to design a cost-efficient organ transplant network. We propose two objective functions, including minimization of total costs and the number of unsatisfied demands, which the second one is one of our contributions. Furthermore, we have interfered with recipient prioritizing by dividing them into high-risk and low-risk recipients into two categories. The organ supply first satisfies the demand of high-risk recipients in order to prevent mortality as much as possible. The remainder is then allocated to low-risk clients. To address the aforementioned gap, we have assumed cold chain vehicles as resources to be allocated for organ transportation from hospitals to TCs, and their capacity constraints are regarded. The movement of vehicles is also restricted by the determined amount of carbon emission allowed by the government.

Problem Description and Formulation

Organ transplant candidates are increasing daily as medical technology advances. Transplantation is divided into two distinct phases: procurement and surgery. OTN’s logistics management and design are centered on the procurement phase, with the surgery phase focusing exclusively on medicine. The procurement step is further subdivided into three stages: matchmaking, transportation route planning, and scheduling of medical teams.

From a planning perspective, organ transplantation articles are divided into two broad categories: (1) those addressing long-term (strategic) decision problems and (2) those addressing short-term (operational) decision problems. The first category entails long-term considerations such as network facility location-allocation and regional configuration design of hierarchical allocation systems in order to maximize societal benefit while lowering overall network expenses. Given that the allocation of organs is the most critical component of short-term organ transplantation decisions, the second category and majority of operational planning research is devoted to studying organ allocation and distribution challenges, particularly kidney and liver allocation problems. This study’s scope is limited to the first category. Given the potential sites, a long-term decision about finding the optimal facilities’ locations will be made. The details of the problem will be enlightened in the following paragraphs.

In general, there are two categories of challenges in supply chain management: incoming and outbound problems. Inventory and collection planning are examples of inbound challenges, whereas supply, distribution, and scheduling are examples of outbound problems. Once the supply is ready, the next step is to distribute the organ to the appropriate recipient while balancing efficiency and equality, as well as expanding donor pools. The incoming dilemma concerns the placement and distribution of organs to ensure a successful transplant. All actions involving the coordination and networking of transplant centers in receiving and transplanting patients with the appropriate centers must be efficient and successful in terms of event planning.

An organ transplant supply chain network that is modeled in this study is depicted in Fig. 2, illustrating the interactions among the constituent facilities. The first stage is once a donor decides to donate an organ to the hospital (1). In order to test the blood and perform the required analyses, a shipping team will be sent to the hospital (2), and then from the hospital to TC transporting the required information and the donor’s blood sample (3). Afterward, the transporter will turn back to the hospital (4). The process of allocating the most appropriate recipient and TC begins at this point. In the event of an operation, the organ harvest procedure will take place in the hospital and the organ/organs will be transported to the TC for transplantation (5). During this time, the accepted recipient is informed and has to attend the TC as soon as possible to undergo the operation (6). It is worth noting that arrows (3) and (4) are depicted with dashes demonstrating the information flows.

Fig. 2
figure 2

Organ transplant supply chain network

Full size image

The hospital receives direct referrals from brain-dead patients or donors. The TC’s responsibility is to register the recipient, sample their blood, and perform the transplantation surgery. To avoid arrow congestion in Fig. 2, two TCs are illustrated. However, they are not different practically.

In this paper, the demand has been studied separately for high-risk and low-risk recipients. In order to have the lowest mortality as possible, the recipients are divided into two groups: The first group includes the recipients who the organ shortage will lead them to mortality (high-risk recipients), and the second one consists of people the deficiency may not bring about death for them (low-risk recipients). Consequently, this study works on prioritizing the patients as well.

Fuzzy programming, rather than being crisp/probabilistic in the traditional sense, is an optimization approach for dealing with issues involving imprecisely described model parameter sets. It covers the modeling components of optimization challenges with imprecisely specified model parameters in the decision context. Triangular fuzzy numbers are commonly used to evaluate and present fuzzy information, and they are particularly well suited to small datasets or data with poor precision. As a result, in this article, we assume that transportation costs and total demand (including high-risk and low-risk recipients) are uncertain, and we seek to ensure that the amount of the items provided to the consumer is likewise uncertain in triangular fuzzy numbers.

In this section, we propose a bi-objective multi-period location-allocation model to design an efficient organ transplantation network, taking uncertainties into account. As previously discussed, there are three types of facilities namely hospitals, shipping agents, and TCs. Due to the given potential sites for facilities and demands for different organs in varying recipient zones, this problem is concerned with issues like finding the optimal sites of the aforementioned facilities, the optimal flows between them, allocating refrigerated vehicles to transportation, monitoring excess carbon emission, and prioritizing the recipients. The model aims to minimize total costs and the unsatisfied demands leading to both mortality and survival.

Notations

The notations used for the mathematical formulation are presented separately, sorted by sets, parameters, and decision variables as follows. The uncertain ones are indicated with a tilde.

Sets

 

I

set of potential hospital locations, i ∈ I

J

set of potential TC locations, j ∈ J

R

set of recipient zones, r ∈ R

O

set of organ types, o ∈ O

SA

set of shipping agent locations, sa ∈ SA

V

set of refrigerated vehicles, v ∈ V

V′

set of shipping agent vehicles, v′ ∈ V′

T

set of time periods, t ∈ T

Parameters

 

ci

fixed cost of establishing a hospital at potential location i

cj

fixed cost of establishing a TC at potential location j

cio

cost of harvest process of organ o at hospital i

cjo

cost of equipping TC j for organ type o

\({\textbf{N}}_{\textbf{i}}^{\textbf{t}}\)

number of donors at hospital i at time period t

\({\boldsymbol{B}}_{\textbf{io}}^{\textbf{t}}\)

number of organ o harvested from a single body at hospital i at time period t

P

total number of available shipping agents at each time period

\({\overset{\sim }{\boldsymbol{D}}}_{\boldsymbol{ro}}^{\boldsymbol{t}}\)

total demand of high-risk recipients in recipient zone r for organ o at time period t

\(\overset{\sim }{\boldsymbol{D}}{\prime}_{\boldsymbol{ro}}^{\boldsymbol{t}}\)

total demand of low-risk recipients recipient zone r for organ o at time period t

\({\overset{\sim }{\boldsymbol{c}}}_{\boldsymbol{i}\boldsymbol{j}}^{\boldsymbol{i}\boldsymbol{\to}\boldsymbol{j}}\)

cost of transporting samples and needed information from hospital i to TC j

\(\overset{\sim }{\boldsymbol{c}}{\prime}_{\boldsymbol{i}\boldsymbol{j}}^{\boldsymbol{i}\boldsymbol{\to}\boldsymbol{j}}\)

cost of transporting an organ from hospital i to TC j

\({\boldsymbol{c}}_{\boldsymbol{r}\boldsymbol{j}}^{\boldsymbol{r}\boldsymbol{\to}\boldsymbol{j}}\)

cost of transporting an individual from recipient zone r to TC j

\({\boldsymbol{c}}_{\boldsymbol{SAi}}^{\left(\boldsymbol{SA}\boldsymbol{\to}\boldsymbol{i}\right)}\)

cost of contract between hospital i and shipping agent sa

\({\boldsymbol{t}}_{\boldsymbol{ijo}}^{\boldsymbol{t}}\)

traveling time of organ o from hospital i to TC j at time period t

Qo

organ o cold ischemia time (CIT)

λ

importance weight of the strategic level costs

disij

the distance between hospital i and TC j

dissai

the distance between hospital i and shipping agent sa

et

amount of CO2 emission per distance unit in period t

Lt

maximum allowable amount of carbon emission in period t determined by the government

capv

capacity of refrigerated vehicle v

capv′

capacity of shipping agent vehicle v′

W1

importance weight of high-risk recipient unsatisfied demands

W2

importance weight of low-risk recipient unsatisfied demands

φ

importance weight of total cost objective function in weighted sum method

1 − φ

importance weight of unsatisfied demand objective function in weighted sum method

PC

penalty cost for each unsatisfied demand

Decision variables

xi

\(\left\{\begin{array}{c}1\ if\ a\ hospital\ is\ established\ at\ location\ i\\ {}\ 0\ otherwise\end{array}\right.\)

xj

\(\left\{\begin{array}{c}1\ if\ a\ TC\ is\ established\ at\ location\ j\\ {}\ 0\ otherwise\end{array}\right.\)

yio

\(\left\{\begin{array}{c}1\ if\ a\ hospital\ is\ established\ at\ location\ i\ and\ equipped\ for\ donation\ of\ organ\ o\\ {}0\kern0.5em otherwise\end{array}\right.\)

yjo

\(\left\{\begin{array}{c}1\ if\ a\ TC\ is\ established\ at\ location\ j\ and\ equipped\ for\ transplantation\ of\ organ\ o\\ {}0\ otherwise\end{array}\right.\)

\({\boldsymbol{z}}_{\boldsymbol{sa}}^{\boldsymbol{t}}\)

\(\left\{\begin{array}{c}\ 1\ if\ shipping\ agent\ sa\ is\ hired\ at\ time\ period\ t\\ {}0\ otherwise\end{array}\right.\)

\({\boldsymbol{z}}_{\boldsymbol{sai}}^{\left(\boldsymbol{sa}\boldsymbol{\to}\boldsymbol{i}\right)\boldsymbol{t}}\)

\(\left\{\begin{array}{c}1\ if\ a\ hospital\ at\ location\ i\ is\ served\ by\ shipping\ agent\ sa, at\ time\ period\ t\\ {}0\ otherwise\end{array}\right.\)

zov

\(\left\{\begin{array}{c}1\ if\ organ\ o\ is\ assigned\ to\ vehicle\ v\ \\ {}0\ otherwise\end{array}\right.\)

d

\(\left\{\begin{array}{c}\ 0\ if\ {\overset{\sim }{D^{\prime}}}_{ro}^t<\sum_{i=1}^I\sum_{j=1}^J{F^{\prime}}_{ijo}^{\left(i\to j\right)t}-{\overset{\sim }{D}}_{ro}^t\\ {}1\ otherwise\end{array}\right.\)

d′

\(\left\{\begin{array}{c}0\ if\ {\overset{\sim }{D}}_{ro}^t<\sum_{i=1}^I\sum_{j=1}^J{F^{\prime}}_{ijo}^{\left(i\to j\right)t}\\ {}1\ otherwise\end{array}\right.\)

\({\boldsymbol{F}}_{\boldsymbol{ijo}}^{\left(\boldsymbol{i}\boldsymbol{\to}\boldsymbol{j}\right)\boldsymbol{t}}\)

flow of information and samples of organ o from hospital to TC j at time period t

\({\overset{\acute{\mkern6mu}}{\boldsymbol{F}}}_{\boldsymbol{ijov}}^{\left(\boldsymbol{i}\boldsymbol{\to}\boldsymbol{j}\right)\boldsymbol{t}}\)

flow of organ o from hospital i to TC j at time period t by vehicle v

\({\boldsymbol{F}}_{\boldsymbol{rjo}}^{\left(\boldsymbol{r}\boldsymbol{\to}\boldsymbol{j}\right)\boldsymbol{t}}\)

flow of recipients moving from their region r to TC j for transplantation at time period t

\({\boldsymbol{A}}_{\boldsymbol{io}}^{\boldsymbol{t}}\)

donor-sourced number of organ o available at hospital i at time period t

\({\boldsymbol{I}}_{\boldsymbol{io}}^{\boldsymbol{t}}\)

Inventory level supply of organ o at hospital i at time period t

\({\boldsymbol{U}}_{\boldsymbol{ro}}^{\boldsymbol{t}}\)

Number of unsatisfied demands in region r leading to mortality (high-risk recipients)

\(\boldsymbol{U}{\prime}_{\boldsymbol{ro}}^{\boldsymbol{t}}\)

Number of unsatisfied demands in region r not leading to mortality (low-risk recipients)

Assumptions

  • Each organ has a specific maximum allowable CIT.

  • Due to the scarcity and perishability of organs’ nature, their transportation requires special consideration. Hence, this affair is not done by shipping agents, and the hospitals are responsible for that with a special type of vehicle.

  • The defined set of vehicles v are exploited for transferring organs to TCs, and they are refrigerated vehicles.

  • The defined set of vehicles v′ are exploited for transporting samples and information from hospitals to TCs and vice versa, and they belong to shipping agents.

  • Each vehicle has a particular capacity.

  • The potential locations for settling the facilities are available and suggested by the experts.

Mathematical Formulation

$${\displaystyle \begin{array}{c}\operatorname{Min}\ \textrm{Z}1=\lambda \left(\ \sum_i^I{c}_i{x}_i+\sum_j^J{c}_j{x}_j+\sum_o^O\sum_j^J{c}_{jo}{y}_{jo}\right)\\ {}+\sum_t^T\sum_o^O\sum_j^J\sum_i^I{c}_{io}{F}_{ij o}^{\left(i\to j\right)t}+\sum_t^T\sum_i^I\sum_{sa}^{SA}{c}_{sa i}^{\left( SA\to i\right)}{z}_{SA i}^{\left( SA\to i\right)t}\\ {}\begin{array}{c}+\sum_{t=1}^T\sum_{o=1}^O\sum_{j=1}^J\sum_{i=1}^I{\tilde{c}}_{ij}^{i\to j}{F}_{ij o}^{\left(i\to j\right)t}+\sum_{t=1}^T\sum_{o=1}^O\sum_{j=1}^J\sum_{i=1}^I\sum_{v=1}^V\overset{\sim }{c}{\prime}_{ij}^{i\to j}{F^{\prime}}_{ij o v}^{\left(i\to j\right)t}\\ {}+\sum_t^T\sum_o^O\sum_j^J\sum_r^R{c}_{rj}^{\left(r\to j\right)}{F}_{rj o}^{\left(r\to j\right)t}\end{array}\end{array}}$$
(1)
$$\operatorname{Min}\ {\textrm{Z}}_2=\sum_r^R\sum_o^O\sum_t^T{W}_1{U}_{ro}^t+\sum_r^R\sum_o^O\sum_t^T{W}_2U{\prime}_{ro}^t$$
(2)

s.t:

$${y}_{io}\le {x}_i\forall i,o$$
(3)
$${y}_{jo}\le {x}_j\forall j,o$$
(4)
$$\sum_{i=1}^I{y}_{io}\ge 1\forall o$$
(5)
$$\sum_{j=1}^J{y}_{jo}\ge 1\forall o$$
(6)
$$\sum_{sa=1}^{SA}{z}_{sa}^t=P\forall t$$
(7)
$${z}_{sa i}^{\left( sa\to i\right)t}\le {z}_{sa}^t\forall i, sa,t$$
(8)
$${y}_{io}^t\le \sum_{sa=1}^{SA}{z}_{sa i}^{\left( sa\to i\right)t}\forall i,o,t$$
(9)
$${z}_{sa}^t\le \sum_{i=1}^I{z}_{sa i}^{\left( sa\to i\right)t}\forall sa,t$$
(10)
$$\sum_{sa=1}^{SA}{z}_{sa i}^{\left( sa\to i\right)t}\le 1\forall i,t$$
(11)
$$\sum_{j=1}^J{F}_{ijo}^{\left(i\to j\right)t}={A}_{io}^t{y}_{io}\forall i,o,t$$
(12)
$${F}_{ijo}^{\left(i\to j\right)t}\le {A}_{io}^t{y}_{jo}\forall i,j,o,t$$
(13)
$$F{\prime}_{ijo v}^{\left(i\to j\right)t}=0\kern0.75em \mid {t}_{ijo}^t>{Q}_o\forall i,j,o,t,v$$
(14)
$$\sum_{v=1}^VF{\prime}_{ijov}^{\left(i\to j\right)t}\le {A}_{io}^t{y}_{jo}\forall i,j,o,t$$
(15)
$$\sum_{j=1}^J\sum_{v=1}^VF{\prime}_{ijov}^{\left(i\to j\right)t}\le {A}_{io}^t{y}_{io}\forall i,o,t$$
(16)
$${A}_{io}^t={N}_i^t{B}_{io}^t\forall i,o,t$$
(17)
$$\sum_{r=1}^R\sum_{j=1}^J{F}_{rjo}^{\left(r\to j\right)t}=\sum_{i=1}^I\sum_{j=1}^J\sum_{v=1}^VF{\prime}_{ijov}^{\left(i\to j\right)t}+\sum_{r=1}^R{U}_{ro}^t+\sum_{r=1}^RU{\prime}_{ro}^t\forall o,t$$
(18)
$$\sum_{r=1}^R{U}_{ro}^t=\left(\sum_{r=1}^R{\overset{\sim }{D}}_{ro}^t-\sum_{i=1}^I\sum_{j=1}^J\sum_{v=1}^V{F^{\prime}}_{ijov}^{\left(i\to j\right)t}\right)\times {d}^{\prime}\forall o,t$$
(19)
$$\sum_{r=1}^RU{\prime}_{ro}^t=\left[\sum_{r=1}^R{\overset{\sim }{D^{\prime}}}_{ro}^t-\left(\sum_{i=1}^I\sum_{j=1}^J\sum_{v=1}^V{F^{\prime}}_{ijov}^{\left(i\to j\right)t}-\sum_{r=1}^R{\overset{\sim }{D}}_{ro}^t\right)\ \left(1-{d}^{\prime}\right)\right]\times d\forall o,t$$
(20)
$${I}_{io}^t={I}_{io}^{t-1}+{A}_{io}^t-\sum_{v=1}^V\sum_{j=1}^J{F^{\prime}}_{ijov}^{\left(i\to j\right)t}\forall i,o,t\mid {I}_{io}^0=0$$
(21)
$$2{e}^t\left[\sum_j^J\sum_i^I\frac{{F^{\prime}}_{ij o v}^{\left(i\to j\right)t}}{cap_v}{dis}_{ij}+\sum_j^J\sum_i^I\frac{F_{ij o}^{\left(i\to j\right)t}}{cap_{v^{\prime }}}\left({dis}_{ij}+{dis}_{sai}\right)\right]\le {L}^t\forall sa,o,t,v,{v}^{\prime }$$
(22)
$$F{\prime}_{ijov}^{\left(i\to j\right)t}\le {cap}_v{z}_{ov}\forall i,j,o,t,v$$
(23)
$${x}_i,{x}_j,{y}_{io},{y}_{jo},{z}_{sa}^t,{z}_{sa i}^t,{z}_{ov},d,{d}^{\prime}\in \left\{0,1\right\}\forall i,j,o,t, sa$$
(24)
$${F}_{ijo}^{\left(i\to j\right)t},F{\prime}_{ijo v}^{\left(i\to j\right)t},{F}_{rjo}^{\left(r\to j\right)t}\ge 0, Integer\forall i,j,o,r,t$$
(25)
$${A}_{io}^t\kern0.5em ,P\ge 0, Integer\forall i,o,t$$
(26)

The objective function (1) minimizes the weighted total costs. It comprises fixed opening costs (including costs of setting up and equipping hospitals and TCs), harvesting process costs, and transportation costs. The last term in this equation refers to the carbon emission costs. Objective function (2) aims to minimize the number of unsatisfied demands considering the importance of mortality and survival weights. According to constraint set (3), a hospital can only serve a special organ donation if it is established. Constraint set (4) does the same for each TC, as well. In constraint sets (5) and (6), it is guaranteed that at least one hospital and one TC must be set up for each organ. Constraint set (7) indicates the total number of shipping agents available to each time period. Constraint set (8) points out that no hospital can be in the service domain of a shipping agent unless that agent is selected. Constraint set (9) ensures that at least one shipping agent covers each hospital. In constraint set (10), we ensure that a shipping agent can only be selected if assigned to at least one hospital to avoid unutilized shipping agents. Constraint set (11) assures that each hospital is covered by no more than one shipping agent. Constraint sets (12) and (13) are associated with the flows of information and samples between hospitals and TCs. These flows are possible if and only if these facilities are established. Constraint set (14) asserts that the flow of an organ from hospital to TC will be zero if the delivery time exceeds the maximum available CIT of that organ. Constraint sets (15) and (16) state that the flow of organs from hospitals to TCs depends on whether these facilities are settled, and also there is a limitation on the amount of flow due to the availability of organs in the hospital. Based on the constraint set (17), we estimate how many organs of each type were supplied at each hospital and each time period. Constraint set (18) shows the equation of total flows from recipient zones to TCs and total flows from hospitals to TCs plus the unsatisfied demand at each time period. At each time period and for each organ, constraint sets (19) and (20) calculate the unsatisfied demand of high-risk and low-risk recipients, respectively. Constraint set (20) is associated with the inventory level of each organ type in each hospital and over each period of time. Constraint set (21) restricts the number of vehicle movements between hospitals and TCs through the maximum allowable amount of carbon emission in period t determined by the government. Constraint set (22) assures that if a vehicle is assigned to an organ at a time period, the capacity of the vehicle should not be violated. Lastly, constraint sets (24–26) identify the type of decision variables.

Solution Approach

The proposed methodology for each small, medium, and large size is straightforward. Therefore, the exact solution can be obtained by employing exact methods and using the Generalized Algebraic Modelling system (GAMS) software in a reasonable time. In the following subsections, we are going to defuzzify the model by Jiménez method, first. Then a weighted sum multi-objective approach is presented in order to solve the problem.

Jiménez Method

Due to the nature of the data in real-world situations, a number of parameters are uncertain. In this research, we, therefore, consider total demand (including high-risk and low-risk recipients) and transportation costs to be possibilistic data represented by triangular fuzzy numbers as shown below:

$${\overset{\sim }{D}}_{ro}^t=\left({D}_{ro(1)}^t,{D}_{ro(2)}^t,{D}_{ro(3)}^t\right)$$
(27)
$${\overset{\sim }{D\prime}}_{ro}^t=\left({D^{\prime}}_{ro(1)}^t,{D^{\prime}}_{ro(2)}^t,{D^{\prime}}_{ro(3)}^t\right)$$
(28)
$${\tilde{c}}_{ij}^{\left(i\to j\right)}=\left({c}_{ij(1)}^{\left(i\to j\right)},{c}_{ij(2)}^{\left(i\to j\right)},{c}_{ij(3)}^{\left(i\to j\right)}\right.$$
(29)
$${\overset{\sim }{c\prime}}_{ij}^{\left(i\to j\right)}=\left({c}_{ij(1)}^{\left(i\to j\right)},{c}_{ij(2)}^{\left(i\to j\right)},{c}_{ij(3)}^{\left(i\to j\right)}\right)$$
(30)

The literature has presented a number of strategies for comparing or ranking fuzzy numbers, although ranking techniques are not necessarily consistent with one another (Wang & Kerre, 1996). Numerous factors, including distinguishability (Bortolan & Degani, 1985), rationality (Nakamura & Hanafusa, 1986), fuzzy or linguistic presentation, and robustness, have been used to support ranking algorithms. In this study, we employ a technique (Jiménez) that confirms all the aforementioned characteristics and, in addition, is computationally effective for solving an LP problem because it maintains linearity.

The Jiménez approach is presented in this section to solve the proposed mixed-integer programming model. This method is one of the most efficient methods of possibility planning that uses the concept of the expected value of fuzzy numbers in ranking numbers. In this method, there is no limit to the possibility of distributing fuzzy values and triangular and trapezoidal distributions can be used (Jiménez, Arenas, Bilbao, & Rodrı, 2007). We now turn to this definition of the two concepts of expected interval and expected value. The expected interval of a fuzzy number such as \(\overset{\sim }{a}\) is defined as follows:

$$EI\left(\overset{\sim }{a}\right)=\left[{E}_{1,}^a\ {E}_2^a\right]=\left[\int_0^1{f}_a^{-1}(r) dr,\int_0^1{g}_a^{-1}(r) dr\ \right]$$
(31)

And the concept of expected value for the fuzzy number \(\overset{\sim }{a}\) is written as follows:

$$EV(I)=\frac{E_1^{a\kern0.5em }+{E}_2^a}{\kern2.5em 2\kern2.5em }$$
(32)

For fuzzy numbers of triangular type with parameters (a1, a2, a3), the expected value and expected interval are calculated as follows (Shahedi et al., 2021):

$$EI\left(\overset{\sim }{a}\right)=\left[{E}_{1,}^a\ {E}_2^a\right]=\left[\frac{1}{2}\left({a}_1+{a}_2\right),\frac{1}{2}\left({a}_2+{a}_3\right)\right], EV\overset{\sim }{(a)}=\frac{1}{4}\left({a}_1+2{a}_2+{a}_3\right)$$
(33)

In the Jimenez method, the ranking method is used to de-fuzzy the constraints of a possibility model. According to this method, for any pair of fuzzy numbers \(\overset{\sim }{a}\) and \(\overset{\sim }{b}\), the degree of more significance or equality of \(\overset{\sim }{a}\) relative to fuzzy number \(\overset{\sim }{b}\) is defined as follows:

$${Degree\ \left(\overset{\sim }{a}\ge \overset{\sim }{b}\right)}={\mu}_M\left(\overset{\sim }{a},\overset{\sim }{b}\right)= degree\ of\ preference\ of\ \overset{\sim }{a}\ over\ \overset{\sim }{b}$$
$${\mu}_M\left(\overset{\sim }{a},\overset{\sim }{b}\right)=\left\{\begin{array}{ll}0& if\ {E}_2^a<{E}_1^b\\ {}\frac{E_2^a-{E}_1^b}{E_2^a+{E}_2^b-{E}_1^a-{E}_1^b}& if\ {E}_1^a-{E}_2^b<0,{E}_2^a\kern0.75em -{E}_1^b>0\\ {}1& if\ {E}_1^a>{E}_2^b\end{array}\right.$$
(34)

If \({\mu}_M\left(\overset{\sim }{a},\overset{\sim }{b}\right)\ge \beta\) and β ∈ [0, 1] is established, \(\overset{\sim }{a}\) is at least greater than or equal to \(\overset{\sim }{b}\) with a β rating. Then:

$${\displaystyle \begin{array}{c}\overset{\sim }{a}x\ge \overset{\sim }{b}\\ {}\frac{E_2^a-{E}_1^b\kern1.5em }{\kern1em {E}_2^a+{E}_2^b-{E}_1^a-{E}_1^b\kern2.25em }\ge \beta \to \beta {E}_1^a+\left(1-\beta \right){E}_2^a\ge \beta {E}_2^b+\left(1-\beta \right){E}_1^b\end{array}}$$
(35)

In equal constraints, de-fuzzy is performed as follows:

$${\displaystyle \begin{array}{c}\overset{\sim }{a}x=\overset{\sim }{b}\\ {}\left\{\begin{array}{c}\left[\left(1-\frac{\beta }{2\ }\right){E}_2^a+\frac{\beta }{2}{E}_1^a\right]x\ge \left(1-\frac{\beta }{2}\right){E}_1^b+\frac{\beta }{2}{E}_2^b\\ {}\left[\left(1-\frac{\beta }{2}\right){E}_1^a+\frac{\beta }{2}{E}_2^a\right]x\le \left(1-\frac{\beta }{2}\right){E}_2^b+\frac{\beta }{2}{E}_1^b\end{array}\right.\end{array}}$$
(36)

And to de-fuzzy the objective function, we will do as follows:

$${\displaystyle \begin{array}{c}\mathit{\operatorname{Min}}\ Z=\overset{\sim }{c}x\\ {} MinZ= EV\left(\overset{\sim }{c}\right).x\end{array}}$$
(37)

Accordingly, the proposed defuzzification approach for the studied problem can be formulated as follows:

The first objective function will be constituted with Equation (38).

$${\displaystyle \begin{array}{l}\operatorname{Min}\ {\textrm{Z}}_1=\lambda \left(\ \sum\nolimits_i^I{c}_i{x}_i+\sum\nolimits_j^J{c}_j{x}_j+\sum\nolimits_o^O\sum\nolimits_j^J{c}_{jo}{y}_{jo}\right)\\ {}+\sum\limits_t^T\sum\limits_o^O\sum\limits_j^J\sum\limits_i^I{c}_{io}{F}_{ij o}^{\left(i\to j\right)t}+\sum\limits_t^T\sum\limits_i^I\sum\limits_{sa}^{SA}{c}_{sa i}^{\left( SA\to i\right)}{z}_{SA i}^{\left( SA\to i\right)t}\\ {}\begin{array}{l}+\sum\limits_t^T\sum\limits_o^O\sum\limits_j^J\sum\limits_i^I\left(\frac{c_{ij(1)}^{\left(i\to j\right)}+2{c}_{ij(2)}^{\left(i\to j\right)}+{c}_{ij(3)}^{\left(i\to j\right)}}{4}\right){F}_{ij o}^{\left(i\to j\right)t}\\ {}\begin{array}{l}+\sum\limits_t^T\sum\limits_o^O\sum\limits_j^J\sum\limits_i^I\sum\limits_{v=1}^V\left(\frac{{c^{\prime}}_{ij(1)}^{\left(i\to j\right)}+2{c^{\prime}}_{ij(2)}^{\left(i\to j\right)}+{c^{\prime}}_{ij(3)}^{\left(i\to j\right)}}{4}\right){F^{\prime}}_{ij o}^{\left(i\to j\right)t}\\ {}+\sum\limits_t^T\sum\limits_o^O\sum\limits_j^J\sum\limits_r^R{c}_{rj}^{\left(r\to j\right)}{F}_{rj o}^{\left(r\to j\right)t}\end{array}\end{array}\end{array}}$$
(38)

Constraint sets (19) and (20) are first linearized and defuzzied as follows:

$$\sum_{r=1}^R\left[\beta \left(\frac{D_{ro(2)}^t+{D}_{ro(3)}^t}{2}\right)+\left(1-\beta \right)\left(\frac{D_{ro(1)}^t+{D}_{ro(2)}^t}{2}\right)\right]\le M{d}^{\prime }+\sum_{i=1}^I\sum_{j=1}^J\sum_{v=1}^V{F^{\prime}}_{ijov}^{\left(i\to j\right)t}\forall o,t$$
(39)
$${d}^{\prime}\le \frac{1}{\sum_{i=1}^I\sum_{j=1}^J\sum_{v=1}^V{F^{\prime}}_{ijov}^{\left(i\to j\right)t}}\sum_{r=1}^R\beta \left(\frac{D_{ro(1)}^t+{D}_{ro(2)}^t}{2}\right)+\left(1-\beta \right)\left(\frac{D_{ro(2)}^t+{D}_{ro(3)}^t}{2}\right)\forall o,t$$
(40)
$$\sum_{r=1}^R\beta \left(\frac{D{\prime}_{ro(2)}^t+D{\prime}_{ro(3)}^t}{2}\right)+\left(1-\beta \right)\left(\frac{D{\prime}_{ro(1)}^t+D{\prime}_{ro(2)}^t}{2}\right)-\sum_{i=1}^I\sum_{j=1}^J\sum_{v=1}^V{F^{\prime}}_{ijov}^{\left(i\to j\right)t}-\sum_{r=1}^R\beta \left(\frac{D_{ro(2)}^t+{D}_{ro(3)}^t}{2}\right)+\left(1-\beta \right)\left(\frac{D_{ro(1)}^t+{D}_{ro(2)}^t}{2}\right)\le Md\forall o,t$$
(41)
$$d-M{d}^{\prime}\le \frac{\sum_{r=1}^R\beta \left(\frac{\Big({D}^{\prime }{\prime}_{ro(1)}^t+{D^{\prime}}_{ro(2)}^t}{2}\right)+\left(1-\beta \right)\left(\frac{{D^{\prime}}_{ro(2)}^t+{D^{\prime}}_{ro(3)}^t}{2}\right)}{\sum_{i=1}^I\sum_{j=1}^J\sum_{v=1}^V{F^{\prime}}_{ijov}^{\left(i\to j\right)t}-\sum_{r=1}^R\beta \left(\frac{D_{ro(1)}^t+{D}_{ro(2)}^t}{2}\right)+\left(1-\beta \right)\left(\frac{D_{ro(2)}^t+{D}_{ro(3)}^t}{2}\right)}\forall o,t$$
(42)
$$\sum_{r=1}^R{U}_{ro}^t\le \left(\sum_{r=1}^R\frac{\beta }{2}\left(\frac{\ {D}_{ro(1)}^t+{D}_{ro(2)}^t}{2}\right)+\left(1-\frac{\beta }{2}\right)\left(\frac{D_{ro(2)}^t+{D}_{ro(3)}^t}{2}\right)-\sum_{i=1}^I\sum_{j=1}^J\sum_{v=1}^V{F^{\prime}}_{ijov}^{\left(i\to j\right)t}\right)\times {d}^{\prime}\forall o,t$$
(43)
$$\sum_{t=1}^T{U}_{ro}^t\ge \left(\sum_{r=1}^R\left(1-\frac{\beta }{2}\right)\left(\frac{D_{ro(1)}^t+{D}_{ro(2)}^t}{2}\right)+\left(\frac{\beta }{2}\right)\left(\frac{D_{ro(2)}^t+{D}_{ro(3)}^t}{2}\right)-\sum_{i=1}^I\sum_{j=1}^J\sum_{v=1}^V{F^{\prime}}_{ijov}^{\left(i\to j\right)t}\right)\times {d}^{\prime}\forall o,t$$
(44)
$$\sum_{r=1}^R{U^{\prime}}_{ro}^t\le \left[\sum_{r=1}^R\left(1-\frac{\beta }{2}\right)\left(\frac{{D^{\prime}}_{ro(2)}^t+{D^{\prime}}_{ro(3)}^t}{2}\right)+\left(\frac{\beta }{2}\right)\left(\frac{{D^{\prime}}_{ro(1)}^t+{D^{\prime}}_{ro(2)}^t}{2}\right)-\left(\sum_{i=1}^I\sum_{j=1}^J\sum_{v=1}^V{F^{\prime}}_{ijov}^{\left(i\to j\right)t}-\sum_{r=1}^R\left(1-\frac{\beta }{2}\right)\left(\frac{D_{ro(2)}^t+{D}_{ro(3)}^t}{2}\right)+\left(\frac{\beta }{2}\right)\left(\frac{D_{ro(1)}^t+{D}_{ro(2)}^t}{2}\right)\right)\ \left(1-{d}^{\prime}\right)\right]\times d\forall o,t$$
(45)
$$\sum_{r=1}^RU{\prime}_{ro}^t\ge \left[\sum_{r=1}^R\left(1-\frac{\beta }{2}\right)\left(\frac{{D^{\prime}}_{ro(1)}^t+{D^{\prime}}_{ro(2)}^t}{2}\right)+\left(\frac{\beta }{2}\right)\left(\frac{{D^{\prime}}_{ro(2)}^t+{D^{\prime}}_{ro(3)}^t}{2}\right)-\left(\sum_{i=1}^I\sum_{j=1}^J\sum_{v=1}^V{F^{\prime}}_{ijov}^{\left(i\to j\right)t}-\sum_{r=1}^R\left(1-\frac{\beta }{2}\right)\left(\frac{D_{ro(1)}^t+{D}_{ro(2)}^t}{2}\right)+\left(\frac{\beta }{2}\right)\left(\frac{D_{ro(2)}^t+{D}_{ro(3)}^t}{2}\right)\right)\ \left(1-{d}^{\prime}\right)\right]\times d\forall o,t$$
(46)

Multi-objective Approach

In order to convert two objective functions into one, the weighted sum method presented by Marler and Arora (2010) is utilized. This method is also the simplest method and probably the most widely used classical method for multi-objective models, which normalizes the set of objectives into a single objective by multiplying each of them with a user-supplied weight (Rabbani et al., 2018). Using the weighted sum approach to solve the given problem requires the selection of scalar weights φi and the minimization of the following composite objective function:

$${\displaystyle \begin{array}{l}F=\sum\limits_{i=1}^k{\varphi}_i{F}_i(x)\\ {}s.t.\sum\limits_{i=1}^k{\varphi}_i=1\\ {}\ {\varphi}_i\ge 0\end{array}}$$
(47)

In our problem, the first objective function is in the scale of cost and the second one represents the number of shortages. Thus, to implement the weighted sum approach, we have considered a penalty cost (determined as PC in formulation) for each unsatisfied demand due to the opinion of decision makers. Consequently, the scale of the second objective function will also be converted to cost, and the weighted sum method can be executed. The composite objective function would be as follows:

$${\displaystyle \begin{array}{l}\operatorname{Min}\ \textrm{Z}=\varphi \left[\lambda \left(\ \sum\nolimits_i^I{c}_i{x}_i+\sum\nolimits_j^J{c}_j{x}_j+\sum\nolimits_o^O\sum\nolimits_j^J{c}_{jo}{y}_{jo}\right)\right.\\ {}+\sum\limits_t^T\sum\limits_o^O\sum\limits_j^J\sum\limits_i^I{c}_{io}{F}_{ij o}^{\left(i\to j\right)t}+\sum\limits_t^T\sum\limits_i^I\sum\limits_{sa}^{SA}{c}_{sa i}^{\left( SA\to i\right)}{z}_{SA i}^{\left( SA\to i\right)t}\\ {}\begin{array}{l}+\sum\limits_t^T\sum\limits_o^O\sum\limits_j^J\sum\limits_i^I\left(\frac{c_{ij(1)}^{\left(i\to j\right)}+2{c}_{ij(2)}^{\left(i\to j\right)}+{c}_{ij(3)}^{\left(i\to j\right)}}{4}\right){F}_{ij o}^{\left(i\to j\right)t}\\ {}\begin{array}{l}+\sum\limits_t^T\sum\limits_o^O\sum\limits_j^J\sum\limits_i^I\sum\limits_{v=1}^V\left(\frac{{c^{\prime}}_{ij(1)}^{\left(i\to j\right)}+2{c^{\prime}}_{ij(2)}^{\left(i\to j\right)}+{c^{\prime}}_{ij(3)}^{\left(i\to j\right)}}{4}\right){F^{\prime}}_{ij o v}^{\left(i\to j\right)t}\\ {}+\sum\limits_t^T\sum\limits_o^O\sum\limits_j^J\sum\limits_r^R\left.{c}_{rj}^{\left(r\to j\right)}{F}_{rj o}^{\left(r\to j\right)t}\right]+ PC\times \left(1-\varphi \right)\left[\sum\limits_r^R\sum\limits_o^O\sum\limits_t^T{W}_1{U}_{ro}^t+\sum\limits_r^R\sum\limits_o^O\sum\limits_t^T{W}_2U{\prime}_{ro}^t\right]\end{array}\end{array}\end{array}}$$
(48)

Numerical Examples

Computational Experiments

In order to validate the effectiveness of the proposed methodology and solution strategy, two numerical examples of small and medium sizes are generated at first. A real case study problem is then applied to demonstrate the applicability and utility of the provided mathematical model in the “Case Study Implementation” section. It is noteworthy that all findings are obtained using GAMS 25.1.2 software with the BARON solver on a core i5 PC with 8 GB of RAM. The aforementioned test problems are presented in the “Results and Model Validation” section, and Table 1 displays the parameter values. The sizes of hospitals, TCs, recipient zones, organs, shipping agents, hospital vehicles, shipping agents vehicles, and time periods are different in each test problem.

Table 1 Parameter ranges for test problems
Full size table

Results and Model Validation

In this section, the values of each of the first and second objective functions and the overall one for small and medium sizes are presented in Table 2. The first and second row corresponds to the small and medium sizes, respectively. As shown in Table 2, increasing the magnitude of the problem will increase CPU execution time and the weighted-sum objective function value (value of Z). The results of the computations conducted on a small scale will then be provided.

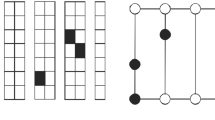
Table 2 Values of objective functions for each test problem size
Full size table

In order to validate the proposed approach, a small-scale test problem (i × j × r × o × sa × v × v′ × t = 6 × 5 × 5 × 2 × 9 × 8 × 9 × 3) is constructed, and the optimal solution is presented in Fig. 3. The parameter values are shown in Table 1. As illustrated in Fig. 3, the nodes determined using i, j, and r correspond to selected hospitals, selected TCs, and the recipient zones. The results are shown for organ type 2 (o = 2). The hatched hospitals and TCs are equipped to process this type of organ. The arrows and associated number of each depict the flows of organs from hospitals to TCs (\({F^{\prime}}_{ijov}^{\left(i\to j\right)t}\)) and the flows of recipients from recipient zones to TCs (\({F}_{rjo}^{\left(r\to j\right)t}\)), in order to have a transplant surgery done. Regarding the number of flows, it is approved that the demand for organs exceeds the supply. As long as the model prioritizes high-risk recipients above low-risk receivers, the demand of high-risk recipients is met first, and the remaining organs are distributed to low-risk recipients. For instance, the unsatisfied demand of recipient zone 2 can be shown as follows:

$$\sum_{t=1}^3{U}_{22}^t=3\kern0.5em and\ \sum_{t=1}^3U{\prime}_{22}^t=9$$
Fig. 3
figure 3

Optimal solution of small-size test problem

Full size image

The matter of CIT is the reason why \({U}_{ro}^t\) is not equal to zero, which indicates that the organ has decomposed before it reaches the recipient.

Case Study Implementation

In real-world applications, a large number of network design issues have been addressed. Strategic location presents a unique challenge in developing nations since site decisions are frequently determined by local officials, which can result in the placement of facilities that may not be cost-effective. On the other hand, what considerably matters is the issue of humans’ lives besides minimizing the costs. Consequently, location-allocation decisions should be made such that organ shortages are kept to a minimum.

This paper considers as an application of the problem at hand the design of an organ transplantation network at the lowest possible cost and the unsatisfied demand simultaneously for one of the most populated provinces of Iran, Khorasan Razavi. This province has 19 main cities designated as recipient zones, 14 hospitals where donors can be accommodated, 8 TCs, and 7 shipping agents. All of them are labeled on the map depicted in Fig. 4. Some facilities are not available in some cities due to the lack of resources. For instance, in the province’s most populated and facilitated city, Mashhad, there are three potential locations for TCs. The recipients from cities like Kashmar should travel to undergo the transplant surgery anyway.

Fig. 4
figure 4

Khorasan Razavi geographical map and the candidate locations of the facilities

Full size image

In order to apply the proposed model to the province of Khorasan Razavi, a portion of the generated parameters are determined by subject matter experts, while the remaining parameters are derived from historical data. For instance, the number and candidate locations of facilities are selected based on the recommendations of specialists. The remaining essential information regarding organ supply and demand has been gathered from the official transplantation organizations in Iran. All costs are estimated in light of previous data. In addition, transportation expenses are computed using the data of a number of transportation service providers. The distances and travel times between different cities within the province have been extracted from google Maps. The proposed model is implemented for the heart (o = 1), liver (o = 2), and lung (o = 3) in three time periods, each of which corresponds to 4 months of the planning horizon. The average CIT (given in hours) for each organ is displayed in Table 3. The costs are stated on the scale of million Tomans.

Table 3 The average CIT for each organ
Full size table

This section analyzes the model to provide some managerial insights. When faced with multiple solutions to a multi-objective problem, decision-makers should evaluate the options and select the optimal one. For this purpose, to assist the decision-makers in finding the best possible choice, Fig. 5 illustrates one of the solutions. Evidently, it is optimal to equip some of the potential facilities with organ processing capabilities. The figure demonstrates, for instance, that among all 14 candidate hospitals, hospital 1 is equipped to receive organ donors of types 1 and 3. Additionally, hospital 9 should be equipped to process all three types of organs. It is not optimum to facilitate other potential hospitals in this respect. Moreover, TCs 3, 4, and 7 are equipped for harvest operation of all three organ types, while TCs 1 and 6 can recite recipients with the demand of organ types 3 and 1, respectively. Additionally, in Fig. 5, arrows indicate the optimal organ flows from hospitals to transplant centers (\({F^{\prime}}_{ijov}^{\left(i\to j\right)t}\)) and the flows of recipients from their zone to the TCs (\({F}_{rjo}^{\left(r\to j\right)t}\)).

Fig. 5
figure 5

Optimal solution of the case study

Full size image

In multi-objective problems, the table of Pareto solutions is one of the most crucial tools for decision-makers. In this regard, Table 4 displays the Pareto solutions of the proposed weighted sum model and the hospitals and TCs to be equipped by a change in the weighted relevance of each objective function (φ). In order to place the two objective functions on the same scale, a penalty cost of 15 has been considered (PC = 15) and multiplied by the second objective function. As is common knowledge, the two present objective functions (cost and unmet demand) are in conflict with each other. In other words, if we want to reduce unmet demand, we must utilize more facilities, such as equipping more transplant centers and hospitals, entering into contracts with more shipping agents, and utilizing more refrigerated vehicles. In this scenario, the cost objective function (Z1) will grow if we place a greater emphasis on reducing unmet demand (Z2) and, subsequently, mortality and transplant rejection. To clarify more, increasing φ concentrates the weighted sum objective function on minimizing Z1. Whereas decreasing φ that leads to the value of 1 − φ having more value than φ, Z2 receives a higher minimization priority.

Table 4 Pareto optimal solutions
Full size table

In addition, according to Table 4, the change in φ affects the quantity and position of the hospitals and TCs to be equipped. For instance, if the importance weight of the cost function is increased, the number of these facilities will decrease, or the ones with the lowest equipping costs will be opened. The scenario is the opposite when the unsatisfied demand function’s importance weight surpasses the one for cost functions. In this situation, the facilities should be equipped that simplify the access of recipients to TCs, before the organs perish. Hence, the decision-makers should make up their mind on choosing the best importance weight (φ) which best fits their priorities and limitations.

Sensitivity Analysis

In this section, the effect of different parameters such as number of donors (N), total demand of high-risk recipients (D), and total demand of low-risk recipients (D′) on the objective functions, namely total cost objective function (Z1) and the number of unsatisfied demand objective function (Z2), will be investigated to analyze the model’s behavior. It is noteworthy that the second objective function has been multiplied by a penalty cost coefficient with a value of 15 to show the results on the diagram more clearly, and in the figures of this section, it is written as “Normalized second objective function value.” It is worth noting that the term change percentage in this section’s figures refers to the percentage of increase and decrease in the parameters’ values.

First, we would like to examine the impact of the number of donors (N) on the first and second objective functions. The value of N in this analysis has been modified slightly to account for the reality that organ transplantation supply can never exceed demand. As depicted in Fig. 6, the total number of unsatisfied demands reduces with the increase in the number of donors. In this context, however, unmet demand will always exist because there are always fewer donors than recipients, and some organs are already lost owing to organ perishability and variations in travel times.

Fig. 6
figure 6

Sensitivity analysis of number of donors on objective functions

Full size image

In order to analyze the effect of high-risk recipients’ total demand (D) on the objective functions, Fig. 7 is presented. As mentioned in previous sections, in this methodology, the priority is on the high-risk recipients. If their demand decrease, the remaining organs will be allocated to the low-risk ones. Therefore, a shortage of organs does not lead to fewer transplantation costs. However, the slight change in the cost objective function is due to the different transportation costs and different types of surgeries. The same conclusion can be drawn for the increase in this type of demand. Moreover, the second objective function is directly related to every type of demand, no matter high-risk or low-risk.

Fig. 7
figure 7

Sensitivity analysis of total demand of high-risk recipients on objective functions

Full size image

Figure 8 depicts the impact of low-risk recipients total demand (D′) on objective functions. Even with a 20% decrease in this type of demand, there are still low-risk recipients whose organ demand cannot be met due to the organ shortage. Therefore, due to the reduction in transport costs between recipient zones and TCs, the value of the cost objective function reduces marginally. With a 70% reduction in this parameter, the supply exceeds the demand, and certain transportation and transplant operation expenses fall, leading to more reduction in the first objective function than the case of 20% decrease. However, the total unsatisfied demand function does not equal zero. This is due to the fact that some organs have passed their CIT and perished in route to the recipient. In addition, since the majority of operational costs correspond to transplant surgery costs, which do not deviate from the 0% change in D′ due to the current lack of supply, the increase in this parameter marginally raises the total cost. This shift is primarily motivated by the transportation costs between recipient zones and TCs. Obviously, the total unmet demand function emerges as a result of grow in low-risk recipient demands.

Fig. 8
figure 8

Sensitivity analysis of total demand of low-risk recipients on objective functions

Full size image

Discussion and Managerial Insights

Some papers, such as Zahiri, Tavakkoli-Moghaddam, and Pishvaee (2014b) and Ahmadvand and Pishvaee (2018a), have addressed the issue of organ transplant network design with the single objective of reducing the total costs, including the cost of establishing and equipping the network’s facilities, surgery operations, and transportation. Unlike our approach, none of the aforementioned articles covers the selection of cold chain vehicles. In this study, transportation restrictions are also based on the government’s carbon emission allowance. Also, in a later work by Zahiri, Tavakkoli-Moghaddam, Mohammadi, et al. (2014a), the prior model is expanded by adding a second objective function of minimizing total time, which includes operation time in hospitals, transport time between facilities, and waiting time at TCs. However, the second objective function in the current paper is the minimization of unmet demand. The implementation of the priority mechanism in the work of Zahiri, Tavakkoli-Moghaddam, Mohammadi, et al. (2014a) is the waiting time, whereas the purpose of this paper is to give high-risk recipients precedence over low-risk recipients. Hence, in order to prevent the risk of mortality in recipients as much as possible, significant consideration has been given to the precious life of humans in this context.

The proposed methodology helps organ transplant supply chain managers allocate an optimal number of cold chain vehicles to transport the organs between hospitals and TCs. Furthermore, the number of these transportations is restricted by the amount of allowed carbon emission determined by the government. Therefore, the suggested OTN is environmentally friendly besides being cost-efficient. Moreover, there has always been a deficiency in this context. The reason is that recipients always outnumber donors, and some organs will perish if their traveling time to the transplant center exceeds their CIT. In the present study, the demand has been evaluated individually for high-risk and low-risk recipients, and a mechanism of prioritization has been established to prevent the mortality of high-risk recipients. Following this strategy, organs will be distributed to high-risk patients first, with the balance going to low-risk recipients. However, there have been some debates on the equity of the clients, in this paper, we have focused on the recipient’s urgency level in the category of maximum benefit.

In the “Sensitivity Analysis” section, a good comprehension of the behavior of objective functions was achieved by modifying the parameters. In light of the findings and conclusions of the analyses, this section provides some practical and managerial insights. According to Fig. 6, hospital managers should increase the number of cold chain vehicles by spending more money to reduce unmet demand. Through this effort, fewer organs will be delivered from hospitals to TCs outside of their Cold Ischemia Times (CITs). Therefore, organ wastage and consequently unsatisfied demand will diminish. Figures 6 and 7 show that the number of unsatisfied demands will grow as the demands of high-risk recipients increase. In this case, managers can increase the number of vehicles based on Fig. 6 in order to lessen the increasing slope of unmet demand.

Conclusion

Organ transplantation is the main approach for treating diseases in their last development stage. In recent years, despite the significant advances in medical science in the field of organ transplantation, a significant percentage of patients die while waiting to receive an organ due to the demand exceeding the supply and the scarcity of organs. Considering the importance of this issue and the direct effect of organ transplantation on patients’ survival, it is necessary to find the most effective means to receive the organ on time and prevent the death of patients. Therefore, designing an efficient organ transplant supply chain network as one of the main subgroups of health care management is vital in balancing demand and supply, choosing the appropriate location of involved facilities, and distributing involved flows between them, and timely transfer of organs to patients. In addition to the above, another challenge in the design of the organ transplant network is the time limit for transporting organs from hospitals to transplant centers, and if it exceeds the CIT determined based on the nature of the organ, consequences such as organ corruption, an increase in the waiting time of the patients will lead to the possibility of their death and, as a result, an increase in the costs of the system. Therefore, it is necessary to determine the mechanism of maintenance and transportation of organs.

In this paper, a bi-objective mixed integer nonlinear programming (MINLP) location-allocation model is proposed to address the design of the organ transplant supply chain network, minimizing the total strategic and operational costs and the number of unmet demands. Due to the imprecise structure of the studied network, the model has been assessed as uncertain. In addition, the organ demand and some transportation costs have been considered triangular fuzzy numbers due to their uncertain nature and lack of historical data, and the approach Jiménez is also used to deal with uncertainty. Some test problems were done to validate the model. In the following, a real case study was conducted in one of Iran’s most populous and prominent provinces. The studied organs were the heart, liver, and lung. Then, several sensitivity analyses were performed on some effective parameters to evaluate their influence on the objective function’s values.

Despite advancements in medical, pharmaceutical, and surgical treatments, there are some limitations in this context. For instance, organ shortage is a global issue that must be addressed at the highest possible international level. With the occurrence of crises and natural disasters beyond human control, the demand for organs also increases with the increase of injured people. In addition, depending on the severity of occurrence, these incidents can lead to damage to facilities or their destruction. Therefore, the development of a mathematical model in the conditions of uncertainty to reduce the costs of transportation and the shortage of organs, choosing the location of the construction of hospitals and transplant centers from among the situations with the highest safety factor, examining the shortest routes for transporting essential items to the injured, taking into account CIT, can be a field for future research. Furthermore, considering different modes of organ transportation, such as air and water transportation in different parts of the network, can be a field for future research. In this type of issue, a trade-off is made between cost and time, and the best option can be chosen depending on the budget limit, the nature of the organ, CIT, and the priority of the goals in the issues. As another limitation of organ transplantation, there has been no consensus over the prioritization of recipients. As previously indicated, this study has divided recipients into two groups: those whose organ deficiency causes their death and those whose organ deficiency does not. Hence, in future studies, the model can be improved by involving other factors such as waiting time. However, some ethical issues can be taken into consideration, such as avoiding biases based on age, life expectancy, and sex. Utilizing other methods of dealing with uncertainty, extending the model to larger scales, and using meta-heuristic algorithms suitable for solving can also be defined as the other subjects of future research. Also, modeling the inventory level of organ types using ABO/Rh rules as a continues time Markov chain (CTMC) and queueing-inventory models similar to Aghsami et al. (2023b) could be interesting work for future research.