1 Introduction

Aluminum alloys are widely used metals in automotive industry due to their mechanical properties. They not only reduce the body weight of the automobile but also provide sufficient strength due to their strength-to-weight ratios. However, they exhibit low ductility and prone to fracture [1]. Hence it is important to understand the formability limits of the aluminum alloy sheets. Uniaxial tensile test is an important test providing fundamental mechanical properties, but it cannot estimate the stretch flange formability limits [2]. To predict the features of the stretch flange formability, several tests are conducted such as Nakajima test, Marciniak test or hole expansion test (HET). In HET, sheet metal, containing a hole at the center, is forced to flow into the die cavity. During the test, hole expands until the initial crack forms. Parmar and Mellor investigated the stress and strain distributions in an annulus of sheet metal exposed to tension. It is recorded that the uniaxial stress state occurs in a narrow range and stress state changes from uniaxial tension at the hole edge to balanced biaxial tension at the outer periphery of the blank [3].

Formability tests are quite expensive and time-consuming processes. In order to reduce the costs of the tests, FE simulations are widely used. Selection of the proper yield function for material has an important effect on the prediction accuracy of FE simulations. Anisotropy occurs in sheet metals due to rolling process and anisotropy strongly affects the deformation behavior of the material. Therefore, it is essential to define anisotropy of the sheet metals for the FE simulations. There have been many studies carried out in order to define the anisotropy of the materials. The first anisotropic yield function was proposed by Hill [4]. Hill48 criterion has a quadratic form and it is quite practical for steels. However, this yield criterion could not give accurate results for aluminum alloys due to their first and second anomalous behaviors [5, 6]. To overcome the anomalous behaviors, Hill proposed three different non-quadratic yield criteria: Hill79 [7], Hill90 [8] and Hill93 [9]. Hill79 yield criterion can describe the first anomalous behavior, while it cannot describe the second anomalous behavior of aluminum alloys and this criterion does not take into consideration the shear components of the stress tensor [10]. Hill90 and Hill93 yield criteria can represent the first and second order anomalous behaviors, but Hill90 criterion need larger CPU times in FE simulations due to its formulation and Hill93 criterion has no shear stress component [11]. Independently from Hill’s criteria, several non-quadratic yield functions have been developed by researchers. Logan and Hosford [12] proposed a non-quadratic yield function for plane stress state. Their criterion does not contain any shear stress component; therefore, it cannot be used for general stress state. Gotoh [13] proposed a fourth-order polynomial yield criterion. He applied this criterion for aluminum alloys and obtained successful results. However, his criterion does not satisfy convexity conditions for some aluminum alloy like AA2090-T3. Bassani [14] developed a non-quadratic yield function which has two different exponents. Budianski [15] suggested a yield function which can be expressed in terms of polar coordinates. However, their models consider only normal anisotropy, therefore these models could not describe the behavior of sheet metals which exhibit planar anisotropy. Barlat et al. applied linear transformation approach to non-quadratic isotropic yield functions which were developed by Hosford [16] and Hershey [17] and developed Yld89 yield criterion. Yld89 yield criterion [18] is comprised of two convex functions and give suitable results for aluminum alloys exhibiting especially low planar anisotropy, but this model is restricted to plane-stress conditions. Then, Barlat generalized his previous model and proposed a yield function which has six parameters defining the material anisotropy for three-dimensional case (Yld91) [19]. Yld91 yield criterion is flexible and practical for aluminum alloy sheets.

There have been also several studies which evaluate the effect of the yield criterion on HET under several loading conditions. Cohen et al. [20] investigated the expansion of the circular hole embedded in an infinite elastoplastic sheet. Two isotropic yield criteria were adopted, and two cases were evaluated. These cases were hole expansion applications under internal pressure and remote tension. It was indicated that, for the first case, power need to create new volume unit is independent from yield function. In contrast, for the second case, external stress became closer to a limit which is sensitive to the yield criteria. Takuda et al. [21] performed FE analyses of HET using Hill48 yield criterion and determined the forming limits of high strength steel sheets. Worswick and Finn [22] modeled stretch-flanging of AA5182-O aluminum alloy with Barlat89, Hill48 and von Mises yield criteria and obtained the most consistent results with Barlat89 criterion. In recent years, many studies have been carried out in order to investigate the effect of the yield criteria on HET for different types of materials [23, 24].

In this study, HET was simulated using implicit FE method and AA6016-O aluminum alloy was used as test material. Von Mises, Hill48 and Yld91 yield criteria were adopted in order to define the plastic behavior of the material and FE analyses were carried out with these material models. Thickness strain distributions along the three directions (rolling, diagonal and transverse) and punch force—displacement curves were predicted from these yield criteria and the predicted results were compared with the experimental results.

This work consists of five sections. In Sect. 2, the mechanical properties of AA6016-O aluminum alloy and tool geometries used in HET are introduced. Section 3 gives information about the numerical studies performed in the study. The FE model of HET, mesh sensitivity study and computed yield surfaces from three yield functions are presented in this section. In Sect. 4, the results obtained from simulations are explained and comparisons between numerical and experimental results are investigated. In the last section, the study is concluded according to the obtained results.

2 Material and method

2.1 Description of the model

Hole expansion process is a stretching test which the blank with a central hole is clamped between the upper and lower dies and then it is subjected to flow into the die cavity by the punch movement. During the process, the hole located at the middle of the blank expands and test is continued until the initial crack forms.

Initial thickness of the material was 1 mm, and the initial hole diameter was 30 mm. Geometry of HET can be seen in Fig. 1.

Fig. 1
figure 1

Dimensions of the components of HET [1]

Full size image

Mechanical properties of AA6016-O aluminum sheet were shown in Table 1.

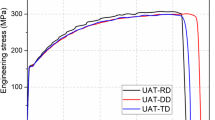
Table 1 Mechanical properties of 6016-O aluminum alloy sheet [1]
Full size table

Here σ0, σ45 and σ90 represent the yield stresses, whereas r0, r45 and r90 represent Lankford coefficients in rolling, diagonal and transversal directions, respectively. Flow curve of AA6016-0 sheet was defined by using Swift hardening law. Swift parameters and flow curve are given in Table 2 and Fig. 2, respectively.

Table 2 Swift parameters of AA6016-0 [1]
Full size table
Fig. 2
figure 2

Flow curve of the AA6016-O sheet [1]

Full size image

Hole expansion ratio (HER) is an important parameter which comprehends the formability limits of the material and can be calculated using Eq. (1) [24].

$${\text{HER}} = \frac{{d - d_{0} }}{{d_{0} }}$$
(1)

Here d0 is the initial hole diameter and d is the diameter after hole expanding process.

2.2 Plasticity models

In order to define plasticity, yield function, flow rule and hardening rule should be defined. Yield function defines a bound which distinguishes the elastic and plastic regions from each other in stress space. In this study, Mises isotropic, Hill quadratic (Hill48) and Barlat non-quadratic (Yld91) anisotropic yield functions were used to define plastic flow. Von Mises yield function can be expressed as [25],

$$f = \sqrt {\frac{3}{2}\left\| {D_{{ij}} } \right\|} - \sigma _{0}$$
(2)

where Dij is the deviatoric part of the stress tensor and σ0 is the yield stress. This yield function ignores the changing of the mechanical properties with respect to the rolling direction of the material. To include the anisotropy, Hill proposed a quadratic yield function which is given in Eq. (3) [4].

$$2f =\, F\left( {\sigma_{yy} - \sigma_{zz} } \right)^{2} + G\left( {\sigma_{zz} - \sigma_{xx} } \right)^{2} + H\left( {\sigma_{xx} - \sigma_{yy} } \right)^{2} + 2L\tau_{yz}^{2} + 2M\tau_{zx}^{2} + 2N\tau_{xy}^{2} = 1$$
(3)

In the above equation, F, G, H, L, M and N are the anisotropy parameters and can be calculated using the yield stress ratios or Lankford parameters individually. In hole expansion and other sheet forming applications, Lankford’s parameters are widely used to calculate these parameters e.g. [26,27,28]. In the present study, anisotropy parameters were calculated according to the yield stress ratios as it seen in the following equations.

$$F = \frac{1}{2}\left( {\frac{1}{{R_{22}^{2} }} + \frac{1}{{R_{33}^{2} }} - \frac{1}{{R_{11}^{2} }}} \right),G = \frac{1}{2}\left( {\frac{1}{{R_{11}^{2} }} + \frac{1}{{R_{33}^{2} }} - \frac{1}{{R_{22}^{2} }}} \right),H = \frac{1}{2}\left( {\frac{1}{{R_{11}^{2} }} + \frac{1}{{R_{22}^{2} }} - \frac{1}{{R_{33}^{2} }}} \right)$$
(4)
$$L = \frac{3}{{2R_{23}^{2} }},M = \frac{3}{{2R_{31}^{2} }},N = \frac{3}{{2R_{12}^{2} }}$$
(5)

Here, Rij represents the yield stress ratio along the different directions of the sheet plane. Yield stress values were normalized with respect to the mean yield stress value. Detailed calculation procedures related to Hill parameters were described in [4] [29].

Yld91 is the other yield function used in this study and it is defined as follows [19, 29]:

$$f = 2\overline{\sigma }^{m} = \left| {S_{1} - S_{2} } \right|^{m} + \left| {S_{2} - S_{3} } \right|^{m} + \left| {S_{3} - S_{1} } \right|^{m}$$
(6)

In equation above, S1-3 represent the principal values of the symmetric matrix Sigiven below.

$$S_{ij} = \left[ {\begin{array}{*{20}c} {\frac{{C_{3} \left( {\sigma_{xx} - \sigma_{yy} } \right) - C_{2} \left( {\sigma_{zz} - \sigma_{xx} } \right)}}{3}} & {C_{6} \sigma_{xy} } & {C_{5} \sigma_{zx} } \\ {C_{6} \sigma_{xy} } & {\frac{{C_{1} \left( {\sigma_{yy} - \sigma_{zz} } \right) - C_{3} \left( {\sigma_{xx} - \sigma_{yy} } \right)}}{3}} & {C_{4} \sigma_{zy} } \\ {C_{5} \sigma_{zx} } & {C_{4} \sigma_{zy} } & {\frac{{C_{2} \left( {\sigma_{zz} - \sigma_{xx} } \right) - C_{1} \left( {\sigma_{yy} - \sigma_{zz} } \right)}}{3}} \\ \end{array} } \right]$$

Here, C1-6 are the anisotropy parameters of the material. Identification procedure of the criterion is explained in the study [30]. The exponent m is a coefficient which is related to the crystal structure of the material. For BCC and FCC, this parameter can be taken as 6 and 8, respectively [30].

In the present work, associated flow rule was adopted to define the direction of the plastic strain increment. Associated flow rule is given in Eq. (7).

$$d\varepsilon^{p} = d\lambda \frac{df}{{d\sigma_{ij} }}$$
(7)

Here, dλ is the proportionality factor, f is the yield function and \(d\varepsilon^{p}\) is the plastic strain increment [10]. Isotropic hardening rule was assumed in this study.

3 Finite element method

HET was modeled in implicit FE code Marc. Blank was meshed with fully integrated solid elements with the dilatational strain constant throughout the element, known as Marc hexa7 [29, 31]. Solid elements are widely used in different engineering problems including relatively thick shell structures. Nguyen et al. proposed consecutive – interpolation four node tetrahedral and eight node hexahedral elements for the 3D analyses. In these works, several benchmark examples were considered, and accuracy of the results obtained by using these element types were proved for linear elasticity, heat transfer and composite structure topics [32, 33]. Present work is focused on metal plasticity and standard FEM framework offered by Marc software where constant dilatational elements, free of volumetric locking, are recommended for use in approximately incompressible analysis, such as large strain metal plasticity in HET. To reduce the solution time, quarter part of the model was generated. Punch, upper and lower dies were modeled as rigid surfaces. To restrict material flow into the die cavity, triangular draw bead was created. Punch stroke was defined as 15 mm in the model. Segment to segment contact algorithm was used to define the contact between the parts. Coefficient of friction between blank and punch was taken as 0.03, whereas it was assumed as 0.3 between blank and die interfaces [1]. In order to apply displacement boundary conditions for upper die and punch, control nodes were assigned to these components. FE model of HET is shown in Fig. 3.

Fig. 3
figure 3

a FE model of HET b Detailed view of triangular draw bead

Full size image

Initially, mesh sensitivity study was carried out. Except for the thickness direction, only the number of elements in the sheet plane was changed and three different grid layouts were considered in the study. The considered element numbers for these layouts are 3200, 7680 and 30720, respectively (Fig. 4). 4 elements were used through thickness direction in all FE models and FE analyses were performed with Yld91 yield criterion in the mesh sensitivity study. Punch force – displacement curves obtained from these layouts were compared with each other and results were given in Fig. 5.

Fig. 4
figure 4

Mesh layouts generated for mesh independency study a 3200 element b 7680 elements c 30720 elements

Full size image
Fig. 5
figure 5

Punch force—stroke curves obtained from different mesh layouts

Full size image

As it seen from the Fig. 5, punch force—stroke results were close to each other. To obtain more precise solutions for thickness strain distributions, second layout was preferred for further studies. Second layout selected for blank is composed of 60 elements in radial direction and 32 elements in circumferential direction. In addition, another mesh sensitivity study was carried out for thickness direction. 1, 2 and 4 elements were used through thickness direction by using second mesh layout. The punch force—stroke results were considered once again, and numerical results were compared with each other for the second mesh sensitivity study (Fig. 6).

Fig. 6
figure 6

Punch force—stroke curves obtained for different element numbers in thickness direction

Full size image

It is seen from Fig. 6 that the predicted punch force–stroke graphs from simulations performed with different element numbers through thickness direction were close to each other. Although the punch force–stroke curves were very similar, 4 elements were selected through the thickness direction to predict the thinning precisely along the hole edge.

Parameters of Hill48 and Yld91 yield functions were calculated based on the yield stress ratios and the calculated parameters for these yield functions are given in Tables 3 and 4, respectively. After determination of the parameters, yield surfaces were computed with Mises, Hill48 and Yld91 yield functions and compared with experimental results in biaxial tensile region as shown in Fig. 7.

Table 3 Yield stress ratios of Hill48 yield criteria
Full size table
Table 4 Anisotropy parameters of Yld91 yield criteria
Full size table
Fig. 7
figure 7

a Yield surfaces obtained from the Mises, Hill48 and Yld91 yield functions b Detailed view of the equibiaxial state

Full size image

It was observed from Fig. 7 that only Yld91 yield criterion could accurately predict the biaxial yield stress ratio. Because, Yld91 criterion has the variable exponent m which provides flexibility to the model. Depending on the value of the exponent m, yield surface shape changes between Tresca’s hexagon and von Mises’s ellipsoid. On the other hand, Hill48 yield function is a generalized form of the von Mises criterion and it has only elliptical shape. Therefore, Yld91 could accurately predict biaxial yield stress ratio.

4 Results and discussion

In the present study, HET was modeled in implicit FE code Marc and FE analyses of the test were performed with von Mises, Hill48 and Yld91 yield functions.

Thickness strain distributions along three directions and punch force—displacement curves were predicted for each yield criterion and the predicted results were compared with the experimental results. Comparisons between the predicted and experimental thickness strain distributions and punch force–displacement curves for each direction are shown in Figs. 8 and 9, respectively.

Fig. 8
figure 8

Comparisons of predicted and experimental thickness strain distributions along three directions

Full size image
Fig. 9
figure 9

Comparison of predicted and experimental punch force—displacement curves

Full size image

It can be seen from the Fig. 8. that, at the hole edge, numerical solutions obtained from three yield functions could predict the thickness strains in rolling and transversal directions approximately. Among them, Hill48 criterion predicted higher strain value at hole edge than von Mises and Yld91 when their absolute values were considered. Yld91 criterion could accurately predict the thickness strain in diagonal direction at the hole edge, whereas von Mises and Hill48 criteria underestimated the experimental thickness strain in the same region. Apart from these results, it was observed that thickness strains decreased suddenly near the hole edge and none of these criteria could capture this decrease.

In general, Yld91 criterion could accurately predict the thickness strains in all directions at the hole edge which is important for failure estimation. Because fracture generally occurs at the hole edge in HET. Yld91 criterion could also successfully captures thickness strain distributions along rolling and transversal directions, whereas Hil48 and von Mises criteria show better success than Yld91 in diagonal direction from the point of thickness strain profile.

As for the punch force—stroke curves in Fig. 9., numerical results obtained from three yield criteria were close to each other, but these predictions were overestimated, when they were compared with the experimental data.

In addition to thickness strain distributions and punch force—displacement curves, HER in 15 mm punch stroke were predicted for each yield criterion and the results are given in Table 5.

Table 5 Hole expansion ratios obtained from different yield criteria
Full size table

Higher HER points out higher ductility. It was observed from Table 5 that, the predicted HER values from yield criteria were different from each other. The differences between HER are based on the differences between the identification procedures of the yield criteria.

5 Conclusions

In the present work, HET of AA6016-0 aluminum alloy was modeled and FE simulations were performed with von Mises, Hill48 and Yld91 yield criteria. In order to include the effects of the out of plane stresses in FE model, blank was meshed with solid elements. After performing FE simulations, thickness strain distributions along the three directions and punch force–displacement curves were predicted for each yield criterion and numerical results were compared with experimental results.

It was observed from the thickness strain distribution results that Yld91 criterion could well capture the experimental thickness strain distribution profiles along rolling and transverse directions, whereas it could not accurately predict the thickness strain distribution along diagonal direction. On the other hand, the predictions along diagonal direction obtained from von Mises and Hill48 yield criteria match with the experiment better compared to Yld91 criterion. As for the thickness strain at hole edge, Yld91 could predict the strain value in all directions while Hill48 and von Mises criteria predict in rolling and transversal directions. From the punch force–displacement curves, it was noticed that the predicted punch force displacement curves from three yield criteria were close each other, but they were overestimated when compared with the experimental results. Anisotropic yield criteria used in this study consider only the yield stress ratios.

As a result, it can be concluded that Yld91 yield criterion has higher prediction capability than Hill48 and von Mises yield criteria and it can be considered as good option in the modelling of AA6016-O alloy.