Eckhaus instability of stationary patterns in hyperbolic reaction–diffusion models on large finite domains

Abstract

We have theoretically investigated the phenomenon of Eckhaus instability of stationary patterns arising in hyperbolic reaction–diffusion models on large finite domains, in both supercritical and subcritical regime. Adopting multiple-scale weakly-nonlinear analysis, we have deduced the cubic and cubic–quintic real Ginzburg–Landau equations ruling the evolution of pattern amplitude close to criticality. Starting from these envelope equations, we have provided the explicit expressions of the most relevant dynamical features characterizing primary and secondary quantized branches of any order: stationary amplitude, existence and stability thresholds and linear growth rate. Particular emphasis is given on the subcritical regime, where cubic and cubic–quintic Ginzburg–Landau equations predict qualitatively different dynamical pictures. As an illustrative example, we have compared the above-mentioned analytical predictions to numerical simulations carried out on the hyperbolic modified Klausmeier model, a conceptual tool used to describe the generation of stationary vegetation stripes over flat arid environments. Our analysis has also allowed to elucidate the role played by inertia during the transient regime, where an unstable patterned state evolves towards a more favorable stable configuration through sequences of phase-slips. In particular, we have inspected the functional dependence of time and location at which wavelength adjustment takes place as well as the possibility to control these quantities, independently of each other.

1 Introduction

Self-organizing patterns are quite ubiquitous in nature and the study of the associated nonlinear spatial processes has become nowadays a sub-area of complexity science. Despite pattern formation is observed in different fields, such as biology, ecology, chemistry and medicine, the underlying phenomena share some common features [1, 2]. For instance, it is widely accepted that regular periodic stationary patterns, that in the one-dimensional case are variously referred to as bands, rolls or stripes, arise from Turing-like instability. It results from the coupling between local interactions and dispersal, even in the absence of heterogeneity of the environment in which the process takes place. In some contexts, the large spatial scale and/or the slow evolution of patterns prevent replicability under laboratory conditions, so that theoretical investigations based upon mathematical models represent an efficient and inexpensive tool to acquire a rigorous understanding on the complex spatio-temporal dynamics. Mathematical models have indeed allowed to get valuable insights on many aspects of pattern dynamics: formation of regular and irregular mosaics, scaling phenomena, spatial modulation of pattern amplitude, transitions from a uniform state to a periodic one as well as between different periodic states [3,4,5,6,7,8]. In particular, it is known that, in a large domain, the equation ruling the spatio-temporal evolution of pattern amplitude close to onset is in the form of a Ginzburg–Landau (GL) equation [9,10,11,12]. This equation also allows to inspect the dependence of the stability of the resulting periodic states on wavelength. Indeed, patterns may undergo different destabilization mechanisms associated with changes in wavelength and amplitude, one of which is the Eckhaus instability (EI) [3,4,5,6,7]. EI acts on the roll phase to compress or dilate pattern wavelength and takes place when a given roll wavelength cannot be accommodated by the environment so that some of them are eventually created or eliminated. The process leading the system to be rearranged in a more favorable configuration is referred to as phase-slip [3, 5, 6].

A large body of literature has successfully addressed the bifurcation analysis of EI in both infinite and finite spatial domains and has also addressed the study of complex intriguing dynamics, such as those associated to quasi-periodic solutions and homoclinic snaking bifurcation structures [3,4,5,6, 8, 13,14,15,16,17,18]. However, none of those works has inspected the EI instability of stationary and quantized Turing patterns in the context of hyperbolic models. As widely reported in previous works [19,20,21,22,23,24,25,26,27], hyperbolic systems bring many advantages. Firstly, they take inertial effects explicitly into account and, thus, allow to overcome to paradox of propagation of disturbances at infinite speed, typical of parabolic models. They also appear more suitable to describe transient phenomena characterized by waves evolving in space over a finite time. Moreover, despite the mathematical convergence of parabolic and hyperbolic models is expected in the long-time limit due to the stationary nature of the excited patterns, the coupling between hyperbolicity and nonlinearity may generate richer transient dynamics.

In particular, the present manuscript addresses the analysis of one-dimensional stationary Turing patterns emerging in a class of two-compartments hyperbolic reaction–diffusion models, where both species undergo self-diffusion, defined on a large finite domain. In some previous works, linear and weakly-nonlinear stability analyses on the homogeneous steady states were carried out over small (in the presence of cross-diffusion [25]) or extended domains (with constant [19] and non-constant [20] inertial times). Here, we aim at addressing the stability and quantization of spatially-periodic patterns, in both supercritical and subcritical regimes.

With this in mind, we aim at deducing, first, the equation governing the evolution of pattern amplitude close to the onset of supercritical and subcritical bifurcation. To this aim, we apply multiple-scale weakly nonlinear expansion which is pushed up to the fifth perturbative order. Depending on the perturbative order at which the expansion is truncated, this procedure allows to build a cubic or cubic–quintic GL equation with real coefficients. Moreover, taking into account the quantization of modes due to the spatial confinement, we address a bifurcation analysis of the EI to accurately describe the existence and stability thresholds of all periodic branches [4]. This investigation is finalized at inspecting the qualitatively different dynamical features captured by the above GL equations.

Theoretical predictions here developed are then validated through a comparison with numerical simulations. To this aim, an illustrative example in which EI takes place in the context of dry-land ecology is here considered: the hyperbolic generalization of the modified Klausmeier model [19, 20, 28,29,30,31]. It represents one of the simplest two-component systems able to predict the formation of vegetation bands in flat arid environments as the result of competition between soil water and vegetation biomass.

The comparison between analytical and numerical results made it possible to address several issues: (i) to validate theoretical predictions on bifurcation analysis developed in the frameworks of cubic and cubic–quintic real GL equations, in both supercritical and subcritical regime; (ii) to investigate how hyperbolicity affects not only transient regime dynamics between different patterned states but also the occurrence of phase slips observed during an Eckhaus-driven restabilizing process; (iii) the feasibility to control, independently of each other, the time and the spatial location at which such phase slips occur.

The manuscript is organized as follows.

In Sect. 2, we present the class of hyperbolic reaction–diffusion models under investigation and develop linear and weakly nonlinear stability analysis. The former allows to deduce the Turing instability threshold, the latter is used to deduce the envelope equations at different perturbative orders.

In Sect.3, we address the bifurcation analysis of the EI. First, we briefly review the most relevant results associated to the supercritical regime in the framework of the cubic GL equation. Then, we inspect the subcritical regime via both cubic and cubic–quintic GL equations. In particular, in all cases, we deduce the expressions of the most relevant dynamical features associated to primary and secondary quantized periodic states: stationary amplitude, existence and stability thresholds and linear growth rate. Finally, this section is concluded with a focus on the difficulties encountered in the theoretical prediction of the phase slip phenomenon.

In Sect. 4, we first validate the theoretical predictions developed in the previous sections by means of a comparison with numerical simulations carried out on the hyperbolic modified Klausmeier model. Then, we address further numerical investigations to inspect the spatio-temporal dependence of phase slip and to emphasize the role played by inertial times.

Concluding remarks are given in the last section.

2 Amplitude equations for hyperbolic reaction–diffusion models

We consider a class of 1D hyperbolic reaction–diffusion models for two species u(x, t) and w(x, t), both undergoing self-diffusion. We denote the w-by-u diffusion ratio by d, the kinetic terms by f(u, w) and g(u, w), the phenomenologically-introduced arbitrary constants by $\gamma _0$ and $\mu _0$ which are related to the inertial times $\tau ^u$ and $\tau ^w$ of the two species by $\gamma _0=1/\tau ^u$ and $\mu _0=d/\tau ^w$. According to Extended Thermodynamics (ET) theory [32], the diffusive fluxes $J^{u}(x,t)$ and $J^{w}(x,t)$ are considered as additional field variables obeying thermodynamically-consistent balance equations that, in the parabolic limit approximation, $\tau ^{u}\rightarrow 0$ and $\tau ^{w}\rightarrow 0$, reduce to classical Fick’s law. In vector form, this model reads:

$$\begin{aligned} \mathbf {U}_{t}+M\mathbf {U}_{x}=\mathbf {N}(\mathbf {U}) \end{aligned}$$

(1)

being:

$$\begin{aligned} \mathbf {U}=\left[ \begin{array}{c} u \\ w \\ J^{u} \\ J^{w} \end{array} \right] , \quad M=\left[ \begin{array}{cccc} 0 &{} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 1 \\ \gamma _{0} &{} 0 &{} 0 &{} 0 \\ 0 &{} \mu _{0} &{} 0 &{} 0 \end{array} \right] , \quad \mathbf {N}=\left[ \begin{array}{c} f(u,w) \\ g(u,w) \\ -\gamma _{0}J^{u} \\ -\frac{\mu _{0}}{d}J^{w} \end{array} \right] {,} \end{aligned}$$

(2)

where subscripts denote partial derivative with respect to the indicated variable. In the literature, the hyperbolic structure (1), (2) has been successfully employed in different contexts, such as plant ecology [19], epidemiology [33], air pollution [34] and chemistry [35].

In order to deduce the conditions for Turing instability let us briefly address linear stability analysis. Let B be a control parameter and $\mathbf {U}^{*}=\left( u^{*},v^{*},0,0\right)$ a positive spatially-homogeneous steady-state satisfying $\mathbf {N(U)}=\mathbf {0}$. By requiring that $\mathbf {U}^{*}$ is stable against spatially-uniform perturbations but unstable with respect to non-homogeneous ones, we get the following restrictions:

$$\begin{aligned} {\left\{ \begin{array}{ll} f_u^{*}+g_w^{*}<0 \\ {f_u^{*}g_w^{*}-f_w^{*}g_u^{*}>0} \\ d f_u^{*} + g_w^{*}> 0 \\ \left( d f_u^{*} + g_w^{*}\right) ^2 - 4 d \left( f_u^{*}g_w^{*} - f_w^{*}g_u^{*}\right) > 0 \end{array}\right. } \end{aligned}$$

(3)

where the asterisk denotes that the function is evaluated at $\mathbf {U}^{*}$.

From (3), it can be easily deduced that the critical values of control parameter $B_{c}$ and wavenumber $q_{c}$ at the onset of Turing instability are obtained by solving:

$$\begin{aligned}&d^2 f_u^{*} + 2d \left( 2 f_w^{*} g_u^{*} - f_u^{*}g_w^{*} \right) + {g_w^{*}}^2 = 0, \end{aligned}$$

(4)

$$\begin{aligned}&q_{c}^{2}=\sqrt{\frac{f_u^{*}g_w^{*}-f_w^{*}g_u^{*}}{d}}. \end{aligned}$$

(5)

Note that, since we deal with the formation of stationary patterns, the hyperbolic structure of system (1), (2) does not affect the expression of the critical parameters at onset, so that the occurrence of Turing instability is ruled by the same conditions found in classical parabolic models [2].

To describe the spatio-temporal evolution of pattern amplitude close to Turing threshold (4), (5), multiple-scale weakly nonlinear analysis is now addressed [3, 6, 8, 36, 37]. To this aim, we consider a small dimensionless parameter $\epsilon$, expand the control parameter B around $B_c$ and the field $\overline{\mathbf {U}}=\mathbf {U}-\mathbf {U}{^{*}}$ as

$$\begin{aligned}&B=B_c+\epsilon ^2 B_2 + \epsilon ^4 B_4 + O(\epsilon ^6),\nonumber \\&\overline{\mathbf {U}}= \epsilon \overline{\mathbf {U}}_1+ \epsilon ^2 \overline{\mathbf {U}}_2+ \epsilon ^3 \overline{\mathbf {U}}_3+ \epsilon ^4 \overline{\mathbf {U}}_4+ \epsilon ^5 \overline{\mathbf {U}}_5+O(\epsilon ^6) \end{aligned}$$

(6)

and introduce different time and spatial scales as follows:

$$\begin{aligned} \begin{aligned}&\frac{\partial }{\partial t} \rightarrow \epsilon ^2\frac{\partial }{\partial T_2}+\epsilon ^4\frac{\partial }{\partial T_4},\\&\frac{\partial }{\partial x} \rightarrow \frac{\partial }{\partial x}+\epsilon \frac{\partial }{\partial X}.\\ \end{aligned} \end{aligned}$$

(7)

After substituting the above expansions into the governing system (1), (2), applying zero-flux boundary conditions over the physical domain $x\in [0,D]$ and collecting terms of the same orders of $\epsilon$, a set of linear equations for the $\overline{\mathbf {U}}_i$ is obtained:

$$\begin{aligned} \begin{array}{lll} \text{ at } \text{ order } \text{1 } &{}{}\quad \quad \quad &{}{}\frac{\partial \overline{\mathbf {U}}_{1}}{\partial x}-K_c^{*}\overline{\mathbf {U}}_{1}=\mathbf {0 } \\ \text{ at } \text{ order } \text{2 } &{}{} &{}{} \frac{\partial \overline{\mathbf {U}}_{2}}{\partial x}-K_c^{*}\overline{\mathbf {U}}_{2}= M^{-1}\, \widetilde{\mathbf {F}}_2 \\ \text{ at } \text{ order } \text{3 } &{}{} &{}{} \frac{\partial \overline{\mathbf {U}}_{3}}{\partial x}-K_c^{*}\overline{\mathbf {U}}_{3}= M^{-1} \, \widetilde{\mathbf {F}}_3 \\ \text{ at } \text{ order } \text{4 } &{}{} &{}{} \frac{\partial \overline{\mathbf {U}}_{4}}{\partial x}-K_c^{*}\overline{\mathbf {U}}_{4}= M^{-1} \, \widetilde{\mathbf {F}}_4 \\ \text{ at } \text{ order } \text{5 } &{}{} &{}{} \frac{\partial \overline{\mathbf {U}}_{5}}{\partial x}-K_c^{*}\overline{\mathbf {U}}_{5}= M^{-1} \, \widetilde{\mathbf {F}}_5 \\ \end{array} \end{aligned}$$

(8)

where the vectors $\widetilde{\mathbf {F}}_j$ $(j=2, \ldots , 5)$ are given by

$$\begin{aligned} \begin{array}{ll} \widetilde{\mathbf {F}}_2=&{} \frac{1}{2}\left[ \left( \overline{\mathbf {U}}_1 \cdot \nabla \right) ^{(2)}\mathbf {N} \right] ^*_{B_c} - M \frac{\partial \overline{\mathbf {U}}_{1}}{\partial X} {,} \\ \widetilde{\mathbf {F}}_3=&{}\left[ \left( \overline{\mathbf {U}}_1 \cdot \nabla \right) \left( \left( \overline{\mathbf {U}}_2 \cdot \nabla \right) \mathbf {N} \right) +\frac{1}{6} \left( \overline{\mathbf {U}}_1 \cdot \nabla \right) ^{(3)}\mathbf {N} \right] ^*_{B_c} - M \frac{\partial \overline{\mathbf {U}}_{2}}{\partial X} - \frac{\partial \overline{\mathbf {U}}_{1}}{\partial T_2} + \mathcal {L} \overline{\mathbf {U}}_{1} {,} \\ \widetilde{\mathbf {F}}_4=&{} \left[ \left( \overline{\mathbf {U}}_1 \cdot \nabla \right) \left( \left( \overline{\mathbf {U}}_3 \cdot \nabla \right) \mathbf {N} \right) +\frac{1}{2} \left( \overline{\mathbf {U}}_2 \cdot \nabla \right) ^{(2)}\mathbf {N} + \frac{1}{2} \left( \overline{\mathbf {U}}_1 \cdot \nabla \right) ^{(2)}\left( \left( \overline{\mathbf {U}}_2 \cdot \nabla \right) \mathbf {N} \right) \right. \\ &{}\left. +\frac{1}{24} \left( \overline{\mathbf {U}}_1 \cdot \nabla \right) ^{(4)}\mathbf {N}\right] ^*_{B_c}+\frac{B_2}{2} \left[ \frac{\text {d} \left[ \left( \overline{\mathbf {U}}_1 \cdot \nabla \right) ^{(2)}\mathbf {N} \right] ^*}{\text {d} B} \right] _{B_c}- M \frac{\partial \overline{\mathbf {U}}_{3}}{\partial X} - \frac{\partial \overline{\mathbf {U}}_{2}}{\partial T_2} + \mathcal {L} \overline{\mathbf {U}}_{2} {,} \\ \widetilde{\mathbf {F}}_5=&{} \left[ \left( \overline{\mathbf {U}}_1 \cdot \nabla \right) \left( \left( \overline{\mathbf {U}}_4 \cdot \nabla \right) \mathbf {N} \right) + \frac{1}{2} \left( \overline{\mathbf {U}}_1 \cdot \nabla \right) ^{(2)}\left( \left( \overline{\mathbf {U}}_3 \cdot \nabla \right) \mathbf {N} \right) + \frac{1}{2} \left( \overline{\mathbf {U}}_2 \cdot \nabla \right) ^{(2)}\left( \left( \overline{\mathbf {U}}_1\cdot \nabla \right) \mathbf {N} \right) \right. \\ &{}\left. +\left( \overline{\mathbf {U}}_2 \cdot \nabla \right) \left( \left( \overline{\mathbf {U}}_3 \cdot \nabla \right) \mathbf {N} \right) + \frac{1}{120} \left( \overline{\mathbf {U}}_1 \cdot \nabla \right) ^{(5)}\mathbf {N}+\frac{1}{6} \left( \overline{\mathbf {U}}_1 \cdot \nabla \right) ^{(3)}\left( \left( \overline{\mathbf {U}}_2 \cdot \nabla \right) \mathbf {N} \right) \right] ^*_{B_c} \\ &{} + \frac{B_2}{6} \left[ \frac{\text {d} \left[ \left( \overline{\mathbf {U}}_1 \cdot \nabla \right) ^{(3)}\mathbf {N}+3\left( \overline{\mathbf {U}}_1 \cdot \nabla \right) \left( \left( \overline{\mathbf {U}}_2 \cdot \nabla \right) \mathbf {N} \right) \right] ^*}{\text {d} B} \right] _{B_c} - M \frac{\partial \overline{\mathbf {U}}_{4}}{\partial X} - \frac{\partial \overline{\mathbf {U}}_{3}}{\partial T_2} - \frac{\partial \overline{\mathbf {U}}_{1}}{\partial T_4} + \mathcal {L} \overline{\mathbf {U}}_{3} + \widetilde{\mathcal {L}}\overline{\mathbf {U}}_{1} {,} \end{array} \end{aligned}$$

(9)

being $\nabla =\partial / \partial \mathbf {U}$, together with

$$\begin{aligned} \begin{array}{lll} K_c^{*}=\left[ \begin{array}{cccc} 0 &{} 0 &{} -1 &{} 0 \\ 0 &{} 0 &{} 0 &{} -\frac{1}{d} \\ f_u^{*} &{} f_w^{*} &{} 0 &{} 0 \\ g_u^{*} &{} g_w^{*} &{} 0 &{} 0 \end{array} \right] , \quad &{} \quad \mathcal {L}=B_{2}\left[ \frac{\text {d}\left( \nabla \mathbf {N}\right) ^*}{\text {d} B}\right] _{B_c}, \quad &{} \quad \widetilde{\mathcal {L}}=B_{4}\left[ \frac{\text {d}\left( \nabla \mathbf {N}\right) ^*}{\text {d} B}\right] _{B_c} + \frac{B_{2}^2}{2}\left[ \frac{\text {d}^2\left( \nabla \mathbf {N}\right) ^*}{\text {d} B^2}\right] _{B_c}. \\ \end{array} \end{aligned}$$

(10)

Moreover, for a generic vector $\mathbf {H}$, the expression $\left( \mathbf {H}\cdot \nabla \right) ^{\left( j\right) }$ stands for the operator

$$\begin{aligned} \mathbf {H}\cdot \nabla =H_{1}\frac{\partial }{\partial u}+H_{2}\frac{ \partial }{\partial w}+H_{3}\frac{\partial }{\partial J^{u}}+H_{4}\frac{ \partial }{\partial J^{w}} \end{aligned}$$

(11)

applied j times.

The set of equations (8)-(10) has to be solved sequentially, as sketched in the Appendix. The removal of secular terms at $O(\epsilon ^3)$ leads to an envelope equation ruling the spatio-temporal evolution of the pattern complex amplitude $\Omega (X,T_2,T_4)$ that takes the form of a real cubic GL equation:

$$\begin{aligned} \frac{\partial {\Omega }}{\partial T_2}=\sigma {\Omega } - L |\Omega |^2\Omega + \nu \frac{\partial ^2 {\Omega }}{\partial X^2} {,} \end{aligned}$$

(12)

which preserves the structure found in classical parabolic models [3, 4, 6, 11]. It is worth noticing that the real coefficients $\sigma$, L and $\nu$ inherit the dependence on the inertial times as follows:

$$\begin{aligned} \begin{aligned}&\sigma \left( \gamma _0,\mu _0\right) =\frac{\Pi }{\Big [d-1+q_c^2d\Big (\frac{d}{\mu _0}-\frac{1}{\gamma _0}\Big )\Big ]},\\&L\left( \gamma _0,\mu _0\right) =\frac{\Gamma }{\Big [d-1+q_c^2d\Big (\frac{d}{\mu _0}-\frac{1}{\gamma _0}\Big )\Big ]},\\&\nu \left( \gamma _0,\mu _0\right) =\frac{\Psi }{\Big [d-1+q_c^2d\Big (\frac{d}{\mu _0}-\frac{1}{\gamma _0}\Big )\Big ]} {,} \end{aligned} \end{aligned}$$

(13)

where the functions $\Pi$, $\Gamma$ and $\Psi$ depend upon the w-by-u diffusion ratio d and the kinetic terms, together with their partial derivatives, but are independent of the inertial times. The explicit expressions of these functions are given in the Appendix for the illustrative example considered in Sect. 4. Therefore, the hyperbolic structure of the system may affect the spatio-temporal evolution of pattern amplitude. In particular, the growth rate $\sigma$ and coefficient $\nu$, that in the pattern forming region are always positive, play a significant role during transient regime. On the other hand, the sign of the Landau coefficient L determines the nature of the dynamical regime: $L > 0$ corresponds to the supercritical regime, whereas $L < 0$ to the subcritical one [19].

Remark

It should be remarked that, to the best of our knowledge, weakly nonlinear analysis in hyperbolic reaction–diffusion systems on large finite domains has been pushed up to the third perturbative order [19, 25], allowing to provide a suitable description of supercritical dynamics only. $\square$

From the removal of secular terms at $O(\epsilon ^4)$, the following compatibility condition for the spatially evolution of the pattern amplitude is obtained [13]:

$$\begin{aligned} k_1 \Omega _{XXX} + k_2 | \Omega |^2 \Omega _{X} +k_3 \Omega _{X} = 0. \end{aligned}$$

(14)

Therefore, to investigate subcritical dynamics, we push weakly nonlinear analysis up to the fifth perturbative order where the removal of secular terms leads to the following envelope equation for the pattern amplitude:

$$\begin{aligned} \frac{\partial \Omega }{\partial T}= \overline{\sigma } \Omega - \overline{L} |\Omega |^2\Omega + \overline{R} |\Omega |^4\Omega + \overline{\nu } \frac{\partial ^2 \Omega }{\partial X^2} {,} \end{aligned}$$

(15)

which is in the form of a real cubic–quintic GL equation. In (15), $\partial /\partial T=\partial /\partial T_2 + \epsilon ^2 \partial /\partial T_4$, the coefficients here appearing are real and represent second-order corrections of the coefficient involved in the cubic GL equation (12), namely $\overline{\sigma }=\sigma +\epsilon ^2 \widetilde{\sigma }$, $\overline{L}=L+\epsilon ^2 \widetilde{L}$, $\overline{\nu }=\nu +\epsilon ^2 \widetilde{\nu }$ and $\overline{R} = \epsilon ^2 \widetilde{R}$. Moreover, each of these coefficients encloses a non trivial dependence on the inertial times which, acting as additional degrees of freedom, may offer a richer scenario of spatio-temporal dynamics with respect to the parabolic counterpart. This statement holds true despite hyperbolic and parabolic models share the same structure of weakly inverted bifurcations to a stationary spatially-periodic state [14,15,16,17, 38, 39]. However, due to the cumbersome expressions here involved, conclusions can be only given through numerical simulations. For this reason, as well as to keep the length of the manuscript within reasonable limits, the full expressions of all the real coefficients involved in Eqs. (12)–(15) will be explicitly given in the Appendix for the illustrative example carried out in Sect. 4.

3 Bifurcation analysis of the Eckhaus instability

The analysis carried out in this section focuses on the formation and stability of stationary 1D Turing patterns originating in the hyperbolic reaction–diffusion system (1), (2) over a large finite domain $D \propto 1/\epsilon$. In detail, the occurrence of the phenomenon of Eckhaus Instability (EI) will be analytically investigated in both supercritical and subcritical regime, with the main aim of quantifying some key dynamical features: stationary amplitude of patterns, existence and stability thresholds of each periodic bifurcating branch and linear growth rate. To address how a non-favorable wavelength may lead to pattern instability, we adopt the standard procedure adopted in the literature [4, 6].

3.1 Supercritical regime (a brief review)

To describe the spatio-temporal evolution of pattern amplitude close to onset of Turing instability in the supercritical regime, it suffices to push weakly nonlinear analysis up to the third perturbative order, where the cubic GL equation (12) is retrieved. We remind that the coefficients $\sigma$ and $\nu$ are always positive whereas the Landau coefficient L is positive in the supercritical regime only. To reduce the number of coefficients here involved, let us apply the following rescaling:

$$\begin{aligned} \tilde{x}=\frac{\pi }{D} x=\frac{\pi }{\epsilon D} X, \quad \tilde{t}=\frac{\pi ^2 \nu }{D^2} t=\frac{\pi ^2 \nu }{\epsilon ^2 D^2} T_2, \quad \tilde{\Omega }=\frac{\epsilon D \sqrt{L}}{\pi \sqrt{\nu }} \Omega , \quad \zeta =\frac{\epsilon ^2 D^2}{\pi ^2 \nu } \sigma , \quad Q = \frac{D}{\pi }q, \end{aligned}$$

(16)

that allows to recast Eq. (12) as:

$$\begin{aligned} \frac{\partial \tilde{\Omega }}{\partial \tilde{t}}=\zeta \tilde{\Omega } - \tilde{\Omega } |\tilde{\Omega }|^2 + \frac{\partial ^2 \tilde{\Omega }}{\partial \tilde{x}^2}. \end{aligned}$$

(17)

For simplicity, let us drop the tilde notation and assume that rolls take the structure:

$$\begin{aligned} \Omega =\Xi e^{iQx}e^{i\theta }, \end{aligned}$$

(18)

where $\Xi$ and Q describe, respectively, the amplitude and the phase of the envelope whereas $\theta$ is an arbitrary constant, to be determined according to boundary conditions. Substituting (18) into (17) gives, apart from the null solution $\Xi =0$, the stationary amplitude:

$$\begin{aligned} \Xi =\sqrt{\zeta - Q^2}. \end{aligned}$$

(19)

Patterned solution (18), (19) exists for $\zeta >Q^2$ and is referred in the literature to as pure mode [4]. It has to be distinguished from the trivial solution $\Omega =0$ which is termed conductive mode.

Note that, according to (16), (18) and the structure of $\overline{\mathbf {U}}_1$ (see (A.13) in the Appendix), the field has total wavenumber $(Q+Q_c)$. The finite domain, however, implies quantization of modes, i.e. not all wavenumbers are admitted but only those integer ones satisfying $(Q_n+Q_c) \in \mathbb {Z}, n \in \mathbb {N}_0$. Let us call

$$\begin{aligned} \Xi _n=\sqrt{\zeta - Q_n^2} \end{aligned}$$

(20)

the quantized amplitude of the n-th mode, that exists for $\zeta >Q_n^2:=\zeta _{e,n}$. Zero-flux boundary conditions, together with quantization of modes, restrict the possible values of $\theta$ to 0 and $\pi$ only. For simplicity, we set $\theta =0$. To address linear stability of patterns, let us apply small perturbations in amplitude and phase of rolls as follows:

$$\begin{aligned} \Omega =\Xi _n(1+\xi )e^{i(Q_n x+\phi )}, \end{aligned}$$

(21)

where $|\xi |, |\phi | \ll 1$. Substituting (21) into (17), keeping the linear terms in $\xi$ and $\phi$ and taking real and imaginary parts, the system ruling the evolution of perturbations results:

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\partial \phi }{\partial t}=2Q_n \frac{\partial \xi }{\partial x} + \frac{\partial ^2 \phi }{\partial x^2} \\ \frac{\partial \xi }{\partial t}=-2\Xi _n^2 \xi +\frac{\partial ^2 \xi }{\partial x^2} - 2Q_n \frac{\partial \phi }{\partial x} \end{array}\right. } \end{aligned}$$

(22)

Then, by assuming:

$$\begin{aligned} {\left\{ \begin{array}{ll} \phi =\hat{\phi }e^{\lambda t + ikx}\\ \xi =\hat{\xi }e^{\lambda t + ikx} \end{array}\right. } \end{aligned}$$

(23)

being $\hat{\phi }$ and $\hat{\xi }$ arbitrary constants and the dimensionless wavenumber $k\ne 0$, the following quadratic equation for the linear growth rate $\lambda$ is obtained:

$$\begin{aligned} \lambda ^2 + 2\left( k^2+\Xi _n^2\right) \lambda + k^2\left( 2\Xi _n^2+k^2-4Q_n^2 \right) =0, \end{aligned}$$

(24)

whose roots are:

$$\begin{aligned} \lambda _n^{(1,2)}=-\Xi _n^2- k^2\pm \sqrt{\Xi _n^4+4Q_n^2k^2}. \end{aligned}$$

(25)

Since the eigenvalue $\lambda _n^{(2)}$ is always negative, the stability of the associated mode depends on $\lambda _n^{(1)}$ which, taking into account (20), can be expressed as:

$$\begin{aligned} \lambda _n^{(1)} = Q_n^2 - k^2 - \zeta +\sqrt{\left( \zeta - Q_n^2 \right) ^2 + 4Q_n^2k^2}. \end{aligned}$$

(26)

Consequently, stable roll solutions in a finite domain satisfy:

$$\begin{aligned} \zeta > \sup _{k\in \mathbb {N}}\left\{ 3Q_n^2 - \frac{1}{2} k^2 \right\} = 3Q_n^2 - \frac{1}{2}:=\zeta _{E,n} {,} \end{aligned}$$

(27)

the last equality of which identifies the well-known Eckhaus parabola in the $(Q,\zeta )$ plane [4, 6].

By means of this approach, we have thus retrieved a well-known result: the primary branch $\Omega _0$ is always stable at onset ($\zeta \ge \zeta _{e,0}$) while all the other branches $\Omega _n$ (with $n\ge 1$) have always n unstable directions at onset and undergo n secondary bifurcations (of pitchfork type) in order to become stable. The final, restabilizing, bifurcation corresponds to the Eckhaus threshold [4]. The analysis developed in the supercritical regime, where pattern amplitude obeys cubic real GL equation (17) can be thus summarized in tabular form, see Table 1.

Moreover, taking into account (13) and (16), we can conclude that the stationary amplitude of each pure mode $\Xi _n$, the existence thresholds $\zeta _{e,n}$ and the Eckhaus thresholds $\zeta _{E,n}$ are unaffected by hyperbolicity, being the ratio $\sigma /\nu$ independent of inertial times. This result is compatible with the stationary nature of the emerging spatially-periodic patterns.

Table 1 Dynamical features predicted by cubic GL equation (17) in the supercritical regime

3.2 Subcritical regime

In this section we aim at describing the pattern amplitude close to onset of a subcritical bifurcation via a real cubic (12) or cubic–quintic (15) GL equation. Although it is known that these amplitude equations may capture different dynamical features, the goal of the subsequent analyses is to detect and emphasize such differences. We keep in mind that the Landau coefficient L is negative in this regime.

3.2.1 Cubic Ginzburg–Landau equation

Starting from cubic GL equation (12), let us rescale the variables as in (16) except for the amplitude:

$$\begin{aligned} \tilde{\Omega }=\frac{\epsilon D \sqrt{-L}}{\pi \sqrt{\nu }} \Omega . \end{aligned}$$

(28)

This allows to recast the cubic GL equation as follows:

$$\begin{aligned} \frac{\partial \tilde{\Omega }}{\partial \tilde{t}}=\zeta \tilde{\Omega } + \tilde{\Omega } |\tilde{\Omega }|^2 + \frac{\partial ^2 \tilde{\Omega }}{\partial \tilde{x}^2}. \end{aligned}$$

(29)

Removing tilde notation and adopting similar arguments as those addressed in the previous subsection, the quantized pure modes can be expressed as:

$$\begin{aligned} \Omega _n=\sqrt{Q_n^2-\zeta } e^{iQ_nx} \end{aligned}$$

(30)

and exist for

$$\begin{aligned} \zeta <Q_n^2:=\zeta _{e,n}. \end{aligned}$$

(31)

For each $Q_n$, the previous expression is representative of two periodic branches that originate from the conductive state through a subcritical pitchfork bifurcation. It is easy to verify that the expression of the eigenvalue determining stability of each bifurcating branch $\lambda _n^{(1)}$ (given in (26)) as well as the condition on pattern stability (given in (27)) are formally unchanged with respect to those found in the supercritical case. However, a key point has to be stressed according to the analysis here carried out: the existence (31) and stability (27) conditions are simultaneously fulfilled in the subcritical regime for $n=0$ only. Results are summarized in Table 2. Therefore, if the pattern amplitude obeyed cubic GL equation (29) close to the onset of a subcritical bifurcation, the sole primary branch $\Omega _0$ would undergo Eckhaus instability [40]. This marks a notably difference with respect to the behavior outlined in the supercritical regime.

Table 2 Dynamical features predicted by cubic GL equation (29) in the subcritical regime

3.2.2 Cubic–Quintic Ginzburg–Landau equation

Let us now inspect whether the real cubic–quintic GL equation (15), obtained by pushing weakly nonlinear expansion up to fifth order, may provide a qualitatively different description of subcritical dynamics. The signs of the coefficients are assumed to be $\overline{\sigma }>0$, $\overline{L}<0$, $\overline{\nu }>0$ and $\widetilde{R}<0$ in order to guarantee that the the primary branch exhibits a weakly inverted bifurcation at onset (i.e., it shows hysteresis) and that such a bifurcation saturates to quintic order [14]. By using the following rescaling of variables:

$$\begin{aligned} \begin{aligned} \tilde{x}=\frac{\pi }{\epsilon D}&X, \quad \tilde{t_2}=\frac{\pi ^2 \overline{\nu }}{\epsilon ^2 D^2} T_2, \quad \tilde{t_4}=\frac{\pi ^2 \overline{\nu }}{\epsilon ^2 D^2} T_4, \quad \tilde{\Omega }=\frac{\epsilon D \sqrt{-\overline{L}}}{\pi \sqrt{\overline{\nu }}} \Omega , \\&\zeta =\frac{\epsilon ^2 D^2}{\pi ^2 \overline{\nu }} \overline{\sigma }, \quad Q = \frac{D}{\pi }q, \quad {\rho }=-\frac{\pi ^2 \overline{\nu }}{D^2 \overline{L}^2} \widetilde{R}, \end{aligned} \end{aligned}$$

(32)

the cubic–quintic GL equation (15) may be recast as:

$$\begin{aligned} \frac{\partial \tilde{\Omega }}{\partial \tilde{t}}=\zeta \tilde{\Omega } + \tilde{\Omega } |\tilde{\Omega }|^2 - {\rho } \tilde{\Omega } |\tilde{\Omega }|^4 + \frac{\partial ^2 \tilde{\Omega }}{\partial \tilde{x}^2} {,} \end{aligned}$$

(33)

being $\partial /\partial \tilde{t}=\partial / \partial \tilde{t_2} + \epsilon ^2 \left( \partial / \partial \tilde{t_4}\right)$. Notice that the coefficients $\zeta$ and $\rho$ are real and positive.

Dropping tilde notation, considering “perfect” rolls structure as in (18) and using similar arguments as those addressed in the previous subsections, the quantized pure modes originating from the turning point can be expressed as $\Omega _n=\Xi _n e^{iQ_nx}$ with:

$$\begin{aligned} \Xi _n=\sqrt{\frac{1 \pm \sqrt{1+4{\rho }\left( \zeta - Q_n^2 \right) }}{2 {\rho }}}. \end{aligned}$$

(34)

The large amplitude branch exists for

$$\begin{aligned} \zeta > Q_n^2 - \frac{1}{4 {\rho }}:=\zeta _{e,n}, \end{aligned}$$

(35)

whereas the small amplitude one exists for

$$\begin{aligned} \zeta _{e,n}< \zeta < Q_n^2. \end{aligned}$$

(36)

Considering (21), (23) and (33), the eigenvalue $\lambda _n^{(1)}$ determining stability of pure modes is given by

$$\begin{aligned} \lambda _n^{(1)} = \Xi _n^2-k^2-2{\rho }\Xi _n^4+\sqrt{4{\rho }^2\Xi _n^8-4{\rho }\Xi _n^6+\Xi _n^4+4Q_n^2k^2} {,} \end{aligned}$$

(37)

that, using (34), allows to deduce the following stability condition for the large amplitude branch:

$$\begin{aligned} \zeta&> \sup _{k\in \mathbb {N}} \left\{ 2Q_n^2 - \frac{1}{4} k^2 - \frac{1}{8 {\rho }} \left[ 1-\sqrt{1-4{\rho }\left( k^2 -4Q_n^2 \right) } \right] \right\} \nonumber \\&=2Q_n^2 - \frac{1}{4} - \frac{1}{8 {\rho }} \left[ 1-\sqrt{1-4{\rho }\left( 1 -4Q_n^2 \right) } \right] :=\zeta _{E,n}, \end{aligned}$$

(38)

the last equality of which defines the Eckhaus threshold predicted by cubic–quintic GL equation. From the comparison between existence (35) and Eckhaus thresholds (38), it is possible to identify which bifurcating branch may undergo EI as:

$$\begin{aligned} \zeta _{e,n}\le \zeta _{E,n} \quad \Leftrightarrow \quad -8{\rho }\left( Q_n^2 - \frac{1}{4} \right) -1 \le \sqrt{1-4{\rho }\left( 1 -4Q_n^2 \right) }. \end{aligned}$$

(39)

Inequality (39) points out that the restabilizing mechanism depends on the order of the bifurcating branch. Indeed, for $n=0$, since quantization of modes implies $\left( Q_0^2 - 1/4\right) \le 0$, the necessary and sufficient condition for the restabilization of the primary branch becomes:

$$\begin{aligned} 2\left( 1-4Q_0^2\right) \rho \le 1 {,} \end{aligned}$$

(40)

that represents a restriction on the allowed values of the coefficient $\rho$. On the other hand, for $n\ge 1$, since $\left( Q_n^2 - 1/4\right) >0$, the inequality (39) is fulfilled for any $\rho >0$, so implying that all the secondary branches exhibit restabilizing Eckhaus bifurcations.

According to this analysis, the existence and consequently the amount of secondary bifurcations originating from periodic branches requires:

$$\begin{aligned} k \le 2 \vert Q_n\vert \sqrt{1+\frac{1}{8 \rho Q_n^2}}:=k_n^{*}, \end{aligned}$$

(41)

with $k \in \mathbb {N}$. Since $\rho >0$, the radicand is always greater than 1, so that $k_n^{*}\ge 2 \vert Q_n\vert$.

Notice that, fulfillment of conditions (39) and (40), as well as the numerical estimation of the quantity $k_n^{*}$ in (41), depends on the value of the coefficient $\rho$ and thus, it has to be checked numerically for the specific model under consideration. This issue will be addressed in the next section.

Therefore, the cubic–quintic GL equation predicts at least four key differences with respect to the cubic counterpart: (i) the range of existence of patterns is bounded from below $\zeta \ge \zeta _{e,n}:=Q_n^2-1/(4\rho )$; (ii) such an existence threshold is smaller than the bifurcation point ($\zeta _n=Q_n^2$) at which periodic branches originate from the conductive state; (iii) the primary branch may undergo EI provided that (40) is satisfied whereas (iv) all the secondary branches undergo EI and the number of restabilizing bifurcations depends on value of $\rho$ through condition (41).

Results contained in this subsection, that represent one of the novelties introduced in this manuscript, are summarized in Table 3.

In the literature [14], Brand and Deissler tackled a similar study on Eckhaus instability and deduced the analog of the Benjamin-Feir-Newell instability criterion for a weakly inverted bifurcation. However, some differences with respect to the present work should be pointed out. Indeed, those authors addressed the analysis on infinite domains only, so that quantization of modes was not investigated. Furthermore, the stability domain for finite-amplitude plane-wave solutions of cubic–quintic Ginzburg–Landau equation that are stable against the Eckhaus sideband instability was provided in terms of wavenumber instead of control parameter.

Table 3 Dynamical features predicted by cubic–quintic GL equation (33) in the subcritical regime

3.3 Spatio-temporal dependence of phase slip

The analysis carried out so far has revealed that the transition from an Eckhaus unstable state towards a more favorable, stable, patterned configuration may occur under different dynamical regimes. This process involves a sequence of transient states during which the wavelength of patterns is adjusted via the formation of amplitude defects and the appearance of phase-slips. Phases-slips are defined as solutions of the real GL equation whose number of zeros varies as a function of time. In other words, assuming the pattern amplitude $\Omega =\Xi (x,t) \text {e}^{i\psi (x,t)}$, a wavelength can only be created or destroyed where the local spatial phase $\psi (x,t)$ is undefined, namely at time instants $(t')$ and locations $(x')$ where $\text {Re}(\Omega (x',t'))=\text {Im}(\Omega (x',t'))=0$ [5, 41, 42].

Unfortunately, the global evolution of a given perturbation cannot be correctly described by a local analysis around a steady state, as the one performed in the previous sections, so that the occurrence in time and the location in space of phase slips is hard to be predicted. To the best of our knowledge, some good approximations of these quantities have been obtained by means of local theories under the assumption that phase slip occurs ‘just’ after an ad-hoc choice of initial data [5, 41], but no explicit expressions have been provided in the general, global, case. Moreover, some works [18, 40, 43] pointed out the possibility to control and vary the time to phase slip only if some ‘free’ model parameters, not involved in the spectrum of the linearized problem, are available. At the same time, those works inspected the dependence of the time to phase slip on the linear growth rate but no mention was given on the functional dependence of the spatial location at which phase slip occurs. Therefore, the issue of controlling, independently of each other, time and space at which phase slip takes place appears to be still unaddressed. This issue will be investigated numerically in Sect. 4.3.

4 An illustrative example: the hyperbolic modified Klausmeier model

In order to validate the theoretical predictions carried out in the previous sections, let us now investigate, as an illustrative example, the occurrence of EI in the context of dry-land ecology. To this aim, let us take into account one of the simplest, conceptual, two-compartment models describing the formation of vegetation stripes in arid environments, i.e. the Klausmeier model [28, 37, 44, 45]. In particular, the analysis will be focused on its modified version [29,30,31] that has been introduced in the literature to model pattern dynamics over flat terrains. Moreover, motivated by the observation of inertial effects [46,47,48,49,50] and long transient regimes [51,52,53] in vegetation patterned dynamics, an hyperbolic generalization was proposed in [19, 20].

In this model, the two species introduced in Sect. 2 are representative of plant biomass u(x, t) and soil–water w(x, t). It is also assumed that $d\gg 1$ measures the water-to-plant diffusion ratio [30], $\tau ^u=1/\gamma _0$ and $\tau ^w=d/\mu _0$ denote the inertial times associated to vegetation and water, respectively. Furthermore, the model encloses a per-capita rate of water uptake proportional to plant biomass, the plant growth rate proportional to water uptake, a linear dependence of plant loss with strength B and a mean annual rainfall represented by the parameter A. According to the above assumptions, the hyperbolic reaction–diffusion model is in the form (1), (2) with kinetic terms given by:

$$\begin{aligned} f(u,w)=u^2w-Bu, \quad \quad g(u,w)=A-u^2w-w. \end{aligned}$$

(42)

In line with the analysis carried out in Sect. 2 , plant mortality B is taken as the main control parameter as it encloses variability due to natural, human and herbivory effects. According to literature data [28, 54], realistic values of plant loss and rainfall belong to the ranges $B\in (0,2)$ and $A\in (0,3)$, respectively. To evaluate the spatio-temporal evolution of pattern dynamics, the governing system is integrated numerically over a finite domain of length D by means of COMSOL Multiphysics [55]. Moreover, the MATLAB package PDE2PATH [56] is used to build up the bifurcation diagrams in both supercritical and subcritical regimes.

In the Appendix we report all the explicit expressions of the quantities arising from linear and weakly nonlinear analysis for the illustrative example here considered.

4.1 Supercritical regime

In the supercritical regime, the following model parameters are chosen: water-to-plant diffusion ratio $d=10^3$ and rainfall $A=2.8$. According to (4), (5), (13), the considered setup gives rise to a critical value of plant loss $B_c=3529\times 10^{-4}$, critical wavenumber $q_c=0.3814$ and Landau coefficient $L=+113\times 10^{-5}>0$. The governing system (1), (2), (42) is integrated over a spatial domain of length $D=200$. For the computation of spatio-temporal dynamics the overall time window here considered is $t \in [0,1.5\times 10^{4}]$.

The bifurcation diagram obtained in the supercritical regime is depicted in Fig. 1, where solid red (dashed black) lines are representative of stable (unstable) branches. In agreement with theoretical predictions (see Table 1), it consists of a primary branch $(n=0)$ and several secondary branches (the cases $n=1,2,3$ are here shown). The primary branch bifurcates supercritically at $B_{e,0}$ giving rise to two stable branches for $B>B_{e,0}$. The secondary branches originate from the conductive state at $B_{e,n}$ and, for $n>1$, undergo $(n-1)$ unstable (pitchfork) bifurcations until they re-stabilize at the Eckhaus threshold $B_{E,n}$. The bifurcation diagram is computed for different values of inertial times achieving the same result, as expected from the analysis carried out in Sect. 3.

Fig. 1

Bifurcation diagram in the supercritical regime. Solid red (dashed black) lines represent stable (unstable) stationary branches. Existence $B_{e,n}$ and Eckhaus $B_{E,n}$ thresholds are indicated in the bottom and in the top part of the figure, respectively

The numerically-computed values of the existence and Eckhaus thresholds are summarized in Table 4 and compared to the theoretical ones given in Table 1. As it can be noticed, the resulting agreement between them is satisfying for all the investigated branches. The agreement gets slightly worse for higher-order branches, as the dimensionless distance from the Turing threshold $\epsilon ^2$ increases, as expected from weakly nonlinear approximation. It should be also remarked that the following inequalities on existence and Eckhaus thresholds, $B_{e,n}>B_{e,n-1}$ and $B_{E,n+1}>B_{E,n}$, hold for any $n\ge 1$.

Table 4 Comparison between theoretically-estimated and numerically-computed bifurcation points for the first four periodic branches characterizing the supercritical regime. The quantity $\epsilon ^2$ represents the dimensionless distance from Turing threshold

In order to check the validity of the bifurcation diagram and, in turn, to confirm the theoretical predictions carried out in Sect. 3.1, let us now integrate numerically the governing systems (1), (2) by varying the control parameter B. In all simulations, the initial condition is assumed to take the form given by (6)$_2$ and (A.13), where the pattern amplitude is taken as a small perturbation of the stationary value for each considered branch $\Omega _n=\sqrt{\zeta -Q_n^2} e^{iQ_nx}$, in line with Eqs. (18), (20). Results are shown in Fig. 2.

Fig. 2

Spatio-temporal evolution of supercritical pattern dynamics obtained integrating numerically the hyperbolic Klausmeier model (1), (2) with the following parameter set: $D=200$, $A=2.8$, $d=10^3$, $\mu _0=10^5$, $\gamma _0=10^2$. In the figures, the control parameter B is varied as follows: a $B>B_{e,0}$, b $B_{e,1}< B < B_{E,1}$, c $B>B_{E,1}$, d $B_{e,2}< B < B_{E,2}$, e $B>B_{E,2}$, f $B_{e,3}< B < B_{E,3}$ and g $B > B_{E,3}$. The different initial conditions here used are specified in the main text

Zero-flux boundary conditions impose that only integer values of the wavenumber are allowed. Therefore, the system will only support periodic patterns whose overall wavenumber $Q_c + Q_n$ are integer. Since $q_c=0.3814$, according to (16), the rescaled value of wavenumber becomes $Q_c=24.28$ and the closest integer is 24, so that the finite geometry shall select a primary mode with wavenumber $Q_c+Q_0 =24$. Considering that $\pi (Q_c +Q_0)/D=2\pi /\Lambda$, with $\Lambda$ the pattern wavelength, the whole computational domain D shall thus accommodate $12\Lambda$. Indeed, by choosing a value $B>B_{e,0}$, starting from a small perturbation of the branch $\Omega _0$, the confirmation of the stability of the primary branch is achieved, as can be seen from Fig. 2a. Analogously, starting from $B_{e,1}<B<B_{E,1}$ and setting as initial condition a small perturbation of the branch $\Omega _1$, the system undergoes a phase slip, during which the number of wavelengths is reduced, and finally it converges towards the stable $\Omega _0$ branch (Fig. 2b). On the contrary, by leaving the previous initial condition unchanged, if the control parameter is set just above the Eckhaus threshold, i.e. $B>B_{E,1}$, the system now stabilizes along the stable branch $\Omega _1$. In this latter case, in fact, the next closest integer is 25, so the finite geometry shall select a mode with wavenumber $Q_c +Q_1=25$ that corresponds to $D=12.5\Lambda$ (see Fig. 2c). Similar conclusions can be drawn for higher-order branches. In detail, Fig. 2d represents the evolution from a small perturbation of the branch $\Omega _2$ (characterized by $Q_c +Q_2=23$ and $D=11.5\Lambda$) by using $B_{e,2}< B < B_{E,2}$. Indeed, in this range of the control parameter, the initial branch is unstable, so the system converges to the stable branch $\Omega _0$ and a phase slip at the boundary of the domain occurs. Instead, if the value of the control parameter is slightly increased to overcome Eckhaus threshold, $B>B_{E,2}$, the branch $\Omega _2$ now stabilizes (see Fig. 2e). Finally, the last two figures correspond to simulations where the initial conditions are set as small perturbations of branch $\Omega _3$ with control parameter slightly smaller ($B_{e,3}< B < B_{E,3}$, Fig. 2f) or larger ($B > B_{E,3}$, Fig. 2g) than the Eckhaus threshold of the corresponding branch. As can be seen, in the former case, the initial branch is unstable and system experiences a transition towards the stable $\Omega _0$ branch whereas, in the latter case, the system stabilizes along the branch $\Omega _3$, consistently with theoretical predictions.

Fig. 3

Diagram of the first three subcritical bifurcating branches. The bifurcation points of the conductive branch $B_{n}$ are indicated in the bottom part of the figure, whereas the Eckhaus thresholds $B_{E,n}$ are shown in the top part

4.2 Subcritical regime

Numerical investigations carried out in the subcritical regime make use of the following parameters: water-to-plant diffusion ratio $d=10^3$ and rainfall $A=0.02$. These parameters provide a critical value of plant loss $B_c=9.378\times 10^{-3}$, critical wavenumber $q_c=5.62\times 10^{-2}$ and Landau coefficient $L=-5.69\times 10^{-5}<0$. As can be noticed, the much smaller value of critical wavenumber suggests that the excited wavelengths are much larger than those observed in the supercritical regime, consistently with previous results [19]. For this reason, the computational domain has been enlarged to $D=1000$. Moreover, since subcritical pattern dynamics are expected to occur over much longer timescales, the spatio-temporal evolution is observed over a wider time window $t \in [2 \times 10^5]$.

Two main considerations can be drawn from the bifurcation diagram obtained in the subcritical regime, shown in Fig. 3. First, the primary branch undergoes a subcritical bifurcation at $B_{0}$ (corresponding to $\zeta =Q_0^2$) where two unstable periodic branches originate from the conductive states, become stable at the Eckhaus threshold $B_{E,0}<B_{0}$ and still survive for $B>B_0$ ($\zeta >Q_0^2$). Second, the secondary branches ($n \ge 1$) undergo a restabilizing bifurcation for $B_{E,n}>B_n$ ($\zeta _{E,n}>\zeta _n$).

Therefore, two striking features appear markedly in contrast with the analysis developed in the framework of cubic GL equation: the existence of periodic solutions beyond the predicted threshold and the occurrence of restabilizing bifurcations for higher order branches too. Evidently, weakly nonlinear analysis developed in Sect. 3.2 fails to describe this phenomenon as it is based on the assumption that pattern amplitude behaves as $O(\epsilon )$ close to onset. The approach based on cubic GL equation appears to be, thus, not suitable to predict the occurrence of restabilizing bifurcations at large amplitudes, whose description requires weakly nonlinear expansion to be pushed forward to higher orders, as done in Sect.3.2.

The features exhibited by the bifurcation diagram in Fig. 3 are, indeed, fully compatible with results obtained in the framework of cubic–quintic GL equation (summarized in Table 3). Several considerations may be addressed on this point. First of all, the occurrence of Eckhaus instability on the primary branch at $\zeta _{E,0}<Q_0^2$ confirms that the numerically-computed value of the coefficient $\widetilde{R}$ is negative and fulfills the restriction (40). Moreover, the secondary branches originating from the unstable conductive state do exhibit Eckhaus re-stabilizing bifurcations for values of the control parameter larger than existence threshold, i.e. $B_{E,n}>B_{e,n}$. Furthermore, each n-th order branch undergoes exactly $(n-1)$ secondary unstable bifurcations (as in the supercritical regime), in agreement with the numerical values of the coefficient $k_n^{*}$ that always fall in the range $n<k_n^{*}<n+1$.

Let us finally comment that the bifurcation diagram drawn in Fig. 3 has been computed for different inertial times (by varying them over different order of magnitudes) obtaining identical results, so verifying the independence of existence and Eckhaus thresholds on inertial effects. The theoretical values of Eckhaus threshold of the first three branches originating from the conductive state arising from cubic and quintic analysis are reported in Table 5. The previous theoretical values are then compared to the numerical ones, obtaining a satisfying agreement in all cases. Of course, theoretical values deviate away from numerical ones as far as the dimensionless distance from the threshold is increased, as expected from weakly nonlinear approximation.

Table 5 Comparison between theoretically-estimated and numerically-computed bifurcation points for the first three periodic branches characterizing the subcritical regime

Let us now inspect the spatio-temporal evolution of patterns resulting from variation of the control parameter B along the different branches characterizing the bifurcation diagram of Fig. 3. To achieve this goal, the governing system is integrated numerically by using the same boundary and initial conditions as the ones adopted in the supercritical regime. Results of this analysis are shown in Fig. 4. According to the previous values of critical parameters together with the scaling of variables (32), the dimensionless value of critical wavenumber becomes $Q_c=17.89$. Therefore, the finite geometry shall select a primary mode with wavenumber $Q_c +Q_0=18$, i.e. the computational domain shall accommodate $D=9\Lambda$. Indeed, by choosing a value $B_{E,0}<B<B_{0}$, starting from a small perturbation of the branch $\Omega _0$, the primary branch results to be stable even for values of the control parameter smaller than the primary bifurcation threshold, so confirming the subcritical character (see Fig. 4a). Let us now set the initial condition as a small perturbation of the branch $\Omega _1$, which is characterized by $Q_c +Q_1=17$ and $D=8.5\Lambda$, and choose a control parameter which falls into the range $B_{1}<B<B_{E,1}$ or $B_{E,1}<B<B_2$, i.e. respectively slightly below or above the Eckhaus threshold of the first secondary branch (predicted by quintic GL equation). Results reveal that, in the former case, the system undergoes a phase slip and finally converges towards the stable $\Omega _0$ branch (see Fig. 4b). In the latter case, the system remains on the stable $\Omega _1$ branch, proving the occurrence of a restabilizing bifurcation (see Fig. 4c). The instability of the last secondary branch for values smaller than Eckhaus threshold can be proved by setting the initial condition as a small perturbation of $\Omega _2$ ($Q_c +Q_2=19$ and $D=9.5\Lambda$) and choosing $B_{2}<B<B_{E,2}$. As shown in Fig. 4d, the system selects a different wavelength and stabilizes along the stable $\Omega _0$ branch. On the contrary, if the control parameter is chosen in such a way that $B>B_{E,2}$, no phase slips occurs and the system stabilizes on the $\Omega _2$ branch, as depicted in Fig. 4e. In all cases, results agree with theoretical predictions developed in Sect. 3.2.1.

Let us finally comment that all the simulations reported in this section have been obtained by integrating numerically the hyperbolic model by using $\mu _0=10^5$ and $\gamma _0=1.1$, that represent a good approximation of the behavior close to the parabolic limit in the subcritical regime. In the next section, the behavior far away from the parabolic limit is explored in more detail.

Fig. 4

Spatio-temporal evolution of subcritical pattern dynamics obtained integrating numerically the hyperbolic Klausmeier model (1), (2) with the following parameter set: $D=1000$, $A=0.02$, $d=10^3$, $\mu _0=10^5$, $\gamma _0=1.1$. The control parameter B is varied as follows: a $B_{E,0}<B<B_{0}$, b $B_{1}<B<B_{E,1}$, c $B_{E,1}<B<B_2$, d $B_{2}<B<B_{E,2}$ and e $B>B_{E,2}$. The different initial conditions here used are specified in the main text

4.3 Spatio-temporal dependence of phase slip

Let us characterize more deeply the phenomenon of phase slip taking place during Eckhaus-driven dynamics, with more emphasis on the role played by hyperbolicity.

As previously mentioned [5, 18, 41, 42], a phase slip may be defined as a solution of the GL equation whose zeros of the pattern amplitude $\vert \Omega (x,t)\vert$ vary as a function of space and time. Let us call $t_{slip}$ and $x_{slip}$, respectively, the first time instant and the spatial location at which such an event takes place. Due to the impossibility to predict these values theoretically, ad-hoc numerical investigations are performed with the twofold aim of: (i) elucidating how inertial times may affect this phenomenon in the supercritical and subcritical regimes and (ii) establishing strategies to control these quantities independently of each other.

Let us now investigate how the time and the space at which phase slip takes place depend on the model parameters and the initial conditions. In this context it will be emphasized how inertial times represent, effectively, additional degrees of freedom that may be used to enrich the scenario of transient dynamics. Indeed, in the parabolic version of the Klausmeier model [28,29,30,31], the linearized problem giving rise to Turing threshold is completely determined by all model parameters, i.e. A, B and d, as deduced in (4), (5). These parameters also specify the stationary amplitude of each branch of quantized periodic state. Consequently, no free parameters are available to characterize the evolution of the system during the transient regime. On the contrary, in the hyperbolic extension (1), (2), (42) it is possible to manage two extra parameters, i.e. $\gamma _0$ and $\mu _0$, that are strictly correlated to the inertial times of the involved species and that are always present in any physical system. As shown in the previous sections, changes applied to inertial times do not yield any variation of existence and stability thresholds, but it is expected that they play a relevant role during transient regime.

To this aim, let us integrate numerically the hyperbolic system by fixing the parameters A, B, d and $\gamma _0$, and varying the phenomenological coefficient $\mu _0$. In the first set of investigations, the parameters are chosen in such a way dynamics fall into the supercritical regime. In particular, the plant loss is chosen in the range $B_{e,2}<B<B_{E,2}$ and the initial condition is set as small perturbation of the unstable branch $\Omega _2$, so that the system is expected to undergo an Eckhaus-driven transition towards the stable branch $\Omega _1$ (as depicted in Fig. 2d). Results are shown in Fig. 5 where $\mu _0$ is varied from $10^2$ to $10^5$. It can be noticed that, as the parameter $\mu _0$ increases, the phase slip takes place earlier, leaving its spatial location at the edges of the domain unaltered. Moreover, dynamics reported from (e) to (a) represent progressive deviations from the parabolic limit and allow to appreciate how much longer transient regimes may be experienced by varying a single inertial-related parameter.

Fig. 5

Spatio-temporal evolution of patterns deduced from numerical integration of the hyperbolic model. The common parameters are: $D=200$, $A=2.8$, $d=1000$, $\gamma _0=100$ and $B_{e,2}< B < B_{E,2}$. The parameter $\mu _0$ is varied as follows: a $\mu _0=100$, b $\mu _0=150$, c $\mu _0=350$, d $\mu _0=500$ and e $\mu _0=10^5$

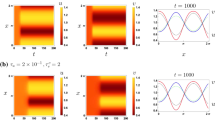
To describe in more detail the control of the only time to phase slip, let us characterize its functional dependence. From the numerical standpoint, keeping in mind (6)$_2$ and (A.13), an useful way to approximate the occurrence of a zero of pattern amplitude consists of searching where and when the current state $\mathbf {U}(x,t)$ crosses the steady-state $\mathbf {U}_S$. To check the validity of the previous statement, let us depict the trajectory followed by the field variables from the initial state $\mathbf {U}_\text {in}$ (taken as small perturbation of the unstable $\Omega _2$ branch) towards the stationary patterned state $\mathbf {U}_\text {end}$ (stable patterned branch $\Omega _0$). As illustrative examples, the trajectories corresponding to three different values of $\mu _0= 20, 10^2$ and $10^5$ are shown in Fig. 6a for the supercritical regime, whereas those corresponding to $\mu _0= 10^2, 10^3$ and $10^5$ for the subcritical one are depicted in Fig. 7a. It is found that, independently of the value of $\mu _0$, all the trajectories cross the steady homogeneous state $\mathbf {U}_{S}$ at the same location: $x_{slip}=84$ in the supercritical regime and $x_{slip}=276$ in the subcritical one. Such an intersection occurs at longer times as the phenomenological parameter $\mu _0$ is reduced, as denoted by the green squares in Figs. 6b and 7b, and consistently with the meaning of inertial time.

Fig. 6

a, b Numerically-computed trajectories $u(x_{slip},t)$ corresponding to supercritical dynamics from a small perturbation of the unstable $\Omega _2$ branch ($\mathbf {U}_\text {in}$) towards the stable patterned $\Omega _0$ branch ($\mathbf {U}_\text {end}$), crossing the homogeneous state $\mathbf {U}_{S}$. Fixed parameters: $B_{e,2}< B < B_{E,2}$, $d=10^3$, $A=2.8$ and $\gamma _0=10^2$. Variables: $\mu _0=20$ (solid blue line), $\mu _0=10^2$ (dashed red line) and $\mu _0=10^5$ (dotted black line). In b, green squares represent the time at which phase slip occurs. c Plot of log(t$_{slip})$ as a function of $-log(\overline{\lambda _2^{(1)}})$. Black squares represent results of numerical simulations for different value of $\mu _0$, the solid red line denotes the linear fit (color figure online)

Fig. 7

Panels, lines and symbols have the same meaning as in Fig. 6, but dynamics falls into subcritical regime. Fixed parameters: $B_2<B<B_{E,2}$, $d=10^3$, $A=0.02$ and $\gamma _0=1.1$. Variables: $\mu _0=10^2$, $\mu _0=10^3$ and $\mu _0=10^5$

The above observations suggest to correlate the time to phase slip $t_{slip}$ with the linear growth rate $\lambda _n^{(1)}$ (see expressions (26) and (37)). Indeed, once the growth factor is recasted in the original time variables, say $\overline{\lambda _n^{(1)}}$, one argues that it depends linearly on the parameters $\nu$ (in the supercritical regime) or $\overline{\nu }$ (in the subcritical one), which both bring the contribution from inertia. Indeed, by plotting the dependence of $t_{slip}$ as a function of $\overline{\lambda _n^{(1)}}$, with $n=2$, two different linear relationships are retrieved in log-log scale, as depicted in Fig. 6c for the supercritical regime (with adjusted r-squared value $r_a^2=0.999$), and in Fig. 7c for the subcritical one ($r_a^2=0.995$). These results confirm that the time to phase slip $t_{slip}$, close to onset, is strictly related to the linear growth rate $\overline{\lambda _{n}^{(1)}}$ in both dynamical regimes.

Notice that the above analysis is carried out by considering values of inertial times falling either in the ranges $\tau ^u<\tau ^w$ and $\tau ^w<\tau ^u$, obtaining the same functional dependence. However, the different signs of the proportionality coefficients deduced in the linear fits indicate that the time to phase slip is negatively correlated with the linear growth rate in the supercritical regime [40], i.e. , whereas it is positively correlated in the subcritical one [18], i.e. .

Results described so far pointed out that the time at which phase slip occurs may be controlled by the linear growth rate, leaving the location unchanged. Let us now inspect whether it is possible to find a strategy to get the opposite scenario, namely the possibility to modulate the location $x_{slip}$ at which wavelength adjustment takes place leaving the time to phase slip unaltered. To this aim, since perfectly-periodic initial conditions may represent an idealization of the reality, let us consider an ecologically-realistic scenario where a defect, localized at $x\equiv x_{def}$ with amplitude a, is present in the initial data, as shown schematically in Fig. 8a. Let us then build the scatterplots representative of location $x_{slip}$ to phase slip as a function of defect position $x_{def}$, obtained for $a=50$. Results shown in Fig. 8b reveal that the spatial location of phase slip can be modulated linearly ($r_a^2=0.999$) by varying the defect position, leaving the time to phase slip almost unchanged. To confirm the above statements, in Fig. 9 some examples of spatiotemporal evolution of patterns obtained for three different locations of a large defect are depicted. As it can be noticed, the time to phase slip is kept almost fixed at $t \simeq 350$.

Therefore, the numerical investigations here proposed suggest different strategies to control, separately, the time and the spatial location at which phase slip takes place.

Fig. 8

The control of the spatial location of phase slip. a Schematics of the initial conditions, where $x_{def}$ denotes the location of a defect and a its amplitude. b Scatterplot representative of the relationship $x_{slip}\left( x_{def}\right)$, where symbols represent results of numerical simulations, the solid line is the computed best linear fit. The amplitude of the defect is set to $a=50$

Fig. 9

Spatiotemporal evolution of patterns with a localized defect in the initial conditions. Parameters are: $D=200$, $A=2.8$, $d=10^3$, $B_{e,2}< B < B_{E,2}$, $\gamma _0=100$, $\mu _0=10^5$, $a=50$ and a $x_{def}=80$ b $x_{def}=100$ c $x_{def}=120$

5 Conclusions

In this paper, a theoretical study on the EI of stationary patterns in a hyperbolic reaction–diffusion system defined over a large finite domain was addressed in the supercritical and subcritical regimes. To this aim, linear and weakly nonlinear analysis were first addressed to deduce the equations governing the pattern amplitude close to criticality. Then, the bifurcation analysis of the EI was carried out to describe existence and stability thresholds of all bifurcating branches. Finally, the above analytical predictions were validated by comparison with results of numerical simulations performed on a conceptual model of interest in dry-lands ecology, the modified Klausmeier model, where stationary vegetation patterns emerge over flat arid terrains. These numerical investigations also allowed to get some insights into the phenomenon of phase-slip.

The main results can be summarized as follows:

(i) It was shown that, while the cubic real GL equation (12) describes satisfactorily well the features associated to primary and secondary branches of periodic solutions in the supercritical regime, it is not able to predict the proper range of existence of such periodic solutions as well as the restabilizing mechanism that n-th order secondary branches, with $n\ge 1$, undergo in the subcritical regime. The above restrictions were overcome by pushing weakly nonlinear analysis up to the fifth order, where the resulting envelope equation takes the form of cubic–quintic GL equation (15). To achieve this goal, it was necessary to deduce the explicit expressions of the main properties of primary and secondary quantized periodic branches (stationary amplitude $\Xi _n$, existence $\zeta _{e,n}$ and stability $\zeta _{E,n}$ thresholds, linear growth rate $\overline{\lambda _n^{(1)}}$) characterizing the bifurcation diagram in the subcritical regime in the framework of quintic GL equation. All these quantities were collected in Tables 1–3. This approach provided the complete description of all ($n\ge 0$) periodic branches appearing in the bifurcation diagram of subcritical modes, as can be noticed from the comparative theoretical-numerical results reported in Tables 4 and 5.

(ii) From the inspection of numerically-computed bifurcation diagrams (see Figs. 1, 3) and spatio-temporal evolution of patterns (see Figs. 2, 4), it was obtained the twofold goal of: validating the theoretical predictions arising from multiple-scale weakly-nonlinear analysis and elucidating the role played by inertial effects that are always present in any physical system. From the theoretical viewpoint, in particular, it was shown that hyperbolicity affects the expression of the linear growth rate but leaves the other quantities (stationary amplitude, existence and stability thresholds) unchanged. This result suggested that the hyperbolic model provides additional degrees of freedom that may be used to better characterize transient regimes, in particular the transition from an Eckhaus-unstable state towards a more favorable stable configuration through sequences of phase-slips.

(iii) The functional dependence of time and location at which wavelength adjustment takes place is investigated numerically with the main goal of finding strategies to control these quantities independently of each other. Our results revealed that the time to phase slip may be modulated by varying the inertial times leaving its location unaltered. Moreover, it was shown that $t_{slip}$ strongly depends upon the linear growth rate $\overline{\lambda _n^{(1)}}$, in both dynamical regimes (as depicted in Figs. 6 and 7). In particular, results indicate that $t_{slip}$ and $\overline{\lambda _n^{(1)}}$ are negatively correlated in the supercritical regime but positively in the subcritical one. On the other hand, it was numerically shown that, by considering a localized defect into the initial conditions, it is possible to modulate the location to phase slip leaving the time to phase slip almost unchanged (see Figs. 8 and 9).

In future works, it is planned to extend bifurcation analysis of EI to the case of oscillatory periodic patterns in the more general framework of hyperbolic reaction–advection–diffusion models, where the instability thresholds are remarkably affected by inertial effects and pattern amplitude close to onset is ruled by complex GL equations.

Appendix

In this Appendix we provide the expressions of the quantities involved in linear and weakly nonlinear analysis for the specific case of the hyperbolic modified Klausmeier model:

$$\begin{aligned} \left[ \begin{array}{c} u \\ w \\ J^{u} \\ J^{w} \end{array} \right] _t + \left[ \begin{array}{cccc} 0 &{} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 1 \\ \gamma _{0} &{} 0 &{} 0 &{} 0 \\ 0 &{} \mu _{0} &{} 0 &{} 0 \end{array} \right] \left[ \begin{array}{c} u \\ w \\ J^{u} \\ J^{w} \end{array} \right] _x = \left[ \begin{array}{c} u^2w-Bu \\ A-u^2w-w \\ -\gamma _{0}J^{u} \\ -\frac{\mu _{0}}{d}J^{w} \end{array} \right] . \end{aligned}$$

(A.1)

As already mentioned, the plant mortality B is taken as the main control parameter.

If $A \le 2B$, the model admits only a steady state of desert-type:

$$\begin{aligned} {\textbf {U}}_D=(0,A,0,0) {,} \end{aligned}$$

(A.2)

while, if $A \ge 2B$, it also admits two states representative of spatially-homogeneous vegetated regions:

$$\begin{aligned} \begin{aligned}&{\textbf {U}}_L=(u_L,w_L, 0,0) {,} \\&{\textbf {U}}_S=(u_S,w_S,0,0) {,} \end{aligned} \end{aligned}$$

(A.3)

where $u_L=\left( A-\sqrt{A^2-4B^2}\right) /(2B)$, $u_S=\left( A+\sqrt{A^2-4B^2}\right) /(2B)$, $w_L=B/u_L$, $w_S=B/u_S$, with $u_L<1<u_S$.

Moreover, in the model under investigation, the only non-zero partial derivatives of kinetics terms take the form:

$$\begin{aligned}&f_{u}^{*}=B,\quad f_{w}^{*}=u_S^2,\quad g_{u}^{*}=-2B,\quad g_{w}^{*}=-\left( 1+u_S^2\right) ,\nonumber \\&f_{uu}^{*}=2B/u_S,\quad f_{uw}^{*}=2u_S,\quad g_{uu}^{*}=-2B/u_S, \quad g_{uw}^{*}=-2u_S,\nonumber \\&f_{uuw}^{*}=2,\quad g_{uuw}^{*}=-2. \end{aligned}$$

(A.4)

Linear stability analysis reveals that the states ${\textbf {U}}_D$ and ${\textbf {U}}_L$ are always stable and unstable, respectively. On the other hand, the state ${\textbf {U}}_S$ is found to be stable against spatially-uniform perturbations if:

$$\begin{aligned} \begin{array}{l} B-1-u_{S}^2 < 0 {,} \\ {B\left( u_{S}^2-1\right) >0,} \end{array} \end{aligned}$$

(A.5)

that are always fulfilled since realistic values of plant loss B are in the range (0, 2) [54] and $u_S>1$. The state ${\textbf {U}}_S$ is also stable under non-homogeneous perturbations if:

$$\begin{aligned} \left\{ \begin{array}{l} dB-\left( 1+u_{S}^{2}\right)<0 \\ \left( dB-1-u_{S}^{2}\right) ^{2}-4dB\left( u_{S}^{2}-1\right) <0 \\ \end{array} \right. \end{aligned}$$

(A.6)

When conditions (A.6) are violated, Turing patterns [2] may originate as a consequence of destabilization of the state ${\textbf {U}}_S$. From (4), (5), the critical values of control parameter $B_{c}$ and wavenumber $q_{c}$ at the onset of Turing instability read:

$$\begin{aligned}&B_{c}=\frac{3u_{S_c}^2-1+2u_{S_{c}}\sqrt{2\left( u_{S_c}^2-1\right) }}{d} {,} \end{aligned}$$

(A.7)

$$\begin{aligned}&q_{c}^{2}=\sqrt{\frac{B_{c}\left( u_{S_c}^2-1\right) }{d}}, \end{aligned}$$

(A.8)

being $u_{S_{c}}=\left( A+\sqrt{A^{2}-4B_{c}^{2}}\right) /\left( 2B_{c}\right)$.

Let us now focus on the results of weakly nonlinear analysis. Applying expansions

$$\begin{aligned} \begin{array}{l} B=B_c+\epsilon ^2 B_2 + \epsilon ^4 B_4 + O(\epsilon ^6), \\ \overline{\mathbf {U}}= \epsilon \overline{\mathbf {U}}_1+ \epsilon ^2 \overline{\mathbf {U}}_2+ \epsilon ^3 \overline{\mathbf {U}}_3+ \epsilon ^4 \overline{\mathbf {U}}_4+ \epsilon ^5 \overline{\mathbf {U}}_5+O(\epsilon ^6) {,}\\ \end{array} \end{aligned}$$

(A.9)

in the model (A.1) and collecting the terms of the same orders of $\epsilon$, the set of linear equation (8) is obtained.

Taking into account (A.4), (A.7), (A.8), the matrix $K_c^{*}$, defined in (10), admits two complex eigenvalues ${{\mp }} iq_c$ with algebraic and geometric multiplicity given by 2 and 1, respectively. By introducing the invertible transform matrix P and the Jordan canonical form $\Upsilon$ of $K_c^{*}$, the general solution of (8)$_1$ can be expressed as:

$$\begin{aligned} \overline{\mathbf {U}}_{1}=Pe^{\Upsilon x}P^{-1}\mathbf {C}_1 {,} \end{aligned}$$

(A.10)

being:

$$\begin{aligned} P=\left[ \begin{array}{cccc} iY_1 &{}{} r_1 &{}{} -iY_1 &{}{} r_1 \\ iY_2 &{}{} r_2 &{}{} -iY_2 &{}{} r_2 \\ Y_3 &{}{} ir_3 &{}{} Y_3 &{}{} -ir_3 \\ Y_4 &{}{} ir_4 &{}{} Y_4 &{}{} -ir_4 \end{array} \right] , \quad \Upsilon =\left[ \begin{array}{cccc} iq_c &{}{} 0 &{}{} 0 &{}{} 0 \\ 1 &{}{} iq_c &{}{} 0 &{}{} 0 \\ 0 &{}{} 0 &{}{} -iq_c &{}{} 0 \\ 0 &{}{} 0 &{}{} 1 &{}{} -iq_c \end{array} \right] , \end{aligned}$$

(A.11)

where the vector $\mathbf {C}_1(X,T_2,T_4)$ is determined by boundary conditions and removal of secular terms, whereas $r_i$ and $Y_i$ $(i=1,...,4)$ are the components of simple and generalized right eigenvectors of $K_c^{*}$, given by:

$$\begin{aligned} \begin{array}{l} r_1=1, \quad r_{2}=r_1\left( q_c^2-B_{c} \right) /u_{S_c}^2, \quad r_{3}=-q_cr_{1}, \quad r_{4}=-dq_cr_{2}, \\ Y_{1}=\frac{2q_cr_{1}}{q_c^{2}-B_{c}}, \quad Y_{2}=0, \quad Y_{3}=q_cY_{1}-r_{1}, \quad Y_{4}=-dr_{2}. \end{array} \end{aligned}$$

(A.12)

The solution at the first perturbative order, satisfying zero-flux boundary conditions, reads

$$\begin{aligned} \overline{\mathbf {U}}_1=\text{ Re }\{\Omega \, \mathbf {r}\, e^{i q_c\, x} \} {,} \end{aligned}$$

(A.13)

being $\mathbf {r}=\left[ r_1, r_2, i r_3, i r_4 \right] ^T$.

On the other hand, the general solution of nonhomogeneous equations (8)$_2$-(8)$_5$ can be expressed as

$$\begin{aligned} \overline{\mathbf {U}}_{j}=Pe^{\Upsilon x}P^{-1}\mathbf {C}_j + P e^{\Upsilon x} \int {e^{-\Upsilon x}} \left( M P\right) ^{-1} \widetilde{\mathbf {F}}_j dx \quad \quad j=2,...,5 {,} \end{aligned}$$

(A.14)

being $\mathbf {C}_j$ the vector of arbitrary constants and the vectors $\widetilde{\mathbf {F}}_j$ $(j=2,...,5)$ are given in (9).

From the removal of secular terms at the third perturbative order, we get the real cubic GL equation

$$\begin{aligned} \frac{\partial {\Omega }}{\partial T_2}=\sigma {\Omega } - L |\Omega |^2\Omega + \nu \frac{\partial ^2 {\Omega }}{\partial X^2} {,} \end{aligned}$$

(A.15)

where the real coefficients $\sigma$, L and $\nu$ are given by:

$$\begin{aligned}&\sigma =\frac{B_2[2u_{S_c}^2(1+u_{S_c}^2)r(1+dr)+B_c(1-u_{S_c}^2)(2+dr)]}{B_cr(1-u_{S_c}^2)\Big [d-1+q_c^2d\Big (\frac{d}{\mu _0}-\frac{1}{\gamma _0}\Big )\Big ]},\nonumber \\&L=-\frac{(6r+8\alpha +4\beta )(1+dr)}{8r\Big [d-1+q_c^2d\Big (\frac{d}{\mu _0}-\frac{1}{\gamma _0}\Big )\Big ]}, \nonumber \\&\nu =\frac{4dq_c^2}{\left( B_c-q_c^2\right) \Big [d-1+q_c^2d\Big (\frac{d}{\mu _0}-\frac{1}{\gamma _0}\Big )\Big ]}, \end{aligned}$$

(A.16)

with

$$\begin{aligned} \begin{aligned}&r=\frac{q_c^2-B_c}{u_{S_c}^2}, \quad \alpha = \frac{\Big (B_c+2r u_{S_c}^2 \Big )\Big [ru_{S_c}^2+B_c\Big (1-u_{S_c}^2\Big )\Big ]}{B_c u_{S_{C} }^2\Big (u_{S_c}^2-1\Big )}, \\&\beta =\frac{\Big (B_c+2u_{S_c}^2r\Big )\Big [B_c(1+4dq_c^2)+ u_{S_c}^2 \Big (r-B_c-4q_c^2(1-dr)\Big )\Big ]}{9 B_c u_{S_c}^2 \Big ( u_{S_c}^2-1\Big )}. \end{aligned} \end{aligned}$$

(A.17)

After that, removing secular terms at $O(\epsilon ^4)$, the following compatibility equation is obtained:

$$\begin{aligned} k_1 \Omega _{XXX} + k_2 | \Omega |^2 \Omega _{X} +k_3 \Omega _{X} = 0 {,} \end{aligned}$$

(A.18)

where

$$\begin{aligned} k_1&= 4 d q_c \nu (\gamma _0 l_4 r_1 - l_3 \mu _0 r_2) - 4 d \gamma _0 \mu _0 \left[ q_c (\omega _{12} r_2 - \omega _{22} r_1) + r_2 (\omega _{32} + l_1 \nu )\right] \nonumber \\&\qquad + 4 \gamma _0 \mu _0 r_1 (\omega _{42} + l_2 \nu ) {,}\nonumber \\ k_2&= \gamma _0 \mu _0 d [r_1 r_2 (2 l_1 r_2+l_2 r_1)+4 r_2 u_{S_c} (\omega _{14} r_2+\omega _{24} r_1-l_1 m_2-l_2 m_1+2 l_1 n_2+2 l_2 n_1) \nonumber \\&\quad \quad +12 r_2 (L l_1-\omega _{31})+12 q_c (\omega _{21} r_1-\omega _{11} r_2)+4 r_2 w_{S_c} (\omega _{14} r_1-l_1 m_1+2 l_1 n_1)]\nonumber \\&\quad \quad +\gamma _0 \mu _0 [12 r_1 (\omega _{41}-L l_2)+4 r_1 u_{S_c} (2 l_2 n_1+2 l_1 n_2-l_2 m_1-l_1 m_2+\omega _{14} r_2+\omega _{24} r_1)\nonumber \\&\quad \quad +4 r_1 w_{S_c} (2 l_1 n_1-l_1 m_1+r_1 \omega _{14})+r_1^2 (l_2 r_1+2 l_1 r_2)]+12 L q_c d (l_3 r_2 \mu _0-l_4 r_1 \gamma _0) {,} \nonumber \\ k_3&= 4 \gamma _0 \mu _0 \{\sigma (l_2 r_1 - d l_1 r_2) + r_1 (\omega _{40} + d q_c \omega _{20})\nonumber \\&\quad \quad + B_2 \left[ r_1 (2 l_1 + 2 u_{S_c}\delta _1 l_2) + d r_2 (l_1 + 2 u_{S_c}\delta _1 l_2)\right] \nonumber \\&\quad \quad + - d r_2 (\omega _{30} + q_c \omega _{10})\} + 4 d q_c \sigma (\gamma _0 l_4 r_1 - l_3 \mu _0 r_2){,} \end{aligned}$$

(A.19)

being $w_{S_C}=B_c/u_{S_c}$, $\delta _1=u_{S_c}\Big (1+ u_{S_c}^2\Big )/\left[ B_c\Big (1- u_{S_c}^2\Big )\right]$ and

$$\begin{aligned} \omega _{10}= & {} {} \frac{ B_2 \left\{ E_1 \left( r_{1}+ 2 r_{2} u_{S_c} \delta _1 \right) +r_{1}^{2}\left[ 2r_{1}q_c\left( \mu _{0}-\gamma _{0}d\right) +\mu _{0}Y_{1}\left( q_c^{2}+\gamma _{0}\right) \right] \right\} }{4q_c^{2}r_{2}Y_{1}\left[ \gamma _{0}\mu _{0}\left( d-1\right) +dq_c^{2}\left( \gamma _{0}d-\mu _{0}\right) \right] } {,} \nonumber \\ \omega _{20}= & {} {} \frac{B_{2}\left( r_{1}+2r_{2} u_{S_c} \delta _1\right) \left\{ r_{1}E_{1}+2q_cY_{1}^{2}\left[ \gamma _{0}\mu _{0}\left( r_{1}+r_{2}\right) -q_c^{2}\left( \gamma _{0}d^{2}r_{2}+\mu _{0}r_{1}\right) \right] \right\} }{4q_c^{2}r_{1}^{2}Y_{1}\left[ \gamma _{0}\mu _{0}\left( d-1\right) +dq_c^{2}\left( \gamma _{0}d-\mu _{0}\right) \right] } \nonumber \\&+\frac{B_{2}\left\{ 2r_{1}^{2}q_c\left( \mu _{0}-\gamma _{0}d\right) +r_{1}\mu _{0}Y_{1}\left( q_c^{2}+\gamma _{0}\right) +2q_c\mu _{0}Y_{1}^{2}\left( \gamma _{0}-q_c^{2}\right) \right\} }{4q_c^{2}Y_{1}\left[ \gamma _{0}\mu _{0}\left( d-1\right) +dq_c^{2}\left( \gamma _{0}d-\mu _{0}\right) \right] } {,}\\ \omega _{30}= & {} {} \frac{B_{2}\left\{ \left( r_{1}+2r_{2} u_{S_c} \delta _1\right) \left[ E_{1}-4q_c^{2}\mu _{0}Y_{1}\left( r_{1}+dr_{2}\right) \right] +r_{1}^{2}\left[ 2r_{1}q_c\left( \mu _{0}-\gamma _{0}d\right) +\mu _{0}Y_{1}\left( \gamma _{0}-3q_c^{2}\right) \right] \right\} }{4q_cr_{2}Y_{1}\left[ \gamma _{0}\mu _{0}\left( d-1\right) +dq_c^{2}\left( \gamma _{0}d-\mu _{0}\right) \right] } {,} \nonumber \\ \omega _{40}= & {} {} \frac{dB_{2}\left( r_{1}+2r_{2} u_{S_c} \delta _1\right) \left\{ r_{1}E_{1}+2q_cY_{1}^{2}\left[ \gamma _{0}\mu _{0}\left( r_{1}+r_{2}\right) -q_c^{2}\left( \gamma _{0}d^{2}r_{2}+\mu _{0}r_{1}\right) \right] -4dq_c^{2}\gamma _{0}r_{1}Y_{1}\left( r_{1}+dr_{2}\right) \right\} }{4q_cr_{1}^{2}Y_{1}\left[ \gamma _{0}\mu _{0}\left( d-1\right) +dq_c^{2}\left( \gamma _{0}d-\mu _{0}\right) \right] } \nonumber \\&+\frac{dB_{2}\left\{ r_{1}^{2}\left[ 2q_c\mu _{0}Y_{1}^{2}\left( \gamma _{0}-q_c^{2}\right) +r_{1}\mu _{0}Y_{1}\left( q_c^{2}+\gamma _{0}\right) +r_{1}^{2}q_c\left( \mu _{0}-\gamma _{0}d\right) \right] -4dq_c^{2}\gamma _{0}r_{1}Y_{1}\left( r_{1}^{2}+r_{1}+dr_{2}\right) \right\} }{4q_cr_{1}^{2}Y_{1}\left[ \gamma _{0}\mu _{0}\left( d-1\right) +dq_c^{2}\left( \gamma _{0}d-\mu _{0}\right) \right] } {,}\\ \omega _{11}= & {} {} \frac{\left( 6 r_1^2 r_2+8q_{1}+4s_{1}\right) E_{1}}{32q_c^{2}r_{2}Y_{1}\left[ \gamma _{0}\mu _{0}\left( d-1\right) +dq_c^{2}\left( \gamma _{0}d-\mu _{0}\right) \right] } + \frac{r_1}{r_2}c_3 {,} \nonumber \\ \omega _{21}= & {} {} \frac{\left( 6 r_1^2 r_2+8q_{1}+4s_{1}\right) \left\{ r_{1}E_{1}+2q_cY_{1}^{2}\left[ \gamma _{0}\mu _{0}\left( r_{1}+r_{2}\right) -q_c^{2}\left( \mu _{0}r_{1}+d^{2}\gamma _{0}r_{2}\right) \right] \right\} }{32Y_{1}q_c^{2}r_{1}^{2}\left[ \gamma _{0}\mu _{0}\left( d-1\right) +dq_c^{2}\left( \gamma _{0}d-\mu _{0}\right) \right] }+c_3 {,} \nonumber \\ \omega _{31}= & {} {} \frac{\left( 6 r_1^2 r_2+8q_{1}+4s_{1}\right) \left[ E_{1}-4q_c^{2}\mu _{0}Y_{1}\left( r_{1}+dr_{2}\right) \right] }{32Y_{1}q_cr_{2}\left[ \gamma _{0}\mu _{0}\left( d-1\right) +dq_c^{2}\left( \gamma _{0}d-\mu _{0}\right) \right] }+\frac{q_c r_1}{r_2}c_3 {,} \\ \omega _{41}= & {} {} \frac{d\left( 6 r_1^2 r_2+8q_{1}+4s_{1}\right) \left\{ r_{1}E_{1}-4dq_c^{2}r_{1}\gamma _{0}Y_{1} \left( r_{1}+dr_{2}\right) + 2q_cY_{1}^{2}\left[ \gamma _{0}\mu _{0}\left( r_{1}+r_{2}\right) -q_c^{2}\left( \mu _{0}r_{1}+d^{2}\gamma _{0}r_{2}\right) \right] \right\} }{32Y_{1}q_cr_{1}^{2}\left[ \gamma _{0}\mu _{0}\left( d-1\right) +dq_c^{2}\left( \gamma _{0}d-\mu _{0}\right) \right] }\\&+d q_c c_3 {,} \nonumber \\ \omega _{12}= & {} {} - \frac{2 r_1^2 \left( \mu _0 + d \gamma _0 \right) p_{42} + Y_1 d q_c \left( q_c^2 p_{12} - \gamma _0 p_{42} \right) \left( 2 q_c Y_1 + r_1 \right) + \mu _0 Y_1 \left( q_c p_{22} - \gamma _0 p_{32} \right) \left( Y1 -r_1 \right) }{4 Y_1 q_c^2 r_1 r_2 \left[ \gamma _{0}\mu _{0}\left( d-1\right) +dq_c^{2}\left( \gamma _{0}d-\mu _{0}\right) \right] } \nonumber \\&- \frac{2 \gamma _0 r_1^2 \left( Y_1 q_c -r_1 \right) \left( d q_c l_4 - l_2 \mu _0 \right) + 2 \mu _0 r_2 d r_1 \left( \gamma _0 l_1 - l_3 q_c \right) }{4 Y_1 q_c^2 r_1 r_2 \left[ \gamma _{0}\mu _{0}\left( d-1\right) +dq_c^{2}\left( \gamma _{0}d-\mu _{0}\right) \right] }, \nonumber \\ \omega _{22}= & {} {} - \frac{ \left( 2 r_1 - Y_1 q_c \right) \left( \gamma _0 d p_{42} + \mu _0 p_{22} \right) - \mu _0 Y_1 \left( q_c r_1 p_{22} - \gamma _0 p_{32} \right) + 2 \gamma _0 r_1\left( Y_1q_c - r_1 \right) \left( d q_c l_4 - l_2 \mu _0 \right) }{4 Y_1 q_c^2 r_1 \left[ \gamma _{0}\mu _{0}\left( d-1\right) +dq_c^{2}\left( \gamma _{0}d-\mu _{0}\right) \right] } \nonumber \\&- \frac{ 2 \mu _0 r_2 d r_1 \left( \gamma _0 l_1 - l_3 q_c \right) + Y_1 d q_c^3 (r_1-1) p_{12} }{4 Y_1 q_c^2 r_1 \left[ \gamma _{0}\mu _{0}\left( d-1\right) +dq_c^{2}\left( \gamma _{0}d-\mu _{0}\right) \right] }, \nonumber \\ \omega _{32}= & {} {} - \frac{\begin{matrix} Y_1 d q_c^3 \left( 2 q_c Y_1 - 3 r_1 \right) p_{12} + \mu _0 \left[ Y_1 q_c \left( Y_1 - r_1 \right) + 10 r_1^2 \right] p_{22} - \gamma _0 \mu _0 Y_1 \left( Y_1 - 5 r_1 \right) \\ p_{32} + 10 \mu _0 r_2 d r_1 \left( \gamma _0 l_1 - l_3 q_c \right) \end{matrix} }{4 Y_1 q_c r_1 r_2 \left[ \gamma _{0}\mu _{0}\left( d-1\right) +dq_c^{2}\left( \gamma _{0}d-\mu _{0}\right) \right] } \nonumber \\&- \frac{ 10 \gamma _0 r_1 \left( Y_1 q_c{-}r_1 \right) \left( d q_c l_4{-}l_2 \mu _0 \right) {-}\gamma _0 d \left[ Y_1^2 q_c{-}5 r_1 \left( 2 r_1{-}Y_1 q_c \right) \right] p_{42}{+}4 \mu _0 r_2 Y_1 d q_c r_1 \left( l_3 q_c{+}\gamma _0 l_1 \right) }{4 Y_1 q_c r_1 r_2 \left[ \gamma _{0}\mu _{0}\left( d-1\right) +dq_c^{2}\left( \gamma _{0}d-\mu _{0}\right) \right] }, \nonumber \\ \omega _{42}= & {} {} - \frac{\begin{matrix}d \gamma _0 \left( 3 Y_1 q_c + 2 r_1 \right) p_{42} -3 Y_1 d q_c^3 p_{12} - 2 \gamma _0 \left( Y_1 q_c +r_1 \right) \left( d p_{22} + p_{12} \right) + \mu _0 \left( Y_1 \gamma _0 + 2 d r_1 q_c \right) \\ p_{32} - \mu _0 \left[ Y_1 q_c + 2 r_1 \left( d-1 \right) \right] p_{22}\end{matrix}}{4 Y_1 q_c r_1 \left[ \gamma _{0}\mu _{0}\left( d-1\right) +dq_c^{2}\left( \gamma _{0}d-\mu _{0}\right) \right] } {,} \end{aligned}$$

$$\begin{aligned} \omega _{13}= & {} {} -\frac{\left( 6 r_1^2 r_2+12s_{1}\right) \left[ dr_{2}\left( r_{1}-4Y_{1}q_c\right) +r_{1}^{2}\right] }{768dq_c^{3}r_{2}Y_{1}} {,} \nonumber \\ \omega _{23}= & {} {} -\frac{\left( 6 r_1^2 r_2+12s_{1}\right) \left[ dr_{2}+4Y_{1}q_c+r_{1}\right] }{768dq_c^{3}Y_{1}} {,} \nonumber \\ \omega _{33}= & {} {} 3q_c\omega _{13} {,} \nonumber \\ \omega _{43}= & {} {} 3dq_c\omega _{23} {,} \nonumber \\ \omega _{14}= & {} {} -\frac{2 r_1 \left[ p_{14} \left( r_1 +d r_2 \right) - 2 d r_2 p_{24} + 2 r_1 p_{34} \right] - 3 Y_1 d q_c r_2 \left( p_{14} - 2 p_{24} \right) }{9 Y_1 d q_c^3 r_2} , \nonumber \\ \omega _{24}= & {} {} - \frac{2 \left[ p_{14} \left( r_1 +d r_2 \right) - 2 d r_2 p_{24} + 2 r_1 p_{34} \right] + 3 Y_1 q_c \left( p_{14} + 2 p_{34} \right) }{9 Y_1 d q_c^3}, \nonumber \\ \omega _{34}= & {} {} -2 \left( q_c \omega _{14} + m_1 \right) , \nonumber \\ \omega _{44}= & {} {} -2 d \left( q_c \omega _{24} + m_2 \right) , \nonumber \\ \omega _{35}= & {} {} -2n_1, \nonumber \\ \omega _{45}= & {} {} -2dn_2,\nonumber \\ E_{1}= & {} {} 2q_cr_{1}\left( \mu _{0}-\gamma _{0}d\right) \left( r_{1}+dr_{2}\right) +Y_{1}\left[ \gamma _{0}\mu _{0}\left( r_{1}+r_{2}\right) +\mu _{0}q_c^{2}\left( r_{1}+dr_{2}\right) +dq_c^{2}r_{2}\left( \mu _{0}-\gamma _{0}d\right) \right] , \nonumber \\ q_{1}= & {} {} \frac{r_{1}\left( B_{c}r_{1}+2u_{S_c}^2r_{2}\right) \left[ r_{2}u_{S_c}^2+B_{c}r_{1}\left( 1-u_{S_c}^2\right) \right] }{B_{c}u_{S_c}^2\left( u_{S_c}^2-1\right) }, \nonumber \\ s_{1}= & {} {} \frac{r_{1}\left( B_{c}r_{1}+2u_{S_c}^2r_{2}\right) \left[ B_{c}r_{1}\left( 1+4dq_c^{2}\right) +u_{S_c}^2 \left( r_{2}-B_{c}r_{1}-4q_c^{2}\left( r_{1}-dr_{2}\right) \right) \right] }{9B_{c}u_{S_c}^2\left( u_{S_c}^2-1\right) }, \nonumber \\ p_{12}= & {} {} \gamma _0 l_1 r_2 d - \mu _0 l_2 r_1, \nonumber \\ p_{22}= & {} {} l_4 q_c r_1 - \gamma _0 l_1 r_2, \nonumber \\ p_{32}= & {} {} l_4 r_1 - l_3 r_2, \nonumber \\ p_{42}= & {} {} l_3 r_2 d q_c - l_2 \mu _0 r_1, \nonumber \\ p_{14}= & {} {} l_1 r_2 u_{S_c} + r_1 \left( l_2 u_{S_c} + l_1 w_{S_c} \right) , \nonumber \\ p_{24}= & {} {} m_3 +2 m_1 q_c, \nonumber \\ p_{34}= & {} {} m_4 + 2 m_2 d q_c. \nonumber \\ n_{1}= & {} {} \frac{r_{1}\left( B_{c}r_{1}+2u_{S_c}^2r_{2}\right) }{2B_{c}u_{S_{c}}\left( u_{S_c}^2-1\right) }, \nonumber \\ n_{2}= & {} {} -B_{c} n_{1} {,} \nonumber \\ m_{1}= & {} {} \frac{1+4dq_c^{2}}{9}n_{1}, \nonumber \\ m_{2}= & {} {} -\frac{B_{c}+4q_c^{2}}{9}n_{1}, \nonumber \\ m_{3}= & {} {} 2q_cm_{1}, \nonumber \\ m_{4}= & {} {} 2dq_cm_{2} {,} \nonumber \\ l_1= & {} {} - \frac{l_3 + r_1}{ q_c}, \nonumber \\ l_2= & {} {} - \frac{r_2 \left( r_1 - Y_1 q_c + l_3 \right) }{q_c r_1}, \nonumber \\ l_4= & {} {} \frac{d r_2 \left( l_3 - Y_1 q_c \right) }{ r_1}. \end{aligned}$$

(A.20)

Finally, $l_3$ and $c_3$ are implicitly given by

$$\begin{aligned}&8 h_1 \left( 3 L k_1 + \nu k_2 \right) + \gamma _0 \mu _0 k_1 h_0 \{ 4 w_{S_c} \left[ l_1 \omega _{14} + r_1 \rho _{12} + 2 r_1 \rho _{10} \right] + l_1 \left( l_1 r_2 + 2 l_2 r_1 \right) + \nonumber \\&\quad + 4 u_{S_c} \left[ l_1 \omega _{24} +l_2 \omega _{14} + r_2 \rho _{12} + r_1 \rho _{22} + 2 \left( r_1 \rho _{20} + r_2 \rho _{10} \right) \right] \} + \nonumber \\&\quad + 8 \gamma _0 \mu _0 k_1 \left[ d q_c \left( \psi _{11} r_2 - \psi _{21} r_1 \right) + \psi _{41} r_1 - d \psi _{31} r_2 \right] = 0 {,} \nonumber \\&(4 k_2 \nu +12 L k_1) h_1-4 \gamma _0 \mu _0 k_1 [d \psi _{31} r_2-\psi _{41} r_1+d q_c (\psi _{21} r_1-\psi _{11} r_2)]+ \nonumber \\&\quad -12 k_1 \nu ([\gamma _0 \mu _0 (d \omega _{11} r_2-\omega _{21} r_1)+d q_c (\gamma _0 \omega _{41} r_1-\mu _0 \omega _{31} r_2)]+ \nonumber \\&\quad +\gamma _0 \mu _0 k_1 h_0 \{3 r_1 (2 \omega _{12} r_2+\omega _{22} r_1)+4 r_1 w_{S_c} (\tau _{12}+2 \tau _{10})\nonumber \\&\quad +4 u_{S_c} [r_1 (\tau _{22}+2 \tau _{20})+r_2 (\tau _{12}+2 \tau _{10})]+ \nonumber \\&\quad +4 \omega _{12} u_{S_c} (m_2+2 n_2)+4 (m_1+2 n_1) (\omega _{22} u_{S_c}+\omega _{12} w_{S_c})\}=0 {,} \end{aligned}$$

(A.21)

where $h_0= d r_2 + r_1$ and $h_1=\gamma _0 \mu _0 \left( d \omega _{12} r_2 - \omega _{22} r_1 \right) + d q_c \left( \gamma _0 \omega _{42} r_1 - \mu _0 r_2 \omega _{32} \right)$.

Then, pushing weakly nonlinear analysis up to the fifth perturbative order, the removal of secular terms leads to the real cubic–quintic GL equation:

$$\begin{aligned} \frac{\partial \Omega }{\partial T}= \overline{\sigma } \Omega - \overline{L} |\Omega |^2\Omega + \overline{R} |\Omega |^4\Omega + \overline{\nu } \frac{\partial ^2 \Omega }{\partial X^2} {,} \end{aligned}$$

(A.22)

where $\overline{\sigma }=\sigma +\epsilon ^2 \widetilde{\sigma }$, $\overline{L}=L+\epsilon ^2 \widetilde{L}$, $\overline{\nu }=\nu +\epsilon ^2 \widetilde{\nu }$ and $\overline{R} = \epsilon ^2 \widetilde{R}$, being the second-order corrections given by

$$\begin{aligned}&\widetilde{\sigma }= \frac{\begin{matrix} \gamma _0 \mu _0 \left\{ h_0 \left[ 4 u_{S_c} \delta _1 \left( B_4 r_2 + B_2 \omega _{20} \right) + B_2^2 \delta _3 r_2 \right] + 2 \left( h_0 + r_1 \right) \left( \omega _{10} B_2 + r_1 B_4 \right) \right\} \\ + 2 \sigma \left[ \gamma _0 \mu _0 \left( d \omega _{10} r_2 - \omega _{20} r_1 \right) + d q_c \left( \gamma _0 \omega _{40} r_1 - \mu _0 \omega _{30} r_2 \right) \right] \end{matrix} }{2 r_1 r_2 \left[ \gamma _0 \mu _0 \left( d-1 \right) + d q_c^2 \left( d \gamma _0 - \mu _0 \right) \right] } {,} \\&\widetilde{L}=\frac{\begin{matrix}\gamma _0 \mu _0 \big \{12 \sigma (\omega _{21} r_1- d \omega _{11} r_2) + (r_1 + d r_2) \big [4 (2 \zeta _{10} + \zeta _{12}) (r_2 u_{S_c} + r_1 w_{S_c})\\ + 4 B_2 [2 u_{S_c} \delta _1 \omega _{21} + \delta _1 r_1 (m_2 + 2 n_2)] \end{matrix}}{4 r_1 r_2 \left[ \gamma _0 \mu _0 \left( d-1 \right) + d q_c^2 \left( d \gamma _0 - \mu _0 \right) \right] } \\&\quad + \frac{\begin{matrix}4 [\omega _{10} w_{S_c} + B_2 (\delta _1 r_2 + \delta _2 r_1)] (m_1 + 2 n_1) + 4 u_{S_c} (m_2 \omega _{10} + m_1 \omega _{20})\\ + 8 u_{S_c} (n_2 \omega _{10} + n_1 \omega _{20}) + 3 r_1 (2 \omega _{10} r_2 + \omega _{20} r_1) + 4 r_1 u_{S_c} (2 \zeta _{20} + \zeta _{22})\big ]\end{matrix}}{4 r_1 r_2 \left[ \gamma _0 \mu _0 \left( d-1 \right) + d q_c^2 \left( d \gamma _0 - \mu _0 \right) \right] } \\&\quad +\frac{\begin{matrix}4 B_2 \omega _{11} (2 r_1 + d r_2)- 4 L (\omega _{20} r_1 - d \omega _{10} r_2) \big \} + 4 L d q_c (\gamma _0 \omega _{40} r_1 - \mu _0 \omega _{30} r_2)\\ - 12 d q_c \sigma (\gamma _0 \omega _{41} r_1 - \mu _0 \omega _{31} r_2)\end{matrix}}{4 r_1 r_2 \left[ \gamma _0 \mu _0 \left( d-1 \right) + d q_c^2 \left( d \gamma _0 - \mu _0 \right) \right] } {,}\\&\widetilde{R}= \frac{\begin{matrix}12 L d q_c (\omega _{31} r_2 \mu _0-\omega _{41} r_1 \gamma _0)-\gamma _0 \mu _0 \big \{12 L (d \omega _{11} r_2-\omega _{21} r_1)\\ +4 r_1^2 [n_2 (2 n_1+m_1)+m_2 (m_1+n_1)]+4 r_1 r_2 m_1 n_1+h_0 \big [r_1^2 (\omega _{23}+3 \omega _{21})\end{matrix}}{4 r_1 r_2 \left[ \gamma _0 \mu _0 \left( d-1 \right) + d q_c^2 \left( d \gamma _0 - \mu _0 \right) \right] }+ \\&\quad \quad + \frac{\begin{matrix}4 r_1 u_{S_c} (\eta _{22}+2 \eta _{20})+2 r_2 (m_1^2+2 n_1^2)+4 m_2 u_{S_c} (\omega _{13}+\omega _{11})+2 r_1 r_2 (\omega _{13}+3 \omega _{11})\\ +4 m_1 u_{S_c} (\omega _{21}+\omega _{23})+8 u_{S_c} (n_2 \omega _{11}+n_1 \omega _{21})\end{matrix}}{4 r_1 r_2 \left[ \gamma _0 \mu _0 \left( d-1 \right) + d q_c^2 \left( d \gamma _0 - \mu _0 \right) \right] } \\&\quad + \frac{\begin{matrix}4 (\eta _{12}+2 \eta _{10}) (r_2 u_{S_c}+r_1 w_{S_c})+4 w_{S_c} [m_1 (\omega _{11}+\omega _{13})+2 n_1 \omega _{11}]\big ]\\ +4 d \big [m_1 r_2 (n_1 r_2+m_2 r_1)+r_1 r_2 (m_1 n_2+m_2 n_1+2 n_1 n_2)\big ]\big \}\end{matrix}}{4 r_1 r_2 \left[ \gamma _0 \mu _0 \left( d-1 \right) + d q_c^2 \left( d \gamma _0 - \mu _0 \right) \right] } {,} \\&\widetilde{\nu }= \frac{B_2 \gamma _0 \mu _0 k_1 \left[ \omega _{12} \left( h_0 + r_1 \right) + 2 u_{S_c} \delta _1 \omega _{22} h_0 \right] - h_1 \left( k_1 \sigma - k_3 \nu \right) }{k_1 r_1 r_2 \left[ \gamma _0 \mu _0 \left( d-1 \right) + d q_c^2 \left( d \gamma _0 - \mu _0 \right) \right] } \\&\quad -\frac{\begin{matrix} k_1 \big \{ \nu d q_c \left[ \gamma _0 \omega _{40} r_1 - \mu _0 \omega _{30} r_2 \right] + \mu _0 \gamma _0 \big [ d q_c \left( r_1 \rho _{21} - r_2 \rho _{11} \right) + \nu \left( d \omega _{10} r_2 - \omega _{20} r_1 \right) \\ + d r_2 \rho _{31} - r_1 \rho _{41} \big ] \big \} \end{matrix}}{k_1 r_1 r_2 \left[ \gamma _0 \mu _0 \left( d-1 \right) + d q_c^2 \left( d \gamma _0 - \mu _0 \right) \right] }{,} \end{aligned}$$

where the coefficients here appearing are given implicitly by

$$\begin{aligned}&\omega _{14} + \rho _{32} - 2 q_c \rho _{12}=0 {,} \\&k_1 l_3 + \gamma _0 k_1 \omega _{10} - \gamma _0 k_3 \omega _{12} + \gamma _0 k_1 \rho _{31} + \gamma _0 k_1 q_c \rho _{11}=0 {,} \\&3 k_1 \omega _{11} - 9 k_1 \omega _{13} - k_2 \omega _{12} + k_1 \psi _{31} - 3 k_1 \psi _{33} + k_1 q_c \psi _{11} - 9 k_1 q_c \psi _{13}=0 {,} \\&3 \omega _{13} + \psi _{33} + 3 q_c \psi _{13}=0 {,} \\&\eta _{34} - 4 \eta _{14} q_c=0 {,} \\&2 m_3 \sigma + \gamma _0 \zeta _{32} - 2 \gamma _0 q_c \zeta _{12}=0 {,} \\&\gamma _0 \omega _{14} + \gamma _0 \tau _{32} + 2 m_3 \nu - 2 \gamma _0 q_c \tau _{12}=0 {,} \\&\eta _{32} \gamma _0 - 2 L m_3 - 2 \eta _{34} \gamma _0 - 2 \eta _{12} \gamma _0 q_c + 8 \eta _{14} \gamma _0 q_c=0 {,} \\&\rho _{42} + d \omega _{24} - 2 d q_c \rho _{22}=0 {,} \\&d k_1 l_4 + k_1 \mu _0 \rho _{41} + d k_1 \mu _0 \omega _{20} - d k_3 \mu _0 \omega _{22} + d k_1 q_c \mu _0 \rho _{21}=0 {,} \\&k_1 \psi _{41} - 3 k_1 \psi _{43} + 3 d k_1 \omega _{21} - 9 d k_1 \omega _{23} - d k_2 \omega _{22} + d k_1 q_c \psi _{21} - 9 d k_1 q_c \psi _{23}=0 {,} \\&\psi _{43} + 3 d \omega _{23} + 3 d q_c \psi _{23}=0 {,} \\&\eta _{42} \mu _0 - 2 \eta _{44} \mu _0 - 2 L d m_4 - 2 d \eta _{22} q_c \mu _0 + 8 d \eta _{24} q_c \mu _0=0 {,} \\&\eta _{44} - 4 d \eta _{24} q_c=0 {,} \\&\mu _0 \zeta _{42} + 2 d m_4 \sigma - 2 d q_c \mu _0 \zeta _{22}=0 {,} \\&\mu _0 \tau _{42} + 2 d m_4 \nu + d \mu _0 \omega _{24} - 2 d q_c \mu _0 \tau _{22}=0 {,} \\&2 \omega _{34} u_{S_c} + B_c l_1^2 - 2 \rho _{22} u_{S_c}^3 + 2 l_1 l_2 u_{S_c}^2 - 2 B_c \rho _{12} u_{S_c} + 4 q_c \rho _{32} u_{S_c}=0 {,} \\&\omega _{35} u_{S_c} - \omega _{34} u_{S_c} - B_c l_1^2 - \rho _{20} u_{S_c}^3 + \rho _{22} u_{S_c}^3 - 2 l_1 l_2 u_{S_c}^2 - B_c \rho _{10} u_{S_c} + B_c \rho _{12} u_{S_c} - 2 q_c \rho _{32} u_{S_c}=0 {,} \\&\quad - k_1 \rho _{21} u_{S_c}^2 + k_1 l_1 + k_1 \omega _{30} - k_3 \omega _{32} - B_2 k_1 l_1 - B_c k_1 \rho _{11} - k_1 q_c \rho _{31} - B_2 2 u_{S_c} \delta _1 k_1 l_2=0 {,} \\&k_1 \psi _{23} u_{S_c}^3 - k_1 \psi _{21} u_{S_c}^3 + 3 k_1 \omega _{31} u_{S_c} - 3 k_1 \omega _{33} u_{S_c} - k_2 \omega _{32} u_{S_c} - k_1 q_c \psi _{31} u_{S_c} + 3 k_1 q_c \psi _{33} u_{S_c} + \\&\quad + 2 k_1 l_1 m_2 u_{S_c}^2 + 2 k_1 l_2 m_1 u_{S_c}^2 - 2 k_1 l_1 n_2 u_{S_c}^2 - 2 k_1 l_2 n_1 u_{S_c}^2 + 2 B_c k_1 l_1 m_1 - 2 B_c k_1 l_1 n_1 + \\&\quad - B_c k_1 \psi _{11} u_{S_c} + B_c k_1 \psi _{13} u_{S_c}=0 {,} \\&12 \omega _{33} u_{S_c} - 4 \psi _{23} u_{S_c}^3 - 4 l_1 m_2 u_{S_c}^2 - 4 l_2 m_1 u_{S_c}^2 - l_2 r_1^2 u_{S_c} - 4 \omega _{14} r_2 u_{S_c}^2 - 4 \omega _{24} r_1 u_{S_c}^2 - 4 B_c l_1 m_1+ \\&\quad - 4 B_c \omega _{14} r_1 - 4 B_c \psi _{13} u_{S_c} - 12 q_c \psi _{33} u_{S_c} - 2 l_1 r_1 r_2 u_{S_c}=0 {,} \\&16 \eta _{34} q_c u_{S_c} - 4 \eta _{24} u_{S_c}^3 - 4 m_1 m_2 u_{S_c}^2 - m_2 r_1^2 u_{S_c} - 4 \omega _{13} r_2 u_{S_c}^2 - 4 \omega _{23} r_1 u_{S_c}^2 - 4 B_c \eta _{14} u_{S_c} + \\&\quad - 4 B_c \omega _{13} r_1 - 2 B_c m_1^2 - 2 m_1 r_1 r_2 u_{S_c}=0 {,} \\&4 B_c m_1^2 - 2 \eta _{22} u_{S_c}^3 + 8 \eta _{24} u_{S_c}^3 + 8 m_1 m_2 u_{S_c}^2 - 4 m_1 n_2 u_{S_c}^2 - 4 m_2 n_1 u_{S_c}^2 + m_2 r_1^2 u_{S_c} - n_2 r_1^2 u_{S_c}+ \\&\quad - 2 \omega _{11} r_2 u_{S_c}^2 + 6 \omega _{13} r_2 u_{S_c}^2 - 2 \omega _{21} r_1 u_{S_c}^2 + 6 \omega _{23} r_1 u_{S_c}^2 - 2 B_c \eta _{12} u_{S_c} + 8 B_c \eta _{14} u_{S_c} - 4 B_c m_1 n_1 + \\&\quad - 2 B_c \omega _{11} r_1 + 6 B_c \omega _{13} r_1 - 4 L m_1 u_{S_c} + 4 \eta _{32} q_c u_{S_c} - 32 \eta _{34} q_c u_{S_c} + 2 m_1 r_1 r_2 u_{S_c} - 2 n_1 r_1 r_2 u_{S_c}=0 {,} \\&\eta _{22} u_{S_c}^3 - B_c n_1^2 - \eta _{20} u_{S_c}^3 - B_c m_1^2 - \eta _{24} u_{S_c}^3 - 2 m_1 m_2 u_{S_c}^2 + 2 m_1 n_2 u_{S_c}^2 + 2 m_2 n_1 u_{S_c}^2 - 2 n_1 n_2 u_{S_c}^2 \\&\quad - B_c \eta _{10} u_{S_c}{+}B_c \eta _{12} u_{S_c}{-}B_c \eta _{14} u_{S_c}{+}2 B_c m_1 n_1{+}2 L m_1 u_{S_c}{-}2 L n_1 u_{S_c} - 2 \eta _{32} q_c u_{S_c} + 4 \eta _{34} q_c u_{S_c}=0 {,} \\&4 m_1 \sigma u_{S_c} - 2 \omega _{10} r_2 u_{S_c}^2 - 2 \omega _{20} r_1 u_{S_c}^2 - 2 B_c \omega _{10} r_1 - 2 B_2 m_1 u_{S_c} - 2 B_c u_{S_c} \zeta _{12} - 2 u_{S_c}^3 \zeta _{22} + 4 q_c u_{S_c} \zeta _{32} + \\&\quad - B_2 \delta _2 r_1^2 u_{S_c} - 2 B_2 2 u_{S_c} \delta _1 m_2 u_{S_c} - 2 B_2 \delta _1 r_1 r_2 u_{S_c}=0 {,} \\&B_2 m_1 - B_2 n_1 - B_c \zeta _{10} + B_c \zeta _{12} - 2 m_1 \sigma + 2 n_1 \sigma - 2 q_c \zeta _{32} - u_{S_c}^2 \zeta _{20} + u_{S_c}^2 \zeta _{22} + \\&\quad + B_2 2 u_{S_c} \delta _1 m_2 - B_2 2 u_{S_c} \delta _1 n_2=0 {,} \\&\omega _{34} u_{S_c} - \tau _{22} u_{S_c}^3 - \omega _{12} r_2 u_{S_c}^2 - \omega _{22} r_1 u_{S_c}^2 - B_c \omega _{12} r_1 - B_c \tau _{12} u_{S_c} + 2 m_1 \nu u_{S_c} + 2 q_c \tau _{32} u_{S_c}=0 {,} \\&\omega _{35} - \omega _{34} - B_c \tau _{10} + B_c \tau _{12} - 2 m_1 \nu + 2 n_1 \nu - 2 q_c \tau _{32} - \tau _{20} u_{S_c}^2 + \tau _{22} u_{S_c}^2=0 {,} \\&2 \omega _{44} u_{S_c} + 2 \rho _{22} u_{S_c} - B_c l_1^2 + 2 \rho _{22} u_{S_c}^3 - 2 l_1 l_2 u_{S_c}^2 + 4 B_c \rho _{12} u_{S_c} + 4 q_c \rho _{42} u_{S_c}=0 {,} \\&\omega _{45} u_{S_c} - \omega _{44} u_{S_c} + \rho _{20} u_{S_c} - \rho _{22} u_{S_c} + B_c l_1^2 + \rho _{20} u_{S_c}^3 - \rho _{22} u_{S_c}^3 + 2 l_1 l_2 u_{S_c}^2 + 2 B_c \rho _{10} u_{S_c}+ \\&\quad - 2 B_c \rho _{12} u_{S_c} - 2 q_c \rho _{42} u_{S_c}=0{,} \\&k_1 \rho _{21} u_{S_c}^2 + k_1 l_2 + k_1 \omega _{40} - k_3 \omega _{42} + k_1 \rho _{21} + 2 B_2 k_1 l_1 + 2 B_c k_1 \rho _{11} - k_1 q_c \rho _{41} + B_2 2 u_{S_c} \delta _1 k_1 l_2=0 {,} \\&k_1 \psi _{21} u_{S_c}^3 - k_1 \psi _{23} u_{S_c}^3 + 3 k_1 \omega _{41} u_{S_c} - 3 k_1 \omega _{43} u_{S_c} - k_2 \omega _{42} u_{S_c} + k_1 \psi _{21} u_{S_c} - k_1 \psi _{23} u_{S_c} - k_1 q_c \psi _{41} u_{S_c} + \\&\quad + 3 k_1 q_c \psi _{43} u_{S_c} - 2 k_1 l_1 m_2 u_{S_c}^2 - 2 k_1 l_2 m_1 u_{S_c}^2 + 2 k_1 l_1 n_2 u_{S_c}^2 + 2 k_1 l_2 n_1 u_{S_c}^2 - 2 B_c k_1 l_1 m_1 + 2 B_c k_1 l_1 n_1 + \\&\quad +2 B_c k_1 \psi _{11} u_{S_c} - 2 B_c k_1 \psi _{13} u_{S_c}=0 {,} \\&12 \omega _{43} u_{S_c} + 4 \psi _{23} u_{S_c} + 4 \psi _{23} u_{S_c}^3 + 4 l_1 m_2 u_{S_c}^2 + 4 l_2 m_1 u_{S_c}^2 + l_2 r_1^2 u_{S_c} + 4 \omega _{14} r_2 u_{S_c}^2 + 4 \omega _{24} r_1 u_{S_c}^2 + \\&\quad + 4 B_c l_1 m_1 + 4 B_c \omega _{14} r_1 + 8 B_c \psi _{13} u_{S_c} - 12 q_c \psi _{43} u_{S_c} + 2 l_1 r_1 r_2 u_{S_c}=0 {,} \\&4 \eta _{24} u_{S_c} + 2 B_c m_1^2 + 4 \eta _{24} u_{S_c}^3 + 4 m_1 m_2 u_{S_c}^2 + m_2 r_1^2 u_{S_c} + 4 \omega _{13} r_2 u_{S_c}^2 + 4 \omega _{23} r_1 u_{S_c}^2 + 8 B_c \eta _{14} u_{S_c} + \\&\quad + 4 B_c \omega _{13} r_1 + 16 \eta _{44} q_c u_{S_c} + 2 m_1 r_1 r_2 u_{S_c}=0 {,} \\&2 \eta _{22} u_{S_c} - 8 \eta _{24} u_{S_c} - 4 B_c m_1^2 + 2 \eta _{22} u_{S_c}^3 - 8 \eta _{24} u_{S_c}^3 - 8 m_1 m_2 u_{S_c}^2 + 4 m_1 n_2 u_{S_c}^2 + 4 m_2 n_1 u_{S_c}^2 + \\&\quad - m_2 r_1^2 u_{S_c} + n_2 r_1^2 u_{S_c} + 2 \omega _{11} r_2 u_{S_c}^2 - 6 \omega _{13} r_2 u_{S_c}^2 + 2 \omega _{21} r_1 u_{S_c}^2 - 6 \omega _{23} r_1 u_{S_c}^2 + 4 B_c \eta _{12} u_{S_c} + \\&\quad - 16 B_c \eta _{14} u_{S_c} + 4 B_c m_1 n_1 + 2 B_c \omega _{11} r_1 - 6 B_c \omega _{13} r_1 - 4 L m_2 u_{S_c} + 4 \eta _{42} q_c u_{S_c} - 32 \eta _{44} q_c u_{S_c}+ \\&\quad - 2 m_1 r_1 r_2 u_{S_c} + 2 n_1 r_1 r_2 u_{S_c}=0 {,} \\&\eta _{20} u_{S_c} - \eta _{22} u_{S_c} + \eta _{24} u_{S_c} + B_c m_1^2 + B_c n_1^2 + \eta _{20} u_{S_c}^3 - \eta _{22} u_{S_c}^3 + \eta _{24} u_{S_c}^3 + 2 m_1 m_2 u_{S_c}^2 - 2 m_1 n_2 u_{S_c}^2 + \\&\quad - 2 m_2 n_1 u_{S_c}^2 + 2 n_1 n_2 u_{S_c}^2 + 2 B_c \eta _{10} u_{S_c} - 2 B_c \eta _{12} u_{S_c} + 2 B_c \eta _{14} u_{S_c} - 2 B_c m_1 n_1 + 2 L m_2 u_{S_c}+ \\&\quad - 2 L n_2 u_{S_c} - 2 \eta _{42} q_c u_{S_c} + 4 \eta _{44} q_c u_{S_c}=0 {,} \\&2 u_{S_c} \zeta _{22} + 2 u_{S_c}^3 \zeta _{22} + 2 \omega _{10} r_2 u_{S_c}^2 + 2 \omega _{20} r_1 u_{S_c}^2 + 2 B_c \omega _{10} r_1 + 4 B_2 m_1 u_{S_c} + 4 B_c u_{S_c} \zeta _{12} + 4 m_2 \sigma u_{S_c} + \\&\quad + 4 q_c u_{S_c} \zeta _{42} + B_2 \delta _2 r_1^2 u_{S_c} + 2 B_2 2 u_{S_c} \delta _1 m_2 u_{S_c} + 2 B_2 \delta _1 r_1 r_2 u_{S_c}=0 {,} \\&\zeta _{20} - \zeta _{22} - 2 B_2 m_1 + 2 B_2 n_1 + 2 B_c \zeta _{10} - 2 B_c \zeta _{12} - 2 m_2 \sigma + 2 n_2 \sigma - 2 q_c \zeta _{42} + u_{S_c}^2 \zeta _{20} - u_{S_c}^2 \zeta _{22} + \\&\quad - B_2 2 u_{S_c} \delta _1 m_2 + B_2 2 u_{S_c} \delta _1 n_2=0 {,} \\&\omega _{44} u_{S_c}{+}\tau _{22} u_{S_c}{+}\tau _{22} u_{S_c}^3 + \omega _{12} r_2 u_{S_c}^2 + \omega _{22} r_1 u_{S_c}^2{+}B_c \omega _{12} r_1 + 2 B_c \tau _{12} u_{S_c} + 2 m_2 \nu u_{S_c} + 2 q_c \tau _{42} u_{S_c}=0 {,} \\&\omega _{45} - \omega _{44} + \tau _{20} - \tau _{22} + 2 B_c \tau _{10} - 2 B_c \tau _{12} - 2 m_2 \nu + 2 n_2 \nu - 2 q_c \tau _{42} + \tau _{20} u_{S_c}^2 - \tau _{22} u_{S_c}^2=0 {} \\ \end{aligned}$$

and $\delta _2=-2 u_{S_c}/\left( 1- u_{S_c}^2\right)$.