Article contents
Scattering rigidity with trapped geodesics
Published online by Cambridge University Press: 04 January 2013
Abstract
We prove that the flat product metric on 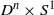 ${D}^{n} \times {S}^{1} $ is scattering rigid where
${D}^{n} \times {S}^{1} $ is scattering rigid where 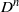 ${D}^{n} $ is the unit ball in
${D}^{n} $ is the unit ball in 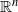 ${ \mathbb{R} }^{n} $ and
${ \mathbb{R} }^{n} $ and 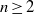 $n\geq 2$. The scattering data (loosely speaking) of a Riemannian manifold with boundary is the map
$n\geq 2$. The scattering data (loosely speaking) of a Riemannian manifold with boundary is the map 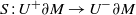 $S: {U}^{+ } \partial M\rightarrow {U}^{- } \partial M$ from unit vectors
$S: {U}^{+ } \partial M\rightarrow {U}^{- } \partial M$ from unit vectors 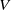 $V$ at the boundary that point inward to unit vectors at the boundary that point outwards. The map (where defined) takes
$V$ at the boundary that point inward to unit vectors at the boundary that point outwards. The map (where defined) takes 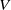 $V$ to
$V$ to 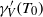 ${ \gamma }_{V}^{\prime } ({T}_{0} )$ where
${ \gamma }_{V}^{\prime } ({T}_{0} )$ where 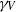 ${\gamma }_{V} $ is the unit speed geodesic determined by
${\gamma }_{V} $ is the unit speed geodesic determined by 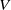 $V$ and
$V$ and 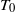 ${T}_{0} $ is the first positive value of
${T}_{0} $ is the first positive value of  $t$ (when it exists) such that
$t$ (when it exists) such that 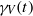 ${\gamma }_{V} (t)$ again lies in the boundary. We show that any other Riemannian manifold
${\gamma }_{V} (t)$ again lies in the boundary. We show that any other Riemannian manifold 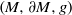 $(M, \partial M, g)$ with boundary
$(M, \partial M, g)$ with boundary 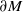 $\partial M$ isometric to
$\partial M$ isometric to 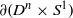 $\partial ({D}^{n} \times {S}^{1} )$ and with the same scattering data must be isometric to
$\partial ({D}^{n} \times {S}^{1} )$ and with the same scattering data must be isometric to 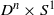 ${D}^{n} \times {S}^{1} $. This is the first scattering rigidity result for a manifold that has a trapped geodesic. The main issue is to show that the unit vectors tangent to trapped geodesics in
${D}^{n} \times {S}^{1} $. This is the first scattering rigidity result for a manifold that has a trapped geodesic. The main issue is to show that the unit vectors tangent to trapped geodesics in 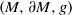 $(M, \partial M, g)$ have measure zero in the unit tangent bundle.
$(M, \partial M, g)$ have measure zero in the unit tangent bundle.
- Type
- Research Article
- Information
- Copyright
- ©2013 Cambridge University Press
References
- 6
- Cited by




