Hostname: page-component-8448b6f56d-m8qmq Total loading time: 0 Render date: 2024-04-24T13:36:11.425Z Has data issue: false hasContentIssue false
  • English
  • Français

Effect of fluid inertia on the dynamics and scaling of neutrally buoyant particles in shear flow

Published online by Cambridge University Press:  13 December 2013

T. Rosén ,
F. Lundell  and
C. K. Aidun
T. Rosén
Affiliation:
Linné FLOW Centre, KTH Mechanics, Royal Institute of Technology, SE-100 44 Stockholm, Sweden
F. Lundell
Affiliation:
Linné FLOW Centre, KTH Mechanics, Royal Institute of Technology, SE-100 44 Stockholm, Sweden Wallenberg Wood Science Center, Royal Institute of Technology, SE-100 44 Stockholm, Sweden
C. K. Aidun*
Affiliation:
George W. Woodruff School of Mechanical Engineering and Parker H. Petit Institute for Bioengineering and Bioscience 801 Ferst Drive, Georgia Institute of Technology, Atlanta, GA 30332-0405, USA
*
†Email address for correspondence: cyrus.aidun@me.gatech.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

The basic dynamics of a prolate spheroidal particle suspended in shear flow is studied using lattice Boltzmann simulations. The spheroid motion is determined by the particle Reynolds number (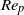${\mathit{Re}}_{p} $) and Stokes number (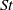$\mathit{St}$), estimating the effects of fluid and particle inertia, respectively, compared with viscous forces on the particle. The particle Reynolds number is defined by 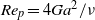${\mathit{Re}}_{p} = 4G{a}^{2} / \nu $, where 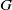$G$ is the shear rate, $a$ is the length of the spheroid major semi-axis and $\nu $ is the kinematic viscosity. The Stokes number is defined as 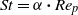$\mathit{St}= \alpha \boldsymbol{\cdot} {\mathit{Re}}_{p} $, where $\alpha $ is the solid-to-fluid density ratio. Here, a neutrally buoyant prolate spheroidal particle (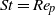$\mathit{St}= {\mathit{Re}}_{p} $) of aspect ratio (major axis/minor axis) 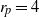${r}_{p} = 4$ is considered. The long-term rotational motion for different initial orientations and 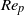${\mathit{Re}}_{p} $ is explained by the dominant inertial effect on the particle. The transitions between rotational states are subsequently studied in detail in terms of nonlinear dynamics. Fluid inertia is seen to cause several bifurcations typical for a nonlinear system with odd symmetry around a double zero eigenvalue. Particle inertia gives rise to centrifugal forces which drives the particle to rotate with the symmetry axis in the flow-gradient plane (tumbling). At high 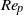${\mathit{Re}}_{p} $, the motion is constrained to this planar motion regardless of initial orientation. At a certain critical Reynolds number, 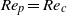${\mathit{Re}}_{p} = {\mathit{Re}}_{c} $, a motionless (steady) state is created through an infinite-period saddle-node bifurcation and consequently the tumbling period near the transition is scaled as 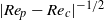$\vert {\mathit{Re}}_{p} - {\mathit{Re}}_{c} {\vert }^{- 1/ 2} $. Analyses in this paper show that if a transition from tumbling to steady state occurs at 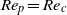${\mathit{Re}}_{p} = {\mathit{Re}}_{c} $, then any parameter 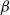$\beta $ (e.g. confinement or particle spacing) that influences the value of 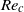${\mathit{Re}}_{c} $, such that 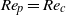${\mathit{Re}}_{p} = {\mathit{Re}}_{c} $ as 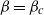$\beta = {\beta }_{c} $, will lead to a period that scales as $\vert \beta - {\beta }_{c} {\vert }^{- 1/ 2} $ and is independent of particle shape or any geometric aspect ratio in the flow.

JFM classification

Complex Fluids: Complex Fluids Multiphase and Particle-laden Flows: Multiphase and Particle-laden Flows Nonlinear Dynamical Systems: Nonlinear Dynamical Systems
Type
Papers
Information
Journal of Fluid Mechanics , Volume 738 , 10 January 2014 , pp. 563 - 590
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aidun, C. K. & Ding, E.-J. 1997 Computational analysis of suspensions in high shear blade coaters. In Euromech 367, Fluid Mechanics of Coating Processes, Proceedings of the Second European Coating Symposium (ECS’97), 22–25 July (ed. P. Bourgin), p. 63. Universite Louis Pasteur, France.Google Scholar
Aidun, C. K. & Lu, Y. 1995 Lattice Boltzmann simulation of solid particles suspended in fluid. J. Stat. Mech. 81, 49–61.Google Scholar
Aidun, C. K., Lu, Y. & Ding, E.-J. 1997 Dynamic simulation of particles suspended in fluid. In The 1997 ASME Fluids Engineering Division Summer Meeting, (FEDSM’97), 22–26 June.Google Scholar
Aidun, C. K., Lu, Y. & Ding, E.-J. 1998 Direct analysis of particulate suspensions with inertia using the discrete Boltzmann equation. J. Fluid Mech. 373, 287–311.Google Scholar
Binder, R. C. 1939 The motion of cylindrical particles in viscous flow. J. Appl. Phys. 10, 711–713.Google Scholar
Bossis, G. & Brady, J. F. 1984 Dynamic simulation of sheared suspensions. J. Chem. Phys. 80, 5141–5154.Google Scholar
Brady, J. F. & Bossis, G. 1988 Stokesian dynamics. Annu. Rev. Fluid Mech. 20, 111–157.Google Scholar
Bretherton, F. P. 1961 Slow viscous motion round a cylinder in a simple shear. J. Fluid Mech. 12, 591–613.Google Scholar
Dellar, P. J. 2001 Bulk and shear viscosities in lattice Boltzmann equations. Phys. Rev. E 64, 031203.Google Scholar
Ding, E.-J. & Aidun, C. K. 2000 The dynamics and scaling law for particles suspended in shear flow with inertia. J. Fluid. Mech. 423, 317–344.Google Scholar
Goldsmith, H. L. & Mason, S. G. 1961 Particle motions in sheared suspensions XIII. The spin and rotation of disks. J. Fluid. Mech. 12, 88–96.Google Scholar
Hale, J. & Koçak, H. 1991 Dynamics and Bifurcations, Texts in Applied Mathematics, vol. 3, Springer.Google Scholar
Huang, H., Yang, X., Krafczyk, M. & Lu, X.-Y. 2012 Rotation of spheroidal particles in Couette flows. J. Fluid. Mech. 692, 369–394.Google Scholar
Jeffery, G. B. 1922 The motion of ellipsoidal particles immersed in a viscous fluid. Proc. R. Soc. Lond. A 102, 161–179.Google Scholar
Karnis, A., Goldsmith, H. L. & Mason, S. G. 1963 Axial migration of particles in Poiseuille flow. Nature 200, 159–160.Google Scholar
Karnis, A., Goldsmith, H. L. & Mason, S. G. 1966 The flow of suspensions through tubes, V. Inertial effects. Can. J. Chem. Engng 44, 181–193.Google Scholar
Ladd, A. J. C. 1994a Numerical simulations of particulate suspensions via a discretized Boltzmann equation, part 1. Theoretical foundation. J. Fluid. Mech. 271, 285–309.Google Scholar
Ladd, A. J. C. 1994b Numerical simulations of particulate suspensions via a discretized Boltzmann equation, part 2. Numerical results. J. Fluid. Mech. 271, 311–339.Google Scholar
Ladd, A. J. C. 1996 Hydrodynamic screening in sedimenting suspensions of non-Brownian spheres. Phys. Rev. Lett. 76, 1392–1395.Google Scholar
Ladd, A. J. C. 1997 Sedimentation of homogeneous suspensions of non-Brownian spheres. Phys. Fluids 9, 491–499.Google Scholar
Leal, L. G. 1980 Particle motions in a viscous fluid. Annu. Rev. Fluid Mech. 12, 435–476.Google Scholar
Lichtenberg, A. J. & Lieberman, M. A. 1992 Regular and Chaotic Dynamics, Applied Mathematical Sciences, vol. 38, Springer.Google Scholar
Lundell, F. & Carlsson, A. 2010 Heavy ellipsoids in creeping shear flow: transitions of the particle rotation rate and orbit shape. Phys. Rev. E 81, 016323.Google Scholar
Mason, S. G. & Manley, R. St J. 1956 Particle motions in sheared suspensions: orientations and interactions of rigid rods. Proc. R. Soc. Lond. A 238, 117–131.Google Scholar
McNamara, G. R. & Zanetti, G. 1988 Use of the Boltzmann equation to simulate lattice-gas automata. Phys. Rev. Lett. 61, 2332–2335.Google Scholar
Saffman, P. G. 1956 On the motion of small spheroidal particles in a viscous liquid. J. Fluid. Mech. 1, 540–553.Google Scholar
Strogatz, S. H. 1994 Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering. Westview Press.Google Scholar
Taylor, G. I. 1923 The motion of ellipsoidal particles in a viscous fluid. Proc. R. Soc. Lond. A 103, 58–61.Google Scholar
Wu, J. & Aidun, C. K. 2010 Simulating 3D deformable particle suspensions using lattice Boltzmann method with discrete external boundary force. Intl J. Numer. Meth. Flow 62, 765–783.Google Scholar
Yu, Z., Phan-Thien, N. & Tanner, R. I. 2007 Rotation of a spheroid in a Couette flow at moderate Reynolds numbers. Phys. Rev. E 76, 026310.Google Scholar
Zettner, C. M. & Yoda, M. 2001 Moderate aspect ratio elliptical cylinders in simple shear with inertia. J. Fluid. Mech. 442, 241–266.Google Scholar