It is well known that, under inertialess conditions, the orientation vector of a torque-free neutrally buoyant spheroid in an ambient simple shear flow rotates along so-called Jeffery orbits, a one-parameter family of closed orbits on the unit sphere centred around the direction of the ambient vorticity (Jeffery, Proc. R. Soc. Lond. A, vol. 102, 1922, pp. 161–179). We characterize analytically the irreversible drift in the orientation of such torque-free spheroidal particles of an arbitrary aspect ratio, across Jeffery orbits, that arises due to weak inertial effects. The analysis is valid in the limit 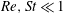$Re,St\ll 1$, where 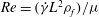$Re=(\dot{{\it\gamma}}L^{2}{\it\rho}_{f})/{\it\mu}$ and 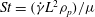$St=(\dot{{\it\gamma}}L^{2}{\it\rho}_{p})/{\it\mu}$ are the Reynolds and Stokes numbers, which, respectively, measure the importance of fluid inertial forces and particle inertia in relation to viscous forces at the particle scale. Here, 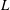$L$ is the semimajor axis of the spheroid, 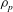${\it\rho}_{p}$ and 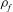${\it\rho}_{f}$ are the particle and fluid densities, 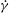$\dot{{\it\gamma}}$ is the ambient shear rate, and 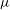${\it\mu}$ is the suspending fluid viscosity. A reciprocal theorem formulation is used to obtain the contributions to the drift due to particle and fluid inertia, the latter in terms of a volume integral over the entire fluid domain. The resulting drifts in orientation at 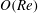$O(Re)$ and 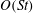$O(St)$ are evaluated, as a function of the particle aspect ratio, for both prolate and oblate spheroids using a vector spheroidal harmonics formalism. It is found that particle inertia, at 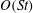$O(St)$, causes a prolate spheroid to drift towards an eventual tumbling motion in the flow–gradient plane. Oblate spheroids, on account of the 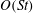$O(St)$ drift, move in the opposite direction, approaching a steady spinning motion about the ambient vorticity axis. The period of rotation in the spinning mode must remain unaltered to all orders in 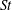$St$. For the tumbling mode, the period remains unaltered at 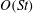$O(St)$. At 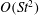$O(St^{2})$, however, particle inertia speeds up the rotation of prolate spheroids. The 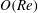$O(Re)$ drift due to fluid inertia drives a prolate spheroid towards a tumbling motion in the flow–gradient plane for all initial orientations and for all aspect ratios. Interestingly, for oblate spheroids, there is a bifurcation in the orientation dynamics at a critical aspect ratio of approximately 0.14. Oblate spheroids with aspect ratios greater than this critical value drift in a direction opposite to that for prolate spheroids, and eventually approach a spinning motion about the ambient vorticity axis starting from any initial orientation. For smaller aspect ratios, a pair of non-trivial repelling orbits emerge from the flow–gradient plane, and divide the unit sphere into distinct basins of orientations that asymptote to the tumbling and spinning modes. With further decrease in the aspect ratio, these repellers move away from the flow–gradient plane, eventually coalescing onto an arc of the great circle in which the gradient–vorticity plane intersects the unit sphere, in the limit of a vanishing aspect ratio. Thus, sufficiently thin oblate spheroids, similar to prolate spheroids, drift towards an eventual tumbling motion irrespective of their initial orientation. The drifts at 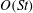$O(St)$ and at 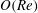$O(Re)$ are combined to obtain the drift for a neutrally buoyant spheroid. The particle inertia contribution remains much smaller than the fluid inertia contribution for most aspect ratios and density ratios of order unity. As a result, the critical aspect ratio for the bifurcation in the orientation dynamics of neutrally buoyant oblate spheroids changes only slightly from its value based only on fluid inertia. The existence of Jeffery orbits implies a rheological indeterminacy, and the dependence of the suspension shear viscosity on initial conditions. For prolate spheroids and oblate spheroids of aspect ratio greater than 0.14, inclusion of inertia resolves the indeterminacy. Remarkably, the existence of the above bifurcation implies that, for a dilute suspension of oblate spheroids with aspect ratios smaller than 0.14, weak stochastic fluctuations (residual Brownian motion being analysed here as an example) play a crucial role in obtaining a shear viscosity independent of the initial orientation distribution. The inclusion of Brownian motion leads to a new smaller critical aspect ratio of approximately 0.013. For sufficiently large 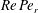$Re\,Pe_{r}$, the peak in the steady-state orientation distribution shifts rapidly from the spinning- to the tumbling-mode location as the spheroid aspect ratio decreases below this critical value; here, 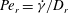$Pe_{r}=\dot{{\it\gamma}}/D_{r}$, with 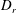$D_{r}$ being the Brownian rotary diffusivity, so that 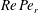$Re\,Pe_{r}$ measures the relative importance of inertial drift and Brownian rotary diffusion. The shear viscosity, plotted as a function of 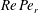$Re\,Pe_{r}$, exhibits a sharp transition from a shear-thickening to a shear-thinning behaviour, as the oblate spheroid aspect ratio decreases below 0.013. Our results are compared in detail to earlier analytical work for limiting cases involving either nearly spherical particles or slender fibres with weak inertia, and to the results of recent numerical simulations at larger values of 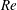$Re$ and $St$.