Hostname: page-component-848d4c4894-75dct Total loading time: 0 Render date: 2024-05-08T05:09:22.153Z Has data issue: false hasContentIssue false
  • English
  • Français

Genesis and evolution of velocity gradients in near-field spatially developing turbulence

Published online by Cambridge University Press:  20 February 2017

I. Paul Open the ORCID record for I. Paul [Opens in a new window] ,
G. Papadakis  and
J. C. Vassilicos
I. Paul*
Affiliation:
Department of Aeronautics, Imperial College London, London SW7 2AZ, UK
G. Papadakis*
Affiliation:
Department of Aeronautics, Imperial College London, London SW7 2AZ, UK
J. C. Vassilicos*
Affiliation:
Department of Aeronautics, Imperial College London, London SW7 2AZ, UK
*
†Email addresses for correspondence: p.immanuvel@imperial.ac.uk, g.papadakis@imperial.ac.uk, j.c.vassilicos@imperial.ac.uk
†Email addresses for correspondence: p.immanuvel@imperial.ac.uk, g.papadakis@imperial.ac.uk, j.c.vassilicos@imperial.ac.uk
†Email addresses for correspondence: p.immanuvel@imperial.ac.uk, g.papadakis@imperial.ac.uk, j.c.vassilicos@imperial.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper investigates the dynamics of velocity gradients for a spatially developing flow generated by a single square element of a fractal square grid at low inlet Reynolds number through direct numerical simulation. This square grid-element is also the fundamental block of a classical grid. The flow along the grid-element centreline is initially irrotational and becomes turbulent further downstream due to the lateral excursions of vortical turbulent wakes from the grid-element bars. We study the generation and evolution of the symmetric and anti-symmetric parts of the velocity gradient tensor for this spatially developing flow using the transport equations of mean strain product and mean enstrophy respectively. The choice of low inlet Reynolds number allows for fine spatial resolution and long simulations, both of which are conducive in balancing the budget equations of the above quantities. The budget analysis is carried out along the grid-element centreline and the bar centreline. The former is observed to consist of two subregions: one in the immediate lee of the grid-element which is dominated by irrotational strain, and one further downstream where both strain and vorticity coexist. In the demarcation area between these two subregions, where the turbulence is inhomogeneous and developing, the energy spectrum exhibits the best 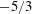$-5/3$ power-law slope. This is the same location where the experiments at much higher inlet Reynolds number show a well-defined 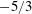$-5/3$ spectrum over more than a decade of frequencies. Yet, the 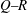$Q{-}R$ diagram, where 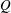$Q$ and 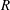$R$ are the second and third invariants of the velocity gradient tensor, remains undeveloped in the near-grid-element region, and both the intermediate and extensive strain-rate eigenvectors align with the vorticity vector. Along the grid-element centreline, the strain is the first velocity gradient quantity generated by the action of pressure Hessian. This strain is then transported downstream by fluctuations and strain self-amplification is activated a little later. Further downstream, vorticity from the bar wakes is brought towards the grid-element centreline, and, through the interaction with strain, leads to the production of enstrophy. The strain-rate tensor has a statistically axial stretching form in the production region, but a statistically biaxial stretching form in the decay region. The usual signatures of velocity gradients such as the shape of 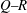$Q{-}R$ diagrams and the alignment of vorticity vector with the intermediate eigenvector are detected only in the decay region even though the local Reynolds number (based on the Taylor length scale) is only between 30 and 40.

JFM classification

Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulence theory Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 815 , 25 March 2017 , pp. 295 - 332
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ashurst, W. M. T., Kerstein, A. R., Kerr, R. M. & Gibson, C. H. 1987 Alignment of vorticity and scalar gradient with strain rate in simulated Navier–Stokes turbulence. Phys. Fluids 30 (8), 2343–2353.CrossRefGoogle Scholar
Balay, S., Abhyankar, S., Adams, M., Brown, J., Brune, P., Buschelman, K., Eijkhout, V., Gropp, W., Kaushik, D., Knepley, M. et al. 2014 Petsc users manual revision 3.5. Tech. Rep., Argonne National Laboratory (ANL).Google Scholar
Bearman, P. W. & Trueman, D. M. 1972 An investigation of the flow around rectangular cylinders. Aeronaut. Q. 23 (03), 229–237.Google Scholar
Betchov, R. 1956 An inequality concerning the production of vorticity in isotropic turbulence. J. Fluid Mech. 1 (05), 497–504.Google Scholar
Betchov, R. 1975 Numerical simulation of isotropic turbulence. Phys. Fluids 18 (10), 1230–1236.Google Scholar
Chong, M. S., Perry, A. E. & Cantwell, B. J. 1990 A general classification of three-dimensional flow fields. Phys. Fluids 2 (5), 765–777.CrossRefGoogle Scholar
Comte-Bellot, G. & Corrsin, S. 1966 The use of a contraction to improve the isotropy of grid-generated turbulence. J. Fluid Mech. 25 (04), 657–682.Google Scholar
Comte-Bellot, G. & Corrsin, S. 1971 Simple Eulerian time correlation of full-and narrow-band velocity signals in grid-generated, isotropic turbulence. J. Fluid Mech. 48 (02), 273–337.CrossRefGoogle Scholar
Donzis, D. A., Yeung, P. K. & Sreenivasan, K. R. 2008 Dissipation and enstrophy in isotropic turbulence: resolution effects and scaling in direct numerical simulations. Phys. Fluids 20 (4), 045108.Google Scholar
Falgout, R. & Yang, U. 2002 Hypre: a library of high performance preconditioners. In Computational Science ICCS 2002, pp. 632–641. Springer.CrossRefGoogle Scholar
Ganapathisubramani, B., Lakshminarasimhan, K. & Clemens, N. T. 2008 Investigation of three-dimensional structure of fine scales in a turbulent jet by using cinematographic stereoscopic particle image velocimetry. J. Fluid Mech. 598, 141–175.Google Scholar
Gomes-Fernandes, R., Ganapathisubramani, B. & Vassilicos, J. C. 2012 Particle image velocimetry study of fractal-generated turbulence. J. Fluid Mech. 711, 306–336.Google Scholar
Gomes-Fernandes, R., Ganapathisubramani, B. & Vassilicos, J. C. 2014 Evolution of the velocity-gradient tensor in a spatially developing turbulent flow. J. Fluid Mech. 756, 252–292.Google Scholar
Gomes-Fernandes, R., Ganapathisubramani, B. & Vassilicos, J. C. 2015 The energy cascade in near-field non-homogeneous non-isotropic turbulence. J. Fluid Mech. 771, 676–705.Google Scholar
Gulitski, G., Kholmyansky, M., Kinzelbach, W., Lüthi, B., Tsinober, A. & Yorish, S. 2007 Velocity and temperature derivatives in high-Reynolds-number turbulent flows in the atmospheric surface layer. Part 1. Facilities, methods and some general results. J. Fluid Mech. 589, 57–81.Google Scholar
Hamlington, P. E., Schumacher, J. & Dahm, W. J. A. 2008a Direct assessment of vorticity alignment with local and nonlocal strain rates in turbulent flows. Phys. Fluids 20 (11), 111703.Google Scholar
Hamlington, P. E., Schumacher, J. & Dahm, W. J. A. 2008b Local and nonlocal strain rate fields and vorticity alignment in turbulent flows. Phys. Rev. E 77 (2), 026303.Google Scholar
Hurst, D. & Vassilicos, J. C. 2007 Scalings and decay of fractal-generated turbulence. Phys. Fluids 19 (3), 035103.Google Scholar
Jiménez, J. 1992 Kinematic alignment effects in turbulent flows. Phys. Fluids A 4 (4), 652–654.Google Scholar
Kerr, R. M. 1987 Histograms of helicity and strain in numerical turbulence. Phys. Rev. Lett. 59 (7), 783–786.Google Scholar
Kholmyansky, M., Tsinober, A. & Yorish, S. 2001 Velocity derivatives in the atmospheric surface layer at Re 𝜆 = 104. Phys. Fluids 13, 311–314.Google Scholar
Kolmogorov, A. N. 1941 The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Dokl. Akad. Nauk SSSR 30, 299–303.Google Scholar
Laizet, S., Nedić, J. & Vassilicos, J. C. 2015a Influence of the spatial resolution on fine-scale features in dns of turbulence generated by a single square grid. Intl J. Comput. Fluid Dyn. 29 (3–5), 286–302.CrossRefGoogle Scholar
Laizet, S., Nedić, J. & Vassilicos, J. C. 2015b The spatial origin of - 5/3 spectra in grid-generated turbulence. Phys. Fluids 27 (6), 065115.CrossRefGoogle Scholar
Laizet, S., Vassilicos, J. C. & Cambon, C. 2013 Interscale energy transfer in decaying turbulence and vorticity–strain-rate dynamics in grid-generated turbulence. Fluid Dyn. Res. 45 (6), 061408.CrossRefGoogle Scholar
Le, H., Moin, P. & Kim, J. 1997 Direct numerical simulation of turbulent flow over a backward-facing step. J. Fluid Mech. 330, 349–374.CrossRefGoogle Scholar
Lu, L. & Papadakis, G. 2011 Investigation of the effect of external periodic flow pulsation on a cylinder wake using linear stability analysis. Phys. Fluids 23 (9), 094105.Google Scholar
Lu, L. & Papadakis, G. 2014 An iterative method for the computation of the response of linearised Navier–Stokes equations to harmonic forcing and application to forced cylinder wakes. Intl J. Numer. Meth. Fluids 74 (11), 794–817.Google Scholar
Mansour, N. N., Kim, J. & Moin, P. 1988 Reynolds-stress and dissipation-rate budgets in a turbulent channel flow. J. Fluid Mech. 194, 15–44.Google Scholar
Maxey, M. R. 1987 The velocity skewness measured in grid turbulence. Phys. Fluids 30 (4), 935–938.Google Scholar
Mazellier, N. & Vassilicos, J. C. 2010 Turbulence without Richardson–Kolmogorov cascade. Phys. Fluids 22 (7), 075101.Google Scholar
Melina, G., Bruce, P. J. K. & Vassilicos, J. C. 2016 Vortex shedding effects in grid-generated turbulence. Phys. Rev. Fluids 1 (4), 044402.Google Scholar
Moin, P. & Mahesh, K. 1998 Direct numerical simulation: a tool in turbulence research. Annu. Rev. Fluid Mech. 30 (1), 539–578.Google Scholar
Norberg, C. 1993 Flow around rectangular cylinders: pressure forces and wake frequencies. J. Wind Engng Ind. Aerodyn. 49 (1), 187–196.Google Scholar
Onishi, R., Baba, Y. & Takahashi, K. 2011 Large-scale forcing with less communication in finite-difference simulations of stationary isotropic turbulence. J. Comput. Phys. 230 (10), 4088–4099.CrossRefGoogle Scholar
Papadakis, G. 2011 New analytic solutions for wave propagation in flexible, tapered vessels with reference to mammalian arteries. J. Fluid Mech. 689, 465–488.CrossRefGoogle Scholar
Rhie, C. M. & Chow, W. L. 1983 Numerical study of the turbulent flow past an airfoil with trailing edge separation. AIAA J. 21 (11), 1525–1532.Google Scholar
Sandham, N. D. & Tsinober, A. 2000 Kinetic energy, enstrophy and strain rate in near-wall turbulence. Adv. Turbul. 8, 407–410.Google Scholar
Schumacher, J., Scheel, J. D., Krasnov, D., Donzis, D. A., Yakhot, V. & Sreenivasan, K. R. 2014 Small-scale universality in fluid turbulence. Proc. Natl Acad. Sci. USA 111 (30), 10961–10965.Google Scholar
Seoud, R. E. & Vassilicos, J. C. 2007 Dissipation and decay of fractal-generated turbulence. Phys. Fluids 19 (10), 105108.Google Scholar
She, Z., Jackson, E. & Orszag, S. A. 1991 Structure and dynamics of homogeneous turbulence: models and simulations. Proc. R. Soc. Lond. A 434, 101–124.Google Scholar
da Silva, C. B. & Pereira, J. C. F. 2008 Invariants of the velocity-gradient, rate-of-strain, and rate-of-rotation tensors across the turbulent/nonturbulent interface in jets. Phys. Fluids 20 (5), 055101.Google Scholar
Simmons, L. F. G. & Salter, C. 1934 Experimental investigation and analysis of the velocity variations in turbulent flow. Proc. R. Soc. Lond. A 145 (854), 212–234.Google Scholar
Sreenivasan, K. R. & Antonia, R. A. 1997 The phenomenology of small-scale turbulence. Annu. Rev. Fluid Mech. 29 (1), 435–472.Google Scholar
Su, L. K. & Dahm, W. J. A. 1996 Scalar imaging velocimetry measurements of the velocity gradient tensor field in turbulent flows. II. Experimental results. Phys. Fluids 8 (7), 1883–1906.Google Scholar
Tavoularis, S., Corrsin, S. & Bennett, J. C. 1978 Velocity-derivative skewness in small Reynolds number, nearly isotropic turbulence. J. Fluid Mech. 88 (1), 63–69.Google Scholar
Taylor, G. I. 1938 Production and dissipation of vorticity in a turbulent fluid. Proc. R. Soc. Lond. A 196, 15–23.Google Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. MIT.Google Scholar
Townsend, A. A. 1980 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
Tsinober, A. 2000 Vortex Stretching Versus Production of Strain/Dissipation, pp. 164–191. Cambridge University Press.Google Scholar
Tsinober, A. 2009 An Informal Conceptual Introduction to Turbulence. Springer.Google Scholar
Tsinober, A., Kit, E. & Dracos, T. 1992 Experimental investigation of the field of velocity gradients in turbulent flows. J. Fluid Mech. 242, 169–192.Google Scholar
Tsinober, A., Shtilman, L., Sinyavskii, A. & Vaisburd, H. 1995 Vortex stretching and enstrophy generation in numerical and laboratory turbulence. In Small-Scale Structures in Three-Dimensional Hydrodynamic and Magnetohydrodynamic Turbulence, pp. 9–16. Springer.Google Scholar
Valente, P. C. & Vassilicos, J. C. 2014 The non-equilibrium region of grid-generated decaying turbulence. J. Fluid Mech. 744, 5–37.Google Scholar
Warhaft, Z. & Jayesh 1992 Probability distribution, conditional dissipation, and transport of passive temperature fluctuations in grid-generated turbulence. Phys. Fluids 4 (10), 2292–2307.Google Scholar
Weitemeyer, S., Reinke, N., Peinke, J. & Hölling, M. 2013 Multi-scale generation of turbulence with fractal grids and an active grid. Fluid Dyn. Res. 45 (6), 061407.Google Scholar
Zhou, Y., Nagata, K., Sakai, Y., Ito, Y. & Hayase, T. 2015 On the evolution of the invariants of the velocity gradient tensor in single-square-grid-generated turbulence. Phys. Fluids 27 (7), 075107.Google Scholar
Zhou, Y., Nagata, K., Sakai, Y., Ito, Y. & Hayase, T. 2016a Enstrophy production and dissipation in developing grid-generated turbulence. Phys. Fluids 28 (2), 025113.Google Scholar
Zhou, Y., Nagata, K., Sakai, Y., Ito, Y. & Hayase, T. 2016b Spatial evolution of the helical behavior and the 2/3 power-law in single-square-grid-generated turbulence. Fluid Dyn. Res. 48 (2), 021404.Google Scholar
Zhou, Y., Nagata, K., Sakai, Y., Suzuki, H., Ito, Y., Terashima, O. & Hayase, T. 2014a Development of turbulence behind the single square grid. Phys. Fluids 26 (4), 045102.Google Scholar
Zhou, Y., Nagata, K., Sakai, Y., Suzuki, H., Ito, Y., Terashima, O. & Hayase, T. 2014b Relevance of turbulence behind the single square grid to turbulence generated by regular-and multiscale-grids. Phys. Fluids 26 (7), 075105.Google Scholar