Hostname: page-component-848d4c4894-p2v8j Total loading time: 0 Render date: 2024-05-01T07:52:55.123Z Has data issue: false hasContentIssue false
  • English
  • Français

RAMSEY’S THEOREM FOR PAIRS AND K COLORS AS A SUB-CLASSICAL PRINCIPLE OF ARITHMETIC

Published online by Cambridge University Press:  19 June 2017

STEFANO BERARDI  and
SILVIA STEILA
STEFANO BERARDI
Affiliation:
DIPARTIMENTO DI INFORMATICA UNIVERSITÀ DEGLI STUDI DI TORINO CORSO SVIZZERA 185 10149 TORINO, ITALYE-mail: stefano@di.unito.it
SILVIA STEILA
Affiliation:
INSTITUTE OF COMPUTER SCIENCE UNIVERSITY OF BERN NEUBRÜCKSTRASSE 10 CH-3012 BERN, SWITZERLANDE-mail: steila@inf.unibe.ch
Get access Rights & Permissions [Opens in a new window]

Abstract

The purpose is to study the strength of Ramsey’s Theorem for pairs restricted to recursive assignments of k-many colors, with respect to Intuitionistic Heyting Arithmetic. We prove that for every natural number 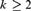$k \ge 2$, Ramsey’s Theorem for pairs and recursive assignments of k colors is equivalent to the Limited Lesser Principle of Omniscience for ${\rm{\Sigma }}_3^0$ formulas over Heyting Arithmetic. Alternatively, the same theorem over intuitionistic arithmetic is equivalent to: for every recursively enumerable infinite k-ary tree there is some 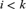$i < k$ and some branch with infinitely many children of index i.

Keywords

03F5503B30Ramsey’s Theoremintuitionistic arithmeticPrinciple of Omniscience
Type
Articles
Information
The Journal of Symbolic Logic , Volume 82 , Issue 2 , June 2017 , pp. 737 - 753
Copyright
Copyright © The Association for Symbolic Logic 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Akama, Y., Berardi, S., Hayashi, S., and Kohlenbach, U., An arithmetical hierarchy of the law of excluded middle and related principles , 19th IEEE Symposium on Logic in Computer Science (LICS 2004), IEEE Computer Society, 2004, pp. 192–201.Google Scholar
Argyros, S. A. and Todorcevic, S., Ramsey Methods in Analysis, Advanced Courses in Mathematics - CRM Barcelona, Birkhäuser, Basel, 2005.CrossRefGoogle Scholar
Berardi, S. and Steila, S., Ramsey Theorem for pairs as a classical principle in intuitionistic arithmetic , 19th International Conference on Types for Proofs and Programs, TYPES 2013 (Matthes, R. and Schubert, A., editors), LIPIcs, vol. 26, Schloss Dagstuhl - Leibniz-Zentrum fuer Informatik, Dagstuhl, 2014, pp. 64–83.Google Scholar
Berardi, S. and Steila, S., An intuitionistic version of Ramsey’s Theorem and its use in Program Termination . Annals of Pure and Applied Logic, vol. 166 (2015), no. 12, pp. 1382–1406.CrossRefGoogle Scholar
Bishop, E., Foundations of Constructive Analysis, McGraw-Hill, New York, NY, 1967.Google Scholar
Brattka, V. and Rakotoniaina, T., On the uniform computational content of Ramsey’s Theorem, 2016, arXiv:1508.00471.Google Scholar
Büchi, J. R., On a decision method in restricted second order arithmetic , Logic, Methodology and Philosophy of Science (Proceeding of the 1960 International Congress) (Nagel, E., Suppes, P., and Tarsk, A., editors), Stanford University Press, Stanford, 1962, pp. 1–11.Google Scholar
Coquand, T., A direct proof of Ramsey’s Theorem , Author’s website, revised in 2011, 1994.Google Scholar
Dorais, F. G., Dzhafarov, D. D., Hirst, J. L., Mileti, J. R., and Shafer, P., On uniform relationships between combinatorial problems . Transactions of the American Mathematical Society, vol. 368 (2016), no. 2, pp. 1321–1359.CrossRefGoogle Scholar
Gasarch, W. I., Proving programs terminate using well-founded orderings , Ramsey’s Theorem, and matrices. Advances in Computers, vol. 97 (2015), pp. 147–200.Google Scholar
Jockusch, C. G., Ramsey’s Theorem and recursion theory , this JOURNAL, vol. 37 (1972), pp. 268–280.Google Scholar
Kreuzer, A. and Kohlenbach, U., Ramsey’s Theorem for pairs and provably recursive functions . Notre Dame Journal of Formal Logic, vol. 50 (2009), no. 4, pp. 427–444.Google Scholar
Lee, C. S., Jones, N. D., and Ben-Amram, A. M., The size-change principle for program termination , Conference Record of POPL 2001 (Hankin, C. and Schmidt, D., editors), ACM, New York, NY, 2001, pp. 81–92.Google Scholar
Podelski, A. and Rybalchenko, A., Transition invariants , 19th IEEE Symposium on Logic in Computer Science (LICS 2004), IEEE Computer Society, 2004, pp. 32–41.Google Scholar
Ramsey, F. P., On a problem in formal logic . Proceedings of the London Mathematical Society, vol. 30 (1930), pp. 264–286.CrossRefGoogle Scholar
Specker, E., Ramsey’s theorem does not hold in recursive set theory , Logic Colloquium ’69 (Proceedings of the Summer School and Colloquium, Manchester, 1969) (Gandy, R. O. and Yates, C. M. E., editors), North-Holland, Amsterdam, 1971, pp. 439–442.Google Scholar
Steila, S., An intuitionistic analysis of size-change termination , 20th International Conference on Types for Proofs and Programs, TYPES 2014 (Herbelin, H., Letouzey, P., and Sozeau, M., editors), LIPIcs, vol. 39, Schloss Dagstuhl - Leibniz-Zentrum fuer Informatik, Dagstuhl, 2015, pp. 288–307.Google Scholar
Vytiniotis, D., Coquand, T., and Wahlstedt, D., Stop when you are almost-full - adventures in constructive termination , Interactive Theorem Proving, ITP 2012 (Beringer, L. and Felty, A. P., editors), Lecture Notes in Computer Science, vol. 7406, Springer, Berlin, Heidelberg, 2012, pp. 250–265.CrossRefGoogle Scholar