Hostname: page-component-76fb5796d-25wd4 Total loading time: 0 Render date: 2024-04-29T22:38:51.882Z Has data issue: false hasContentIssue false
  • English
  • Français

A simple proof of Euler's continued fraction of e1/M

Published online by Cambridge University Press:  14 June 2016

Joseph Tonien
Joseph Tonien*
Affiliation:
School of Computing and Information Technology, University of Wollongong, Australia e-mail: joseph_tonien@uow.edu.au
Get access Rights & Permissions [Opens in a new window]

Extract

A continued fraction is an expression of the form

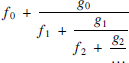
and we will denote it by the notation [f0, (g0, f1), (g1, f2), (g2, f3), … ]. If the numerators gi are all equal to 1 then we will use a shorter notation [f0, f1, f2, f3, … ]. A simple continued fraction is a continued fraction with all the gi coefficients equal to 1 and with all the fi coefficients positive integers except perhaps f0.

The finite continued fraction [f0, (g0, f1), (g1, f2),…, (gk–1, fk)] is called the k th convergent of the infinite continued fraction [f0, (g0, f1), (g1, f2),…]. We define

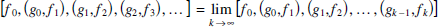
if this limit exists and in this case we say that the infinite continued fraction converges.

Type
Research Article
Information
The Mathematical Gazette , Volume 100 , Issue 548 , July 2016 , pp. 279 - 287
Copyright
Copyright © Mathematical Association 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Euler, L., De fractionibus continuis dissertatio, Commentarii academiae scientiarum Petropolitanae 9 (1744) pp. 98–137 also available at http://eulerarchive.maa.org/pages/E071.htmlGoogle Scholar
2.Hermite, C., Sur la fonction exponentielle, Comptes rendus de l'Académie des sciences Paris (1873) pp. 18-24, pp. 74-79, pp. 226-233, pp. 285-293.Google Scholar
3.Olds, C. D., The simple continued fraction expansion of e, Amer. Math. Monthly 77 (1970) pp. 968–974.CrossRefGoogle Scholar
4.Cohn, H., A short proof of the simple continued fraction expansion of e, Amer. Math. Monthly 113 (2006) pp. 57–62.Google Scholar
5.Osler, T. J., A proof of the continued fraction expansion of e 1/M, Amer. Math. Monthly 113 (2006) pp. 62–66.Google Scholar
6.Borwein, J. M., van der Poorten, A. J., Shallit, J. O. and Zudilin, W., Neverending fractions: an introduction to continued fractions, Cambridge University Press (2014) pp. 45–49.CrossRefGoogle Scholar
7.Rose, H. E., A course in number theory (2nd edn.), Oxford University Press (1994) Excercises 15, 16, pp. 143-144.Google Scholar
8.Khrushchev, S., On Euler's differential methods for continued fractions, Electronic transactions on numerical analysis 25 (2006) pp. 178–200.Google Scholar