Hostname: page-component-848d4c4894-hfldf Total loading time: 0 Render date: 2024-05-03T09:41:28.597Z Has data issue: false hasContentIssue false
  • English
  • Français

Differential equations in Banach spaces

Published online by Cambridge University Press:  17 April 2009

E.S. Noussair
E.S. Noussair
Affiliation:
School of Mathematics, University of New South Wales, Kensington, New South Wales.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let H be a fixed Hilbert space and B(H, H) be the Banach space of bounded linear operators from H to H with the uniform operator topology. Oscillation criteria are obtained for the operator differential equation

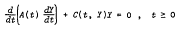
where the coefficients A, C are linear operators from B(H, H) to B(H, H), for each t ≤ 0. A solution Y: R+ → B(H, H) is said to be oscillatory if there exists a sequence of points ti ∈ R+, so that ti → ∞ as i → ∞, and Y(ti) fails to have a bounded inverse. The main theorem states that a solution Y is oscillatory if an associated scalar differential equation is oscillatory.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 9 , Issue 2 , October 1973 , pp. 219 - 226
Copyright
Copyright © Australian Mathematical Society 1973

References

[1]Hayden, T.L. and Howard, H.C., “Oscillation of differential equations in Banach spaces”, Ann. Mat. Pura Appi. 85 (1970), 383–394.CrossRefGoogle Scholar
[2]Mille, Einar, “Non-oscillation theorems”, Trans. Amer. Math. Soc. 64 (1948), 235–252.Google Scholar
[3]Leighton, Walter, “On self-adjoint differential equations of second order”, J. London Math. Soc. 27 (1952), 37–47.CrossRefGoogle Scholar
[4]Loomis, Lynn H. and Sternberg, Shlomo, Advanced calculus (Addison-Wesley, Reading, Massachusetts; London; Don Mills, Ontario; 1968).Google Scholar
[5]Noussair, E.S., “Comparison and oscillation theorems for matrix differential inequalities”, Trans. Amer. Math. Soc. 160 (1971), 203–215.Google Scholar
[6]Noussair, E.S. and Swanson, C.A., “Oscillation criteria for differential systems”, J. Math. Anal. Appi. 36 (1971), 575–580.CrossRefGoogle Scholar
[7]Picone, M., “Un teorema sulle soluzioni delle equazioni lineari ellittiche autoaggiunte alle derivate parziali del secondo ordine”, Atti. R. Accad. Lincei Rend. Cl. Sci. Fis. Mat. Natur. (5) 20 (1911), 213–219.Google Scholar
[8]Swanson, C.A., “An identity for elliptic equations with applications”, Trans. Amer. Math. Soc. 134 (1968), 325–333.CrossRefGoogle Scholar