Hostname: page-component-848d4c4894-75dct Total loading time: 0 Render date: 2024-05-01T12:35:59.046Z Has data issue: false hasContentIssue false
  • English
  • Français

Calculus on Gaussian and Poisson white noises

Published online by Cambridge University Press:  22 January 2016

Yoshifusa Ito  and
Izumi Kubo
Yoshifusa Ito
Affiliation:
Nagoya University College of Medical Technology, Higashi-ku, Nagoya 461, Japan
Izumi Kubo
Affiliation:
Hiroshima University, Naka-ku, Hiroshima 730, Japan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

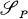Recently one of the authors has introduced the concept of generalized Poisson functionals and discussed the differentiation, renormalization, stochastic integrals etc. ([8], [9]), analogously to the works of T. Hida ([3], [4], [5]). Here we introduce a transformation for Poisson fnnctionals with the idea as in the case of Gaussian white noise (cf. [10], [11], [12], [13]). Then we can discuss the differentiation, renormalization, multiple Wiener integrals etc. in a way completely parallel with the Gaussian case. The only one exceptional point, which is most significant, is that the multiplications are described by

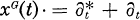for the Gaussian case,

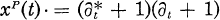for the Poisson case,

as will be stated in Section 5. Conversely, those formulae characterize the types of white noises.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 111 , September 1988 , pp. 41 - 84
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1988

References

[1] Aronszajn, N., Theory of reproducing kernel, Trans. Amer. Math. Soc., 68 (1950), 337–404.CrossRefGoogle Scholar
[2] Hida, T., Generalized multiple Wiener integrals, Proc. J. Acad., 54, Ser. A, (1978), 55–58.Google Scholar
[3] Hida, T., Analysis of Brownian functionals, Carleton Math. Lee. Notes No. 13, 2nd Ed. (1978) [c] Hida, T.: Brownian motion, Springer-Verlag, New York, Heidelberg, Berlin (1980).Google Scholar
[4] Hida, T., Causal calculus of Brownian functionals and its applications, Statistics and related topics, ed. Csörgő, M. et al. North Holland Publishing Company (1981).Google Scholar
[5] Hida, T., White noise analysis and its applications, Proceedings of the International Mathematical Conference, Singapore 1981, (1982).Google Scholar
[6] Hida, T. and Ikeda, N., Analysis on Hilbert space with reproducing kernel arising from multiple Wiener integral, Proc. 5th Berkeley Symp. on Math. Stat, and Prob. Vol. II, Part 1, (1967), 117–143.Google Scholar
[7] Ito, K., Multiple Wiener integral, J. Math. Soc. Japan, 3 (1951), 157–169.Google Scholar
[8] Ito, Y., On a generalization of non-linear Poisson functionals, Math. Eep. Toyama Univ., 3 (1980), 111–122.Google Scholar
[9] Ito, Y., Generalized Poisson functionals, Prob. Th. Rel. Fields, 77 (1988), 1–28.CrossRefGoogle Scholar
[10] Kubo, I. and Takenaka, S., Calculus on Gaussian white noises I, Proc. Japan Acad., 56 Ser. A, No. 8, (1980), 376–380.Google Scholar
[11] Kubo, I. and Takenaka, S., Calculus on Gaussian white noises II, Proc. Japan Acad., 56 Ser. A, No. 9, (1980), 411–416.Google Scholar
[12] Kubo, I. and Takenaka, S., Calculus on Gaussian white noises III, Proc. Japan Acad., 57 Ser. A, No. 9 (1981), 433–437.Google Scholar
[13] Kubo, I. and Takenaka, S., Calculus on Gaussian white noises IV, Proc. Japan Acad., 58 Ser. A, No. 9 (1982), 186–189.Google Scholar
[14] Kuo, H.-H., Gaussian measures in Banach spaces, Lect. Notes in Math., 463, Springer-Verlag, (1975).Google Scholar
[15] Segal, I., Tensor algebra over Hilbert spaces I, Trans. Amer. Math. Soc., 81 (1956),106–134.Google Scholar
[16] Segal, I., Tensor algebra over Hilbert spaces II, Ann. of Math., 63 (1956), 160–175.Google Scholar
[17] Wick, G. C., The evaluation of the collision of matrix, Phys. Rev., 80 (1950), 268–272.Google Scholar
[18] Wiener, N. and Wintner, A., Discrete chaos, Amer. J. Math., 65 (1943), 279–298.CrossRefGoogle Scholar