Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Hoffmann-Ostenhof, T
1979.
Lower and upper bounds to the decay of the ground state one-electron density of helium-like systems.
Journal of Physics A: Mathematical and General,
Vol. 12,
Issue. 8,
p.
1181.
Hoffmann-Ostenhof, T
1980.
A comparison theorem for differential inequalities with applications in quantum mechanics.
Journal of Physics A: Mathematical and General,
Vol. 13,
Issue. 2,
p.
417.
Carmona, R.
and
Simon, B.
1981.
Pointwise bounds on eigenfunctions and wave packets inN-body quantum systems.
Communications in Mathematical Physics,
Vol. 80,
Issue. 1,
p.
59.
Ahlrichs, Reinhart
Hoffmann-Ostenhof, Maria
Hoffmann-Ostenhof, Thomas
and
Morgan, John D.
1981.
Bounds on the decay of electron densities with screening.
Physical Review A,
Vol. 23,
Issue. 5,
p.
2106.
Froese, R.
Herbst, I.
Hoffmann-Ostenhof, M.
and
Hoffmann-Ostenhof, T.
1983.
L2-lower bounds to solutions of one-body Schrödinger equations.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 95,
Issue. 1-2,
p.
25.
Froese, Richard
and
Herbst, Ira
1983.
Exponential lower bounds to solutions of the Schr�dinger equation: Lower bounds for the spherical average.
Communications in Mathematical Physics,
Vol. 92,
Issue. 1,
p.
71.
Amrein, Werner O.
1984.
Bornes inférieurs pour des fonctions propres de l'opérateur de Schrödinger.
Journées équations aux dérivées partielles,
p.
1.
Froese, R.
1984.
Bound states in N-body quantum systems.
Physica A: Statistical Mechanics and its Applications,
Vol. 124,
Issue. 1-3,
p.
311.
Hinz, Andreas M.
1984.
Obere Schranken f�r Eigenfunktionen eines Operators ??+q.
Mathematische Zeitschrift,
Vol. 185,
Issue. 2,
p.
291.
Herbst, Ira W.
1986.
Lower bounds in cones for solutions to the schrödinger equation.
Journal d'Analyse Mathématique,
Vol. 47,
Issue. 1,
p.
151.
Donnelly, Harold
1988.
Geometry and Analysis on Manifolds.
Vol. 1339,
Issue. ,
p.
106.
Donnelly, Harold
1988.
Lower bounds for eigenfunctions on Riemannian manifolds.
Mathematische Annalen,
Vol. 279,
Issue. 4,
p.
653.
Hoffmann-Ostenhof, M.
1990.
On the asymptotic decay of L2-solutions of one-body Schrödinger equations in unbounded domains.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 115,
Issue. 1-2,
p.
65.
Duyckaerts, Thomas
Zhang, Xu
and
Zuazua, Enrique
2008.
On the optimality of the observability inequalities for parabolic and hyperbolic systems with potentials.
Annales de l'Institut Henri Poincaré C, Analyse non linéaire,
Vol. 25,
Issue. 1,
p.
1.
Herbst, I.
and
Skibsted, E.
2017.
Decay of eigenfunctions of elliptic PDE's, II.
Advances in Mathematics,
Vol. 306,
Issue. ,
p.
177.
Akduman, Setenay
and
Pankov, Alexander
2017.
Exponential decay of eigenfunctions of Schrödinger operators on infinite metric graphs.
Complex Variables and Elliptic Equations,
Vol. 62,
Issue. 7,
p.
957.
Elton, Daniel M.
2020.
Decay rates at infinity for solutions to periodic Schrödinger equations.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 150,
Issue. 3,
p.
1113.
Gontier, David
Lewin, Mathieu
and
Nazar, Faizan Q.
2021.
The Nonlinear Schrödinger Equation for Orthonormal Functions: Existence of Ground States.
Archive for Rational Mechanics and Analysis,
Vol. 240,
Issue. 3,
p.
1203.
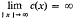 . Applications to the asymptotic decay of the bound states of a Hamiltonian are given.
. Applications to the asymptotic decay of the bound states of a Hamiltonian are given.



