1. INTRODUCTION
With the growing military and civilian demands for navigation and detection systems, more and more sensors are installed on moving platforms such as trucks, ships and aircraft. In order to obtain target locations, these sensors need to know the real-time attitude information of their platforms to rectify radar measurements. However, the attitude angles provided by the Inertial Navigation System (INS) are biased because of the accumulated errors in the Inertial Measurement Units (IMU) of INS. In addition, the sensors have native systematic biases which are usually called offset biases. The attitude biases and offset biases always influence the sensor measurements simultaneously and their adverse influences are coupled. It is impossible for a single sensor to rectify these biases. Fortunately, in order to estimate and compensate for these biases, many error registration methods have been proposed; this is one of the key technologies to be tackled first in sensor networking and directly affects the accuracies of the sensor networks in target tracking, fusion, and recognition.
At present, the methods for registration are mostly focused on the networks composed of stationary radars and the algorithms used include the parameter estimation methods such as weighted mean (Burke, Reference Burke1966), least square (Sudano, Reference Sudano1993), maximum likelihood (Zhou and Henry, Reference Zhou and Henry1997), and the state estimation methods such as Kalman Filter [KF] (Kousuge and Okada, Reference Kousuge and Okada1996), Unscented Kalman Filter [UKF] (Li et al., Reference Li, Leung and Zhou2004), EM method (Li and Leung, Reference Li and Leung2006), and so on. The difficulty for mobile radar registration, which is different from stationary radars, is to estimate offset biases of radars and attitude biases of platforms simultaneously. The influences of the attitude biases on radar measurements are nonlinear and related to the geometry between target(s) and radars. They take on the form of varying radar measurement errors and are coupled with the native offset biases of radars. In order to solve the coupling problems, Dela Cruz et al., (Reference Dela Cruz, Alouani, Rice and Blair1992); Helmick and Rice, (Reference Helmick and Rice1993); Wang et al., (Reference Wang, Chen and Jia2012) have made some efforts.
A two-stepped method was proposed by Dela Cruz et al., (Reference Dela Cruz, Alouani, Rice and Blair1992), which first estimated radar offset biases using a KF without considering the influences of attitude biases, that is, all the attitude biases were set zeroes. Subsequently, another KF was used to merely estimate attitude biases by using raw radar measurements rectified by the offset bias estimates obtained from the first step. This method ignored the coupling. That is, the offset biases were solved independently of the attitude biases. The model proposed by Helmick and Rice (Reference Helmick and Rice1993) considered the coupling influences adequately, however, it assumed that the sensors were close enough (e.g., they were located on the same platform). For models proposed by Dela Cruz et al., (Reference Dela Cruz, Alouani, Rice and Blair1992) and Helmick and Rice (Reference Helmick and Rice1993), they both selected relative offset biases and relative attitude biases as their system state variables. So, their methods could only obtain the relative bias estimates. However, the absolute bias estimates of each sensor are very important for the Integrated Situation Awareness (ISA) in large regions, which cannot be obtained by their methods. Wang et al., (Reference Wang, Chen and Jia2012) used all the absolute biases as state variables. They gave the equivalent measurement error expressions induced by the attitude biases by using linearization. Then, an Optimized Bias Estimation Model (OBEM) was proposed which omitted radar pitch and roll biases in the state vector when establishing the registration equations. However, OBEM did not make the best of equivalent error expressions to simplify the models and the reasons for poor estimate results of roll and pitch biases have not been fully explained.
In fact, the All Augmented Model (AAM) in Wang et al., (Reference Wang, Chen and Jia2012), which is the basic model for the moving platform registration, and OBEM are both linearized models, so, the errors caused by linearization may be the main reason for the poor estimates of attitude biases. In order to analyse the effects of the linearization, we establish the nonlinear registration models and use Square Root Unscented Kalman Filter (SRUKF), as can be seen in Merwe and Wan (Reference Merwe and Wan2001). In addition, based on the equivalent error expressions given in this paper, an Attitude Bias Conversion Model (ABCM) is proposed, in which the attitude biases are converted to radar measurement errors. This changes the coupling characteristic from multiplicative to additive and simplifies the modelling process. ABCM also uses all the absolute radar offset biases and attitude biases as the state variables to establish nonlinear equivalent measurement equations and use SRUKF as filter. Theorem 1 in Appendix B and the simulation results prove that the linearization is not the main reason for poor estimates of the attitude biases. The estimate results of ABCM-SRUKF are very close to OBEM because the former's estimate values of roll and pitch biases are zeros and the latter sets them to zeros, which suggest that observability is the main reason for poor estimates. To simplify the problems, in this paper, it is assumed that all the systematic biases are time-invariant parameters. It is also assumed that both radars have accurate position information for themselves; they are synchronized and have the same sampling intervals.
This paper is organized as follows: In section 2, the detailed descriptions of ABCM-SRUKF and the other comparative models such as AAM, OBEM, et al., are given. Then, in Section 3, we test the comparative models and ABCM-SRUKF with a simulated track data. Conclusions are given in Section 4. In Appendices A and B, the validity of the model is verified and the estimate errors induced by the linearization are analysed.
2. REGISTRATION MODELS
The problem addressed in this work can be stated as follows. Consider the ith radar, where i=1, 2, which is installed on the ith moving ship. The geographic coordinates of the ith ship are latitude Ls i, longitude Rs i, and altitude H i, which are known in real time. Three-axis gyro-stabilized platform of radar can steadily track local East-North-Up (ENU) frame. Chapter 2 of Progri's pioneering work (Progri, Reference Progri2011) provides an excellent environment description of local and global reference coordinates and an illustration of various potential applications of this technology. For the ENU frame, its origin o locates at the centre of the gyro-stabilized platform, three mutually orthogonal axes x, y, and z refer to the directions of East, North and Up, respectively. The plane xoy is horizontal. The output Cartesian coordinates of the gyro-stabilized platform is defined as platform frame, which has the same origin as the ENU frame, but its axes have angle biases with the corresponding axes of the ENU. These biases are attitude biases. Figure 1 shows the conversion process from the platform frame to ENU, where x p, yp, and z p denotes x, y, and z axis of platform frame, respectively, and the axes drawn in dashed lines are the intermediate axes. As shown in Figure 1, the transition of the target coordinates from the platform frame to ENU is accomplished by first rotating about the y-axis of the platform frame by the roll angle Δψ, then rotating about the intermediate x-axis by the pitch angle Δη, and rotating about the final z-axis by the yaw angle Δϕ. Customarily, the polarities of Δϕ and Δψ abide by the left-hand rule, while Δψ abides by the right-hand rule.

Figure 1. Conversion from the platform frame to ENU.
Radar measurements are based on measurement frame which shares the same origin with the platform frame. There are azimuth and elevation biases between the corresponding axes of two frames. The measurements of the targets from the ith radar include the range r i, the azimuth θ i, and the elevation ε i, which contain the true target position information (such as the true range r it, azimuth θ it, and elevation ε it), radar offset biases (such as the range bias Δr i, the gain of the range k ri, azimuth Δθ i, and elevation Δε i), the attitude biases of gyro-stabilized platform (such as the yaw bias Δϕ i, pitch Δη i, and roll Δψ i), and random measurement errors (such as the range error δ ri, azimuth δ θi, and elevation δ εi) which are zero-mean, Gaussian with known standard deviations.
The main work for mobile radar registration is to estimate radar offset biases and attitude biases simultaneously using both radars’ raw measurements. Figure 2 is the main procedures usually used to establish mathematic models. First, radar offset biases and random measurement errors included in the raw measurements are removed to obtain the True Target Coordinates (t.t.c.) in the platform frame. Then, the conversion to ENU is accomplished according to the attitude biases. Finally, the conversion from ENU to the Earth-Centered Earth-Fixed (ECEF) frame (see Zhou et al., Reference Zhou, Henry and Martin1999) is used to obtain the t.t.c. in a common reference frame. The theoretical basis for the alignment algorithm is that the t.t.c. included in both radars’ raw measurements are equal when they are converted to a common reference frame.

Figure 2. The general procedure for mobile radar registration.
From Figure 2, we know that the whole process is complicated and the conversion from the platform frame to ENU needs three rotation transformations. If we use the equivalent error expressions caused by the attitude biases, we can write out the t.t.c. in ENU frame directly from radar measurements. When the nonlinear filter is used for the model, such as SRUKF, the linearization process can also be deleted. As shown in Figure 3, the main modelling procedures are given step by step as follows:

Figure 3. The block diagram of ABCM-SRUKF.
2.1. Selection of the State Vector
Usually, for the moving radar registration equations, the offset and attitude biases of both radars are written sequentially in the state vector as (the order can be changed):
where the superscript “T” denotes the matrix or vector transposition.
According to (Wang et al., Reference Wang, Chen and Jia2012), in the first-order linearized equations of the systematic bias estimation models, the coefficients of the azimuth bias of radar i and the yaw bias of platform i are equivalent and both biases are linearly dependent. In this situation, if Equation (1) was used as state vector to establish the registration equations, the system is unobservable, and the estimates obtained individually for both biases are meaningless. On the contrary, when the subtraction of the yaw bias from the azimuth bias serves as one variable, the system is observable. That is, the state vector should be selected as:
In view of this, all the linearized models will select Equation (2) as their state vectors. Since all the biases are selected as the state variables, this kind of model is called the All Augmented Model (AAM) by Wang et al. (Reference Wang, Chen and Jia2012).
As for the nonlinear models, given the multiplicative coupling of biases and the existence of high-order terms, it is impossible to use (Δθ i–Δϕ i) as one variable when nonlinear filter (such as UKF) is used. Both biases are estimated separately, that is, Equation (1) is selected as the state vector. However, the linear dependences are still in being although they were testified in the linearized models, that is, the estimates for each variable are meaningless when they are used separately. On the contrary, if they are combined as one term or used simultaneously, they become meaningful, which can be seen in the following simulations. For convenience of comparison, the subtractions of both biases’ estimates are used in the nonlinear models when we compute the Root Mean Square Errors (RMSE).
2.2. True Target Coordinates in ENU Frame
Given the true target coordinates in radar iENU frame as [x i, yi, zi], and the attitude biases of the platform i as [Δϕ i, Δη i, Δψ i], Wang et al., (Reference Wang, Chen and Jia2012) derived the expressions for the equivalent measurement errors of the attitude biases as:
According to Equations (3)–(5), given the ith radar measurements at time “k” (r i(k), θ i(k), ε i(k)), the systematic biases (Δr i(k), k ri(k), Δθ i(k), Δε i(k)), and the random measurement errors (δr i(k), δ θi(k), δ εi(k)), the t.t.c. in the ENU frame can be written as:

where ![]() ,
, ![]() .
.
For simplicity, the time argument “k” is omitted in Equation (6). Since the true range of the target r it cannot be obtained, it can be approximated by the range measurement r i, and:

2.3. Transition from ENU to ECEF Frame
According to Zhou et al., (Reference Zhou, Henry and Martin1999), given the ith radar geographic coordinates, it is convenient to transform the t.t.c. from ENU to ECEF frame as:
where:
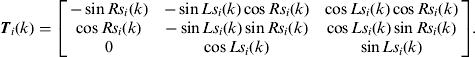
and:
 denotes the t.t.c. in the ECEF frame obtained from the measurements of the ith radar.
denotes the t.t.c. in the ECEF frame obtained from the measurements of the ith radar.Xis(k) denotes the ith radar ECEF coordinates converted from its geographic coordinates.
T i(k) is the rotation matrix.
Xis(k) and T i(k) are only correlated with the geographic coordinates of the ith radar at time k.
2.4. Nonlinear ABCM Based on the SRUKF (ABCM-SRUKF)
In view of the fact that the true coordinates of the same target in the ECEF frame denoted by the different radar measurements are equal, we can obtain:
Equation (9) can be rewritten in the form of nonlinear measurement (registration) equations as:
where:
ZABCM(k)=X2s(k)−X1s(k);
 ;
;w(k)=[w1T(k), w2T(k)]T.
In Equation (10), all the offset biases and attitude biases are assumed to be constants, then, the state equations can be written as
In Equation (11), the state transition matrix is a unit matrix and the process noises for systematic biases are assumed to be zeroes.
Here, the model that converts the attitude biases into radar measurement errors and does not use the rotation transformation is called ABCM. The UKF proposed by Julier and Uhlmann (Reference Julier and Uhlmann2004), whose theoretical basis is the unscented transformation, can apply to nonlinear models and the computation burden does not increase much compared with a KF. SRUKF is the improvement of UKF which can ensure consistent estimation. For a detailed description of SRUKF see: Julier and Uhlmann (Reference Julier and Uhlmann2004); Li et al. (Reference Li, Wang, Rizos, Mumford and Ding2006); Jwo et al., (Reference Jwo and Lai2009); and Xu et al., (Reference Xu, Li, Rizos and Xu2010). In this paper, SRUKF is used for the nonlinear models composed of Equations (10) and (11), and we call this algorithm ABCM-SRUKF. The complete algorithm block diagram for ABCM-SRUKF is given in Figure 3 and the flowchart for ABCM-SRUKF is given in Figure 4.
In order to compare ABCM-SRUKF, nonlinear AAM and linearized ABCM (which is equivalent to linearized AAM) are given below.
2.5. Comparative Models
2.5.1. Nonlinear AAM based on SRUKF (AAM-SRUKF)
The dynamic equations of AAM are established according to the mechanisms of radar measurements.
First, the t.t.c. in radar i platform frame can be written as:

where ρ i(k)=θ i(k)−Δθ i(k)−δ θi(k), μ i(k)=ε i(k)−Δε i(k)−δ εi(k).
Secondly, transition from the platform frame to ENU can be written as:
where:
Xi_ENU(k) denotes the t.t.c. in the ith radar ENU frame.
Ti_p2ENU(k) is an orthogonal matrix which denotes the rotation matrix from the platform frame to ENU.
and:

where:
 ;
;  ;
; ;
; ;
; ;
;  ;
; ;
;  ;
;  .
.
Thirdly, substituting Equations (12), (13) into Equation (7), the t.t.c. in ECEF frame can be written as:
Fourthly, the nonlinear AAM registration equations can be written as:
Equations (11) and (15) are the dynamic equations for the nonlinear AAM, and SRUKF can be used to estimate the offset and attitude biases simultaneously.

Figure 4. The complete algorithm flowchart for ABCM-SRUKF.
2.5.2. Linearized AAM based on Kalman filter (AAM-KF)
The linearized model of Equation (15) and Equation (2) were used as the state vector. The description of linearized AAM can be written as:
where:
ZAAM(k)=X2s(k)−X1s(k)+T2(k)X2(k)−T1(k)X1(k),
 ,
,H(k)=[T1(k)A1(k),−T2(k)A2(k),D1(k),−D2(k)],
C(k)=[C1(k),−C2(k)],
A i(k)=∂Xi_p(k)∂βi(k),
Ci(k)=∂Xi_p(k)/∂wi(k)
βi(k)=[Δr i(k), k ri(k), Δθ i(k), Δε i(k)]T,
wi(k)=[δ ri(k), δ θi(k), δ εi(k)]T,
 ,
,
The state equations can be written as:
Using KF for the dynamic equations composed of Equations (16) and (17), the model can be called the all augmented model based on a KF.
2.5.3. Linearized ABCM Based on Kalman Filter (ABCM-KF)
Selecting Equation (1) as the state vector, Equation (10) can be linearized by using the first-order Maclaurin expansion, then, KF can be used for estimation. This model is named as ABCM based on KF. ABCM-KF is equivalent to AAM-KF in essence, which will be proved in appendix A.
The comparisons of the models mentioned above can be seen in Table 1, where different rows denote different models mentioned in this paper. The column of ‘System variables’ denotes all the variables used in the state vectors of different models. The column of ‘Characteristic of the model’ denotes the characteristic of the dynamic equations. The column of ‘Filter’ denotes the filter used for different models.
Table 1. Comparison of AAM, ABCM, and OBEM.

3. SIMULATION RESULTS
In order to analyse the performance of ABCM-SRUKF and another three algorithms OBEM (Wang et al., Reference Wang, Chen and Jia2012), AAM-SRUKF and ABCM-KF, which are equivalent in essence to AAM-KF(Wang et al., Reference Wang, Chen and Jia2012), they are all compared in the same test environment. The system test setup block diagram of ABCM-SRUKF can be seen in Figure 5, which is also applicable to the other three algorithms.

Figure 5. System test setup block diagram.
The four alignment algorithms mentioned above are tested by generating a common track for two radars installed on different ships. It is assumed that Ship 1 and Ship 2 are moving with a constant velocity model and the initial geographical coordinates are [40°, 116°, 10m], [40·4°, 115·8°, 10m], respectively. The initial states of both ships in their native ENU frames are the same, i.e., [0,10m/s,0,10m/s,0,0]. In the state vector, the variables denote x-coordinate, x-velocity, y-coordinate, y-velocity, z-coordinate, and z-velocity, respectively. The standard deviations of both ships’ process noises are equal which are given in x, y, and z coordinates by 0·1m/s 2, 0·1m/s 2, and 0m/s 2, respectively. The fusion centre is located at the initial position of Ship 1. The constant velocity model is also used for the target. The initial state of the target in fusion centre is [60km, −150m/s, 50km, 0m/s, 5km, 1m/s]. The standard deviations of the process noises in x, y, and z coordinates are set to 1m/s 2, 1m/s 2, and 0·1m/s 2, respectively. The geometry of radars and target is shown in Figure 6. The true offset biases of both radars are assumed to be constants and equal as Δr i=300m, k ri=0·01, Δθ i=2°, Δε i=2°, respectively. The standard deviations of the random measurement noises for both radars are σ ri=50m, σ θi=0·5°, and σ εi=0·5°, respectively. The attitude biases of both platforms are also assumed to be constant and equal as Δϕ i=1°, Δη i=1°, and Δψ i=1°, respectively. It is assumed that both radars are synchronized with the same sampling intervals T=5s. 200 scans of the target are simulated and the number of Monte Carlo runs is set to 100. For length limitation, only the estimation results of radar 1 are given below.

Figure 6. The geometry of radar and target.
Figure 7 are the RMSEs of Radar 1 offset bias estimates, where the green lines represent the results of ABCM-KF, the blue lines represent OBEM-KF, the red lines represent ABCM-SRUKF, and the magenta lines represent AAM-SRUKF.
Figure 7(a) represents the gross range bias which is the sum of the range bias and the range bias induced by the gain of the range.
Figure 7(b) is the equivalent azimuth bias which is the subtraction of the yaw bias from azimuth bias.
Figure 7(c) is the elevation bias.

Figure 7. RMSEs of Radar 1 bias estimates. (a) gross range bias; (b) equivalent azimuth bias; (c) elevation bias.
Compared with the other three models, the attitude bias estimates of ABCM-SRUKF are always zeros regardless of the different attitude bias magnitudes, because in ABCM, the target location information weakens the influences of the attitude biases and restricts their amplitude of variation, which can be seen from the equivalent radar measurement error expressions at Equations (3)–(5). On the contrary, there is no weakening in AAM, which leads to bigger attitude estimate magnitudes (see Figure 8). In reality, attitude biases are usually small, then, the estimate errors will be unacceptable. According to Equation (5), the big estimate errors of attitude biases influence the estimate accuracies of radar elevation biases. So, ABCM-SRUKF has the best estimation results for elevation biases. For pitch and roll biases, OBEM sets them to zeros, which coincides with the results of ABCM-SRUKF. So, they have the similar estimate accuracies in elevation biases. Figure 7(b) shows that the RMSE of the subtraction of yaw bias from azimuth bias is less than 0·3°, which verifies the correctness of the selection of state vector.

Figure 8. RMSEs of the attitude bias estimates of both platforms. (a) pitch bias; (b) roll bias.
The RMSEs of pitch and roll biases estimated by three models (except OBEM) are given in Figure 8. The results show that the estimates deviate from the true values significantly. It is not ideal for the three models to estimate the attitude biases.
Figure 9 shows the RMSEs of Radar 1 measurements rectified by offset bias estimates. Since the attitude estimate errors are large, the attitude biases are omitted when the raw measurements are rectified. In Figure 9, the black lines represent the RMSE curves of raw measurements. Figure 9(c) shows that ABCM-SRUKF and OBEM have significant performances on rectifying z-coordinate errors.

Figure 9. RMSEs of Radar 1 measurements rectified by the offset bias estimation results. (a) x-coordinate; (b) y-coordinate; (c) z-coordinate.
Comparing four methods above, it is obvious that ABCM-SRUKF and OBEM have better and closer performance. Besides that, the former has simplified process for modelling and the idea of the conversion from attitude biases to measurement errors is both novel and prospective. It can be applied to all the detection systems with attitude biases and it does not need linearization. However, the latter has lower system state dimension, which can reduce the computation burden. Both algorithms have their own merits and they can be used for mobile radar registration.
4. CONCLUSIONS
For mobile 3-D radar registration, Wang et al., (Reference Wang, Chen and Jia2012) gave the equivalent measurement error expressions caused by the attitude biases. According to these expressions, they proposed Optimized Bias Estimation Model (OBEM), which is a linearized model and omits pitch and roll biases to establish registration model. Compared with All Augmented Model (AAM), which uses all the radar offset biases and platform attitude biases as state vector for registration, OBEM can obtain better elevation bias estimates and its calibration effects on radar raw measurements are better than AAM. However, OBEM cannot explain why the estimates of the attitude biases are poor. In order to testify the influences of linearization on the attitude bias estimates, in this paper, the nonlinear AAM and ABCM are proposed which use SRUKF as filter. ABCM uses the equivalent measurement error expressions to convert radar measurements to ENU frame directly without using rotation transformation, which simplifies the modelling process. Appendix A proves that linearized AAM and ABCM are equivalent in essence, and it also proves the validity of the derivations of the equivalent measurement error expressions at Equations (3)–(5). Appendix B gives the influences of linearization on attitude bias estimates mathematically and explains that the linearization is not the main reason for the poor estimates of attitude biases. The simulation results in Appendix B prove these results.
The observability proof for AAM in proposition 1 in Wang et al., (Reference Wang, Chen and Jia2012) and good estimate results for yaw bias in OBEM remind us that other dependencies may exist for pitch and roll biases with radar offset biases.
According to Equations (3)–(5), ![]() , and
, and ![]() should serve as one variable to keep the observability of the system. We will develop this method in our future work.
should serve as one variable to keep the observability of the system. We will develop this method in our future work.
ACKNOWLEDGEMENTS
This work was supported in part by the National Natural Science Foundation of China 61032001, 61102165, 61002006 and Special Foundation Program for Mountain Tai Scholars of China.The authors would like to thank Giftet Inc. for its outstanding support and for enabling Dr. Progri to write portions of this article.
APPENDIX A
In order to testify the validity of the equivalent measurement error expressions caused by the attitude biases, the true target coordinates in ENU frame obtained from two different methods should be compared, that is, from the ABCM method and the rotation transformation method. The following are the derivations.
A1. THE ABCM METHOD
A first-order Taylor series expansion can be made for the nonlinear ABCM Equation (6) about zero systematic biases and random measurement errors as:
where:
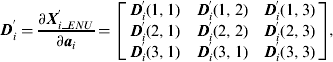
where the elements of matrix ![]() can be written further as:
can be written further as:
A2. THE ROTATION TRANSFORMATION METHOD
Xi_ENU obtained by using the first-order linearization can be written out as:
In Equation (A15), Xi, Ai, and Ci are the same as those in Equation (16), and the higher-order minor terms are omitted. Also, the only term which contains the attitude biases is ΔiXi which can be rewritten as:
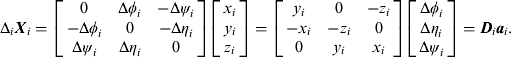
Then, Equation (A15) can be rewritten as:
Comparing Di in (A16) with ![]() in Equation (A6), we can obtain:
in Equation (A6), we can obtain:
According to Equations (A1), (A3), (A4), (A5), and (A17):
Equation (A19) proves the equivalence between ABCM and the normal model, which also proves the validity of the equivalent radar measurement error expressions caused by the attitude biases.
APPENDIX B
B1. THEOREM 1
Incorrect covariance of measurement noises induced by linearization is not the main factor to affect the estimate accuracy.
B2. PROOF
In order to analyse the effects of the incorrect covariance of the measurement noises in ABCM, we use the linearized model of ABCM which consists of Equations (24) and (25) based on Seo et al., (Reference Seo, Lee and Park2006).
Assuming that the complete information on the initial state covariance P(0) and the measurement noise covariance R(k) are not known, the KF designed for Equations (24) and (25) is no longer optimal, it can be expressed by:
where:
are model representations of P(0) and R(k) respectively. ΔP(0) and ΔR(k) denote the respective modelling errors. Then, the mean-squared error of the estimate is expressed by:
where P(k+1) is an actual covariance matrix of the suboptimal estimate in (B1)–(B5), and:
From Equation (B7):
Proceeding in this way and substituting Equations (B5) and (B8) into Equation (B7), we can obtain:
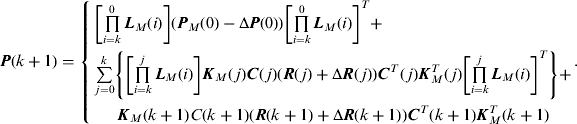
Let ![]() and ΔPR denote the mean-squared errors of the estimation caused by ΔP(0) and ΔR(k), respectively, according to Equation (B9), we have
and ΔPR denote the mean-squared errors of the estimation caused by ΔP(0) and ΔR(k), respectively, according to Equation (B9), we have
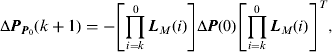

According to Equations (B10) and (B11), the influences of the incorrect initial covariance on P(k+1) will diminish with time. In view of this, the errors of the equivalent measurement error covariance in Equation (24) caused by linearization are probably the main factor. Following is the computation of ΔR(j) in (B11).
For nonlinear registration model Equation (27), it can be written in the exact first-order Maclaurin series as:
where E(β, w)=[Ex, Ey, Ez]T denotes the exact remainder terms in x, y, and z coordinate, respectively.
In Equation (B12), there are 10 variables, so, each element of E contains 10×10=100 terms. Since the coefficients of the attitude biases are smaller than 1, for the sake of simplicity of analysis, the errors caused by the attitude biases will not be considered. Then, each direction in E has only 49 terms. From Equation (B12), we can obtain:



where:
 ;
;  ;
; ; and
; and 
Using the well-known inequalities:
and substituting the true bias values in the standard deviation for random measurement error terms in Equations (B13)–(B15), the maximum values of Ex, Ey, and Ez, respectively will be obtained.
Then:
where diag(V) denotes a square matrix whose main diagonal elements are composed of the elements of vector V, and the other elements are zeros. Substituting Equation (B17) into Equation (B11), the upper bounds of ΔPR can be calculated.
Figure A1 is the square root of the diagonal elements of covariance matrix of the estimate. The thick lines represent the covariance of the linearized model using KF, and dotted lines represent the actual covariance upper bounds considering errors caused by linearization. For the range upper bounds, it's a little bigger, because in Equation (B13), Equation (B17) and the absolute value for each term can amplify the errors, and the number of the terms in Equation (B13) is large. Despite the amplification, the upper bound is only about 100 m bigger than the calculated one. The upper bounds for the other biases are very close to the calculated values which show that the effects of the linearization errors are small.

Figure A1. Estimated covariance considering linearization errors
From Equations (B13)–(B15), we know that the second-order remainder terms are smaller by an order of magnitude than the first-order terms. In addition, Figure A1 proves that the incorrect covariance of P(0) and R(k) are not the main factors for the poor estimates of the attitude biases and that the instability of the system should be the main factor. According to the definition of stability, when the system is stable, the adverse effects of P(0) will be diminished with time automatically which can be seen in Qin et al., (Reference Qin, Zhang and Wang1998). One of the sufficient conditions for stability is the controllability and observability of the system. Though it is not the necessary condition, the instability of the model we used in this paper shows that the system may be uncontrollable or unobservable, which will be studied in our future work.




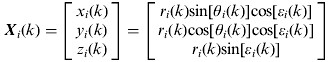 ,
,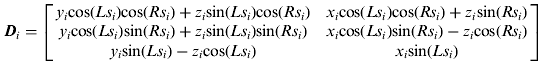 ,
,










