1 Introduction
1.1 Background
Let ![]() ${\mathfrak g}$ be a symmetrisable Kac–Moody algebra and
${\mathfrak g}$ be a symmetrisable Kac–Moody algebra and ![]() $\theta :{\mathfrak g}\rightarrow {\mathfrak g}$ an involutive Lie algebra automorphism. In the theory of quantum symmetric pairs, one considers quantum group analogues of the fixed Lie subalgebra
$\theta :{\mathfrak g}\rightarrow {\mathfrak g}$ an involutive Lie algebra automorphism. In the theory of quantum symmetric pairs, one considers quantum group analogues of the fixed Lie subalgebra ![]() ${\mathfrak g}^\theta =\{x\in {\mathfrak g}\mid \theta (x)=x\}$. The main objects of investigation are certain subalgebras
${\mathfrak g}^\theta =\{x\in {\mathfrak g}\mid \theta (x)=x\}$. The main objects of investigation are certain subalgebras ![]() ${\mathcal B}_{\mathbf {c}}$ of the quantised enveloping algebra
${\mathcal B}_{\mathbf {c}}$ of the quantised enveloping algebra ![]() ${U_q(\mathfrak {g})}$ which specialise to
${U_q(\mathfrak {g})}$ which specialise to ![]() $U\left ({\mathfrak g}^\theta \right )$ in a suitable limit
$U\left ({\mathfrak g}^\theta \right )$ in a suitable limit ![]() $q\rightarrow 1$. The subalgebras
$q\rightarrow 1$. The subalgebras ![]() ${\mathcal B}_{\mathbf {c}}$ satisfy the (right) coideal property
${\mathcal B}_{\mathbf {c}}$ satisfy the (right) coideal property ![]() ${\varDelta }({\mathcal B}_{\mathbf {c}})\subset {\mathcal B}_{\mathbf {c}}\otimes {U_q(\mathfrak {g})}$, where
${\varDelta }({\mathcal B}_{\mathbf {c}})\subset {\mathcal B}_{\mathbf {c}}\otimes {U_q(\mathfrak {g})}$, where ![]() ${\varDelta }$ denotes the coproduct of
${\varDelta }$ denotes the coproduct of ![]() ${U_q(\mathfrak {g})}$, and we refer to them as quantum symmetric pair coideal subalgebras.
${U_q(\mathfrak {g})}$, and we refer to them as quantum symmetric pair coideal subalgebras.
For ![]() ${\mathfrak g}$ of finite type, a comprehensive theory of quantum symmetric pairs was developed by G. Letzter in [Reference LetzterLet99]. This theory was extended to the Kac–Moody case in [Reference KolbKol14] for involutive automorphisms of the second kind of
${\mathfrak g}$ of finite type, a comprehensive theory of quantum symmetric pairs was developed by G. Letzter in [Reference LetzterLet99]. This theory was extended to the Kac–Moody case in [Reference KolbKol14] for involutive automorphisms of the second kind of ![]() ${\mathfrak g}$. Such involutions are determined by Satake diagrams
${\mathfrak g}$. Such involutions are determined by Satake diagrams ![]() $(X,\tau )$, where X is a subset of the nodes I of the underlying Dynkin diagram and
$(X,\tau )$, where X is a subset of the nodes I of the underlying Dynkin diagram and ![]() $\tau :I\rightarrow I$ is an involutive diagram automorphism. The subset
$\tau :I\rightarrow I$ is an involutive diagram automorphism. The subset ![]() $X\subset I$ has to be of finite type, and the pair
$X\subset I$ has to be of finite type, and the pair ![]() $(X,\tau )$ has to satisfy the compatibility conditions given in [Reference KolbKol14, Definition 2.3]. It was observed by V. Regelskis and B. Vlaar in [Reference Regelskis and VlaarRV20] that these conditions can be slightly weakened and that the theory extends to a setting of generalised Satake diagrams
$(X,\tau )$ has to satisfy the compatibility conditions given in [Reference KolbKol14, Definition 2.3]. It was observed by V. Regelskis and B. Vlaar in [Reference Regelskis and VlaarRV20] that these conditions can be slightly weakened and that the theory extends to a setting of generalised Satake diagrams ![]() $(X,\tau )$ – see Section 2.3.
$(X,\tau )$ – see Section 2.3.
The theory of quantum symmetric pairs has been evolving rapidly over the past decade. In [Reference Bao and WangBW18], H. Bao and W. Wang initiated a program to extend Lusztig’s theory of canonical bases to the setting of quantum symmetric pairs. This program fed into a general construction of a universal K-matrix in [Reference Balagović and KolbBK19], which is the quantum symmetric pair analogue of the universal R-matrix for quantum groups. A centrepiece in both constructions was a notion of bar involution for quantum symmetric pairs, which appeared independently in [Reference Ehrig and StroppelES18] and [Reference Bao and WangBW18]. These developments led to a flurry of activity aiming to extend many quantum group related constructions to the setting of quantum symmetric pairs.
1.2 The problem
One of the outstanding problems in the theory of quantum symmetric pairs is to give an explicit, conceptual and simple description of the algebra ![]() ${\mathcal B}_{\mathbf {c}}$ in terms of generators and relations for all generalised Satake diagrams
${\mathcal B}_{\mathbf {c}}$ in terms of generators and relations for all generalised Satake diagrams ![]() $(X,\tau )$. In the present paper we solve this problem completely. To describe previous work and to formulate our results, we recall the definition of the quantum symmetric pair coideal subalgebra
$(X,\tau )$. In the present paper we solve this problem completely. To describe previous work and to formulate our results, we recall the definition of the quantum symmetric pair coideal subalgebra ![]() ${\mathcal B}_{\mathbf {c}}$ in terms of the pair
${\mathcal B}_{\mathbf {c}}$ in terms of the pair ![]() $(X,\tau )$.
$(X,\tau )$.
Let ![]() $U=U_q({\mathfrak g}')$ be the quantised enveloping algebra of the derived Lie algebra
$U=U_q({\mathfrak g}')$ be the quantised enveloping algebra of the derived Lie algebra ![]() ${\mathfrak g}'=[{\mathfrak g},{\mathfrak g}]$ with standard generators
${\mathfrak g}'=[{\mathfrak g},{\mathfrak g}]$ with standard generators  $E_i, F_i, K_i^{\pm 1}$ for
$E_i, F_i, K_i^{\pm 1}$ for ![]() $i\in I$, defined over the field
$i\in I$, defined over the field ![]() ${\mathbb K}=k(q)$ of rational functions in an indeterminate q. Let
${\mathbb K}=k(q)$ of rational functions in an indeterminate q. Let ![]() ${\mathcal M}_X\subset U$ be the subalgebra generated by
${\mathcal M}_X\subset U$ be the subalgebra generated by  $E_i, F_i, K_i^{\pm 1}$ for
$E_i, F_i, K_i^{\pm 1}$ for ![]() $i\in X$ and let
$i\in X$ and let ![]() $U^0_\Theta $ be the subalgebra generated by
$U^0_\Theta $ be the subalgebra generated by  $K_j, K_i K_{\tau (i)}^{-1}$ for
$K_j, K_i K_{\tau (i)}^{-1}$ for ![]() $j\in X, i\in I\setminus X$. Let W be the Weyl group of
$j\in X, i\in I\setminus X$. Let W be the Weyl group of ![]() ${\mathfrak g}$ and let
${\mathfrak g}$ and let ![]() $w_X$ be the longest element in the parabolic subgroup of W for the subset X. We write
$w_X$ be the longest element in the parabolic subgroup of W for the subset X. We write ![]() $T_{w_X}$ to denote the corresponding Lusztig automorphism. By construction,
$T_{w_X}$ to denote the corresponding Lusztig automorphism. By construction, ![]() $U^0_\Theta $ is the group algebra of the subgroup
$U^0_\Theta $ is the group algebra of the subgroup ![]() $Q^\Theta =\{\beta \in Q\mid \beta =-w_X\tau (\beta )\}$ of the root lattice Q. Let
$Q^\Theta =\{\beta \in Q\mid \beta =-w_X\tau (\beta )\}$ of the root lattice Q. Let ![]() $K_\beta $ for
$K_\beta $ for ![]() $\beta \in Q^\Theta $ be the corresponding basis element of
$\beta \in Q^\Theta $ be the corresponding basis element of ![]() $U^0_\Theta $. For each
$U^0_\Theta $. For each ![]() $i\in I\setminus X$, define
$i\in I\setminus X$, define
 $$ \begin{align} B_i=F_i- c_iT_{w_X}\left(E_{\tau(i)}\right)K_i^{-1}, \end{align} $$
$$ \begin{align} B_i=F_i- c_iT_{w_X}\left(E_{\tau(i)}\right)K_i^{-1}, \end{align} $$where ![]() $c_i\in {\mathbb K}^\ast $. For a good theory, we need to assume that the parameters
$c_i\in {\mathbb K}^\ast $. For a good theory, we need to assume that the parameters ![]() ${\mathbf {c}}=(c_i)_{i\in I\setminus X}$ belong to the set
${\mathbf {c}}=(c_i)_{i\in I\setminus X}$ belong to the set
 $$ \begin{align} {\mathcal C}=\left\{{\mathbf{c}}=(c_i)_{i\in I\setminus X}\in ({\mathbb K}^\times)^{I\setminus X}\mid c_i=c_{\tau(i)} \text{ if}\ \left(\alpha_i,w_X\left(\alpha_{\tau(i)}\right)\right)=0\right\}. \end{align} $$
$$ \begin{align} {\mathcal C}=\left\{{\mathbf{c}}=(c_i)_{i\in I\setminus X}\in ({\mathbb K}^\times)^{I\setminus X}\mid c_i=c_{\tau(i)} \text{ if}\ \left(\alpha_i,w_X\left(\alpha_{\tau(i)}\right)\right)=0\right\}. \end{align} $$By definition, the quantum symmetric pair coideal subalgebra ![]() ${\mathcal B}_{\mathbf {c}}$ for
${\mathcal B}_{\mathbf {c}}$ for ![]() ${\mathbf {c}}=(c_i)_{i\in I\setminus X}\in {\mathcal C}$ is the subalgebra of U generated by
${\mathbf {c}}=(c_i)_{i\in I\setminus X}\in {\mathcal C}$ is the subalgebra of U generated by ![]() ${\mathcal M}_X$,
${\mathcal M}_X$, ![]() $U^0_\Theta $ and the elements
$U^0_\Theta $ and the elements ![]() $B_i$ given by equation (1.1). For
$B_i$ given by equation (1.1). For ![]() $j\in X$ we also write
$j\in X$ we also write ![]() $B_j=F_j$.
$B_j=F_j$.
The algebra ![]() ${\mathcal B}_{\mathbf {c}}$ has a filtration
${\mathcal B}_{\mathbf {c}}$ has a filtration ![]() ${\mathcal F}$ defined by a degree function given by
${\mathcal F}$ defined by a degree function given by
 $$ \begin{align} \begin{aligned} \deg(B_i)&=1 \qquad \text{for}\ i\in I\setminus X,\\ \deg(h)&=0 \qquad \text{for}\ h\in {\mathcal M}_X U^0_\Theta. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \deg(B_i)&=1 \qquad \text{for}\ i\in I\setminus X,\\ \deg(h)&=0 \qquad \text{for}\ h\in {\mathcal M}_X U^0_\Theta. \end{aligned} \end{align} $$For ![]() $i,j\in I$, let
$i,j\in I$, let ![]() $S_{ij}(x,y)\in {\mathbb K}[x,y]$ be the quantum Serre polynomial given by equation (2.1). Let
$S_{ij}(x,y)\in {\mathbb K}[x,y]$ be the quantum Serre polynomial given by equation (2.1). Let  $\left (a_{ij}\right )_{i,j\in I}$ be the generalised Cartan matrix of
$\left (a_{ij}\right )_{i,j\in I}$ be the generalised Cartan matrix of ![]() ${\mathfrak g}$. By definition, one has
${\mathfrak g}$. By definition, one has ![]() $S_{ij}\left (B_i,B_j\right )\in {\mathcal F}_{\deg \left (i,j\right )}({\mathcal B}_{\mathbf {c}})$, where
$S_{ij}\left (B_i,B_j\right )\in {\mathcal F}_{\deg \left (i,j\right )}({\mathcal B}_{\mathbf {c}})$, where
 $$ \begin{align*} \deg(i,j)=\begin{cases} 2-a_{ij} & \text{if}\ i,j\in I\setminus X,\\ 1-a_{ij} & \text{if}\ i\in I\setminus X, j\in X,\\ 1 & \text{if}\ i\in X, j\in I\setminus X,\\ 0& \text{if}\ i,j\in X.\\ \end{cases} \end{align*} $$
$$ \begin{align*} \deg(i,j)=\begin{cases} 2-a_{ij} & \text{if}\ i,j\in I\setminus X,\\ 1-a_{ij} & \text{if}\ i\in I\setminus X, j\in X,\\ 1 & \text{if}\ i\in X, j\in I\setminus X,\\ 0& \text{if}\ i,j\in X.\\ \end{cases} \end{align*} $$A finer analysis implies that there exist elements ![]() $C_{ij}({\mathbf {c}})\in {\mathcal F}_{\deg \left (i,j\right )-1}({\mathcal B}_{\mathbf {c}})$ such that
$C_{ij}({\mathbf {c}})\in {\mathcal F}_{\deg \left (i,j\right )-1}({\mathcal B}_{\mathbf {c}})$ such that ![]() $S_{ij}\left (B_i,B_j\right )=C_{ij}({\mathbf {c}})$ for all
$S_{ij}\left (B_i,B_j\right )=C_{ij}({\mathbf {c}})$ for all ![]() $i,j\in I$. Let
$i,j\in I$. Let ![]() ${\mathcal M}_X^+$ denote the subalgebra of U generated by all
${\mathcal M}_X^+$ denote the subalgebra of U generated by all ![]() $E_j$ for
$E_j$ for ![]() $j\in X$. The following theorem was proved in [Reference LetzterLet02] for
$j\in X$. The following theorem was proved in [Reference LetzterLet02] for ![]() ${\mathfrak g}$ of finite type and was extended to the Kac–Moody case in [Reference KolbKol14]:
${\mathfrak g}$ of finite type and was extended to the Kac–Moody case in [Reference KolbKol14]:
Theorem 1.1 [Reference LetzterLet02, Theorem 7.4], [Reference KolbKol14, Theorem 7.1]
Let ![]() ${\mathbf {c}}\in {\mathcal C}$. The algebra
${\mathbf {c}}\in {\mathcal C}$. The algebra ![]() ${\mathcal B}_{\mathbf {c}}$ is generated over
${\mathcal B}_{\mathbf {c}}$ is generated over  ${\mathcal M}_X^+ U^0_\Theta $ by the elements
${\mathcal M}_X^+ U^0_\Theta $ by the elements ![]() $B_i$ for
$B_i$ for ![]() $i\in I$ subject to the following relations:
$i\in I$ subject to the following relations:
 $$ \begin{align} K_\beta B_i &=q^{-\left(\beta, \alpha_i\right)} B_i K_\beta &&\text{for all}\ \beta\in Q^\Theta, i\in I,\nonumber\\ E_iB_j-B_jE_i&=\delta_{ij}\frac{K_i-K_i^{-1}}{q_i-q_i^{-1}} &&\text{for all}\ i\in X,j\in I,\nonumber\\ S_{ij}\left(B_i,B_j\right)&=C_{ij}({\mathbf{c}}) && \text{for all}\ i,j\in I, i\neq j. \end{align} $$
$$ \begin{align} K_\beta B_i &=q^{-\left(\beta, \alpha_i\right)} B_i K_\beta &&\text{for all}\ \beta\in Q^\Theta, i\in I,\nonumber\\ E_iB_j-B_jE_i&=\delta_{ij}\frac{K_i-K_i^{-1}}{q_i-q_i^{-1}} &&\text{for all}\ i\in X,j\in I,\nonumber\\ S_{ij}\left(B_i,B_j\right)&=C_{ij}({\mathbf{c}}) && \text{for all}\ i,j\in I, i\neq j. \end{align} $$ We call the relations (1.4) the quantum Serre relations for ![]() ${\mathcal B}_{\mathbf {c}}$. In order to obtain defining relations for
${\mathcal B}_{\mathbf {c}}$. In order to obtain defining relations for ![]() ${\mathcal B}_{\mathbf {c}}$, it remains to determine these quantum Serre relations explicitly.
${\mathcal B}_{\mathbf {c}}$, it remains to determine these quantum Serre relations explicitly.
1.3 Previous results
It follows from [Reference KolbKol14, Lemma 5.11, Theorem 7.3] that ![]() $C_{ij}({\mathbf {c}})=0$ if
$C_{ij}({\mathbf {c}})=0$ if ![]() $i\in X$ or
$i\in X$ or ![]() $\tau (i)\notin \{i,j\}$. Hence it remains to determine the relations (1.4) explicitly in the following three cases:
$\tau (i)\notin \{i,j\}$. Hence it remains to determine the relations (1.4) explicitly in the following three cases:
(I)
 $\tau (i)=i$ and
$\tau (i)=i$ and  $i,j\in I\setminus X$.
$i,j\in I\setminus X$.(II)
 $\tau (i)=i$ and
$\tau (i)=i$ and  $i\in I\setminus X$,
$i\in I\setminus X$,  $j\in X$.
$j\in X$.(III)
 $\tau (i)=j$ and
$\tau (i)=j$ and  $i,j\in I\setminus X$.
$i,j\in I\setminus X$.
For all Satake diagrams of finite type, the relations (1.4) were determined explicitly in [Reference LetzterLet03, Theorem 7.1] by a subtle method involving the coproduct ![]() ${\varDelta }$ of U. Letzter’s method was extended to the Kac–Moody case in [Reference KolbKol14, Section 7] and was used to determine the relations (1.4) in the case
${\varDelta }$ of U. Letzter’s method was extended to the Kac–Moody case in [Reference KolbKol14, Section 7] and was used to determine the relations (1.4) in the case  $\left \lvert a_{ij}\right \rvert \le 2$. A general formula for
$\left \lvert a_{ij}\right \rvert \le 2$. A general formula for ![]() $C_{ij}({\mathbf {c}})$ in case (III) was obtained in [Reference Balagović and KolbBK15, Theorem 3.6], again using Letzter’s coproduct method. In [Reference Balagović and KolbBK15, Theorem 3.9] it was observed that cases (I) and (II) should allow a uniform treatment, but explicit formulas were still elusive for
$C_{ij}({\mathbf {c}})$ in case (III) was obtained in [Reference Balagović and KolbBK15, Theorem 3.6], again using Letzter’s coproduct method. In [Reference Balagović and KolbBK15, Theorem 3.9] it was observed that cases (I) and (II) should allow a uniform treatment, but explicit formulas were still elusive for  $\left \lvert a_{ij}\right \rvert>3$.
$\left \lvert a_{ij}\right \rvert>3$.
Following [Reference Chen, Lu and WangCLW20], we call a quantum symmetric pair quasi-split if ![]() $X=\emptyset $. Case (II) does not appear in the quasi-split setting. Explicit formulas for the quantum Serre relations (1.4) in the quasi-split case (I) were given in [Reference Chen, Lu and WangCLW20] in terms of so-called
$X=\emptyset $. Case (II) does not appear in the quasi-split setting. Explicit formulas for the quantum Serre relations (1.4) in the quasi-split case (I) were given in [Reference Chen, Lu and WangCLW20] in terms of so-called ![]() $\imath$divided powers for
$\imath$divided powers for ![]() ${\mathcal B}_{\mathbf {c}}$. The methods in [Reference Chen, Lu and WangCLW20] are calculational but do not involve Letzter’s coproduct method.
${\mathcal B}_{\mathbf {c}}$. The methods in [Reference Chen, Lu and WangCLW20] are calculational but do not involve Letzter’s coproduct method.
Using Letzter’s coproduct method, H. de Clercq was able to derive expressions for the quantum Serre relations (1.4) in general. Cases (I) and (II) are treated in [Reference de ClercqdC19, Theorems 3.13, 3.19] by combinatorially involved and unwieldy formulas. Nonetheless, in case (I), de Clercq was able to use her formulas to extend the quantum Serre relations from [Reference Chen, Lu and WangCLW20] from the quasi-split case to the case of general pairs ![]() $(X,\tau )$ [Reference de ClercqdC19, Theorem 4.7]. This extension of results was also performed in [Reference Chen, Lu and WangCLW21] in a more general setting of higher Serre relations. A conceptual and compact expression for the quantum Serre relations in case (II), however, remained to be found.
$(X,\tau )$ [Reference de ClercqdC19, Theorem 4.7]. This extension of results was also performed in [Reference Chen, Lu and WangCLW21] in a more general setting of higher Serre relations. A conceptual and compact expression for the quantum Serre relations in case (II), however, remained to be found.
In a new approach [Reference Casper, Kolb and YakimovCKY21], W. R. Casper and the present authors also found explicit, conceptual formulas for the quantum Serre relations (1.4) in the quasi-split case. The resulting relations are expressed in terms of continuous q-Hermite polynomials. The formulas are obtained using the star product interpretation of quantum symmetric pairs from [Reference Kolb and YakimovKY20]. Continuous q-Hermite polynomials differ from the ![]() $\imath$divided powers in [Reference Chen, Lu and WangCLW20], but the resulting descriptions of the quantum Serre relations bear many similarities. The method in [Reference Casper, Kolb and YakimovCKY21] involves minimal calculations.
$\imath$divided powers in [Reference Chen, Lu and WangCLW20], but the resulting descriptions of the quantum Serre relations bear many similarities. The method in [Reference Casper, Kolb and YakimovCKY21] involves minimal calculations.
In the present paper we further develop the star product interpretation of quantum symmetric pairs to give a conceptual and uniform treatment of the quantum Serre relations (1.4) in all three cases (I), (II) and (III) for arbitrary generalised Satake diagrams. This, in particular, settles the hardest and subtlest case, (II). We give a complete description of the defining relations of ![]() ${\mathcal B}_{\mathbf {c}}$ by closed formulas, which is independent of any of the previous approaches and is based on minimal calculations with star products.
${\mathcal B}_{\mathbf {c}}$ by closed formulas, which is independent of any of the previous approaches and is based on minimal calculations with star products.
1.4 Statement of results
To formulate our results, we need three families of ![]() ${\mathcal M}_X^+$-valued orthogonal polynomials. For
${\mathcal M}_X^+$-valued orthogonal polynomials. For ![]() $i\in I\setminus X$ define
$i\in I\setminus X$ define
 $$ \begin{align} {\mathcal Z}_i=q_i c_i \partial^R_{\tau(i)}\left(T_{w_X}\left(E_{\tau(i)}\right)\right), \end{align} $$
$$ \begin{align} {\mathcal Z}_i=q_i c_i \partial^R_{\tau(i)}\left(T_{w_X}\left(E_{\tau(i)}\right)\right), \end{align} $$where  $\partial ^R_{\tau (i)}$ is the Lusztig–Kashiwara skew derivation for U (see Section 2.1). The element
$\partial ^R_{\tau (i)}$ is the Lusztig–Kashiwara skew derivation for U (see Section 2.1). The element ![]() ${\mathcal Z}_i$ belongs to
${\mathcal Z}_i$ belongs to ![]() ${\mathcal M}_X^+$ and hence commutes with
${\mathcal M}_X^+$ and hence commutes with ![]() $B_\ell $ for all
$B_\ell $ for all ![]() $\ell \in I\setminus X$.
$\ell \in I\setminus X$.
A) The rescaled univariate q-Hermite polynomials 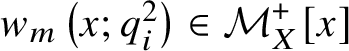 $w_m\left (x;q_i^2\right )\in {\mathcal M}_X^+[x]$ are defined for
$w_m\left (x;q_i^2\right )\in {\mathcal M}_X^+[x]$ are defined for ![]() $m\in {\mathbb N}$ by the initial conditions
$m\in {\mathbb N}$ by the initial conditions  $w_0\left (x;q_i^2\right )=1$,
$w_0\left (x;q_i^2\right )=1$,  $w_1\left (x;q_i^2\right )=x$ and the recursion
$w_1\left (x;q_i^2\right )=x$ and the recursion
 $$ \begin{align*} w_{m+1}\left(x;q_i^2\right)= x w_m\left(x;q_i^2\right)- \frac{1-q_i^{2m}}{\left(q_i-q_i^{-1}\right)^2} {\mathcal Z}_i w_{m-1}\left(x;q_i^2\right). \end{align*} $$
$$ \begin{align*} w_{m+1}\left(x;q_i^2\right)= x w_m\left(x;q_i^2\right)- \frac{1-q_i^{2m}}{\left(q_i-q_i^{-1}\right)^2} {\mathcal Z}_i w_{m-1}\left(x;q_i^2\right). \end{align*} $$The polynomials  $w_m\left (x;q_i^2\right )$ are rescaled versions of the univariate continuous q-Hermite polynomials defined, for example, in [Reference Koekoek, Lesky and SwarttouwKLS10, 14.26] (see Sections 4.1 and 5.1 for details).
$w_m\left (x;q_i^2\right )$ are rescaled versions of the univariate continuous q-Hermite polynomials defined, for example, in [Reference Koekoek, Lesky and SwarttouwKLS10, 14.26] (see Sections 4.1 and 5.1 for details).
B) The rescaled bivariate continuous q-Hermite polynomials  $w_{m,n}(x,y;q_i^2,q_i^{a_{ij}})\in {\mathcal M}_X^+[x,y]$ for
$w_{m,n}(x,y;q_i^2,q_i^{a_{ij}})\in {\mathcal M}_X^+[x,y]$ for ![]() $m,n\in {\mathbb N}$ are defined by the initial condition
$m,n\in {\mathbb N}$ are defined by the initial condition  $w_{0,n}(x,y;q_i^2,q_i^{a_{ij}})=w_n(y;q_i^2)$ for all
$w_{0,n}(x,y;q_i^2,q_i^{a_{ij}})=w_n(y;q_i^2)$ for all ![]() $n\in {\mathbb N}$ and the recursion
$n\in {\mathbb N}$ and the recursion
 $$ \begin{align*} x w_{m,n}\left(x,y;q_i^2,q_i^{a_{ij}}\right) & = w_{m+1,n}\left(x,y;q_i^2, q_i^{a_{ij}}\right) +\frac{1-q_i^{2m}}{\left(q_i-q_i^{-1}\right)^2} {\mathcal Z}_i w_{m-1,n}\left(x,y; q_i^2,q_i^{a_{ij}}\right)\\ &\quad + \frac{q_i^{2m}\left(1-q_i^{2n}\right)}{\left(q_i-q_i^{-1}\right)^2}q_i^{a_{ij}}{\mathcal Z}_i w_{m,n-1}\left(x,y;q_i^2,q_i^{a_{ij}}\right). \end{align*} $$
$$ \begin{align*} x w_{m,n}\left(x,y;q_i^2,q_i^{a_{ij}}\right) & = w_{m+1,n}\left(x,y;q_i^2, q_i^{a_{ij}}\right) +\frac{1-q_i^{2m}}{\left(q_i-q_i^{-1}\right)^2} {\mathcal Z}_i w_{m-1,n}\left(x,y; q_i^2,q_i^{a_{ij}}\right)\\ &\quad + \frac{q_i^{2m}\left(1-q_i^{2n}\right)}{\left(q_i-q_i^{-1}\right)^2}q_i^{a_{ij}}{\mathcal Z}_i w_{m,n-1}\left(x,y;q_i^2,q_i^{a_{ij}}\right). \end{align*} $$The polynomials 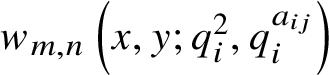 $w_{m,n}\left (x,y;q_i^2,q_i^{a_{ij}}\right )$ are rescaled versions of the bivariate continuous q-Hermite polynomials
$w_{m,n}\left (x,y;q_i^2,q_i^{a_{ij}}\right )$ are rescaled versions of the bivariate continuous q-Hermite polynomials ![]() $H_{m,n}(x,y;q,r)$, which were first introduced and studied in [Reference Casper, Kolb and YakimovCKY21] (see Sections 4.1 and 5.1 for details).
$H_{m,n}(x,y;q,r)$, which were first introduced and studied in [Reference Casper, Kolb and YakimovCKY21] (see Sections 4.1 and 5.1 for details).
C) The rescaled deformed Chebyshev polynomials  $u_n\left (x;q_i^2,q_i^{2a_{ij}}\right )\in {\mathcal M}_X^+[x]$ are defined for
$u_n\left (x;q_i^2,q_i^{2a_{ij}}\right )\in {\mathcal M}_X^+[x]$ are defined for ![]() $n\in {\mathbb N}$ by
$n\in {\mathbb N}$ by 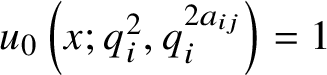 $u_0\left (x;q_i^2,q_i^{2a_{ij}}\right )=1$,
$u_0\left (x;q_i^2,q_i^{2a_{ij}}\right )=1$,  $u_1\left (x;q_i^2,q_i^{2a_{ij}}\right )=x$ and the recursion
$u_1\left (x;q_i^2,q_i^{2a_{ij}}\right )=x$ and the recursion
 $$ \begin{align*} u_{n+1}\left(x;q_i^2,q_i^{2a_{ij}}\right)= xu_n\left(x;q_i^2,q_i^{2a_{ij}}\right) - \frac{q_i^{-2a_{ij}}-q_i^{2(n+1)}}{\left(1-q_i^{2(n+1)}\right)\left(q_i-q_i^{-1}\right)^2}{\mathcal Z}_i u_{n-1}\left(x;q_i^2,q_i^{2a_{ij}}\right). \end{align*} $$
$$ \begin{align*} u_{n+1}\left(x;q_i^2,q_i^{2a_{ij}}\right)= xu_n\left(x;q_i^2,q_i^{2a_{ij}}\right) - \frac{q_i^{-2a_{ij}}-q_i^{2(n+1)}}{\left(1-q_i^{2(n+1)}\right)\left(q_i-q_i^{-1}\right)^2}{\mathcal Z}_i u_{n-1}\left(x;q_i^2,q_i^{2a_{ij}}\right). \end{align*} $$The polynomials  $u_n\left (x;q_i^2,q_i^{2a_{ij}}\right )$ are obtained by rescaling from a family of univariate orthogonal polynomials
$u_n\left (x;q_i^2,q_i^{2a_{ij}}\right )$ are obtained by rescaling from a family of univariate orthogonal polynomials ![]() $C_n(x;q,r)\in {\mathbb K}[x]$ for
$C_n(x;q,r)\in {\mathbb K}[x]$ for ![]() $n\in {\mathbb N}$,
$n\in {\mathbb N}$, ![]() $r\in {\mathbb K}$, which we call deformed Chebyshev polynomials of the second kind. The polynomials
$r\in {\mathbb K}$, which we call deformed Chebyshev polynomials of the second kind. The polynomials ![]() $C_n(x;q,r)$ are defined by the initial conditions
$C_n(x;q,r)$ are defined by the initial conditions ![]() $C_0(x; q, r) =1$,
$C_0(x; q, r) =1$, ![]() $C_1(x; q, r) =2x$ and the recursion
$C_1(x; q, r) =2x$ and the recursion
 $$\begin{align*}C_{n+1}(x; q, r) = 2x C_{n}(x; q, r) - \frac{r^{-1}-q^{n+1}}{1 - q^{n+1}} C_{n-1}(x; q, r). \end{align*}$$
$$\begin{align*}C_{n+1}(x; q, r) = 2x C_{n}(x; q, r) - \frac{r^{-1}-q^{n+1}}{1 - q^{n+1}} C_{n-1}(x; q, r). \end{align*}$$In the case ![]() $r=1$, we recover the classical Chebyshev polynomials of the second kind. We investigate this new sequence of orthogonal polynomials in Section 4.5, obtaining two generating functions for them. The first is
$r=1$, we recover the classical Chebyshev polynomials of the second kind. We investigate this new sequence of orthogonal polynomials in Section 4.5, obtaining two generating functions for them. The first is
 $$\begin{align*}\sum_{n=0}^\infty C_n(x;q,r) \frac{s^n}{1-q^{n+2}} =\frac{1}{1-2xs+r^{-1}s^2} {}_{3}\phi_2\left(\begin{array}{c} q,x_1s,x_2s \\qa_1s,qa_2s\end{array};q,q^2\right), \end{align*}$$
$$\begin{align*}\sum_{n=0}^\infty C_n(x;q,r) \frac{s^n}{1-q^{n+2}} =\frac{1}{1-2xs+r^{-1}s^2} {}_{3}\phi_2\left(\begin{array}{c} q,x_1s,x_2s \\qa_1s,qa_2s\end{array};q,q^2\right), \end{align*}$$where ![]() $x_{1,2}$ and
$x_{1,2}$ and ![]() $a_{1,2}$ are the roots of the polynomials
$a_{1,2}$ are the roots of the polynomials
and ![]() ${}_{3}\phi _2$ is the basic hypergeometric function [Reference Koekoek, Lesky and SwarttouwKLS10, 1.10]. The second generating function in Proposition 4.8 displays the connection to classical Chebyshev polynomials of the second kind.
${}_{3}\phi _2$ is the basic hypergeometric function [Reference Koekoek, Lesky and SwarttouwKLS10, 1.10]. The second generating function in Proposition 4.8 displays the connection to classical Chebyshev polynomials of the second kind.
These three families of rescaled orthogonal polynomials provide the main ingredients to write down the defining relations (1.4) in cases (I) and (II). For any ![]() ${\mathbb K}$-algebra A, any noncommutative polynomial
${\mathbb K}$-algebra A, any noncommutative polynomial ![]() $w(x,y)=\sum _{s,t}\lambda _{st} x^s y^t\in A[x,y]$ and any
$w(x,y)=\sum _{s,t}\lambda _{st} x^s y^t\in A[x,y]$ and any ![]() $a_1, a_2,a_3\in A$, we write
$a_1, a_2,a_3\in A$, we write
 $$ \begin{align} a_3 \curvearrowright w(a_1,a_2) = \sum_{s,t} a_1^{s} a_3 a_2^{t} \lambda_{st}. \end{align} $$
$$ \begin{align} a_3 \curvearrowright w(a_1,a_2) = \sum_{s,t} a_1^{s} a_3 a_2^{t} \lambda_{st}. \end{align} $$Note that the coefficients ![]() $\lambda _{st}\in A$ are written at the very right side in equation (1.6), which will be crucial in case (II). With these notations we are able to formulate the main result of this paper:
$\lambda _{st}\in A$ are written at the very right side in equation (1.6), which will be crucial in case (II). With these notations we are able to formulate the main result of this paper:
Theorem 1.2. For any symmetrisable Kac–Moody algebra ![]() ${\mathfrak g}$, generalised Satake diagram
${\mathfrak g}$, generalised Satake diagram ![]() $(X,\tau )$ and
$(X,\tau )$ and ![]() ${\mathbf {c}}\in {\mathcal C}$, the relations (1.4) in Theorem 1.1 are given as follows:
${\mathbf {c}}\in {\mathcal C}$, the relations (1.4) in Theorem 1.1 are given as follows:
Cases (I) and (II): If ![]() $i\in I\setminus X$ with
$i\in I\setminus X$ with ![]() $\tau (i)=i$ and
$\tau (i)=i$ and ![]() $j\in I$ with
$j\in I$ with ![]() $j\neq i$, then
$j\neq i$, then
 $$ \begin{align} &\sum_{n=0}^{1-a_{ij}}(-1)^n \begin{bmatrix} 1-a_{ij}\\ n\end{bmatrix}_{q_i} B_j \curvearrowright w_{1-a_{ij}-n,n}\left(B_i, B_i;q_i^2,q_i^{a_{ij}}\right) \nonumber\\ &\quad = \delta_{j\in X}\left(\frac{q_i^{-a_{ij}\left(a_{ij}+1\right)}\left(q_i^2;q_i^2\right)_{-a_{ij}}}{\left(q_i-q_i^{-1}\right)^2\left(q_j-q_j^{-1}\right)}\partial_j^R({\mathcal Z}_i)K_j u_{-a_{ij}-1}\left(B_i;q_i^2,q_i^{2a_{ij}}\right)\right. \nonumber\\ & \qquad\left. - \frac{q_i^{a_{ij}\left(a_{ij}+1\right)}\left(q_i^{-2};q_i^{-2}\right)_{-a_{ij}}}{\left(q_i-q_i^{-1}\right)^2\left(q_j-q_j^{-1}\right)} K_j^{-1 }\partial_j^L({\mathcal Z}_i) u_{-a_{ij}-1}\left(B_i;q_i^{-2},q_i^{-2a_{ij}}\right) \right). \end{align} $$
$$ \begin{align} &\sum_{n=0}^{1-a_{ij}}(-1)^n \begin{bmatrix} 1-a_{ij}\\ n\end{bmatrix}_{q_i} B_j \curvearrowright w_{1-a_{ij}-n,n}\left(B_i, B_i;q_i^2,q_i^{a_{ij}}\right) \nonumber\\ &\quad = \delta_{j\in X}\left(\frac{q_i^{-a_{ij}\left(a_{ij}+1\right)}\left(q_i^2;q_i^2\right)_{-a_{ij}}}{\left(q_i-q_i^{-1}\right)^2\left(q_j-q_j^{-1}\right)}\partial_j^R({\mathcal Z}_i)K_j u_{-a_{ij}-1}\left(B_i;q_i^2,q_i^{2a_{ij}}\right)\right. \nonumber\\ & \qquad\left. - \frac{q_i^{a_{ij}\left(a_{ij}+1\right)}\left(q_i^{-2};q_i^{-2}\right)_{-a_{ij}}}{\left(q_i-q_i^{-1}\right)^2\left(q_j-q_j^{-1}\right)} K_j^{-1 }\partial_j^L({\mathcal Z}_i) u_{-a_{ij}-1}\left(B_i;q_i^{-2},q_i^{-2a_{ij}}\right) \right). \end{align} $$Case (III): If ![]() $i,j\in I\setminus X$ and
$i,j\in I\setminus X$ and ![]() $\tau (i)=j\neq i$, then
$\tau (i)=j\neq i$, then
 $$ \begin{align*} S_{ij}\left(B_i,B_j\right)=\frac{q_i^{a_{ij}-2} \left(q_i^{2};q_i^{2}\right)_{1-a_{ij}}}{\left(q_i-q_i^{-1}\right)^2} B_i^{-a_{ij}} K_j K_i^{-1}{\mathcal Z}_i + \frac{\left(q_i^{-2};q_i^{-2}\right)_{1-a_{ij}}}{\left(q_i-q_i^{-1}\right)^2}B_i^{-a_{ij}} K_i K_j^{-1} {\mathcal Z}_j. \end{align*} $$
$$ \begin{align*} S_{ij}\left(B_i,B_j\right)=\frac{q_i^{a_{ij}-2} \left(q_i^{2};q_i^{2}\right)_{1-a_{ij}}}{\left(q_i-q_i^{-1}\right)^2} B_i^{-a_{ij}} K_j K_i^{-1}{\mathcal Z}_i + \frac{\left(q_i^{-2};q_i^{-2}\right)_{1-a_{ij}}}{\left(q_i-q_i^{-1}\right)^2}B_i^{-a_{ij}} K_i K_j^{-1} {\mathcal Z}_j. \end{align*} $$In all other cases, the relation (1.4) is given by ![]() $S_{ij}\left (B_i,B_j\right )=0$.
$S_{ij}\left (B_i,B_j\right )=0$.
By the definition of the rescaled bivariate continuous q-Hermite polynomials in B) above we have ![]() $w_{m,n}(x,y)=x^my^n + $ lower order terms in
$w_{m,n}(x,y)=x^my^n + $ lower order terms in ![]() ${\mathcal M}_X^+[x,y]$. Hence the left-hand side of equation (1.7) takes the form of
${\mathcal M}_X^+[x,y]$. Hence the left-hand side of equation (1.7) takes the form of ![]() $S_{ij}\left (B_i,B_j\right )+$ lower order terms in
$S_{ij}\left (B_i,B_j\right )+$ lower order terms in ![]() ${\mathcal F}_{\deg \left (i,j\right )-1}({\mathcal B}_{\mathbf {c}})$. These lower order terms are concisely encoded by the rescaled bivariate continuous q-Hermite polynomials.
${\mathcal F}_{\deg \left (i,j\right )-1}({\mathcal B}_{\mathbf {c}})$. These lower order terms are concisely encoded by the rescaled bivariate continuous q-Hermite polynomials.
We will show in Proposition 4.4 that the left-hand side of equation (1.7) can be expressed in terms of rescaled univariate continuous q-Hermite polynomials as
 $$ \begin{align*} \sum_{n=0}^{1-a_{ij}}(-1)^n \begin{bmatrix} 1-a_{ij}\\ n\end{bmatrix}_{q_i} w_{1-a_{ij}-n}\left(B_i;q_i^2\right)B_j w_n\left(B_i;q_i^{-2}\right). \end{align*} $$
$$ \begin{align*} \sum_{n=0}^{1-a_{ij}}(-1)^n \begin{bmatrix} 1-a_{ij}\\ n\end{bmatrix}_{q_i} w_{1-a_{ij}-n}\left(B_i;q_i^2\right)B_j w_n\left(B_i;q_i^{-2}\right). \end{align*} $$However, this expression has to be interpreted with care. In case (II), following convention (1.6), all powers of ![]() ${\mathcal Z}_i$ for
${\mathcal Z}_i$ for  $w_{1-a_{ij}-n}\left (B_i;q_i^2\right )$ have to be written to the right side of the factor
$w_{1-a_{ij}-n}\left (B_i;q_i^2\right )$ have to be written to the right side of the factor ![]() $B_j$. This subtlety is not relevant in case (I), as then
$B_j$. This subtlety is not relevant in case (I), as then ![]() ${\mathcal Z}_i$ and
${\mathcal Z}_i$ and ![]() $B_j$ commute.
$B_j$ commute.
As mentioned before, the formula in case (III) already appeared in [Reference Balagović and KolbBK15, Theorem 3.6], but we give an independent proof using star products.
1.5 Methods
Recall the filtration ![]() ${\mathcal F}$ of
${\mathcal F}$ of ![]() ${\mathcal B}_{\mathbf {c}}$ defined by equation (1.3). The associated graded algebra
${\mathcal B}_{\mathbf {c}}$ defined by equation (1.3). The associated graded algebra ![]() $\mathrm {gr}({\mathcal B}_{\mathbf {c}})$ is isomorphic to the partial parabolic subalgebra
$\mathrm {gr}({\mathcal B}_{\mathbf {c}})$ is isomorphic to the partial parabolic subalgebra
 $$ \begin{align*} {\mathcal A}={\mathbb K}\left\langle F_i, E_j,K_\beta\mid i\in I, j\in X, \beta \in Q^\Theta \right\rangle \subset U. \end{align*} $$
$$ \begin{align*} {\mathcal A}={\mathbb K}\left\langle F_i, E_j,K_\beta\mid i\in I, j\in X, \beta \in Q^\Theta \right\rangle \subset U. \end{align*} $$We lift the isomorphism ![]() ${\mathrm {gr}}({\mathcal B}_{\mathbf {c}})\cong {\mathcal A}$ to an explicit
${\mathrm {gr}}({\mathcal B}_{\mathbf {c}})\cong {\mathcal A}$ to an explicit ![]() ${\mathbb K}$-linear isomorphism
${\mathbb K}$-linear isomorphism ![]() $\psi :{\mathcal B}_{\mathbf {c}} \rightarrow {\mathcal A}$, which we call the Letzter map, as a similar map appeared in [Reference LetzterLet19]. We use the Letzter map to push forward the algebra structure of
$\psi :{\mathcal B}_{\mathbf {c}} \rightarrow {\mathcal A}$, which we call the Letzter map, as a similar map appeared in [Reference LetzterLet19]. We use the Letzter map to push forward the algebra structure of ![]() ${\mathcal B}_{\mathbf {c}}$ to a new algebra structure
${\mathcal B}_{\mathbf {c}}$ to a new algebra structure ![]() $({\mathcal A},\ast )$ on the vector space
$({\mathcal A},\ast )$ on the vector space ![]() ${\mathcal A}$. The algebra structure
${\mathcal A}$. The algebra structure ![]() $({\mathcal A},\ast )$ is a star product on the
$({\mathcal A},\ast )$ is a star product on the ![]() ${\mathbb N}$-graded algebra
${\mathbb N}$-graded algebra ![]() ${\mathcal A}$ in the sense of [Reference Kolb and YakimovKY20, Definition 5.1]. This means in particular that the algebra
${\mathcal A}$ in the sense of [Reference Kolb and YakimovKY20, Definition 5.1]. This means in particular that the algebra ![]() $({\mathcal A},\ast )$ has the same generating set as
$({\mathcal A},\ast )$ has the same generating set as ![]() ${\mathcal A}$ and that its defining relations are those of
${\mathcal A}$ and that its defining relations are those of ![]() ${\mathcal A}$ re-expressed in terms of the star product
${\mathcal A}$ re-expressed in terms of the star product ![]() $\ast $. To obtain the quantum Serre relations (1.4) for
$\ast $. To obtain the quantum Serre relations (1.4) for ![]() ${\mathcal B}_{\mathbf {c}}$, it hence suffices to rewrite the quantum Serre relations
${\mathcal B}_{\mathbf {c}}$, it hence suffices to rewrite the quantum Serre relations ![]() $S_{ij}\left (F_i,F_j\right )=0$ for
$S_{ij}\left (F_i,F_j\right )=0$ for ![]() ${\mathcal A}$ in terms of the star product on
${\mathcal A}$ in terms of the star product on ![]() ${\mathcal A}$.
${\mathcal A}$.
To describe the star product on ![]() ${\mathcal A}$, we use Radford’s biproduct decomposition [Reference RadfordRad85] for the negative parabolic subalgebra of U, to obtain a tensor product decomposition
${\mathcal A}$, we use Radford’s biproduct decomposition [Reference RadfordRad85] for the negative parabolic subalgebra of U, to obtain a tensor product decomposition
Here ![]() ${\mathcal H}={\mathcal F}_0({\mathcal B})={\mathcal A}_0$, and
${\mathcal H}={\mathcal F}_0({\mathcal B})={\mathcal A}_0$, and ![]() ${\mathcal R}_X$ is a subalgebra of coinvariants which is generated in degree
${\mathcal R}_X$ is a subalgebra of coinvariants which is generated in degree ![]() $1$. The star product on
$1$. The star product on ![]() ${\mathcal A}$ is uniquely determined by the maps
${\mathcal A}$ is uniquely determined by the maps
 $$ \begin{align} \mu^L_f(u)=f\ast u - fu \qquad \text{for}\ f\in ({\mathcal R}_X)_1={\mathcal R}_X\cap {\mathcal A}_1, u\in {\mathcal R}_X. \end{align} $$
$$ \begin{align} \mu^L_f(u)=f\ast u - fu \qquad \text{for}\ f\in ({\mathcal R}_X)_1={\mathcal R}_X\cap {\mathcal A}_1, u\in {\mathcal R}_X. \end{align} $$These maps can be expressed in terms of twisted Lusztig–Kashiwara skew derivations  $\partial _{i,X}^{L/R}=T_{w_X}\circ \partial _i^{L/R}\circ T_{w_X}^{-1}$. In cases (I) and (II), inductive arguments based on the maps (1.9) show that
$\partial _{i,X}^{L/R}=T_{w_X}\circ \partial _i^{L/R}\circ T_{w_X}^{-1}$. In cases (I) and (II), inductive arguments based on the maps (1.9) show that
 $$ \begin{align} F_i^mF_jF_i^n= F_j&\curvearrowright w_{m,n}\left(F_i\stackrel{\ast}{,}F_i;q_i^2,q_i^{a_{ij}}\right)\nonumber\\ &\quad + \delta_{j\in X}\left(\partial^R_j({\mathcal Z}_i)K_j \rho_{m,n}(F_i)^\ast + K_j^{-1}\partial_j^L({\mathcal Z}_i)\sigma_{m,n}(F_i)^\ast\right) \end{align} $$
$$ \begin{align} F_i^mF_jF_i^n= F_j&\curvearrowright w_{m,n}\left(F_i\stackrel{\ast}{,}F_i;q_i^2,q_i^{a_{ij}}\right)\nonumber\\ &\quad + \delta_{j\in X}\left(\partial^R_j({\mathcal Z}_i)K_j \rho_{m,n}(F_i)^\ast + K_j^{-1}\partial_j^L({\mathcal Z}_i)\sigma_{m,n}(F_i)^\ast\right) \end{align} $$for some polynomials ![]() $\rho _{m,n}(x), \sigma _{m,n}(x)\in {\mathcal M}_X^+[x]$ (see Proposition 5.3 and Lemma 5.5). The symbol
$\rho _{m,n}(x), \sigma _{m,n}(x)\in {\mathcal M}_X^+[x]$ (see Proposition 5.3 and Lemma 5.5). The symbol ![]() $\ast $ appearing on the right hand side of this equation indicates that all polynomials are evaluated in
$\ast $ appearing on the right hand side of this equation indicates that all polynomials are evaluated in ![]() $({\mathcal A},\ast )$, see Section 5.1 for the precise notation. To obtain formula (1.7), we thus need to determine the quantum Serre combination
$({\mathcal A},\ast )$, see Section 5.1 for the precise notation. To obtain formula (1.7), we thus need to determine the quantum Serre combination
 $$ \begin{align} \sum_{n=0}^{1-a_{ij}}(-1)^n \begin{bmatrix} 1-a_{ij}\\ n\end{bmatrix}_{q_i} \rho_{1-a_{ij}-n}(F_i)^\ast, \end{align} $$
$$ \begin{align} \sum_{n=0}^{1-a_{ij}}(-1)^n \begin{bmatrix} 1-a_{ij}\\ n\end{bmatrix}_{q_i} \rho_{1-a_{ij}-n}(F_i)^\ast, \end{align} $$and similarly for ![]() $\sigma _{m,n}$. The inductive argument from Lemma 5.5 provides recursive formulas for
$\sigma _{m,n}$. The inductive argument from Lemma 5.5 provides recursive formulas for ![]() $\rho _{m,n}(x)$ and
$\rho _{m,n}(x)$ and ![]() $\sigma _{m,n}(x)$. Using a generalisation of the bar involution for
$\sigma _{m,n}(x)$. Using a generalisation of the bar involution for ![]() ${\mathcal B}_{\mathbf {c}}$, which was implicit in [Reference Appel and VlaarAV20] and was made explicit in [Reference KolbKol21], we show that it suffices to consider the quantum Serre combination (1.11). In Section 5.6 we determine formula (1.11) using a generating function approach which naturally leads to the deformed Chebyshev polynomials of the second kind.
${\mathcal B}_{\mathbf {c}}$, which was implicit in [Reference Appel and VlaarAV20] and was made explicit in [Reference KolbKol21], we show that it suffices to consider the quantum Serre combination (1.11). In Section 5.6 we determine formula (1.11) using a generating function approach which naturally leads to the deformed Chebyshev polynomials of the second kind.
1.6 Organisation of the paper
In Section 2 we fix notation and present background material on quantum groups and quantum symmetric pairs. In particular, in Sections 2.2 and 2.3 we recall how Radford’s biproduct leads to the tensor product decomposition (1.8). Moreover, we define the Letzter map in Section 2.5 and recall the generalised bar involution in Section 2.6.
Section 3 develops the star product on the partial parabolic subalgebra ![]() ${\mathcal A}$. After recalling the definition of a star product in Section 3.1, we determine the maps
${\mathcal A}$. After recalling the definition of a star product in Section 3.1, we determine the maps ![]() $\mu _f^L$ for
$\mu _f^L$ for ![]() $({\mathcal A},\ast )$ in Section 3.2. In Section 3.3 we then determine the values of the twisted skew derivations
$({\mathcal A},\ast )$ in Section 3.2. In Section 3.3 we then determine the values of the twisted skew derivations  $\partial ^{L/R}_{i,X}$, which will be needed later to derive equation (1.10).
$\partial ^{L/R}_{i,X}$, which will be needed later to derive equation (1.10).
In Section 4 we discuss the three families of orthogonal polynomials given before in A), B) and C). We first recall the univariate and bivariate continuous q-Hermite polynomials and list essential properties of their rescaled versions in Section 4.1. In Section 4.3 we show how the quantum Serre combination of  $w_{m,n}\left (x,y;q_i^2,q_i^{2a_{ij}}\right )$ can be expressed in terms of
$w_{m,n}\left (x,y;q_i^2,q_i^{2a_{ij}}\right )$ can be expressed in terms of  $w_m\left (x;q_i^2\right )$ and
$w_m\left (x;q_i^2\right )$ and  $w_m\left (x;q_i^{-2}\right )$. In Section 4.5 we introduce the deformed Chebyshev polynomials of the second kind and determine two generating functions for them.
$w_m\left (x;q_i^{-2}\right )$. In Section 4.5 we introduce the deformed Chebyshev polynomials of the second kind and determine two generating functions for them.
The final section contains the proof of Theorem 1.2. In Section 5.3 we derive equation (1.7) in case (I). In Section 5.4 we derive equation (1.10) in the subtle case (II). The quantum Serre combination (1.11) is determined in Section 5.6. This allows us to prove formula (1.7) also in case (II). Finally, Section 5.8 contains the proof in case (III) of Theorem 1.2.
2 Quantum symmetric pairs and partial parabolic subalgebras
In this introductory section we expand on the notation given in Section 1.2 and recall some standard constructions for quantised enveloping algebras, in particular the decomposition of a quantised standard parabolic as a Radford biproduct [Reference RadfordRad85]. We then recall that quantum symmetric pair coideal subalgebras ![]() ${\mathcal B}_{\mathbf {c}}$ have a filtration such that the associated graded algebra is isomorphic to a large subalgebra
${\mathcal B}_{\mathbf {c}}$ have a filtration such that the associated graded algebra is isomorphic to a large subalgebra ![]() ${\mathcal A}$ of a quantised standard parabolic. This isomorphism can be lifted to a filtered linear isomorphism
${\mathcal A}$ of a quantised standard parabolic. This isomorphism can be lifted to a filtered linear isomorphism ![]() $\psi :{\mathcal B}_{\mathbf {c}}\rightarrow {\mathcal A}$, which we call the Letzter map. This map provides the interpretation of
$\psi :{\mathcal B}_{\mathbf {c}}\rightarrow {\mathcal A}$, which we call the Letzter map. This map provides the interpretation of ![]() ${\mathcal B}_{\mathbf {c}}$ as a star product deformation of
${\mathcal B}_{\mathbf {c}}$ as a star product deformation of ![]() ${\mathcal A}$ in Section 3.
${\mathcal A}$ in Section 3.
2.1 The setting
Let ![]() ${\mathfrak g}$ be a symmetrisable Kac–Moody algebra with generalised Cartan matrix
${\mathfrak g}$ be a symmetrisable Kac–Moody algebra with generalised Cartan matrix  $\left (a_{ij}\right )_{i,j\in I}$, where I is a finite set. Let
$\left (a_{ij}\right )_{i,j\in I}$, where I is a finite set. Let ![]() $\{d_i\mid i\in I\}$ be a set of relatively prime positive integers such that the matrix
$\{d_i\mid i\in I\}$ be a set of relatively prime positive integers such that the matrix ![]() $\left (d_ia_{ij}\right )$ is symmetric. Let
$\left (d_ia_{ij}\right )$ is symmetric. Let ![]() $\Pi =\{\alpha _i\mid i\in I\}$ be the set of simple roots for
$\Pi =\{\alpha _i\mid i\in I\}$ be the set of simple roots for ![]() ${\mathfrak g}$ and let
${\mathfrak g}$ and let ![]() $Q={\mathbb Z}\Pi $ be the root lattice. Consider the symmetric bilinear form
$Q={\mathbb Z}\Pi $ be the root lattice. Consider the symmetric bilinear form ![]() $(\cdot ,\cdot ):Q\times Q \rightarrow {\mathbb Z}$ defined by
$(\cdot ,\cdot ):Q\times Q \rightarrow {\mathbb Z}$ defined by ![]() $\left (\alpha _i,\alpha _j\right )=d_ia_{ij}$ for all
$\left (\alpha _i,\alpha _j\right )=d_ia_{ij}$ for all ![]() $i,j\in I$. Let W be the corresponding Weyl group with simple reflections
$i,j\in I$. Let W be the corresponding Weyl group with simple reflections ![]() $s_i$ for
$s_i$ for ![]() $i\in I$. Let
$i\in I$. Let ![]() ${\mathfrak g}'=[{\mathfrak g},{\mathfrak g}]$ be the derived subalgebra of
${\mathfrak g}'=[{\mathfrak g},{\mathfrak g}]$ be the derived subalgebra of ![]() ${\mathfrak g}$.
${\mathfrak g}$.
Throughout the paper, we fix a field k of characteristic ![]() $0$ and set
$0$ and set ![]() ${\mathbb K}=k(q)$. The quantised enveloping algebra
${\mathbb K}=k(q)$. The quantised enveloping algebra ![]() $U=U_q({\mathfrak g}')$ is the
$U=U_q({\mathfrak g}')$ is the ![]() ${\mathbb K}$-algebra with generators
${\mathbb K}$-algebra with generators  $E_i, F_i, K_i^{\pm 1}$ for
$E_i, F_i, K_i^{\pm 1}$ for ![]() $i \in I$ and defining relations given in [Reference LusztigLus94, 3.1]. In particular, the generators
$i \in I$ and defining relations given in [Reference LusztigLus94, 3.1]. In particular, the generators ![]() $E_i, F_i$ satisfy the quantum Serre relations
$E_i, F_i$ satisfy the quantum Serre relations
for all ![]() $i,j\in I$, where
$i,j\in I$, where
 $$ \begin{align} S_{ij}(x,y)=\sum_{\ell=0}^{1-a_{ij}}(-1)^\ell \genfrac{[}{]}{0pt}{}{1-a_{ij}}{\ell}_{q_i}x^{1-a_{ij}-\ell}y x^\ell \in {\mathbb K}[x,y], \end{align} $$
$$ \begin{align} S_{ij}(x,y)=\sum_{\ell=0}^{1-a_{ij}}(-1)^\ell \genfrac{[}{]}{0pt}{}{1-a_{ij}}{\ell}_{q_i}x^{1-a_{ij}-\ell}y x^\ell \in {\mathbb K}[x,y], \end{align} $$with ![]() $q_i=q^{d_i}$ denoting the quantum Serre polynomial [Reference LusztigLus94, Corollary 33.1.5]. The algebra U is a Hopf algebra with coproduct
$q_i=q^{d_i}$ denoting the quantum Serre polynomial [Reference LusztigLus94, Corollary 33.1.5]. The algebra U is a Hopf algebra with coproduct ![]() ${\varDelta }$ given by
${\varDelta }$ given by
 $$ \begin{align} {\varDelta}(E_i){=}E_i\otimes 1+ K_i\otimes E_i, \qquad {\varDelta}(F_i){=}F_i\otimes K_i^{-1}+1 \otimes F_i, \qquad {\varDelta}(K_i){=}K_i\otimes K_i, \end{align} $$
$$ \begin{align} {\varDelta}(E_i){=}E_i\otimes 1+ K_i\otimes E_i, \qquad {\varDelta}(F_i){=}F_i\otimes K_i^{-1}+1 \otimes F_i, \qquad {\varDelta}(K_i){=}K_i\otimes K_i, \end{align} $$for all ![]() $i\in I$. For
$i\in I$. For ![]() $\beta =\sum _{i\in I}n_i \alpha _i\in Q$, write
$\beta =\sum _{i\in I}n_i \alpha _i\in Q$, write ![]() $K_\beta =\prod _{i\in I}K_i^{n_i}$.
$K_\beta =\prod _{i\in I}K_i^{n_i}$.
We write ![]() ${\mathbb N}=\{0,1,2,\dotsc \}$ and let
${\mathbb N}=\{0,1,2,\dotsc \}$ and let ![]() $Q^+={\mathbb N}\Pi $ be the positive cone in the root lattice. For any
$Q^+={\mathbb N}\Pi $ be the positive cone in the root lattice. For any ![]() $\mu \in Q^+$ we let
$\mu \in Q^+$ we let  $U^+_\mu =\mathrm {span}_{\mathbb K}\left \{E_{i_1} \dotsm E_{i_\ell }\mid \sum _{j=1}^\ell \alpha _{i_j}=\mu \right \}$ be the corresponding root space, where
$U^+_\mu =\mathrm {span}_{\mathbb K}\left \{E_{i_1} \dotsm E_{i_\ell }\mid \sum _{j=1}^\ell \alpha _{i_j}=\mu \right \}$ be the corresponding root space, where ![]() $\mathrm {span}_{\mathbb K}$ denotes the
$\mathrm {span}_{\mathbb K}$ denotes the ![]() ${\mathbb K}$-linear span. Moreover, define
${\mathbb K}$-linear span. Moreover, define 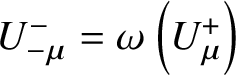 $U^-_{-\mu }=\omega \left (U^+_\mu \right )$, where
$U^-_{-\mu }=\omega \left (U^+_\mu \right )$, where ![]() $\omega :U\rightarrow U$ is the algebra automorphism given in [Reference LusztigLus94, 3.1.3]. We will use the Lusztig–Kashiwara skew derivations
$\omega :U\rightarrow U$ is the algebra automorphism given in [Reference LusztigLus94, 3.1.3]. We will use the Lusztig–Kashiwara skew derivations 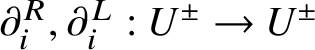 $\partial ^R_i, \partial ^L_i:U^\pm \rightarrow U^\pm $ for
$\partial ^R_i, \partial ^L_i:U^\pm \rightarrow U^\pm $ for ![]() $i\in I$, which are uniquely determined by
$i\in I$, which are uniquely determined by
 $$ \begin{align} E_i y - y E_i &=\frac{K_i \partial^L_i(y) - \partial^R_i(y)K_i^{-1}}{q_i-q_i^{-1}} , \end{align} $$
$$ \begin{align} E_i y - y E_i &=\frac{K_i \partial^L_i(y) - \partial^R_i(y)K_i^{-1}}{q_i-q_i^{-1}} , \end{align} $$ $$ \begin{align} F_i x - x F_i &= \frac{K_i^{-1} \partial^L_i(x) - \partial^R_i(x)K_i}{q_i-q_i^{-1}}, \end{align} $$
$$ \begin{align} F_i x - x F_i &= \frac{K_i^{-1} \partial^L_i(x) - \partial^R_i(x)K_i}{q_i-q_i^{-1}}, \end{align} $$for ![]() $x\in U^+$ and
$x\in U^+$ and ![]() $y\in U^-$ [Reference LusztigLus94, Proposition 3.1.6]. The skew derivations
$y\in U^-$ [Reference LusztigLus94, Proposition 3.1.6]. The skew derivations ![]() $\partial _i^L$ and
$\partial _i^L$ and ![]() $\partial _i^R$ satisfy the relations
$\partial _i^R$ satisfy the relations
 $$ \begin{align} \partial_i^L(fg)&=\partial_i^L(f)g +q^{\left(\alpha_i,\mu\right)}f \partial_i^L(g), \end{align} $$
$$ \begin{align} \partial_i^L(fg)&=\partial_i^L(f)g +q^{\left(\alpha_i,\mu\right)}f \partial_i^L(g), \end{align} $$ $$ \begin{align} \partial_i^R(fg)&=q^{\left(\alpha_i,\nu\right)}\partial_i^R(f)g +f \partial_i^R(g), \end{align} $$
$$ \begin{align} \partial_i^R(fg)&=q^{\left(\alpha_i,\nu\right)}\partial_i^R(f)g +f \partial_i^R(g), \end{align} $$for all ![]() $f\in U^-_{-\mu }$,
$f\in U^-_{-\mu }$, ![]() $g\in U^-_{-\nu }$ and for all
$g\in U^-_{-\nu }$ and for all ![]() $f\in U^+_{\mu }$,
$f\in U^+_{\mu }$, ![]() $g\in U^+_{\nu }$.
$g\in U^+_{\nu }$.
For any ![]() $i\in I$, let
$i\in I$, let ![]() $T_i:U\rightarrow U$ be the algebra automorphism denoted by
$T_i:U\rightarrow U$ be the algebra automorphism denoted by  $T^{\prime \prime }_{i,1}$ in [Reference LusztigLus94, 37.1]. The skew derivations
$T^{\prime \prime }_{i,1}$ in [Reference LusztigLus94, 37.1]. The skew derivations ![]() $\partial _i^L$ and
$\partial _i^L$ and ![]() $\partial _i^R$ detect elements in the intersection
$\partial _i^R$ detect elements in the intersection ![]() $U^\pm \cap T_i\left (U^{\pm }\right )$. More precisely, for
$U^\pm \cap T_i\left (U^{\pm }\right )$. More precisely, for ![]() $x\in U^+$ and
$x\in U^+$ and ![]() $y\in U^-$ we have the following equivalences [Reference LusztigLus94, 38.1.6, 37.2.4]:
$y\in U^-$ we have the following equivalences [Reference LusztigLus94, 38.1.6, 37.2.4]:
 $$ \begin{align} x&\in T_i^{-1}(U^+) & &\Longleftrightarrow & \partial_i^L(x)&=0,\end{align} $$
$$ \begin{align} x&\in T_i^{-1}(U^+) & &\Longleftrightarrow & \partial_i^L(x)&=0,\end{align} $$ $$ \begin{align} x&\in T_i(U^+) & &\Longleftrightarrow & \partial_i^R(x)&=0,\end{align} $$
$$ \begin{align} x&\in T_i(U^+) & &\Longleftrightarrow & \partial_i^R(x)&=0,\end{align} $$ $$ \begin{align} y&\in T_i^{-1}(U^-) & &\Longleftrightarrow & \partial_i^L(y)&=0,\end{align} $$
$$ \begin{align} y&\in T_i^{-1}(U^-) & &\Longleftrightarrow & \partial_i^L(y)&=0,\end{align} $$ $$ \begin{align} y&\in T_i(U^-) & &\Longleftrightarrow & \partial_i^R(y)&=0,\end{align} $$
$$ \begin{align} y&\in T_i(U^-) & &\Longleftrightarrow & \partial_i^R(y)&=0,\end{align} $$ Given a subset ![]() $X \subseteq I$, denote
$X \subseteq I$, denote
 $$\begin{align*}Q_X=\sum_{j\in X} {\mathbb Z} \alpha_j \quad \text{and} \quad Q_X^+=\sum_{j\in X}{\mathbb N} \alpha_j. \end{align*}$$
$$\begin{align*}Q_X=\sum_{j\in X} {\mathbb Z} \alpha_j \quad \text{and} \quad Q_X^+=\sum_{j\in X}{\mathbb N} \alpha_j. \end{align*}$$We write ![]() ${\mathcal M}_X$ to denote the subalgebra of U generated by
${\mathcal M}_X$ to denote the subalgebra of U generated by  $\left \{E_j, F_j, K_j^{\pm 1}\mid j\in X\right \}$, and
$\left \{E_j, F_j, K_j^{\pm 1}\mid j\in X\right \}$, and ![]() ${\mathcal M}^+_X$ and
${\mathcal M}^+_X$ and ![]() ${\mathcal M}^-_X$ for the subalgebras generated by
${\mathcal M}^-_X$ for the subalgebras generated by  $\left \{E_j\mid j\in X\right \}$ and
$\left \{E_j\mid j\in X\right \}$ and 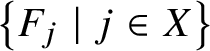 $\left \{F_j\mid j\in X\right \}$, respectively. We write
$\left \{F_j\mid j\in X\right \}$, respectively. We write ![]() $G_X^+$ and
$G_X^+$ and ![]() $G_X^-$ to denote the subalgebras of U generated by
$G_X^-$ to denote the subalgebras of U generated by  $\left \{E_jK_j^{-1}\mid j\in X\right \}$ and
$\left \{E_jK_j^{-1}\mid j\in X\right \}$ and  $\left \{F_jK_j\mid j\in X\right \}$, respectively. Moreover, we write
$\left \{F_jK_j\mid j\in X\right \}$, respectively. Moreover, we write ![]() $G^\pm $ for
$G^\pm $ for ![]() $G^\pm _I$.
$G^\pm _I$.
2.2 Parabolic subalgebras
Let ![]() $X\subseteq I$ be a subset of finite type. The parabolic subalgebra
$X\subseteq I$ be a subset of finite type. The parabolic subalgebra
 $$ \begin{align*} {\mathcal P}_X={\mathbb K}\left\langle F_i, E_j, K_i^{\pm 1}\mid i\in I, j\in X\right\rangle \end{align*} $$
$$ \begin{align*} {\mathcal P}_X={\mathbb K}\left\langle F_i, E_j, K_i^{\pm 1}\mid i\in I, j\in X\right\rangle \end{align*} $$is a Hopf subalgebra of U, and the corresponding Levi factor
 $$ \begin{align*} {\mathcal L}_X={\mathbb K}\left\langle F_j, E_j, K_i^{\pm 1}\mid i\in I, j\in X\right\rangle \end{align*} $$
$$ \begin{align*} {\mathcal L}_X={\mathbb K}\left\langle F_j, E_j, K_i^{\pm 1}\mid i\in I, j\in X\right\rangle \end{align*} $$is a Hopf subalgebra of ![]() ${\mathcal P}_X$. The parabolic subalgebra and the Levi factor have respective triangular decompositions
${\mathcal P}_X$. The parabolic subalgebra and the Levi factor have respective triangular decompositions
 $$ \begin{align} {\mathcal P}_X\cong {\mathcal M}_X^+ \otimes U^0 \otimes U^- \quad \text{and} \quad {\mathcal L}_X \cong {\mathcal M}_X^+\otimes U^0 \otimes {\mathcal M}_X^-. \end{align} $$
$$ \begin{align} {\mathcal P}_X\cong {\mathcal M}_X^+ \otimes U^0 \otimes U^- \quad \text{and} \quad {\mathcal L}_X \cong {\mathcal M}_X^+\otimes U^0 \otimes {\mathcal M}_X^-. \end{align} $$There is a surjective Hopf algebra homomorphism ![]() $\pi _X:{\mathcal P}_X\rightarrow {\mathcal L}_X$ defined by
$\pi _X:{\mathcal P}_X\rightarrow {\mathcal L}_X$ defined by
The structure of Hopf algebras with a projection onto a Hopf subalgebra was investigated in detail by D. Radford in [Reference RadfordRad85]. In the following we recall some of his results in our setting. All the material in this section is known to experts, but we include some proofs for the convenience of the reader.
Consider the left coaction of ![]() ${\mathcal L}_X$ on
${\mathcal L}_X$ on ![]() ${\mathcal P}_X$ given by
${\mathcal P}_X$ given by
and define a subalgebra ![]() ${\mathcal R}_X\subset {\mathcal P}_X$ by
${\mathcal R}_X\subset {\mathcal P}_X$ by
The algebra ![]() ${\mathcal R}_X$ is a right
${\mathcal R}_X$ is a right ![]() ${\mathcal L}_X$-module algebra under the right adjoint action given by
${\mathcal L}_X$-module algebra under the right adjoint action given by ![]() ${\mbox{ad}}_r(h)(a)= S\left (h_{(1)}\right )a h_{(2)}$ for all
${\mbox{ad}}_r(h)(a)= S\left (h_{(1)}\right )a h_{(2)}$ for all ![]() $a\in {\mathcal R}_X, h\in {\mathcal L}_X$. Hence we can form the smash product
$a\in {\mathcal R}_X, h\in {\mathcal L}_X$. Hence we can form the smash product ![]() ${\mathcal L}_X\otimes {\mathcal R}_X$, which is an associative algebra with the multiplication
${\mathcal L}_X\otimes {\mathcal R}_X$, which is an associative algebra with the multiplication
 $$ \begin{align*} (h\otimes a)(h'\otimes a') = h h^{\prime}_{(1)} \otimes {\mbox{ad}}_r\left(h^{\prime}_{(2)}\right)(a)a'. \end{align*} $$
$$ \begin{align*} (h\otimes a)(h'\otimes a') = h h^{\prime}_{(1)} \otimes {\mbox{ad}}_r\left(h^{\prime}_{(2)}\right)(a)a'. \end{align*} $$The following theorem is obtained by translating [Reference RadfordRad85, Theorem 3(d)] from left to right:
Theorem 2.1. The multiplication map ![]() ${\mathcal L}_X \otimes {\mathcal R}_X \rightarrow {\mathcal P}_X$ is an isomorphism of algebras.
${\mathcal L}_X \otimes {\mathcal R}_X \rightarrow {\mathcal P}_X$ is an isomorphism of algebras.
Remark 2.2. The statement of [Reference RadfordRad85, Theorem 3] goes beyond Theorem 2.1. The algebra ![]() ${\mathcal R}_X$ is a Hopf algebra in the category of right Yetter–Drinfeld modules over
${\mathcal R}_X$ is a Hopf algebra in the category of right Yetter–Drinfeld modules over ![]() ${\mathcal L}_X$. One can thus form Radford’s biproduct
${\mathcal L}_X$. One can thus form Radford’s biproduct ![]() ${\mathcal L}_X\times {\mathcal R}_X$ (also known as the bosonisation [Reference MajidMaj94]), which is a Hopf algebra that coincides with the smash product
${\mathcal L}_X\times {\mathcal R}_X$ (also known as the bosonisation [Reference MajidMaj94]), which is a Hopf algebra that coincides with the smash product ![]() ${\mathcal L}_X\otimes {\mathcal R}_X$ as an algebra. By [Reference RadfordRad85, Theorem 3(d)], the multiplication map
${\mathcal L}_X\otimes {\mathcal R}_X$ as an algebra. By [Reference RadfordRad85, Theorem 3(d)], the multiplication map ![]() ${\mathcal L}_X \times {\mathcal R}_X \rightarrow {\mathcal P}_X$ is an isomorphism of Hopf algebras. We will only need the algebra structure on
${\mathcal L}_X \times {\mathcal R}_X \rightarrow {\mathcal P}_X$ is an isomorphism of Hopf algebras. We will only need the algebra structure on ![]() ${\mathcal L}_X\otimes {\mathcal R}_X$.
${\mathcal L}_X\otimes {\mathcal R}_X$.
Formula (2.2) for the coproduct of ![]() $F_i$ implies that
$F_i$ implies that ![]() $F_i\in {\mathcal R}_X$ for all
$F_i\in {\mathcal R}_X$ for all ![]() $i\in I\setminus X$. Moreover, as
$i\in I\setminus X$. Moreover, as ![]() ${\mathcal R}_X$ is invariant under the right adjoint action of
${\mathcal R}_X$ is invariant under the right adjoint action of ![]() ${\mathcal L}_X$, we obtain
${\mathcal L}_X$, we obtain ![]() ${\mbox{ad}}_r({\mathcal L}_X)(F_i) \subseteq {\mathcal R}_X$ for all
${\mbox{ad}}_r({\mathcal L}_X)(F_i) \subseteq {\mathcal R}_X$ for all ![]() $i\in I\setminus X$.
$i\in I\setminus X$.
Corollary 2.3. The algebra ![]() ${\mathcal R}_X$ is generated by the subspaces
${\mathcal R}_X$ is generated by the subspaces ![]() ${\mbox{ad}}_r({\mathcal L}_X)(F_i)$ for all
${\mbox{ad}}_r({\mathcal L}_X)(F_i)$ for all ![]() $i\in I\setminus X$.
$i\in I\setminus X$.
Proof. Let ![]() $V_X\subset {\mathcal P}_X$ be the subalgebra generated by the subspaces
$V_X\subset {\mathcal P}_X$ be the subalgebra generated by the subspaces ![]() ${\mbox{ad}}_r({\mathcal L}_X)(F_i)$ for all
${\mbox{ad}}_r({\mathcal L}_X)(F_i)$ for all ![]() $i\in I\setminus X$. As observed already, we have
$i\in I\setminus X$. As observed already, we have ![]() $V_X\subseteq {\mathcal R}_X$. The subalgebra of
$V_X\subseteq {\mathcal R}_X$. The subalgebra of ![]() ${\mathcal P}_X$ generated by
${\mathcal P}_X$ generated by ![]() $V_X$ and
$V_X$ and ![]() ${\mathcal L}_X$ coincides with
${\mathcal L}_X$ coincides with ![]() ${\mathcal P}_X$. Hence the formula
${\mathcal P}_X$. Hence the formula ![]() $a h = h_{(1)} {\mbox{ad}}_r\left (h_{(2)}\right )(a)$ for
$a h = h_{(1)} {\mbox{ad}}_r\left (h_{(2)}\right )(a)$ for ![]() $a\in V_X$,
$a\in V_X$, ![]() $h\in {\mathcal L}_X$ implies that the multiplication map
$h\in {\mathcal L}_X$ implies that the multiplication map ![]() ${\mathcal L}_X\otimes V_X\rightarrow {\mathcal P}_X$ is surjective. Now the inclusion
${\mathcal L}_X\otimes V_X\rightarrow {\mathcal P}_X$ is surjective. Now the inclusion ![]() $V_X\subseteq {\mathcal R}_X$ and Theorem 2.1 imply that
$V_X\subseteq {\mathcal R}_X$ and Theorem 2.1 imply that ![]() $V_X={\mathcal R}_X$.
$V_X={\mathcal R}_X$.
For all ![]() $j\in X$,
$j\in X$, ![]() $i\in I\setminus X$ one has
$i\in I\setminus X$ one has  ${\mbox{ad}}_r\left (E_j\right )(F_i)=-K_j^{-1}\left [E_j,F_i\right ]=0$. Hence by the triangular decomposition (2.11) for
${\mbox{ad}}_r\left (E_j\right )(F_i)=-K_j^{-1}\left [E_j,F_i\right ]=0$. Hence by the triangular decomposition (2.11) for ![]() ${\mathcal L}_X$ we get
${\mathcal L}_X$ we get ![]() ${\mbox{ad}}_r({\mathcal L}_X)(F_i)={\mbox{ad}}_r\left ({\mathcal M}^-_X\right )(F_i)\subset U^-$. By Theorem 2.1, Corollary 2.3 and the triangular decompositions (2.11), we get that the multiplication map
${\mbox{ad}}_r({\mathcal L}_X)(F_i)={\mbox{ad}}_r\left ({\mathcal M}^-_X\right )(F_i)\subset U^-$. By Theorem 2.1, Corollary 2.3 and the triangular decompositions (2.11), we get that the multiplication map
is an isomorphism of algebras.
We can also describe the subalgebra ![]() ${\mathcal R}_X\subset U^-$ in terms of the Lusztig automorphisms:
${\mathcal R}_X\subset U^-$ in terms of the Lusztig automorphisms:
Lemma 2.4. We have
 $$ \begin{align*} {\mathcal R}_X=\left\{a\in U^-\mid T_j^{-1}(a)\in U^- \text{ for all}\ j\in X\right\}=\bigcap_{j\in X} \left(U^-\cap T_j\left(U^-\right)\right). \end{align*} $$
$$ \begin{align*} {\mathcal R}_X=\left\{a\in U^-\mid T_j^{-1}(a)\in U^- \text{ for all}\ j\in X\right\}=\bigcap_{j\in X} \left(U^-\cap T_j\left(U^-\right)\right). \end{align*} $$Proof. Let ![]() $j\in X$. We first show that
$j\in X$. We first show that  $T_j^{-1}({\mathcal R}_X)\subset U^-$. By Corollary 2.3 it suffices to show that
$T_j^{-1}({\mathcal R}_X)\subset U^-$. By Corollary 2.3 it suffices to show that  $T_j^{-1}\left ({\mbox{ad}}_r\left ({\mathcal M}_X^-\right )(F_i)\right )\subset U^-$ for any
$T_j^{-1}\left ({\mbox{ad}}_r\left ({\mathcal M}_X^-\right )(F_i)\right )\subset U^-$ for any ![]() $i\in I\setminus X$. We have
$i\in I\setminus X$. We have  $T_j^{-1}(F_i)\in U^-$. Now we proceed by induction. Assume that
$T_j^{-1}(F_i)\in U^-$. Now we proceed by induction. Assume that ![]() $u\in {\mathcal R}_X$ satisfies
$u\in {\mathcal R}_X$ satisfies  $T_j^{-1}(u)\in U^-$ and let
$T_j^{-1}(u)\in U^-$ and let ![]() $\ell \in X$. Then we get
$\ell \in X$. Then we get
 $$ \begin{align*} T_j^{-1}({\mbox{ad}}_r(F_\ell)(u))&=T_j^{-1}\left(-F_\ell K_\ell u K_{\ell}^{-1} + u F_\ell\right), \end{align*} $$
$$ \begin{align*} T_j^{-1}({\mbox{ad}}_r(F_\ell)(u))&=T_j^{-1}\left(-F_\ell K_\ell u K_{\ell}^{-1} + u F_\ell\right), \end{align*} $$which by the induction hypothesis lies in ![]() $U^-$ if
$U^-$ if ![]() $\ell \neq j$. In the case
$\ell \neq j$. In the case ![]() $\ell =j$, this formula becomes
$\ell =j$, this formula becomes
 $$ \begin{align*} T_j^{-1}({\mbox{ad}}_r(F_\ell)(u))=\left[T_\ell^{-1}(u), E_\ell\right] K_\ell \stackrel{\text{(2.9)}}{=} \frac{1}{q_\ell-q_\ell^{-1}}\partial_\ell^R\left(T_\ell^{-1}(u)\right)\in U^-. \end{align*} $$
$$ \begin{align*} T_j^{-1}({\mbox{ad}}_r(F_\ell)(u))=\left[T_\ell^{-1}(u), E_\ell\right] K_\ell \stackrel{\text{(2.9)}}{=} \frac{1}{q_\ell-q_\ell^{-1}}\partial_\ell^R\left(T_\ell^{-1}(u)\right)\in U^-. \end{align*} $$This implies that  $T_j^{-1}\left ({\mbox{ad}}_r\left ({\mathcal M}_X^-\right )(F_i)\right )\subseteq U^-$, as required.
$T_j^{-1}\left ({\mbox{ad}}_r\left ({\mathcal M}_X^-\right )(F_i)\right )\subseteq U^-$, as required.
Conversely, assume that ![]() $u\in U^-$ satisfies
$u\in U^-$ satisfies  $T_j^{-1}(u)\in U^-$ for all
$T_j^{-1}(u)\in U^-$ for all ![]() $j\in X$. We want to show that
$j\in X$. We want to show that ![]() $u\in {\mathcal R}_X$. For any
$u\in {\mathcal R}_X$. For any ![]() $j\in X$ the decomposition (2.12) implies that the multiplication map
$j\in X$ the decomposition (2.12) implies that the multiplication map
 $$ \begin{align} {\mathbb K}\left[F_j\right]\otimes \left({\mathcal M}_X^-\cap T_j\left({\mathcal M}_X^-\right)\right)\otimes {\mathcal R}_X\rightarrow U^- \end{align} $$
$$ \begin{align} {\mathbb K}\left[F_j\right]\otimes \left({\mathcal M}_X^-\cap T_j\left({\mathcal M}_X^-\right)\right)\otimes {\mathcal R}_X\rightarrow U^- \end{align} $$is a linear isomorphism. Write ![]() $u=\sum _m h_m\otimes v_m$ with linearly independent
$u=\sum _m h_m\otimes v_m$ with linearly independent  $h_m\in {\mathcal M}_X^-\cong {\mathbb K}\left [F_j\right ]\otimes \left ({\mathcal M}_X^-\cap T_j\left ({\mathcal M}_X^-\right )\right )$ and
$h_m\in {\mathcal M}_X^-\cong {\mathbb K}\left [F_j\right ]\otimes \left ({\mathcal M}_X^-\cap T_j\left ({\mathcal M}_X^-\right )\right )$ and ![]() $v_m\in {\mathcal R}_X$. Then the relations
$v_m\in {\mathcal R}_X$. Then the relations 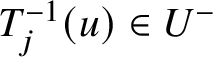 $T_j^{-1}(u)\in U^-$ and
$T_j^{-1}(u)\in U^-$ and 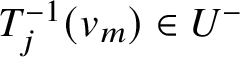 $T_j^{-1}(v_m)\in U^-$ imply that
$T_j^{-1}(v_m)\in U^-$ imply that ![]() $h_m\in \left ({\mathcal M}_X^-\cap T_j\left ({\mathcal M}_X^-\right )\right )$. By [Reference LusztigLus94, Lemma 1.2.15] we have
$h_m\in \left ({\mathcal M}_X^-\cap T_j\left ({\mathcal M}_X^-\right )\right )$. By [Reference LusztigLus94, Lemma 1.2.15] we have
 $$ \begin{align*} \bigcap_{j\in X} \left({\mathcal M}_X^-\cap T_j\left({\mathcal M}_X^-\right)\right)\stackrel{\text{(2.10)}}{=} \left\{y\in {\mathcal M}_X^-\mid\partial^R_j(y)=0 \text{ for all}\ j\in X\right\} = {\mathbb K}. \end{align*} $$
$$ \begin{align*} \bigcap_{j\in X} \left({\mathcal M}_X^-\cap T_j\left({\mathcal M}_X^-\right)\right)\stackrel{\text{(2.10)}}{=} \left\{y\in {\mathcal M}_X^-\mid\partial^R_j(y)=0 \text{ for all}\ j\in X\right\} = {\mathbb K}. \end{align*} $$Hence all ![]() $h_m$ are scalars, which implies that
$h_m$ are scalars, which implies that ![]() $u\in {\mathcal R}_X$.
$u\in {\mathcal R}_X$.
Remark 2.5. In formula (2.13) we used the decomposition  ${\mathcal M}_X^-\cong {\mathbb K}\left [F_j\right ]\otimes \left ({\mathcal M}_X^-\cap T_j\left ({\mathcal M}_X^-\right )\right )$, which holds by the Poincaré–Birkhoff–Witt theorem for the finite type quantum enveloping algebra
${\mathcal M}_X^-\cong {\mathbb K}\left [F_j\right ]\otimes \left ({\mathcal M}_X^-\cap T_j\left ({\mathcal M}_X^-\right )\right )$, which holds by the Poincaré–Birkhoff–Witt theorem for the finite type quantum enveloping algebra ![]() ${\mathcal M}_X$. By Lemma 2.4 and the decomposition (2.12) in the case where
${\mathcal M}_X$. By Lemma 2.4 and the decomposition (2.12) in the case where ![]() $\lvert X\rvert =1$, we now have the same decomposition
$\lvert X\rvert =1$, we now have the same decomposition
for any ![]() $i\in I$ also in infinite type.
$i\in I$ also in infinite type.
To rewrite the statement of Lemma 2.4 we note the following fact:
Lemma 2.6. Let ![]() $w\in W$ be an element with reduced expression
$w\in W$ be an element with reduced expression ![]() $w=s_{i_1}s_{i_2} \dotsm s_{i_m}$. Then the following relations hold:
$w=s_{i_1}s_{i_2} \dotsm s_{i_m}$. Then the following relations hold:
 $$ \begin{align} U^- \cap T_w^{-1}\left(U^-\right)&= U^- \cap T^{-1}_{i_m}\left(U^-\right)\cap T^{-1}_{i_m} T^{-1}_{i_{m-1}}\left(U^-\right) \cap \dotsb \cap T^{-1}_w\left(U^-\right). \end{align} $$
$$ \begin{align} U^- \cap T_w^{-1}\left(U^-\right)&= U^- \cap T^{-1}_{i_m}\left(U^-\right)\cap T^{-1}_{i_m} T^{-1}_{i_{m-1}}\left(U^-\right) \cap \dotsb \cap T^{-1}_w\left(U^-\right). \end{align} $$Proof. It suffices to prove equation (2.16), as equation (2.15) then follows by application of ![]() $T_w$. We prove equation (2.16) by induction on the length
$T_w$. We prove equation (2.16) by induction on the length ![]() $l(w)=m$ of w. For
$l(w)=m$ of w. For ![]() $m=1$ there is nothing to show. Now assume that
$m=1$ there is nothing to show. Now assume that ![]() $w=s_i w'$, where
$w=s_i w'$, where ![]() $l(w)=l(w')+1$. Then
$l(w)=l(w')+1$. Then ![]() $T_w=T_i T_w'$, and formula (2.14) gives us
$T_w=T_i T_w'$, and formula (2.14) gives us
 $$ \begin{align*} T^{-1}_w\left(U^-\right)&=T^{-1}_{w'} T^{-1}_i \left({\mathbb K}[F_i] \otimes \left(U^-\cap T_i\left(U^-\right)\right)\right)\\ &= T_{w'}^{-1}\left({\mathbb K}[E_iK_i] \otimes \left(T_i^{-1}\left(U^-\right)\cap U^-\right) \right)\\ &= {\mathbb K}\left[T_{w'}^{-1}(E_iK_i)\right] \otimes \left(T_w^{-1}\left(U^-\right) \cap T_{w'}^{-1}\left(U^-\right)\right). \end{align*} $$
$$ \begin{align*} T^{-1}_w\left(U^-\right)&=T^{-1}_{w'} T^{-1}_i \left({\mathbb K}[F_i] \otimes \left(U^-\cap T_i\left(U^-\right)\right)\right)\\ &= T_{w'}^{-1}\left({\mathbb K}[E_iK_i] \otimes \left(T_i^{-1}\left(U^-\right)\cap U^-\right) \right)\\ &= {\mathbb K}\left[T_{w'}^{-1}(E_iK_i)\right] \otimes \left(T_w^{-1}\left(U^-\right) \cap T_{w'}^{-1}\left(U^-\right)\right). \end{align*} $$By [Reference LusztigLus94, Proposition 40.2.1] we have  $T_{w'}^{-1}(E_i)\in U^+$, and hence the triangular decomposition
$T_{w'}^{-1}(E_i)\in U^+$, and hence the triangular decomposition ![]() $U^+\otimes U^0 \otimes U^-\cong U$ implies that
$U^+\otimes U^0 \otimes U^-\cong U$ implies that
 $$ \begin{align*} U^- \cap T^{-1}_w\left(U^-\right) = U^- \cap T_w^{-1}\left(U^-\right) \cap T_{w'}^{-1}\left(U^-\right). \end{align*} $$
$$ \begin{align*} U^- \cap T^{-1}_w\left(U^-\right) = U^- \cap T_w^{-1}\left(U^-\right) \cap T_{w'}^{-1}\left(U^-\right). \end{align*} $$Now equation (2.16) follows by the induction hypothesis.
Let ![]() $w_X$ denote the longest element in the finite parabolic subgroup
$w_X$ denote the longest element in the finite parabolic subgroup ![]() $W_X$ of the Weyl group W. There is a diagram automorphism
$W_X$ of the Weyl group W. There is a diagram automorphism ![]() $\tau _X:X\rightarrow X$ such that
$\tau _X:X\rightarrow X$ such that ![]() $w_X\left (\alpha _j\right )=-\alpha _{\tau _X\left (j\right )}$ for all
$w_X\left (\alpha _j\right )=-\alpha _{\tau _X\left (j\right )}$ for all ![]() $j\in X$.
$j\in X$.
Corollary 2.7. We have ![]() ${\mathcal R}_X=U^-\cap T_{w_X}\left (U^-\right )$.
${\mathcal R}_X=U^-\cap T_{w_X}\left (U^-\right )$.
Proof. For any ![]() $j\in X$, we can write
$j\in X$, we can write ![]() $w_X=s_j w'$ for some
$w_X=s_j w'$ for some ![]() $w'\in W_X$ with
$w'\in W_X$ with ![]() $l(w')=l(w_X)-1$. Hence equation (2.15) and Lemma 2.4 imply that
$l(w')=l(w_X)-1$. Hence equation (2.15) and Lemma 2.4 imply that
 $$ \begin{align*} U^-\cap T_{w_X}\left(U^-\right) \subseteq \bigcap_{j\in X} \left(U^- \cap T_j\left(U^-\right)\right)={\mathcal R}_X. \end{align*} $$
$$ \begin{align*} U^-\cap T_{w_X}\left(U^-\right) \subseteq \bigcap_{j\in X} \left(U^- \cap T_j\left(U^-\right)\right)={\mathcal R}_X. \end{align*} $$The converse inclusion is verified similarly to the first part of the proof of Lemma 2.4. Again it suffices to show that ![]() ${\mbox{ad}}_r\left ({\mathcal M}_X^-\right )(F_i) \subseteq U^-\cap T_{w_X}\left (U^-\right )$ for all
${\mbox{ad}}_r\left ({\mathcal M}_X^-\right )(F_i) \subseteq U^-\cap T_{w_X}\left (U^-\right )$ for all ![]() $i\in I\setminus X$. By [Reference LusztigLus94, Proposition 40.2.1] we have
$i\in I\setminus X$. By [Reference LusztigLus94, Proposition 40.2.1] we have  $T_{w_X}^{-1}(F_i)\in U^-$, and hence
$T_{w_X}^{-1}(F_i)\in U^-$, and hence ![]() $F_i\in U^-\cap T_{w_X}\left (U^-\right )$. If
$F_i\in U^-\cap T_{w_X}\left (U^-\right )$. If ![]() $u\in U^-\cap T_{w_X}\left (U^-\right )$ and
$u\in U^-\cap T_{w_X}\left (U^-\right )$ and ![]() $\ell \in X$, then
$\ell \in X$, then
 $$ \begin{align*} T_{w_X}^{-1}({\mbox{ad}}_r(F_\ell)(u))=\left[T_{w_X}^{-1}(u), E_{\tau_X(\ell)}\right]K_{\tau_X(\ell)} \stackrel{\text{(2.9)}}{=} \frac{1}{q_\ell-q_\ell^{-1}} \partial_{\tau_X(\ell)}^R\left(T_{w_X}^{-1}(u)\right)\in U^-. \end{align*} $$
$$ \begin{align*} T_{w_X}^{-1}({\mbox{ad}}_r(F_\ell)(u))=\left[T_{w_X}^{-1}(u), E_{\tau_X(\ell)}\right]K_{\tau_X(\ell)} \stackrel{\text{(2.9)}}{=} \frac{1}{q_\ell-q_\ell^{-1}} \partial_{\tau_X(\ell)}^R\left(T_{w_X}^{-1}(u)\right)\in U^-. \end{align*} $$This implies inductively that  $T_{w_X}^{-1}\left ({\mbox{ad}}_r\left ({\mathcal M}_X^-\right )(F_i)\right )\subset U^-$ and completes the proof of the corollary.
$T_{w_X}^{-1}\left ({\mbox{ad}}_r\left ({\mathcal M}_X^-\right )(F_i)\right )\subset U^-$ and completes the proof of the corollary.
2.3 Partial parabolic subalgebras
Consider a subset of finite type ![]() $X\subseteq I$ and a map
$X\subseteq I$ and a map ![]() $\tau :I\rightarrow I$ which is an involutive diagram automorphism such that
$\tau :I\rightarrow I$ which is an involutive diagram automorphism such that ![]() $\tau (X)=X$ and
$\tau (X)=X$ and ![]() $w_X\left (\alpha _j\right )=-\alpha _{\tau \left (j\right )}$ for all
$w_X\left (\alpha _j\right )=-\alpha _{\tau \left (j\right )}$ for all ![]() $j\in X$. Following [Reference Regelskis and VlaarRV20], we call a pair
$j\in X$. Following [Reference Regelskis and VlaarRV20], we call a pair ![]() $(X,\tau )$ with these properties a compatible decoration. The map
$(X,\tau )$ with these properties a compatible decoration. The map ![]() $\Theta =-w_X\circ \tau :Q\rightarrow Q$ is an involutive automorphism of the root lattice. Define
$\Theta =-w_X\circ \tau :Q\rightarrow Q$ is an involutive automorphism of the root lattice. Define ![]() $Q^\Theta =\{\beta \in Q\mid \Theta (\beta )=\beta \}$ and
$Q^\Theta =\{\beta \in Q\mid \Theta (\beta )=\beta \}$ and  $U^0_\Theta ={\mathbb K}\left \langle K_\beta \mid \beta \in Q^\Theta \right \rangle $. As
$U^0_\Theta ={\mathbb K}\left \langle K_\beta \mid \beta \in Q^\Theta \right \rangle $. As ![]() $Q^\Theta $ is generated by the elements of the set
$Q^\Theta $ is generated by the elements of the set  $\left \{\alpha _i-\alpha _{\tau \left (i\right )},\alpha _j\mid i\in I\setminus X, j\in X\right \}$, we see that
$\left \{\alpha _i-\alpha _{\tau \left (i\right )},\alpha _j\mid i\in I\setminus X, j\in X\right \}$, we see that
 $$ \begin{align*} U^0_\Theta={\mathbb K} \left\langle K_j^{\pm 1}, K_i K_{\tau\left(i\right)}^{-1}\mid j\in X, i\in I \right\rangle. \end{align*} $$
$$ \begin{align*} U^0_\Theta={\mathbb K} \left\langle K_j^{\pm 1}, K_i K_{\tau\left(i\right)}^{-1}\mid j\in X, i\in I \right\rangle. \end{align*} $$Consider the subalgebra ![]() ${\mathcal A}={\mathcal A}(X,\tau )\subset U$ defined by
${\mathcal A}={\mathcal A}(X,\tau )\subset U$ defined by
 $$ \begin{align*} {\mathcal A}={\mathbb K}\left\langle F_i, E_j, K_\beta\mid i\in I, j\in X, \Theta(\beta)=\beta\right\rangle. \end{align*} $$
$$ \begin{align*} {\mathcal A}={\mathbb K}\left\langle F_i, E_j, K_\beta\mid i\in I, j\in X, \Theta(\beta)=\beta\right\rangle. \end{align*} $$We call ![]() ${\mathcal A}$ the partial parabolic subalgebra corresponding to the pair
${\mathcal A}$ the partial parabolic subalgebra corresponding to the pair ![]() $(X,\tau )$. By definition,
$(X,\tau )$. By definition, ![]() ${\mathcal A}$ is contained in the standard parabolic subalgebra
${\mathcal A}$ is contained in the standard parabolic subalgebra ![]() ${\mathcal P}_X$, with the only difference being that
${\mathcal P}_X$, with the only difference being that  ${\mathcal A}\cap U^0=U^0_\Theta $ is not the whole torus. In particular,
${\mathcal A}\cap U^0=U^0_\Theta $ is not the whole torus. In particular, ![]() ${\mathcal A}$ has the triangular decomposition
${\mathcal A}$ has the triangular decomposition
 $$ \begin{align} {\mathcal A}\cong {\mathcal M}_X^+ \otimes U^0_\Theta \otimes U^-. \end{align} $$
$$ \begin{align} {\mathcal A}\cong {\mathcal M}_X^+ \otimes U^0_\Theta \otimes U^-. \end{align} $$Additionally, consider the subalgebra ![]() ${\mathcal H}={\mathcal H}(X,\tau )\subset U$ defined by
${\mathcal H}={\mathcal H}(X,\tau )\subset U$ defined by
 $$ \begin{align*} {\mathcal H}={\mathbb K} \left\langle E_j, F_j, K_\beta\mid j\in X, \Theta(\beta)=\beta\right\rangle={\mathcal M}_X U^0_\Theta. \end{align*} $$
$$ \begin{align*} {\mathcal H}={\mathbb K} \left\langle E_j, F_j, K_\beta\mid j\in X, \Theta(\beta)=\beta\right\rangle={\mathcal M}_X U^0_\Theta. \end{align*} $$We call ![]() ${\mathcal H}$ the partial Levi factor corresponding to the generalised Satake diagram
${\mathcal H}$ the partial Levi factor corresponding to the generalised Satake diagram ![]() $(X,\tau )$. The partial Levi factor
$(X,\tau )$. The partial Levi factor ![]() ${\mathcal H}$ has a triangular decomposition
${\mathcal H}$ has a triangular decomposition
 $$ \begin{align} {\mathcal H} \cong {\mathcal M}^+_X \otimes U_\Theta^0 \otimes {\mathcal M}^-_X. \end{align} $$
$$ \begin{align} {\mathcal H} \cong {\mathcal M}^+_X \otimes U_\Theta^0 \otimes {\mathcal M}^-_X. \end{align} $$The partial parabolic subalgebra ![]() ${\mathcal A}$ is not a subbialgebra of U. However, the partial Levi factor
${\mathcal A}$ is not a subbialgebra of U. However, the partial Levi factor ![]() ${\mathcal H}$ is a Hopf subalgebra of U. Comparison of the triangular decompositions (2.17) and (2.18) with the decomposition (2.12) implies that the multiplication map
${\mathcal H}$ is a Hopf subalgebra of U. Comparison of the triangular decompositions (2.17) and (2.18) with the decomposition (2.12) implies that the multiplication map
is an isomorphism.
2.4 Quantum symmetric pairs
Let ![]() $(X,\tau )$ be a generalised Satake diagram. Following [Reference Regelskis and VlaarRV20], this means that
$(X,\tau )$ be a generalised Satake diagram. Following [Reference Regelskis and VlaarRV20], this means that ![]() $(X,\tau )$ is a compatible decoration, as described at the beginning of Section 2.3, and additionally that for
$(X,\tau )$ is a compatible decoration, as described at the beginning of Section 2.3, and additionally that for ![]() $i\in I\setminus X$ and
$i\in I\setminus X$ and ![]() $j\in X$ the implication
$j\in X$ the implication
holds. The condition (2.19) is weaker than condition (3) in [Reference KolbKol14, Definition 2.3]. As explained in [Reference Regelskis and VlaarRV20, Section 4.1], the results of [Reference KolbKol14] remain valid in this more general setting. Following [Reference KolbKol14] we recall the definition of the quantum symmetric pair coideal subalgebra corresponding to the generalised Satake diagram ![]() $(X,\tau )$. Recall the set of parameters
$(X,\tau )$. Recall the set of parameters ![]() ${\mathcal C}$ defined by equation (1.2). For any
${\mathcal C}$ defined by equation (1.2). For any ![]() ${\mathbf {c}}=(c_i)_{i\in I\setminus X}\in {\mathcal C}$, let
${\mathbf {c}}=(c_i)_{i\in I\setminus X}\in {\mathcal C}$, let ![]() ${\mathcal B}_{\mathbf {c}}$ denote the subalgebra of U generated by the partial Levi factor
${\mathcal B}_{\mathbf {c}}$ denote the subalgebra of U generated by the partial Levi factor ![]() ${\mathcal H}$ and the elements
${\mathcal H}$ and the elements
 $$ \begin{align} B_i=F_i - c_i T_{w_X}\left(E_{\tau(i)}\right) K_i^{-1} \quad \text{for all }{i\in I\setminus X}. \end{align} $$
$$ \begin{align} B_i=F_i - c_i T_{w_X}\left(E_{\tau(i)}\right) K_i^{-1} \quad \text{for all }{i\in I\setminus X}. \end{align} $$Remark 2.8. In [Reference KolbKol14], quantum symmetric pairs depend on a second family of parameters ![]() ${\textbf {{s}}}=(s_i)_{i\in I\setminus X}$ in a certain subset
${\textbf {{s}}}=(s_i)_{i\in I\setminus X}$ in a certain subset ![]() ${\mathcal S}\subset {\mathbb K}^{I\setminus X}$. The corresponding coideal subalgebras are then denoted by
${\mathcal S}\subset {\mathbb K}^{I\setminus X}$. The corresponding coideal subalgebras are then denoted by ![]() ${\mathcal B}_{{\mathbf {c}},{\textbf {{s}}}}$. By [Reference KolbKol14, Theorem 7.1], for any
${\mathcal B}_{{\mathbf {c}},{\textbf {{s}}}}$. By [Reference KolbKol14, Theorem 7.1], for any ![]() ${\textbf {{s}}}\in {\mathcal S}$ the algebra
${\textbf {{s}}}\in {\mathcal S}$ the algebra ![]() ${\mathcal B}_{{\mathbf {c}},{\textbf {{s}}}}$ is isomorphic to
${\mathcal B}_{{\mathbf {c}},{\textbf {{s}}}}$ is isomorphic to ![]() ${\mathcal B}_{{\mathbf {c}}}$. As we only aim to establish defining relations for
${\mathcal B}_{{\mathbf {c}}}$. As we only aim to establish defining relations for ![]() ${\mathcal B}_{{\mathbf {c}},{\textbf {{s}}}}$, it suffices to consider the case where
${\mathcal B}_{{\mathbf {c}},{\textbf {{s}}}}$, it suffices to consider the case where ![]() ${\textbf {{s}}}=(0,0, \dotsc ,0)$.
${\textbf {{s}}}=(0,0, \dotsc ,0)$.
Recall that the algebra ![]() ${\mathcal B}_{\mathbf {c}}$ has a natural
${\mathcal B}_{\mathbf {c}}$ has a natural ![]() ${\mathbb N}$-filtration
${\mathbb N}$-filtration ![]() ${\mathcal F}_\ast $ defined via the degree function (1.3). Hence
${\mathcal F}_\ast $ defined via the degree function (1.3). Hence ![]() ${\mathcal F}_n({\mathcal B}_{\mathbf {c}})$ is the
${\mathcal F}_n({\mathcal B}_{\mathbf {c}})$ is the ![]() ${\mathbb K}$-linear span of all monomials in the generators of
${\mathbb K}$-linear span of all monomials in the generators of ![]() ${\mathcal B}_{\mathbf {c}}$, where each monomial contains at most n factors
${\mathcal B}_{\mathbf {c}}$, where each monomial contains at most n factors ![]() $B_i$, with
$B_i$, with ![]() $i\in I\setminus X$. Let
$i\in I\setminus X$. Let ![]() ${\mathrm {gr}}({\mathcal B}_{\mathbf {c}})$ be the associated graded algebra. It follows from [Reference KolbKol14, Theorem 7.1] that there exists a surjective algebra homomorphism
${\mathrm {gr}}({\mathcal B}_{\mathbf {c}})$ be the associated graded algebra. It follows from [Reference KolbKol14, Theorem 7.1] that there exists a surjective algebra homomorphism
given by ![]() $\varphi (F_i)=B_i$ for all
$\varphi (F_i)=B_i$ for all ![]() $i\in I\setminus X$ and
$i\in I\setminus X$ and ![]() $\varphi (h)=h$ for all
$\varphi (h)=h$ for all ![]() $h\in {\mathcal H}$. Moreover, the triangular decomposition (2.17) for
$h\in {\mathcal H}$. Moreover, the triangular decomposition (2.17) for ![]() ${\mathcal A}$ and [Reference KolbKol14, Proposition 6.2] imply that
${\mathcal A}$ and [Reference KolbKol14, Proposition 6.2] imply that ![]() $\varphi $ is an isomorphism.
$\varphi $ is an isomorphism.
The partial parabolic subalgebra ![]() ${\mathcal A}$ is
${\mathcal A}$ is ![]() ${\mathbb N}$-graded via the degree function given by
${\mathbb N}$-graded via the degree function given by
 $$ \begin{align*} \deg(F_i)&=1 \qquad \text{for all}\ i\in I\setminus X,\\ \deg(h)&=0 \qquad \text{for all}\ h\in {\mathcal H}. \end{align*} $$
$$ \begin{align*} \deg(F_i)&=1 \qquad \text{for all}\ i\in I\setminus X,\\ \deg(h)&=0 \qquad \text{for all}\ h\in {\mathcal H}. \end{align*} $$With this grading, the map ![]() $\varphi $ in formula (2.21) is an isomorphism of graded algebras. For any
$\varphi $ in formula (2.21) is an isomorphism of graded algebras. For any ![]() $n\in {\mathbb N}$ we let
$n\in {\mathbb N}$ we let ![]() ${\mathcal A}_n$ denote the n-th graded component of
${\mathcal A}_n$ denote the n-th graded component of ![]() ${\mathcal A}$ and we write
${\mathcal A}$ and we write  ${\mathcal A}_{<n}=\bigoplus _{m=0}^{n-1}{\mathcal A}_m$.
${\mathcal A}_{<n}=\bigoplus _{m=0}^{n-1}{\mathcal A}_m$.
2.5 The Letzter map
Let ![]() $U^{\mathrm {poly}}$ denote the subalgebra of U generated by
$U^{\mathrm {poly}}$ denote the subalgebra of U generated by ![]() ${\mathcal A}$ and the elements
${\mathcal A}$ and the elements  $\widetilde {E}_i=E_iK_i^{-1}$,
$\widetilde {E}_i=E_iK_i^{-1}$,  $K_i^{-1}$ for all
$K_i^{-1}$ for all ![]() $i\in I\setminus X$. Observe that
$i\in I\setminus X$. Observe that ![]() ${\mathcal B}_{\mathbf {c}}\subset U^{\mathrm {poly}}$, as
${\mathcal B}_{\mathbf {c}}\subset U^{\mathrm {poly}}$, as  $T_{w_X}\left (E_{\tau (i)}\right )K_i^{-1}\in {\mathcal A} \widetilde {E}_{\tau (i)}{\mathcal A}$. Let
$T_{w_X}\left (E_{\tau (i)}\right )K_i^{-1}\in {\mathcal A} \widetilde {E}_{\tau (i)}{\mathcal A}$. Let ![]() $I_\tau $ be a set of representatives of
$I_\tau $ be a set of representatives of ![]() $\tau $-orbits in
$\tau $-orbits in ![]() $I\setminus X$. In analogy to the definition of
$I\setminus X$. In analogy to the definition of ![]() $V_X$ in the proof of Corollary 2.3, let
$V_X$ in the proof of Corollary 2.3, let ![]() $V_X^+\subset {\mathcal P}_X$ be the subalgebra generated by the subspaces
$V_X^+\subset {\mathcal P}_X$ be the subalgebra generated by the subspaces  ${\mbox{ad}}_r({\mathcal L}_X)\left (\widetilde {E}_i\right )={\mbox{ad}}_r\left ({\mathcal M}_X^+\right )\left (\widetilde {E}_i\right )$ for
${\mbox{ad}}_r({\mathcal L}_X)\left (\widetilde {E}_i\right )={\mbox{ad}}_r\left ({\mathcal M}_X^+\right )\left (\widetilde {E}_i\right )$ for ![]() $i\in I\setminus X$. The triangular decomposition
$i\in I\setminus X$. The triangular decomposition
 $$ \begin{align*} U\cong U^- \otimes U^0 \otimes G^+ \cong {\mathcal A} \otimes {\mathbb K}\left[K_i^{\pm 1}\mid i\in I_\tau\right]\otimes V_X^+ \end{align*} $$
$$ \begin{align*} U\cong U^- \otimes U^0 \otimes G^+ \cong {\mathcal A} \otimes {\mathbb K}\left[K_i^{\pm 1}\mid i\in I_\tau\right]\otimes V_X^+ \end{align*} $$implies that there is a direct sum decomposition of vector spaces
 $$ \begin{align} U^{\mathrm{poly}} \cong {\mathcal A} \oplus U^{\mathrm{poly}} \mathrm{span}_{\mathbb K}\left\{\widetilde{E}_i, K_i^{-1}\mid i\in I\setminus X\right\} {\mathcal H}. \end{align} $$
$$ \begin{align} U^{\mathrm{poly}} \cong {\mathcal A} \oplus U^{\mathrm{poly}} \mathrm{span}_{\mathbb K}\left\{\widetilde{E}_i, K_i^{-1}\mid i\in I\setminus X\right\} {\mathcal H}. \end{align} $$Let
denote the ![]() ${\mathbb K}$-linear projection with respect to the direct sum decomposition (2.22).
${\mathbb K}$-linear projection with respect to the direct sum decomposition (2.22).
Remark 2.9. For ![]() ${\mathfrak g}$ of finite type, the map
${\mathfrak g}$ of finite type, the map ![]() $\psi $ is the restriction to
$\psi $ is the restriction to ![]() $U^{\mathrm {poly}}$ of a projection map
$U^{\mathrm {poly}}$ of a projection map ![]() ${\mathcal P}:{U_q(\mathfrak {g})} \rightarrow {\mathcal A}$ given in [Reference LetzterLet19, (4.9)]. The restriction to
${\mathcal P}:{U_q(\mathfrak {g})} \rightarrow {\mathcal A}$ given in [Reference LetzterLet19, (4.9)]. The restriction to ![]() $U^{\mathrm {poly}}$ has the advantage that the kernel of
$U^{\mathrm {poly}}$ has the advantage that the kernel of ![]() $\psi $ is a left ideal in
$\psi $ is a left ideal in ![]() $U^{\mathrm {poly}}$. This will be relevant in the proof of Lemma 2.11.
$U^{\mathrm {poly}}$. This will be relevant in the proof of Lemma 2.11.
As ![]() ${\mathcal B}_{\mathbf {c}}$ is a subalgebra of
${\mathcal B}_{\mathbf {c}}$ is a subalgebra of ![]() $U^{\mathrm {poly}}$, we can restrict the map
$U^{\mathrm {poly}}$, we can restrict the map ![]() $\psi $ to
$\psi $ to ![]() ${\mathcal B}_{\mathbf {c}}$. We call the map
${\mathcal B}_{\mathbf {c}}$. We call the map ![]() $\psi :{\mathcal B}_{\mathbf {c}}\rightarrow {\mathcal A}$ the Letzter map. The algebra
$\psi :{\mathcal B}_{\mathbf {c}}\rightarrow {\mathcal A}$ the Letzter map. The algebra ![]() ${\mathcal B}_{\mathbf {c}}$ is filtered by the filtration
${\mathcal B}_{\mathbf {c}}$ is filtered by the filtration ![]() ${\mathcal F}_\ast $ given in Section 2.4. The algebra
${\mathcal F}_\ast $ given in Section 2.4. The algebra ![]() ${\mathcal A}$ is graded and hence also filtered. By construction, the Letzter map
${\mathcal A}$ is graded and hence also filtered. By construction, the Letzter map ![]() $\psi :{\mathcal B}_{\mathbf {c}}\rightarrow {\mathcal A}$ is a linear map of filtered vector spaces. Let
$\psi :{\mathcal B}_{\mathbf {c}}\rightarrow {\mathcal A}$ is a linear map of filtered vector spaces. Let
be the associated graded map, and recall the isomorphism ![]() $\varphi $ from formula (2.21). The composition
$\varphi $ from formula (2.21). The composition ![]() ${\mathrm {gr}}(\psi )\circ \varphi :{\mathcal A} \rightarrow {\mathcal A}$ is
${\mathrm {gr}}(\psi )\circ \varphi :{\mathcal A} \rightarrow {\mathcal A}$ is ![]() ${\mathcal H}$-linear and satisfies
${\mathcal H}$-linear and satisfies
for all ![]() $i_1,\dotsc , i_\ell \in I$. Hence
$i_1,\dotsc , i_\ell \in I$. Hence ![]() ${\mathrm {gr}}(\psi )\circ \varphi ={\mathrm {id}}_{\mathcal A}$. This implies that
${\mathrm {gr}}(\psi )\circ \varphi ={\mathrm {id}}_{\mathcal A}$. This implies that ![]() ${\mathrm {gr}}(\psi )=\varphi ^{-1}$ is a linear isomorphism. This proves the following lemma which is also contained in [Reference LetzterLet19, Corollary 4.4] for
${\mathrm {gr}}(\psi )=\varphi ^{-1}$ is a linear isomorphism. This proves the following lemma which is also contained in [Reference LetzterLet19, Corollary 4.4] for ![]() ${\mathfrak g}$ of finite type:
${\mathfrak g}$ of finite type:
Lemma 2.10. The Letzter map ![]() $\psi :{\mathcal B}_{\mathbf {c}}\rightarrow {\mathcal A}$ is a linear isomorphism.
$\psi :{\mathcal B}_{\mathbf {c}}\rightarrow {\mathcal A}$ is a linear isomorphism.
We collect some additional properties of the Letzter map:
Lemma 2.11. The Letzter map ![]() $\psi :{\mathcal B}_{\mathbf {c}}\rightarrow {\mathcal A}$ has the following properties:
$\psi :{\mathcal B}_{\mathbf {c}}\rightarrow {\mathcal A}$ has the following properties:
(1)
 $\psi (ab) = \psi (a\psi (b))$ for all
$\psi (ab) = \psi (a\psi (b))$ for all  $a,b\in {\mathcal B}_{\mathbf {c}}$.
$a,b\in {\mathcal B}_{\mathbf {c}}$.(2)
 $\psi (h_1bh_2) = h_1\psi (b) h_2$ for all
$\psi (h_1bh_2) = h_1\psi (b) h_2$ for all  $b\in {\mathcal B}_{\mathbf {c}}$,
$b\in {\mathcal B}_{\mathbf {c}}$,  $h_1,h_2\in {\mathcal H}$.
$h_1,h_2\in {\mathcal H}$.(3)
 $\psi (T_i(b))=T_i(\psi (b))$ for all
$\psi (T_i(b))=T_i(\psi (b))$ for all  $i\in X$.
$i\in X$.(4)
 $\psi (ab)-\psi (a)\psi (b)\in {\mathcal A}_{<m+n}$ for all
$\psi (ab)-\psi (a)\psi (b)\in {\mathcal A}_{<m+n}$ for all  $a\in {\mathcal F}_m({\mathcal B}_{\mathbf {c}})$,
$a\in {\mathcal F}_m({\mathcal B}_{\mathbf {c}})$,  $b\in {\mathcal F}_n({\mathcal B}_{\mathbf {c}})$.
$b\in {\mathcal F}_n({\mathcal B}_{\mathbf {c}})$.
Proof. The kernel of the projection map (2.23) is a left ideal in ![]() $U^{\mathrm {poly}}$. Hence the kernel of the Letzter map is a left ideal in
$U^{\mathrm {poly}}$. Hence the kernel of the Letzter map is a left ideal in ![]() ${\mathcal B}_{\mathbf {c}}$. This implies statement (1). Similarly, statement (2) follows from the fact that the decomposition (2.22) is a sum of
${\mathcal B}_{\mathbf {c}}$. This implies statement (1). Similarly, statement (2) follows from the fact that the decomposition (2.22) is a sum of ![]() ${\mathcal H}$-bimodules. And statement (3) holds because both summands in the decomposition (2.22) are invariant under
${\mathcal H}$-bimodules. And statement (3) holds because both summands in the decomposition (2.22) are invariant under ![]() $T_i$ for
$T_i$ for ![]() $i\in X$.
$i\in X$.
Recall from the discussion before Lemma 2.10 that the Letzter map ![]() $\psi :{\mathcal B}_{\mathbf {c}}\rightarrow {\mathcal A}$ is a linear isomorphism of filtered vector spaces, and that the associated graded map
$\psi :{\mathcal B}_{\mathbf {c}}\rightarrow {\mathcal A}$ is a linear isomorphism of filtered vector spaces, and that the associated graded map ![]() ${\mathrm {gr}}(\psi ):{\mathrm {gr}}({\mathcal B}_{\mathbf {c}})\rightarrow {\mathcal A}$ is an algebra isomorphism. This implies statement (4).
${\mathrm {gr}}(\psi ):{\mathrm {gr}}({\mathcal B}_{\mathbf {c}})\rightarrow {\mathcal A}$ is an algebra isomorphism. This implies statement (4).
2.6 An antilinear isomorphism of quantum symmetric pair coideals
Let ![]() $\overline {\phantom {m}}:U\rightarrow U$,
$\overline {\phantom {m}}:U\rightarrow U$, ![]() $u\mapsto \overline {u}$, be the Lusztig bar involution defined in [Reference LusztigLus94, 3.1.12]. Denote by
$u\mapsto \overline {u}$, be the Lusztig bar involution defined in [Reference LusztigLus94, 3.1.12]. Denote by ![]() $\rho _X$ and
$\rho _X$ and ![]() $\rho _X^\vee $ the half sum of positive roots and of coroots, respectively, for the root system corresponding to
$\rho _X^\vee $ the half sum of positive roots and of coroots, respectively, for the root system corresponding to ![]() $X \subseteq I$. For any
$X \subseteq I$. For any  ${\mathbf {c}}=(c_i)_{i\in I\setminus X}\in {\mathbb K}^{I\setminus X}$, define
${\mathbf {c}}=(c_i)_{i\in I\setminus X}\in {\mathbb K}^{I\setminus X}$, define  ${\mathbf {c}}'=\left (c_i'\right )\in {\mathbb K}^{I\setminus X}$ by
${\mathbf {c}}'=\left (c_i'\right )\in {\mathbb K}^{I\setminus X}$ by
 $$ \begin{align} c_i'=(-1)^{2\alpha_i\left(\rho_X^\vee\right)}q^{\left(\alpha_i,\Theta\left(\alpha_i\right)-2\rho_X\right)} \overline{c_{\tau(i)}} \end{align} $$
$$ \begin{align} c_i'=(-1)^{2\alpha_i\left(\rho_X^\vee\right)}q^{\left(\alpha_i,\Theta\left(\alpha_i\right)-2\rho_X\right)} \overline{c_{\tau(i)}} \end{align} $$for all ![]() $i\in I\setminus X$. Note that
$i\in I\setminus X$. Note that ![]() ${\mathbf {c}}\in {\mathcal C}$ if and only if
${\mathbf {c}}\in {\mathcal C}$ if and only if ![]() ${\mathbf {c}}'\in {\mathcal C}$. In the following we will compare the quantum symmetric pair coideal subalgebras
${\mathbf {c}}'\in {\mathcal C}$. In the following we will compare the quantum symmetric pair coideal subalgebras ![]() ${\mathcal B}_{\mathbf {c}}$ and
${\mathcal B}_{\mathbf {c}}$ and ![]() ${\mathcal B}_{{\mathbf {c}}'}$. To indicate the parameters, we write
${\mathcal B}_{{\mathbf {c}}'}$. To indicate the parameters, we write ![]() $B_i'$ for the generators (2.20) of
$B_i'$ for the generators (2.20) of ![]() ${\mathcal B}_{{\mathbf {c}}'}$ for
${\mathcal B}_{{\mathbf {c}}'}$ for ![]() $i\in I\setminus X$.
$i\in I\setminus X$.
In [Reference Appel and VlaarAV20, Theorem 7.4], Appel and Vlaar considered an extended version of the quasi K-matrix constructed in [Reference Balagović and KolbBK19]. Using this extended version of the quasi K-matrix, one obtains the following theorem, a proof of which in our notation can be found in [Reference KolbKol21, Corollary 4.1]:
Theorem 2.12. For any ![]() ${\mathbf {c}}\in {\mathcal C}$ there exists a k-algebra isomorphism
${\mathbf {c}}\in {\mathcal C}$ there exists a k-algebra isomorphism ![]() $\Phi :{\mathcal B}_{\mathbf {c}}\rightarrow {\mathcal B}_{{\mathbf {c}}'}$ such that
$\Phi :{\mathcal B}_{\mathbf {c}}\rightarrow {\mathcal B}_{{\mathbf {c}}'}$ such that
In particular, we have ![]() $\Phi (q)=q^{-1}$ and
$\Phi (q)=q^{-1}$ and ![]() $\Phi (K_\beta )=K_{-\beta }$ for all
$\Phi (K_\beta )=K_{-\beta }$ for all ![]() $\beta \in Q^\Theta $.
$\beta \in Q^\Theta $.
3 The star product on the partial parabolic subalgebra
In this section we recall the general notion of a star product on an ![]() ${\mathbb N}$-graded algebra A. We then recall the fact that
${\mathbb N}$-graded algebra A. We then recall the fact that ![]() ${\mathcal B}_{\mathbf {c}}$ can be viewed as a star product deformation of the partial parabolic subalgebra
${\mathcal B}_{\mathbf {c}}$ can be viewed as a star product deformation of the partial parabolic subalgebra ![]() ${\mathcal A}$. To describe this star product, we need to know the action of certain twisted skew derivations
${\mathcal A}$. To describe this star product, we need to know the action of certain twisted skew derivations  $\partial ^L_{i,X}$ on
$\partial ^L_{i,X}$ on ![]() ${\mathcal R}_X$. In Lemmas 3.4, 3.5, 3.6 and 3.7 we calculate the required values of
${\mathcal R}_X$. In Lemmas 3.4, 3.5, 3.6 and 3.7 we calculate the required values of  $\partial ^L_{i,X}$ explicitly.
$\partial ^L_{i,X}$ explicitly.
3.1 Star products
We will extensively use the notion of star product algebras and their properties from [Reference Kolb and YakimovKY20]. For an ![]() ${\mathbb N}$-graded
${\mathbb N}$-graded ![]() ${\mathbb K}$-algebra
${\mathbb K}$-algebra  $A=\bigoplus _{j\in {\mathbb N}} A_j$ and
$A=\bigoplus _{j\in {\mathbb N}} A_j$ and ![]() $m\in {\mathbb N}$, denote
$m\in {\mathbb N}$, denote  $A_{<m}=\bigoplus _{j=0}^{m-1}A_j$ and
$A_{<m}=\bigoplus _{j=0}^{m-1}A_j$ and  $A_{\le m}=\bigoplus _{j=0}^{m}A_j$.
$A_{\le m}=\bigoplus _{j=0}^{m}A_j$.
Definition 3.1. Assume that  $A=\bigoplus _{j\in {\mathbb N}} A_j$ is an
$A=\bigoplus _{j\in {\mathbb N}} A_j$ is an ![]() ${\mathbb N}$-graded
${\mathbb N}$-graded ![]() ${\mathbb K}$-algebra. A star product on A is an associative bilinear operation
${\mathbb K}$-algebra. A star product on A is an associative bilinear operation ![]() $* : A \times A \to A$ such that
$* : A \times A \to A$ such that
A star product ![]() $\ast $ on A is called
$\ast $ on A is called ![]() $0$-equivariant if
$0$-equivariant if
In this setting, ![]() $(A,\ast )$ is a filtered algebra with
$(A,\ast )$ is a filtered algebra with ![]() ${\mathcal F}_m (A) := A_{\leq m}$ and
${\mathcal F}_m (A) := A_{\leq m}$ and
If A is generated in degrees ![]() $0$ and
$0$ and ![]() $1$, then
$1$, then ![]() $(A,*)$ is generated by
$(A,*)$ is generated by ![]() ${\mathcal F}_1 (A)$ and we have the following properties [Reference Kolb and YakimovKY20, Lemma 5.2.(ii)]:
${\mathcal F}_1 (A)$ and we have the following properties [Reference Kolb and YakimovKY20, Lemma 5.2.(ii)]:
Lemma 3.2. Let A be an ![]() ${\mathbb N}$-graded
${\mathbb N}$-graded ![]() ${\mathbb K}$-algebra generated in degrees
${\mathbb K}$-algebra generated in degrees ![]() $0$ and
$0$ and ![]() $1$.
$1$.
(i) Every
 $0$-equivariant star product on A is uniquely determined by the
$0$-equivariant star product on A is uniquely determined by the  ${\mathbb K}$-linear map
${\mathbb K}$-linear map  $\mu ^L:A_1\to \mathrm {End}_{{\mathbb K}}(A)$,
$\mu ^L:A_1\to \mathrm {End}_{{\mathbb K}}(A)$,  $$\begin{align*}\mu^L_f(a) = f * a - f a \qquad \text{for all}\ f \in A_1, a \in A. \end{align*}$$
$$\begin{align*}\mu^L_f(a) = f * a - f a \qquad \text{for all}\ f \in A_1, a \in A. \end{align*}$$(ii) If U is a graded subalgebra of A such that
 $A_0 U = U A_0 = A$, then every
$A_0 U = U A_0 = A$, then every  $0$-equivariant star product on A is uniquely determined by the
$0$-equivariant star product on A is uniquely determined by the  ${\mathbb K}$-linear map
${\mathbb K}$-linear map  $\mu ^L : U_1 \to {\mathrm {Hom}}_{{\mathbb K}}(U,A)$,
$\mu ^L : U_1 \to {\mathrm {Hom}}_{{\mathbb K}}(U,A)$,  $$\begin{align*}\mu^L_f(u) = f*u - fu \qquad \text{for all}\ f \in U_1, u \in U. \end{align*}$$
$$\begin{align*}\mu^L_f(u) = f*u - fu \qquad \text{for all}\ f \in U_1, u \in U. \end{align*}$$
3.2 The pullback of the algebra structure on  ${\mathcal B}_{\mathbf {c}}$
${\mathcal B}_{\mathbf {c}}$
We can use the Letzter map ![]() $\psi :{\mathcal B}_{\mathbf {c}}\rightarrow {\mathcal A}$ to define a new algebra structure
$\psi :{\mathcal B}_{\mathbf {c}}\rightarrow {\mathcal A}$ to define a new algebra structure ![]() $\ast $ on
$\ast $ on ![]() ${\mathcal A}$ by
${\mathcal A}$ by
By Lemma 2.11(4) the binary operation ![]() $\ast $ defines a star product on
$\ast $ defines a star product on ![]() ${\mathcal A}$, and by Lemma 2.11(2) this star product is
${\mathcal A}$, and by Lemma 2.11(2) this star product is ![]() $0$-equivariant. Hence Lemma 3.2 implies that the star product
$0$-equivariant. Hence Lemma 3.2 implies that the star product ![]() $\ast $ on
$\ast $ on ![]() ${\mathcal A}$ is uniquely determined by the family of maps
${\mathcal A}$ is uniquely determined by the family of maps  $\mu ^L_f\in {\mathrm {Hom}}_{{\mathbb K}}({\mathcal R}_X,{\mathcal A})$ for all
$\mu ^L_f\in {\mathrm {Hom}}_{{\mathbb K}}({\mathcal R}_X,{\mathcal A})$ for all ![]() $f\in ({\mathcal R}_X)_1={\mathcal R}_X\cap {\mathcal A}_1$ defined by
$f\in ({\mathcal R}_X)_1={\mathcal R}_X\cap {\mathcal A}_1$ defined by
 $$ \begin{align*} \mu_f^L(u) = f\ast u - fu \qquad \text{for all}\ u\in {\mathcal R}_X. \end{align*} $$
$$ \begin{align*} \mu_f^L(u) = f\ast u - fu \qquad \text{for all}\ u\in {\mathcal R}_X. \end{align*} $$As  $\mu ^L_{{\mbox{ad}}_r(h)(f)}(u)=S\left (h_{(1)}\right )\mu _f^L\left (h_{(2)}u\right )$ for all
$\mu ^L_{{\mbox{ad}}_r(h)(f)}(u)=S\left (h_{(1)}\right )\mu _f^L\left (h_{(2)}u\right )$ for all ![]() $f\in ({\mathcal R}_X)_1$,
$f\in ({\mathcal R}_X)_1$, ![]() $h\in {\mathcal H}$ and
$h\in {\mathcal H}$ and ![]() $u\in {\mathcal R}_X$, the
$u\in {\mathcal R}_X$, the ![]() $0$-equivariant star product
$0$-equivariant star product ![]() $\ast $ on
$\ast $ on ![]() ${\mathcal A}$ is uniquely determined by the maps
${\mathcal A}$ is uniquely determined by the maps  $\mu _{F_i}^L$ for
$\mu _{F_i}^L$ for ![]() $i\in I\setminus X$. In the following lemma, we determine these maps:
$i\in I\setminus X$. In the following lemma, we determine these maps:
Lemma 3.3. For all ![]() $i\in I\setminus X$ and all
$i\in I\setminus X$ and all ![]() $u\in {\mathcal R}_X$, we have
$u\in {\mathcal R}_X$, we have
 $$ \begin{align} F_i\ast u = F_i u - c_i \frac{q^{-\left(\alpha_i,\Theta\left(\alpha_i\right)\right)}}{q_i-q_i^{-1}}K_{-\alpha_i-\Theta\left(\alpha_i\right)} T_{w_X} \circ \partial_{\tau(i)}^L\circ T_{w_X}^{-1}(u). \end{align} $$
$$ \begin{align} F_i\ast u = F_i u - c_i \frac{q^{-\left(\alpha_i,\Theta\left(\alpha_i\right)\right)}}{q_i-q_i^{-1}}K_{-\alpha_i-\Theta\left(\alpha_i\right)} T_{w_X} \circ \partial_{\tau(i)}^L\circ T_{w_X}^{-1}(u). \end{align} $$Proof. Write ![]() $u=\psi (b)$ for some
$u=\psi (b)$ for some ![]() $b\in {\mathcal B}_{\mathbf {c}}$. Using Lemma 2.11(1) and (3), we calculate
$b\in {\mathcal B}_{\mathbf {c}}$. Using Lemma 2.11(1) and (3), we calculate
 $$ \begin{align*} F_i\ast u &= \psi(B_i b)\\ &= \psi\left(\left(F_i - c_i T_{w_X}\left(E_{\tau(i)}\right)K_i^{-1}\right)\psi(b) \right)\\ &= F_i u - c_i q^{-\left(\alpha_i,\Theta\left(\alpha_i\right)\right)} \psi\left(K_i^{-1}\left[T_{w_X}\left(E_{\tau(i)}\right),u\right] \right)\\ &= F_i u - c_i q^{-\left(\alpha_i,\Theta\left(\alpha_i\right)\right)} T_{w_X}\left(\psi\left(K_{w_X\left(\alpha_i\right)}^{-1}\left[E_{\tau(i)}, T_{w_X}^{-1}(u)\right] \right)\right). \end{align*} $$
$$ \begin{align*} F_i\ast u &= \psi(B_i b)\\ &= \psi\left(\left(F_i - c_i T_{w_X}\left(E_{\tau(i)}\right)K_i^{-1}\right)\psi(b) \right)\\ &= F_i u - c_i q^{-\left(\alpha_i,\Theta\left(\alpha_i\right)\right)} \psi\left(K_i^{-1}\left[T_{w_X}\left(E_{\tau(i)}\right),u\right] \right)\\ &= F_i u - c_i q^{-\left(\alpha_i,\Theta\left(\alpha_i\right)\right)} T_{w_X}\left(\psi\left(K_{w_X\left(\alpha_i\right)}^{-1}\left[E_{\tau(i)}, T_{w_X}^{-1}(u)\right] \right)\right). \end{align*} $$Using equation (2.3) and the definition of the projection ![]() $\psi $, we obtain
$\psi $, we obtain
 $$ \begin{align*} F_i\ast u &= F_i u - c_i \frac{q^{-\left(\alpha_i,\Theta\left(\alpha_i\right)\right)}}{q_i-q_i^{-1}} T_{w_X} \left(K_{w_X\left(\alpha_i\right)}^{-1} K_{\tau(i)} \partial^L_{\tau(i)}\left(T_{w_X}^{-1}(u)\right) \right)\\ &= F_i u - c_i \frac{q^{-\left(\alpha_i,\Theta\left(\alpha_i\right)\right)}}{q_i-q_i^{-1}} K_{-\alpha_i - \Theta\left(\alpha_i\right)} T_{w_X} \left( \partial^L_{\tau(i)}\left( T_{w_X}^{-1}(u)\right)\right), \end{align*} $$
$$ \begin{align*} F_i\ast u &= F_i u - c_i \frac{q^{-\left(\alpha_i,\Theta\left(\alpha_i\right)\right)}}{q_i-q_i^{-1}} T_{w_X} \left(K_{w_X\left(\alpha_i\right)}^{-1} K_{\tau(i)} \partial^L_{\tau(i)}\left(T_{w_X}^{-1}(u)\right) \right)\\ &= F_i u - c_i \frac{q^{-\left(\alpha_i,\Theta\left(\alpha_i\right)\right)}}{q_i-q_i^{-1}} K_{-\alpha_i - \Theta\left(\alpha_i\right)} T_{w_X} \left( \partial^L_{\tau(i)}\left( T_{w_X}^{-1}(u)\right)\right), \end{align*} $$which gives the desired formula.
3.3 Twisted skew derivations
Recall Corollary 2.7 and the subalgebra ![]() $G_X^+$ defined in Section 2.1. The decomposition (2.12) implies that
$G_X^+$ defined in Section 2.1. The decomposition (2.12) implies that ![]() $T_{w_X}:U^-\rightarrow G_X^+\otimes {\mathcal R}_X$ is an algebra isomorphism. To shorten notation, define twisted skew derivations
$T_{w_X}:U^-\rightarrow G_X^+\otimes {\mathcal R}_X$ is an algebra isomorphism. To shorten notation, define twisted skew derivations  $\partial ^L_{i,X}, \partial ^R_{i,X}:G_X^+\otimes {\mathcal R}_X \rightarrow G_X^+\otimes {\mathcal R}_X$ by
$\partial ^L_{i,X}, \partial ^R_{i,X}:G_X^+\otimes {\mathcal R}_X \rightarrow G_X^+\otimes {\mathcal R}_X$ by
 $$ \begin{align*} \partial^{L}_{i,X}=T_{w_X} \circ \partial^{L}_i \circ T_{w_X}^{-1}, \qquad \partial^{R}_{i,X}=T_{w_X} \circ \partial^{R}_i \circ T_{w_X}^{-1}, \end{align*} $$
$$ \begin{align*} \partial^{L}_{i,X}=T_{w_X} \circ \partial^{L}_i \circ T_{w_X}^{-1}, \qquad \partial^{R}_{i,X}=T_{w_X} \circ \partial^{R}_i \circ T_{w_X}^{-1}, \end{align*} $$for all ![]() $i\in I$. The skew derivation properties (2.5) and (2.6) of
$i\in I$. The skew derivation properties (2.5) and (2.6) of ![]() $\partial ^L_i$ and
$\partial ^L_i$ and ![]() $\partial ^R_i$ imply
$\partial ^R_i$ imply
 $$ \begin{align} \partial_{i,X}^L(fg)&=\partial_{i,X}^L(f)g +q^{\left(w_X\left(\alpha_i\right),\mu\right)}f \partial_{i,X}^L(g) \end{align} $$
$$ \begin{align} \partial_{i,X}^L(fg)&=\partial_{i,X}^L(f)g +q^{\left(w_X\left(\alpha_i\right),\mu\right)}f \partial_{i,X}^L(g) \end{align} $$ $$ \begin{align} \partial_{i,X}^R(fg)&=q^{\left(w_X\left(\alpha_i\right),\nu\right)}\partial_{i,X}^R(f)g +f \partial_{i,X}^R(g) \end{align} $$
$$ \begin{align} \partial_{i,X}^R(fg)&=q^{\left(w_X\left(\alpha_i\right),\nu\right)}\partial_{i,X}^R(f)g +f \partial_{i,X}^R(g) \end{align} $$for all  $f\in \left (G_X^+\otimes {\mathcal R}_X\right )_{-\mu }$,
$f\in \left (G_X^+\otimes {\mathcal R}_X\right )_{-\mu }$,  $g\in \left (G_X^+\otimes {\mathcal R}_X\right )_{-\nu }$. To understand the star product better, we need to know the action of the twisted skew derivation
$g\in \left (G_X^+\otimes {\mathcal R}_X\right )_{-\nu }$. To understand the star product better, we need to know the action of the twisted skew derivation  $\partial ^L_{i,X}$ on the elements of
$\partial ^L_{i,X}$ on the elements of ![]() ${\mathcal R}_X$.
${\mathcal R}_X$.
Lemma 3.4. For any ![]() $i\in I \setminus X$ we have
$i\in I \setminus X$ we have
 $$ \begin{align} \partial^L_{i,X}(F_i) = q^{\left(\alpha_i,\alpha_i-w_X\left(\alpha_i\right)\right)} K_{\alpha_i-w_X\left(\alpha_i\right)} \partial_i^R\left(T_{w_X}(E_i)\right). \end{align} $$
$$ \begin{align} \partial^L_{i,X}(F_i) = q^{\left(\alpha_i,\alpha_i-w_X\left(\alpha_i\right)\right)} K_{\alpha_i-w_X\left(\alpha_i\right)} \partial_i^R\left(T_{w_X}(E_i)\right). \end{align} $$Proof. We apply 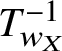 $T_{w_X}^{-1}$ to equation (2.4) for
$T_{w_X}^{-1}$ to equation (2.4) for ![]() $x=T_{w_X}(E_i)$ and compare with equation (2.3) to obtain
$x=T_{w_X}(E_i)$ and compare with equation (2.3) to obtain
 $$ \begin{align*} &\frac{T_{w_X}^{-1}\left(\partial_i^R\left(T_{w_X}(E_i)\right)K_i\right) - T_{w_X}^{-1}\left(K_i^{-1}\partial^L_i\left(T_{w_X}(E_i)\right)\right)}{q_i-q_i^{-1}}\\ &\quad=\left[E_i, T_{w_X}^{-1}(F_i)\right] =\frac{K_i\partial^L_i\left(T_{w_X}^{-1}(F_i)\right)-\partial_i^R\left(T_{w_X}^{-1}(F_i)\right)K_i^{-1}}{q_i-q_i^{-1}}. \end{align*} $$
$$ \begin{align*} &\frac{T_{w_X}^{-1}\left(\partial_i^R\left(T_{w_X}(E_i)\right)K_i\right) - T_{w_X}^{-1}\left(K_i^{-1}\partial^L_i\left(T_{w_X}(E_i)\right)\right)}{q_i-q_i^{-1}}\\ &\quad=\left[E_i, T_{w_X}^{-1}(F_i)\right] =\frac{K_i\partial^L_i\left(T_{w_X}^{-1}(F_i)\right)-\partial_i^R\left(T_{w_X}^{-1}(F_i)\right)K_i^{-1}}{q_i-q_i^{-1}}. \end{align*} $$Comparing the summands involving ![]() $K_i$, we obtain
$K_i$, we obtain
 $$ \begin{align*} T_{w_X}^{-1}\left(\partial_i^R\left(T_{w_X}(E_i)\right)K_i\right)=K_i\partial^L_i\left(T_{w_X}^{-1}(F_i)\right) \end{align*} $$
$$ \begin{align*} T_{w_X}^{-1}\left(\partial_i^R\left(T_{w_X}(E_i)\right)K_i\right)=K_i\partial^L_i\left(T_{w_X}^{-1}(F_i)\right) \end{align*} $$and hence
 $$ \begin{align*} T_{w_X}\left(\partial_i^L\left(T_{w_X}^{-1}(F_i)\right) \right)&= K_{w_X\left(\alpha_i\right)}^{-1}\partial_i^R\left(T_{w_X}(E_i)\right)K_i\\ &=q^{\left(\alpha_i,\alpha_i-w_X\left(\alpha_i\right)\right)} K_{\alpha_i-w_X\left(\alpha_i\right)}\partial_i^R\left(T_{w_X}(E_i)\right), \end{align*} $$
$$ \begin{align*} T_{w_X}\left(\partial_i^L\left(T_{w_X}^{-1}(F_i)\right) \right)&= K_{w_X\left(\alpha_i\right)}^{-1}\partial_i^R\left(T_{w_X}(E_i)\right)K_i\\ &=q^{\left(\alpha_i,\alpha_i-w_X\left(\alpha_i\right)\right)} K_{\alpha_i-w_X\left(\alpha_i\right)}\partial_i^R\left(T_{w_X}(E_i)\right), \end{align*} $$which confirms the statement of the lemma.
For simplicity, define
 $$\begin{align*}Z_i=\partial_i^R\left(T_{w_X}(E_i)\right)\in U^+_{w_X\left(\alpha_i\right)-\alpha_i} \qquad \text{for any}\ i\in I\setminus X. \end{align*}$$
$$\begin{align*}Z_i=\partial_i^R\left(T_{w_X}(E_i)\right)\in U^+_{w_X\left(\alpha_i\right)-\alpha_i} \qquad \text{for any}\ i\in I\setminus X. \end{align*}$$As ![]() $w_X(\alpha _i)-\alpha _i\in Q_X^+$, we get
$w_X(\alpha _i)-\alpha _i\in Q_X^+$, we get ![]() $Z_i\in {\mathcal M}_X^+$ and hence we have
$Z_i\in {\mathcal M}_X^+$ and hence we have
 $$ \begin{align} \left[Z_i,F_j\right]=0 \qquad \text{for all}\ i,j\in I \setminus X. \end{align} $$
$$ \begin{align} \left[Z_i,F_j\right]=0 \qquad \text{for all}\ i,j\in I \setminus X. \end{align} $$Recall the nonsymmetric quantum integer ![]() $(n)_p$ defined by
$(n)_p$ defined by  $(n)_p=\sum _{j=0}^{n-1}p^j$ for any
$(n)_p=\sum _{j=0}^{n-1}p^j$ for any ![]() $n\in {\mathbb N}$,
$n\in {\mathbb N}$, ![]() $p\in {\mathbb K}$.
$p\in {\mathbb K}$.
Lemma 3.5. For any ![]() $i\in I\setminus X$ and
$i\in I\setminus X$ and ![]() $n\in {\mathbb N}$, we have
$n\in {\mathbb N}$, we have
 $$ \begin{align} \partial_{i,X}^L\left(F_i^n\right)=q^{\left(\alpha_i,\alpha_i-w_X\left(\alpha_i\right)\right)}(n)_{q_i^2}K_{\alpha_i-w_X\left(\alpha_i\right)} Z_i F_i^{n-1}. \end{align} $$
$$ \begin{align} \partial_{i,X}^L\left(F_i^n\right)=q^{\left(\alpha_i,\alpha_i-w_X\left(\alpha_i\right)\right)}(n)_{q_i^2}K_{\alpha_i-w_X\left(\alpha_i\right)} Z_i F_i^{n-1}. \end{align} $$Proof. For ![]() $n=1$, equation (3.6) holds by Lemma 3.4. We proceed by induction on n. For
$n=1$, equation (3.6) holds by Lemma 3.4. We proceed by induction on n. For ![]() $n>1$ we calculate
$n>1$ we calculate
 $$ \begin{align*} \partial_{i,X}^L\left(F_i^n\right) &\stackrel{\text{(3.2)}}{=}\partial_{i,X}^L(F_i)F_i^{n-1} + q^{\left(w_X\left(\alpha_i\right),\alpha_i\right)} F_i\partial_{i,X}^L\left(F_i^{n-1}\right)\\ &\stackrel{\text{(3.4)}}{=}q^{\left(\alpha_i,\alpha_i-w_X\left(\alpha_i\right)\right)} K_{\alpha_i-w_X\left(\alpha_i\right)}Z_i F_i^{n-1} + F_i q^{\left(\alpha_i,\alpha_i\right)} (n-1)_{q_i^2} K_{\alpha_i-w_X\left(\alpha_i\right)} Z_i F_i^{n-2}\\ &\stackrel{\phantom{\text{(3.2)}}}{=} q^{\left(\alpha_i,\alpha_i-w_X\left(\alpha_i\right)\right)} (n)_{q_i^2} K_{\alpha_i-w_X\left(\alpha_i\right)} Z_i F_i^{n-1}, \end{align*} $$
$$ \begin{align*} \partial_{i,X}^L\left(F_i^n\right) &\stackrel{\text{(3.2)}}{=}\partial_{i,X}^L(F_i)F_i^{n-1} + q^{\left(w_X\left(\alpha_i\right),\alpha_i\right)} F_i\partial_{i,X}^L\left(F_i^{n-1}\right)\\ &\stackrel{\text{(3.4)}}{=}q^{\left(\alpha_i,\alpha_i-w_X\left(\alpha_i\right)\right)} K_{\alpha_i-w_X\left(\alpha_i\right)}Z_i F_i^{n-1} + F_i q^{\left(\alpha_i,\alpha_i\right)} (n-1)_{q_i^2} K_{\alpha_i-w_X\left(\alpha_i\right)} Z_i F_i^{n-2}\\ &\stackrel{\phantom{\text{(3.2)}}}{=} q^{\left(\alpha_i,\alpha_i-w_X\left(\alpha_i\right)\right)} (n)_{q_i^2} K_{\alpha_i-w_X\left(\alpha_i\right)} Z_i F_i^{n-1}, \end{align*} $$where we also used the fact that ![]() $Z_i$ and
$Z_i$ and ![]() $F_i$ commute by equation (3.5).
$F_i$ commute by equation (3.5).
We will need similar relations for  ${\mbox{ad}}_r\left (F_j\right )\left (F_i^n\right )$, which lies in
${\mbox{ad}}_r\left (F_j\right )\left (F_i^n\right )$, which lies in ![]() ${\mathcal R}_X$ for
${\mathcal R}_X$ for ![]() $j\in X$.
$j\in X$.
Lemma 3.6. For any ![]() $u\in {\mathcal R}_X$,
$u\in {\mathcal R}_X$, ![]() $j\in X$ and
$j\in X$ and ![]() $i\in I\setminus X$, we have
$i\in I\setminus X$, we have
 $$ \begin{align} \partial_{i,X}^L\left({\mbox{ad}}_r\left(F_j\right)(u)\right) = - \frac{1}{q_j-q_j^{-1}} \partial_{\tau(j),X}^R \circ \partial_{i,X}^L(u). \end{align} $$
$$ \begin{align} \partial_{i,X}^L\left({\mbox{ad}}_r\left(F_j\right)(u)\right) = - \frac{1}{q_j-q_j^{-1}} \partial_{\tau(j),X}^R \circ \partial_{i,X}^L(u). \end{align} $$Proof. For ![]() $u\in ({\mathcal R}_X)_{-\mu }$ and
$u\in ({\mathcal R}_X)_{-\mu }$ and ![]() $j\in X$ we calculate
$j\in X$ we calculate
 $$ \begin{align} T_{w_X}^{-1}\left({\mbox{ad}}_r\left(F_j\right)(u)\right)& \stackrel{\phantom{\text{(2.9)}}}{=}T_{w_X}^{-1}\left(u F_j - q^{-\left(\alpha_j,\mu\right)}F_j u\right)\nonumber\\ &\stackrel{\phantom{\text{(2.9)}}}{=} - T_{w_X}^{-1}(u) E_{\tau\left(j\right)} K_{\tau\left(j\right)} + q^{-\left(\alpha_j,\mu\right)} E_{\tau\left(j\right)} K_{\tau\left(j\right)} T_{w_X}^{-1}(u)\nonumber\\ &\stackrel{\phantom{\text{(2.9)}}}{=} \left[E_{\tau\left(j\right)}, T_{w_X}^{-1}(u)\right] K_{\tau\left(j\right)}\nonumber\\ &\stackrel{\text{(2.9)}}{=} - \frac{1}{q_j-q_j^{-1}} \partial^R_{\tau\left(j\right)}\circ T_{w_X}^{-1}(u). \end{align} $$
$$ \begin{align} T_{w_X}^{-1}\left({\mbox{ad}}_r\left(F_j\right)(u)\right)& \stackrel{\phantom{\text{(2.9)}}}{=}T_{w_X}^{-1}\left(u F_j - q^{-\left(\alpha_j,\mu\right)}F_j u\right)\nonumber\\ &\stackrel{\phantom{\text{(2.9)}}}{=} - T_{w_X}^{-1}(u) E_{\tau\left(j\right)} K_{\tau\left(j\right)} + q^{-\left(\alpha_j,\mu\right)} E_{\tau\left(j\right)} K_{\tau\left(j\right)} T_{w_X}^{-1}(u)\nonumber\\ &\stackrel{\phantom{\text{(2.9)}}}{=} \left[E_{\tau\left(j\right)}, T_{w_X}^{-1}(u)\right] K_{\tau\left(j\right)}\nonumber\\ &\stackrel{\text{(2.9)}}{=} - \frac{1}{q_j-q_j^{-1}} \partial^R_{\tau\left(j\right)}\circ T_{w_X}^{-1}(u). \end{align} $$Hence we obtain
 $$ \begin{align*} \partial_{i,X}^L\left({\mbox{ad}}_r\left(F_j\right)(u)\right) &= - \frac{1}{q_j-q_j^{-1}} T_{w_X}\circ \partial^L_i \circ \partial^R_{\tau\left(j\right)}\circ T_{w_X}^{-1}(u)\\ &= - \frac{1}{q_j-q_j^{-1}} T_{w_X}\circ \partial^R_{\tau\left(j\right)} \circ \partial^L_i \circ T_{w_X}^{-1}(u)\\ &= - \frac{1}{q_j-q_j^{-1}} \partial_{\tau\left(j\right),X}^R \circ \partial_{i,X}^L(u), \end{align*} $$
$$ \begin{align*} \partial_{i,X}^L\left({\mbox{ad}}_r\left(F_j\right)(u)\right) &= - \frac{1}{q_j-q_j^{-1}} T_{w_X}\circ \partial^L_i \circ \partial^R_{\tau\left(j\right)}\circ T_{w_X}^{-1}(u)\\ &= - \frac{1}{q_j-q_j^{-1}} T_{w_X}\circ \partial^R_{\tau\left(j\right)} \circ \partial^L_i \circ T_{w_X}^{-1}(u)\\ &= - \frac{1}{q_j-q_j^{-1}} \partial_{\tau\left(j\right),X}^R \circ \partial_{i,X}^L(u), \end{align*} $$which is the desired formula.
By equation (3.7), we will need to understand the action of  $\partial _{j,X}^R$ on
$\partial _{j,X}^R$ on ![]() $G_X^+\otimes {\mathcal R}_X$. Equation (3.8) implies that
$G_X^+\otimes {\mathcal R}_X$. Equation (3.8) implies that
 $$ \begin{align} \partial_{j,X}^R(u)=-\left(q_j-q_j^{-1}\right) {\mbox{ad}}_r\left(F_{\tau\left(j\right)}\right)(u) \qquad \text{for all}\ u\in {\mathcal R}_X, j\in X. \end{align} $$
$$ \begin{align} \partial_{j,X}^R(u)=-\left(q_j-q_j^{-1}\right) {\mbox{ad}}_r\left(F_{\tau\left(j\right)}\right)(u) \qquad \text{for all}\ u\in {\mathcal R}_X, j\in X. \end{align} $$Moreover, by Lemma 3.4 we have
 $$ \begin{align} T_{w_X}^{-1}\left(K_{\alpha_i-w_X\left(\alpha_i\right)}Z_i\right) = q^{\left(\alpha_i, w_X\left(\alpha_i\right)-\alpha_i\right)} \partial_i^L\circ T_{w_X}^{-1}(F_i), \end{align} $$
$$ \begin{align} T_{w_X}^{-1}\left(K_{\alpha_i-w_X\left(\alpha_i\right)}Z_i\right) = q^{\left(\alpha_i, w_X\left(\alpha_i\right)-\alpha_i\right)} \partial_i^L\circ T_{w_X}^{-1}(F_i), \end{align} $$and hence
 $$ \begin{align*} \partial_{\tau\left(j\right),X}^R\left(K_{\alpha_i-w_X\left(\alpha_i\right)}Z_i\right)= q^{\left(\alpha_i, w_X\left(\alpha_i\right)-\alpha_i\right)} \partial_{\tau\left(j\right),X}^R \circ \partial_{i,X}^L (F_i), \end{align*} $$
$$ \begin{align*} \partial_{\tau\left(j\right),X}^R\left(K_{\alpha_i-w_X\left(\alpha_i\right)}Z_i\right)= q^{\left(\alpha_i, w_X\left(\alpha_i\right)-\alpha_i\right)} \partial_{\tau\left(j\right),X}^R \circ \partial_{i,X}^L (F_i), \end{align*} $$which implies that  $\partial _{\tau \left (j\right ),X}^R\left (K_{\alpha _i-w_X\left (\alpha _i\right )}Z_i\right )\in \left (G_X^+\right )_{w_X\left (\alpha _i\right )-\alpha _i-\alpha _j}$.
$\partial _{\tau \left (j\right ),X}^R\left (K_{\alpha _i-w_X\left (\alpha _i\right )}Z_i\right )\in \left (G_X^+\right )_{w_X\left (\alpha _i\right )-\alpha _i-\alpha _j}$.
Lemma 3.7. For any ![]() $i\in I\setminus X$,
$i\in I\setminus X$, ![]() $j\in X$ and
$j\in X$ and ![]() $1\le n\in {\mathbb N}$, we have
$1\le n\in {\mathbb N}$, we have
 $$ \begin{align} \partial^L_{i,X}\left({\mbox{ad}}_r\left(F_j\right)\left(F_i^n\right)\right)&= \frac{q^{\left(\alpha_i+\alpha_j,\alpha_i+\alpha_j-w_X\left(\alpha_i\right)\right)-n\left(\alpha_i,\alpha_j\right)}}{q_j-q_j^{-1}} (n)_{q_i^2} K_{\alpha_i+\alpha_j-w_X\left(\alpha_i\right)} \partial^R_j(Z_i) F_i^{n-1}\nonumber\\ & \quad + q^{\left(\alpha_i,\alpha_i-w_X\left(\alpha_i\right)\right)}(n)_{q_i^2} K_{\alpha_i-w_X\left(\alpha_i\right)}Z_i {\mbox{ad}}_r\left(F_j\right)\left(F_i^{n-1}\right). \end{align} $$
$$ \begin{align} \partial^L_{i,X}\left({\mbox{ad}}_r\left(F_j\right)\left(F_i^n\right)\right)&= \frac{q^{\left(\alpha_i+\alpha_j,\alpha_i+\alpha_j-w_X\left(\alpha_i\right)\right)-n\left(\alpha_i,\alpha_j\right)}}{q_j-q_j^{-1}} (n)_{q_i^2} K_{\alpha_i+\alpha_j-w_X\left(\alpha_i\right)} \partial^R_j(Z_i) F_i^{n-1}\nonumber\\ & \quad + q^{\left(\alpha_i,\alpha_i-w_X\left(\alpha_i\right)\right)}(n)_{q_i^2} K_{\alpha_i-w_X\left(\alpha_i\right)}Z_i {\mbox{ad}}_r\left(F_j\right)\left(F_i^{n-1}\right). \end{align} $$Proof. By equation (2.3) we have
 $$ \begin{align*} \!\left[E_{\tau\left(j\right)},T_{w_X}^{-1}\left(K_{\alpha_i-w_X\left(\alpha_i\right)}Z_i\right)\right]=\frac{K_{\tau\left(j\right)}\partial^L_{\tau\left(j\right)}\left(T_{w_X}^{-1}\left(K_{\alpha_i-w_X\left(\alpha_i\right)}Z_i\right)\right)-\partial^R_{\tau\left(j\right)}\left(T_{w_X}^{-1}\left(K_{\alpha_i-w_X\left(\alpha_i\right)}Z_i\right)\right)K_{\tau\left(j\right)}^{-1}}{q_j-q_j^{-1}}. \end{align*} $$
$$ \begin{align*} \!\left[E_{\tau\left(j\right)},T_{w_X}^{-1}\left(K_{\alpha_i-w_X\left(\alpha_i\right)}Z_i\right)\right]=\frac{K_{\tau\left(j\right)}\partial^L_{\tau\left(j\right)}\left(T_{w_X}^{-1}\left(K_{\alpha_i-w_X\left(\alpha_i\right)}Z_i\right)\right)-\partial^R_{\tau\left(j\right)}\left(T_{w_X}^{-1}\left(K_{\alpha_i-w_X\left(\alpha_i\right)}Z_i\right)\right)K_{\tau\left(j\right)}^{-1}}{q_j-q_j^{-1}}. \end{align*} $$Applying ![]() $T_{w_X}$ to this equation, we obtain
$T_{w_X}$ to this equation, we obtain
 $$ \begin{align*} &\frac{K_j^{-1}\partial_{\tau\left(j\right),X}^L\left(K_{\alpha_i-w_X\left(\alpha_i\right)}Z_i\right)-\partial_{\tau\left(j\right),X}^R\left(K_{\alpha_i-w_X\left(\alpha_i\right)}Z_i\right)K_{j}}{q_j-q_j^{-1}}\\ &\quad =-\left[F_j K_j, K_{\alpha_i-w_X\left(\alpha_i\right)}Z_i\right]\\ &\quad = - K_{\alpha_i-w_X\left(\alpha_i\right)}\left[F_j,Z_i\right]K_j\\ &\quad = - K_{\alpha_i-w_X\left(\alpha_i\right)} \frac{K_j^{-1}\partial_j^L(Z_i) - \partial_j^R(Z_i)K_j}{q_j-q_j^{-1}} K_j. \end{align*} $$
$$ \begin{align*} &\frac{K_j^{-1}\partial_{\tau\left(j\right),X}^L\left(K_{\alpha_i-w_X\left(\alpha_i\right)}Z_i\right)-\partial_{\tau\left(j\right),X}^R\left(K_{\alpha_i-w_X\left(\alpha_i\right)}Z_i\right)K_{j}}{q_j-q_j^{-1}}\\ &\quad =-\left[F_j K_j, K_{\alpha_i-w_X\left(\alpha_i\right)}Z_i\right]\\ &\quad = - K_{\alpha_i-w_X\left(\alpha_i\right)}\left[F_j,Z_i\right]K_j\\ &\quad = - K_{\alpha_i-w_X\left(\alpha_i\right)} \frac{K_j^{-1}\partial_j^L(Z_i) - \partial_j^R(Z_i)K_j}{q_j-q_j^{-1}} K_j. \end{align*} $$Using the fact that 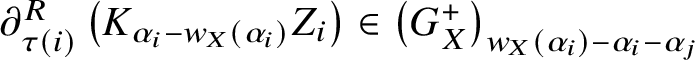 $\partial _{\tau (i)}^R\left (K_{\alpha _i-w_X\left (\alpha _i\right )}Z_i\right ) \in \left (G_X^+\right )_{w_X\left (\alpha _i\right )-\alpha _i-\alpha _j}$ proved before Lemma 3.7, and collecting terms in
$\partial _{\tau (i)}^R\left (K_{\alpha _i-w_X\left (\alpha _i\right )}Z_i\right ) \in \left (G_X^+\right )_{w_X\left (\alpha _i\right )-\alpha _i-\alpha _j}$ proved before Lemma 3.7, and collecting terms in ![]() $U^+K_{\alpha _i+2\alpha _j-w_X\left (\alpha _i\right )}$, we obtain
$U^+K_{\alpha _i+2\alpha _j-w_X\left (\alpha _i\right )}$, we obtain
 $$ \begin{align*} \partial_{\tau\left(j\right),X}^R\left(K_{\alpha_i-w_X\left(\alpha_i\right)} Z_i\right) =-q^{-\left(\alpha_j,w_X\left(\alpha_i\right)-\alpha_i-\alpha_j\right)} K_{\alpha_i-w_X\left(\alpha_i\right)+\alpha_j}\partial^R_j(Z_i). \end{align*} $$
$$ \begin{align*} \partial_{\tau\left(j\right),X}^R\left(K_{\alpha_i-w_X\left(\alpha_i\right)} Z_i\right) =-q^{-\left(\alpha_j,w_X\left(\alpha_i\right)-\alpha_i-\alpha_j\right)} K_{\alpha_i-w_X\left(\alpha_i\right)+\alpha_j}\partial^R_j(Z_i). \end{align*} $$We can use this formula and the skew derivation property (3.3) to calculate
 $$ \begin{align*} \partial^L_{i,X}\left({\mbox{ad}}_r\left(F_j\right)\left(F_i^n\right)\right) &\stackrel{\text{(3.7)}}{=} \frac{-1}{q_j-q_j^{-1}} \partial_{\tau\left(j\right),X}^R \circ \partial_{i,X}^L\left(F_i^n\right)\\ &\stackrel{\text{(3.6)}}{=} \frac{-1}{q_j-q_j^{-1}} \partial_{\tau\left(j\right),X}^R \left(q^{\left(\alpha_i,\alpha_i-w_X\left(\alpha_i\right)\right)}(n)_{q_i^2}K_{\alpha_i-w_X\left(\alpha_i\right)} Z_i F_i^{n-1} \right)\\ &\stackrel{\text{\phantom{(3.7)}}}{=} \frac{q^{\left(\alpha_i+\alpha_j,\alpha_i+\alpha_j-w_X\left(\alpha_i\right)\right)-n\left(\alpha_i,\alpha_j\right)}}{q_j-q_j^{-1}} (n)_{q_i^2} K_{\alpha_i+\alpha_j-w_X\left(\alpha_i\right)} \partial_j^R(Z_i) F_i^{n-1}\\ & \qquad \qquad \quad + q^{\left(\alpha_i,\alpha_i-w_X\left(\alpha_i\right)\right)}(n)_{q_i^2} K_{\alpha_i-w_X\left(\alpha_i\right)}Z_i {\mbox{ad}}_r\left(F_j\right)\left(F_i^{n-1}\right), \end{align*} $$
$$ \begin{align*} \partial^L_{i,X}\left({\mbox{ad}}_r\left(F_j\right)\left(F_i^n\right)\right) &\stackrel{\text{(3.7)}}{=} \frac{-1}{q_j-q_j^{-1}} \partial_{\tau\left(j\right),X}^R \circ \partial_{i,X}^L\left(F_i^n\right)\\ &\stackrel{\text{(3.6)}}{=} \frac{-1}{q_j-q_j^{-1}} \partial_{\tau\left(j\right),X}^R \left(q^{\left(\alpha_i,\alpha_i-w_X\left(\alpha_i\right)\right)}(n)_{q_i^2}K_{\alpha_i-w_X\left(\alpha_i\right)} Z_i F_i^{n-1} \right)\\ &\stackrel{\text{\phantom{(3.7)}}}{=} \frac{q^{\left(\alpha_i+\alpha_j,\alpha_i+\alpha_j-w_X\left(\alpha_i\right)\right)-n\left(\alpha_i,\alpha_j\right)}}{q_j-q_j^{-1}} (n)_{q_i^2} K_{\alpha_i+\alpha_j-w_X\left(\alpha_i\right)} \partial_j^R(Z_i) F_i^{n-1}\\ & \qquad \qquad \quad + q^{\left(\alpha_i,\alpha_i-w_X\left(\alpha_i\right)\right)}(n)_{q_i^2} K_{\alpha_i-w_X\left(\alpha_i\right)}Z_i {\mbox{ad}}_r\left(F_j\right)\left(F_i^{n-1}\right), \end{align*} $$where we also used equation (3.9) in the last step.
4 Continuous q-Hermite polynomials and deformed Chebyshev polynomials of the second kind
We recall the family of bivariate continuous q-Hermite polynomials introduced in [Reference Casper, Kolb and YakimovCKY21]. Here we will need rescaled versions of these polynomials with coefficients in the algebra ![]() ${\mathcal M}_X^+$. To express the defining relations of
${\mathcal M}_X^+$. To express the defining relations of ![]() ${\mathcal B}_{\mathbf {c}}$ we will consider quantum Serre combinations of bivariate q-Hermite polynomials, which we therefore discuss in some detail. We also introduce a new class of deformed Chebyshev polynomials of the second kind in preparation for the quantum Serre relations in the subtle case
${\mathcal B}_{\mathbf {c}}$ we will consider quantum Serre combinations of bivariate q-Hermite polynomials, which we therefore discuss in some detail. We also introduce a new class of deformed Chebyshev polynomials of the second kind in preparation for the quantum Serre relations in the subtle case ![]() $i\in I\setminus X$,
$i\in I\setminus X$, ![]() $j\in X$, discussed in Section 5.7.
$j\in X$, discussed in Section 5.7.
4.1 Bivariate continuous q-Hermite polynomials
Recall the univariate continuous q-Hermite polynomials ![]() $H_m(x;q)$ defined recursively for all
$H_m(x;q)$ defined recursively for all ![]() $m\in {\mathbb Z}$ by
$m\in {\mathbb Z}$ by ![]() $H_{-m}(x;q)=0$ for
$H_{-m}(x;q)=0$ for ![]() $m<0$,
$m<0$, ![]() $H_{0}(x;q)=1$ and
$H_{0}(x;q)=1$ and
(see [Reference Koekoek, Lesky and SwarttouwKLS10, 14.26]). The following family of bivariate continuous q-Hermite polynomials ![]() $H_{m,n}(x,y;q,r)$ was introduced in [Reference Casper, Kolb and YakimovCKY21]:
$H_{m,n}(x,y;q,r)$ was introduced in [Reference Casper, Kolb and YakimovCKY21]:
Definition 4.1. Let ![]() $r\in {\mathbb K}$. The bivariate continuous q-Hermite polynomials
$r\in {\mathbb K}$. The bivariate continuous q-Hermite polynomials ![]() $H_{m,n}(x,y;q,r)$ are defined for all
$H_{m,n}(x,y;q,r)$ are defined for all ![]() $m,n\in {\mathbb Z}$ by
$m,n\in {\mathbb Z}$ by ![]() $H_{0,n}(x,y;q,r)=H_n(y;q)$ and the recursion
$H_{0,n}(x,y;q,r)=H_n(y;q)$ and the recursion
 $$ \begin{align} 2x H_{m,n}(x,y;q,r) &= H_{m+1,n}(x,y;q,r) + (1-q^m)H_{m-1,n}(x,y;q,r)\nonumber\\ &\quad + q^m(1-q^n)r H_{m,n-1}(x,y;q,r), \end{align} $$
$$ \begin{align} 2x H_{m,n}(x,y;q,r) &= H_{m+1,n}(x,y;q,r) + (1-q^m)H_{m-1,n}(x,y;q,r)\nonumber\\ &\quad + q^m(1-q^n)r H_{m,n-1}(x,y;q,r), \end{align} $$where we set ![]() $H_{-m,n}(x,y;q,r) =0$ for
$H_{-m,n}(x,y;q,r) =0$ for ![]() $m>0, n \in {\mathbb Z}$ and
$m>0, n \in {\mathbb Z}$ and ![]() $H_{m,-n}(x,y;q,r)=0\ m \in {\mathbb Z}, n>0$.
$H_{m,-n}(x,y;q,r)=0\ m \in {\mathbb Z}, n>0$.
It was shown in [Reference Casper, Kolb and YakimovCKY21] that the bivariate continuous q-Hermite polynomials form a family of orthogonal polynomials with many desirable properties. In particular, they satisfy the symmetry condition
Moreover, by [Reference Casper, Kolb and YakimovCKY21, (3.4)] the bivariate q-Hermite polynomials ![]() $H_{m,n}(x,y;q,r)$ can be expressed in terms of the univariate continuous q-Hermite polynomials by the formula
$H_{m,n}(x,y;q,r)$ can be expressed in terms of the univariate continuous q-Hermite polynomials by the formula
 $$ \begin{align} H_{m,n}(x,y;q,r)=\sum_{k=0}^{\min\left(m,n\right)}\frac{(-1)^kq^{{k\choose 2}}(q;q)_m (q;q)_n r^k}{(q;q)_{m-k}(q;q)_{n-k}(q;q)_k} H_{m-k}(x;q) H_{n-k}(y;q), \end{align} $$
$$ \begin{align} H_{m,n}(x,y;q,r)=\sum_{k=0}^{\min\left(m,n\right)}\frac{(-1)^kq^{{k\choose 2}}(q;q)_m (q;q)_n r^k}{(q;q)_{m-k}(q;q)_{n-k}(q;q)_k} H_{m-k}(x;q) H_{n-k}(y;q), \end{align} $$where  $(t;q)_k=\prod _{j=0}^{k-1}\left (1-tq^j\right )$ denotes the q-Pochhammer symbol. Note that the coefficient inside the sum in equation (4.3) is a polynomial in q.
$(t;q)_k=\prod _{j=0}^{k-1}\left (1-tq^j\right )$ denotes the q-Pochhammer symbol. Note that the coefficient inside the sum in equation (4.3) is a polynomial in q.
In the following we will encounter rescaled versions of the continuous q-Hermite polynomials with coefficients in an associative algebra ![]() ${\mathcal M}$ over
${\mathcal M}$ over ![]() ${\mathbb K}$. Let
${\mathbb K}$. Let ![]() ${\mathcal M}[x]={\mathcal M}\otimes _{\mathbb K} {\mathbb K}[x]$ and
${\mathcal M}[x]={\mathcal M}\otimes _{\mathbb K} {\mathbb K}[x]$ and ![]() ${\mathcal M}[x,y]={\mathcal M}\otimes _{\mathbb K} {\mathbb K}[x,y]$ be the algebras of polynomials in one or two variables with coefficients in
${\mathcal M}[x,y]={\mathcal M}\otimes _{\mathbb K} {\mathbb K}[x,y]$ be the algebras of polynomials in one or two variables with coefficients in ![]() ${\mathcal M}$.
${\mathcal M}$.
Lemma 4.2. Let ![]() $b^2\in {\mathcal M}\setminus \{0\}$ and let b be a formal square root of
$b^2\in {\mathcal M}\setminus \{0\}$ and let b be a formal square root of ![]() $b^2$.
$b^2$.
(1) For all
 $m,n\in {\mathbb N}$, the expressions (4.4)define polynomials in
$m,n\in {\mathbb N}$, the expressions (4.4)define polynomials in $$ \begin{align} w_m(x)=(b/2)^m H_m\left(\frac{x}{b};q^2\right) \qquad \text{and} \qquad w_{m,n}(x,y)= (b/2)^{m+n} H_{m,n}\left(\frac{x}{b},\frac{y}{b};q^2,r\right) \end{align} $$
$$ \begin{align} w_m(x)=(b/2)^m H_m\left(\frac{x}{b};q^2\right) \qquad \text{and} \qquad w_{m,n}(x,y)= (b/2)^{m+n} H_{m,n}\left(\frac{x}{b},\frac{y}{b};q^2,r\right) \end{align} $$ ${\mathcal M}[x]$ and
${\mathcal M}[x]$ and  ${\mathcal M}[x,y]$, respectively.
${\mathcal M}[x,y]$, respectively.(2) The polynomials
 $w_m(x)$ for
$w_m(x)$ for  $m\in {\mathbb N}$ are uniquely determined by
$m\in {\mathbb N}$ are uniquely determined by  $w_0(x)=1$,
$w_0(x)=1$,  $w_1(x)=x$ and the recursion (4.5)
$w_1(x)=x$ and the recursion (4.5) $$ \begin{align} x w_m(x) = w_{m+1}(x) +\frac{b^2}{4} \left(1-q^{2m}\right)w_{m-1}(x). \end{align} $$
$$ \begin{align} x w_m(x) = w_{m+1}(x) +\frac{b^2}{4} \left(1-q^{2m}\right)w_{m-1}(x). \end{align} $$(3) The polynomials
 $w_{m,n}(x)$ are uniquely determined by
$w_{m,n}(x)$ are uniquely determined by  $w_{0,n}(x,y)=w_n(y)$ for all
$w_{0,n}(x,y)=w_n(y)$ for all  $n\in {\mathbb N}$ and by the recursion (4.6)where we set
$n\in {\mathbb N}$ and by the recursion (4.6)where we set $$ \begin{align} x w_{m,n}(x,y)&= w_{m+1,n}(x,y) +\frac{b^2}{4} \left(1-q^{2m}\right)w_{m-1,n}(x,y)\nonumber\\ & \quad + \frac{b^2}{4} q^{2m}\left(1-q^{2n}\right)r w_{m,n-1}(x,y), \end{align} $$
$$ \begin{align} x w_{m,n}(x,y)&= w_{m+1,n}(x,y) +\frac{b^2}{4} \left(1-q^{2m}\right)w_{m-1,n}(x,y)\nonumber\\ & \quad + \frac{b^2}{4} q^{2m}\left(1-q^{2n}\right)r w_{m,n-1}(x,y), \end{align} $$ $w_{-1,n}(x,y)=w_{m,-1}(x,y)=0$.
$w_{-1,n}(x,y)=w_{m,-1}(x,y)=0$.(4) For all
 $m,n\in {\mathbb N}$, the relation (4.7)holds with
$m,n\in {\mathbb N}$, the relation (4.7)holds with $$ \begin{align} w_{m,n}(x,y)=\sum_{k=0}^{\min\left(m,n\right)}r^k q^{k(m+n)}\eta(k) \begin{bmatrix}m\\k\end{bmatrix}_q \begin{bmatrix}n\\k \end{bmatrix}_q[k]^!_q w_{m-k}(x) w_{n-k}(y) \end{align} $$
$$ \begin{align} w_{m,n}(x,y)=\sum_{k=0}^{\min\left(m,n\right)}r^k q^{k(m+n)}\eta(k) \begin{bmatrix}m\\k\end{bmatrix}_q \begin{bmatrix}n\\k \end{bmatrix}_q[k]^!_q w_{m-k}(x) w_{n-k}(y) \end{align} $$ $\eta (k)=\left (q-q^{-1}\right )^k q^{-k(k+1)/2} \left (b^2/4\right )^k$.
$\eta (k)=\left (q-q^{-1}\right )^k q^{-k(k+1)/2} \left (b^2/4\right )^k$.
Proof. The recursion (4.2) implies that ![]() $H_{m,n}\left (x,y;q^2,r\right )$ is a polynomial with leading term
$H_{m,n}\left (x,y;q^2,r\right )$ is a polynomial with leading term ![]() $x^my^n$, and that if a monomial
$x^my^n$, and that if a monomial ![]() $x^iy^j$ appears in
$x^iy^j$ appears in ![]() $H_{m,n}\left (x,y;q^2,r\right )$ with nonzero coefficient, then
$H_{m,n}\left (x,y;q^2,r\right )$ with nonzero coefficient, then ![]() $i+j\equiv m+n \bmod 2$. This implies that equations (4.4) indeed define polynomials in
$i+j\equiv m+n \bmod 2$. This implies that equations (4.4) indeed define polynomials in ![]() ${\mathcal M}[x]$ and
${\mathcal M}[x]$ and ![]() ${\mathcal M}[x,y]$. This proves (1). Properties (2) and (3) are obtained by replacing x and y by
${\mathcal M}[x,y]$. This proves (1). Properties (2) and (3) are obtained by replacing x and y by ![]() $x/b$ and
$x/b$ and ![]() $y/b$, respectively, and q by
$y/b$, respectively, and q by ![]() $q^2$ in the recursions (4.1) and (4.2). Property (4) follows from equation (4.3) and the relations
$q^2$ in the recursions (4.1) and (4.2). Property (4) follows from equation (4.3) and the relations
 $$ \begin{align*} \left(q^2,q^2\right)_k&=(-1)^k q^{k(k+1)/2}\left(q-q^{-1}\right)^k[k]_q^!, \qquad \frac{\left(q^2;q^2\right)_n}{\left(q^2;q^2\right)_m \left(q^2;q^2\right)_{n-m}}&= q^{m(n-m)}\begin{bmatrix}n \\ m \end{bmatrix}_{q} \end{align*} $$
$$ \begin{align*} \left(q^2,q^2\right)_k&=(-1)^k q^{k(k+1)/2}\left(q-q^{-1}\right)^k[k]_q^!, \qquad \frac{\left(q^2;q^2\right)_n}{\left(q^2;q^2\right)_m \left(q^2;q^2\right)_{n-m}}&= q^{m(n-m)}\begin{bmatrix}n \\ m \end{bmatrix}_{q} \end{align*} $$for ![]() $n\ge m$.
$n\ge m$.
4.2 A relation between q-Hermite polynomials for  $q^2$ and
$q^2$ and  $q^{-2}$
$q^{-2}$
In the following we fix ![]() $b^2\in {\mathcal M}$ and we let
$b^2\in {\mathcal M}$ and we let ![]() $w_m(x)\in {\mathcal M}[x]$ be the polynomial defined by equation (4.4). Moreover, set
$w_m(x)\in {\mathcal M}[x]$ be the polynomial defined by equation (4.4). Moreover, set
 $$ \begin{align} v_m(x)=\sum_{k=0}^{\left\lfloor m/2 \right\rfloor} (-1)^k q^k \eta(k) \frac{[m]^!_q}{[m-2k]^!_q [k]^!_q} w_{m-2k}(x) \in {\mathcal M}[x], \end{align} $$
$$ \begin{align} v_m(x)=\sum_{k=0}^{\left\lfloor m/2 \right\rfloor} (-1)^k q^k \eta(k) \frac{[m]^!_q}{[m-2k]^!_q [k]^!_q} w_{m-2k}(x) \in {\mathcal M}[x], \end{align} $$where, as before,  $\eta (k)=\left (q-q^{-1}\right )^k q^{-k(k+1)/2} \left (b^2/4\right )^k$. In the following we set
$\eta (k)=\left (q-q^{-1}\right )^k q^{-k(k+1)/2} \left (b^2/4\right )^k$. In the following we set ![]() $w_k(x)=0$ for all
$w_k(x)=0$ for all ![]() $k< 0$, and hence in the definition (4.8) of
$k< 0$, and hence in the definition (4.8) of ![]() $v_m(x)$ we may take the sum over all nonnegative integers k.
$v_m(x)$ we may take the sum over all nonnegative integers k.
Lemma 4.3. The polynomials ![]() $v_m(x)$ satisfy the recursion
$v_m(x)$ satisfy the recursion
 $$ \begin{align} x v_m(x)= v_{m+1}(x) + \frac{b^2}{4}\left(1-q^{-2m}\right) v_{m-1}(x) \end{align} $$
$$ \begin{align} x v_m(x)= v_{m+1}(x) + \frac{b^2}{4}\left(1-q^{-2m}\right) v_{m-1}(x) \end{align} $$with ![]() $v_0(x)=1$ and
$v_0(x)=1$ and ![]() $v_1(x)=x$. Hence we have
$v_1(x)=x$. Hence we have
 $$ \begin{align} v_m(x) = (b/2)^m H_m\left(\frac{x}{b};q^{-2}\right) \end{align} $$
$$ \begin{align} v_m(x) = (b/2)^m H_m\left(\frac{x}{b};q^{-2}\right) \end{align} $$for all ![]() $m\in {\mathbb N}$.
$m\in {\mathbb N}$.
Proof. Using the definition (4.8) of ![]() $v_m(x)$ and the recursion (4.5), we calculate
$v_m(x)$ and the recursion (4.5), we calculate
 $$ \begin{align*} xv_m(x) &- \frac{b^2}{4}\left(1-q^{-2m}\right)v_{m-1}(x)\\ &=\sum_{k=0}^{\left\lfloor m/2 \right\rfloor} (-1)^k q^k \eta(k) \frac{[m]^!_q}{[m-2k]^!_q [k]^!_q} \left(w_{m-2k+1}(x) + \frac{b^2}{4} \left(1-q^{2(m-2k)}\right)w_{m-2k-1}(x)\right)\\ & \quad-\frac{b^2}{4}\left(1-q^{-2m}\right)\sum_{k=0}^{\left\lfloor (m-1)/2 \right\rfloor} (-1)^k q^k \eta(k) \frac{[m-1]^!_q}{[m-1-2k]^!_q [k]^!_q}w_{m-1-2k}(x)\\ &= w_{m+1}(x) +\sum_{k\ge 1} (-1)^k q^k \eta(k) \frac{[m]^!_q}{[m+1-2k]^!_q [k]^!_q} \cdot\\ & \quad \cdot\left([m+1-2k]_q + [k]_q\left(q^{m-k+1} + q^{-m+k-1}\right) \right)w_{m+1-2k}(x)\\ &=v_{m+1}(x). \end{align*} $$
$$ \begin{align*} xv_m(x) &- \frac{b^2}{4}\left(1-q^{-2m}\right)v_{m-1}(x)\\ &=\sum_{k=0}^{\left\lfloor m/2 \right\rfloor} (-1)^k q^k \eta(k) \frac{[m]^!_q}{[m-2k]^!_q [k]^!_q} \left(w_{m-2k+1}(x) + \frac{b^2}{4} \left(1-q^{2(m-2k)}\right)w_{m-2k-1}(x)\right)\\ & \quad-\frac{b^2}{4}\left(1-q^{-2m}\right)\sum_{k=0}^{\left\lfloor (m-1)/2 \right\rfloor} (-1)^k q^k \eta(k) \frac{[m-1]^!_q}{[m-1-2k]^!_q [k]^!_q}w_{m-1-2k}(x)\\ &= w_{m+1}(x) +\sum_{k\ge 1} (-1)^k q^k \eta(k) \frac{[m]^!_q}{[m+1-2k]^!_q [k]^!_q} \cdot\\ & \quad \cdot\left([m+1-2k]_q + [k]_q\left(q^{m-k+1} + q^{-m+k-1}\right) \right)w_{m+1-2k}(x)\\ &=v_{m+1}(x). \end{align*} $$This confirms the recursion (4.9). The second statement holds by Lemma 4.2(1) and (2) with q replaced by ![]() $q^{-1}$.
$q^{-1}$.
4.3 Serre combinations of bivariate continuous q-Hermite polynomials
The following identity is the crucial ingredient needed in the following sections to express the quantum Serre relations for quantum symmetric pairs in terms of univariate continuous q-Hermite polynomials:
Proposition 4.4. Let ![]() $a\in -{\mathbb N}$ and assume that
$a\in -{\mathbb N}$ and assume that ![]() $r=q^a$. Then the polynomials
$r=q^a$. Then the polynomials ![]() $w_m(x), v_n(x)\in {\mathcal M}[x]$ and
$w_m(x), v_n(x)\in {\mathcal M}[x]$ and ![]() $w_{m,n}(x,y)\in {\mathcal M}[x,y]$ defined by equations (4.4) and (4.8) satisfy the relation
$w_{m,n}(x,y)\in {\mathcal M}[x,y]$ defined by equations (4.4) and (4.8) satisfy the relation
 $$ \begin{align*} \sum_{n=0}^{1-a} (-1)^n \begin{bmatrix} 1-a\\ n \end{bmatrix}_q w_{1-a-n,n}(x,y) &= \sum_{n=0}^{1-a} (-1)^n \begin{bmatrix} 1-a\\ n \end{bmatrix}_q w_{1-a-n}(x)\,v_n(y) \\ &= \sum_{n=0}^{1-a} (-1)^n \begin{bmatrix} 1-a\\ n \end{bmatrix}_q v_{1-a-n}(x)\,w_{n}(y). \end{align*} $$
$$ \begin{align*} \sum_{n=0}^{1-a} (-1)^n \begin{bmatrix} 1-a\\ n \end{bmatrix}_q w_{1-a-n,n}(x,y) &= \sum_{n=0}^{1-a} (-1)^n \begin{bmatrix} 1-a\\ n \end{bmatrix}_q w_{1-a-n}(x)\,v_n(y) \\ &= \sum_{n=0}^{1-a} (-1)^n \begin{bmatrix} 1-a\\ n \end{bmatrix}_q v_{1-a-n}(x)\,w_{n}(y). \end{align*} $$Proof. For ![]() $r=q^a$ and any
$r=q^a$ and any ![]() $b^2\in {\mathcal M}$, we use equation (4.7) to calculate
$b^2\in {\mathcal M}$, we use equation (4.7) to calculate
 $$ \begin{align*} &\sum_{n=0}^{1-a} (-1)^n \begin{bmatrix} 1-a\\ n \end{bmatrix}_q w_{1-a-n,n}(x,y)\\ & \qquad\qquad\qquad = \sum_{n=0}^{1-a} (-1)^n \begin{bmatrix} 1-a\\ n \end{bmatrix}_q \sum_{k\ge 0} q^{k}\eta(k)\begin{bmatrix} 1-a-n\\ k \end{bmatrix}_q \begin{bmatrix} n\\ k \end{bmatrix}_q [k]^!_q w_{1-a-n-k}(x)w_{n-k}(y), \end{align*} $$
$$ \begin{align*} &\sum_{n=0}^{1-a} (-1)^n \begin{bmatrix} 1-a\\ n \end{bmatrix}_q w_{1-a-n,n}(x,y)\\ & \qquad\qquad\qquad = \sum_{n=0}^{1-a} (-1)^n \begin{bmatrix} 1-a\\ n \end{bmatrix}_q \sum_{k\ge 0} q^{k}\eta(k)\begin{bmatrix} 1-a-n\\ k \end{bmatrix}_q \begin{bmatrix} n\\ k \end{bmatrix}_q [k]^!_q w_{1-a-n-k}(x)w_{n-k}(y), \end{align*} $$where again ![]() $w_n(x)=0$ for
$w_n(x)=0$ for ![]() $n<0$. Setting
$n<0$. Setting ![]() $\ell =n+k$ and
$\ell =n+k$ and ![]() $m=k$, we obtain
$m=k$, we obtain
 $$ \begin{align*} \sum_{n=0}^{1-a} (-1)^n &\begin{bmatrix} 1-a\\ n \end{bmatrix}_q w_{1-a-n,n}(x,y)\\ &= \sum_{\ell=0}^{1-a} (-1)^\ell \begin{bmatrix} 1-a\\ \ell \end{bmatrix}_q \sum_{m\ge 0} (-1)^mq^m \eta(m)\frac{[\ell]^!_q}{[\ell-2m]^!_q [m]^!_q} w_{1-a-\ell}(x) w_{\ell-2m}(y)\\ &=\sum_{\ell=0}^{1-a} (-1)^\ell \begin{bmatrix} 1-a\\ \ell \end{bmatrix}_q w_{1-a-\ell}(x) v_{\ell}(y), \end{align*} $$
$$ \begin{align*} \sum_{n=0}^{1-a} (-1)^n &\begin{bmatrix} 1-a\\ n \end{bmatrix}_q w_{1-a-n,n}(x,y)\\ &= \sum_{\ell=0}^{1-a} (-1)^\ell \begin{bmatrix} 1-a\\ \ell \end{bmatrix}_q \sum_{m\ge 0} (-1)^mq^m \eta(m)\frac{[\ell]^!_q}{[\ell-2m]^!_q [m]^!_q} w_{1-a-\ell}(x) w_{\ell-2m}(y)\\ &=\sum_{\ell=0}^{1-a} (-1)^\ell \begin{bmatrix} 1-a\\ \ell \end{bmatrix}_q w_{1-a-\ell}(x) v_{\ell}(y), \end{align*} $$which proves the first identity of the proposition. On the other hand, setting ![]() $\ell =1-a-n+k$ and
$\ell =1-a-n+k$ and ![]() $m=k$, we obtain
$m=k$, we obtain
 $$ \begin{align*} \sum_{n=0}^{1-a}& (-1)^n \begin{bmatrix} 1-a\\ n \end{bmatrix}_q w_{1-a-n,n}(x,y)\\ &=(-1)^{1-a} \sum_{\ell=0}^{1-a} (-1)^\ell \begin{bmatrix} 1-a\\ \ell \end{bmatrix}_q \sum_{m\ge 0} (-1)^mq^m \eta(m)\frac{[\ell]^!_q}{[\ell-2m]^!_q [m]^!_q} w_{\ell-2m}(x) w_{1-a-\ell}(y)\\ &=(-1)^{1-a}\sum_{\ell=0}^{1-a} (-1)^\ell \begin{bmatrix} 1-a\\ \ell \end{bmatrix}_q v_{\ell}(x) w_{1-a-\ell}(y) =\sum_{\ell=0}^{1-a} (-1)^\ell \begin{bmatrix} 1-a\\ \ell \end{bmatrix}_q v_{1-a-\ell}(x) w_{\ell}(y), \end{align*} $$
$$ \begin{align*} \sum_{n=0}^{1-a}& (-1)^n \begin{bmatrix} 1-a\\ n \end{bmatrix}_q w_{1-a-n,n}(x,y)\\ &=(-1)^{1-a} \sum_{\ell=0}^{1-a} (-1)^\ell \begin{bmatrix} 1-a\\ \ell \end{bmatrix}_q \sum_{m\ge 0} (-1)^mq^m \eta(m)\frac{[\ell]^!_q}{[\ell-2m]^!_q [m]^!_q} w_{\ell-2m}(x) w_{1-a-\ell}(y)\\ &=(-1)^{1-a}\sum_{\ell=0}^{1-a} (-1)^\ell \begin{bmatrix} 1-a\\ \ell \end{bmatrix}_q v_{\ell}(x) w_{1-a-\ell}(y) =\sum_{\ell=0}^{1-a} (-1)^\ell \begin{bmatrix} 1-a\\ \ell \end{bmatrix}_q v_{1-a-\ell}(x) w_{\ell}(y), \end{align*} $$which proves the second identity.
4.4 Bar invariance of deformed quantum Serre polynomials
Assume that the ![]() ${\mathbb K}$-algebra
${\mathbb K}$-algebra ![]() ${\mathcal M}$ has a bar involution
${\mathcal M}$ has a bar involution
which is a k-algebra isomorphism such that ![]() $\overline {q}^{\mathcal M}=q^{-1}$. We extend
$\overline {q}^{\mathcal M}=q^{-1}$. We extend ![]() $\overline {\phantom {m}}^{\mathcal M}$ to a bar involution on
$\overline {\phantom {m}}^{\mathcal M}$ to a bar involution on ![]() ${\mathcal M}[x]$ and
${\mathcal M}[x]$ and ![]() ${\mathcal M}[x,y]$ by application of
${\mathcal M}[x,y]$ by application of ![]() $\overline {\phantom {m}}^{\mathcal M}$ to the coefficients of any polynomial. Again, we consider the polynomials
$\overline {\phantom {m}}^{\mathcal M}$ to the coefficients of any polynomial. Again, we consider the polynomials ![]() $w_m(x), v_m(x)$ and
$w_m(x), v_m(x)$ and ![]() $w_{m,n}(x,y)$ formed with respect to a fixed element
$w_{m,n}(x,y)$ formed with respect to a fixed element ![]() $b^2\in {\mathcal M}\setminus \{0\}$. Define
$b^2\in {\mathcal M}\setminus \{0\}$. Define  $(b')^2=\overline {b^2}^{\mathcal M}$ and let
$(b')^2=\overline {b^2}^{\mathcal M}$ and let ![]() $w_m'(x), v_m'(x)$ and
$w_m'(x), v_m'(x)$ and ![]() $w_{m,n}'(x,y)$ be the corresponding polynomials formed with respect to the element
$w_{m,n}'(x,y)$ be the corresponding polynomials formed with respect to the element ![]() $(b')^2$.
$(b')^2$.
Lemma 4.5. Retain the setting of Proposition 4.4 and set  $(b')^2=\overline {b^2}^{\mathcal M}$. Then the relations
$(b')^2=\overline {b^2}^{\mathcal M}$. Then the relations
 $$ \begin{align} \overline{w_n(x)}^{\mathcal M}=v_n'(x) \qquad \text{and} \qquad \overline{v_n(x)}^{\mathcal M}=w_n'(x) \end{align} $$
$$ \begin{align} \overline{w_n(x)}^{\mathcal M}=v_n'(x) \qquad \text{and} \qquad \overline{v_n(x)}^{\mathcal M}=w_n'(x) \end{align} $$hold in ![]() ${\mathcal M}[x]$ for all
${\mathcal M}[x]$ for all ![]() $n\in {\mathbb N}$.
$n\in {\mathbb N}$.
Proof. By Lemmas 4.2(2) and 4.3, we have  $\overline {w_0(x)}^{\mathcal M}=1=v_0'(x)$ and
$\overline {w_0(x)}^{\mathcal M}=1=v_0'(x)$ and  $\overline {w_1(x)}^{\mathcal M}=x=v_1'(x)$, and the recursions (4.5) and (4.9) inductively imply the first relation in equation (4.11). The second relation is obtained analogously.
$\overline {w_1(x)}^{\mathcal M}=x=v_1'(x)$, and the recursions (4.5) and (4.9) inductively imply the first relation in equation (4.11). The second relation is obtained analogously.
This lemma and Proposition 4.4 allow us to describe the behaviour of the deformed quantum Serre polynomial under the bar involution.
Corollary 4.6. Retain the setting of Proposition 4.4 and set 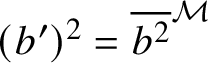 $(b')^2=\overline {b^2}^{\mathcal M}$. Then the relation
$(b')^2=\overline {b^2}^{\mathcal M}$. Then the relation
 $$ \begin{align*} \overline{\sum_{n=0}^{1-a}(-1)^n \begin{bmatrix} 1-a\\ n \end{bmatrix}_q w_{1-a-n,n}(x,y)}^{\mathcal M} = \sum_{n=0}^{1-a}(-1)^n \begin{bmatrix} 1-a\\ n \end{bmatrix}_q w_{1-a-n,n}'(x,y) \end{align*} $$
$$ \begin{align*} \overline{\sum_{n=0}^{1-a}(-1)^n \begin{bmatrix} 1-a\\ n \end{bmatrix}_q w_{1-a-n,n}(x,y)}^{\mathcal M} = \sum_{n=0}^{1-a}(-1)^n \begin{bmatrix} 1-a\\ n \end{bmatrix}_q w_{1-a-n,n}'(x,y) \end{align*} $$holds in ![]() ${\mathcal M}[x,y]$.
${\mathcal M}[x,y]$.
Proof. By Lemma 4.5 and Proposition 4.4, we have
 $$ \begin{align*} \overline{\sum_{n=0}^{1-a} (-1)^n \begin{bmatrix} 1-a\\ n \end{bmatrix}_q w_{1-a-n,n}(x,y)}^{\mathcal M} &= \sum_{n=0}^{1-a} (-1)^n \begin{bmatrix} 1-a\\ n \end{bmatrix}_q \overline{w_{1-a-n}(x)}^{\mathcal M}\overline{v_n(y)}^{\mathcal M}\\ &=\sum_{n=0}^{1-a} (-1)^n \begin{bmatrix} 1-a\\ n \end{bmatrix}_q v_{1-a-n}'(x)\,w_n'(y)\\ &= \sum_{n=0}^{1-a} (-1)^n \begin{bmatrix} 1-a\\ n \end{bmatrix}_q w_{1-a-n,n}'(x,y), \end{align*} $$
$$ \begin{align*} \overline{\sum_{n=0}^{1-a} (-1)^n \begin{bmatrix} 1-a\\ n \end{bmatrix}_q w_{1-a-n,n}(x,y)}^{\mathcal M} &= \sum_{n=0}^{1-a} (-1)^n \begin{bmatrix} 1-a\\ n \end{bmatrix}_q \overline{w_{1-a-n}(x)}^{\mathcal M}\overline{v_n(y)}^{\mathcal M}\\ &=\sum_{n=0}^{1-a} (-1)^n \begin{bmatrix} 1-a\\ n \end{bmatrix}_q v_{1-a-n}'(x)\,w_n'(y)\\ &= \sum_{n=0}^{1-a} (-1)^n \begin{bmatrix} 1-a\\ n \end{bmatrix}_q w_{1-a-n,n}'(x,y), \end{align*} $$as desired.
4.5 Deformed Chebyshev polynomials of the second kind
For any ![]() $r\in {\mathbb K}$ consider the sequence of polynomials given by the recursion formula
$r\in {\mathbb K}$ consider the sequence of polynomials given by the recursion formula
 $$ \begin{align} C_{n+1}(x; q, r) = 2x C_{n}(x; q, r) - \frac{r^{-1}-q^{n+1}}{1 - q^{n+1}} C_{n-1}(x; q, r), \qquad n \geq 0, \end{align} $$
$$ \begin{align} C_{n+1}(x; q, r) = 2x C_{n}(x; q, r) - \frac{r^{-1}-q^{n+1}}{1 - q^{n+1}} C_{n-1}(x; q, r), \qquad n \geq 0, \end{align} $$subject to the initial conditions
It is clear from the recursion and the initial conditions that in the case ![]() $r=1$ we recover the Chebyshev polynomials of the second kind:
$r=1$ we recover the Chebyshev polynomials of the second kind:
For background on the classical Chebyshev polynomials, see, for example, [Reference Magnus, Oberhettinger and SoniMOS69, Sect. 5.7].
Example 4.7. By direct computation, one obtains
 $$ \begin{align} C_2(x;q,r)&= 4 x^2- \frac{r^{-1}-q^2}{\left(1-q^2\right)}, \end{align} $$
$$ \begin{align} C_2(x;q,r)&= 4 x^2- \frac{r^{-1}-q^2}{\left(1-q^2\right)}, \end{align} $$ $$ \begin{align} C_3(x;q,r)&=8x^3 - 2x\left( \frac{r^{-1}-q^2}{1-q^2} + \frac{r^{-1}-q^3}{1-q^3} \right). \end{align} $$
$$ \begin{align} C_3(x;q,r)&=8x^3 - 2x\left( \frac{r^{-1}-q^2}{1-q^2} + \frac{r^{-1}-q^3}{1-q^3} \right). \end{align} $$ By Favard’s theorem, ![]() $\{C_n(x;q,r)\}_{n=0}^\infty $ is a sequence of orthogonal polynomials with respect to a Borel measure when q and r are real and
$\{C_n(x;q,r)\}_{n=0}^\infty $ is a sequence of orthogonal polynomials with respect to a Borel measure when q and r are real and ![]() $\lvert q\rvert < 1 \leq r^{-1}$. We will call them deformed Chebyshev polynomials of the second kind. If q and r are viewed as indeterminates, then
$\lvert q\rvert < 1 \leq r^{-1}$. We will call them deformed Chebyshev polynomials of the second kind. If q and r are viewed as indeterminates, then
 $$\begin{align*}\left(1-q^2\right) \dotsm (1-q^n) C_n(x; q, r) \in {\mathbb Z}\left[q,r^{-1}\right] \qquad \text{for}\ n \geq 2. \end{align*}$$
$$\begin{align*}\left(1-q^2\right) \dotsm (1-q^n) C_n(x; q, r) \in {\mathbb Z}\left[q,r^{-1}\right] \qquad \text{for}\ n \geq 2. \end{align*}$$The rescaled polynomials
 $$\begin{align*}\widetilde{C}_n(x; q, r) = r^{n/2} C_n\left(r^{-1/2} x; q, r\right) \end{align*}$$
$$\begin{align*}\widetilde{C}_n(x; q, r) = r^{n/2} C_n\left(r^{-1/2} x; q, r\right) \end{align*}$$satisfy the recursion
 $$\begin{align}\widetilde{C}_{n+1}(x; q, r) = 2x \widetilde{C}_{n}(x; q, r) - \frac{1- r q^{n+1}}{1 - q^{n+1}} \widetilde{C}_{n-1}(x; q, r), \qquad n \geq 0 \end{align}$$
$$\begin{align}\widetilde{C}_{n+1}(x; q, r) = 2x \widetilde{C}_{n}(x; q, r) - \frac{1- r q^{n+1}}{1 - q^{n+1}} \widetilde{C}_{n-1}(x; q, r), \qquad n \geq 0 \end{align}$$and the same initial conditions as ![]() $C_{n}(x; q, r)$. In our recursion for the deformed Chebyshev polynomials (4.12) we used
$C_{n}(x; q, r)$. In our recursion for the deformed Chebyshev polynomials (4.12) we used ![]() $r^{-1}$ instead of r because the recursion (4.15a) naturally leads to expressions involving q-Pochhammer symbols.
$r^{-1}$ instead of r because the recursion (4.15a) naturally leads to expressions involving q-Pochhammer symbols.
Next we provide explicit formulas for two generating functions for the deformed Chebyshev polynomials. In an appropriate field extension of ![]() ${\mathbb K}=k(q)$, define
${\mathbb K}=k(q)$, define
 $$ \begin{align} x_{1,2}=x\pm \sqrt{x^2-1}, \qquad a_{1,2}=x\pm \sqrt{x^2-r^{-1}}, \qquad \widetilde{a}_{1,2} = r^{-1}\left(x\pm \sqrt{x^2-r}\right), \end{align} $$
$$ \begin{align} x_{1,2}=x\pm \sqrt{x^2-1}, \qquad a_{1,2}=x\pm \sqrt{x^2-r^{-1}}, \qquad \widetilde{a}_{1,2} = r^{-1}\left(x\pm \sqrt{x^2-r}\right), \end{align} $$which satisfy the relations
 $$ \begin{align*} 1-2xs+s^2&=(1- x_1s)(1-x_2s), \\ 1-2xs+r^{-1}s^2&=(1-a_1s)(1-a_2s),\\ 1-2r^{-1} xs+r^{-1}s^2&=\left(1-\widetilde{a}_1s\right)\left(1-\widetilde{a}_2s\right). \end{align*} $$
$$ \begin{align*} 1-2xs+s^2&=(1- x_1s)(1-x_2s), \\ 1-2xs+r^{-1}s^2&=(1-a_1s)(1-a_2s),\\ 1-2r^{-1} xs+r^{-1}s^2&=\left(1-\widetilde{a}_1s\right)\left(1-\widetilde{a}_2s\right). \end{align*} $$Recall the definition of the basic hypergeometric function ![]() ${}_{3}\phi _2$[Reference Koekoek, Lesky and SwarttouwKLS10, 1.10], and define
${}_{3}\phi _2$[Reference Koekoek, Lesky and SwarttouwKLS10, 1.10], and define
 $$ \begin{align} \eta\left(\begin{matrix} x \\s \end{matrix};q\right)&=\frac{1}{1-2xs+r^{-1}s^2} {}_{3}\phi_2\left(\begin{array}{c} q,x_1s,x_2s \\qa_1s,qa_2s\end{array};q,q^2\right)\\ &=\sum_{k=0}^\infty \frac{(x_1s;q)_k(x_2s;q)_k}{(a_1s;q)_{k+1}(a_2s;q)_{k+1}}q^{2k}. \nonumber \end{align} $$
$$ \begin{align} \eta\left(\begin{matrix} x \\s \end{matrix};q\right)&=\frac{1}{1-2xs+r^{-1}s^2} {}_{3}\phi_2\left(\begin{array}{c} q,x_1s,x_2s \\qa_1s,qa_2s\end{array};q,q^2\right)\\ &=\sum_{k=0}^\infty \frac{(x_1s;q)_k(x_2s;q)_k}{(a_1s;q)_{k+1}(a_2s;q)_{k+1}}q^{2k}. \nonumber \end{align} $$As the basic hypergeometric function  ${}_{3}\phi _2\left (\begin {array}{c} q,x_1s,x_2s \\qa_1s,qa_2s\end {array};q,q^2\right )$ is analytic at
${}_{3}\phi _2\left (\begin {array}{c} q,x_1s,x_2s \\qa_1s,qa_2s\end {array};q,q^2\right )$ is analytic at ![]() $s=0$, so is
$s=0$, so is  $\eta \left (\begin {matrix} x \\s \end {matrix};q\right )$. Analogously,
$\eta \left (\begin {matrix} x \\s \end {matrix};q\right )$. Analogously,
 $$\begin{align*}\widetilde{\eta} \left(\begin{matrix} x \\s \end{matrix};q\right)=\frac{1}{1-2xs+s^2} {}_{3}\phi_2\left(\begin{array}{c} q, q \widetilde{a}_1s, q \widetilde{a}_2 s \\qx_1s,qx_2s\end{array};q,q r\right) \end{align*}$$
$$\begin{align*}\widetilde{\eta} \left(\begin{matrix} x \\s \end{matrix};q\right)=\frac{1}{1-2xs+s^2} {}_{3}\phi_2\left(\begin{array}{c} q, q \widetilde{a}_1s, q \widetilde{a}_2 s \\qx_1s,qx_2s\end{array};q,q r\right) \end{align*}$$is analytic at ![]() $s=0$.
$s=0$.
Proposition 4.8. We have
 $$ \begin{align*} \eta\left(\begin{matrix} x \\s \end{matrix};q, r\right)&= \sum_{n=0}^\infty C_n(x;q,r) \frac{s^n}{1-q^{n+2}} \end{align*} $$
$$ \begin{align*} \eta\left(\begin{matrix} x \\s \end{matrix};q, r\right)&= \sum_{n=0}^\infty C_n(x;q,r) \frac{s^n}{1-q^{n+2}} \end{align*} $$and
 $$ \begin{align*} \widetilde{\eta}\left(\begin{matrix} x \\s \end{matrix};q, r\right)&= \sum_{n=0}^\infty \frac{\left(q^2;q\right)_n}{(qr;q)_{n+1}} \widetilde{C}_n(x;q,r) s^n = \sum_{n=0}^\infty \frac{\left(q^2;q\right)_n}{(qr;q)_{n+1}} C_n\left(r^{-1/2}x;q,r\right) \left(r^{1/2} s\right)^n. \end{align*} $$
$$ \begin{align*} \widetilde{\eta}\left(\begin{matrix} x \\s \end{matrix};q, r\right)&= \sum_{n=0}^\infty \frac{\left(q^2;q\right)_n}{(qr;q)_{n+1}} \widetilde{C}_n(x;q,r) s^n = \sum_{n=0}^\infty \frac{\left(q^2;q\right)_n}{(qr;q)_{n+1}} C_n\left(r^{-1/2}x;q,r\right) \left(r^{1/2} s\right)^n. \end{align*} $$ The first generating function will play a key role in Sections 5.5 and 5.6. In the special case ![]() $r=1$, the second one reduces to the standard generating function for the Chebyshev polynomials of the second kind:
$r=1$, the second one reduces to the standard generating function for the Chebyshev polynomials of the second kind:
 $$\begin{align*}\sum_{n=0}^\infty U_n(x) s^n = \left(1 - 2xs +s^2\right)^{-1}. \end{align*}$$
$$\begin{align*}\sum_{n=0}^\infty U_n(x) s^n = \left(1 - 2xs +s^2\right)^{-1}. \end{align*}$$Proof. For simplicity of notation, we suppress the arguments s and q of the functions ![]() $\eta $ and
$\eta $ and ![]() $\widetilde {\eta }$. Consider the Taylor expansion
$\widetilde {\eta }$. Consider the Taylor expansion
 $$\begin{align*}\eta(x)= \sum_{n=0}^\infty f_n(x;q) s^n \end{align*}$$
$$\begin{align*}\eta(x)= \sum_{n=0}^\infty f_n(x;q) s^n \end{align*}$$in the variable s with Taylor coefficients ![]() $f_n(x;q)$. We have
$f_n(x;q)$. We have
 $$ \begin{align*} \eta(qs) &= \sum_{k=0}^\infty \frac{(qx_1s;q)_k(qx_2s;q)_k}{(qa_1s;q)_{k+1}(qa_2s;q)_{k+1}}q^{2k} \\ &= q^{-2} \frac{(1-a_1s)(1-a_2s)}{(1-x_1s)(1-x_2s)} \sum_{k=1}^\infty \frac{(x_1s;q)_k(x_2s;q)_k}{(a_1s;q)_{k+1}(a_2s;q)_{k+1}}q^{2k}\\ &= q^{-2} \frac{(1-a_1s)(1-a_2s)}{(1-x_1s)(1-x_2s)} \left(\eta(s)-\frac{1}{(1-a_1s)(1-a_2s)}\right)\\ &= q^{-2} \frac{1-2xs+r^{-1}s^2}{1-2xs+s^2} \left(\eta(s)-\frac{1}{1-2xs+r^{-1}s^2}\right), \end{align*} $$
$$ \begin{align*} \eta(qs) &= \sum_{k=0}^\infty \frac{(qx_1s;q)_k(qx_2s;q)_k}{(qa_1s;q)_{k+1}(qa_2s;q)_{k+1}}q^{2k} \\ &= q^{-2} \frac{(1-a_1s)(1-a_2s)}{(1-x_1s)(1-x_2s)} \sum_{k=1}^\infty \frac{(x_1s;q)_k(x_2s;q)_k}{(a_1s;q)_{k+1}(a_2s;q)_{k+1}}q^{2k}\\ &= q^{-2} \frac{(1-a_1s)(1-a_2s)}{(1-x_1s)(1-x_2s)} \left(\eta(s)-\frac{1}{(1-a_1s)(1-a_2s)}\right)\\ &= q^{-2} \frac{1-2xs+r^{-1}s^2}{1-2xs+s^2} \left(\eta(s)-\frac{1}{1-2xs+r^{-1}s^2}\right), \end{align*} $$and thus
 $$ \begin{align*} q^2\left(1-2xs+s^2\right) \eta(qs) = \left(1-2xs+r^{-1}s^2\right) \eta(s)-1. \end{align*} $$
$$ \begin{align*} q^2\left(1-2xs+s^2\right) \eta(qs) = \left(1-2xs+r^{-1}s^2\right) \eta(s)-1. \end{align*} $$Comparing the coefficients of ![]() $s^{n+1}$ in the Taylor series expansion of both sides at
$s^{n+1}$ in the Taylor series expansion of both sides at ![]() $s=0$ gives
$s=0$ gives
 $$ \begin{align*} &q^{n+3} f_{n+1}(x;q) -2 q^{n+2}x f_{n}(x;q) + q^{n+1} f_{n-1}(x;q) \\ &\quad = f_{n+1}(x;q) - 2x f_{n}(x;q) + r^{-1}f_{n-1}(x;q) - \delta_{n,-1}. \end{align*} $$
$$ \begin{align*} &q^{n+3} f_{n+1}(x;q) -2 q^{n+2}x f_{n}(x;q) + q^{n+1} f_{n-1}(x;q) \\ &\quad = f_{n+1}(x;q) - 2x f_{n}(x;q) + r^{-1}f_{n-1}(x;q) - \delta_{n,-1}. \end{align*} $$Hence, ![]() $f_n(x;q)$ are uniquely determined by the recursion
$f_n(x;q)$ are uniquely determined by the recursion
 $$ \begin{align*} \left(1-q^{n+3}\right) f_{n+1}(x;q) = 2x\left(1-q^{n+2}\right) f_{n}(x;q) - \left(r^{-1}-q^{n+1}\right)f_{n-1}(x;q) + \delta_{n,-1}, \end{align*} $$
$$ \begin{align*} \left(1-q^{n+3}\right) f_{n+1}(x;q) = 2x\left(1-q^{n+2}\right) f_{n}(x;q) - \left(r^{-1}-q^{n+1}\right)f_{n-1}(x;q) + \delta_{n,-1}, \end{align*} $$with the initial condition ![]() $f_n(x;q)=0$ for
$f_n(x;q)=0$ for ![]() $n<0$. Comparing this to the recursion (4.12) and the initial conditions (4.13) gives
$n<0$. Comparing this to the recursion (4.12) and the initial conditions (4.13) gives
 $$\begin{align*}f_n(x;q) = C_n(x; q, r)/\left(1-q^{n+2}\right) \qquad \text{for}\ n \geq 0, \end{align*}$$
$$\begin{align*}f_n(x;q) = C_n(x; q, r)/\left(1-q^{n+2}\right) \qquad \text{for}\ n \geq 0, \end{align*}$$which proves the first generating function identity. Similarly, for the second identity, one first shows that
 $$ \begin{align*} \widetilde{\eta}(qs) = (qr)^{-1} \frac{1-2xs+s^2}{1-2 r^{-1} q xs+ r^{-1} q^2 s^2} \left(\widetilde{\eta}(s)-\frac{1}{1-2xs+s^2}\right), \end{align*} $$
$$ \begin{align*} \widetilde{\eta}(qs) = (qr)^{-1} \frac{1-2xs+s^2}{1-2 r^{-1} q xs+ r^{-1} q^2 s^2} \left(\widetilde{\eta}(s)-\frac{1}{1-2xs+s^2}\right), \end{align*} $$and then proceeds as before.
5 Generators and relations for  ${\mathcal B}_{\mathbf {c}}$
${\mathcal B}_{\mathbf {c}}$
We are now ready to deduce the quantum Serre relations (1.4) for ![]() ${\mathcal B}_{\mathbf {c}}$. Cases (I) and (III) from Section 1.3, where
${\mathcal B}_{\mathbf {c}}$. Cases (I) and (III) from Section 1.3, where ![]() $i,j\in I\setminus X$, are treated in Sections 5.3 and 5.8, respectively, and are rather straightforward generalisations of the calculations in the quasi-split setting in [Reference Casper, Kolb and YakimovCKY21]. The bulk of this section, Sections 5.4 through 5.7, is devoted to the subtle case (II), where
$i,j\in I\setminus X$, are treated in Sections 5.3 and 5.8, respectively, and are rather straightforward generalisations of the calculations in the quasi-split setting in [Reference Casper, Kolb and YakimovCKY21]. The bulk of this section, Sections 5.4 through 5.7, is devoted to the subtle case (II), where ![]() $i\in I\setminus X$ and
$i\in I\setminus X$ and ![]() $j\in X$, and which does not exist in the quasi-split setting.
$j\in X$, and which does not exist in the quasi-split setting.
5.1  ${\mathcal M}_X^+$-valued orthogonal polynomials
${\mathcal M}_X^+$-valued orthogonal polynomials
For a suitable choice of ![]() $b^2\in {\mathcal M}_X^+$, the recursions (4.5) and (4.6) translate into the recursions given in A) and B) in Section 1.4. Indeed, recall that
$b^2\in {\mathcal M}_X^+$, the recursions (4.5) and (4.6) translate into the recursions given in A) and B) in Section 1.4. Indeed, recall that  ${\mathcal Z}_i=q_ic_i \partial _{\tau (i)}^R\left (T_{w_X\left (E_{\tau (i)}\right )}\right )$ for
${\mathcal Z}_i=q_ic_i \partial _{\tau (i)}^R\left (T_{w_X\left (E_{\tau (i)}\right )}\right )$ for ![]() $i\in I\setminus X$ and set
$i\in I\setminus X$ and set
 $$ \begin{align*} b_i^2= \frac{4}{\left(q_i-q_i^{-1}\right)^2}{\mathcal Z}_i\in {\mathcal M}_X^+. \end{align*} $$
$$ \begin{align*} b_i^2= \frac{4}{\left(q_i-q_i^{-1}\right)^2}{\mathcal Z}_i\in {\mathcal M}_X^+. \end{align*} $$For  $b^2=b_i^2$, the rescaled continuous q-Hermite polynomials
$b^2=b_i^2$, the rescaled continuous q-Hermite polynomials ![]() $w_m(x)$ defined for
$w_m(x)$ defined for ![]() $m\in {\mathbb N}$ by
$m\in {\mathbb N}$ by
 $$ \begin{align} w_m(x) = (b_i/2)^m H_m\left(\frac{x}{b_i};q_i^2\right) \in {\mathbb K}\left[b_i^2,x\right] \subset {\mathcal M}_X^+[x] \end{align} $$
$$ \begin{align} w_m(x) = (b_i/2)^m H_m\left(\frac{x}{b_i};q_i^2\right) \in {\mathbb K}\left[b_i^2,x\right] \subset {\mathcal M}_X^+[x] \end{align} $$satisfy the initial conditions and recursion A) in Section 1.4. Hence we get  $w_m(x)=w_m\left (x,q_i^2\right )$. Similarly,
$w_m(x)=w_m\left (x,q_i^2\right )$. Similarly,
 $$ \begin{align} v_m(x) = (b_i/2)^m H_m\left(\frac{x}{b_i};q_i^{-2}\right) \in {\mathbb K}\left[b_i^2,x\right] \subset {\mathcal M}_X^+[x] \end{align} $$
$$ \begin{align} v_m(x) = (b_i/2)^m H_m\left(\frac{x}{b_i};q_i^{-2}\right) \in {\mathbb K}\left[b_i^2,x\right] \subset {\mathcal M}_X^+[x] \end{align} $$satisfy recursion A) in Section 1.4 with  $q_i^{2m}$ replaced by
$q_i^{2m}$ replaced by  $q_i^{-2m}$. Hence we get
$q_i^{-2m}$. Hence we get  $v_m(x)=w_m\left (x,q_i^{-2}\right )$. Finally, for
$v_m(x)=w_m\left (x,q_i^{-2}\right )$. Finally, for ![]() $i\in I\setminus X$ and
$i\in I\setminus X$ and ![]() $j\in I$, the rescaled bivariate continuous q-Hermite polynomials
$j\in I$, the rescaled bivariate continuous q-Hermite polynomials
 $$ \begin{align} w_{m,n}(x,y) = (b_i/2)^{m+n} H_{m,n}\left(\frac{x}{b_i},\frac{y}{b_i};q_i^2,q_i^{a_{ij}}\right) \in {\mathbb K}\left[b_i^2,x,y\right] \subset {\mathcal M}_X^+[x,y] \end{align} $$
$$ \begin{align} w_{m,n}(x,y) = (b_i/2)^{m+n} H_{m,n}\left(\frac{x}{b_i},\frac{y}{b_i};q_i^2,q_i^{a_{ij}}\right) \in {\mathbb K}\left[b_i^2,x,y\right] \subset {\mathcal M}_X^+[x,y] \end{align} $$satisfy the initial conditions and recursion B) in Section 1.4. Hence we get  $w_{m,n}(x,y)=w_{m,n}\left (x,y;q_i^2,q_i^{a_{ij}}\right )$. By Lemma 4.2 we have
$w_{m,n}(x,y)=w_{m,n}\left (x,y;q_i^2,q_i^{a_{ij}}\right )$. By Lemma 4.2 we have
for all ![]() $n\in {\mathbb N}$. All through Section 5, the notations
$n\in {\mathbb N}$. All through Section 5, the notations ![]() $w_m(x)$,
$w_m(x)$, ![]() $v_m(x)$ and
$v_m(x)$ and ![]() $w_{m,n}(x,y)$ will refer to these special instances of the polynomials investigated in Section 4. In particular, we may freely use the results of Section 4. To keep notation short we will suppress the dependence on i and j.
$w_{m,n}(x,y)$ will refer to these special instances of the polynomials investigated in Section 4. In particular, we may freely use the results of Section 4. To keep notation short we will suppress the dependence on i and j.
We will evaluate the polynomials ![]() $w_m(x)$,
$w_m(x)$, ![]() $v_m(x)$ and
$v_m(x)$ and ![]() $w_{m,n}(x,y)$ on elements in the algebra
$w_{m,n}(x,y)$ on elements in the algebra ![]() $({\mathcal A},\ast )$. To distinguish the different algebra structures on
$({\mathcal A},\ast )$. To distinguish the different algebra structures on ![]() ${\mathcal A}$, we introduce some notation. For any
${\mathcal A}$, we introduce some notation. For any ![]() $u\in {\mathcal A}$ and any
$u\in {\mathcal A}$ and any ![]() $n\in {\mathbb N}$, we write
$n\in {\mathbb N}$, we write
 $$ \begin{align*} u^{\ast n}= \underbrace{u\ast u\ast \dotsb \ast u}_{n\ \text{factors}}. \end{align*} $$
$$ \begin{align*} u^{\ast n}= \underbrace{u\ast u\ast \dotsb \ast u}_{n\ \text{factors}}. \end{align*} $$For any polynomial ![]() $w(x)=\sum _{n}\lambda _n x^n\in {\mathcal A}[x]$ and any
$w(x)=\sum _{n}\lambda _n x^n\in {\mathcal A}[x]$ and any ![]() $u\in {\mathcal A}$, we write
$u\in {\mathcal A}$, we write
 $$ \begin{align} w(u)^\ast = \sum_n \lambda_n \ast u^{\ast n}. \end{align} $$
$$ \begin{align} w(u)^\ast = \sum_n \lambda_n \ast u^{\ast n}. \end{align} $$For any polynomial ![]() $w(x,y)=\sum _{s,t}\lambda _{st} x^s y^t\in {\mathcal A}[x,y]$ and any
$w(x,y)=\sum _{s,t}\lambda _{st} x^s y^t\in {\mathcal A}[x,y]$ and any ![]() $a_1, a_2, a_3 \in {\mathcal A}$, we write
$a_1, a_2, a_3 \in {\mathcal A}$, we write
 $$ \begin{align} a_3 \curvearrowright w(a_1 \stackrel{\ast}{,} a_2) = \sum_{s,t} a_1^{\ast s} \ast a_3 \ast a_2^{\ast t}\ast \lambda_{st}. \end{align} $$
$$ \begin{align} a_3 \curvearrowright w(a_1 \stackrel{\ast}{,} a_2) = \sum_{s,t} a_1^{\ast s} \ast a_3 \ast a_2^{\ast t}\ast \lambda_{st}. \end{align} $$Remark 5.1. Note that we write the coefficients ![]() $\lambda _{st}$ on the right side in equation (5.6). This will not be relevant in Section 5.3, where we will consider expressions of the form
$\lambda _{st}$ on the right side in equation (5.6). This will not be relevant in Section 5.3, where we will consider expressions of the form ![]() $F_j \curvearrowright w_{m,n}(F_i\stackrel {\ast }{,}F_i)$ for
$F_j \curvearrowright w_{m,n}(F_i\stackrel {\ast }{,}F_i)$ for ![]() $i,j\in I\setminus X$. Indeed, the coefficients of the rescaled bivariate continuous q-Hermite polynomials
$i,j\in I\setminus X$. Indeed, the coefficients of the rescaled bivariate continuous q-Hermite polynomials ![]() $w_{m,n}(x,y)$ involve only powers of
$w_{m,n}(x,y)$ involve only powers of ![]() $b_i^2$, which commutes with
$b_i^2$, which commutes with ![]() $F_k$ for all
$F_k$ for all ![]() $k\in I\setminus X$.
$k\in I\setminus X$.
However, in Section 5.4 we will consider the insertion operation ![]() $F_j \curvearrowright w_{m,n}(F_i\stackrel {\ast }{,}F_i)$ for
$F_j \curvearrowright w_{m,n}(F_i\stackrel {\ast }{,}F_i)$ for ![]() $i\in I\setminus X$ and
$i\in I\setminus X$ and ![]() $j\in X$. In this case,
$j\in X$. In this case, ![]() $b_i^2$ does not commute with
$b_i^2$ does not commute with ![]() $F_j$, and it will turn out crucial to have the coefficients
$F_j$, and it will turn out crucial to have the coefficients ![]() $\lambda _{st}$ on the right side in equation (5.6).
$\lambda _{st}$ on the right side in equation (5.6).
5.2 The powers of  $F_i$ for
$F_i$ for  $\tau (i)=i$
$\tau (i)=i$
Fix ![]() $i\in I\setminus X$ with
$i\in I\setminus X$ with ![]() $\tau (i)=i$. The following proposition expresses
$\tau (i)=i$. The following proposition expresses ![]() $F_i^n$ for
$F_i^n$ for ![]() $n\in {\mathbb N}$ in terms of the star product
$n\in {\mathbb N}$ in terms of the star product ![]() $\ast $ on
$\ast $ on ![]() ${\mathcal A}$. Recall equations (5.1) and (5.5) and the recursion (4.5).
${\mathcal A}$. Recall equations (5.1) and (5.5) and the recursion (4.5).
Proposition 5.2. Let ![]() $i\in I\setminus X$ with
$i\in I\setminus X$ with ![]() $\tau (i)=i$. The relation
$\tau (i)=i$. The relation
holds in ![]() ${\mathcal A}$ for any
${\mathcal A}$ for any ![]() $m\in {\mathbb N}$.
$m\in {\mathbb N}$.
Proof. The relation (5.7) holds for ![]() $m=0$ and
$m=0$ and ![]() $m=1$. We proceed by induction on m. By Lemmas 3.3 and 3.5 we have
$m=1$. We proceed by induction on m. By Lemmas 3.3 and 3.5 we have
 $$ \begin{align*} F_i\ast F_i^m&\stackrel{\phantom{\text{(3.6)}}}{=} F_i^{m+1} - c_i \frac{q^{\left(\alpha_i,w_X\left(\alpha_i\right)\right)}}{q_i-q_i^{-1}} K_{w_X\left(\alpha_i\right)-\alpha_i} \partial_{i,X}^L\left(F_i^{m}\right)\\ &\stackrel{\text{(3.6)}}{=} F_i^{m+1} - \frac{c_i q_i^2}{q_i-q_i^{-1}} (m)_{q_i^2} Z_i F_i^{m-1}\\ &\stackrel{\phantom{\text{(3.6)}}}{=} F_i^{m+1} + \frac{b_i^2}{4} \left(1-q_i^{2m}\right) F_i^{m-1}. \end{align*} $$
$$ \begin{align*} F_i\ast F_i^m&\stackrel{\phantom{\text{(3.6)}}}{=} F_i^{m+1} - c_i \frac{q^{\left(\alpha_i,w_X\left(\alpha_i\right)\right)}}{q_i-q_i^{-1}} K_{w_X\left(\alpha_i\right)-\alpha_i} \partial_{i,X}^L\left(F_i^{m}\right)\\ &\stackrel{\text{(3.6)}}{=} F_i^{m+1} - \frac{c_i q_i^2}{q_i-q_i^{-1}} (m)_{q_i^2} Z_i F_i^{m-1}\\ &\stackrel{\phantom{\text{(3.6)}}}{=} F_i^{m+1} + \frac{b_i^2}{4} \left(1-q_i^{2m}\right) F_i^{m-1}. \end{align*} $$Hence by the induction hypothesis and equation (4.5), we get
 $$ \begin{align*} F_i^{m+1} = F_i\ast w_m(F_i)^\ast - \frac{b_i^2}{4} \left(1-q_i^{2m}\right) w_{m-1}(F_i)^\ast = w_{m+1}(F_i)^\ast, \end{align*} $$
$$ \begin{align*} F_i^{m+1} = F_i\ast w_m(F_i)^\ast - \frac{b_i^2}{4} \left(1-q_i^{2m}\right) w_{m-1}(F_i)^\ast = w_{m+1}(F_i)^\ast, \end{align*} $$which completes the induction step.
5.3 The quantum Serre relation for  $\tau (i)=i\neq j$ where
$\tau (i)=i\neq j$ where  $i,j\in I\setminus X$
$i,j\in I\setminus X$
We now want to rewrite the quantum Serre relation ![]() $S_{ij}\left (F_i,F_j\right )=0$ for
$S_{ij}\left (F_i,F_j\right )=0$ for ![]() $\tau (i)=i$, with
$\tau (i)=i$, with ![]() $i,j\in I\setminus X$, in terms of the star product on the algebra
$i,j\in I\setminus X$, in terms of the star product on the algebra ![]() ${\mathcal A}$. Recall the rescaled bivariate q-Hermite polynomials (5.3), the insertion operator defined by equation (5.6) and the recursion (4.6).
${\mathcal A}$. Recall the rescaled bivariate q-Hermite polynomials (5.3), the insertion operator defined by equation (5.6) and the recursion (4.6).
Proposition 5.3. Let ![]() $i,j\in I\setminus X$ with
$i,j\in I\setminus X$ with ![]() $\tau (i)=i\neq j$. Then the relation
$\tau (i)=i\neq j$. Then the relation
holds in ![]() ${\mathcal A}$ for any
${\mathcal A}$ for any ![]() $m,n\in {\mathbb N}$.
$m,n\in {\mathbb N}$.
Proof. We prove equation (5.8) by induction on m. For ![]() $m=0$ the relation holds by Proposition 5.2 and equation (5.4). Now fix
$m=0$ the relation holds by Proposition 5.2 and equation (5.4). Now fix ![]() $m,n\in {\mathbb N}$. Equations (3.1), (3.2) and (3.6) imply
$m,n\in {\mathbb N}$. Equations (3.1), (3.2) and (3.6) imply
 $$ \begin{align} F_i\ast F_i^mF_jF_i^n &= F_i^{m+1} F_j F_i^n - \frac{c_i q^{\left(\alpha_i,w_X\left(\alpha_i\right)\right)}}{q_i-q_i^{-1}} K_{w_X\left(\alpha_i\right)-\alpha_i} \partial^L_{i,X}\left(F_i^mF_jF_i^n\right)\nonumber\\ &= F_i^{m+1} F_j F_i^n - \frac{c_i q^{\left(\alpha_i,\alpha_i\right)}}{q_i-q_i^{-1}} (m)_{q_i^2} Z_i F_i^{m-1}F_j F_i^n \nonumber\\ &\quad - \frac{c_i q^{\left(\alpha_i,(m+1)\alpha_i+\alpha_j\right)}}{q_i-q_i^{-1}} (n)_{q_i^2} Z_i F_i^{m}F_j F_i^{n-1} \nonumber\\ &= F_i^{m+1} F_j F_i^n + \frac{b_i^2}{4} \left(1-q_i^{2m}\right) F_i^{m-1}F_j F_i^n \nonumber\\ &\quad + \frac{b_i^2}{4} q_i^{2m+a_{ij}}\left(1-q_i^{2n}\right) F_i^{m}F_j F_i^{n-1}. \end{align} $$
$$ \begin{align} F_i\ast F_i^mF_jF_i^n &= F_i^{m+1} F_j F_i^n - \frac{c_i q^{\left(\alpha_i,w_X\left(\alpha_i\right)\right)}}{q_i-q_i^{-1}} K_{w_X\left(\alpha_i\right)-\alpha_i} \partial^L_{i,X}\left(F_i^mF_jF_i^n\right)\nonumber\\ &= F_i^{m+1} F_j F_i^n - \frac{c_i q^{\left(\alpha_i,\alpha_i\right)}}{q_i-q_i^{-1}} (m)_{q_i^2} Z_i F_i^{m-1}F_j F_i^n \nonumber\\ &\quad - \frac{c_i q^{\left(\alpha_i,(m+1)\alpha_i+\alpha_j\right)}}{q_i-q_i^{-1}} (n)_{q_i^2} Z_i F_i^{m}F_j F_i^{n-1} \nonumber\\ &= F_i^{m+1} F_j F_i^n + \frac{b_i^2}{4} \left(1-q_i^{2m}\right) F_i^{m-1}F_j F_i^n \nonumber\\ &\quad + \frac{b_i^2}{4} q_i^{2m+a_{ij}}\left(1-q_i^{2n}\right) F_i^{m}F_j F_i^{n-1}. \end{align} $$Hence by the induction hypothesis and equation (4.6) for ![]() $r=q^{a_{ij}}$ we get
$r=q^{a_{ij}}$ we get
 $$ \begin{align*} F_i^{m+1}F_j F_i^n &= F_i\ast \left( F_j \curvearrowright w_{m,n}(F_i\stackrel{\ast}{,}F_i)\right) - \frac{b_i^2}{4}\left(1-q_i^{2m}\right)F_j \curvearrowright w_{m-1,n}(F_i\stackrel{\ast}{,}F_i)\\ & \quad -\frac{b_i^2}{4} q_i^{2m+a_{ij}}\left(1-q_i^{2n}\right)F_j \curvearrowright w_{m,n-1}(F_i\stackrel{\ast}{,}F_i)\\ &= F_j\curvearrowright \left(x\cdot w_{m,n} - \frac{b_i^2}{4}\left(1-q_i^{2m}\right) w_{m-1,n} \right.\\ &\quad \left. -\frac{b_i^2}{4} q_i^{2m+a_{ij}}\left(1-q_i^{2n}\right) w_{m,n-1} \right)(F_i\stackrel{\ast}{,}F_i)\\ &=F_j \curvearrowright w_{m+1,n}(F_i\stackrel{\ast}{,}F_i), \end{align*} $$
$$ \begin{align*} F_i^{m+1}F_j F_i^n &= F_i\ast \left( F_j \curvearrowright w_{m,n}(F_i\stackrel{\ast}{,}F_i)\right) - \frac{b_i^2}{4}\left(1-q_i^{2m}\right)F_j \curvearrowright w_{m-1,n}(F_i\stackrel{\ast}{,}F_i)\\ & \quad -\frac{b_i^2}{4} q_i^{2m+a_{ij}}\left(1-q_i^{2n}\right)F_j \curvearrowright w_{m,n-1}(F_i\stackrel{\ast}{,}F_i)\\ &= F_j\curvearrowright \left(x\cdot w_{m,n} - \frac{b_i^2}{4}\left(1-q_i^{2m}\right) w_{m-1,n} \right.\\ &\quad \left. -\frac{b_i^2}{4} q_i^{2m+a_{ij}}\left(1-q_i^{2n}\right) w_{m,n-1} \right)(F_i\stackrel{\ast}{,}F_i)\\ &=F_j \curvearrowright w_{m+1,n}(F_i\stackrel{\ast}{,}F_i), \end{align*} $$which completes the induction step.
With this proposition we are able to express the quantum Serre relation ![]() $S_{ij}\left (F_i,F_j\right )=0$ in
$S_{ij}\left (F_i,F_j\right )=0$ in ![]() ${\mathcal A}$ in terms of the star product. Recall equations (5.1)–(5.3).
${\mathcal A}$ in terms of the star product. Recall equations (5.1)–(5.3).
Theorem 5.4. Let ![]() $i,j\in I\setminus X$ with
$i,j\in I\setminus X$ with ![]() $\tau (i)=i\neq j$. Then the relation
$\tau (i)=i\neq j$. Then the relation
 $$ \begin{align*} \sum_{n=0}^{1-a_{ij}}(-1)^n \begin{bmatrix} 1-a_{ij}\\ n \end{bmatrix}_{q_i} F_j \curvearrowright w_{1-a_{ij}-n,n}(F_i \stackrel{\ast}{,}F_i) =0 \end{align*} $$
$$ \begin{align*} \sum_{n=0}^{1-a_{ij}}(-1)^n \begin{bmatrix} 1-a_{ij}\\ n \end{bmatrix}_{q_i} F_j \curvearrowright w_{1-a_{ij}-n,n}(F_i \stackrel{\ast}{,}F_i) =0 \end{align*} $$holds in the algebra ![]() $({\mathcal A},\ast )$. This relation can be rewritten as
$({\mathcal A},\ast )$. This relation can be rewritten as
 $$ \begin{align*} \sum_{n=0}^{1-a_{ij}}(-1)^n \begin{bmatrix} 1-a_{ij}\\ n \end{bmatrix}_{q_i} w_{1-a_{ij}-n}(F_i)^\ast \ast F_j \ast v_{n}(F_i)^\ast =0. \end{align*} $$
$$ \begin{align*} \sum_{n=0}^{1-a_{ij}}(-1)^n \begin{bmatrix} 1-a_{ij}\\ n \end{bmatrix}_{q_i} w_{1-a_{ij}-n}(F_i)^\ast \ast F_j \ast v_{n}(F_i)^\ast =0. \end{align*} $$Proof. The first statement is a direct consequence of the quantum Serre relation ![]() $S_{ij}\left (F_i,F_j\right )=0$ and Proposition 5.3. The second statement then follows from Proposition 4.4 with
$S_{ij}\left (F_i,F_j\right )=0$ and Proposition 5.3. The second statement then follows from Proposition 4.4 with ![]() $a=a_{ij}$.
$a=a_{ij}$.
In view of the isomorphism ![]() $\psi :{\mathcal B}_{\mathbf {c}}\rightarrow ({\mathcal A},\ast )$, Theorem 5.4 proves case (I) of Theorem 1.2.
$\psi :{\mathcal B}_{\mathbf {c}}\rightarrow ({\mathcal A},\ast )$, Theorem 5.4 proves case (I) of Theorem 1.2.
5.4 A recursive formula in the case  $\tau (i)=i\neq j$ where
$\tau (i)=i\neq j$ where  $i\in I\setminus X$ and
$i\in I\setminus X$ and  $j\in X$
$j\in X$
Assume that ![]() $i\in I\setminus X$ with
$i\in I\setminus X$ with ![]() $\tau (i)=i$ and
$\tau (i)=i$ and ![]() $j\in X$. Recall from equation (1.5) that in this case we write
$j\in X$. Recall from equation (1.5) that in this case we write
 $$ \begin{align} &{\mathcal Z}_i=c_iq_i Z_i=c_iq_i \partial_i^R\left(T_{w_X}(E_i)\right). \end{align} $$
$$ \begin{align} &{\mathcal Z}_i=c_iq_i Z_i=c_iq_i \partial_i^R\left(T_{w_X}(E_i)\right). \end{align} $$Moreover, we set
 $$ \begin{align} d_{ij}=\partial_j^R({\mathcal Z}_i)K_j, \qquad \widetilde{d_{ij}}=K_j^{-1}\partial_j^L({\mathcal Z}_i), \end{align} $$
$$ \begin{align} d_{ij}=\partial_j^R({\mathcal Z}_i)K_j, \qquad \widetilde{d_{ij}}=K_j^{-1}\partial_j^L({\mathcal Z}_i), \end{align} $$so that equation (2.4) now reads
 $$ \begin{align} \left[F_j,{\mathcal Z}_i\right] = \frac{\widetilde{d_{ij}}-d_{ij}}{q_j-q_j^{-1}}. \end{align} $$
$$ \begin{align} \left[F_j,{\mathcal Z}_i\right] = \frac{\widetilde{d_{ij}}-d_{ij}}{q_j-q_j^{-1}}. \end{align} $$Recall from Section 2.6 that it is convenient to simultaneously consider the parameters ![]() ${\mathbf {c}}=(c_i)_{i\in I\setminus X}\in {\mathcal C}$ and
${\mathbf {c}}=(c_i)_{i\in I\setminus X}\in {\mathcal C}$ and  ${\mathbf {c}}'=\left (c_i'\right )_{i\in I\setminus X}\in {\mathcal C}$ related by equation (2.24). We write
${\mathbf {c}}'=\left (c_i'\right )_{i\in I\setminus X}\in {\mathcal C}$ related by equation (2.24). We write ![]() ${\mathcal Z}_i'$,
${\mathcal Z}_i'$, ![]() $d^{\prime }_{ij}$,
$d^{\prime }_{ij}$, ![]() $\widetilde {d^{\prime }_{ij}}$ to denote the elements (5.10) and (5.11) corresponding to the parameter family
$\widetilde {d^{\prime }_{ij}}$ to denote the elements (5.10) and (5.11) corresponding to the parameter family ![]() ${\mathbf {c}}'$. It follows from [Reference Balagović and KolbBK15, Lemma 2.9] and [Reference Bao and WangBW21, Theorem 4.1] that
${\mathbf {c}}'$. It follows from [Reference Balagović and KolbBK15, Lemma 2.9] and [Reference Bao and WangBW21, Theorem 4.1] that
 $$ \begin{align} \overline{{\mathcal Z}_i}=\overline{c_i} q_i (-1)^{2\alpha_i\left(\rho_X^\vee\right)}q^{\left(\alpha_i,\Theta\left(\alpha_i\right)-2\rho_X\right)} \partial_i^R\left(T_{w_X}(E_i)\right)={\mathcal Z}^{\prime}_i. \end{align} $$
$$ \begin{align} \overline{{\mathcal Z}_i}=\overline{c_i} q_i (-1)^{2\alpha_i\left(\rho_X^\vee\right)}q^{\left(\alpha_i,\Theta\left(\alpha_i\right)-2\rho_X\right)} \partial_i^R\left(T_{w_X}(E_i)\right)={\mathcal Z}^{\prime}_i. \end{align} $$Moreover, we have ![]() $d_{ij}\in K_j{\mathcal M}_X^+$ and
$d_{ij}\in K_j{\mathcal M}_X^+$ and  $\widetilde {d_{ij}}\in K_j^{-1}{\mathcal M}_X^+$. Hence, applying the bar involution to equation (5.12) gives us
$\widetilde {d_{ij}}\in K_j^{-1}{\mathcal M}_X^+$. Hence, applying the bar involution to equation (5.12) gives us
 $$ \begin{align*} \overline{\widetilde{d_{ij}}}=d^{\prime}_{ij}, \qquad \overline{d_{ij}}=\widetilde{d^{\prime}_{ij}}. \end{align*} $$
$$ \begin{align*} \overline{\widetilde{d_{ij}}}=d^{\prime}_{ij}, \qquad \overline{d_{ij}}=\widetilde{d^{\prime}_{ij}}. \end{align*} $$These relations will be used in the proof of Theorem 5.10.
The following lemma provides a formula similar to equation (5.9) in the present setting:
Lemma 5.5. Let ![]() $i\in I\setminus X$, with
$i\in I\setminus X$, with ![]() $\tau (i)=i$ and
$\tau (i)=i$ and ![]() $j\in X$. Then the relation
$j\in X$. Then the relation
 $$ \begin{align} F_i\ast F_i^mF_j F_i^n &= F_i^{m+1} F_j F_i^n \nonumber\\ &\quad + \left(1-q_i^{2m}\right) F_i^{m-1} F_j F_i^n \frac{b_i^2}{4} + q_i^{2 m + a_{ij}} \left(1-q_i^{2n}\right) F_i^m F_j F_i^{n-1}\frac{b_i^2}{4} \nonumber\\ & \quad+ \frac{q_i^{(m-1)a_{ij}} \left(1-q_i^{2m}\right)}{\lambda_{ij}} d_{ij} F_i^{m+n-1} -\frac{q_i^{-(m-1)a_{ij}} \left(1-q_i^{2(m+n)}\right)}{\lambda_{ij}} \widetilde{d_{ij}} F_i^{m+n-1} \end{align} $$
$$ \begin{align} F_i\ast F_i^mF_j F_i^n &= F_i^{m+1} F_j F_i^n \nonumber\\ &\quad + \left(1-q_i^{2m}\right) F_i^{m-1} F_j F_i^n \frac{b_i^2}{4} + q_i^{2 m + a_{ij}} \left(1-q_i^{2n}\right) F_i^m F_j F_i^{n-1}\frac{b_i^2}{4} \nonumber\\ & \quad+ \frac{q_i^{(m-1)a_{ij}} \left(1-q_i^{2m}\right)}{\lambda_{ij}} d_{ij} F_i^{m+n-1} -\frac{q_i^{-(m-1)a_{ij}} \left(1-q_i^{2(m+n)}\right)}{\lambda_{ij}} \widetilde{d_{ij}} F_i^{m+n-1} \end{align} $$holds in ![]() ${\mathcal A}$ for all
${\mathcal A}$ for all ![]() $m,n\in {\mathbb N}$ with
$m,n\in {\mathbb N}$ with  $b_i^2=4 {\mathcal Z}_i/\left (q_i-q_i^{-1}\right )^2$ and
$b_i^2=4 {\mathcal Z}_i/\left (q_i-q_i^{-1}\right )^2$ and  $\lambda _{ij}=\left (q_i-q_i^{-1}\right )^2\left (q_j-q_j^{-1}\right )$.
$\lambda _{ij}=\left (q_i-q_i^{-1}\right )^2\left (q_j-q_j^{-1}\right )$.
Proof. For all ![]() $m,n\in {\mathbb N}$, we have
$m,n\in {\mathbb N}$, we have
 $$ \begin{align} F_i^m F_j F_i^n= q^{n\left(\alpha_j,\alpha_i\right)} F_i^{m+n} F_j - q^{n\left(\alpha_j,\alpha_i\right)} F_i^m {\mbox{ad}}_r\left(F_j\right)\left(F_i^n\right), \end{align} $$
$$ \begin{align} F_i^m F_j F_i^n= q^{n\left(\alpha_j,\alpha_i\right)} F_i^{m+n} F_j - q^{n\left(\alpha_j,\alpha_i\right)} F_i^m {\mbox{ad}}_r\left(F_j\right)\left(F_i^n\right), \end{align} $$and hence equation (3.1) implies
 $$ \begin{align} F_i\ast F_i^mF_j F_i^n &= F_i^{m+1} F_j F_i^n - \frac{c_i q^{\left(\alpha_i,w_X\left(\alpha_i\right)+n\alpha_j\right)}}{q_i-q_i^{-1}} K_{w_X\left(\alpha_i\right)-\alpha_i} \partial_{i,X}^L\left(F_i^{m+n}\right) F_j\nonumber\\ & \quad + \frac{c_i q^{\left(\alpha_i,w_X\left(\alpha_i\right)+n\alpha_j\right)}}{q_i-q_i^{-1}} K_{w_X\left(\alpha_i\right)-\alpha_i} \partial_{i,X}^L\left(F_i^m {\mbox{ad}}_r\left(F_j\right)\left(F_i^n\right)\right). \end{align} $$
$$ \begin{align} F_i\ast F_i^mF_j F_i^n &= F_i^{m+1} F_j F_i^n - \frac{c_i q^{\left(\alpha_i,w_X\left(\alpha_i\right)+n\alpha_j\right)}}{q_i-q_i^{-1}} K_{w_X\left(\alpha_i\right)-\alpha_i} \partial_{i,X}^L\left(F_i^{m+n}\right) F_j\nonumber\\ & \quad + \frac{c_i q^{\left(\alpha_i,w_X\left(\alpha_i\right)+n\alpha_j\right)}}{q_i-q_i^{-1}} K_{w_X\left(\alpha_i\right)-\alpha_i} \partial_{i,X}^L\left(F_i^m {\mbox{ad}}_r\left(F_j\right)\left(F_i^n\right)\right). \end{align} $$In view of the skew derivation property (3.2), equations (3.6) and (3.11) allow us to rewrite this as
 $$ \begin{align*} F_i\ast F_i^mF_j F_i^n &= F_i^{m+1} F_j F_i^n - \frac{c_i q^{\left(\alpha_i,\alpha_i+n\alpha_j\right)}}{q_i-q_i^{-1}} (m+n)_{q_i^2} Z_i F_i^{m+n-1} F_j\\ & \quad + \frac{c_i q^{\left(\alpha_i,\alpha_i+n\alpha_j\right)}}{q_i-q_i^{-1}} (m)_{q_i^2} Z_i F_i^{m-1} {\mbox{ad}}_r\left(F_j\right)\left(F_i^n\right)\\ & \quad +\frac{c_i q^{(m+1)\left(\alpha_i,\alpha_i+\alpha_j\right)-\left(\alpha_j,w_X\left(\alpha_i\right)-\alpha_i-\alpha_j\right)}}{\left(q_i-q_i^{-1}\right)\left(q_j-q_j^{-1}\right)} (n)_{q_i^2} K_j \partial_j^R(Z_i) F_i^{m+n-1}\\ & \quad + \frac{c_i q^{\left(\alpha_i,(m+1)\alpha_i+n\alpha_j\right)}}{q_i-q_i^{-1}} (n)_{q_i^2} Z_i F_i^m {\mbox{ad}}_r\left(F_j\right)\left(F_i^{n-1}\right). \end{align*} $$
$$ \begin{align*} F_i\ast F_i^mF_j F_i^n &= F_i^{m+1} F_j F_i^n - \frac{c_i q^{\left(\alpha_i,\alpha_i+n\alpha_j\right)}}{q_i-q_i^{-1}} (m+n)_{q_i^2} Z_i F_i^{m+n-1} F_j\\ & \quad + \frac{c_i q^{\left(\alpha_i,\alpha_i+n\alpha_j\right)}}{q_i-q_i^{-1}} (m)_{q_i^2} Z_i F_i^{m-1} {\mbox{ad}}_r\left(F_j\right)\left(F_i^n\right)\\ & \quad +\frac{c_i q^{(m+1)\left(\alpha_i,\alpha_i+\alpha_j\right)-\left(\alpha_j,w_X\left(\alpha_i\right)-\alpha_i-\alpha_j\right)}}{\left(q_i-q_i^{-1}\right)\left(q_j-q_j^{-1}\right)} (n)_{q_i^2} K_j \partial_j^R(Z_i) F_i^{m+n-1}\\ & \quad + \frac{c_i q^{\left(\alpha_i,(m+1)\alpha_i+n\alpha_j\right)}}{q_i-q_i^{-1}} (n)_{q_i^2} Z_i F_i^m {\mbox{ad}}_r\left(F_j\right)\left(F_i^{n-1}\right). \end{align*} $$Using the relation  $(m+n)_{q_i^2}=(m)_{q_i^2} + q_i^{2m}(n)_{q_i^2}$ and equation (5.15) for the third and fifth terms, we obtain
$(m+n)_{q_i^2}=(m)_{q_i^2} + q_i^{2m}(n)_{q_i^2}$ and equation (5.15) for the third and fifth terms, we obtain
 $$ \begin{align*} &F_i\ast F_i^mF_j F_i^n = F_i^{m+1} F_j F_i^n - \frac{c_i q_i^2}{q_i-q_i^{-1}}\left( (m)_{q_i^2} Z_i F_i^{m-1} F_j F_i^n + \right. \\ &\qquad\qquad\qquad\left. + q_i^{2 m + a_{ij}} (n)_{q_i^2} Z_i F_i^m F_j F_i^{n-1}\right) +\frac{c_i q_i^{(2m+2)-(n-2)a_{ij}}}{\left(q_i-q_i^{-1}\right)\left(q_j-q_j^{-1}\right)} (n)_{q_i^2} F_i^{m+n-1} \partial_j^R(Z_i) K_j. \end{align*} $$
$$ \begin{align*} &F_i\ast F_i^mF_j F_i^n = F_i^{m+1} F_j F_i^n - \frac{c_i q_i^2}{q_i-q_i^{-1}}\left( (m)_{q_i^2} Z_i F_i^{m-1} F_j F_i^n + \right. \\ &\qquad\qquad\qquad\left. + q_i^{2 m + a_{ij}} (n)_{q_i^2} Z_i F_i^m F_j F_i^{n-1}\right) +\frac{c_i q_i^{(2m+2)-(n-2)a_{ij}}}{\left(q_i-q_i^{-1}\right)\left(q_j-q_j^{-1}\right)} (n)_{q_i^2} F_i^{m+n-1} \partial_j^R(Z_i) K_j. \end{align*} $$Using the notation of equations (5.10) and (5.11) and the commutation relation (5.12), one transforms this equation into equation (5.14).
Recall the insertion operation defined by equation (5.6) and the rescaled bivariate continuous q-Hermite polynomials ![]() $w_{m,n}(x,y)$ defined by equation (5.3). The recursion (5.14) implies that there exist polynomials
$w_{m,n}(x,y)$ defined by equation (5.3). The recursion (5.14) implies that there exist polynomials ![]() $\rho _{m,n}(x), \sigma _{m,n}(x)\in {\mathcal M}_X^+[x]$ such that
$\rho _{m,n}(x), \sigma _{m,n}(x)\in {\mathcal M}_X^+[x]$ such that
 $$ \begin{align} F_i^m F_j F_i^n = F_j\curvearrowright w_{m,n}(F_i\stackrel{\ast}{,}F_i) + d_{ij} \rho_{m,n}(F_i)^\ast + \widetilde{d_{ij}} \sigma_{m,n}(F_i)^\ast. \end{align} $$
$$ \begin{align} F_i^m F_j F_i^n = F_j\curvearrowright w_{m,n}(F_i\stackrel{\ast}{,}F_i) + d_{ij} \rho_{m,n}(F_i)^\ast + \widetilde{d_{ij}} \sigma_{m,n}(F_i)^\ast. \end{align} $$For ![]() $m=0$, we have
$m=0$, we have ![]() $F_jF_i^n=F_j\curvearrowright w_n(F_i)^\ast $ and hence
$F_jF_i^n=F_j\curvearrowright w_n(F_i)^\ast $ and hence ![]() $\rho _{0,n}(x)=\sigma _{0,n}(x)=0$ for all
$\rho _{0,n}(x)=\sigma _{0,n}(x)=0$ for all ![]() $n\in {\mathbb N}$. We can translate the recursion (5.14) into recursive formulas for
$n\in {\mathbb N}$. We can translate the recursion (5.14) into recursive formulas for ![]() $\rho _{m,n}(x)$ and
$\rho _{m,n}(x)$ and ![]() $\sigma _{m,n}(x)$.
$\sigma _{m,n}(x)$.
Lemma 5.6. With the ansatz (5.17), the recursion (5.14) is equivalent to the recursions
 $$ \begin{align} q_i^{a_{ij}} x\rho_{m,n}(x)&= \rho_{m+1,n}(x) +\left(1-q_i^{2m}\right)\rho_{m-1,n}(x) \frac{b_i^2}{4}\nonumber\\& \quad + \left(1-q_i^{2n}\right)q_i^{2m+a_{ij}} \rho_{m,n-1}(x) \frac{b_i^2}{4} + \frac{q_i^{(m-1)a_{ij}}\left(1-q_i^{2m}\right)}{\lambda_{ij}} w_{m+n-1}(x),\\q_i^{-a_{ij}} x\sigma_{m,n}(x)&= \sigma_{m+1,n}(x) +\left(1-q_i^{2m}\right) \sigma_{m-1,n}(x) \frac{b_i^2}{4}\nonumber\\& \quad + \left(1-q_i^{2n}\right)q_i^{2m+a_{ij}} \sigma_{m,n-1}(x) \frac{b_i^2}{4} - \frac{q_i^{-(m-1)a_{ij}}\left(1-q_i^{2(m+n)}\right)}{\lambda_{ij}} w_{m+n-1}(x)\nonumber \end{align} $$
$$ \begin{align} q_i^{a_{ij}} x\rho_{m,n}(x)&= \rho_{m+1,n}(x) +\left(1-q_i^{2m}\right)\rho_{m-1,n}(x) \frac{b_i^2}{4}\nonumber\\& \quad + \left(1-q_i^{2n}\right)q_i^{2m+a_{ij}} \rho_{m,n-1}(x) \frac{b_i^2}{4} + \frac{q_i^{(m-1)a_{ij}}\left(1-q_i^{2m}\right)}{\lambda_{ij}} w_{m+n-1}(x),\\q_i^{-a_{ij}} x\sigma_{m,n}(x)&= \sigma_{m+1,n}(x) +\left(1-q_i^{2m}\right) \sigma_{m-1,n}(x) \frac{b_i^2}{4}\nonumber\\& \quad + \left(1-q_i^{2n}\right)q_i^{2m+a_{ij}} \sigma_{m,n-1}(x) \frac{b_i^2}{4} - \frac{q_i^{-(m-1)a_{ij}}\left(1-q_i^{2(m+n)}\right)}{\lambda_{ij}} w_{m+n-1}(x)\nonumber \end{align} $$for all ![]() $m,n\in {\mathbb N}$.
$m,n\in {\mathbb N}$.
From now on we focus on the polynomials ![]() $\rho _{m,n}$ only. In Section 5.6 we will determine the Serre combination of the polynomials
$\rho _{m,n}$ only. In Section 5.6 we will determine the Serre combination of the polynomials ![]() $\rho _{m,n}$. The Serre combination of the polynomials
$\rho _{m,n}$. The Serre combination of the polynomials ![]() $\sigma _{m,n}$ can then be obtained with the help of the isomorphism
$\sigma _{m,n}$ can then be obtained with the help of the isomorphism ![]() $\Phi $ from Section 2.6.
$\Phi $ from Section 2.6.
We produce an unscaled version of the recursion (5.18). Define polynomials ![]() $U_{m,n}(x;q,r)\in {\mathbb K}[x]$ recursively by
$U_{m,n}(x;q,r)\in {\mathbb K}[x]$ recursively by ![]() $U_{0,n}(x;q,r)=0$ for all
$U_{0,n}(x;q,r)=0$ for all ![]() $n\in {\mathbb N}$ and
$n\in {\mathbb N}$ and
 $$ \begin{align} 2x U_{m,n}(x)&= U_{m+1,n}(x) + (1-q^m) r^{-1} U_{m-1,n}(x) + q^m(1-q^n)U_{m,n-1}(x) \nonumber\\ & \quad +(1-q^m) H_{m+n-1}(x). \end{align} $$
$$ \begin{align} 2x U_{m,n}(x)&= U_{m+1,n}(x) + (1-q^m) r^{-1} U_{m-1,n}(x) + q^m(1-q^n)U_{m,n-1}(x) \nonumber\\ & \quad +(1-q^m) H_{m+n-1}(x). \end{align} $$The following statement is an immediate consequence of equation (5.18):
Lemma 5.7. The relation
 $$ \begin{align*} \rho_{m,n}(x)=\frac{q_i^{(m-2)a_{ij}}}{\lambda_{ij}} \left(b_i/2\right)^{m+n-2} U_{m,n}\left(\frac{x}{b_i};q_i^2,q_i^{2a_{ij}}\right) \end{align*} $$
$$ \begin{align*} \rho_{m,n}(x)=\frac{q_i^{(m-2)a_{ij}}}{\lambda_{ij}} \left(b_i/2\right)^{m+n-2} U_{m,n}\left(\frac{x}{b_i};q_i^2,q_i^{2a_{ij}}\right) \end{align*} $$holds for all ![]() $m,n\in {\mathbb N}$ with
$m,n\in {\mathbb N}$ with 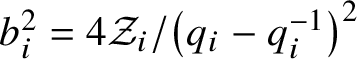 $b_i^2=4{\mathcal Z}_i/\left (q_i-q_i^{-1}\right )^2$.
$b_i^2=4{\mathcal Z}_i/\left (q_i-q_i^{-1}\right )^2$.
5.5 A generating function approach for  $\tau (i)=i\neq j$ where
$\tau (i)=i\neq j$ where  $i\in I\setminus X$ and
$i\in I\setminus X$ and  $j\in X$
$j\in X$
Define a generating function
 $$ \begin{align*} \psi\left(\begin{matrix} x \\s,t\end{matrix};q\right)=\sum_{m,n\ge 0} \frac{H_{m+n}(x;q)}{(q;q)_m(q;q)_n}s^mt^n. \end{align*} $$
$$ \begin{align*} \psi\left(\begin{matrix} x \\s,t\end{matrix};q\right)=\sum_{m,n\ge 0} \frac{H_{m+n}(x;q)}{(q;q)_m(q;q)_n}s^mt^n. \end{align*} $$Using the recursions (4.1) and (4.2) and induction over m, one obtains
Hence [Reference Casper, Kolb and YakimovCKY21, Theorem 2.7] implies that
 $$ \begin{align*} \psi\left(\begin{matrix} x \\s,t\end{matrix};q\right) = \frac{(st;q)_\infty}{\left\lvert\left(se^{i\theta},te^{i\theta};q\right)_\infty\right\rvert^2} \end{align*} $$
$$ \begin{align*} \psi\left(\begin{matrix} x \\s,t\end{matrix};q\right) = \frac{(st;q)_\infty}{\left\lvert\left(se^{i\theta},te^{i\theta};q\right)_\infty\right\rvert^2} \end{align*} $$for ![]() $x=\cos (\theta )$. Following [Reference Casper, Kolb and YakimovCKY21, Section 3.1], we have
$x=\cos (\theta )$. Following [Reference Casper, Kolb and YakimovCKY21, Section 3.1], we have
 $$ \begin{align*} \psi\left(\begin{matrix} x \\qs,t\end{matrix};q\right) = \frac{1-2xs+s^2}{1-ts} \psi\left(\begin{matrix} x \\s,t\end{matrix};q\right). \end{align*} $$
$$ \begin{align*} \psi\left(\begin{matrix} x \\qs,t\end{matrix};q\right) = \frac{1-2xs+s^2}{1-ts} \psi\left(\begin{matrix} x \\s,t\end{matrix};q\right). \end{align*} $$In terms of 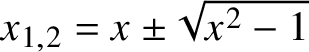 $x_{1,2}=x\pm \sqrt {x^2-1}$, defined in equation (4.16), this can be rewritten as
$x_{1,2}=x\pm \sqrt {x^2-1}$, defined in equation (4.16), this can be rewritten as
 $$ \begin{align} \psi\left(\begin{matrix} x \\qs,t\end{matrix};q\right) = \frac{(1-x_1s)(1-x_2s)}{1-ts} \psi\left(\begin{matrix} x \\s,t\end{matrix};q\right). \end{align} $$
$$ \begin{align} \psi\left(\begin{matrix} x \\qs,t\end{matrix};q\right) = \frac{(1-x_1s)(1-x_2s)}{1-ts} \psi\left(\begin{matrix} x \\s,t\end{matrix};q\right). \end{align} $$Now recall the polynomials ![]() $U_{m,n}(x;q,r)$ defined by the recursion (5.19) and consider the generating function
$U_{m,n}(x;q,r)$ defined by the recursion (5.19) and consider the generating function
 $$ \begin{align} \phi\left(\begin{matrix} x \\s,t\end{matrix};q\right) = \sum_{m,n\ge 0} \frac{U_{m,n}(x;q,r)}{(q;q)_m(q;q)_n}s^mt^n. \end{align} $$
$$ \begin{align} \phi\left(\begin{matrix} x \\s,t\end{matrix};q\right) = \sum_{m,n\ge 0} \frac{U_{m,n}(x;q,r)}{(q;q)_m(q;q)_n}s^mt^n. \end{align} $$The initial condition ![]() $U_{0,n}(x;q,r)=0$ implies that
$U_{0,n}(x;q,r)=0$ implies that
 $$ \begin{align} \phi\left(\begin{matrix} x \\0,t\end{matrix};q\right)=0. \end{align} $$
$$ \begin{align} \phi\left(\begin{matrix} x \\0,t\end{matrix};q\right)=0. \end{align} $$Finally, recall the definition (4.17) of the function  $\eta \left (\begin {matrix} x \\s \end {matrix};q\right )$, which is analytic at
$\eta \left (\begin {matrix} x \\s \end {matrix};q\right )$, which is analytic at ![]() $s=0$.
$s=0$.
Lemma 5.8. The relation
 $$ \begin{align} \phi\left(\begin{matrix} x \\s,t\end{matrix};q\right)=-s^2 \eta\left(\begin{matrix} x \\s \end{matrix};q\right) \psi\left(\begin{matrix} x \\s,t\end{matrix};q\right) \end{align} $$
$$ \begin{align} \phi\left(\begin{matrix} x \\s,t\end{matrix};q\right)=-s^2 \eta\left(\begin{matrix} x \\s \end{matrix};q\right) \psi\left(\begin{matrix} x \\s,t\end{matrix};q\right) \end{align} $$holds as an identity of formal power series in s and t with coefficients in ![]() ${\mathbb K}[x]$.
${\mathbb K}[x]$.
Proof. The recursion (5.19) implies that
 $$ \begin{align*} 2x \phi\left(\begin{matrix} x \\s,t\end{matrix};q\right)&= \frac{1}{s}\left( \phi\left(\begin{matrix} x \\s,t\end{matrix};q\right) - \phi\left(\begin{matrix} x \\qs,t\end{matrix};q\right)\right)\\ &\quad + s r^{-1} \phi\left(\begin{matrix} x \\s,t\end{matrix};q\right) + t \phi\left(\begin{matrix} x \\qs,t\end{matrix};q\right) +s \psi\left(\begin{matrix} x \\s,t\end{matrix}; q\right), \end{align*} $$
$$ \begin{align*} 2x \phi\left(\begin{matrix} x \\s,t\end{matrix};q\right)&= \frac{1}{s}\left( \phi\left(\begin{matrix} x \\s,t\end{matrix};q\right) - \phi\left(\begin{matrix} x \\qs,t\end{matrix};q\right)\right)\\ &\quad + s r^{-1} \phi\left(\begin{matrix} x \\s,t\end{matrix};q\right) + t \phi\left(\begin{matrix} x \\qs,t\end{matrix};q\right) +s \psi\left(\begin{matrix} x \\s,t\end{matrix}; q\right), \end{align*} $$and hence
 $$ \begin{align*} (1-ts) \phi\left(\begin{matrix} x \\qs,t\end{matrix};q\right)=\left(1-2xs + r^{-1}s^2\right) \phi\left(\begin{matrix} x \\s,t\end{matrix};q\right) + s^2 \psi\left(\begin{matrix} x \\s,t\end{matrix};q\right). \end{align*} $$
$$ \begin{align*} (1-ts) \phi\left(\begin{matrix} x \\qs,t\end{matrix};q\right)=\left(1-2xs + r^{-1}s^2\right) \phi\left(\begin{matrix} x \\s,t\end{matrix};q\right) + s^2 \psi\left(\begin{matrix} x \\s,t\end{matrix};q\right). \end{align*} $$This relation can be rewritten as
 $$ \begin{align*} \phi\left(\begin{matrix} x \\s,t\end{matrix};q\right)= \frac{1-ts}{(1-a_1s)(1-a_2s)} \phi\left(\begin{matrix} x \\qs,t\end{matrix};q\right) - \frac{s^2}{(1-a_1s)(1-a_2s)} \psi\left(\begin{matrix} x \\s,t\end{matrix};q\right), \end{align*} $$
$$ \begin{align*} \phi\left(\begin{matrix} x \\s,t\end{matrix};q\right)= \frac{1-ts}{(1-a_1s)(1-a_2s)} \phi\left(\begin{matrix} x \\qs,t\end{matrix};q\right) - \frac{s^2}{(1-a_1s)(1-a_2s)} \psi\left(\begin{matrix} x \\s,t\end{matrix};q\right), \end{align*} $$where  $a_{1,2}=x\pm \sqrt {x^2-r^{-1}}$ satisfy the relation
$a_{1,2}=x\pm \sqrt {x^2-r^{-1}}$ satisfy the relation ![]() $1-2xs+r^{-1}s^2=(1-a_1s)(1-a_2s)$, see equation (4.16). By induction over n, this formula together with equation (5.20) gives
$1-2xs+r^{-1}s^2=(1-a_1s)(1-a_2s)$, see equation (4.16). By induction over n, this formula together with equation (5.20) gives
 $$ \begin{align*} \phi\left(\begin{matrix} x \\s,t\end{matrix};q\right)&= \frac{(ts;q)_n}{(a_1s;q)_n(a_2s;q)_n} \phi\left(\begin{matrix} x \\q^ns,t\end{matrix};q\right)\\ &\quad - s^2 \sum_{k=0}^{n-1}\frac{q^{2k}(x_1s;q)_k(x_2s;q)_k}{(a_1s;q)_{k+1}(a_2s;q)_{k+1}} \psi\left(\begin{matrix} x \\s,t\end{matrix};q\right). \end{align*} $$
$$ \begin{align*} \phi\left(\begin{matrix} x \\s,t\end{matrix};q\right)&= \frac{(ts;q)_n}{(a_1s;q)_n(a_2s;q)_n} \phi\left(\begin{matrix} x \\q^ns,t\end{matrix};q\right)\\ &\quad - s^2 \sum_{k=0}^{n-1}\frac{q^{2k}(x_1s;q)_k(x_2s;q)_k}{(a_1s;q)_{k+1}(a_2s;q)_{k+1}} \psi\left(\begin{matrix} x \\s,t\end{matrix};q\right). \end{align*} $$Now we argue analytically for ![]() $q\in {\mathbb C}$ with
$q\in {\mathbb C}$ with ![]() $\lvert q\rvert <1$. In the limit
$\lvert q\rvert <1$. In the limit ![]() $n\to \infty $, the first term in this expression vanishes by equation (5.22), and hence we get the desired formula (5.23).
$n\to \infty $, the first term in this expression vanishes by equation (5.22), and hence we get the desired formula (5.23).
5.6 The quantum Serre combination of the polynomials  $\rho _{m,n}$
$\rho _{m,n}$
To simplify notation, set ![]() $N=1-a_{ij}$ and
$N=1-a_{ij}$ and ![]() $q=q_i$. By equation (5.17) and Lemma 5.7, we need to determine the following polynomial:
$q=q_i$. By equation (5.17) and Lemma 5.7, we need to determine the following polynomial:
 $$ \begin{align} \sum_{m=0}^N(-1)^m\begin{bmatrix}N\\m\end{bmatrix}_{q}\rho_{N-m,m}(x) &=(-1)^N \sum_{m=0}^N(-1)^m\begin{bmatrix}N\\m\end{bmatrix}_{q}\rho_{m,N-m}(x)\\ &=(-1)^N \frac{q^{2(N-1)}}{\lambda_{ij}}\left(b_i/2\right)^{N-2}P_N(x/b_i;q), \nonumber \end{align} $$
$$ \begin{align} \sum_{m=0}^N(-1)^m\begin{bmatrix}N\\m\end{bmatrix}_{q}\rho_{N-m,m}(x) &=(-1)^N \sum_{m=0}^N(-1)^m\begin{bmatrix}N\\m\end{bmatrix}_{q}\rho_{m,N-m}(x)\\ &=(-1)^N \frac{q^{2(N-1)}}{\lambda_{ij}}\left(b_i/2\right)^{N-2}P_N(x/b_i;q), \nonumber \end{align} $$where
 $$ \begin{align} P_N(x;q)=\sum_{m=0}^N (-1)^m\begin{bmatrix}N\\m\end{bmatrix}_q q^{(1-N)m} U_{m,N-m}\left(x;q^2,q^{2(1-N)}\right). \end{align} $$
$$ \begin{align} P_N(x;q)=\sum_{m=0}^N (-1)^m\begin{bmatrix}N\\m\end{bmatrix}_q q^{(1-N)m} U_{m,N-m}\left(x;q^2,q^{2(1-N)}\right). \end{align} $$Up to an overall factor, the polynomial ![]() $P_N(x;q)$ is a deformed Chebyshev polynomial of the second kind, as defined in Section 4.5.
$P_N(x;q)$ is a deformed Chebyshev polynomial of the second kind, as defined in Section 4.5.
Lemma 5.9. For any ![]() $N\in {\mathbb N}$, we have
$N\in {\mathbb N}$, we have
 $$ \begin{align} P_N(x;q)=(-1)^{N-1} q^{(1-N)N}\left(q^2;q^2\right)_{N-1} C_{N-2}\left(x;q^2, q^{2(1-N)}\right). \end{align} $$
$$ \begin{align} P_N(x;q)=(-1)^{N-1} q^{(1-N)N}\left(q^2;q^2\right)_{N-1} C_{N-2}\left(x;q^2, q^{2(1-N)}\right). \end{align} $$Proof. By Proposition 4.8, Lemma 5.8 and equation (5.21) we have
 $$ \begin{align} P_N(x;q)&=\sum_{m=0}^N(-1)^{m-1}\begin{bmatrix}N\\m\end{bmatrix}_q q^{(1-N)m}\left(q^2;q^2\right)_m \cdot\nonumber\\ & \quad \cdot\sum_{k=2}^m \frac{C_{k-2}\left(x;q^2, q^{2(1-N)}\right)}{1-q^{2k}} \frac{H_{N-k}\left(x;q^2\right)}{\left(q^2,q^2\right)_{m-k}}\nonumber\\ &=\sum_{k=2}^N \frac{\omega_{N,k}(q)}{1-q^{2k}} C_{k-2}\left(x;q^2, q^{2(1-N)}\right) H_{N-k}\left(x;q^2\right), \end{align} $$
$$ \begin{align} P_N(x;q)&=\sum_{m=0}^N(-1)^{m-1}\begin{bmatrix}N\\m\end{bmatrix}_q q^{(1-N)m}\left(q^2;q^2\right)_m \cdot\nonumber\\ & \quad \cdot\sum_{k=2}^m \frac{C_{k-2}\left(x;q^2, q^{2(1-N)}\right)}{1-q^{2k}} \frac{H_{N-k}\left(x;q^2\right)}{\left(q^2,q^2\right)_{m-k}}\nonumber\\ &=\sum_{k=2}^N \frac{\omega_{N,k}(q)}{1-q^{2k}} C_{k-2}\left(x;q^2, q^{2(1-N)}\right) H_{N-k}\left(x;q^2\right), \end{align} $$where
 $$ \begin{align*} \omega_{N,k}(q)=\sum_{m=k}^N (-1)^{m-1}\begin{bmatrix}N\\m\end{bmatrix}_q \frac{\left(q^2;q^2\right)_m}{\left(q^2;q^2\right)_{m-k}}q^{(1-N)m}. \end{align*} $$
$$ \begin{align*} \omega_{N,k}(q)=\sum_{m=k}^N (-1)^{m-1}\begin{bmatrix}N\\m\end{bmatrix}_q \frac{\left(q^2;q^2\right)_m}{\left(q^2;q^2\right)_{m-k}}q^{(1-N)m}. \end{align*} $$Using the relation  $\left (q^2;q^2\right )_m=(-1)^m q^{m(m+1)/2}\left (q-q^{-1}\right )^m [m]^!_q$ and setting
$\left (q^2;q^2\right )_m=(-1)^m q^{m(m+1)/2}\left (q-q^{-1}\right )^m [m]^!_q$ and setting ![]() $\ell =m-k$, we obtain
$\ell =m-k$, we obtain
 $$ \begin{align*} \omega_{N,k}(q)=- q^{k(k+1)/2}q^{(1-N)k}\left(q-q^{-1}\right)^k \frac{[N]^!_q}{[N-k]^!_q} \sum_{\ell=0}^{N-k}(-1)^\ell \begin{bmatrix}N-k\\ \ell\end{bmatrix}_q q^{\ell(k-N+1)}. \end{align*} $$
$$ \begin{align*} \omega_{N,k}(q)=- q^{k(k+1)/2}q^{(1-N)k}\left(q-q^{-1}\right)^k \frac{[N]^!_q}{[N-k]^!_q} \sum_{\ell=0}^{N-k}(-1)^\ell \begin{bmatrix}N-k\\ \ell\end{bmatrix}_q q^{\ell(k-N+1)}. \end{align*} $$By [Reference LusztigLus94, 1.3.4], we obtain
 $$ \begin{align*} \omega_{N,k}(q)=\begin{cases} 0 & \text{if}\ k\neq N,\\ (-1)^{N-1} \left(q^2;q^2\right)_N q^{(1-N)N}& \text{if}\ k=N. \end{cases} \end{align*} $$
$$ \begin{align*} \omega_{N,k}(q)=\begin{cases} 0 & \text{if}\ k\neq N,\\ (-1)^{N-1} \left(q^2;q^2\right)_N q^{(1-N)N}& \text{if}\ k=N. \end{cases} \end{align*} $$Inserting this into equation (5.27), we obtain the desired formula.
Inserting equation (5.26) into equation (5.24), we obtain
 $$ \begin{align} &\sum_{m=0}^N(-1)^m\begin{bmatrix}N\\m\end{bmatrix}_{q}\rho_{N-m,m}(x) \nonumber\\ &\quad =- \frac{q^{(N-2)(1-N)}}{\lambda_{ij}}\left(\frac{b_i}{2}\right)^{N-2} \left(q^2;q^2\right)_{N-1} C_{N-2}\left(x/b_i;q^2, q^{2(1-N)}\right). \end{align} $$
$$ \begin{align} &\sum_{m=0}^N(-1)^m\begin{bmatrix}N\\m\end{bmatrix}_{q}\rho_{N-m,m}(x) \nonumber\\ &\quad =- \frac{q^{(N-2)(1-N)}}{\lambda_{ij}}\left(\frac{b_i}{2}\right)^{N-2} \left(q^2;q^2\right)_{N-1} C_{N-2}\left(x/b_i;q^2, q^{2(1-N)}\right). \end{align} $$5.7 The quantum Serre relation for  $\tau (i)=i$ where
$\tau (i)=i$ where  $i\in I\setminus X$ and
$i\in I\setminus X$ and  $j\in X$
$j\in X$
We are now in a position to write down the deformed quantum Serre relation (1.4) in the case ![]() $i\in I\setminus X$,
$i\in I\setminus X$, ![]() $\tau (i)=i$ and
$\tau (i)=i$ and ![]() $j\in X$. Recall the antilinear algebra isomorphism
$j\in X$. Recall the antilinear algebra isomorphism ![]() $\Phi :{\mathcal B}_{\mathbf {c}}\rightarrow {\mathcal B}_{{\mathbf {c}}'}$ from Theorem 2.12. Using the parameters
$\Phi :{\mathcal B}_{\mathbf {c}}\rightarrow {\mathcal B}_{{\mathbf {c}}'}$ from Theorem 2.12. Using the parameters ![]() ${\mathbf {c}}$ and
${\mathbf {c}}$ and ![]() ${\mathbf {c}}'$, we obtain two star products
${\mathbf {c}}'$, we obtain two star products ![]() $\ast $ and
$\ast $ and ![]() $\ast '$ on
$\ast '$ on ![]() ${\mathcal A}$ such that
${\mathcal A}$ such that ![]() ${\mathcal B}_{\mathbf {c}}\cong ({\mathcal A},\ast )$ and
${\mathcal B}_{\mathbf {c}}\cong ({\mathcal A},\ast )$ and ![]() ${\mathcal B}_{{\mathbf {c}}'}\cong ({\mathcal A},\ast ')$, respectively. Under these identifications we may consider
${\mathcal B}_{{\mathbf {c}}'}\cong ({\mathcal A},\ast ')$, respectively. Under these identifications we may consider ![]() $\Phi $ as an antilinear algebra isomorphism
$\Phi $ as an antilinear algebra isomorphism
Also recall the elements  $b_i^2=4{\mathcal Z}_i/\left (q_i-q_i^{-1}\right )^2$ and write
$b_i^2=4{\mathcal Z}_i/\left (q_i-q_i^{-1}\right )^2$ and write  $\left (b_i^2\right )'=4{\mathcal Z}_i'/\left (q_i-q_i^{-1}\right )^2$. By equation (5.13) we have
$\left (b_i^2\right )'=4{\mathcal Z}_i'/\left (q_i-q_i^{-1}\right )^2$. By equation (5.13) we have
 $$ \begin{align} \Phi\left(b_i^2\right)=\overline{b_i^2}=\left(b_i'\right)^2 \end{align} $$
$$ \begin{align} \Phi\left(b_i^2\right)=\overline{b_i^2}=\left(b_i'\right)^2 \end{align} $$With these notational preliminaries, we are ready to prove our main result:
Theorem 5.10. Let ![]() $i\in I\setminus X$ with
$i\in I\setminus X$ with ![]() $\tau (i)=i$ and
$\tau (i)=i$ and ![]() $j\in X$. Then the relation
$j\in X$. Then the relation
 $$ \begin{align*} \sum_{n=0}^{1-a_{ij}}(-1)^n \begin{bmatrix} 1-a_{ij}\\ n \end{bmatrix}_{q_i} F_j \curvearrowright w_{1-a_{ij}-n,n}(F_i\stackrel{\ast}{,}F_i) + C + D =0 \end{align*} $$
$$ \begin{align*} \sum_{n=0}^{1-a_{ij}}(-1)^n \begin{bmatrix} 1-a_{ij}\\ n \end{bmatrix}_{q_i} F_j \curvearrowright w_{1-a_{ij}-n,n}(F_i\stackrel{\ast}{,}F_i) + C + D =0 \end{align*} $$holds in the algebra ![]() $({\mathcal A},\ast )$, where
$({\mathcal A},\ast )$, where
 $$ \begin{align}C&= -\frac{d_{ij}}{\lambda_{ij}} q_i^{-a_{ij}\left(a_{ij} +1\right)} \left(q_i^2; q_i^2\right)_{-a_{ij}} \left(\frac{b_i}{2}\right)^{-a_{ij}-1} C_{-a_{ij}-1} \left(\frac{F_i}{b_i}; q_i^2, q_i^{2 a_{ij}}\right)^\ast, \end{align} $$
$$ \begin{align}C&= -\frac{d_{ij}}{\lambda_{ij}} q_i^{-a_{ij}\left(a_{ij} +1\right)} \left(q_i^2; q_i^2\right)_{-a_{ij}} \left(\frac{b_i}{2}\right)^{-a_{ij}-1} C_{-a_{ij}-1} \left(\frac{F_i}{b_i}; q_i^2, q_i^{2 a_{ij}}\right)^\ast, \end{align} $$ $$ \begin{align}D&= \frac{\widetilde{d_{ij}}}{\lambda_{ij}}q_i^{a_{ij}\left(a_{ij} +1\right)} \left(q_i^{-2}; q_i^{-2}\right)_{-a_{ij}} \left(\frac{b_i}{2}\right)^{-a_{ij}-1} C_{-a_{ij}-1} \left(\frac{F_i}{b_i}; q_i^{-2}, q_i^{-2 a_{ij}}\right)^\ast. \end{align} $$
$$ \begin{align}D&= \frac{\widetilde{d_{ij}}}{\lambda_{ij}}q_i^{a_{ij}\left(a_{ij} +1\right)} \left(q_i^{-2}; q_i^{-2}\right)_{-a_{ij}} \left(\frac{b_i}{2}\right)^{-a_{ij}-1} C_{-a_{ij}-1} \left(\frac{F_i}{b_i}; q_i^{-2}, q_i^{-2 a_{ij}}\right)^\ast. \end{align} $$Proof. By equation (5.17) we have the relation
 $$ \begin{align} 0=\sum_{n=0}^{1-a_{ij}} (-1)^n \begin{bmatrix}1-a_{ij} \\ n \end{bmatrix}_{q_i}F_i^{1-a_{ij} - n} F_j F_i^n = A+C+D \end{align} $$
$$ \begin{align} 0=\sum_{n=0}^{1-a_{ij}} (-1)^n \begin{bmatrix}1-a_{ij} \\ n \end{bmatrix}_{q_i}F_i^{1-a_{ij} - n} F_j F_i^n = A+C+D \end{align} $$in ![]() ${\mathcal A}$, with
${\mathcal A}$, with
 $$ \begin{align} A&= \sum_{n=0}^{1-a_{ij}} (-1)^n \begin{bmatrix}1-a_{ij} \\ n \end{bmatrix}_{q_i} F_j \curvearrowright w_{1- a_{ij} -n, n}(F_i\stackrel{\ast}{,}F_i) \\C&= d_{ij} \sum_{n=0}^{1-a_{ij}} (-1)^n \begin{bmatrix}1-a_{ij} \\ n \end{bmatrix}_{q_i} \rho_{1-a_{ij} - n, n}(F_i)^*,\nonumber \\D&= \widetilde{d_{ij}} \sum_{n=0}^{1-a_{ij}} (-1)^n \begin{bmatrix}1-a_{ij} \\ n \end{bmatrix}_{q_i} \sigma_{1-a_{ij} - n, n}(F_i)^*.\nonumber \end{align} $$
$$ \begin{align} A&= \sum_{n=0}^{1-a_{ij}} (-1)^n \begin{bmatrix}1-a_{ij} \\ n \end{bmatrix}_{q_i} F_j \curvearrowright w_{1- a_{ij} -n, n}(F_i\stackrel{\ast}{,}F_i) \\C&= d_{ij} \sum_{n=0}^{1-a_{ij}} (-1)^n \begin{bmatrix}1-a_{ij} \\ n \end{bmatrix}_{q_i} \rho_{1-a_{ij} - n, n}(F_i)^*,\nonumber \\D&= \widetilde{d_{ij}} \sum_{n=0}^{1-a_{ij}} (-1)^n \begin{bmatrix}1-a_{ij} \\ n \end{bmatrix}_{q_i} \sigma_{1-a_{ij} - n, n}(F_i)^*.\nonumber \end{align} $$By equation (5.28) we obtain
 $$ \begin{align*} C&= -\frac{d_{ij}}{\lambda_{ij}} \left( \frac{b_i}{2} \right)^{-a_{ij}-1} q_i^{-a_{ij}\left(a_{ij} +1\right)} \left(q_i^2; q_i^2\right)_{-a_{ij}} C_{-a_{ij}-1} \left(\frac{F_i}{b_i}; q_i^2, q_i^{2 a_{ij}}\right)^\ast, \end{align*} $$
$$ \begin{align*} C&= -\frac{d_{ij}}{\lambda_{ij}} \left( \frac{b_i}{2} \right)^{-a_{ij}-1} q_i^{-a_{ij}\left(a_{ij} +1\right)} \left(q_i^2; q_i^2\right)_{-a_{ij}} C_{-a_{ij}-1} \left(\frac{F_i}{b_i}; q_i^2, q_i^{2 a_{ij}}\right)^\ast, \end{align*} $$which proves equation (5.30). For the parameters ![]() ${\mathbf {c}}'\in {\mathcal C}$ defined by equation (2.24), we write equation (5.32) as
${\mathbf {c}}'\in {\mathcal C}$ defined by equation (2.24), we write equation (5.32) as
Equation (5.29) and Corollary 4.6 imply that ![]() $\Phi (A)=A'$. Hence we obtain
$\Phi (A)=A'$. Hence we obtain
Relation (5.11) implies that
 $$ \begin{gather*} C= K_j p_C(F_i)^\ast, \qquad C'= K_j p_C'(F_i)^\ast, \\ D= K_j^{-1} p_D(F_i)^\ast, \qquad D'= K_j^{-1} p_D'(F_i)^\ast, \end{gather*} $$
$$ \begin{gather*} C= K_j p_C(F_i)^\ast, \qquad C'= K_j p_C'(F_i)^\ast, \\ D= K_j^{-1} p_D(F_i)^\ast, \qquad D'= K_j^{-1} p_D'(F_i)^\ast, \end{gather*} $$for some polynomials ![]() $p_C(x), p_D(x), p_C'(x), p_D'(x)\in {\mathcal M}_X^+[x]$. As
$p_C(x), p_D(x), p_C'(x), p_D'(x)\in {\mathcal M}_X^+[x]$. As 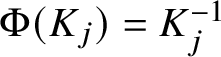 $\Phi (K_j)=K_j^{-1}$, equation (5.34) hence implies that
$\Phi (K_j)=K_j^{-1}$, equation (5.34) hence implies that ![]() $\Phi (C)=D'$ and
$\Phi (C)=D'$ and ![]() $\Phi (D)=C'$. This gives us
$\Phi (D)=C'$. This gives us
 $$ \begin{align*} D&=\Phi^{-1}(C')\\ &=\frac{\widetilde{d_{ij}}}{\lambda_{ij}}\left( \frac{b_i}{2} \right)^{-a_{ij}-1} q_i^{a_{ij}\left(a_{ij} +1\right)} \left(q_i^{-2}; q_i^{-2}\right)_{-a_{ij}} C_{-a_{ij}-1} \left(\frac{F_i}{b_i}; q_i^{-2}, q_i^{-2 a_{ij}}\right)^\ast, \end{align*} $$
$$ \begin{align*} D&=\Phi^{-1}(C')\\ &=\frac{\widetilde{d_{ij}}}{\lambda_{ij}}\left( \frac{b_i}{2} \right)^{-a_{ij}-1} q_i^{a_{ij}\left(a_{ij} +1\right)} \left(q_i^{-2}; q_i^{-2}\right)_{-a_{ij}} C_{-a_{ij}-1} \left(\frac{F_i}{b_i}; q_i^{-2}, q_i^{-2 a_{ij}}\right)^\ast, \end{align*} $$which proves equation (5.31).
For ![]() $n\in {\mathbb N}$, set
$n\in {\mathbb N}$, set
 $$ \begin{align*} u_n\left(x;q_i^2,q_i^{2a_{ij}}\right)=\left(\frac{b_i}{2}\right)^n C_n\left(\frac{x}{b_i};q_i^2,q_i^{2a_{ij}}\right)\in {\mathcal M}_X^+[x]. \end{align*} $$
$$ \begin{align*} u_n\left(x;q_i^2,q_i^{2a_{ij}}\right)=\left(\frac{b_i}{2}\right)^n C_n\left(\frac{x}{b_i};q_i^2,q_i^{2a_{ij}}\right)\in {\mathcal M}_X^+[x]. \end{align*} $$The polynomials  $u_n\left (x;q_i^2,q_i^{2a_{ij}}\right )$ satisfy the initial conditions and recursion given in C) in Section (1.4). With this notation we get
$u_n\left (x;q_i^2,q_i^{2a_{ij}}\right )$ satisfy the initial conditions and recursion given in C) in Section (1.4). With this notation we get
 $$ \begin{align*} C&= -\frac{d_{ij}}{\lambda_{ij}} q_i^{-a_{ij}\left(a_{ij} +1\right)} \left(q_i^2; q_i^2\right)_{-a_{ij}} u_{-a_{ij}-1} \left(F_i; q_i^2, q_i^{2 a_{ij}}\right)^\ast,\\ D&= \frac{\widetilde{d_{ij}}}{\lambda_{ij}}q_i^{a_{ij}\left(a_{ij} +1\right)} \left(q_i^{-2}; q_i^{-2}\right)_{-a_{ij}} u_{-a_{ij}-1} \left(F_i; q_i^{-2}, q_i^{-2 a_{ij}}\right)^\ast. \end{align*} $$
$$ \begin{align*} C&= -\frac{d_{ij}}{\lambda_{ij}} q_i^{-a_{ij}\left(a_{ij} +1\right)} \left(q_i^2; q_i^2\right)_{-a_{ij}} u_{-a_{ij}-1} \left(F_i; q_i^2, q_i^{2 a_{ij}}\right)^\ast,\\ D&= \frac{\widetilde{d_{ij}}}{\lambda_{ij}}q_i^{a_{ij}\left(a_{ij} +1\right)} \left(q_i^{-2}; q_i^{-2}\right)_{-a_{ij}} u_{-a_{ij}-1} \left(F_i; q_i^{-2}, q_i^{-2 a_{ij}}\right)^\ast. \end{align*} $$Inserting these expressions for C and D and equation (5.11) into the formula in Theorem 5.10, we obtain case (II) of Theorem 1.2 under the isomorphism ![]() $\psi :{\mathcal B}_{\mathbf {c}}\rightarrow ({\mathcal A},\ast )$.
$\psi :{\mathcal B}_{\mathbf {c}}\rightarrow ({\mathcal A},\ast )$.
Remark 5.11. We can use the formula from Proposition 4.4 to rewrite the term A given by equation (5.33) as
 $$ \begin{align*} A = \sum_{n=0}^{1-a_{ij}}(-1)^n \begin{bmatrix} 1-a_{ij}\\ n \end{bmatrix}_{q_i} w_{1-a_{ij}-n}(F_i)^\ast \ast F_j \ast v_{n}(F_i)^\ast. \end{align*} $$
$$ \begin{align*} A = \sum_{n=0}^{1-a_{ij}}(-1)^n \begin{bmatrix} 1-a_{ij}\\ n \end{bmatrix}_{q_i} w_{1-a_{ij}-n}(F_i)^\ast \ast F_j \ast v_{n}(F_i)^\ast. \end{align*} $$However, following Remark 5.1, this formula needs to be interpreted such that any coefficients  $b_i^k\in {\mathcal M}_X^+$ coming from
$b_i^k\in {\mathcal M}_X^+$ coming from ![]() $w_{1-a_{ij}-n}(F_i)^\ast $ are moved to the right hand side of the factor
$w_{1-a_{ij}-n}(F_i)^\ast $ are moved to the right hand side of the factor ![]() $F_j$.
$F_j$.
Example 5.12. The formulas in Theorem 5.10 allow us to write down explicit expressions for the deformed quantum Serre relations in the case ![]() $\tau (i)=i\in I\setminus X$ and
$\tau (i)=i\in I\setminus X$ and ![]() $j\in X$. We obtain
$j\in X$. We obtain
 $$\begin{align*}\sum_{n=0}^{1-a_{ij}} (-1)^n \begin{bmatrix}1-a_{ij} \\ n \end{bmatrix}_{q_i} F_j \curvearrowright w_{1- a_{ij} -n, n}(F_i\stackrel{\ast}{,}F_i) =\begin{cases} 0 & \text{if}\ a_{ij}=0,\\ -\displaystyle\frac{q_i d_{ij} + q_i^{-1}\widetilde{d_{ij}}}{\left(q_i-q_i^{-1}\right)\left(q_j-q_j^{-1}\right)}& \text{if}\ a_{ij}=-1,\\ [2]_{q_i}\displaystyle\frac{q_id_{ij} - q_i^{-1}\widetilde{d_{ij}}}{q_j-q_j^{-1}} F_i & \mbox{if}\ a_{ij}=-2. \end{cases} \end{align*}$$
$$\begin{align*}\sum_{n=0}^{1-a_{ij}} (-1)^n \begin{bmatrix}1-a_{ij} \\ n \end{bmatrix}_{q_i} F_j \curvearrowright w_{1- a_{ij} -n, n}(F_i\stackrel{\ast}{,}F_i) =\begin{cases} 0 & \text{if}\ a_{ij}=0,\\ -\displaystyle\frac{q_i d_{ij} + q_i^{-1}\widetilde{d_{ij}}}{\left(q_i-q_i^{-1}\right)\left(q_j-q_j^{-1}\right)}& \text{if}\ a_{ij}=-1,\\ [2]_{q_i}\displaystyle\frac{q_id_{ij} - q_i^{-1}\widetilde{d_{ij}}}{q_j-q_j^{-1}} F_i & \mbox{if}\ a_{ij}=-2. \end{cases} \end{align*}$$Under the identification ![]() ${\mathcal B}_{\mathbf {c}}\cong ({\mathcal A},\ast )$, these relations coincide with the relations given in [Reference KolbKol14, Theorem 7.8] in the reformulation given in [Reference Balagović and KolbBK15, Theorem 3.9]. Note that
${\mathcal B}_{\mathbf {c}}\cong ({\mathcal A},\ast )$, these relations coincide with the relations given in [Reference KolbKol14, Theorem 7.8] in the reformulation given in [Reference Balagović and KolbBK15, Theorem 3.9]. Note that ![]() ${\mathcal Z}_i$ in the present paper coincides with
${\mathcal Z}_i$ in the present paper coincides with ![]() $-q_ic_i{\mathcal Z}_i$ in [Reference Balagović and KolbBK15]. For
$-q_ic_i{\mathcal Z}_i$ in [Reference Balagović and KolbBK15]. For ![]() $a_{ij}=-3$, we obtain the new relation
$a_{ij}=-3$, we obtain the new relation
 $$ \begin{align*} & \sum_{n=0}^{1-a_{ij}} (-1)^n \begin{bmatrix}1-a_{ij} \\ n \end{bmatrix}_{q_i} F_j \curvearrowright w_{1- a_{ij} -n, n}(F_i\stackrel{\ast}{,}F_i)\\ &\quad = - [2]_{q_i} \frac{q_i^3-q_i^{-3}}{q_j-q_j^{-1}} \left(d_{ij}+\widetilde{d_{ij}}\right) F_i^{\ast 2} - \frac{q_i^3-q_i^{-3}}{\left(q_i-q_i^{-1}\right)^2\left(q_j-q_j^{-1}\right)} \left(q_i^3d_{ij}+q_i^{-3}\widetilde{d_{ij}}\right) {\mathcal Z}_i. \end{align*} $$
$$ \begin{align*} & \sum_{n=0}^{1-a_{ij}} (-1)^n \begin{bmatrix}1-a_{ij} \\ n \end{bmatrix}_{q_i} F_j \curvearrowright w_{1- a_{ij} -n, n}(F_i\stackrel{\ast}{,}F_i)\\ &\quad = - [2]_{q_i} \frac{q_i^3-q_i^{-3}}{q_j-q_j^{-1}} \left(d_{ij}+\widetilde{d_{ij}}\right) F_i^{\ast 2} - \frac{q_i^3-q_i^{-3}}{\left(q_i-q_i^{-1}\right)^2\left(q_j-q_j^{-1}\right)} \left(q_i^3d_{ij}+q_i^{-3}\widetilde{d_{ij}}\right) {\mathcal Z}_i. \end{align*} $$In the special case where ![]() $a_{ji}=-1$ with
$a_{ji}=-1$ with ![]() $q_i=q$ and
$q_i=q$ and ![]() $q_j=q^3$, this formula reproduces the formula given in [Reference Regelskis and VlaarRV20, (4.19)].
$q_j=q^3$, this formula reproduces the formula given in [Reference Regelskis and VlaarRV20, (4.19)].
5.8 The quantum Serre relation for  $\tau (i)=j$ where
$\tau (i)=j$ where  $i,j\in I\setminus X$
$i,j\in I\setminus X$
All through this subsection we assume that ![]() $i,j\in I\setminus X$ with
$i,j\in I\setminus X$ with ![]() $\tau (i)=j\neq i$. In this case, equation (3.1) implies that
$\tau (i)=j\neq i$. In this case, equation (3.1) implies that
 $$ \begin{align} F_i\ast u = F_i u - c_i\frac{q^{\left(\alpha_i,w_X\left(\alpha_j\right)\right)}}{q_i-q_i^{-1}} K_{w_X\left(\alpha_j\right)-\alpha_i} \partial_{j,X}^L(u) \end{align} $$
$$ \begin{align} F_i\ast u = F_i u - c_i\frac{q^{\left(\alpha_i,w_X\left(\alpha_j\right)\right)}}{q_i-q_i^{-1}} K_{w_X\left(\alpha_j\right)-\alpha_i} \partial_{j,X}^L(u) \end{align} $$for all ![]() $u\in {\mathcal R}_X$. Hence for any
$u\in {\mathcal R}_X$. Hence for any ![]() $n\in {\mathbb N}$, we have
$n\in {\mathbb N}$, we have ![]() $F_i^{\ast n}=F_i^n$ and
$F_i^{\ast n}=F_i^n$ and
 $$ \begin{align} F_j\ast F_i^n &\stackrel{\phantom{\text{(3.6)}}}{=}F_j F_i^n - c_j\frac{q^{\left(\alpha_j,w_X\left(\alpha_i\right)\right)}}{q_i-q_i^{-1}} K_{w_X\left(\alpha_i\right)-\alpha_j} \partial_{i,X}^L\left(F_i^n\right)\nonumber \\ &\stackrel{\text{(3.6)}}{=} F_j F_i^n - c_j\frac{q^{\left(\alpha_i,\alpha_j\right)}}{q_i-q_i^{-1}} (n)_{q_i^2}K_i K_j^{-1} Z_i F_i^{n-1}\nonumber\\ &\stackrel{\phantom{\text{(3.6)}}}{=}F_j F_i^n -c_j\frac{q_i^{na_{ij}-2n+2}}{q_i-q_i^{-1}} (n)_{q_i^2} F_i^{n-1} K_i K_j^{-1}Z_i. \end{align} $$
$$ \begin{align} F_j\ast F_i^n &\stackrel{\phantom{\text{(3.6)}}}{=}F_j F_i^n - c_j\frac{q^{\left(\alpha_j,w_X\left(\alpha_i\right)\right)}}{q_i-q_i^{-1}} K_{w_X\left(\alpha_i\right)-\alpha_j} \partial_{i,X}^L\left(F_i^n\right)\nonumber \\ &\stackrel{\text{(3.6)}}{=} F_j F_i^n - c_j\frac{q^{\left(\alpha_i,\alpha_j\right)}}{q_i-q_i^{-1}} (n)_{q_i^2}K_i K_j^{-1} Z_i F_i^{n-1}\nonumber\\ &\stackrel{\phantom{\text{(3.6)}}}{=}F_j F_i^n -c_j\frac{q_i^{na_{ij}-2n+2}}{q_i-q_i^{-1}} (n)_{q_i^2} F_i^{n-1} K_i K_j^{-1}Z_i. \end{align} $$Moreover, one shows by induction on m, using equations (5.35), (3.2) and (3.4), that
 $$ \begin{align} F_i^{\ast m} \ast F_j F_i^n = F_i^m F_j F_i^n - c_i \frac{q_i^{2n-(n-1)a_{ij}}}{q_i-q_i^{-1}} (m)_{q_i^2}F_i^{m+n-1} K_j K_i^{-1} Z_j. \end{align} $$
$$ \begin{align} F_i^{\ast m} \ast F_j F_i^n = F_i^m F_j F_i^n - c_i \frac{q_i^{2n-(n-1)a_{ij}}}{q_i-q_i^{-1}} (m)_{q_i^2}F_i^{m+n-1} K_j K_i^{-1} Z_j. \end{align} $$Inserting equation (5.36) into equation (5.37), we obtain
 $$ \begin{align} F_i^m F_j F_i^n &= F_i^{\ast m}\ast F_j \ast F_i^{\ast n} + c_i \frac{q_i^{2n-(n-1)a_{ij}}}{q_i-q_i^{-1}} (m)_{q_i^2} F_i^{m+n-1} K_j K_i^{-1} Z_j \nonumber\\ & \quad + c_j\frac{q_i^{na_{ij}-2n+2}}{q_i-q_i^{-1}} (n)_{q_i^2} F_i^{m+n-1} K_i K_j^{-1}Z_i. \end{align} $$
$$ \begin{align} F_i^m F_j F_i^n &= F_i^{\ast m}\ast F_j \ast F_i^{\ast n} + c_i \frac{q_i^{2n-(n-1)a_{ij}}}{q_i-q_i^{-1}} (m)_{q_i^2} F_i^{m+n-1} K_j K_i^{-1} Z_j \nonumber\\ & \quad + c_j\frac{q_i^{na_{ij}-2n+2}}{q_i-q_i^{-1}} (n)_{q_i^2} F_i^{m+n-1} K_i K_j^{-1}Z_i. \end{align} $$Using the relations
 $$ \begin{align*} \sum_{n=0}^\ell (-1)^n \begin{bmatrix}\ell \\ n \end{bmatrix}_{q} q^{n(\ell + 1)} =\left(q^2;q^2\right)_\ell, \qquad \sum_{n=0}^\ell (-1)^n \begin{bmatrix}\ell \\ n \end{bmatrix}_{q} q^{n(\ell-1)}=0, \end{align*} $$
$$ \begin{align*} \sum_{n=0}^\ell (-1)^n \begin{bmatrix}\ell \\ n \end{bmatrix}_{q} q^{n(\ell + 1)} =\left(q^2;q^2\right)_\ell, \qquad \sum_{n=0}^\ell (-1)^n \begin{bmatrix}\ell \\ n \end{bmatrix}_{q} q^{n(\ell-1)}=0, \end{align*} $$which hold for all ![]() $\ell \in {\mathbb N}$, one shows that
$\ell \in {\mathbb N}$, one shows that
 $$ \begin{align} \sum_{n=0}^{1-a_{ij}} (-1)^n \begin{bmatrix}1-a_{ij} \\ n \end{bmatrix}_{q_i} q_i^{n\left(2-a_{ij}\right)}\left(1-a_{ij}-n\right)_{q_i^2} &=-\frac{q_i^{-1}\left(q_i^{2};q_i^{2}\right)_{1-a_{ij}}}{q_i-q_i^{-1}}, \end{align} $$
$$ \begin{align} \sum_{n=0}^{1-a_{ij}} (-1)^n \begin{bmatrix}1-a_{ij} \\ n \end{bmatrix}_{q_i} q_i^{n\left(2-a_{ij}\right)}\left(1-a_{ij}-n\right)_{q_i^2} &=-\frac{q_i^{-1}\left(q_i^{2};q_i^{2}\right)_{1-a_{ij}}}{q_i-q_i^{-1}}, \end{align} $$ $$ \begin{align} \sum_{n=0}^{1-a_{ij}} (-1)^n \begin{bmatrix}1-a_{ij} \\ n \end{bmatrix}_{q_i} q_i^{n\left(a_{ij}-2\right)}(n)_{q_i^2} &=-\frac{q_i^{-1}\left(q_i^{-2};q_i^{-2}\right)_{1-a_{ij}}}{q_i-q_i^{-1}}. \end{align} $$
$$ \begin{align} \sum_{n=0}^{1-a_{ij}} (-1)^n \begin{bmatrix}1-a_{ij} \\ n \end{bmatrix}_{q_i} q_i^{n\left(a_{ij}-2\right)}(n)_{q_i^2} &=-\frac{q_i^{-1}\left(q_i^{-2};q_i^{-2}\right)_{1-a_{ij}}}{q_i-q_i^{-1}}. \end{align} $$Using equations (5.38), (5.39) and (5.40), we can now rewrite the quantum Serre relation ![]() $S_{ij}\left (F_i,F_j\right )=0$ in terms of the star product
$S_{ij}\left (F_i,F_j\right )=0$ in terms of the star product ![]() $\ast $ on
$\ast $ on ![]() ${\mathcal A}$. One obtains the following result:
${\mathcal A}$. One obtains the following result:
Theorem 5.13. Let ![]() $i,j\in I\setminus X$ with
$i,j\in I\setminus X$ with ![]() $\tau (i)=j\neq i$ and set
$\tau (i)=j\neq i$ and set ![]() $N=1-a_{ij}$. Then the relation
$N=1-a_{ij}$. Then the relation
 $$ \begin{align*} & \sum_{n=0}^{N}(-1)^n\begin{bmatrix}N \\ n \end{bmatrix}_{q_i} F_i^{\ast (N-n)}\ast F_j \ast F_i^{\ast n}\\ &\quad =\frac{c_i q_i^{-N} \left(q_i^{2};q_i^{2}\right)_{N}}{\left(q_i-q_i^{-1}\right)^2} F_i^{\ast(N-1)} K_j K_i^{-1}Z_j + \frac{c_jq_i \left(q_i^{-2};q_i^{-2}\right)_{N}}{\left(q_i-q_i^{-1}\right)^2}F_i^{\ast(N-1)} K_i K_j^{-1} Z_i \end{align*} $$
$$ \begin{align*} & \sum_{n=0}^{N}(-1)^n\begin{bmatrix}N \\ n \end{bmatrix}_{q_i} F_i^{\ast (N-n)}\ast F_j \ast F_i^{\ast n}\\ &\quad =\frac{c_i q_i^{-N} \left(q_i^{2};q_i^{2}\right)_{N}}{\left(q_i-q_i^{-1}\right)^2} F_i^{\ast(N-1)} K_j K_i^{-1}Z_j + \frac{c_jq_i \left(q_i^{-2};q_i^{-2}\right)_{N}}{\left(q_i-q_i^{-1}\right)^2}F_i^{\ast(N-1)} K_i K_j^{-1} Z_i \end{align*} $$holds in the algebra ![]() $({\mathcal A},\ast )$.
$({\mathcal A},\ast )$.
With the relation ![]() ${\mathcal Z}_i=c_iq_iZ_j$, this theorem turns into case (III) of Theorem 1.2 under the isomorphism
${\mathcal Z}_i=c_iq_iZ_j$, this theorem turns into case (III) of Theorem 1.2 under the isomorphism ![]() $\psi :{\mathcal B}_{\mathbf {c}}\rightarrow ({\mathcal A},\ast )$.
$\psi :{\mathcal B}_{\mathbf {c}}\rightarrow ({\mathcal A},\ast )$.
Acknowledgments
We are grateful to the referee for valuable comments and corrections which helped us to improve the exposition.
Conflicts of Interest
None.
Financial Support
The research of the second named author was supported by NSF grants DMS-1901830 and DMS-2131243 and by Bulgarian Science Fund grant DN02/05.