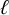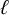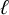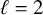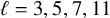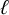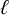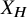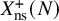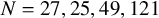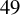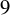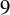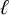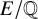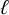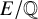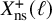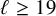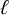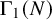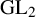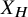1 Introduction
To an elliptic curve E over a number field K, one can associate representations

of the absolute Galois group
. If E does not have complex multiplication (CM), then the images of these representations are open [Reference SerreSer72], and thus of finite index. It is conjectured ([Reference ZywinaZyw15a, Conjecture 1.12], [Reference SutherlandSut16, Conjecture 1.1]) that
![]() $\rho _{E, \ell }$
is surjective for non-CM
$\rho _{E, \ell }$
is surjective for non-CM
![]() $E/\mathbb {Q}$
for all
$E/\mathbb {Q}$
for all
![]() $\ell> 37$
and that there is an absolute bound on the index of
$\ell> 37$
and that there is an absolute bound on the index of
![]() $\rho _E(G_{\mathbb {Q}})$
.
$\rho _E(G_{\mathbb {Q}})$
.
Concordant with his watershed papers [Reference MazurMaz77b, Reference MazurMaz78] classifying rational points on the modular curves
![]() $X_1(N)$
and
$X_1(N)$
and
![]() $X_0(N)$
of prime level, Mazur proposed the following program (labeled ‘Program B’) in his article [Reference MazurMaz77a]:
$X_0(N)$
of prime level, Mazur proposed the following program (labeled ‘Program B’) in his article [Reference MazurMaz77a]:
‘Given a number field K and a subgroup H of
![]() $\operatorname {GL}_2({\widehat {\mathbb {Z}}}) \simeq \prod _p \operatorname {GL}_2 (\mathbb {Z}_p)$
, classify all elliptic curves
$\operatorname {GL}_2({\widehat {\mathbb {Z}}}) \simeq \prod _p \operatorname {GL}_2 (\mathbb {Z}_p)$
, classify all elliptic curves
![]() $E/K$
whose associated Galois representation on torsion points maps
$E/K$
whose associated Galois representation on torsion points maps
![]() $\operatorname {\mathrm {Gal}}({\overline {K}}/K)$
into
$\operatorname {\mathrm {Gal}}({\overline {K}}/K)$
into
![]() $H \leq \operatorname {GL}_2 ({\widehat {\mathbb {Z}}})$
.’
$H \leq \operatorname {GL}_2 ({\widehat {\mathbb {Z}}})$
.’
Mazur’s Program B has seen substantial progress over the past decade: for prime level, see [Reference Bilu and ParentBP11, Reference Bilu, Parent and RebolledoBPR13, Reference ZywinaZyw15a, Reference SutherlandSut16, Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+19, Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+21, Reference Le Fourn and LemosLFL21]; for prime power level, see [Reference Rouse and Zureick-BrownRZB15, Reference Sutherland and ZywinaSZ17]; for multi-prime level, see [Reference ZywinaZyw15b, Reference Daniels and González-JiménezDGJ, Reference González-Jiménez and Lozano-RobledoGJLR16, Reference Brau and JonesBJ16, Reference MorrowMor19, Reference Jones and McMurdyJM22, Reference Daniels and Lozano-RobledoDLR, Reference Daniels and MorrowDM, Reference Daniels, Lozano-Robledo and MorrowDLRM21, Rak21, Reference Barbulescu and ShindeBS22]; and for CM curves, see [Reference Bourdon and ClarkBC20, Reference Lozano-RobledoLR, Reference Campagna and PengoCP, Reference LombardoLom17].
1.1 Main theorem
Our main theorem addresses almost all of the remaining groups of prime power level. For each open subgroup H of
![]() $\operatorname {GL}_2({\widehat {\mathbb {Z}}})$
, we use
$\operatorname {GL}_2({\widehat {\mathbb {Z}}})$
, we use
![]() $X_H$
to denote the modular curve whose noncuspidal K-rational points classify elliptic curves
$X_H$
to denote the modular curve whose noncuspidal K-rational points classify elliptic curves
![]() $E/K$
for which
$E/K$
for which
![]() $\rho _E(G_K)$
is contained in H (see Section 2.3 for a precise definition).
$\rho _E(G_K)$
is contained in H (see Section 2.3 for a precise definition).
Remark 1.1. We write
![]() $\rho _{E,\ell ^{\infty }}(G_K){\,=\,} H$
to indicate that H is conjugate to the inverse image of
$\rho _{E,\ell ^{\infty }}(G_K){\,=\,} H$
to indicate that H is conjugate to the inverse image of
![]() $\rho _{E,\ell ^{\infty }}(G_K)$
under the projection
$\rho _{E,\ell ^{\infty }}(G_K)$
under the projection
![]() $\operatorname {GL}_2({\widehat {\mathbb {Z}}})\to \operatorname {GL}_2(\mathbb {Z}_{\ell })$
. In general, we are only interested in the image of
$\operatorname {GL}_2({\widehat {\mathbb {Z}}})\to \operatorname {GL}_2(\mathbb {Z}_{\ell })$
. In general, we are only interested in the image of
![]() $\rho _E$
up to conjugacy (the exact image depends on a choice of basis).
$\rho _E$
up to conjugacy (the exact image depends on a choice of basis).
Definition 1.2. Let
![]() $\ell $
be a prime, let H be an open subgroup of
$\ell $
be a prime, let H be an open subgroup of
![]() $\operatorname {GL}_2({\widehat {\mathbb {Z}}})$
of
$\operatorname {GL}_2({\widehat {\mathbb {Z}}})$
of
![]() $\ell $
-power level, and let K be a number field. We say that a point
$\ell $
-power level, and let K be a number field. We say that a point
![]() $P \in X_H(K)$
is exceptional if
$P \in X_H(K)$
is exceptional if
![]() $X_H(K)$
is finite and P corresponds to a non-CM elliptic curve
$X_H(K)$
is finite and P corresponds to a non-CM elliptic curve
![]() $E/K$
. We call an element of K exceptional if it is the j-invariant of an exceptional point. If there is a non-CM elliptic curve
$E/K$
. We call an element of K exceptional if it is the j-invariant of an exceptional point. If there is a non-CM elliptic curve
![]() $E/K$
such that
$E/K$
such that
![]() $j(E)$
is exceptional and
$j(E)$
is exceptional and
![]() $\rho _{E,\ell ^{\infty }}(G_K)=H$
(as opposed to a subgroup of H), then we refer to H as K-exceptional; we may omit K when
$\rho _{E,\ell ^{\infty }}(G_K)=H$
(as opposed to a subgroup of H), then we refer to H as K-exceptional; we may omit K when
![]() $K = \mathbb {Q}$
.
$K = \mathbb {Q}$
.
For
![]() $K=\mathbb {Q}$
, the known exceptional j-invariants of prime power level are listed in Table 1 along with the known exceptional points on
$K=\mathbb {Q}$
, the known exceptional j-invariants of prime power level are listed in Table 1 along with the known exceptional points on
![]() $X_H$
for exceptional subgroups H of prime power level that do not contain
$X_H$
for exceptional subgroups H of prime power level that do not contain
![]() $-I$
; the groups of prime level appear in both [Reference SutherlandSut16] and [Reference ZywinaZyw15a].
$-I$
; the groups of prime level appear in both [Reference SutherlandSut16] and [Reference ZywinaZyw15a].
Table 1 Known (and conjecturally all) exceptional groups and j-invariants of prime power level. When
![]() $-I \not \in H$
, we list models of elliptic curves
$-I \not \in H$
, we list models of elliptic curves
![]() $E/\mathbb {Q}$
for which
$E/\mathbb {Q}$
for which
![]() $\rho _{E,\ell ^{\infty }}(G_{\mathbb {Q}})=H$
. The Magma script checkimages.m in the software repository associated with this paper [Reference Rouse, Sutherland and Zureick-BrownRSZB21] verifies each line of this table. Generators for the arithmetically maximal groups can be found in Appendix B.
$\rho _{E,\ell ^{\infty }}(G_{\mathbb {Q}})=H$
. The Magma script checkimages.m in the software repository associated with this paper [Reference Rouse, Sutherland and Zureick-BrownRSZB21] verifies each line of this table. Generators for the arithmetically maximal groups can be found in Appendix B.

Remark 1.3. For the H and j listed in Table 1, if
![]() $-I \in H$
, then all but finitely many elliptic curves with
$-I \in H$
, then all but finitely many elliptic curves with
![]() $j(E) = j$
have
$j(E) = j$
have
![]() $\ell $
-adic image equal to H (rather than a proper subgroup). If
$\ell $
-adic image equal to H (rather than a proper subgroup). If
![]() $H' \subsetneq H$
is a proper subgroup such that
$H' \subsetneq H$
is a proper subgroup such that
![]() $H = \langle H',-I\rangle $
and
$H = \langle H',-I\rangle $
and
![]() $E/\mathbb {Q}$
is an elliptic curve with
$E/\mathbb {Q}$
is an elliptic curve with
![]() $\ell $
-adic image H and
$\ell $
-adic image H and
![]() $j(E) \ne 1728$
, then there are
$j(E) \ne 1728$
, then there are
![]() $[N_{\operatorname {GL}_{2}(\mathbb {Z}_{\ell })}(H) : N_{\operatorname {GL}_{2}(\mathbb {Z}_{\ell })}(H')]$
quadratic twists
$[N_{\operatorname {GL}_{2}(\mathbb {Z}_{\ell })}(H) : N_{\operatorname {GL}_{2}(\mathbb {Z}_{\ell })}(H')]$
quadratic twists
![]() $E'$
of E whose
$E'$
of E whose
![]() $\ell $
-adic image is
$\ell $
-adic image is
![]() $H'$
; see Section 10.
$H'$
; see Section 10.
Remark 1.4. If
![]() $P \in X_H(K)$
corresponds to an elliptic curve E, then
$P \in X_H(K)$
corresponds to an elliptic curve E, then
![]() $\rho _E(G_K)$
may be a proper subgroup of H. For example, any elliptic curve
$\rho _E(G_K)$
may be a proper subgroup of H. For example, any elliptic curve
![]() $E/\mathbb {Q}$
with j-invariant
$E/\mathbb {Q}$
with j-invariant
![]() $-11^2$
admits a rational 11-isogeny, which forces
$-11^2$
admits a rational 11-isogeny, which forces
![]() $\rho _{E,11^{\infty }}(G_{\mathbb {Q}})$
to lie in the Borel group
$\rho _{E,11^{\infty }}(G_{\mathbb {Q}})$
to lie in the Borel group
![]() $B(11)$
, but
$B(11)$
, but
![]() $\rho _{E,11^{\infty }}(G_{\mathbb {Q}})$
is generically the index-5 subgroup
$\rho _{E,11^{\infty }}(G_{\mathbb {Q}})$
is generically the index-5 subgroup
![]() $\langle \left [\begin {smallmatrix} 10 & 1 \\ 0 & 10 \end {smallmatrix}\right ], \left [\begin {smallmatrix} 3 & 0 \\ 0 & 2 \end {smallmatrix}\right ] \rangle $
with label 11.60.1.4. In this example,
$\langle \left [\begin {smallmatrix} 10 & 1 \\ 0 & 10 \end {smallmatrix}\right ], \left [\begin {smallmatrix} 3 & 0 \\ 0 & 2 \end {smallmatrix}\right ] \rangle $
with label 11.60.1.4. In this example,
![]() $-11^2$
is an exceptional j-invariant and 11.60.1.4 is an exceptional group, but
$-11^2$
is an exceptional j-invariant and 11.60.1.4 is an exceptional group, but
![]() $B(11)$
is not an exceptional group, because no non-CM elliptic curve over
$B(11)$
is not an exceptional group, because no non-CM elliptic curve over
![]() $\mathbb {Q}$
has
$\mathbb {Q}$
has
![]() $11$
-adic image
$11$
-adic image
![]() $B(11)$
. The group
$B(11)$
. The group
![]() $B(11)={\texttt {11.12.1.1}}$
appears in Table 11 along with 13 other groups H of prime power level for which a similar phenomenon occurs.
$B(11)={\texttt {11.12.1.1}}$
appears in Table 11 along with 13 other groups H of prime power level for which a similar phenomenon occurs.
Conjecture 1.5. Table 1 lists all rational exceptional j-invariants of prime power level.
Theorem 1.6. Let
![]() $\ell $
be a prime, let
$\ell $
be a prime, let
![]() $E/\mathbb {Q}$
be an elliptic curve without complex multiplication, and let
$E/\mathbb {Q}$
be an elliptic curve without complex multiplication, and let
![]() $H = \rho _{E,{\ell }^{\infty }}(G_{\mathbb {Q}})$
. Exactly one of the following is true:
$H = \rho _{E,{\ell }^{\infty }}(G_{\mathbb {Q}})$
. Exactly one of the following is true:
-
(i) the modular curve
 $X_H$
is isomorphic to
$X_H$
is isomorphic to
 $\mathbb {P}^1$
or an elliptic curve of rank one, in which case H is identified in [Reference Sutherland and ZywinaSZ17, Corollary 1.6] and
$\mathbb {P}^1$
or an elliptic curve of rank one, in which case H is identified in [Reference Sutherland and ZywinaSZ17, Corollary 1.6] and
 $\langle H,-I\rangle $
is listed in [Reference Sutherland and ZywinaSZ17, Tables 1–4];
$\langle H,-I\rangle $
is listed in [Reference Sutherland and ZywinaSZ17, Tables 1–4]; -
(ii) the modular curve
 $X_H$
has an exceptional rational point, and H is listed in Table 1;
$X_H$
has an exceptional rational point, and H is listed in Table 1; -
(iii)
 $H \leq N_{\operatorname {\mathrm {ns}}}(3^3), N_{\operatorname {\mathrm {ns}}}(5^2), N_{\operatorname {\mathrm {ns}}}(7^2), N_{\operatorname {\mathrm {ns}}}(11^2)$
or
$H \leq N_{\operatorname {\mathrm {ns}}}(3^3), N_{\operatorname {\mathrm {ns}}}(5^2), N_{\operatorname {\mathrm {ns}}}(7^2), N_{\operatorname {\mathrm {ns}}}(11^2)$
or
 $N_{\operatorname {\mathrm {ns}}}(\ell )$
for some
$N_{\operatorname {\mathrm {ns}}}(\ell )$
for some
 $\ell \ge 19$
;
$\ell \ge 19$
; -
(iv) H is a subgroup of one of the groups labeled
 $\mathrm {{\texttt {49.147.9.1}}}$
or
$\mathrm {{\texttt {49.147.9.1}}}$
or
 $\mathrm {{\texttt {49.196.9.1}}}$
.
$\mathrm {{\texttt {49.196.9.1}}}$
.
See Subsection 2.4 for a discussion of the group labels, and see Tables 2 and 3 for a summary of the groups H that appear in Theorem 1.6 for
![]() $\ell \leq 37$
.
$\ell \leq 37$
.
Table 2 Arithmetically maximal groups of
![]() $\ell $
-power level with
$\ell $
-power level with
![]() $\ell \leq 17$
for which
$\ell \leq 17$
for which
![]() $X_H(\mathbb {Q})$
is unknown; each has rank
$X_H(\mathbb {Q})$
is unknown; each has rank
![]() $=$
genus, rational CM points, no rational cusps and no known exceptional points.
$=$
genus, rational CM points, no rational cusps and no known exceptional points.

Table 3 Numerical summary of open
![]() $H\leq \operatorname {GL}_2({\widehat {\mathbb {Z}}})$
of prime power level that can conjecturally occur as
$H\leq \operatorname {GL}_2({\widehat {\mathbb {Z}}})$
of prime power level that can conjecturally occur as
![]() $\rho _{E,{\ell }^{\infty }}(G_{\mathbb {Q}})$
for
$\rho _{E,{\ell }^{\infty }}(G_{\mathbb {Q}})$
for
![]() $E/\mathbb {Q}$
without CM. The starred primes depend on the conjecture that
$E/\mathbb {Q}$
without CM. The starred primes depend on the conjecture that
![]() $N_{\operatorname {\mathrm {ns}}}(\ell )$
for
$N_{\operatorname {\mathrm {ns}}}(\ell )$
for
![]() $\ell> 17$
and the groups from Table 2 do not occur. See the file sample.txt in [Reference Rouse, Sutherland and Zureick-BrownRSZB21] for a list of elliptic curves over
$\ell> 17$
and the groups from Table 2 do not occur. See the file sample.txt in [Reference Rouse, Sutherland and Zureick-BrownRSZB21] for a list of elliptic curves over
![]() $\mathbb {Q}$
that realise each of the subgroups in this table.
$\mathbb {Q}$
that realise each of the subgroups in this table.

We conjecture that in cases (iii) and (iv), the curve
![]() $X_H$
has no exceptional rational points; see Section 9 for a discussion of evidence for this conjecture. For the six groups in Table 2, the genus of
$X_H$
has no exceptional rational points; see Section 9 for a discussion of evidence for this conjecture. For the six groups in Table 2, the genus of
![]() $X_H$
is 9, 12, 14, 69 or 511, and for each isogeny factor A of
$X_H$
is 9, 12, 14, 69 or 511, and for each isogeny factor A of
![]() $J_H$
, the analytic rank of A is equal to the dimension of A. We were not able to provably determine the rational points on these curves; see Section 9 for a more detailed discussion of these cases.
$J_H$
, the analytic rank of A is equal to the dimension of A. We were not able to provably determine the rational points on these curves; see Section 9 for a more detailed discussion of these cases.
Remark 1.7. The recent groundbreaking work of [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+19, Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+21] yields a complete classification of the possible
![]() $13$
-adic and
$13$
-adic and
![]() $17$
-adic images for elliptic curves over
$17$
-adic images for elliptic curves over
![]() $\mathbb {Q}$
; these are the only primes other than
$\mathbb {Q}$
; these are the only primes other than
![]() $\ell = 2$
for which this is currently known.
$\ell = 2$
for which this is currently known.
1.2 Outline of proof
The proof of Theorem 1.6 breaks down into the following steps:
-
○ We begin by computing the collection
 ${\mathcal S}$
of arithmetically maximal subgroups of prime power level; see Section 3 and the tables in Appendix B.
${\mathcal S}$
of arithmetically maximal subgroups of prime power level; see Section 3 and the tables in Appendix B. -
○ For
 $H \in {\mathcal S}$
, we compute the isogeny decomposition of
$H \in {\mathcal S}$
, we compute the isogeny decomposition of
 $J_H$
and the analytic ranks of its simple factors; see Sections 5 and 6.
$J_H$
and the analytic ranks of its simple factors; see Sections 5 and 6. -
○ For many
 $H \in {\mathcal S}$
, we compute equations for
$H \in {\mathcal S}$
, we compute equations for
 $X_H$
and
$X_H$
and
 $j_H\colon X_H \to X(1)$
; see Section 7.
$j_H\colon X_H \to X(1)$
; see Section 7. -
○ For most
 $H \in {\mathcal S}$
with
$H \in {\mathcal S}$
with
 $-I \in H$
, we determine
$-I \in H$
, we determine
 $X_H(\mathbb {Q})$
; see Sections 4, 5, 8.
$X_H(\mathbb {Q})$
; see Sections 4, 5, 8. -
○ For
 $H \in {\mathcal S}$
with
$H \in {\mathcal S}$
with
 $-I \not \in H$
, we compute equations for the universal curve
$-I \not \in H$
, we compute equations for the universal curve
 $E \to U$
, where
$E \to U$
, where
 $U \subset X_H$
is the locus of points with
$U \subset X_H$
is the locus of points with
 $j \ne 0, 1728,\infty $
; see Section 10.
$j \ne 0, 1728,\infty $
; see Section 10.
Analyses of many of the relevant
![]() $X_H$
already exist in the literature, which is summarised in Section 4; the remaining cases are listed in Table 5. Some are routine; for example, some of the genus 2 curves in Section 8 have rank zero Jacobians and are handled with no additional work by Magma’s Chabauty0 command, but many require novel arguments.
$X_H$
already exist in the literature, which is summarised in Section 4; the remaining cases are listed in Table 5. Some are routine; for example, some of the genus 2 curves in Section 8 have rank zero Jacobians and are handled with no additional work by Magma’s Chabauty0 command, but many require novel arguments.
-
○ We use the moduli enumeration of Section 5 to show that
 $X_H({\mathbb F}_p)$
and therefore
$X_H({\mathbb F}_p)$
and therefore
 $X_H(\mathbb {Q})$
is empty in several cases without needing equations for
$X_H(\mathbb {Q})$
is empty in several cases without needing equations for
 $X_H$
; see Table 7.
$X_H$
; see Table 7. -
○ In Section 8, a few curves admit an involution
 $\iota $
such that the map
$\iota $
such that the map
 $P \mapsto P - \iota (P)$
projects to the torsion subgroup of the Jacobian, and we ‘sieve’ with this map. In one case, we are only able to compute an upper bound on
$P \mapsto P - \iota (P)$
projects to the torsion subgroup of the Jacobian, and we ‘sieve’ with this map. In one case, we are only able to compute an upper bound on
 $J_H(\mathbb {Q})_{{\operatorname {tors}}}$
but are then able to circumvent this via sieving.
$J_H(\mathbb {Q})_{{\operatorname {tors}}}$
but are then able to circumvent this via sieving. -
○ In Section 7, we compute canonical models of two high genus curves (genus 36 and 43); and in Section 8.6, we use these models to set up a nontrivial local computation to show that
 $X_H(\mathbb {Q}_p)$
is empty, where p divides the level of H and is thus the only possible prime of bad reduction.
$X_H(\mathbb {Q}_p)$
is empty, where p divides the level of H and is thus the only possible prime of bad reduction. -
○ The curve
 $X_H$
from Section 8.7 has genus 41, and we were not able to compute a model;
$X_H$
from Section 8.7 has genus 41, and we were not able to compute a model;
 $X_H$
maps to
$X_H$
maps to
 $X_{\mathrm {ns}}^{+}(11)$
, which is a rank 1 elliptic curve, and we perform an ‘equationless’ Mordell–Weil sieve (via moduli) to show that
$X_{\mathrm {ns}}^{+}(11)$
, which is a rank 1 elliptic curve, and we perform an ‘equationless’ Mordell–Weil sieve (via moduli) to show that
 $X_H(\mathbb {Q})$
is empty.
$X_H(\mathbb {Q})$
is empty. -
○ Throughout, our approaches are heavily informed by the isogeny decompositions and analytic ranks computed in Section 6. In the end, for a rigorous proof, we often do not need to know that the analytic and algebraic ranks agree, but some cases in Section 8 rely on this and thus make crucial use of Appendix A.
-
○ Appendix A contains an additional novelty: we make use of the Jacobian of a connected but geometrically disconnected curve.
1.3 Applications
In [Reference GreenbergGre12], Greenberg shows that if
![]() $\ell $
is a prime number and
$\ell $
is a prime number and
![]() $E/\mathbb {Q}$
is an elliptic with a cyclic
$E/\mathbb {Q}$
is an elliptic with a cyclic
![]() $\ell $
-isogeny, then
$\ell $
-isogeny, then
![]() $\rho _{E,\ell ^{\infty }}(G_{\mathbb {Q}})$
is as large as possible given the existence of the isogeny if
$\rho _{E,\ell ^{\infty }}(G_{\mathbb {Q}})$
is as large as possible given the existence of the isogeny if
![]() $\ell> 7$
, or the existence of
$\ell> 7$
, or the existence of
![]() $\ell $
-power isogenies if
$\ell $
-power isogenies if
![]() $\ell = 5$
. The
$\ell = 5$
. The
![]() $\ell = 7$
case is handled in [Reference Greenberg, Rubin, Silverberg and StollGRSS14]. As a consequence of our work, we obtain a classification of the
$\ell = 7$
case is handled in [Reference Greenberg, Rubin, Silverberg and StollGRSS14]. As a consequence of our work, we obtain a classification of the
![]() $3$
-adic image for a non-CM elliptic curve
$3$
-adic image for a non-CM elliptic curve
![]() $E/\mathbb {Q}$
with a rational
$E/\mathbb {Q}$
with a rational
![]() $3$
-isogeny.
$3$
-isogeny.
Corollary 1.1. Suppose that
![]() $E/\mathbb {Q}$
is a non-CM elliptic curve with a rational
$E/\mathbb {Q}$
is a non-CM elliptic curve with a rational
![]() $3$
-isogeny, and let
$3$
-isogeny, and let
![]() $H = \langle \rho _{E,3^{\infty }}(G_{\mathbb {Q}}), -I \rangle $
. Then exactly one of the following is true:
$H = \langle \rho _{E,3^{\infty }}(G_{\mathbb {Q}}), -I \rangle $
. Then exactly one of the following is true:
-
(i)
 $[\operatorname {GL}_{2}(\mathbb {Z}_{3}) : H] = 4$
, and H has label
$[\operatorname {GL}_{2}(\mathbb {Z}_{3}) : H] = 4$
, and H has label
 $\mathrm {\texttt {3.4.0.1}}$
;
$\mathrm {\texttt {3.4.0.1}}$
; -
(ii)
 $[\operatorname {GL}_{2}(\mathbb {Z}_{3}) : H] = 12$
, and H has label
$[\operatorname {GL}_{2}(\mathbb {Z}_{3}) : H] = 12$
, and H has label
 $\mathrm {\texttt {3.12.0.1}}$
,
$\mathrm {\texttt {3.12.0.1}}$
,
 $\mathrm {\texttt {9.12.0.1}}$
, or
$\mathrm {\texttt {9.12.0.1}}$
, or
 $\mathrm {\texttt {9.12.0.2}}$
;
$\mathrm {\texttt {9.12.0.2}}$
; -
(iii)
 $[\operatorname {GL}_{2}(\mathbb {Z}_{3}) : H] = 36$
, and H has label
$[\operatorname {GL}_{2}(\mathbb {Z}_{3}) : H] = 36$
, and H has label
 $\mathrm {\texttt {9.36.0.1}}$
,
$\mathrm {\texttt {9.36.0.1}}$
,
 $\mathrm {\texttt {9.36.0.2}}, \mathrm {\texttt {9.36.0.3}}, \mathrm {\texttt {9.36.0.4}}, \mathrm {\texttt {9.36.0.5}}$
,
$\mathrm {\texttt {9.36.0.2}}, \mathrm {\texttt {9.36.0.3}}, \mathrm {\texttt {9.36.0.4}}, \mathrm {\texttt {9.36.0.5}}$
,
 $\mathrm {\texttt {9.36.0.6}}, \mathrm {\texttt {9.36.0.7}}, \mathrm {\texttt {9.36.0.8}}, \mathrm {\texttt {9.36.0.9}}$
, or
$\mathrm {\texttt {9.36.0.6}}, \mathrm {\texttt {9.36.0.7}}, \mathrm {\texttt {9.36.0.8}}, \mathrm {\texttt {9.36.0.9}}$
, or
 $\mathrm {\texttt {27.36.0.1}}$
.
$\mathrm {\texttt {27.36.0.1}}$
.
In each case, the relevant modular curve has genus zero and infinitely many rational points. Moreover,
![]() $\rho _{E,3^{\infty }}(G_{\mathbb {Q}})$
(which may have index two in H) contains all matrices congruent to the identity matrix modulo
$\rho _{E,3^{\infty }}(G_{\mathbb {Q}})$
(which may have index two in H) contains all matrices congruent to the identity matrix modulo
![]() $27$
and all matrices
$27$
and all matrices
![]() $\left [\begin {smallmatrix} \lambda & 0 \\ 0 & \lambda \end {smallmatrix}\right ]$
with
$\left [\begin {smallmatrix} \lambda & 0 \\ 0 & \lambda \end {smallmatrix}\right ]$
with
![]() $\lambda \in \mathbb {Z}_{3}$
and
$\lambda \in \mathbb {Z}_{3}$
and
![]() $\lambda \equiv 1 \pmod {9}$
.
$\lambda \equiv 1 \pmod {9}$
.
This result plays a role in the classification of odd-degree isolated points on
![]() $X_{1}(N)$
given in [Reference Bourdon, Gill, Rouse and WatsonBGRW20]. In [Reference Lombardo and TrontoLT, Reference Lombardo and TrontoLT21], Lombardo and Tronto study the degree of the extension
$X_{1}(N)$
given in [Reference Bourdon, Gill, Rouse and WatsonBGRW20]. In [Reference Lombardo and TrontoLT, Reference Lombardo and TrontoLT21], Lombardo and Tronto study the degree of the extension
![]() $\mathbb {Q}(E[N],N^{-1} \alpha )/\mathbb {Q}(E[N])$
, where
$\mathbb {Q}(E[N],N^{-1} \alpha )/\mathbb {Q}(E[N])$
, where
![]() $\alpha \in E(\mathbb {Q})$
is a point of infinite order and the presence of scalars in
$\alpha \in E(\mathbb {Q})$
is a point of infinite order and the presence of scalars in
![]() $\rho _{E,\ell ^{\infty }}(G_{\mathbb {Q}})$
is used to bound certain Galois cohomology groups. Corollary 1.1 gives precise information about the scalars present in the
$\rho _{E,\ell ^{\infty }}(G_{\mathbb {Q}})$
is used to bound certain Galois cohomology groups. Corollary 1.1 gives precise information about the scalars present in the
![]() $3$
-adic image.
$3$
-adic image.
An additional application of Theorem 1.6 is a very fast ‘algebraic’ algorithm to compute all of the
![]() $\ell $
-adic Galois images of a given non-CM elliptic curve
$\ell $
-adic Galois images of a given non-CM elliptic curve
![]() $E/\mathbb {Q}$
; this algorithm is described in Section 11. By exploiting the classification of
$E/\mathbb {Q}$
; this algorithm is described in Section 11. By exploiting the classification of
![]() $\ell $
-adic Galois images of CM elliptic curves obtained by Lozano-Robledo [Reference Lozano-RobledoLR], we can extend this algorithm to also handle CM elliptic curves over
$\ell $
-adic Galois images of CM elliptic curves obtained by Lozano-Robledo [Reference Lozano-RobledoLR], we can extend this algorithm to also handle CM elliptic curves over
![]() $\mathbb {Q}$
(and, more generally, any CM elliptic curve over its minimal field of definition), as described in Section 12. An implementation of this algorithm is available in the GitHub repository associated to this paper [Reference Rouse, Sutherland and Zureick-BrownRSZB21], and we have applied it to the elliptic curves
$\mathbb {Q}$
(and, more generally, any CM elliptic curve over its minimal field of definition), as described in Section 12. An implementation of this algorithm is available in the GitHub repository associated to this paper [Reference Rouse, Sutherland and Zureick-BrownRSZB21], and we have applied it to the elliptic curves
![]() $E/\mathbb {Q}$
in the L-functions and Modular Forms Database (LMFDB) [LMF] as well as two other large databases of elliptic curves over
$E/\mathbb {Q}$
in the L-functions and Modular Forms Database (LMFDB) [LMF] as well as two other large databases of elliptic curves over
![]() $\mathbb {Q}$
[Reference Stein and WatkinsSW02, Reference Balakrishnan, Ho, Kaplan, Spicer, Stein and WeigandtBHK+16]. This data has now been added to the LMFDB, where it extends existing
$\mathbb {Q}$
[Reference Stein and WatkinsSW02, Reference Balakrishnan, Ho, Kaplan, Spicer, Stein and WeigandtBHK+16]. This data has now been added to the LMFDB, where it extends existing
![]() $2$
-adic and mod-
$2$
-adic and mod-
![]() $\ell $
Galois image data that was previously available. As a result, the
$\ell $
Galois image data that was previously available. As a result, the
![]() $\ell $
-adic images
$\ell $
-adic images
![]() $\rho _{E,\ell ^{\infty }}(G_{\mathbb {Q}})$
are now known for all elliptic curves
$\rho _{E,\ell ^{\infty }}(G_{\mathbb {Q}})$
are now known for all elliptic curves
![]() $E/\mathbb {Q}$
of conductor up to
$E/\mathbb {Q}$
of conductor up to
![]() $500000$
and every prime
$500000$
and every prime
![]() $\ell $
.
$\ell $
.
Other applications abound; examples include [Reference Jones and RouseJR10, Reference Cerchia and RouseCR21, Reference Lombardo and TrontoLT, Reference GužvićGuž21, Reference Bourdon, Gill, Rouse and WatsonBGRW20, Reference González-Jiménez and NajmanGJN20, Reference Bourdon, Ejder, Liu, Odumodu and VirayBEL+19, Reference González-Jiménez and Lozano-RobledoGJLR18, Reference González-Jiménez and Lozano-RobledoGJLR17, Reference Daniels, Lozano-Robledo, Najman and SutherlandDLRNS18, Reference ReiterRei21, Reference Chiloyan and Lozano-RobledoCLR21, Reference Barbulescu and ShindeBS22].
1.4 Code
We make extensive use of the computer algebra system Magma [Reference Bosma, Cannon and PlayoustBCP97]. Code verifying the computational claims made in this paper is available at the GitHub repository https://github.com/AndrewVSutherland/ell-adic-galois-images, which also includes related algorithms and data.
2 The Modular curves
 $X_H$
$X_H$
2.1 Notation
In this article,
![]() $\ell $
and p denote primes, and N is a positive integer. We define
$\ell $
and p denote primes, and N is a positive integer. We define
with the understanding that
![]() $\mathbb {Z}(1)$
is the zero ring and
$\mathbb {Z}(1)$
is the zero ring and
![]() $\operatorname {GL}_2(1)$
and
$\operatorname {GL}_2(1)$
and
![]() $\operatorname {SL}_2(1)$
are trivial groups. We then have
$\operatorname {SL}_2(1)$
are trivial groups. We then have
![]() ${\widehat {\mathbb {Z}}}=\varprojlim \mathbb {Z}(N)$
and
${\widehat {\mathbb {Z}}}=\varprojlim \mathbb {Z}(N)$
and
![]() $\operatorname {GL}_2({\widehat {\mathbb {Z}}})=\varprojlim \operatorname {GL}_2(N)$
and natural projection maps
$\operatorname {GL}_2({\widehat {\mathbb {Z}}})=\varprojlim \operatorname {GL}_2(N)$
and natural projection maps
We view
![]() $\mathbb {Z}(N)^2$
as a
$\mathbb {Z}(N)^2$
as a
![]() $\mathbb {Z}(N)$
-module of column vectors equipped with a left action of
$\mathbb {Z}(N)$
-module of column vectors equipped with a left action of
![]() $\operatorname {GL}_2(N)$
via matrix-vector multiplication.
$\operatorname {GL}_2(N)$
via matrix-vector multiplication.
For
![]() $N>1$
, we use
$N>1$
, we use
![]() $B(N)$
to denote the Borel subgroup of
$B(N)$
to denote the Borel subgroup of
![]() $\operatorname {GL}_2(N)$
consisting of upper triangular matrices,
$\operatorname {GL}_2(N)$
consisting of upper triangular matrices,
![]() $C_{\operatorname {\mathrm {sp}}}(N)$
to denote the split Cartan subgroup of diagonal matrices in
$C_{\operatorname {\mathrm {sp}}}(N)$
to denote the split Cartan subgroup of diagonal matrices in
![]() $\operatorname {GL}_2(N)$
and
$\operatorname {GL}_2(N)$
and
![]() $C_{\operatorname {\mathrm {ns}}}(N)$
to denote the nonsplit Cartan subgroup of
$C_{\operatorname {\mathrm {ns}}}(N)$
to denote the nonsplit Cartan subgroup of
![]() $\operatorname {GL}_2(N)$
, which can be constructed by picking an imaginary quadratic order
$\operatorname {GL}_2(N)$
, which can be constructed by picking an imaginary quadratic order
![]() $\mathcal O$
in which every prime
$\mathcal O$
in which every prime
![]() $\ell |N$
is inert and embedding
$\ell |N$
is inert and embedding
![]() $(\mathcal O/N\mathcal O)^{\times }$
in
$(\mathcal O/N\mathcal O)^{\times }$
in
![]() $\operatorname {GL}_2(N)$
via its action on a
$\operatorname {GL}_2(N)$
via its action on a
![]() $\mathbb {Z}(N)$
-basis for
$\mathbb {Z}(N)$
-basis for
![]() $\mathcal O/N\mathcal O$
(see Section 12), which is unique up to conjugacy. We use
$\mathcal O/N\mathcal O$
(see Section 12), which is unique up to conjugacy. We use
![]() $N_{\operatorname {\mathrm {sp}}}(N)$
to denote the subgroup of the normaliser of
$N_{\operatorname {\mathrm {sp}}}(N)$
to denote the subgroup of the normaliser of
![]() $C_{\operatorname {\mathrm {sp}}}(N)$
in
$C_{\operatorname {\mathrm {sp}}}(N)$
in
![]() $\operatorname {GL}_2(N)$
whose projection to
$\operatorname {GL}_2(N)$
whose projection to
![]() $\operatorname {GL}_2(M)$
contains
$\operatorname {GL}_2(M)$
contains
![]() $C_{\operatorname {\mathrm {sp}}}(M)$
with index 2 for all
$C_{\operatorname {\mathrm {sp}}}(M)$
with index 2 for all
![]() $M>2$
dividing N, which is unique up to conjugacy and equal to the normaliser when
$M>2$
dividing N, which is unique up to conjugacy and equal to the normaliser when
![]() $N>2$
is a prime power; we similarly define
$N>2$
is a prime power; we similarly define
![]() $N_{\operatorname {\mathrm {ns}}}(N)$
. If G is a subgroup of the projectivisation
$N_{\operatorname {\mathrm {ns}}}(N)$
. If G is a subgroup of the projectivisation
![]() $\operatorname {PGL}_2(N)$
of
$\operatorname {PGL}_2(N)$
of
![]() $\operatorname {GL}_2(N)$
, then we denote by
$\operatorname {GL}_2(N)$
, then we denote by
![]() $G(N)$
the preimage of G in
$G(N)$
the preimage of G in
![]() $\operatorname {GL}_2(N)$
.
$\operatorname {GL}_2(N)$
.
2.2 Group theory and Galois representations
Let
![]() $N \ge 1$
be an integer, let k be a perfect field of characteristic coprime to N, and let
$N \ge 1$
be an integer, let k be a perfect field of characteristic coprime to N, and let
. A basis
![]() $(P_1,P_2)$
of
$(P_1,P_2)$
of
![]() $E[N]({\overline {k}})$
determines an isomorphism
$E[N]({\overline {k}})$
determines an isomorphism
![]() $E[N]({\overline {k}}) \overset \sim \rightarrow \mathbb {Z}(N)^2$
via the map
$E[N]({\overline {k}}) \overset \sim \rightarrow \mathbb {Z}(N)^2$
via the map
![]() $P_i \mapsto e_i$
. This gives rise to an isomorphism
$P_i \mapsto e_i$
. This gives rise to an isomorphism
![]() $\iota \colon \operatorname {\mathrm {Aut}} \left ( E[N]({\overline {k}})\right ) \simeq \operatorname {GL}_2(N)$
as follows: for
$\iota \colon \operatorname {\mathrm {Aut}} \left ( E[N]({\overline {k}})\right ) \simeq \operatorname {GL}_2(N)$
as follows: for
![]() $\phi \in \operatorname {\mathrm {Aut}} \left (E[N]({\overline {k}})\right )$
such that
$\phi \in \operatorname {\mathrm {Aut}} \left (E[N]({\overline {k}})\right )$
such that
 $$ \begin{align*} \phi(P_1) = &\, aP_1 + cP_2 \\ \phi(P_2) = &\, bP_1 + dP_2, \end{align*} $$
$$ \begin{align*} \phi(P_1) = &\, aP_1 + cP_2 \\ \phi(P_2) = &\, bP_1 + dP_2, \end{align*} $$
we define

which yields a Galois representation
![]() $G_k \to \operatorname {GL}_2(N)$
given by
$G_k \to \operatorname {GL}_2(N)$
given by
![]() $\sigma \mapsto \iota (\sigma _N)$
, where
$\sigma \mapsto \iota (\sigma _N)$
, where
![]() $\sigma _N$
is the automorphism of
$\sigma _N$
is the automorphism of
![]() $E[N]({\overline {k}})$
induced by
$E[N]({\overline {k}})$
induced by
![]() $\sigma $
.
$\sigma $
.
Remark 2.1. Our choice of
![]() $\iota $
corresponds to the left action of
$\iota $
corresponds to the left action of
![]() $\operatorname {GL}_2(N)$
on
$\operatorname {GL}_2(N)$
on
![]() $\mathbb {Z}(N)^2$
. Many sources are ambiguous about the choice of left vs. right action; this ambiguity often makes no difference (see [Reference Rouse and Zureick-BrownRZB15, Remark 2.2]), but it does when
$\mathbb {Z}(N)^2$
. Many sources are ambiguous about the choice of left vs. right action; this ambiguity often makes no difference (see [Reference Rouse and Zureick-BrownRZB15, Remark 2.2]), but it does when
![]() $H\le \operatorname {GL}_2(N)$
is not conjugate to its transpose. Our choice here is consistent with [Reference SutherlandSut16, Reference Sutherland and ZywinaSZ17], but differs from [Reference Rouse and Zureick-BrownRZB15], which uses right actions.
$H\le \operatorname {GL}_2(N)$
is not conjugate to its transpose. Our choice here is consistent with [Reference SutherlandSut16, Reference Sutherland and ZywinaSZ17], but differs from [Reference Rouse and Zureick-BrownRZB15], which uses right actions.
For each elliptic curve
![]() $E/k$
, we fix a system of compatible bases for
$E/k$
, we fix a system of compatible bases for
![]() $E[N]({\overline {k}})$
for all
$E[N]({\overline {k}})$
for all
![]() $N\ge 1$
coprime to the characteristic of k, meaning if
$N\ge 1$
coprime to the characteristic of k, meaning if
![]() $N=N_1N_2$
, then the bases for
$N=N_1N_2$
, then the bases for
![]() $E[N_1]({\overline {k}})$
and
$E[N_1]({\overline {k}})$
and
![]() $E[N_2]({\overline {k}})$
are the images of the basis for
$E[N_2]({\overline {k}})$
are the images of the basis for
![]() $E[N]({\overline {k}})$
under multiplication by
$E[N]({\overline {k}})$
under multiplication by
![]() $N_2$
and
$N_2$
and
![]() $N_1$
, respectively. Let
$N_1$
, respectively. Let
![]() $\iota _E\colon \! \operatorname {\mathrm {Aut}}(E[N]({\overline {k}})) \overset \sim \longrightarrow \operatorname {GL}_2(N)$
denote the isomorphism determined by the basis for
$\iota _E\colon \! \operatorname {\mathrm {Aut}}(E[N]({\overline {k}})) \overset \sim \longrightarrow \operatorname {GL}_2(N)$
denote the isomorphism determined by the basis for
![]() $E[N]({\overline {k}})$
, and define the Galois representation
$E[N]({\overline {k}})$
, and define the Galois representation
![]() $\rho _{E,N}\colon G_k\to \operatorname {GL}_2(N)$
via
$\rho _{E,N}\colon G_k\to \operatorname {GL}_2(N)$
via
![]() . When k has characteristic zero, we shall also use
. When k has characteristic zero, we shall also use
![]() $\iota _E$
to denote the isomorphism
$\iota _E$
to denote the isomorphism
![]() $\iota _E\colon \operatorname {\mathrm {Aut}}(E_{\mathrm {tor}}({\overline {k}})) \overset \sim \longrightarrow \operatorname {GL}_2({\widehat {\mathbb {Z}}})$
determined by this system of bases and use it to define the Galois representation
$\iota _E\colon \operatorname {\mathrm {Aut}}(E_{\mathrm {tor}}({\overline {k}})) \overset \sim \longrightarrow \operatorname {GL}_2({\widehat {\mathbb {Z}}})$
determined by this system of bases and use it to define the Galois representation
![]() $\rho _E\colon G_k\to \operatorname {GL}_2({\widehat {\mathbb {Z}}})$
via
$\rho _E\colon G_k\to \operatorname {GL}_2({\widehat {\mathbb {Z}}})$
via
![]() . If k is a number field and
. If k is a number field and
![]() ${\mathfrak p}$
is a prime of good reduction for E, for each
${\mathfrak p}$
is a prime of good reduction for E, for each
![]() $N\ge 1$
coprime to
$N\ge 1$
coprime to
![]() $N({\mathfrak p})$
, we shall use the reduction of our chosen basis for
$N({\mathfrak p})$
, we shall use the reduction of our chosen basis for
![]() $E[N]({\overline {k}})$
as a basis for
$E[N]({\overline {k}})$
as a basis for
![]() $E_{\mathfrak p}[N](\overline {\mathbb F}_{\mathfrak p})$
.
$E_{\mathfrak p}[N](\overline {\mathbb F}_{\mathfrak p})$
.
For a subgroup
![]() $H \leq \operatorname {GL}_2({\widehat {\mathbb {Z}}})$
, we use
$H \leq \operatorname {GL}_2({\widehat {\mathbb {Z}}})$
, we use
![]() $H(N)$
to denote the image
$H(N)$
to denote the image
![]() $\pi _N(H)$
of H under
$\pi _N(H)$
of H under
![]() $\pi _N$
. An open subgroup
$\pi _N$
. An open subgroup
![]() $H \leq \operatorname {GL}_2({\widehat {\mathbb {Z}}})$
contains the kernel of
$H \leq \operatorname {GL}_2({\widehat {\mathbb {Z}}})$
contains the kernel of
![]() $\pi _N\colon \operatorname {GL}_2({\widehat {\mathbb {Z}}})\to \operatorname {GL}_2(N)$
for some
$\pi _N\colon \operatorname {GL}_2({\widehat {\mathbb {Z}}})\to \operatorname {GL}_2(N)$
for some
![]() $N\ge 1$
; the least such N is the level of H, in which case
$N\ge 1$
; the least such N is the level of H, in which case
![]() $H = \pi _N^{-1}(H(N))$
is completely determined by
$H = \pi _N^{-1}(H(N))$
is completely determined by
![]() $\pi _N(H)$
. We will typically work directly with subgroups of
$\pi _N(H)$
. We will typically work directly with subgroups of
![]() $\operatorname {GL}_2(N)$
instead of
$\operatorname {GL}_2(N)$
instead of
![]() $\operatorname {GL}_2({\widehat {\mathbb {Z}}})$
, with the understanding that every subgroup of
$\operatorname {GL}_2({\widehat {\mathbb {Z}}})$
, with the understanding that every subgroup of
![]() $\operatorname {GL}_2(N)$
uniquely determines an open subgroup of
$\operatorname {GL}_2(N)$
uniquely determines an open subgroup of
![]() $\operatorname {GL}_2({\widehat {\mathbb {Z}}})$
as its inverse image under
$\operatorname {GL}_2({\widehat {\mathbb {Z}}})$
as its inverse image under
![]() $\pi _N$
; we may use the symbol H to denote both H and
$\pi _N$
; we may use the symbol H to denote both H and
![]() $\pi _N(H)$
, which we note have the same index
$\pi _N(H)$
, which we note have the same index
![]() $[\operatorname {GL}_2({\widehat {\mathbb {Z}}}):H]=[\operatorname {GL}_2(N):\pi _N(H)]$
. We define the level of a subgroup
$[\operatorname {GL}_2({\widehat {\mathbb {Z}}}):H]=[\operatorname {GL}_2(N):\pi _N(H)]$
. We define the level of a subgroup
![]() $H \leq \operatorname {GL}_2(N)$
to be the level of
$H \leq \operatorname {GL}_2(N)$
to be the level of
![]() $\pi _N^{-1}(H)$
.
$\pi _N^{-1}(H)$
.
We may also identify open subgroups of
![]() $\operatorname {GL}_2(\mathbb {Z}_{\ell })$
with their preimages in
$\operatorname {GL}_2(\mathbb {Z}_{\ell })$
with their preimages in
![]() $\operatorname {GL}_2({\widehat {\mathbb {Z}}})$
under the projection map
$\operatorname {GL}_2({\widehat {\mathbb {Z}}})$
under the projection map
![]() $\operatorname {GL}_2({\widehat {\mathbb {Z}}})\to \operatorname {GL}_2(\mathbb {Z}_{\ell })$
. For any
$\operatorname {GL}_2({\widehat {\mathbb {Z}}})\to \operatorname {GL}_2(\mathbb {Z}_{\ell })$
. For any
![]() $e\ge 0$
, we may identify
$e\ge 0$
, we may identify
![]() $H\le \operatorname {GL}_2(\ell ^e)$
with the corresponding open subgroups of
$H\le \operatorname {GL}_2(\ell ^e)$
with the corresponding open subgroups of
![]() $\operatorname {GL}_2(\mathbb {Z}_{\ell })$
or
$\operatorname {GL}_2(\mathbb {Z}_{\ell })$
or
![]() $\operatorname {GL}_2({\widehat {\mathbb {Z}}})$
of the same index. In what follows, we shall only be interested in subgroups of
$\operatorname {GL}_2({\widehat {\mathbb {Z}}})$
of the same index. In what follows, we shall only be interested in subgroups of
![]() $\operatorname {GL}_2({\widehat {\mathbb {Z}}})$
up to conjugacy and view each subgroup H as a representative of its conjugacy class. All inclusions
$\operatorname {GL}_2({\widehat {\mathbb {Z}}})$
up to conjugacy and view each subgroup H as a representative of its conjugacy class. All inclusions
![]() $H_1\le H_2$
of subgroups of
$H_1\le H_2$
of subgroups of
![]() $\operatorname {GL}_2({\widehat {\mathbb {Z}}})$
should be understood to indicate that
$\operatorname {GL}_2({\widehat {\mathbb {Z}}})$
should be understood to indicate that
![]() $H_1$
is conjugate to a subgroup of
$H_1$
is conjugate to a subgroup of
![]() $H_2$
.
$H_2$
.
2.3 Modular curves
Let H be a subgroup of
![]() $\operatorname {GL}_2(N)$
of level N. We define the modular curve
$\operatorname {GL}_2(N)$
of level N. We define the modular curve
![]() $Y_H$
(respectively,
$Y_H$
(respectively,
![]() $X_H$
) to be the coarse moduli space of the stack
$X_H$
) to be the coarse moduli space of the stack
![]() $\mathcal {M}^0_H$
(respectively,
$\mathcal {M}^0_H$
(respectively,
![]() $\mathcal {M}_H$
), over
$\mathcal {M}_H$
), over
![]() $\operatorname {\mathrm {Spec}} \mathbb {Z}[1/N]$
, which parametrises elliptic curves (respectively, generalised elliptic curves) with H-level structure. Equivalently, by [Reference Deligne and RapoportDR73, IV-3.1] (see also [Reference Rouse and Zureick-BrownRZB15, Lemma 2.1]),
$\operatorname {\mathrm {Spec}} \mathbb {Z}[1/N]$
, which parametrises elliptic curves (respectively, generalised elliptic curves) with H-level structure. Equivalently, by [Reference Deligne and RapoportDR73, IV-3.1] (see also [Reference Rouse and Zureick-BrownRZB15, Lemma 2.1]),
![]() $X_H$
is isomorphic to the coarse space of the stack quotient
$X_H$
is isomorphic to the coarse space of the stack quotient
![]() $X(N)/H$
, where
$X(N)/H$
, where
![]() $X(N)$
is the classical modular curve parametrising full level structures.
$X(N)$
is the classical modular curve parametrising full level structures.
More precisely, an H-level structure on an elliptic curve
![]() $E/{\overline {k}}$
is an equivalence class
$E/{\overline {k}}$
is an equivalence class
![]() $[\iota ]_H$
of isomorphisms
$[\iota ]_H$
of isomorphisms
![]() $\iota \colon E[N]({\overline {k}})\to \mathbb {Z}(N)^2$
, where
$\iota \colon E[N]({\overline {k}})\to \mathbb {Z}(N)^2$
, where
![]() $\iota \sim \iota '$
if
$\iota \sim \iota '$
if
![]() $\iota = h\circ \iota '$
for some
$\iota = h\circ \iota '$
for some
![]() $h\in H$
. The set
$h\in H$
. The set
![]() $Y_H({\overline {k}})$
consists of equivalence classes of pairs
$Y_H({\overline {k}})$
consists of equivalence classes of pairs
![]() $(E,[\iota ]_H)$
, where
$(E,[\iota ]_H)$
, where
![]() $(E,[\iota ]_H)\sim (E',[\iota ']_H)$
if there is an isomorphism
$(E,[\iota ]_H)\sim (E',[\iota ']_H)$
if there is an isomorphism
![]() $\phi \colon E\to E'$
for which the induced isomorphism
$\phi \colon E\to E'$
for which the induced isomorphism
![]() $\phi _N\colon E[N]\to E'[N]$
satisfies
$\phi _N\colon E[N]\to E'[N]$
satisfies
![]() $\iota \sim \iota '\circ \phi _N$
. Equivalently,
$\iota \sim \iota '\circ \phi _N$
. Equivalently,
![]() $Y_H({\overline {k}})$
consists of pairs
$Y_H({\overline {k}})$
consists of pairs
![]() $(j(E),\alpha )$
, where
$(j(E),\alpha )$
, where
![]() $\alpha =HgA_E$
is a double coset in
$\alpha =HgA_E$
is a double coset in
![]() $H\backslash \operatorname {GL}_2(N)/A_E$
, where
$H\backslash \operatorname {GL}_2(N)/A_E$
, where
![]() with
with
![]() .
.
Each
![]() $\sigma \in G_k$
induces an isomorphism
$\sigma \in G_k$
induces an isomorphism
![]() $E^{\sigma }[N]\to E[N]$
defined by
$E^{\sigma }[N]\to E[N]$
defined by
![]() $P \mapsto \sigma ^{-1}(P)$
, which we denote
$P \mapsto \sigma ^{-1}(P)$
, which we denote
![]() $\sigma ^{-1}$
. We define a right
$\sigma ^{-1}$
. We define a right
![]() $G_k$
-action on
$G_k$
-action on
![]() $Y_H({\overline {k}})$
via
$Y_H({\overline {k}})$
via
![]() $(E,[\iota ]_H)\mapsto (E^{\sigma },[\iota \circ \sigma ^{-1}]_H)$
. The set of k-rational points
$(E,[\iota ]_H)\mapsto (E^{\sigma },[\iota \circ \sigma ^{-1}]_H)$
. The set of k-rational points
![]() $Y_H(k)$
consists of the elements in
$Y_H(k)$
consists of the elements in
![]() $Y_H({\overline {k}})$
that are fixed by this
$Y_H({\overline {k}})$
that are fixed by this
![]() $G_k$
-action. Each
$G_k$
-action. Each
![]() $P\in Y_H(k)$
is represented by a pair
$P\in Y_H(k)$
is represented by a pair
![]() $(E,[\iota ]_H)\in Y_H(k)$
such that E is defined over k and for all
$(E,[\iota ]_H)\in Y_H(k)$
such that E is defined over k and for all
![]() $\sigma \in G_k$
there exist
$\sigma \in G_k$
there exist
![]() $\varphi \in \operatorname {\mathrm {Aut}}(E_{{\overline {k}}})$
and
$\varphi \in \operatorname {\mathrm {Aut}}(E_{{\overline {k}}})$
and
![]() $h\in H$
such that
$h\in H$
such that
as shown in [Reference ZywinaZyw15b, Lemma 3.1].Footnote
1
Equivalently, a pair
![]() $(j(E),\alpha )$
with
$(j(E),\alpha )$
with
![]() $\alpha =HgA_E$
lies in the set
$\alpha =HgA_E$
lies in the set
![]() $Y_H(k)$
if and only if we have
$Y_H(k)$
if and only if we have
![]() $j(E)\in k$
and
$j(E)\in k$
and
![]() $Hg\rho _{E,N}(\sigma ) A_E=HgA_E$
for all
$Hg\rho _{E,N}(\sigma ) A_E=HgA_E$
for all
![]() $\sigma \in G_k$
.
$\sigma \in G_k$
.
Remark 2.1. For an elliptic curve
![]() $E/k$
, if
$E/k$
, if
![]() $\rho _{E,N}(G_k)\le H$
, then there exists an isomorphism
$\rho _{E,N}(G_k)\le H$
, then there exists an isomorphism
![]() $\iota \colon E[N]\overset \sim \rightarrow \mathbb {Z}(N)^2$
for which
$\iota \colon E[N]\overset \sim \rightarrow \mathbb {Z}(N)^2$
for which
![]() $(E, [\iota ]_H)\in Y_H(k)$
. Conversely, assuming
$(E, [\iota ]_H)\in Y_H(k)$
. Conversely, assuming
![]() $\textrm {char}(k)\ne 2,3$
, if
$\textrm {char}(k)\ne 2,3$
, if
![]() $(E, [\iota ]_H)\in Y_H(k)$
, then for every twist
$(E, [\iota ]_H)\in Y_H(k)$
, then for every twist
![]() $E'$
of E, there is an isomorphism
$E'$
of E, there is an isomorphism
![]() $\iota '\colon E'[N]\overset \sim \rightarrow \mathbb {Z}(N)^2$
with
$\iota '\colon E'[N]\overset \sim \rightarrow \mathbb {Z}(N)^2$
with
![]() $(E', [\iota ']_H)\in Y_H(k)$
, and for at least one
$(E', [\iota ']_H)\in Y_H(k)$
, and for at least one
![]() $E'$
, we have
$E'$
, we have
![]() $\rho _{E',N}(G_k)\le H$
, as we now show.
$\rho _{E',N}(G_k)\le H$
, as we now show.
If
![]() $E'$
is a twist of E, then there is an isomorphism
$E'$
is a twist of E, then there is an isomorphism
![]() $\phi \colon E^{\prime }_{\bar k}\overset {\sim }{\to }E_{\bar k}$
that induces an isomorphism
$\phi \colon E^{\prime }_{\bar k}\overset {\sim }{\to }E_{\bar k}$
that induces an isomorphism
![]() $\phi _N\colon E'[N]({\overline {k}})\overset {\sim }{\to }E[N]({\overline {k}})$
, and for
$\phi _N\colon E'[N]({\overline {k}})\overset {\sim }{\to }E[N]({\overline {k}})$
, and for
![]() the pairs
the pairs
![]() $(E,[\iota ]_H)$
and
$(E,[\iota ]_H)$
and
![]() $(E',[\iota ']_H)$
represent the same point in
$(E',[\iota ']_H)$
represent the same point in
![]() $Y_H({\overline {k}})$
; thus if
$Y_H({\overline {k}})$
; thus if
![]() $(E,[\iota ]_H)$
lies in
$(E,[\iota ]_H)$
lies in
![]() $Y_H(k)$
, then so does
$Y_H(k)$
, then so does
![]() $(E',[\iota ']_H)$
.
$(E',[\iota ']_H)$
.
If the point
![]() $(E,[\iota ]_H)=(j(E),\alpha )$
lies in
$(E,[\iota ]_H)=(j(E),\alpha )$
lies in
![]() $Y_H(k)$
, say for
$Y_H(k)$
, say for
![]() $\alpha =HgA_E$
, then
$\alpha =HgA_E$
, then
![]() $\rho _{E,N}(G_k)$
must lie in
$\rho _{E,N}(G_k)$
must lie in
![]() $g^{-1}HgA_E$
. In other words, up to conjugacy in
$g^{-1}HgA_E$
. In other words, up to conjugacy in
![]() $\operatorname {GL}_2(N)$
, the subgroups
$\operatorname {GL}_2(N)$
, the subgroups
![]() $\rho _{E,N}(G_k)$
and H can differ only by elements of
$\rho _{E,N}(G_k)$
and H can differ only by elements of
![]() $A_E$
, which for
$A_E$
, which for
![]() $\textrm {char}(k)\ne 2,3$
is cyclic of order 2, 4, 6, the last two occurring only for
$\textrm {char}(k)\ne 2,3$
is cyclic of order 2, 4, 6, the last two occurring only for
![]() $j(E)=0,1728$
. When
$j(E)=0,1728$
. When
![]() $\#A_E=2$
, every twist of E is a quadratic twist, and [Reference SutherlandSut16, Lemma 5.24] implies that there is a quadratic twist
$\#A_E=2$
, every twist of E is a quadratic twist, and [Reference SutherlandSut16, Lemma 5.24] implies that there is a quadratic twist
![]() $E'$
of E for which
$E'$
of E for which
![]() $\rho _{E',N}(G_k)\le H$
. Otherwise E has potential CM, and we may apply Proposition 12.1, which also addresses quartic and sextic twists. These results assume k is a number field, but the arguments apply whenever
$\rho _{E',N}(G_k)\le H$
. Otherwise E has potential CM, and we may apply Proposition 12.1, which also addresses quartic and sextic twists. These results assume k is a number field, but the arguments apply whenever
![]() $A_E$
is cyclic (including
$A_E$
is cyclic (including
![]() $\textrm {char}(k)= 2,3$
provided
$\textrm {char}(k)= 2,3$
provided
![]() $j(E)\ne 0,1728$
).
$j(E)\ne 0,1728$
).
Remark 2.2. The elliptic curves
with
![]() $j(E)=j(E') = 0$
are cubic twists that correspond to the same point in
$j(E)=j(E') = 0$
are cubic twists that correspond to the same point in
![]() $X_0(2)(\mathbb {Q})$
, but E has a rational point of order 2 and
$X_0(2)(\mathbb {Q})$
, but E has a rational point of order 2 and
![]() $\rho _{E,2}(G_{\mathbb {Q}}) = B(2)$
, while
$\rho _{E,2}(G_{\mathbb {Q}}) = B(2)$
, while
![]() $E'$
has no rational points of order 2 and
$E'$
has no rational points of order 2 and
![]() $\rho _{E',2}(G_{\mathbb {Q}}) = \operatorname {GL}_2(2)$
. In particular, [Reference Rouse and Zureick-BrownRZB15, Lemma 2.1] is incorrectly stated: it holds only up to twist.
$\rho _{E',2}(G_{\mathbb {Q}}) = \operatorname {GL}_2(2)$
. In particular, [Reference Rouse and Zureick-BrownRZB15, Lemma 2.1] is incorrectly stated: it holds only up to twist.
The complement
![]() is the set of cusps of
is the set of cusps of
![]() $X_H$
and corresponds to generalised elliptic curves with H-level structure. The set of k-rational cusps
$X_H$
and corresponds to generalised elliptic curves with H-level structure. The set of k-rational cusps
![]() $X_H^{\infty }(k)$
can be alternatively described as follows. Let
$X_H^{\infty }(k)$
can be alternatively described as follows. Let
![]() . We define a right
. We define a right
![]() $G_k$
-action on
$G_k$
-action on
![]() $H\backslash \operatorname {GL}_2(N)/U(N)$
via
$H\backslash \operatorname {GL}_2(N)/U(N)$
via
![]() $hgu\mapsto hg\chi _N(\sigma )u$
, where
$hgu\mapsto hg\chi _N(\sigma )u$
, where
![]() is defined by
is defined by
![]() $\sigma (\zeta _N)=\zeta _N^e$
. By [Reference Deligne and RapoportDR73, IV-5.3],
$\sigma (\zeta _N)=\zeta _N^e$
. By [Reference Deligne and RapoportDR73, IV-5.3],
![]() $X_H^{\infty }(k)$
is in bijection with the subset of
$X_H^{\infty }(k)$
is in bijection with the subset of
![]() $H\backslash \operatorname {GL}_2(N)/U(N)$
fixed by
$H\backslash \operatorname {GL}_2(N)/U(N)$
fixed by
![]() $\chi _N(G_k)$
.
$\chi _N(G_k)$
.
We define the genus
![]() $g(H)$
of H and
$g(H)$
of H and
![]() $\pi _N^{-1}(H)$
to be the genus of each of the geometric connected components of the modular curve
$\pi _N^{-1}(H)$
to be the genus of each of the geometric connected components of the modular curve
![]() $X_H$
, which can be directly computed from H via the usual formula
$X_H$
, which can be directly computed from H via the usual formula
if we take
![]() , let
, let
![]() $i(\Gamma _H)=[\operatorname {SL}_2(N):\Gamma _H]$
, let
$i(\Gamma _H)=[\operatorname {SL}_2(N):\Gamma _H]$
, let
![]() $\nu _2$
(respectively,
$\nu _2$
(respectively,
![]() $\nu _3$
) count the right cosets of
$\nu _3$
) count the right cosets of
![]() $\Gamma _H$
in
$\Gamma _H$
in
![]() $\operatorname {SL}_2(N)$
that contain a conjugate of
$\operatorname {SL}_2(N)$
that contain a conjugate of
![]() $\left [\begin {smallmatrix} 0 & 1 \\ -1 & 0 \end {smallmatrix}\right ]$
(respectively,
$\left [\begin {smallmatrix} 0 & 1 \\ -1 & 0 \end {smallmatrix}\right ]$
(respectively,
![]() $\left [\begin {smallmatrix} 0 & 1 \\ -1 & -1 \end {smallmatrix}\right ]$
) and let
$\left [\begin {smallmatrix} 0 & 1 \\ -1 & -1 \end {smallmatrix}\right ]$
) and let
![]() $\nu _{\infty }(\Gamma _H)$
count the orbits of
$\nu _{\infty }(\Gamma _H)$
count the orbits of
![]() $\Gamma _H\backslash \operatorname {SL}_2(N)$
under the right action of
$\Gamma _H\backslash \operatorname {SL}_2(N)$
under the right action of
![]() $\left [\begin {smallmatrix} 1 & 1 \\ 0 & 1 \end {smallmatrix}\right ]$
. The function GL2Genus in the file gl2.m in [Reference Rouse, Sutherland and Zureick-BrownRSZB21] implements this computation.
$\left [\begin {smallmatrix} 1 & 1 \\ 0 & 1 \end {smallmatrix}\right ]$
. The function GL2Genus in the file gl2.m in [Reference Rouse, Sutherland and Zureick-BrownRSZB21] implements this computation.
We define the index
![]() $i(H)$
of H to be the integer
$i(H)$
of H to be the integer
![]() $[\operatorname {GL}_2({\widehat {\mathbb {Z}}})\!:\!H]=[\operatorname {GL}_2(N)\!:\!H(N)]$
.
$[\operatorname {GL}_2({\widehat {\mathbb {Z}}})\!:\!H]=[\operatorname {GL}_2(N)\!:\!H(N)]$
.
Remark 2.3. For
![]() $H\le \operatorname {GL}_2({\widehat {\mathbb {Z}}})$
of level N, the inverse image
$H\le \operatorname {GL}_2({\widehat {\mathbb {Z}}})$
of level N, the inverse image
![]() $\Gamma $
of
$\Gamma $
of
![]() $\Gamma _H\leq \operatorname {SL}_2(N)$
in
$\Gamma _H\leq \operatorname {SL}_2(N)$
in
![]() $\operatorname {SL}_2(\mathbb {Z})$
is a congruence subgroup of some level
$\operatorname {SL}_2(\mathbb {Z})$
is a congruence subgroup of some level
![]() $M|N$
, but M may be strictly smaller than N; see [Reference Sutherland and ZywinaSZ17] for examples. In any case, the base change of
$M|N$
, but M may be strictly smaller than N; see [Reference Sutherland and ZywinaSZ17] for examples. In any case, the base change of
![]() $X_H$
to
$X_H$
to
![]() $\mathbb {Q}(\zeta _N)$
breaks into connected components that are geometrically connected and are each isomorphic over
$\mathbb {Q}(\zeta _N)$
breaks into connected components that are geometrically connected and are each isomorphic over
![]() $\mathbb {C}$
to the modular curve
$\mathbb {C}$
to the modular curve
![]() $X_{\Gamma }$
obtained by taking the quotient of the extended upper half plane by
$X_{\Gamma }$
obtained by taking the quotient of the extended upper half plane by
![]() $\Gamma $
.
$\Gamma $
.
Remark 2.4. For
![]() $H\le \operatorname {GL}_2(N)$
, if
$H\le \operatorname {GL}_2(N)$
, if
![]() $\det H = \mathbb {Z}(N)^{\times }$
, then
$\det H = \mathbb {Z}(N)^{\times }$
, then
![]() $X_H$
is geometrically connected. We mostly consider the case where
$X_H$
is geometrically connected. We mostly consider the case where
![]() $\det H = \mathbb {Z}(N)^{\times }$
in this paper, although in Appendix A, we make use of the case
$\det H = \mathbb {Z}(N)^{\times }$
in this paper, although in Appendix A, we make use of the case
![]() $H = \{I\}$
, where
$H = \{I\}$
, where
![]() $X_H = X(N)$
. When
$X_H = X(N)$
. When
![]() $\det H < \mathbb {Z}(N)^{\times }$
is a proper subgroup,
$\det H < \mathbb {Z}(N)^{\times }$
is a proper subgroup,
![]() $X_H$
is still a curve defined over
$X_H$
is still a curve defined over
![]() $\mathbb {Q}$
, but it is not geometrically connected; its connected components are defined over
$\mathbb {Q}$
, but it is not geometrically connected; its connected components are defined over
![]() $\mathbb {Q}(\zeta _N)^H$
, indexed (via the Weil pairing on the level structures) by cosets of
$\mathbb {Q}(\zeta _N)^H$
, indexed (via the Weil pairing on the level structures) by cosets of
![]() $\det H$
and isomorphic (over
$\det H$
and isomorphic (over
![]() $\mathbb {Q}(\zeta _N)^H$
) to
$\mathbb {Q}(\zeta _N)^H$
) to
![]() $X_{\Gamma }$
. See Appendix A where this is worked out in more detail for
$X_{\Gamma }$
. See Appendix A where this is worked out in more detail for
![]() $X(N)$
, and Example 6.3, where we discuss the isogeny decomposition of the ‘Jacobian’ of such an
$X(N)$
, and Example 6.3, where we discuss the isogeny decomposition of the ‘Jacobian’ of such an
![]() $X_H$
.
$X_H$
.
2.4 Subgroup labels
To help organise our work, we introduce the following labeling convention for uniquely identifying (conjugacy classes of) open subgroups H of
![]() $\operatorname {GL}_2({\widehat {\mathbb {Z}}})$
, which will also serve as labels of the corresponding modular curves
$\operatorname {GL}_2({\widehat {\mathbb {Z}}})$
, which will also serve as labels of the corresponding modular curves
![]() $X_H$
. All the subgroups we shall consider satisfy
$X_H$
. All the subgroups we shall consider satisfy
![]() $\det (H)={\widehat {\mathbb {Z}}}^{\times }$
and have labels of the form
$\det (H)={\widehat {\mathbb {Z}}}^{\times }$
and have labels of the form
where N, i, g, n are the decimal representations of integers
![]() $N,i,g,n$
defined as follows:
$N,i,g,n$
defined as follows:
-
○
 $N=N(H)$
is the level of H;
$N=N(H)$
is the level of H; -
○
 $i=i(H)$
is the index of H;
$i=i(H)$
is the index of H; -
○
 $g=g(H)$
is the genus of H;
$g=g(H)$
is the genus of H; -
○
 $n\ge 1$
is an ordinal indicating the position of H among all subgroups of the same level, index and genus with
$n\ge 1$
is an ordinal indicating the position of H among all subgroups of the same level, index and genus with
 $\det (H)={\widehat {\mathbb {Z}}}^{\times }$
under the ordering defined below.
$\det (H)={\widehat {\mathbb {Z}}}^{\times }$
under the ordering defined below.
To define the ordinal n, we must totally order the set
![]() $S(N,i,g)$
of open subgroups of
$S(N,i,g)$
of open subgroups of
![]() $\operatorname {GL}_2({\widehat {\mathbb {Z}}})$
of level N, index i and genus g with
$\operatorname {GL}_2({\widehat {\mathbb {Z}}})$
of level N, index i and genus g with
![]() $\det (H)={\widehat {\mathbb {Z}}}^{\times }$
, and we want this ordering to be efficiently computable. With this in mind, we define the following invariants for each
$\det (H)={\widehat {\mathbb {Z}}}^{\times }$
, and we want this ordering to be efficiently computable. With this in mind, we define the following invariants for each
![]() $H\in S(N,i,g)$
:
$H\in S(N,i,g)$
:
-
○ the parent list of H is the lexicographically ordered list of labels of the subgroups
 $G\leq \operatorname {GL}_2({\widehat {\mathbb {Z}}})$
of which H is a maximal subgroup;
$G\leq \operatorname {GL}_2({\widehat {\mathbb {Z}}})$
of which H is a maximal subgroup; -
○ the orbit signature of H as the ordered list of triples
 $(e,s,m)$
, where m counts orbits of
$(e,s,m)$
, where m counts orbits of
 $\mathbb {Z}(N)^2$
under the left-action of H of size s and exponent e (the least integer that kills every element of the orbit);Footnote
2
$\mathbb {Z}(N)^2$
under the left-action of H of size s and exponent e (the least integer that kills every element of the orbit);Footnote
2
-
○ the class signature of H is the ordered set of tuples
 $(o,d,t,s,m)$
, where m counts the conjugacy classes of elements of
$(o,d,t,s,m)$
, where m counts the conjugacy classes of elements of
 $H\le \operatorname {GL}_2(N)$
of size s whose elements have order o, determinant d and trace t;
$H\le \operatorname {GL}_2(N)$
of size s whose elements have order o, determinant d and trace t; -
○ the minimal conjugate of H is the least subgroup of
 $\operatorname {GL}_2(N)$
conjugate to H, where subgroups of
$\operatorname {GL}_2(N)$
conjugate to H, where subgroups of
 $\operatorname {GL}_2(N)$
are ordered lexicographically as ordered lists of tuples of integers
$\operatorname {GL}_2(N)$
are ordered lexicographically as ordered lists of tuples of integers
 $(a,b,c,d)$
with
$(a,b,c,d)$
with
 $a,b,c,d\in [0,N-1]$
corresponding to the matrix
$a,b,c,d\in [0,N-1]$
corresponding to the matrix
 $\left [\begin {smallmatrix} a & b \\ c & d \end {smallmatrix}\right ]\in H$
.
$\left [\begin {smallmatrix} a & b \\ c & d \end {smallmatrix}\right ]\in H$
.
We now totally order the set
![]() $S(N,i,g,d)$
lexicographically by parent list, orbit signature, class signature and minimal conjugate; these invariants are intentionally ordered according to the difficulty of computing them, and in most cases the first two or three suffice to distinguish every element of
$S(N,i,g,d)$
lexicographically by parent list, orbit signature, class signature and minimal conjugate; these invariants are intentionally ordered according to the difficulty of computing them, and in most cases the first two or three suffice to distinguish every element of
![]() $S(N,i,g,d)$
, meaning we rarely need to compute minimal conjugates, which is by far the most expensive invariant to compute.
$S(N,i,g,d)$
, meaning we rarely need to compute minimal conjugates, which is by far the most expensive invariant to compute.
Example 2.1. Let
![]() $H=N_{\operatorname {\mathrm {ns}}}(11^2)$
be the normaliser of the nonsplit Cartan subgroup of
$H=N_{\operatorname {\mathrm {ns}}}(11^2)$
be the normaliser of the nonsplit Cartan subgroup of
![]() $\mathbb {Z}(11^2)$
, which has level
$\mathbb {Z}(11^2)$
, which has level
![]() $11^2=121$
and index
$11^2=121$
and index
![]() $5\cdot 11^3 = 6655$
. There are just two subgroups
$5\cdot 11^3 = 6655$
. There are just two subgroups
![]() $H\le \operatorname {GL}_2(11^2)$
of index 6655 (up to conjugacy), only one of which has
$H\le \operatorname {GL}_2(11^2)$
of index 6655 (up to conjugacy), only one of which has
![]() $\det (H)={\widehat {\mathbb {Z}}}^{\times }$
, so computing
$\det (H)={\widehat {\mathbb {Z}}}^{\times }$
, so computing
![]() $g(H)=511$
suffices to determine the label 121.6655.511.1 of
$g(H)=511$
suffices to determine the label 121.6655.511.1 of
![]() $N_{\operatorname {\mathrm {ns}}}(11^2)$
.
$N_{\operatorname {\mathrm {ns}}}(11^2)$
.
If we instead take
![]() $H=N_{\operatorname {\mathrm {ns}}}(11)$
with level 11 and index 55, we find there are two subgroups of
$H=N_{\operatorname {\mathrm {ns}}}(11)$
with level 11 and index 55, we find there are two subgroups of
![]() $\operatorname {GL}_2(11)$
of index 55; they have genus 1 and determinant index 1 and thus belong to the set
$\operatorname {GL}_2(11)$
of index 55; they have genus 1 and determinant index 1 and thus belong to the set
![]() $S(11,55,1,1)$
. These subgroups
$S(11,55,1,1)$
. These subgroups
![]() and
and
![]() have parent list
have parent list
![]() $(\texttt {1.1.0.1})$
and orbit signature
$(\texttt {1.1.0.1})$
and orbit signature
![]() $(1,1,1), (11,120,1)$
. Their class signatures begin
$(1,1,1), (11,120,1)$
. Their class signatures begin
![]() $(1,1,2,1,1), (2,1,9,1,1), (2,10,0,12,1)$
but differ in the fourth tuple, which is
$(1,1,2,1,1), (2,1,9,1,1), (2,10,0,12,1)$
but differ in the fourth tuple, which is
![]() $(3,1,10,2,1)$
for
$(3,1,10,2,1)$
for
![]() $H_1$
but
$H_1$
but
![]() $(3,1,10,8,1)$
for
$(3,1,10,8,1)$
for
![]() $H_2$
, meaning
$H_2$
, meaning
![]() $H_1$
contains a conjugacy class of size 2 whose elements have order 3, determinant 1, and trace 10, but
$H_1$
contains a conjugacy class of size 2 whose elements have order 3, determinant 1, and trace 10, but
![]() $H_2$
does not. It follows that the labels of
$H_2$
does not. It follows that the labels of
![]() $H_1$
and
$H_1$
and
![]() $H_2$
are 11.55.1.1 and 11.55.1.2, and that
$H_2$
are 11.55.1.1 and 11.55.1.2, and that
![]() $N_{\operatorname {\mathrm {ns}}}(11)=H_1$
.
$N_{\operatorname {\mathrm {ns}}}(11)=H_1$
.
Remark 2.2. This labeling system can be extended to arbitrary open
![]() $H\le \operatorname {GL}_2({\widehat {\mathbb {Z}}})$
using labels of the form M.d.m-N.i.g.n, where M.d.m uniquely identifies
$H\le \operatorname {GL}_2({\widehat {\mathbb {Z}}})$
using labels of the form M.d.m-N.i.g.n, where M.d.m uniquely identifies
![]() $\det (H)\le {\widehat {\mathbb {Z}}}^{\times }$
according to its level
$\det (H)\le {\widehat {\mathbb {Z}}}^{\times }$
according to its level
![]() $M|N$
, index
$M|N$
, index
![]() $d:=[{\widehat {\mathbb {Z}}}^{\times }\!\!:\!\det (H)]$
and an ordinal m that distinguishes
$d:=[{\widehat {\mathbb {Z}}}^{\times }\!\!:\!\det (H)]$
and an ordinal m that distinguishes
![]() $\det (H)$
among the open subgroups
$\det (H)$
among the open subgroups
![]() $D\le {\widehat {\mathbb {Z}}}^{\times }$
of level M and index d.Footnote
3
To define m, we order the index d subgroups
$D\le {\widehat {\mathbb {Z}}}^{\times }$
of level M and index d.Footnote
3
To define m, we order the index d subgroups
![]() $D\le (\mathbb {Z}/M\mathbb {Z})^{\times }$
lexicographically according to the lists of labels
$D\le (\mathbb {Z}/M\mathbb {Z})^{\times }$
lexicographically according to the lists of labels
![]() $\texttt {M.a}$
of Conrey characters
$\texttt {M.a}$
of Conrey characters
![]() $\chi _M(a,\cdot )$
of modulus M whose kernels contain D; see [Reference Best, Bober, Booker, Costa, Cremona, Maarten, Lee, Lowry-Duda, Roe, Sutherland and VoightBBB+21, Section 3.2] for the definition of
$\chi _M(a,\cdot )$
of modulus M whose kernels contain D; see [Reference Best, Bober, Booker, Costa, Cremona, Maarten, Lee, Lowry-Duda, Roe, Sutherland and VoightBBB+21, Section 3.2] for the definition of
![]() $\chi _M(a,\cdot )$
. We then redefine N and i to be the relative level and index of H as a subgroup of the preimage G of
$\chi _M(a,\cdot )$
. We then redefine N and i to be the relative level and index of H as a subgroup of the preimage G of
![]() $\det (H)$
in
$\det (H)$
in
![]() $\operatorname {GL}_2({\widehat {\mathbb {Z}}})$
: this means N is the least positive integer for which
$\operatorname {GL}_2({\widehat {\mathbb {Z}}})$
: this means N is the least positive integer for which
![]() $H=\pi _N^{-1}(\pi _N(H))$
, where
$H=\pi _N^{-1}(\pi _N(H))$
, where
![]() $\pi _N\colon G\to G(N)$
is the reduction map and
$\pi _N\colon G\to G(N)$
is the reduction map and
![]() $i=[G:H]$
. This convention ensures that if
$i=[G:H]$
. This convention ensures that if
![]() $E/K$
has Galois image
$E/K$
has Galois image
![]() $\rho _E(G_K)=H$
, the values of N, i, g in the label of
$\rho _E(G_K)=H$
, the values of N, i, g in the label of
![]() $\rho _E(G_L)$
will be the same for every finite extension
$\rho _E(G_L)$
will be the same for every finite extension
![]() $L/K$
.
$L/K$
.
3 Arithmetically maximal subgroups
Definition 3.1. We define an open subgroup
![]() $H \le \operatorname {GL}_2({\widehat {\mathbb {Z}}})$
to be arithmetically maximal if
$H \le \operatorname {GL}_2({\widehat {\mathbb {Z}}})$
to be arithmetically maximal if
-
(i)
 $\det (H)={\widehat {\mathbb {Z}}}^{\times }$
,
$\det (H)={\widehat {\mathbb {Z}}}^{\times }$
, -
(ii) H contains an element conjugate to
 $\left [\begin {smallmatrix} 1 & 0 \\ 0 & -1 \end {smallmatrix}\right ]$
or
$\left [\begin {smallmatrix} 1 & 0 \\ 0 & -1 \end {smallmatrix}\right ]$
or
 $\left [\begin {smallmatrix} 1 & 1 \\ 0 & -1 \end {smallmatrix}\right ]$
,
$\left [\begin {smallmatrix} 1 & 1 \\ 0 & -1 \end {smallmatrix}\right ]$
, -
(iii)
 $j(X_H(\mathbb {Q}))$
is finite and
$j(X_H(\mathbb {Q}))$
is finite and
 $j(X_K(\mathbb {Q}))$
is infinite for all
$j(X_K(\mathbb {Q}))$
is infinite for all
 $H< K\le \operatorname {GL}_2({\widehat {\mathbb {Z}}})$
.
$H< K\le \operatorname {GL}_2({\widehat {\mathbb {Z}}})$
.
Properties of the Weil pairing imply that if
![]() $H = \rho _E(G_{\mathbb {Q}})$
, then
$H = \rho _E(G_{\mathbb {Q}})$
, then
![]() $\det (H)= \mathbb {Z}^{\times }$
, and more generally, that if E is an elliptic curve over a number field K and
$\det (H)= \mathbb {Z}^{\times }$
, and more generally, that if E is an elliptic curve over a number field K and
![]() $H=\rho _E(G_K)$
, then
$H=\rho _E(G_K)$
, then
![]() $[\mathbb {Z}^{\times }:\det (H)]=[K:K\cap \mathbb {Q}^{\mathrm {cyc}}]$
. In particular, condition (i) holds for every H that arises as
$[\mathbb {Z}^{\times }:\det (H)]=[K:K\cap \mathbb {Q}^{\mathrm {cyc}}]$
. In particular, condition (i) holds for every H that arises as
![]() $\rho _E(G_{\mathbb {Q}})$
for an elliptic curve
$\rho _E(G_{\mathbb {Q}})$
for an elliptic curve
![]() $E/\mathbb {Q}$
. Condition (ii) is a necessary and sufficient condition for
$E/\mathbb {Q}$
. Condition (ii) is a necessary and sufficient condition for
![]() $X_{H}$
to have noncuspidal real points, by Proposition 3.5 of [Reference ZywinaZyw15b], and it follows from Proposition 3.1 of [Reference Sutherland and ZywinaSZ17] that every genus zero H of prime power level
$X_{H}$
to have noncuspidal real points, by Proposition 3.5 of [Reference ZywinaZyw15b], and it follows from Proposition 3.1 of [Reference Sutherland and ZywinaSZ17] that every genus zero H of prime power level
![]() $N=\ell ^e$
that satisfies equations (i) and (ii) has infinitely many
$N=\ell ^e$
that satisfies equations (i) and (ii) has infinitely many
![]() $\mathbb {Q}$
-points (the assumption
$\mathbb {Q}$
-points (the assumption
![]() $-I\in H$
is not used in the proof of Proposition 3.1 in [Reference Sutherland and ZywinaSZ17]). For odd
$-I\in H$
is not used in the proof of Proposition 3.1 in [Reference Sutherland and ZywinaSZ17]). For odd
![]() $\ell $
, the matrices in condition (ii) are conjugate in
$\ell $
, the matrices in condition (ii) are conjugate in
![]() $\operatorname {GL}_2(N)$
, and only the first is needed. This definition differs slightly from that used in [Reference Rouse and Zureick-BrownRZB15, Definition 3.1] for
$\operatorname {GL}_2(N)$
, and only the first is needed. This definition differs slightly from that used in [Reference Rouse and Zureick-BrownRZB15, Definition 3.1] for
![]() $\ell =2$
.
$\ell =2$
.
Let
![]() ${\mathcal S}_{\ell }(\mathbb {Q})$
be the set of arithmetically maximal subgroups of
${\mathcal S}_{\ell }(\mathbb {Q})$
be the set of arithmetically maximal subgroups of
![]() $\ell $
-power level, and let
$\ell $
-power level, and let
![]() ${\mathcal S}_{\ell }^{\infty }(\mathbb {Q})$
be the set of open subgroups of
${\mathcal S}_{\ell }^{\infty }(\mathbb {Q})$
be the set of open subgroups of
![]() $\operatorname {GL}_2({\widehat {\mathbb {Z}}})$
of
$\operatorname {GL}_2({\widehat {\mathbb {Z}}})$
of
![]() $\ell $
-power level for which
$\ell $
-power level for which
![]() $j(X_H(\mathbb {Q}))$
is infinite.
$j(X_H(\mathbb {Q}))$
is infinite.
The sets
![]() ${\mathcal S}_{\ell }^{\infty }(\mathbb {Q})$
are explicitly determined in [Reference Sutherland and ZywinaSZ17] (and in [Reference Rouse and Zureick-BrownRZB15] for
${\mathcal S}_{\ell }^{\infty }(\mathbb {Q})$
are explicitly determined in [Reference Sutherland and ZywinaSZ17] (and in [Reference Rouse and Zureick-BrownRZB15] for
![]() $\ell =2$
) and have cardinalities
$\ell =2$
) and have cardinalities
![]() $1208,47,23,15,2,11$
for
$1208,47,23,15,2,11$
for
![]() $\ell =2,3,5,7,11,13$
and cardinality
$\ell =2,3,5,7,11,13$
and cardinality
![]() $1$
for all
$1$
for all
![]() $\ell>13$
.Footnote
4
To enumerate the set
$\ell>13$
.Footnote
4
To enumerate the set
![]() ${\mathcal S}_{\ell }(\mathbb {Q})$
, it would suffice to enumerate the maximal subgroups of all the groups in
${\mathcal S}_{\ell }(\mathbb {Q})$
, it would suffice to enumerate the maximal subgroups of all the groups in
![]() ${\mathcal S}_{\ell }^{\infty }(\mathbb {Q})$
, but we take a slightly different approach and use our knowledge of
${\mathcal S}_{\ell }^{\infty }(\mathbb {Q})$
, but we take a slightly different approach and use our knowledge of
![]() ${\mathcal S}_{\ell }^{\infty }(\mathbb {Q})$
to derive an upper bound on the level of the groups in
${\mathcal S}_{\ell }^{\infty }(\mathbb {Q})$
to derive an upper bound on the level of the groups in
![]() ${\mathcal S}_{\ell }(\mathbb {Q})$
.
${\mathcal S}_{\ell }(\mathbb {Q})$
.
Lemma 3.2. Let
![]() for
for
![]() $\ell =2,3,5,7,11,13$
, respectively, and let
$\ell =2,3,5,7,11,13$
, respectively, and let
![]() for all primes
for all primes
![]() $\ell>13$
. Then
$\ell>13$
. Then
![]() $\ell ^{e_{\ell }}$
is an upper bound on the level of every
$\ell ^{e_{\ell }}$
is an upper bound on the level of every
![]() $H\in {\mathcal S}_{\ell }^{\infty }(\mathbb {Q})$
and
$H\in {\mathcal S}_{\ell }^{\infty }(\mathbb {Q})$
and
![]() $\ell ^{e_{\ell }+1}$
is an upper bound on the level of every
$\ell ^{e_{\ell }+1}$
is an upper bound on the level of every
![]() $H\in {\mathcal S}_{\ell }(\mathbb {Q})$
.
$H\in {\mathcal S}_{\ell }(\mathbb {Q})$
.
Proof. The bound for
![]() $H\in {\mathcal S}_{\ell }^{\infty }(\mathbb {Q})$
follows from [Reference Sutherland and ZywinaSZ17, Corollary 1.6] and its associated data. The bound for
$H\in {\mathcal S}_{\ell }^{\infty }(\mathbb {Q})$
follows from [Reference Sutherland and ZywinaSZ17, Corollary 1.6] and its associated data. The bound for
![]() $H\in {\mathcal S}_{\ell }(\mathbb {Q})$
follows from [Reference Sutherland and ZywinaSZ17, Lemma 3.7] for
$H\in {\mathcal S}_{\ell }(\mathbb {Q})$
follows from [Reference Sutherland and ZywinaSZ17, Lemma 3.7] for
![]() $\ell \le 13$
(note
$\ell \le 13$
(note
![]() $e_2\ge 2$
); and for
$e_2\ge 2$
); and for
![]() $\ell>13$
, we can apply [Reference SerreSer98, Lemma 3, pages IV-23], since
$\ell>13$
, we can apply [Reference SerreSer98, Lemma 3, pages IV-23], since
![]() $e_{\ell }=0$
.
$e_{\ell }=0$
.
Lemma 3.2 reduces the problem of enumerating the sets
![]() ${\mathcal S}_{\ell }(\mathbb {Q})$
to a finite computation in
${\mathcal S}_{\ell }(\mathbb {Q})$
to a finite computation in
![]() $\operatorname {GL}_2(\ell ^{e_{\ell }+1})$
. This computation can be further constrained by computing the maximal index
$\operatorname {GL}_2(\ell ^{e_{\ell }+1})$
. This computation can be further constrained by computing the maximal index
![]() $i_{\ell }$
of any maximal subgroup of
$i_{\ell }$
of any maximal subgroup of
![]() $H_0\in {\mathcal S}_{\ell }^{\infty }(\mathbb {Q})$
and then enumerating all (conjugacy classes of) subgroups of
$H_0\in {\mathcal S}_{\ell }^{\infty }(\mathbb {Q})$
and then enumerating all (conjugacy classes of) subgroups of
![]() $\operatorname {GL}_2(\ell ^{e_{\ell }+1})$
of index at most
$\operatorname {GL}_2(\ell ^{e_{\ell }+1})$
of index at most
![]() $i_{\ell }$
, which can be efficiently accomplished using algorithms for subgroup enumeration that are implemented in Magma and other computer algebra systems. The advantages of this approach are that it enumerates subgroups up to conjugacy in
$i_{\ell }$
, which can be efficiently accomplished using algorithms for subgroup enumeration that are implemented in Magma and other computer algebra systems. The advantages of this approach are that it enumerates subgroups up to conjugacy in
![]() $\operatorname {GL}_2({\widehat {\mathbb {Z}}})$
, rather than up to conjugacy in
$\operatorname {GL}_2({\widehat {\mathbb {Z}}})$
, rather than up to conjugacy in
![]() $H_0$
, and it includes all subgroups that have the same level and index of any
$H_0$
, and it includes all subgroups that have the same level and index of any
![]() $H\in {\mathcal S}_{\ell }(\mathbb {Q})$
, as well as all of the groups that contain them, which may be needed to compute the group labels defined in the previous section.
$H\in {\mathcal S}_{\ell }(\mathbb {Q})$
, as well as all of the groups that contain them, which may be needed to compute the group labels defined in the previous section.
Table 4 summarises this computation. The ‘subgroups’ row counts the number of subgroups
![]() $H\le \operatorname {GL}_2({\widehat {\mathbb {Z}}})$
of
$H\le \operatorname {GL}_2({\widehat {\mathbb {Z}}})$
of
![]() $\ell $
-power level with
$\ell $
-power level with
![]() $\det (H)={\widehat {\mathbb {Z}}}^{\times }$
that satisfy the level and index bounds in the first two rows, and the last three rows list the maximum level, index and genus that arise among the groups
$\det (H)={\widehat {\mathbb {Z}}}^{\times }$
that satisfy the level and index bounds in the first two rows, and the last three rows list the maximum level, index and genus that arise among the groups
![]() $H\in {\mathcal S}_{\ell }(\mathbb {Q})$
.
$H\in {\mathcal S}_{\ell }(\mathbb {Q})$
.
Table 4 Summary of arithmetically maximal
![]() $H\leq \operatorname {GL}_2({\widehat {\mathbb {Z}}})$
of
$H\leq \operatorname {GL}_2({\widehat {\mathbb {Z}}})$
of
![]() $\ell $
-power level for
$\ell $
-power level for
![]() $\ell \le 37$
. The level and index bounds are those implied by Lemma 3.2 and the paragraph following; the max level, index and genus rows are the maximum values realised by arithmetically maximal groups.
$\ell \le 37$
. The level and index bounds are those implied by Lemma 3.2 and the paragraph following; the max level, index and genus rows are the maximum values realised by arithmetically maximal groups.

4 Bookkeeping
By [Reference MazurMaz78], [Reference SerreSer81, Section 8.4] and [Reference Bilu and ParentBP11], if
![]() $\ell \geq 17$
and
$\ell \geq 17$
and
![]() $\rho _{E,\ell }$
is not surjective, then either
$\rho _{E,\ell }$
is not surjective, then either
![]() $\ell = 17$
or
$\ell = 17$
or
![]() $37$
and
$37$
and
![]() $j(E)$
is listed in Table 1, or the image
$j(E)$
is listed in Table 1, or the image
![]() $\rho _{E,\ell }(G_{\mathbb {Q}})$
is a subgroup of
$\rho _{E,\ell }(G_{\mathbb {Q}})$
is a subgroup of
![]() $N_{\operatorname {\mathrm {ns}}}(\ell )$
. In the latter case, for
$N_{\operatorname {\mathrm {ns}}}(\ell )$
. In the latter case, for
![]() $\ell \equiv 1\pmod {3}$
, the image must be equal to
$\ell \equiv 1\pmod {3}$
, the image must be equal to
![]() $N_{\operatorname {\mathrm {ns}}}(\ell )$
(not a proper subgroup); and for
$N_{\operatorname {\mathrm {ns}}}(\ell )$
(not a proper subgroup); and for
![]() $\ell \equiv 2\pmod {3}$
, the image is either
$\ell \equiv 2\pmod {3}$
, the image is either
![]() $N_{\operatorname {\mathrm {ns}}}(\ell )$
or the index-3 subgroup
$N_{\operatorname {\mathrm {ns}}}(\ell )$
or the index-3 subgroup
by [Reference ZywinaZyw15a, Proposition 1.13]. Recent work by le Fourn and Lemos [Reference Le Fourn and LemosLFL21, Theorem 1.2] shows that if
![]() $\ell> 1.4\times 10^7$
, then
$\ell> 1.4\times 10^7$
, then
![]() $\rho _{E,\ell }(G_{\mathbb {Q}})$
cannot be a proper subgroup of
$\rho _{E,\ell }(G_{\mathbb {Q}})$
cannot be a proper subgroup of
![]() $N_{\operatorname {\mathrm {ns}}}(\ell )$
.
$N_{\operatorname {\mathrm {ns}}}(\ell )$
.
Numerous individual cases remain. See Tables 12–17 in Appendix B for a list of all arithmetically maximal
![]() $H\le \operatorname {GL}_2({\widehat {\mathbb {Z}}})$
of
$H\le \operatorname {GL}_2({\widehat {\mathbb {Z}}})$
of
![]() $\ell $
-power level for
$\ell $
-power level for
![]() $\ell \leq 37$
, and see Table 4 for a numerical summary of this data. Many of the corresponding modular curves
$\ell \leq 37$
, and see Table 4 for a numerical summary of this data. Many of the corresponding modular curves
![]() $X_H$
are already handled in the literature, and these account for most of the exceptional points listed in Table 1. Below is a summary of prior results.
$X_H$
are already handled in the literature, and these account for most of the exceptional points listed in Table 1. Below is a summary of prior results.
-
1. Ligozat determined the rational points on
 $X_0(N)$
for
$X_0(N)$
for
 $N = 27,49,11,17,19$
with labels 27.36.1.1, 49.56.1.1, 11.12.1.1, 17.18.1.1, 19.20.1.1 in [Reference LigozatLig75, 5.2.3.1]; there are exceptional points for
$N = 27,49,11,17,19$
with labels 27.36.1.1, 49.56.1.1, 11.12.1.1, 17.18.1.1, 19.20.1.1 in [Reference LigozatLig75, 5.2.3.1]; there are exceptional points for
 $N = 11,17$
.
$N = 11,17$
. -
2. Ligozat addressed
 $X_{S_4}(11)$
with label 11.55.1.2 in [Reference LigozatLig77, Proposition 4.4.8.1].
$X_{S_4}(11)$
with label 11.55.1.2 in [Reference LigozatLig77, Proposition 4.4.8.1]. -
3. Kenku determined the rational points on
 $X_0(13^2)$
(labeled 169.182.8.1) [Reference KenkuKen80] and on
$X_0(13^2)$
(labeled 169.182.8.1) [Reference KenkuKen80] and on
 $X_0(125)$
(labeled 125.150.8.1) [Reference KenkuKen81]; the modular curve
$X_0(125)$
(labeled 125.150.8.1) [Reference KenkuKen81]; the modular curve
 $X_0(5,25)$
with label 25.150.8.1 is isomorphic to
$X_0(5,25)$
with label 25.150.8.1 is isomorphic to
 $X_0(125)$
and thus also handled by Kenku.
$X_0(125)$
and thus also handled by Kenku. -
4. The curves
 $X_{\operatorname {\mathrm {sp}}}^+(25)$
and
$X_{\operatorname {\mathrm {sp}}}^+(25)$
and
 $X_{\operatorname {\mathrm {sp}}}^+(49)$
have labels 25.375.22.1 and 49.1372.94.1; they are isomorphic to
$X_{\operatorname {\mathrm {sp}}}^+(49)$
have labels 25.375.22.1 and 49.1372.94.1; they are isomorphic to
 $X_0^+(25^2)$
and
$X_0^+(25^2)$
and
 $X_0^+(49^2)$
and are thus handled by Momose and Shimura [Reference Momose and ShimuraMS02, Theorems 0.1 and 3.14] and by Momose [Reference MomoseMom86, Theorem 3.6].
$X_0^+(49^2)$
and are thus handled by Momose and Shimura [Reference Momose and ShimuraMS02, Theorems 0.1 and 3.14] and by Momose [Reference MomoseMom86, Theorem 3.6]. -
5. Momose also handled
 $X_{\operatorname {\mathrm {sp}}}^+(11)$
with label 11.66.2.1 in [Reference MomoseMom84, Theorem 0.1].
$X_{\operatorname {\mathrm {sp}}}^+(11)$
with label 11.66.2.1 in [Reference MomoseMom84, Theorem 0.1]. -
6. The curves
 $X_{\operatorname {\mathrm {ns}}}^+(13)$
and
$X_{\operatorname {\mathrm {ns}}}^+(13)$
and
 $X_{\operatorname {\mathrm {sp}}}^+(13)$
labeled 13.78.3.1 and 13.91.3.1 are handled via nonabelian Chabauty by Balakrishnan et al. in [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+19].
$X_{\operatorname {\mathrm {sp}}}^+(13)$
labeled 13.78.3.1 and 13.91.3.1 are handled via nonabelian Chabauty by Balakrishnan et al. in [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+19]. -
7. The curves
 $X_{S_4}(13)$
and
$X_{S_4}(13)$
and
 $X_{\operatorname {\mathrm {ns}}}^+(17)$
labeled 13.91.3.2 and 17.136.6.1 are handled via nonabelian Chabauty by Balakrishnan et al. in [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+21].
$X_{\operatorname {\mathrm {ns}}}^+(17)$
labeled 13.91.3.2 and 17.136.6.1 are handled via nonabelian Chabauty by Balakrishnan et al. in [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+21]. -
8. Rouse and Zureick-Brown addressed all
 $X_H$
of
$X_H$
of
 $2$
-power level in [Reference Rouse and Zureick-BrownRZB15].
$2$
-power level in [Reference Rouse and Zureick-BrownRZB15]. -
9. The group with label 7.42.1.1 is the index 2 subgroup of
 $N_{\operatorname {\mathrm {sp}}}(7)$
containing the elements of
$N_{\operatorname {\mathrm {sp}}}(7)$
containing the elements of
 $C_{\operatorname {\mathrm {sp}}}(7)$
with square determinant and the elements of
$C_{\operatorname {\mathrm {sp}}}(7)$
with square determinant and the elements of
 $N_{\operatorname {\mathrm {sp}}}(7) - C_{\operatorname {\mathrm {sp}}}(7)$
with nonsquare determinant, handled by [Reference SutherlandSut12a, Section 3] and [Reference ZywinaZyw15a, Remark 4.3]. There is one exceptional j-invariant, which is interesting because elliptic curves with this mod 7 image admit a rational 7-isogeny locally everywhere but not globally; this is the unique example of this phenomenon over
$N_{\operatorname {\mathrm {sp}}}(7) - C_{\operatorname {\mathrm {sp}}}(7)$
with nonsquare determinant, handled by [Reference SutherlandSut12a, Section 3] and [Reference ZywinaZyw15a, Remark 4.3]. There is one exceptional j-invariant, which is interesting because elliptic curves with this mod 7 image admit a rational 7-isogeny locally everywhere but not globally; this is the unique example of this phenomenon over
 $\mathbb {Q}$
for any prime
$\mathbb {Q}$
for any prime
 $\ell $
.
$\ell $
. -
10. Zywina addressed all remaining curves of prime level
 $\ell \leq 37$
except
$\ell \leq 37$
except
 $N_{\operatorname {\mathrm {ns}}}(\ell )$
in [Reference ZywinaZyw15a].
$N_{\operatorname {\mathrm {ns}}}(\ell )$
in [Reference ZywinaZyw15a]. -
11. Elkies showed that the curve 9.81.1.1 has no rational points in [Reference ElkiesElk06, p. 5].
-
12. Noncuspidal points on the modular curves labeled 49.168.12.1 and 49.168.12.2 are ‘
 $7$
-exceptional’ in the sense of [Reference Greenberg, Rubin, Silverberg and StollGRSS14, Definition 1.1].Footnote
5
By [Reference Greenberg, Rubin, Silverberg and StollGRSS14, page 3], the only
$7$
-exceptional’ in the sense of [Reference Greenberg, Rubin, Silverberg and StollGRSS14, Definition 1.1].Footnote
5
By [Reference Greenberg, Rubin, Silverberg and StollGRSS14, page 3], the only
 $7$
-exceptional elliptic curves are CM curves with
$7$
-exceptional elliptic curves are CM curves with
 $j = -15^3$
and
$j = -15^3$
and
 $j = 255^3$
, which give rise to two points on the curve with label 49.168.12.2.
$j = 255^3$
, which give rise to two points on the curve with label 49.168.12.2. -
13. The groups with labels 25.150.4.1, 25.150.4.2, 25.150.4.5 and 25.150.4.6 correspond to elliptic curves
 $E/\mathbb {Q}$
that admit a rational
$E/\mathbb {Q}$
that admit a rational
 $5$
-isogeny with
$5$
-isogeny with
 $5$
-adic image of index divisible by
$5$
-adic image of index divisible by
 $25$
; their existence is ruled out by [Reference GreenbergGre12, Theorem 2].
$25$
; their existence is ruled out by [Reference GreenbergGre12, Theorem 2]. -
14. The genus 2 rank 2 curves 25.50.2.1 and 25.75.2.1 are handled by Balakrishnan et al. in [Reference Balakrishnan, Dogra, Müller, Tuitman and VonkBDM+21, 4.3]. Each has a single exceptional j-invariant, and the minimal conductors for the two j-invariants are 396900 and 21175, respectively.
Of the 210 arithmetically maximal subgroups in Table 3, only 32 are not addressed above. Five are the groups
![]() $N_{\mathrm {ns}}(\ell )$
for
$N_{\mathrm {ns}}(\ell )$
for
![]() $19\le \ell \le 37$
; the remaining 27 are listed in Table 5.
$19\le \ell \le 37$
; the remaining 27 are listed in Table 5.
Table 5 The arithmetically maximal subgroups of
![]() $\ell $
-power level for
$\ell $
-power level for
![]() $\ell \le 17$
not addressed by previous results. Subgroups marked with asterisks are the subgroups H listed in Table 2 for which we are not able to determine
$\ell \le 17$
not addressed by previous results. Subgroups marked with asterisks are the subgroups H listed in Table 2 for which we are not able to determine
![]() $X_H(\mathbb {Q})$
.
$X_H(\mathbb {Q})$
.

5 Counting
 ${\mathbb F}_q$
-points on
${\mathbb F}_q$
-points on
 $X_H$
$X_H$
For any prime power
![]() $q=p^e$
coprime to N and
$q=p^e$
coprime to N and
![]() $H\le \operatorname {GL}_2(N)$
, we may consider the modular curve
$H\le \operatorname {GL}_2(N)$
, we may consider the modular curve
![]() $X_H$
over the finite field
$X_H$
over the finite field
![]() ${\mathbb F}_q$
. We can count
${\mathbb F}_q$
. We can count
![]() ${\mathbb F}_q$
-rational points on
${\mathbb F}_q$
-rational points on
![]() $X_H$
via
$X_H$
via
by counting fixed points of a right
![]() $G_{{\mathbb F}_q}$
-action on certain double coset spaces of
$G_{{\mathbb F}_q}$
-action on certain double coset spaces of
![]() $\operatorname {GL}_2(N)$
defined in Subsection 2.3. In this section, we explain how to do this explicitly and efficiently via a refinement of the method proposed in [Reference ZywinaZyw15b, Section 3]. Applications include:
$\operatorname {GL}_2(N)$
defined in Subsection 2.3. In this section, we explain how to do this explicitly and efficiently via a refinement of the method proposed in [Reference ZywinaZyw15b, Section 3]. Applications include:
-
○ checking for p-adic obstructions to rational points (by checking if
 $\#X_H({\mathbb F}_p)=0$
);
$\#X_H({\mathbb F}_p)=0$
); -
○ computing the zeta function of
 $X_H/{\mathbb F}_p$
(by computing
$X_H/{\mathbb F}_p$
(by computing
 $\#X_H({\mathbb F}_{p^r})$
for
$\#X_H({\mathbb F}_{p^r})$
for
 $1\le r\le g(H)$
);
$1\le r\le g(H)$
); -
○ determining the isogeny decomposition of
 $\operatorname {\mathrm {Jac}}(X_H)$
;
$\operatorname {\mathrm {Jac}}(X_H)$
; -
○ determining the analytic rank of
 $\operatorname {\mathrm {Jac}}(X_H)$
.
$\operatorname {\mathrm {Jac}}(X_H)$
.
The last two are described in Section 6. None require an explicit model for
![]() $X_H$
.
$X_H$
.
5.1 Counting points
If we put
![]() , we can use the permutation representation provided by the right
, we can use the permutation representation provided by the right
![]() $G_{{\mathbb F}_q}$
-action on the coset space
$G_{{\mathbb F}_q}$
-action on the coset space
![]() $[\overline {H}\backslash \operatorname {GL}_2(N)]$
to compute
$[\overline {H}\backslash \operatorname {GL}_2(N)]$
to compute
as the number of
![]() $\left [\begin {smallmatrix} 1 & 1 \\ 0 & 1 \end {smallmatrix}\right ]$
-orbits of
$\left [\begin {smallmatrix} 1 & 1 \\ 0 & 1 \end {smallmatrix}\right ]$
-orbits of
![]() $[\overline {H}\backslash \operatorname {GL}_2(N)]$
stable under the action of
$[\overline {H}\backslash \operatorname {GL}_2(N)]$
stable under the action of
![]() $\left [\begin {smallmatrix} q & 0 \\ 0 & 1 \end {smallmatrix}\right ]$
, which we note depends only on
$\left [\begin {smallmatrix} q & 0 \\ 0 & 1 \end {smallmatrix}\right ]$
, which we note depends only on
![]() $q\bmod N$
; if one expects to compute
$q\bmod N$
; if one expects to compute
![]() $\#X_H^{\infty }({\mathbb F}_q)$
for many finite fields
$\#X_H^{\infty }({\mathbb F}_q)$
for many finite fields
![]() ${\mathbb F}_q$
(as when computing the L-function of
${\mathbb F}_q$
(as when computing the L-function of
![]() $X_H/\mathbb {Q}$
, for example), one can simply precompute a table of rational cusp counts indexed by
$X_H/\mathbb {Q}$
, for example), one can simply precompute a table of rational cusp counts indexed by
![]() $(\mathbb {Z}/N\mathbb {Z})^{\times }$
.
$(\mathbb {Z}/N\mathbb {Z})^{\times }$
.
To compute
 $$ \begin{align} \#Y_H({\mathbb F}_q) = \sum_{j(E)\in k} \#(H\backslash \operatorname{GL}_2(N)/A_E)^{G_{{\mathbb F}_q}}, \end{align} $$
$$ \begin{align} \#Y_H({\mathbb F}_q) = \sum_{j(E)\in k} \#(H\backslash \operatorname{GL}_2(N)/A_E)^{G_{{\mathbb F}_q}}, \end{align} $$
we first note that
![]() , so we may replace H with
, so we may replace H with
![]() $\overline {H}$
and work with the quotient
$\overline {H}$
and work with the quotient
![]() $A_E/\pm I$
, which is trivial for
$A_E/\pm I$
, which is trivial for
![]() $j(E)\ne 0,1728$
. It then suffices to count elements of
$j(E)\ne 0,1728$
. It then suffices to count elements of
![]() $[\overline {H}\backslash \operatorname {GL}_2(N)]$
fixed by
$[\overline {H}\backslash \operatorname {GL}_2(N)]$
fixed by
![]() $G_{{\mathbb F}_q}$
using the action of the Frobenius endomorphism
$G_{{\mathbb F}_q}$
using the action of the Frobenius endomorphism
![]() $\pi $
on
$\pi $
on
![]() $E[N]$
with respect to some basis; we are free to choose any basis we like, since the number of elements of
$E[N]$
with respect to some basis; we are free to choose any basis we like, since the number of elements of
![]() $[\overline {H}\backslash \operatorname {GL}_2(N)]$
fixed by a matrix in
$[\overline {H}\backslash \operatorname {GL}_2(N)]$
fixed by a matrix in
![]() $\operatorname {GL}_2(N)$
is invariant under conjugation. By [Reference Duke and TóthDT02, Theorem 2.1], we can use the reduction modulo N of the integer matrix
$\operatorname {GL}_2(N)$
is invariant under conjugation. By [Reference Duke and TóthDT02, Theorem 2.1], we can use the reduction modulo N of the integer matrix

where
![]() $a,b,\Delta ,d\in \mathbb {Z}$
are defined as follows. Let
$a,b,\Delta ,d\in \mathbb {Z}$
are defined as follows. Let
![]() , let
, let
![]() , let
, let
![]() , and let
, and let
![]() if
if
![]() $\mathbb {Z}[\pi ]\ne \mathbb {Z}$
, and let
$\mathbb {Z}[\pi ]\ne \mathbb {Z}$
, and let
![]() otherwise, so that we always have
otherwise, so that we always have
and let
![]() . We then have
. We then have
![]() $\operatorname {\mathrm {tr}} A_{\pi }\equiv \operatorname {\mathrm {tr}} \pi \bmod N$
and
$\operatorname {\mathrm {tr}} A_{\pi }\equiv \operatorname {\mathrm {tr}} \pi \bmod N$
and
![]() $\det A_{\pi }\equiv q\bmod N$
. We note that
$\det A_{\pi }\equiv q\bmod N$
. We note that
![]() $A_{\pi }$
is uniquely determined by
$A_{\pi }$
is uniquely determined by
![]() $\operatorname {\mathrm {tr}}\pi $
and
$\operatorname {\mathrm {tr}}\pi $
and
![]() $\Delta $
and represents an element of
$\Delta $
and represents an element of
![]() $\operatorname {GL}_2(N)$
for every integer N coprime to q.
$\operatorname {GL}_2(N)$
for every integer N coprime to q.
Let
![]() $\chi _{\overline {H}}\colon \operatorname {GL}_2(N)\to \mathbb {Z}_{\ge 0}$
denote the character of the permutation representation given by the right
$\chi _{\overline {H}}\colon \operatorname {GL}_2(N)\to \mathbb {Z}_{\ge 0}$
denote the character of the permutation representation given by the right
![]() $\operatorname {GL}_2(N)$
-set
$\operatorname {GL}_2(N)$
-set
![]() $[\overline {H}\backslash \operatorname {GL}_2(N)]$
. Each term in equation (5.1) for
$[\overline {H}\backslash \operatorname {GL}_2(N)]$
. Each term in equation (5.1) for
![]() $j(E)\ne 0,1728$
can be computed as
$j(E)\ne 0,1728$
can be computed as
![]() $\chi _{\overline {H}}(A_{\pi })$
. It follows from the theory of complex multiplication that for each imaginary quadratic discriminant
$\chi _{\overline {H}}(A_{\pi })$
. It follows from the theory of complex multiplication that for each imaginary quadratic discriminant
![]() $\Delta $
for which the norm equation (5.3) has a solution with
$\Delta $
for which the norm equation (5.3) has a solution with
![]() $a>0$
coprime to q, there are exactly
$a>0$
coprime to q, there are exactly
![]() $h(\Delta )$
ordinary j-invariants of elliptic curves over
$h(\Delta )$
ordinary j-invariants of elliptic curves over
![]() ${\mathbb F}_q$
with
${\mathbb F}_q$
with
![]() $\operatorname {\mathrm {disc}}(R_{\pi })=\Delta $
, where
$\operatorname {\mathrm {disc}}(R_{\pi })=\Delta $
, where
![]() $h(\Delta )$
is the class number; see [Reference SutherlandSut11, Proposition 1], for example. We thus compute the number of
$h(\Delta )$
is the class number; see [Reference SutherlandSut11, Proposition 1], for example. We thus compute the number of
![]() ${\mathbb F}_q$
-points on
${\mathbb F}_q$
-points on
![]() $X_H$
corresponding to ordinary
$X_H$
corresponding to ordinary
![]() $j(E)\ne 0,1728$
via
$j(E)\ne 0,1728$
via
 $$ \begin{align} \#X_H^{\mathrm{{ord}'}}({\mathbb F}_q) = \sum_{\substack{0<a<2\sqrt{q}\\ \gcd(a,q)=1}}\ \sum_{\substack{4q=a^2-b^2\Delta\\ \Delta <-4}} h(\Delta)\chi_{\overline{H}}\bigl(A(a,b,\Delta)\bigr). \end{align} $$
$$ \begin{align} \#X_H^{\mathrm{{ord}'}}({\mathbb F}_q) = \sum_{\substack{0<a<2\sqrt{q}\\ \gcd(a,q)=1}}\ \sum_{\substack{4q=a^2-b^2\Delta\\ \Delta <-4}} h(\Delta)\chi_{\overline{H}}\bigl(A(a,b,\Delta)\bigr). \end{align} $$
To count supersingular points in
![]() $X_H({\mathbb F}_q)$
with
$X_H({\mathbb F}_q)$
with
![]() $j\ne 0,1728$
, we rely on the following lemma.
$j\ne 0,1728$
, we rely on the following lemma.
Lemma 5.1. Let
![]() $q=p^e$
be a prime power, let
$q=p^e$
be a prime power, let
![]() $H\le \operatorname {GL}_2(N)$
with
$H\le \operatorname {GL}_2(N)$
with
![]() $\gcd (q,N)=1$
, let
$\gcd (q,N)=1$
, let
![]() $h'=\lfloor h(-4p)/2\rfloor $
, and let
$h'=\lfloor h(-4p)/2\rfloor $
, and let
![]() $s_0=1$
for
$s_0=1$
for
![]() $p\equiv 2\bmod 3$
and
$p\equiv 2\bmod 3$
and
![]() $s_0=0$
otherwise. The number
$s_0=0$
otherwise. The number
![]() $\#X_H^{\mathrm {ss'}}({\mathbb F}_q)$
of
$\#X_H^{\mathrm {ss'}}({\mathbb F}_q)$
of
![]() ${\mathbb F}_q$
-points on
${\mathbb F}_q$
-points on
![]() $X_H$
corresponding to supersingular
$X_H$
corresponding to supersingular
![]() $j(E)\ne 0,1728$
can be computed as follows.
$j(E)\ne 0,1728$
can be computed as follows.
-
○ If
 $p\le 3$
, then
$p\le 3$
, then
 $\#X_H^{\mathrm {ss'}}({\mathbb F}_q)=0$
.
$\#X_H^{\mathrm {ss'}}({\mathbb F}_q)=0$
. -
○ If e is odd and
 $p\equiv 1\bmod 4$
, then
$p\equiv 1\bmod 4$
, then  $$\begin{align*}\#X_H^{\mathrm{ss'}}({\mathbb F}_q) = (h'-s_0)\chi_{\overline{H}}\bigl(A(0,p^{(e-1)/2},-4p)\bigr). \end{align*}$$
$$\begin{align*}\#X_H^{\mathrm{ss'}}({\mathbb F}_q) = (h'-s_0)\chi_{\overline{H}}\bigl(A(0,p^{(e-1)/2},-4p)\bigr). \end{align*}$$
-
○ If e is odd and
 $p\equiv 3\bmod 4$
, then
$p\equiv 3\bmod 4$
, then  $$ \begin{align*} \#X_H^{\mathrm{ss'}}({\mathbb F}_q) = h'\chi_{\overline{H}}\bigl(A(0,2p^{(e-1)/2},-p)\bigr) + (h'-s_0)\chi_{\overline{H}}\bigl(A(0,p^{(e-1)/2},-4p)\bigr). \end{align*} $$
$$ \begin{align*} \#X_H^{\mathrm{ss'}}({\mathbb F}_q) = h'\chi_{\overline{H}}\bigl(A(0,2p^{(e-1)/2},-p)\bigr) + (h'-s_0)\chi_{\overline{H}}\bigl(A(0,p^{(e-1)/2},-4p)\bigr). \end{align*} $$
-
○ If e is even then
 $$\begin{align*}\#X_H^{\mathrm{ss'}}({\mathbb F}_q) = \Biggl(\frac{p-6+2\left(\frac{-3}{p}\right)+3\left(\frac{-4}{p}\right)}{12}\Biggr) \chi_{\overline{H}}\bigl(A(2p^{e/2},0,1)\bigr). \end{align*}$$
$$\begin{align*}\#X_H^{\mathrm{ss'}}({\mathbb F}_q) = \Biggl(\frac{p-6+2\left(\frac{-3}{p}\right)+3\left(\frac{-4}{p}\right)}{12}\Biggr) \chi_{\overline{H}}\bigl(A(2p^{e/2},0,1)\bigr). \end{align*}$$
Proof. These formulas are derived from [Reference SchoofSch87, Theorem 4.6] by discarding
![]() ${\mathbb F}_q$
-isomorphism classes with
${\mathbb F}_q$
-isomorphism classes with
![]() $j(E)=0,1728$
and dividing by 2 to count j-invariants rather than counting
$j(E)=0,1728$
and dividing by 2 to count j-invariants rather than counting
![]() ${\mathbb F}_q$
-isomorphism classes. For
${\mathbb F}_q$
-isomorphism classes. For
![]() $p=2,3$
, there are no supersingular
$p=2,3$
, there are no supersingular
![]() $j(E)\ne 0,1728$
, and for
$j(E)\ne 0,1728$
, and for
![]() $p>3$
and
$p>3$
and
![]() $j(E)\ne 0,1728$
, we only need to consider supersingular
$j(E)\ne 0,1728$
, we only need to consider supersingular
![]() ${\mathbb F}_q$
-isomorphism classes with trace
${\mathbb F}_q$
-isomorphism classes with trace
![]() $a=0$
and
$a=0$
and
![]() $\Delta =-0,-4p$
when e is odd, and with trace
$\Delta =-0,-4p$
when e is odd, and with trace
![]() $a=2p^{e/2}$
and
$a=2p^{e/2}$
and
![]() $\Delta =1$
when e is even. In each case, the number of supersingular
$\Delta =1$
when e is even. In each case, the number of supersingular
![]() ${\mathbb F}_q$
-isomorphism classes with j-invariant
${\mathbb F}_q$
-isomorphism classes with j-invariant
![]() $0,1728$
that we need to discard can be determined using Table 6 below.
$0,1728$
that we need to discard can be determined using Table 6 below.
Table 6
![]() ${\mathbb F}_{p^e}$
-isomorphism classes of elliptic curves with j-invariant
${\mathbb F}_{p^e}$
-isomorphism classes of elliptic curves with j-invariant
![]() $0$
or
$0$
or
![]() $1728$
.
$1728$
.

For
![]() $j(E)=0,1728$
, rather than computing double cosets fixed by
$j(E)=0,1728$
, rather than computing double cosets fixed by
![]() $G_k$
, we instead compute a weighted sum of
$G_k$
, we instead compute a weighted sum of
![]() $\chi _{\overline {H}}(A_{\pi })$
over k-isomorphism classes of elliptic curves with
$\chi _{\overline {H}}(A_{\pi })$
over k-isomorphism classes of elliptic curves with
![]() $j(E)=0,1728$
via the table below. If we extend the permutation character
$j(E)=0,1728$
via the table below. If we extend the permutation character
![]() $\chi _{\overline {H}}$
to the group ring
$\chi _{\overline {H}}$
to the group ring
![]() $\mathbb {Q}[\operatorname {GL}_2(N)]$
, we can compute the number of k-rational points of
$\mathbb {Q}[\operatorname {GL}_2(N)]$
, we can compute the number of k-rational points of
![]() $X_H$
above
$X_H$
above
![]() $j=0,1728\in X(1)$
via
$j=0,1728\in X(1)$
via
 $$\begin{align*}\# X_H^{j=0}({\mathbb F}_q)= \chi_{\overline{H}}\left(\sum_{\substack{j(E)=0\\p\ne 2}} \frac{A(a,b,\Delta)}{\#\operatorname{\mathrm{Aut}}(E)} \right), \qquad \#X_H^{j=1728}({\mathbb F}_q) = \chi_{\overline{H}}\left(\sum_{\substack{j(E)=1728\\p\ne 3}} \frac{A(a,b,\Delta)}{\#\operatorname{\mathrm{Aut}}(E)} \right), \end{align*}$$
$$\begin{align*}\# X_H^{j=0}({\mathbb F}_q)= \chi_{\overline{H}}\left(\sum_{\substack{j(E)=0\\p\ne 2}} \frac{A(a,b,\Delta)}{\#\operatorname{\mathrm{Aut}}(E)} \right), \qquad \#X_H^{j=1728}({\mathbb F}_q) = \chi_{\overline{H}}\left(\sum_{\substack{j(E)=1728\\p\ne 3}} \frac{A(a,b,\Delta)}{\#\operatorname{\mathrm{Aut}}(E)} \right), \end{align*}$$
where the sums are over
![]() ${\mathbb F}_q$
-isomorphism classes of elliptic curves
${\mathbb F}_q$
-isomorphism classes of elliptic curves
![]() $E/{\mathbb F}_q$
, and the values of
$E/{\mathbb F}_q$
, and the values of
![]() $a,b,\Delta $
are listed in Table 6. These values are derived from [Reference WaterhouseWat69] and [Reference SchoofSch87], and we note that for each triple
$a,b,\Delta $
are listed in Table 6. These values are derived from [Reference WaterhouseWat69] and [Reference SchoofSch87], and we note that for each triple
![]() $(|a|,b,\Delta )$
with
$(|a|,b,\Delta )$
with
![]() $|a|>0$
listed in the table with multiplicity m, the triples
$|a|>0$
listed in the table with multiplicity m, the triples
![]() $(a,b,\Delta )$
and
$(a,b,\Delta )$
and
![]() $(-a,b,\Delta )$
each occur with multiplicity
$(-a,b,\Delta )$
each occur with multiplicity
![]() $m/2$
.
$m/2$
.
To sum up, for any
![]() $H\le \operatorname {GL}_2(N)$
, we can compute
$H\le \operatorname {GL}_2(N)$
, we can compute
![]() $\#X_H({\mathbb F}_q)$
as
$\#X_H({\mathbb F}_q)$
as
where each term in the sum is computed using the permutation representation
![]() $[\overline {H}\backslash \operatorname {GL}_2(N)]$
: the term
$[\overline {H}\backslash \operatorname {GL}_2(N)]$
: the term
![]() $\#X_H^{\infty }({\mathbb F}_q)$
is computed by counting
$\#X_H^{\infty }({\mathbb F}_q)$
is computed by counting
![]() $\left [\begin {smallmatrix} q & 0 \\ 0 & q \end {smallmatrix}\right ]$
-stable
$\left [\begin {smallmatrix} q & 0 \\ 0 & q \end {smallmatrix}\right ]$
-stable
![]() $\left [\begin {smallmatrix} 1 & 1 \\ 0 & 1 \end {smallmatrix}\right ]$
-orbits, and the remaining terms are weighted sums of values of the permutation character
$\left [\begin {smallmatrix} 1 & 1 \\ 0 & 1 \end {smallmatrix}\right ]$
-orbits, and the remaining terms are weighted sums of values of the permutation character
![]() $\chi _{\overline {H}}$
on the matrices
$\chi _{\overline {H}}$
on the matrices
![]() $A(a,b,\Delta )$
arising for elliptic curves
$A(a,b,\Delta )$
arising for elliptic curves
![]() $E/{\mathbb F}_q$
. A Magma implementation of the formula in equation (5.5) is provided by the function GL2PointCount in the file gl2.m in [Reference Rouse, Sutherland and Zureick-BrownRSZB21].
$E/{\mathbb F}_q$
. A Magma implementation of the formula in equation (5.5) is provided by the function GL2PointCount in the file gl2.m in [Reference Rouse, Sutherland and Zureick-BrownRSZB21].
Example 5.2. Consider
![]() $H=\{\left [\begin {smallmatrix} 1 & * \\ 0 & * \end {smallmatrix}\right ]\}\le \operatorname {GL}_2(13)$
with label 13.168.2.1. The modular curve
$H=\{\left [\begin {smallmatrix} 1 & * \\ 0 & * \end {smallmatrix}\right ]\}\le \operatorname {GL}_2(13)$
with label 13.168.2.1. The modular curve
![]() $X_H=X_1(13)$
parametrises elliptic curves with a rational point of order 13. Over
$X_H=X_1(13)$
parametrises elliptic curves with a rational point of order 13. Over
![]() ${\mathbb F}_{37}$
, there are four such elliptic curves, up to
${\mathbb F}_{37}$
, there are four such elliptic curves, up to
![]() ${\mathbb F}_{37}$
-isomorphism, each with 12 points of order 13 with distinct j-invariants
${\mathbb F}_{37}$
-isomorphism, each with 12 points of order 13 with distinct j-invariants
![]() $0$
,
$0$
,
![]() $16$
,
$16$
,
![]() $26=1728$
,
$26=1728$
,
![]() $35$
(none are supersingular) and automorphism groups of order 6, 2, 4, 2, respectively. We thus expect
$35$
(none are supersingular) and automorphism groups of order 6, 2, 4, 2, respectively. We thus expect
![]() $\#Y_H({\mathbb F}_{37}) = 12/6 + 12/2 + 12/4 + 12/2 = 17$
, and one can check that 6 of the 12 cusps of
$\#Y_H({\mathbb F}_{37}) = 12/6 + 12/2 + 12/4 + 12/2 = 17$
, and one can check that 6 of the 12 cusps of
![]() $X_1(13)$
are
$X_1(13)$
are
![]() ${\mathbb F}_{37}$
-rational (those of width of 13). This agrees with the fact that there are 23 rational points on the mod-37 reduction of the genus 2 curve
${\mathbb F}_{37}$
-rational (those of width of 13). This agrees with the fact that there are 23 rational points on the mod-37 reduction of the genus 2 curve
![]() $y^2+(x^3+x+1)y=x^5+x^4$
, which is a
$y^2+(x^3+x+1)y=x^5+x^4$
, which is a
![]() $\mathbb {Z}[1/13]$
-model for
$\mathbb {Z}[1/13]$
-model for
![]() $X_H=X_1(13)$
.
$X_H=X_1(13)$
.
To compute
![]() $\#X_H({\mathbb F}_{37})$
using the algorithm proposed above, we apply equation (5.5), which does not require us to enumerate elliptic curves with a point of order 13. We compute
$\#X_H({\mathbb F}_{37})$
using the algorithm proposed above, we apply equation (5.5), which does not require us to enumerate elliptic curves with a point of order 13. We compute
![]() $\#X_H^{\infty }({\mathbb F}_{37})=6$
by noting that the coset space
$\#X_H^{\infty }({\mathbb F}_{37})=6$
by noting that the coset space
![]() $[\overline {H}\backslash \operatorname {GL}_2(13)]$
has twelve
$[\overline {H}\backslash \operatorname {GL}_2(13)]$
has twelve
![]() $\left [\begin {smallmatrix} 1 & 1 \\ 0 & 1 \end {smallmatrix}\right ]$
-orbits, six of size 1 and six of size 13, the latter of which are stable under the action of
$\left [\begin {smallmatrix} 1 & 1 \\ 0 & 1 \end {smallmatrix}\right ]$
-orbits, six of size 1 and six of size 13, the latter of which are stable under the action of
![]() $\left [\begin {smallmatrix} 37 & 0 \\ 0 & 1 \end {smallmatrix}\right ]\equiv \left [\begin {smallmatrix} 11 & 0 \\ 0 & 1 \end {smallmatrix}\right ]$
. Enumerating integers
$\left [\begin {smallmatrix} 37 & 0 \\ 0 & 1 \end {smallmatrix}\right ]\equiv \left [\begin {smallmatrix} 11 & 0 \\ 0 & 1 \end {smallmatrix}\right ]$
. Enumerating integers
![]() $a\in [1,\lfloor 2\sqrt {37}\rfloor ]$
yields 17 triples
$a\in [1,\lfloor 2\sqrt {37}\rfloor ]$
yields 17 triples
![]() $(a,b,\Delta )$
with
$(a,b,\Delta )$
with
![]() $\Delta < -4$
that satisfy the norm equation (5.3). Among these, only
$\Delta < -4$
that satisfy the norm equation (5.3). Among these, only
![]() $A(1,1,-147)$
fixes an element of
$A(1,1,-147)$
fixes an element of
![]() $[\overline {H}\backslash \operatorname {GL}_2(13)]$
, and from equation (5.4), we obtain
$[\overline {H}\backslash \operatorname {GL}_2(13)]$
, and from equation (5.4), we obtain
To compute
![]() $\#X_H^{\mathrm {ss'}}({\mathbb F}_{37})$
, we apply Lemma 5.1 and find that
$\#X_H^{\mathrm {ss'}}({\mathbb F}_{37})$
, we apply Lemma 5.1 and find that
![]() $\chi _{\overline {H}}(A(0,0,-4\cdot 37))=0$
, so
$\chi _{\overline {H}}(A(0,0,-4\cdot 37))=0$
, so
![]() $\#X_H^{\mathrm {ss'}}({\mathbb F}_q) =0$
. Using Table 6, we compute
$\#X_H^{\mathrm {ss'}}({\mathbb F}_q) =0$
. Using Table 6, we compute
 $$ \begin{align*} \#X_H^{j=0}({\mathbb F}_{37}) &= \chi_{\overline{H}}(A(\pm 1,7,-3)/6 + A(\pm 10, 4,-3)/6 + A(\pm 11,3,-3)/6)=2+0+0=2\\ \#X_H^{j=1728}({\mathbb F}_{37}) &= \chi_{\overline{H}}(A(\pm 2,6,-4)/4 + A(\pm 12, 1,-4)/4)=0+3=3, \end{align*} $$
$$ \begin{align*} \#X_H^{j=0}({\mathbb F}_{37}) &= \chi_{\overline{H}}(A(\pm 1,7,-3)/6 + A(\pm 10, 4,-3)/6 + A(\pm 11,3,-3)/6)=2+0+0=2\\ \#X_H^{j=1728}({\mathbb F}_{37}) &= \chi_{\overline{H}}(A(\pm 2,6,-4)/4 + A(\pm 12, 1,-4)/4)=0+3=3, \end{align*} $$
and equation (5.5) then yields
 $$ \begin{align*} \#X_H({\mathbb F}_{37}) &= \#X_H^{\infty}({\mathbb F}_{37}) + \#X_H^{\mathrm{ord'}}({\mathbb F}_{37}) +\#X_H^{\mathrm{ss'}}({\mathbb F}_{37}) +\#X_H^{j=0}({\mathbb F}_{37}) +\#X_H^{j=1728}({\mathbb F}_{37})\\ &= 6 + 12 + 0 + 2 + 3 = 23. \end{align*} $$
$$ \begin{align*} \#X_H({\mathbb F}_{37}) &= \#X_H^{\infty}({\mathbb F}_{37}) + \#X_H^{\mathrm{ord'}}({\mathbb F}_{37}) +\#X_H^{\mathrm{ss'}}({\mathbb F}_{37}) +\#X_H^{j=0}({\mathbb F}_{37}) +\#X_H^{j=1728}({\mathbb F}_{37})\\ &= 6 + 12 + 0 + 2 + 3 = 23. \end{align*} $$
In contrast to the method described in [Reference ZywinaZyw15b, Section 3], in our computation above, we did not enumerate elliptic curves or j-invariants over
![]() ${\mathbb F}_q$
, nor did we compute any Hilbert class polynomials (a commonly used but inefficient way to compute
${\mathbb F}_q$
, nor did we compute any Hilbert class polynomials (a commonly used but inefficient way to compute
![]() $A_{\pi }$
). Instead, we enumerated possible Frobenius traces
$A_{\pi }$
). Instead, we enumerated possible Frobenius traces
![]() $a>0$
, solved norm equations, computed class numbers and computed values of the permutation character
$a>0$
, solved norm equations, computed class numbers and computed values of the permutation character
![]() $\chi _{\overline {H}}$
. This can be viewed as an algorithmic generalisation of the Eichler–Selberg trace formula that works for any open
$\chi _{\overline {H}}$
. This can be viewed as an algorithmic generalisation of the Eichler–Selberg trace formula that works for any open
![]() $H\le \operatorname {GL}_2({\widehat {\mathbb {Z}}})$
. It has roughly the same asymptotic complexity as the trace formula (the dependence on q is
$H\le \operatorname {GL}_2({\widehat {\mathbb {Z}}})$
. It has roughly the same asymptotic complexity as the trace formula (the dependence on q is
![]() $\tilde O(q^{1/2})$
if we ignore the cost of computing class numbers, which in practice we simply look up in a table such as those available for
$\tilde O(q^{1/2})$
if we ignore the cost of computing class numbers, which in practice we simply look up in a table such as those available for
![]() $|D|\le 2^{40}$
in the LMFDB). But the constant factors are better, and even for groups that do not contain the
$|D|\le 2^{40}$
in the LMFDB). But the constant factors are better, and even for groups that do not contain the
![]() $\operatorname {GL}_2$
-analog of
$\operatorname {GL}_2$
-analog of
![]() $\Gamma _1(N)$
, we are always able to work at level N rather than level
$\Gamma _1(N)$
, we are always able to work at level N rather than level
![]() $N^2$
, as typically required by generalisations of the trace formula to handle congruence subgroups that do not contain
$N^2$
, as typically required by generalisations of the trace formula to handle congruence subgroups that do not contain
![]() $\Gamma _1(N)$
.
$\Gamma _1(N)$
.
5.2 Local obstructions
An easy application of this point counting algorithm is checking for local obstructions to rational points on the arithmetically maximal modular curves
![]() $X_H$
. For
$X_H$
. For
![]() $X_H$
of genus g, it suffices to compute
$X_H$
of genus g, it suffices to compute
![]() $\#X({\mathbb F}_p)$
for
$\#X({\mathbb F}_p)$
for
![]() $p < \lfloor 2g\sqrt {p}\rfloor $
, since the Weil bounds force
$p < \lfloor 2g\sqrt {p}\rfloor $
, since the Weil bounds force
![]() $\#X({\mathbb F}_p)>0$
for all larger primes p. Doing this for the 210 arithmetically maximal groups summarised in Table 4 yields Theorem 5.1, whose results are summarised in Table 7.
$\#X({\mathbb F}_p)>0$
for all larger primes p. Doing this for the 210 arithmetically maximal groups summarised in Table 4 yields Theorem 5.1, whose results are summarised in Table 7.
Theorem 5.1. For
![]() $\ell \le 37$
, the arithmetically maximal
$\ell \le 37$
, the arithmetically maximal
![]() $H\le \operatorname {GL}_2({\widehat {\mathbb {Z}}})$
of
$H\le \operatorname {GL}_2({\widehat {\mathbb {Z}}})$
of
![]() $\ell $
-power level for which
$\ell $
-power level for which
![]() $X_H$
has no
$X_H$
has no
![]() ${\mathbb F}_{p}$
-points for some prime
${\mathbb F}_{p}$
-points for some prime
![]() $p\ne \ell $
are precisely those listed in Table 7.
$p\ne \ell $
are precisely those listed in Table 7.
Table 7 Arithmetically maximal
![]() $H\le \operatorname {GL}_2({\widehat {\mathbb {Z}}})$
of
$H\le \operatorname {GL}_2({\widehat {\mathbb {Z}}})$
of
![]() $\ell $
-power level for which
$\ell $
-power level for which
![]() $X_H$
has no
$X_H$
has no
![]() ${\mathbb F}_p$
-points for some prime
${\mathbb F}_p$
-points for some prime
![]() $p\ne \ell \le 37$
.
$p\ne \ell \le 37$
.

6 Computing the isogeny decomposition and analytic rank of
 $J_H$
$J_H$
Let H be an open subgroup of
![]() $\operatorname {GL}_2({\widehat {\mathbb {Z}}})$
. In this section, we explain how the point-counting algorithm described in the previous section can be used to determine the isogeny factors of the Jacobian
$\operatorname {GL}_2({\widehat {\mathbb {Z}}})$
. In this section, we explain how the point-counting algorithm described in the previous section can be used to determine the isogeny factors of the Jacobian
![]() as modular abelian varieties; this decomposition can then be used to compute the analytic rank of
as modular abelian varieties; this decomposition can then be used to compute the analytic rank of
![]() $J_H$
. To simplify the exposition, we shall assume that
$J_H$
. To simplify the exposition, we shall assume that
![]() $\det (H)={\widehat {\mathbb {Z}}}^{\times }$
, which holds in all the cases of interest to us here, but the methods we describe can also be applied when
$\det (H)={\widehat {\mathbb {Z}}}^{\times }$
, which holds in all the cases of interest to us here, but the methods we describe can also be applied when
![]() $\det (H)\ne {\widehat {\mathbb {Z}}}^{\times }$
; see Example 6.3 for details.
$\det (H)\ne {\widehat {\mathbb {Z}}}^{\times }$
; see Example 6.3 for details.
The Jacobian
![]() $J_H$
is an abelian variety over
$J_H$
is an abelian variety over
![]() $\mathbb {Q}$
that has good reduction at all primes p that do not divide the level N of H. It follows from Theorem A.7 that the simple factors of
$\mathbb {Q}$
that has good reduction at all primes p that do not divide the level N of H. It follows from Theorem A.7 that the simple factors of
![]() $J_H$
are each
$J_H$
are each
![]() $\mathbb {Q}$
-isogenous to the modular abelian variety associated to the Galois orbit of a (not necessarily new, normalised) eigenform of weight 2 for
$\mathbb {Q}$
-isogenous to the modular abelian variety associated to the Galois orbit of a (not necessarily new, normalised) eigenform of weight 2 for
![]() $\Gamma _1(N)\cap \Gamma _0(N^2)$
. We may decompose this space of modular forms as
$\Gamma _1(N)\cap \Gamma _0(N^2)$
. We may decompose this space of modular forms as
 $$\begin{align*}S_2\bigl(\Gamma_1(N)\cap\Gamma_0(N^2)\bigr)=\bigoplus_{\operatorname{\mathrm{cond}}(\chi)|N}\!\!\!S_2\bigl(\Gamma_0(N^2),[\chi]\bigr), \end{align*}$$
$$\begin{align*}S_2\bigl(\Gamma_1(N)\cap\Gamma_0(N^2)\bigr)=\bigoplus_{\operatorname{\mathrm{cond}}(\chi)|N}\!\!\!S_2\bigl(\Gamma_0(N^2),[\chi]\bigr), \end{align*}$$
where
![]() $[\chi ]$
denotes the Galois orbit of the Dirichlet character
$[\chi ]$
denotes the Galois orbit of the Dirichlet character
![]() $\chi $
and the direct sum varies over Galois orbits of Dirichlet characters of modulus
$\chi $
and the direct sum varies over Galois orbits of Dirichlet characters of modulus
![]() $N^2$
whose conductor divides N. The Galois orbit of a normalised eigenform
$N^2$
whose conductor divides N. The Galois orbit of a normalised eigenform
![]() $f\in S_2(\Gamma _0(N^2),[\chi ])$
has an associated trace form
$f\in S_2(\Gamma _0(N^2),[\chi ])$
has an associated trace form
![]() $\operatorname {\mathrm {Tr}}(f)$
(see [Reference Best, Bober, Booker, Costa, Cremona, Maarten, Lee, Lowry-Duda, Roe, Sutherland and VoightBBB+21, Section 4.5]), which has an integral q-expansion
$\operatorname {\mathrm {Tr}}(f)$
(see [Reference Best, Bober, Booker, Costa, Cremona, Maarten, Lee, Lowry-Duda, Roe, Sutherland and VoightBBB+21, Section 4.5]), which has an integral q-expansion
with
; and for each prime p, the coefficient
![]() $a_p$
is the Frobenius trace of the abelian variety
$a_p$
is the Frobenius trace of the abelian variety
![]() $A_f/\mathbb {Q}$
of dimension
$A_f/\mathbb {Q}$
of dimension
![]() $\dim f$
associated to f via the Eichler–Shimura correspondence; equivalently,
$\dim f$
associated to f via the Eichler–Shimura correspondence; equivalently,
![]() $a_p$
is the pth (arithmetically normalised) Dirichlet coefficient of the L-function
$a_p$
is the pth (arithmetically normalised) Dirichlet coefficient of the L-function
![]() $L(A_f,s)=\prod _{f\in [f]}L(f,s)$
.
$L(A_f,s)=\prod _{f\in [f]}L(f,s)$
.
Let
![]() be the Galois orbits of eigenforms
be the Galois orbits of eigenforms
![]() $f\in S_2(\Gamma _1(N)\cap \Gamma _0(N^2))$
with
$f\in S_2(\Gamma _1(N)\cap \Gamma _0(N^2))$
with
![]() $\dim f\le \dim J_H=g(H)$
. Theorem A.7 implies that there is a sequence of nonnegative integers
$\dim f\le \dim J_H=g(H)$
. Theorem A.7 implies that there is a sequence of nonnegative integers
![]() $e(H)=(e_1,\ldots ,e_m)$
for which we have
$e(H)=(e_1,\ldots ,e_m)$
for which we have
 $$\begin{align*}L(J_H,s) = \prod_{i=1}^m L(A_{f_i},s)^{e_i}, \end{align*}$$
$$\begin{align*}L(J_H,s) = \prod_{i=1}^m L(A_{f_i},s)^{e_i}, \end{align*}$$
and this sequence also satisfies
![]() $\sum _i e_i\dim f_i =g(H)$
. Now let
$\sum _i e_i\dim f_i =g(H)$
. Now let
![]() $T(B)$
be the
$T(B)$
be the
![]() $n\times m$
integer matrix whose ith column is
$n\times m$
integer matrix whose ith column is
![]() $[a_1(\operatorname {\mathrm {Tr}}(f_i)),a_2(\operatorname {\mathrm {Tr}}(f_i)),a_3(\operatorname {\mathrm {Tr}}(f_i)),a_5(\operatorname {\mathrm {Tr}}(f_i)),\ldots ,a_p(\operatorname {\mathrm {Tr}}(f_i)),\ldots ]$
, where p varies over the
$[a_1(\operatorname {\mathrm {Tr}}(f_i)),a_2(\operatorname {\mathrm {Tr}}(f_i)),a_3(\operatorname {\mathrm {Tr}}(f_i)),a_5(\operatorname {\mathrm {Tr}}(f_i)),\ldots ,a_p(\operatorname {\mathrm {Tr}}(f_i)),\ldots ]$
, where p varies over the
![]() $n-1$
primes bounded by B that do not divide the level of H, and let
$n-1$
primes bounded by B that do not divide the level of H, and let
![]() $a(H;B)$
be the vector of integers
$a(H;B)$
be the vector of integers
![]() $[g(H),a_2(H),a_3(H),\ldots ,a_p(H),\ldots ]$
, where
$[g(H),a_2(H),a_3(H),\ldots ,a_p(H),\ldots ]$
, where
![]() $a_p(H)$
denotes the trace of the Frobenius endomorphism of
$a_p(H)$
denotes the trace of the Frobenius endomorphism of
![]() $J_H$
at a prime
$J_H$
at a prime
![]() $p\le B$
not dividing the level of H, which we can compute as
$p\le B$
not dividing the level of H, which we can compute as
![]() $a_p(H)= p+1-\#X_H({\mathbb F}_p)$
via equation (5.5). For
$a_p(H)= p+1-\#X_H({\mathbb F}_p)$
via equation (5.5). For
![]() $B\ge 1$
, we have
$B\ge 1$
, we have
and it follows from an effective form of multiplicity 1 for the Selberg class [Reference Kaczorowski and PerelliKP01, Reference SoundararajanSou04] that for all sufficiently large B, the matrix
![]() $T(B)$
and the vector
$T(B)$
and the vector
![]() $a(H,B)$
uniquely determine the vector
$a(H,B)$
uniquely determine the vector
![]() $e(H)$
. Indeed, there are only finitely many sequences of nonnegative integers that sum to
$e(H)$
. Indeed, there are only finitely many sequences of nonnegative integers that sum to
![]() $g(H)$
, and the corresponding L-functions are all distinguished by their Dirichlet coefficients
$g(H)$
, and the corresponding L-functions are all distinguished by their Dirichlet coefficients
![]() $a_p$
on the set of primes
$a_p$
on the set of primes
![]() $p\nmid N$
by strong multiplicity 1; for each pair of these L-functions, there is some smallest
$p\nmid N$
by strong multiplicity 1; for each pair of these L-functions, there is some smallest
![]() $p\nmid N$
for which the
$p\nmid N$
for which the
![]() $a_p$
differ, and we can take B to be the maximum of this p over all pairs. We note that L-functions of modular forms and all products of such L-functions not only lie in the Selberg class but also satisfy the polynomial Euler product condition used in [Reference Kaczorowski and PerelliKP01] and the weaker condition required by [Reference SoundararajanSou04].
$a_p$
differ, and we can take B to be the maximum of this p over all pairs. We note that L-functions of modular forms and all products of such L-functions not only lie in the Selberg class but also satisfy the polynomial Euler product condition used in [Reference Kaczorowski and PerelliKP01] and the weaker condition required by [Reference SoundararajanSou04].
This suggests the following approach to determining the exponents in the factorisation
![]() $L(J_H,s)=\prod _i L(A_{f_i},s)^{e_i}$
, from which both the analytic rank of
$L(J_H,s)=\prod _i L(A_{f_i},s)^{e_i}$
, from which both the analytic rank of
![]() $J_H$
and its isogeny-factor decomposition can be derived. We first determine the set
$J_H$
and its isogeny-factor decomposition can be derived. We first determine the set
![]() $S(H)$
, which we note depends only on the genus and level of H. We then determine a value of B for which the
$S(H)$
, which we note depends only on the genus and level of H. We then determine a value of B for which the
![]() $\#S(H)$
columns of
$\#S(H)$
columns of
![]() $T(B)$
become linearly independent over
$T(B)$
become linearly independent over
![]() $\mathbb {Q}$
: for example, by starting with a value of B that makes
$\mathbb {Q}$
: for example, by starting with a value of B that makes
![]() $T(B)$
a square matrix and successively increasing B by some constant factor
$T(B)$
a square matrix and successively increasing B by some constant factor
![]() $\alpha>1$
. Finally, we compute the vector
$\alpha>1$
. Finally, we compute the vector
![]() $a(H;B)$
by computing
$a(H;B)$
by computing
![]() $p+1-\#X_H({\mathbb F}_p)$
for primes
$p+1-\#X_H({\mathbb F}_p)$
for primes
![]() $p\le B$
not dividing the level of H and determine
$p\le B$
not dividing the level of H and determine
![]() $e(H)$
as the necessarily unique solution to the linear system
$e(H)$
as the necessarily unique solution to the linear system
![]() $T(B)x=a(H;B)$
.
$T(B)x=a(H;B)$
.
This approach is remarkably effective in practice. For the 210 arithmetically maximal H arising for
![]() $\ell \le 37$
, the value of B never exceeds 3000, and the matrix
$\ell \le 37$
, the value of B never exceeds 3000, and the matrix
![]() $T(B)$
with linear independent columns typically has fewer than 100 rows. To compute
$T(B)$
with linear independent columns typically has fewer than 100 rows. To compute
![]() $T(B)$
, we use precomputed trace form data stored in the LMFDB along with additional data available in the file cmfdata.txt in [Reference Rouse, Sutherland and Zureick-BrownRSZB21] that we computed to handle cases where the set
$T(B)$
, we use precomputed trace form data stored in the LMFDB along with additional data available in the file cmfdata.txt in [Reference Rouse, Sutherland and Zureick-BrownRSZB21] that we computed to handle cases where the set
![]() $S(H)$
contains Galois orbits of eigenforms that are not currently stored in the LMFDB, using the methods described in [Reference Best, Bober, Booker, Costa, Cremona, Maarten, Lee, Lowry-Duda, Roe, Sutherland and VoightBBB+21].
$S(H)$
contains Galois orbits of eigenforms that are not currently stored in the LMFDB, using the methods described in [Reference Best, Bober, Booker, Costa, Cremona, Maarten, Lee, Lowry-Duda, Roe, Sutherland and VoightBBB+21].
Remark 6.1. There are special cases in which we know the isogeny factors of
![]() $J_H$
a priori and need not apply the approach described above in order to determine the vector
$J_H$
a priori and need not apply the approach described above in order to determine the vector
![]() $e(H)$
. When H is the Borel subgroup of level N, we have
$e(H)$
. When H is the Borel subgroup of level N, we have
![]() $X_H=X_0(N)$
and the isogeny factors of
$X_H=X_0(N)$
and the isogeny factors of
![]() $J_H$
are the modular abelian varieties associated to the eigenforms
$J_H$
are the modular abelian varieties associated to the eigenforms
![]() $f\in S_2(\Gamma _0(N))$
. When H is the normaliser of a nonsplit Cartan subgroup of prime power level
$f\in S_2(\Gamma _0(N))$
. When H is the normaliser of a nonsplit Cartan subgroup of prime power level
![]() $\ell ^n$
, we have
$\ell ^n$
, we have
![]() $X_H=X_{\operatorname {\mathrm {ns}}}^+(\ell ^n)$
and the isogeny factors of
$X_H=X_{\operatorname {\mathrm {ns}}}^+(\ell ^n)$
and the isogeny factors of
![]() $J_H$
are the modular abelian varieties associated to the eigenforms in
$J_H$
are the modular abelian varieties associated to the eigenforms in
![]() $f\in S_2^{\mathrm {new}}(\Gamma _0(\ell ^{2r}))$
with Fricke eigenvalue 1, for
$f\in S_2^{\mathrm {new}}(\Gamma _0(\ell ^{2r}))$
with Fricke eigenvalue 1, for
![]() $1\le r\le n$
. And when H is the normaliser of a split Cartan subgroup of level
$1\le r\le n$
. And when H is the normaliser of a split Cartan subgroup of level
![]() $\ell ^n$
, we have
$\ell ^n$
, we have
![]() $X_H=X_{\operatorname {\mathrm {sp}}}^+(\ell ^r)$
and the isogeny factors of
$X_H=X_{\operatorname {\mathrm {sp}}}^+(\ell ^r)$
and the isogeny factors of
![]() $J_H$
are the modular abelian varieties associated to the eigenforms in
$J_H$
are the modular abelian varieties associated to the eigenforms in
![]() $f\in S_2(\Gamma _0(\ell ^{2n}))$
with Fricke eigenvalue 1, as shown by Chen [Reference ChenChe04].
$f\in S_2(\Gamma _0(\ell ^{2n}))$
with Fricke eigenvalue 1, as shown by Chen [Reference ChenChe04].
Having determined the vector
![]() $e(H)=[e_1,\ldots ,e_m]$
, we compute the rank of
$e(H)=[e_1,\ldots ,e_m]$
, we compute the rank of
![]() $J_H$
as
$J_H$
as
![]() $\sum _i e_ir_i$
, where each
$\sum _i e_ir_i$
, where each
![]() $r_i$
is the sum of the analytic ranks of the eigenforms in the ith Galois orbit
$r_i$
is the sum of the analytic ranks of the eigenforms in the ith Galois orbit
![]() $[f_i]$
(one expects them to have the same rank as
$[f_i]$
(one expects them to have the same rank as
![]() $f_i$
; this is true for all of the modular forms in the LMFDB and for all of the modular forms that we computed). The method used to rigorously compute the analytic ranks of these modular forms is described in [Reference Best, Bober, Booker, Costa, Cremona, Maarten, Lee, Lowry-Duda, Roe, Sutherland and VoightBBB+21, Section 9].
$f_i$
; this is true for all of the modular forms in the LMFDB and for all of the modular forms that we computed). The method used to rigorously compute the analytic ranks of these modular forms is described in [Reference Best, Bober, Booker, Costa, Cremona, Maarten, Lee, Lowry-Duda, Roe, Sutherland and VoightBBB+21, Section 9].
Example 6.2. Consider the group
![]() $H{\,=\,}\langle \left [\begin {smallmatrix} 4 & 1 \\ 21 & 2 \end {smallmatrix}\right ],\left [\begin {smallmatrix} 11 & 0 \\ 0 & 19 \end {smallmatrix}\right ]\rangle {\,\le \,} \operatorname {GL}_2(27)$
with label 27.36.3.1. Eleven Galois orbits of eigenforms
$H{\,=\,}\langle \left [\begin {smallmatrix} 4 & 1 \\ 21 & 2 \end {smallmatrix}\right ],\left [\begin {smallmatrix} 11 & 0 \\ 0 & 19 \end {smallmatrix}\right ]\rangle {\,\le \,} \operatorname {GL}_2(27)$
with label 27.36.3.1. Eleven Galois orbits of eigenforms
![]() $f\in S_2(\Gamma _1(27)\cap \Gamma _0(27^2))$
have
$f\in S_2(\Gamma _1(27)\cap \Gamma _0(27^2))$
have
![]() $\dim f{\,\le \,} g(H){\,=\,} 3$
, with LMFDB labels 243.2.a.a, 27.2.a.a, 243.2.a.b, 243.2.c.a, 243.2.a.c, 81.2.c.a, 243.2.a.d, 81.2.a.a, 243.2.c.b, 243.2.a.e, and 243.2.a.f. For
$\dim f{\,\le \,} g(H){\,=\,} 3$
, with LMFDB labels 243.2.a.a, 27.2.a.a, 243.2.a.b, 243.2.c.a, 243.2.a.c, 81.2.c.a, 243.2.a.d, 81.2.a.a, 243.2.c.b, 243.2.a.e, and 243.2.a.f. For
![]() $B =73$
the
$B =73$
the
![]() $21\times 11$
matrix
$21\times 11$
matrix
![]() $T(B)$
has independent columns. Computing
$T(B)$
has independent columns. Computing
![]() $\#X_H({\mathbb F}_p)$
for
$\#X_H({\mathbb F}_p)$
for
![]() $p{\,=\,}2,5,7,11,\ldots , 73$
yields
$p{\,=\,}2,5,7,11,\ldots , 73$
yields
, and the linear system

has the unique solution
![]() $e(H)=[1,0,0,0,0,0,1,0,0,0,0]^{\mathrm {T}}$
corresponding to the Galois orbits 243.2.a.a and 243.2.a.d of dimensions 1 and 2 with analytic ranks 1 and 0, respectively; thus
$e(H)=[1,0,0,0,0,0,1,0,0,0,0]^{\mathrm {T}}$
corresponding to the Galois orbits 243.2.a.a and 243.2.a.d of dimensions 1 and 2 with analytic ranks 1 and 0, respectively; thus
![]() $J_H$
has analytic rank 1.
$J_H$
has analytic rank 1.
We used the method described above to compute the analytic ranks and the decomposition of
![]() $J_H$
up to isogeny for all but one of the arithmetically maximal subgroups of
$J_H$
up to isogeny for all but one of the arithmetically maximal subgroups of
![]() $\ell $
-power level for
$\ell $
-power level for
![]() $\ell \le 37$
. The sole exception is the group H with label 121.605.41.1 of level
$\ell \le 37$
. The sole exception is the group H with label 121.605.41.1 of level
![]() $121$
, where we were unable to compute all of the elements of
$121$
, where we were unable to compute all of the elements of
![]() $S(H)$
(we were able to do this for the group 121.6655.511.1 corresponding to
$S(H)$
(we were able to do this for the group 121.6655.511.1 corresponding to
![]() $N_{\mathrm { ns}}(121)$
by restricting to eigenforms
$N_{\mathrm { ns}}(121)$
by restricting to eigenforms
![]() $f\in S_2(\Gamma _0(\ell ^{2n}))$
via the optimisation noted above). Computing all of the elements of
$f\in S_2(\Gamma _0(\ell ^{2n}))$
via the optimisation noted above). Computing all of the elements of
![]() $S(H)$
in this case would require decomposing the newspaces
$S(H)$
in this case would require decomposing the newspaces
![]() $S_2^{\mathrm {new}}(\Gamma _0(11^4),[\chi ])$
for all Dirichlet characters of modulus
$S_2^{\mathrm {new}}(\Gamma _0(11^4),[\chi ])$
for all Dirichlet characters of modulus
![]() $11^4$
and conductor dividing
$11^4$
and conductor dividing
![]() $11^2$
, which we found impractical in the two cases where
$11^2$
, which we found impractical in the two cases where
![]() $\operatorname {\mathrm {cond}}(\chi )=11^2$
(the corresponding newspaces have
$\operatorname {\mathrm {cond}}(\chi )=11^2$
(the corresponding newspaces have
![]() $\mathbb {Q}$
-dimensions 10550 and 42200).
$\mathbb {Q}$
-dimensions 10550 and 42200).
For the group 121.605.41.1, we apply the alternative strategy of verifying a candidate value for
![]() $e(H)$
by checking Fourier coefficients up to the Sturm bound. We first use the subset of
$e(H)$
by checking Fourier coefficients up to the Sturm bound. We first use the subset of
![]() $S(H)$
that we know to find a candidate
$S(H)$
that we know to find a candidate
![]() $e(H)=[e_1,\ldots ,e_m]$
that works even for B much larger than necessary to ensure that the columns of
$e(H)=[e_1,\ldots ,e_m]$
that works even for B much larger than necessary to ensure that the columns of
![]() $T(B)$
are linearly independent. To rigorously verify this candidate, it suffices to compare the Dirichlet coefficients
$T(B)$
are linearly independent. To rigorously verify this candidate, it suffices to compare the Dirichlet coefficients
![]() $b_n,c_n\in \mathbb {Z}$
of the L-functions
$b_n,c_n\in \mathbb {Z}$
of the L-functions
 $$\begin{align*}L(J_H,s)= \sum_{n=1}^{\infty} b_n n^{-s}\qquad\text{and}\qquad \prod_i L(A_{f_i},s)^{e_i}=\sum_{n=1}^{\infty} c_nn^{-s}, \end{align*}$$
$$\begin{align*}L(J_H,s)= \sum_{n=1}^{\infty} b_n n^{-s}\qquad\text{and}\qquad \prod_i L(A_{f_i},s)^{e_i}=\sum_{n=1}^{\infty} c_nn^{-s}, \end{align*}$$
for n up to the Sturm bound for the space
![]() $S_2\bigl (\Gamma _1(N)\cap \Gamma _0(N^2)\bigr )$
, which is
$S_2\bigl (\Gamma _1(N)\cap \Gamma _0(N^2)\bigr )$
, which is
![]() . The integers
. The integers
![]() $c_n$
uniquely determine the Fourier coefficients
$c_n$
uniquely determine the Fourier coefficients
![]() $a_n$
that appear in the q-expansion of the modular from
$a_n$
that appear in the q-expansion of the modular from
![]() for
for
![]() $n\le B$
, which uniquely determines F.Footnote
6
$n\le B$
, which uniquely determines F.Footnote
6
Both L-functions are defined by an Euler product, so it suffices to check
![]() $b_q=c_q$
for prime powers
$b_q=c_q$
for prime powers
![]() $q\le B$
. We compute the
$q\le B$
. We compute the
![]() $c_q$
by computing Euler factors of
$c_q$
by computing Euler factors of
![]() $\prod _{f\in [f_i]}L(f,s)$
at all primes
$\prod _{f\in [f_i]}L(f,s)$
at all primes
![]() $p\le B$
using the modular symbols functionality in Magma. For
$p\le B$
using the modular symbols functionality in Magma. For
![]() $11\!\nmid \! q$
, we compute the
$11\!\nmid \! q$
, we compute the
![]() $b_q$
by computing
$b_q$
by computing
![]() $\#X_H({\mathbb F}_{p^r})$
for
$\#X_H({\mathbb F}_{p^r})$
for
![]() $1\le r\le \log _p B$
via the point counting algorithm described in the previous section (these point counts determine enough coefficients of the degree-82 L-polynomial of
$1\le r\le \log _p B$
via the point counting algorithm described in the previous section (these point counts determine enough coefficients of the degree-82 L-polynomial of
![]() $J_H$
at p to determine the
$J_H$
at p to determine the
![]() $a_q$
for
$a_q$
for
![]() $q\le B$
). To compute the Euler factor of
$q\le B$
). To compute the Euler factor of
![]() $L(J_H,s)$
at 11 (which determines the
$L(J_H,s)$
at 11 (which determines the
![]() $a_q$
for
$a_q$
for
![]() $11|q$
), we use the
$11|q$
), we use the
![]() $\operatorname {GL}_2$
-modular symbols functionality in the Magma package ModFrmGL2 recently developed by Assaf [Reference AssafAss21]. The most time-consuming part of this process is computing the
$\operatorname {GL}_2$
-modular symbols functionality in the Magma package ModFrmGL2 recently developed by Assaf [Reference AssafAss21]. The most time-consuming part of this process is computing the
![]() $c_q$
for
$c_q$
for
![]() $q\le B=322\,102$
, which takes 15–20 hours. It takes about 15 minutes to compute the
$q\le B=322\,102$
, which takes 15–20 hours. It takes about 15 minutes to compute the
![]() $b_q$
for
$b_q$
for
![]() $11\nmid q$
and another 15 or 20 minutes to compute the Euler factor of
$11\nmid q$
and another 15 or 20 minutes to compute the Euler factor of
![]() $L(J_H,s)$
at 11. Magma scripts that reproduce all three computations and verify that the results match are available at [Reference Rouse, Sutherland and Zureick-BrownRSZB21].
$L(J_H,s)$
at 11. Magma scripts that reproduce all three computations and verify that the results match are available at [Reference Rouse, Sutherland and Zureick-BrownRSZB21].
Example 6.3. We remark that these methods apply to groups with nonsurjective determinant as well. While for such H,
![]() $X_H(\mathbb {Q})$
is empty (see the discussion after Definition 3.1) and
$X_H(\mathbb {Q})$
is empty (see the discussion after Definition 3.1) and
![]() $X_H$
is connected but not geometrically connected, the sheafification of the functor
$X_H$
is connected but not geometrically connected, the sheafification of the functor
![]() $\operatorname {\mathrm {Pic}}^0 X_H$
is still representable by an abelian variety
$\operatorname {\mathrm {Pic}}^0 X_H$
is still representable by an abelian variety
![]() $J_H$
over
$J_H$
over
![]() $\mathbb {Q}$
; see Remark 2.4 and Appendix A, where it is also proved that the isogeny factors of
$\mathbb {Q}$
; see Remark 2.4 and Appendix A, where it is also proved that the isogeny factors of
![]() $J_H$
are twists
$J_H$
are twists
![]() $A_{f \otimes \chi }$
of factors of
$A_{f \otimes \chi }$
of factors of
![]() $J_1(N^2)$
, where N is the level of H and
$J_1(N^2)$
, where N is the level of H and
![]() $\chi $
is a Dirichlet character of modulus N.
$\chi $
is a Dirichlet character of modulus N.
One can compute the decomposition of
![]() $J_H$
via the methods of this section. At primes
$J_H$
via the methods of this section. At primes
![]() $p \nmid N$
whose reduction mod N is not an element of
$p \nmid N$
whose reduction mod N is not an element of
![]() $\det (H)$
, the point count
$\det (H)$
, the point count
![]() $X_H({\mathbb F}_p)$
is zero (again by the Weil pairing), and one can show that the trace of Frobenius acting on
$X_H({\mathbb F}_p)$
is zero (again by the Weil pairing), and one can show that the trace of Frobenius acting on
![]() $H^1$
is also zero; for consistency, we also remark that since for such p none of the geometric connected components of
$H^1$
is also zero; for consistency, we also remark that since for such p none of the geometric connected components of
![]() $X_{H,{\mathbb F}_p}$
are defined over
$X_{H,{\mathbb F}_p}$
are defined over
![]() ${\mathbb F}_p$
, the trace of Frobenius acting on
${\mathbb F}_p$
, the trace of Frobenius acting on
![]() $H^0$
(and by duality, also on
$H^0$
(and by duality, also on
![]() $H^2$
) are zero.
$H^2$
) are zero.
For example, consider the group
![]() $H=\langle \left [\begin {smallmatrix} 8 & 0 \\ 0 & 1 \end {smallmatrix}\right ],\left [\begin {smallmatrix} 1 & 3 \\ 0 & 8 \end {smallmatrix}\right ]\rangle \le \operatorname {GL}_2(9)$
with label 9.3.1-9.108.1.1. One has
$H=\langle \left [\begin {smallmatrix} 8 & 0 \\ 0 & 1 \end {smallmatrix}\right ],\left [\begin {smallmatrix} 1 & 3 \\ 0 & 8 \end {smallmatrix}\right ]\rangle \le \operatorname {GL}_2(9)$
with label 9.3.1-9.108.1.1. One has
![]() $\det (H) = \{\pm 1\}$
, which has index 3;
$\det (H) = \{\pm 1\}$
, which has index 3;
![]() $X_H$
is connected but geometrically disconnected, and the geometric components are each isomorphic (over
$X_H$
is connected but geometrically disconnected, and the geometric components are each isomorphic (over
![]() ${\overline {\mathbb {Q}}}$
) to
${\overline {\mathbb {Q}}}$
) to
![]() $E_{{\overline {\mathbb {Q}}}}$
, where
$E_{{\overline {\mathbb {Q}}}}$
, where
![]() $E/\mathbb {Q}$
is the elliptic curve with newform 27.2.a.a. Following the procedure outlined in Example 6.2, we find that over
$E/\mathbb {Q}$
is the elliptic curve with newform 27.2.a.a. Following the procedure outlined in Example 6.2, we find that over
![]() $J_H$
decomposes (over
$J_H$
decomposes (over
![]() $\mathbb {Q}$
) as
$\mathbb {Q}$
) as
![]() $E \times A$
, where A is the simple abelian surface corresponding to the newform orbit 81.2.c.a. The abelian surface A is not geometrically simple; in fact,
$E \times A$
, where A is the simple abelian surface corresponding to the newform orbit 81.2.c.a. The abelian surface A is not geometrically simple; in fact,
![]() $A_{{\overline {\mathbb {Q}}}} \sim E_{{\overline {\mathbb {Q}}}}^2$
, and the newform orbit 81.2.c.a is the twist of the newform 27.2.a.a by the Dirichlet character orbit 9.c.
$A_{{\overline {\mathbb {Q}}}} \sim E_{{\overline {\mathbb {Q}}}}^2$
, and the newform orbit 81.2.c.a is the twist of the newform 27.2.a.a by the Dirichlet character orbit 9.c.
7 Computing equations for
 $X_H$
with
$X_H$
with
 $-I \in H$
$-I \in H$
We now discuss the computation of equations for
![]() $X_H$
for arithmetically maximal H containing
$X_H$
for arithmetically maximal H containing
![]() $-I$
of
$-I$
of
![]() $\ell $
-power level for
$\ell $
-power level for
![]() $3\le \ell \le 13$
; see Section 10 for the case
$3\le \ell \le 13$
; see Section 10 for the case
![]() $-I \not \in H$
.
$-I \not \in H$
.
In [Reference Rouse and Zureick-BrownRZB15], Rouse and Zureick-Brown construct the modular curves
![]() $X_{H}$
as covers of
$X_{H}$
as covers of
![]() $X_{\widetilde {H}}$
, where
$X_{\widetilde {H}}$
, where
![]() $\widetilde {H}$
is a supergroup of H for which
$\widetilde {H}$
is a supergroup of H for which
![]() $[\widetilde {H} : H]$
is minimal. Because we are only recording equations for arithmetically maximal subgroups, in any case where we compute the covering
$[\widetilde {H} : H]$
is minimal. Because we are only recording equations for arithmetically maximal subgroups, in any case where we compute the covering
![]() $X_{H} \to X_{\widetilde {H}}$
, the genus of
$X_{H} \to X_{\widetilde {H}}$
, the genus of
![]() $X_{\widetilde {H}}$
is zero or one. In all cases, we consider the genus of
$X_{\widetilde {H}}$
is zero or one. In all cases, we consider the genus of
![]() $X_{\widetilde {H}}$
is zero, and we know a specific function
$X_{\widetilde {H}}$
is zero, and we know a specific function
![]() $x \in \mathbb {Q}(X_{\widetilde {H}})$
so that
$x \in \mathbb {Q}(X_{\widetilde {H}})$
so that
![]() $\mathbb {Q}(X_{\widetilde {H}}) = \mathbb {Q}(x)$
. The models are computed by constructing elements of the function field of
$\mathbb {Q}(X_{\widetilde {H}}) = \mathbb {Q}(x)$
. The models are computed by constructing elements of the function field of
![]() $\mathbb {Q}(X_{H})$
built using products of weight
$\mathbb {Q}(X_{H})$
built using products of weight
![]() $2$
Eisenstein series whose Fourier expansions are simple to compute and for which it is easy to describe the action of
$2$
Eisenstein series whose Fourier expansions are simple to compute and for which it is easy to describe the action of
![]() $\operatorname {GL}_2(N)$
on them. In this way, we find a generator y for
$\operatorname {GL}_2(N)$
on them. In this way, we find a generator y for
![]() $\mathbb {Q}(X_{H})$
and then compute the action of H-coset representatives of
$\mathbb {Q}(X_{H})$
and then compute the action of H-coset representatives of
![]() $\widetilde {H}$
on it. This allows us to compute the minimal polynomial for y over
$\widetilde {H}$
on it. This allows us to compute the minimal polynomial for y over
![]() $\mathbb {Q}(x)$
, which gives a plane model for
$\mathbb {Q}(x)$
, which gives a plane model for
![]() $X_{H}$
. We use the method of Novocin and van Hoeij [Reference van Hoeij and NovocinvHN05] to reduce the resulting algebraic function field and obtain a simple model.
$X_{H}$
. We use the method of Novocin and van Hoeij [Reference van Hoeij and NovocinvHN05] to reduce the resulting algebraic function field and obtain a simple model.
We now describe another approach for computing the canonical model of a high genus curve, which we use to compute equations of
![]() $X_{\operatorname {\mathrm {ns}}}^{+}(27)$
(label 27.243.12.1) and
$X_{\operatorname {\mathrm {ns}}}^{+}(27)$
(label 27.243.12.1) and
![]() $X_{H}$
, where H has label 27.729.43.1 or 25.625.36.1. Given
$X_{H}$
, where H has label 27.729.43.1 or 25.625.36.1. Given
![]() $H \leq \operatorname {GL}_{2}(N)$
, there is a natural action of H on the field of modular functions for
$H \leq \operatorname {GL}_{2}(N)$
, there is a natural action of H on the field of modular functions for
![]() $\Gamma (N)$
with coefficients in
$\Gamma (N)$
with coefficients in
![]() $\mathbb {Q}(\zeta _{N})$
. In particular,
$\mathbb {Q}(\zeta _{N})$
. In particular,
![]() $\left [\begin {smallmatrix} a & b \\ c & d \end {smallmatrix}\right ] \in \operatorname {SL}_{2}(N)$
acts via
$\left [\begin {smallmatrix} a & b \\ c & d \end {smallmatrix}\right ] \in \operatorname {SL}_{2}(N)$
acts via
![]() $f | \left [\begin {smallmatrix} a & b \\ c & d \end {smallmatrix}\right ] = f\left (\frac {az+b}{cz+d}\right )$
, while the matrix
$f | \left [\begin {smallmatrix} a & b \\ c & d \end {smallmatrix}\right ] = f\left (\frac {az+b}{cz+d}\right )$
, while the matrix
![]() $h = \left [\begin {smallmatrix} 1 & 0 \\ 0 & d \end {smallmatrix}\right ]$
acts by sending
$h = \left [\begin {smallmatrix} 1 & 0 \\ 0 & d \end {smallmatrix}\right ]$
acts by sending
![]() $f = \sum a(n) q^{n}$
to
$f = \sum a(n) q^{n}$
to
![]() $f | h = \sum \sigma _{d}(a(n)) q^{n}$
, where
$f | h = \sum \sigma _{d}(a(n)) q^{n}$
, where
![]() $\sigma _{d}$
is the automorphism of
$\sigma _{d}$
is the automorphism of
![]() $\mathbb {Q}(\zeta _{N})$
sending
$\mathbb {Q}(\zeta _{N})$
sending
![]() $\sigma _{d}(\zeta _{N}) = \zeta _{N}^{d}$
. One can extend this map to a natural map on
$\sigma _{d}(\zeta _{N}) = \zeta _{N}^{d}$
. One can extend this map to a natural map on
![]() $M_{2k}(\Gamma (N), \mathbb {Q}(\zeta _{N}))$
of the space of weight
$M_{2k}(\Gamma (N), \mathbb {Q}(\zeta _{N}))$
of the space of weight
![]() $2k$
modular forms for
$2k$
modular forms for
![]() $\Gamma (N)$
with Fourier coefficients in
$\Gamma (N)$
with Fourier coefficients in
![]() $\mathbb {Q}(\zeta _{N})$
. To do so, given a form
$\mathbb {Q}(\zeta _{N})$
. To do so, given a form
![]() $F \in M_{2k}(\Gamma (N), \mathbb {Q}(\zeta _{N}))$
, define
$F \in M_{2k}(\Gamma (N), \mathbb {Q}(\zeta _{N}))$
, define
![]() $f = \frac {E_{4}(z)^{k} E_{6}(z)^{k}}{\Delta (z)^{k}} F$
, a modular function for
$f = \frac {E_{4}(z)^{k} E_{6}(z)^{k}}{\Delta (z)^{k}} F$
, a modular function for
![]() $\Gamma (N)$
, and
$\Gamma (N)$
, and

Here
(with
![]() $q = e^{2 \pi i z}$
) and
$q = e^{2 \pi i z}$
) and
are the classical weight
![]() $4$
and
$4$
and
![]() $6$
Eisenstein series, respectively.
$6$
Eisenstein series, respectively.
Given H, our goal is to find q-expansions for a basis for
![]() $S_{2}(\Gamma (N), \mathbb {Q}(\zeta _{N}))^{H}$
. This problem has been considered before in [Reference Banwait and CremonaBC14] and recently in [Reference ZywinaZyw21] and [Reference AssafAss21]. Instead, we continue our approach from [Reference Rouse and Zureick-BrownRZB15] of first computing the space of weight
$S_{2}(\Gamma (N), \mathbb {Q}(\zeta _{N}))^{H}$
. This problem has been considered before in [Reference Banwait and CremonaBC14] and recently in [Reference ZywinaZyw21] and [Reference AssafAss21]. Instead, we continue our approach from [Reference Rouse and Zureick-BrownRZB15] of first computing the space of weight
![]() $2$
Eisenstein series for H. Compared to other methods, our method has the disadvantage of requiring a much larger number of Fourier coefficients. However, it only requires working with modular forms defined on H, and our method may be substantially more efficient if the index of
$2$
Eisenstein series for H. Compared to other methods, our method has the disadvantage of requiring a much larger number of Fourier coefficients. However, it only requires working with modular forms defined on H, and our method may be substantially more efficient if the index of
![]() $\Gamma (N)$
in H is large. The addition of modular forms functionality to PARI/GP in [Reference Belabas and CohenBC18] uses the strategy of multiplying Eisenstein series.
$\Gamma (N)$
in H is large. The addition of modular forms functionality to PARI/GP in [Reference Belabas and CohenBC18] uses the strategy of multiplying Eisenstein series.
The next task is to construct the Fourier coefficients of weight
![]() $2$
cusp forms from those of the Eisenstein series. We do this by multiplying triples of weight
$2$
cusp forms from those of the Eisenstein series. We do this by multiplying triples of weight
![]() $2$
Eisenstein series together to obtain a large collection of weight
$2$
Eisenstein series together to obtain a large collection of weight
![]() $6$
modular forms. Because we know how each weight
$6$
modular forms. Because we know how each weight
![]() $2$
Eisenstein series transforms under matrices in
$2$
Eisenstein series transforms under matrices in
![]() $\operatorname {GL}_{2}(N)$
, we can keep track of the values of these products of the Eisenstein series at each cusp of
$\operatorname {GL}_{2}(N)$
, we can keep track of the values of these products of the Eisenstein series at each cusp of
![]() $X_{H}$
. There is no reason to expect that this is the entirety of the space of weight
$X_{H}$
. There is no reason to expect that this is the entirety of the space of weight
![]() $6$
modular forms because weight
$6$
modular forms because weight
![]() $2$
modular forms must have a zero at each elliptic point of order
$2$
modular forms must have a zero at each elliptic point of order
![]() $2$
and a double zero at each elliptic point of order
$2$
and a double zero at each elliptic point of order
![]() $3$
. One can use the Riemann–Roch theorem to compute that the dimension of the subspace of weight
$3$
. One can use the Riemann–Roch theorem to compute that the dimension of the subspace of weight
![]() $6$
modular forms with a zero of order
$6$
modular forms with a zero of order
![]() $\geq 3$
at each elliptic point of order
$\geq 3$
at each elliptic point of order
![]() $2$
and zero of order
$2$
and zero of order
![]() $\geq 6$
at each elliptic point of order
$\geq 6$
at each elliptic point of order
![]() $3$
is
$3$
is
![]() $3 \nu _{\infty }(\Gamma _{H}) + 5(g-1)$
. This allows one to avoid computing products of all triples of weight
$3 \nu _{\infty }(\Gamma _{H}) + 5(g-1)$
. This allows one to avoid computing products of all triples of weight
![]() $2$
Eisenstein series.
$2$
Eisenstein series.
Next, one applies Hecke operators to compute the full space of weight
![]() $6$
modular forms. In [Reference KatoKat04], Kato defines a family of Hecke operators
$6$
modular forms. In [Reference KatoKat04], Kato defines a family of Hecke operators
![]() $T(n) \left [\begin {smallmatrix} n & 0 \\ 0 & 1 \end {smallmatrix}\right ]^{*}$
for modular forms on
$T(n) \left [\begin {smallmatrix} n & 0 \\ 0 & 1 \end {smallmatrix}\right ]^{*}$
for modular forms on
![]() $\Gamma (N)$
and gives their action on Fourier expansions for
$\Gamma (N)$
and gives their action on Fourier expansions for
![]() $\gcd (n,N) = 1$
. As noted by Kato, this normalisation commutes with the action of
$\gcd (n,N) = 1$
. As noted by Kato, this normalisation commutes with the action of
![]() $\operatorname {GL}_{2}(N)$
, but it does not preserve the connected components of
$\operatorname {GL}_{2}(N)$
, but it does not preserve the connected components of
![]() $X(N)$
.
$X(N)$
.
Let w be the width of the cusp at
![]() $\infty $
for
$\infty $
for
![]() $\Gamma _H$
, and suppose that
$\Gamma _H$
, and suppose that
![]() $f(z) = \sum _{n=0}^{\infty } a(n) q^{n/w}$
is a modular form of weight k for
$f(z) = \sum _{n=0}^{\infty } a(n) q^{n/w}$
is a modular form of weight k for
![]() $\Gamma _{H}$
,
$\Gamma _{H}$
,
![]() $q = e^{2 \pi i z}$
. Then Kato’s formulas show that if p is a prime with
$q = e^{2 \pi i z}$
. Then Kato’s formulas show that if p is a prime with
![]() $p \equiv \pm 1 \pmod {N}$
$p \equiv \pm 1 \pmod {N}$
 $$\begin{align*}\left(\sum_{n=0}^{\infty} a(n) q^{n/w}\right) | T(p) = \sum_{n=0}^{\infty} a(pn) q^{n/w} + p^{k-1} \sum_{n \equiv 0 \pmod{p}}^{\infty} a(n/p) q^{n/w}. \end{align*}$$
$$\begin{align*}\left(\sum_{n=0}^{\infty} a(n) q^{n/w}\right) | T(p) = \sum_{n=0}^{\infty} a(pn) q^{n/w} + p^{k-1} \sum_{n \equiv 0 \pmod{p}}^{\infty} a(n/p) q^{n/w}. \end{align*}$$
The case
![]() $p \equiv -1 \pmod {N}$
requires
$p \equiv -1 \pmod {N}$
requires
![]() , so we conjugate H to contain M.
, so we conjugate H to contain M.
We choose the smallest prime
![]() $p \equiv \pm 1 \pmod {N}$
and apply the Hecke operator
$p \equiv \pm 1 \pmod {N}$
and apply the Hecke operator
![]() $T(p)$
to all the products of three weight
$T(p)$
to all the products of three weight
![]() $2$
Eisenstein series. While we are not guaranteed to obtain the entire space
$2$
Eisenstein series. While we are not guaranteed to obtain the entire space
![]() $M_{6}(\Gamma (N), \mathbb {Q}(\zeta _{N}))^{H}$
, in the cases under consideration we do. It is not difficult to see how the Hecke operator affects values at the cusps, and in this way, we obtain a basis for the space
$M_{6}(\Gamma (N), \mathbb {Q}(\zeta _{N}))^{H}$
, in the cases under consideration we do. It is not difficult to see how the Hecke operator affects values at the cusps, and in this way, we obtain a basis for the space
![]() $S_{6}(\Gamma (N), \mathbb {Q}(\zeta _{N}))^{H}$
. We apply the same tools to obtain a basis for the space
$S_{6}(\Gamma (N), \mathbb {Q}(\zeta _{N}))^{H}$
. We apply the same tools to obtain a basis for the space
![]() $S_{8}(\Gamma (N), \mathbb {Q}(\zeta _{N}))^{H}$
.
$S_{8}(\Gamma (N), \mathbb {Q}(\zeta _{N}))^{H}$
.
Let h be a meromorphic modular form on
![]() $\Gamma (N)$
. We use the elementary observation that since the zero sets of
$\Gamma (N)$
. We use the elementary observation that since the zero sets of
![]() $E_{4}(z)$
and
$E_{4}(z)$
and
![]() $E_{6}(z)$
are disjoint,
$E_{6}(z)$
are disjoint,
![]() $h\in S_{2}(\Gamma (N), \mathbb {Q}(\zeta _{N}))^{H}$
if and only if
$h\in S_{2}(\Gamma (N), \mathbb {Q}(\zeta _{N}))^{H}$
if and only if
![]() $h E_{4} \in S_{6}(\Gamma (N), \mathbb {Q}(\zeta _{N}))^{H}$
and
$h E_{4} \in S_{6}(\Gamma (N), \mathbb {Q}(\zeta _{N}))^{H}$
and
![]() $h E_{6} \in S_{8}(\Gamma (N), \mathbb {Q}(\zeta _N))^{H}$
. In this way, one obtains q-expansions for the weight
$h E_{6} \in S_{8}(\Gamma (N), \mathbb {Q}(\zeta _N))^{H}$
. In this way, one obtains q-expansions for the weight
![]() $2$
cusps forms for H. From these, we can easily obtain the canonical map for
$2$
cusps forms for H. From these, we can easily obtain the canonical map for
![]() $X_{H}$
and its image in
$X_{H}$
and its image in
![]() $\mathbb {P}^{g-1}$
and then check whether the curve is hyperelliptic. Let
$\mathbb {P}^{g-1}$
and then check whether the curve is hyperelliptic. Let
![]() $\Omega $
be the sheaf of holomorphic
$\Omega $
be the sheaf of holomorphic
![]() $1$
-forms on the curve
$1$
-forms on the curve
![]() $X_{H}$
. If
$X_{H}$
. If
![]() $g(H) \geq 3$
and
$g(H) \geq 3$
and
![]() $X_{H}$
is not hyperelliptic, the canonical ring
$X_{H}$
is not hyperelliptic, the canonical ring
![]() $R = \oplus _{d \geq 0} H^{0}(X_{H}, \Omega ^{\otimes d})$
is generated in degree
$R = \oplus _{d \geq 0} H^{0}(X_{H}, \Omega ^{\otimes d})$
is generated in degree
![]() $1$
[Reference Voight and Zureick-BrownVZB22, Chapter 2].
$1$
[Reference Voight and Zureick-BrownVZB22, Chapter 2].
Finally, we seek to identify
![]() $j(z)$
as a ratio of two elements of the canonical ring. From a computational standpoint, it is easier to write
$j(z)$
as a ratio of two elements of the canonical ring. From a computational standpoint, it is easier to write
 $$\begin{align*}j(z) = \frac{1728 E_{4}(z)^{3}}{E_{4}(z)^{3} - E_{6}(z)^{2}} \end{align*}$$
$$\begin{align*}j(z) = \frac{1728 E_{4}(z)^{3}}{E_{4}(z)^{3} - E_{6}(z)^{2}} \end{align*}$$
and find representations of
![]() $E_{4}(z)$
and
$E_{4}(z)$
and
![]() $E_{6}(z)$
as ratios of elements of the canonical ring. Let
$E_{6}(z)$
as ratios of elements of the canonical ring. Let
![]() $h(z)$
be an element of the canonical ring of weight
$h(z)$
be an element of the canonical ring of weight
![]() $k-4$
. Then
$k-4$
. Then
![]() $E_{4}(z) = \frac {f(z)}{h(z)}$
for some
$E_{4}(z) = \frac {f(z)}{h(z)}$
for some
![]() $f(z)$
in the canonical ring if and only if
$f(z)$
in the canonical ring if and only if
![]() $h(z) E_{4}(z) dz^{k/2}$
is a holomorphic
$h(z) E_{4}(z) dz^{k/2}$
is a holomorphic
![]() $k/2$
-form. Diamond and Shurman [Reference Diamond and ShurmanDS05, p. 86] show that
$k/2$
-form. Diamond and Shurman [Reference Diamond and ShurmanDS05, p. 86] show that
where
![]() $\{x_{2,i} \}$
is the set of elliptic points of order
$\{x_{2,i} \}$
is the set of elliptic points of order
![]() $2$
,
$2$
,
![]() $\{ x_{3,i} \}$
is the set of elliptic points of order
$\{ x_{3,i} \}$
is the set of elliptic points of order
![]() $3$
and
$3$
and
![]() $\{ x_{i} \}$
is the set of cusps on
$\{ x_{i} \}$
is the set of cusps on
![]() $X_{H}$
. Let
$X_{H}$
. Let
![]() $D = -\sum x_{2,i} - \sum x_{3,i} - \sum 2x_{i}$
. Then
$D = -\sum x_{2,i} - \sum x_{3,i} - \sum 2x_{i}$
. Then
![]() $h(z) E_{4}(z) dz^{k/2}$
is holomorphic if and only if
$h(z) E_{4}(z) dz^{k/2}$
is holomorphic if and only if
![]() $h(z) dz^{(k-4)/2} \in L^{(k-4)/2}(D)$
, the space of meromorphic
$h(z) dz^{(k-4)/2} \in L^{(k-4)/2}(D)$
, the space of meromorphic
![]() $(k-4)/2$
-forms with poles at most at D. We have (by Lemma VII.4.11 from Miranda [Reference MirandaMir95]) that
$(k-4)/2$
-forms with poles at most at D. We have (by Lemma VII.4.11 from Miranda [Reference MirandaMir95]) that
![]() $L^{(k-4)/2}(D) \simeq L(D + ((k-4)/2)K)$
, where K is the canonical divisor. Riemann–Roch now guarantees the existence of such a D, provided that
$L^{(k-4)/2}(D) \simeq L(D + ((k-4)/2)K)$
, where K is the canonical divisor. Riemann–Roch now guarantees the existence of such a D, provided that
A similar calculation shows that
![]() $E_{6}$
is a ratio of a holomorphic
$E_{6}$
is a ratio of a holomorphic
![]() $(k/2)$
-form and a holomorphic
$(k/2)$
-form and a holomorphic
![]() $((k-6)/2)$
-form, provided that
$((k-6)/2)$
-form, provided that
With these bounds, one can use the q-expansions of the weight
![]() $2$
cusp forms to compute the q-expansions of the modular forms of weight k that correspond to elements of the canonical ring and use linear algebra to compute a ratio that is equal to
$2$
cusp forms to compute the q-expansions of the modular forms of weight k that correspond to elements of the canonical ring and use linear algebra to compute a ratio that is equal to
![]() $E_{4}(z)$
and
$E_{4}(z)$
and
![]() $E_{6}(z)$
.
$E_{6}(z)$
.
This technique is used to compute the canonical models of
![]() $X_{\operatorname {\mathrm {ns}}}^{+}(25)$
,
$X_{\operatorname {\mathrm {ns}}}^{+}(25)$
,
![]() $X_{\operatorname {\mathrm {ns}}}^{+}(27)$
, a genus
$X_{\operatorname {\mathrm {ns}}}^{+}(27)$
, a genus
![]() $43$
curve with label 27.729.43.1 and a genus
$43$
curve with label 27.729.43.1 and a genus
![]() $36$
curve with label 25.625.36.1. A variant of this technique was used to compute a model of a genus
$36$
curve with label 25.625.36.1. A variant of this technique was used to compute a model of a genus
![]() $3$
modular curve defined over
$3$
modular curve defined over
![]() $\mathbb {Q}(\zeta _{3})$
(see Subsection 9.1). We compute models for all of the arithmetically maximal modular curves with
$\mathbb {Q}(\zeta _{3})$
(see Subsection 9.1). We compute models for all of the arithmetically maximal modular curves with
![]() $3 \leq \ell \leq 13$
with the exceptions of
$3 \leq \ell \leq 13$
with the exceptions of
![]() $X_{\mathrm {s}}^{+}(49)$
with label 49.1372.94.1, which is known not to have any noncuspidal non-CM rational points, 121.605.41.1 which is shown not to have any rational points in Section 8.7 and
$X_{\mathrm {s}}^{+}(49)$
with label 49.1372.94.1, which is known not to have any noncuspidal non-CM rational points, 121.605.41.1 which is shown not to have any rational points in Section 8.7 and
![]() $X_{\operatorname {\mathrm {ns}}}^{+}(121)$
with label 121.6655.511.1. For the genus
$X_{\operatorname {\mathrm {ns}}}^{+}(121)$
with label 121.6655.511.1. For the genus
![]() $69$
curve
$69$
curve
![]() $X_{\operatorname {\mathrm {ns}}}^{+}(49)$
, we obtain a singular plane model, but we are unable to apply the method of Novocin and van Hoeij to simplify the equation.
$X_{\operatorname {\mathrm {ns}}}^{+}(49)$
, we obtain a singular plane model, but we are unable to apply the method of Novocin and van Hoeij to simplify the equation.
Example 7.1. Consider the modular curve
![]() $X_H= X_{\operatorname {\mathrm {ns}}}^{+}(27)$
with label 27.243.12.1. We compute the Fourier expansions of the
$X_H= X_{\operatorname {\mathrm {ns}}}^{+}(27)$
with label 27.243.12.1. We compute the Fourier expansions of the
![]() $8$
Eisenstein series in
$8$
Eisenstein series in
![]() $M_{2}(\Gamma (27),\mathbb {Q}(\zeta _{27}))^{H}$
, which are elements of
$M_{2}(\Gamma (27),\mathbb {Q}(\zeta _{27}))^{H}$
, which are elements of
![]() $\mathbb {Q}(\zeta _{27})[[q^{1/27}]]$
, and multiply triples of these together. There are
$\mathbb {Q}(\zeta _{27})[[q^{1/27}]]$
, and multiply triples of these together. There are
![]() $120$
such triples; however, the subspace of
$120$
such triples; however, the subspace of
![]() $M_{6}(\Gamma (27),\mathbb {Q}(\zeta _{27}))^{H}$
with triple zeros at the
$M_{6}(\Gamma (27),\mathbb {Q}(\zeta _{27}))^{H}$
with triple zeros at the
![]() $19$
elliptic points of order
$19$
elliptic points of order
![]() $2$
has dimension
$2$
has dimension
![]() $82$
. The first
$82$
. The first
![]() $82$
triples that we try are linearly independent in
$82$
triples that we try are linearly independent in
![]() $M_{6}(\Gamma (27),\mathbb {Q}(\zeta _{27}))^{H}$
.
$M_{6}(\Gamma (27),\mathbb {Q}(\zeta _{27}))^{H}$
.
The smallest prime
![]() $p \equiv \pm 1 \pmod {27}$
is
$p \equiv \pm 1 \pmod {27}$
is
![]() $p = 53$
. We apply the Hecke operator
$p = 53$
. We apply the Hecke operator
![]() $T(53)$
to the first
$T(53)$
to the first
![]() $19$
weight
$19$
weight
![]() $6$
forms we computed in the last step and find that these are linearly independent, while for the remaining
$6$
forms we computed in the last step and find that these are linearly independent, while for the remaining
![]() $63$
forms g,
$63$
forms g,
![]() $g | T(53)$
is a linear combination of the forms we already have. This gives us a basis for
$g | T(53)$
is a linear combination of the forms we already have. This gives us a basis for
![]() $M_{6}(\Gamma (27),\mathbb {Q}(\zeta _{27}))^{H}$
, which has dimension
$M_{6}(\Gamma (27),\mathbb {Q}(\zeta _{27}))^{H}$
, which has dimension
![]() $101$
. We then identify the subspace of cusp forms, which has dimension
$101$
. We then identify the subspace of cusp forms, which has dimension
![]() $92$
.
$92$
.
Next we find a basis for
![]() $M_{8}(\Gamma (27),\mathbb {Q}(\zeta _{27}))^{H}$
by multiplying together
$M_{8}(\Gamma (27),\mathbb {Q}(\zeta _{27}))^{H}$
by multiplying together
![]() $4$
-tuples of weight
$4$
-tuples of weight
![]() $2$
Eisenstein series. We obtain
$2$
Eisenstein series. We obtain
![]() $113$
linearly independent forms this way and
$113$
linearly independent forms this way and
![]() $38$
additional forms by applying
$38$
additional forms by applying
![]() $T(53)$
. This gives us a basis for
$T(53)$
. This gives us a basis for
![]() $M_{8}(\Gamma (27),\mathbb {Q}(\zeta _{27}))^{H}$
, which has dimension
$M_{8}(\Gamma (27),\mathbb {Q}(\zeta _{27}))^{H}$
, which has dimension
![]() $151$
. The subspace of cusp forms has dimension
$151$
. The subspace of cusp forms has dimension
![]() $142$
.
$142$
.
Next, we compute the subspace of
![]() $\mathbb {Q}(\zeta _{27})[[q^{1/27}]]$
spanned by the forms
$\mathbb {Q}(\zeta _{27})[[q^{1/27}]]$
spanned by the forms
![]() $g_{6}/E_{4}$
, where
$g_{6}/E_{4}$
, where
![]() $g_{6} \in S_{6}(\Gamma (27),\mathbb {Q}(\zeta _{27}))^{H}$
, and intersect this with the subspace of
$g_{6} \in S_{6}(\Gamma (27),\mathbb {Q}(\zeta _{27}))^{H}$
, and intersect this with the subspace of
![]() $\mathbb {Q}(\zeta _{27})[[q^{1/27}]]$
spanned by the forms
$\mathbb {Q}(\zeta _{27})[[q^{1/27}]]$
spanned by the forms
![]() $g_{8}/E_{6}$
, where
$g_{8}/E_{6}$
, where
![]() $g_{8} \in S_{8}(\Gamma (27),\mathbb {Q}(\zeta _{27}))^{H}$
. This subspace has dimension
$g_{8} \in S_{8}(\Gamma (27),\mathbb {Q}(\zeta _{27}))^{H}$
. This subspace has dimension
![]() $12$
, so it must equal
$12$
, so it must equal
![]() $S_{2}(\Gamma (27),\mathbb {Q}(\zeta _{27}))^{H}$
. We compute an LLL-reduced basis for this latter space and an LLL-reduced basis for the space of quadratic relations and find that it has dimension
$S_{2}(\Gamma (27),\mathbb {Q}(\zeta _{27}))^{H}$
. We compute an LLL-reduced basis for this latter space and an LLL-reduced basis for the space of quadratic relations and find that it has dimension
![]() $45$
. This shows that the image of the canonical map is not a rational normal curve (for in this case, the space of quadratic relations would have dimension
$45$
. This shows that the image of the canonical map is not a rational normal curve (for in this case, the space of quadratic relations would have dimension
![]() $55$
), and hence
$55$
), and hence
![]() $X_H$
is not hyperelliptic and the curve
$X_H$
is not hyperelliptic and the curve
![]() $X_H$
is given by the intersection of our
$X_H$
is given by the intersection of our
![]() $45$
quadrics in
$45$
quadrics in
![]() $\mathbb {P}^{11}$
.
$\mathbb {P}^{11}$
.
The Riemann–Roch calculation described above shows that
![]() $E_{4}$
is a ratio of an element of
$E_{4}$
is a ratio of an element of
![]() $H^{0}(X_H, \Omega ^{5})$
and one in
$H^{0}(X_H, \Omega ^{5})$
and one in
![]() $H^{0}(X_H,\Omega ^{3})$
, while
$H^{0}(X_H,\Omega ^{3})$
, while
![]() $E_{6}$
is a ratio of elements in
$E_{6}$
is a ratio of elements in
![]() $H^{0}(X_H,\Omega ^{6})$
and one in
$H^{0}(X_H,\Omega ^{6})$
and one in
![]() $H^{0}(X_H,\Omega ^{3})$
. We obtain Fourier expansions of the modular forms of weight
$H^{0}(X_H,\Omega ^{3})$
. We obtain Fourier expansions of the modular forms of weight
![]() $2r$
corresponding to elements of
$2r$
corresponding to elements of
![]() $H^{0}(X_H,\Omega ^{r})$
by multiplying together forms in
$H^{0}(X_H,\Omega ^{r})$
by multiplying together forms in
![]() $S_{2}(\Gamma (27),\mathbb {Q}(\zeta _{27}))^{H}$
. A linear algebra calculation then finds (many) representations of
$S_{2}(\Gamma (27),\mathbb {Q}(\zeta _{27}))^{H}$
. A linear algebra calculation then finds (many) representations of
![]() $E_{4}$
and
$E_{4}$
and
![]() $E_{6}$
in the desired form. From this, the map
$E_{6}$
in the desired form. From this, the map
![]() $j \colon X_H \to \mathbb {P}^{1}$
can be constructed.
$j \colon X_H \to \mathbb {P}^{1}$
can be constructed.
We do not reproduce the model in this paper (the file modelfile27.243.12.1.txt in [Reference Rouse, Sutherland and Zureick-BrownRSZB21] contains Magma code to compute it), but the coefficients are quite small: the largest absolute value of a coefficient is
![]() $4$
. Point searching on this model finds
$4$
. Point searching on this model finds
![]() $8$
rational points. Two of these
$8$
rational points. Two of these
![]() $8$
points are in the base locus of the map from
$8$
points are in the base locus of the map from
![]() $X_H \to \mathbb {P}^{1}$
, and more care is needed to compute their image on the j-line (both map to
$X_H \to \mathbb {P}^{1}$
, and more care is needed to compute their image on the j-line (both map to
![]() $j = 1728$
). The remaining
$j = 1728$
). The remaining
![]() $6$
points map to
$6$
points map to
![]() $j = -3375$
,
$j = -3375$
,
![]() $j = 287496$
,
$j = 287496$
,
![]() $j = -884736$
,
$j = -884736$
,
![]() $j = 16581375$
,
$j = 16581375$
,
![]() $j = -147197952000$
and
$j = -147197952000$
and
![]() $j = -262537412640768000$
, all of which are CM points. The total time required for the computation of the model and the map to the j-line is about
$j = -262537412640768000$
, all of which are CM points. The total time required for the computation of the model and the map to the j-line is about
![]() $12$
minutes.
$12$
minutes.
8 Analysis of rational points
In this section, we determine the rational points on
![]() $X_H(\mathbb {Q})$
for each of the 21 arithmetically maximal subgroups that appear in Table 5 without an asterisk.
$X_H(\mathbb {Q})$
for each of the 21 arithmetically maximal subgroups that appear in Table 5 without an asterisk.
8.1 Genus 1
The three curves of genus 1 listed in Table 5 have labels
whose rational points are as follows:
-
○ 9.12.1.1 is a degree
 $3$
cover of
$3$
cover of
 $X_{0}(3)$
isomorphic to the elliptic curve
$X_{0}(3)$
isomorphic to the elliptic curve
 $y^{2} + y = x^{3}$
. It has three rational points, two of which are cusps; the other is a CM point with
$y^{2} + y = x^{3}$
. It has three rational points, two of which are cusps; the other is a CM point with
 $j = 0$
.
$j = 0$
. -
○ 9.54.1.1 also known as
 $X_{\operatorname {\mathrm {sp}}}^{+}(9)$
is also isomorphic to
$X_{\operatorname {\mathrm {sp}}}^{+}(9)$
is also isomorphic to
 $y^{2} + y = x^{3}$
(different j-map). In this case, the curve has one cusp and two CM points:
$y^{2} + y = x^{3}$
(different j-map). In this case, the curve has one cusp and two CM points:
 $j = 8000$
and
$j = 8000$
and
 $j = -32768$
.
$j = -32768$
. -
○ 27.36.1.2 is isomorphic to the elliptic curve
 $y^2 + y = x^3 + 2$
; it has three rational points, two of which are cusps; the other is a CM point with
$y^2 + y = x^3 + 2$
; it has three rational points, two of which are cusps; the other is a CM point with
 $j = 0$
.
$j = 0$
.
The file check-for-sporadic-points.m in [Reference Rouse, Sutherland and Zureick-BrownRSZB21] verifies these computations.
8.2 Genus 2
The curves corresponding to the labels
have genus 2 and rank 0. The first two curves are isomorphic and have minimal Weierstrass model
![]() $y^{2} + (x^{3} + 1)y = -5x^{3} - 7$
, and
$y^{2} + (x^{3} + 1)y = -5x^{3} - 7$
, and
![]() $y^{2} + (x^{3} + 1)y = -2x^{3} - 7$
is a minimal Weierstrass model for the third curve. Using Magma’s RankBound command, it is straightforward to see that the Jacobians of these curves have rank zero; and using the command Chabauty0, one finds that each has two rational points. In each case, the rational points are cusps.
$y^{2} + (x^{3} + 1)y = -2x^{3} - 7$
is a minimal Weierstrass model for the third curve. Using Magma’s RankBound command, it is straightforward to see that the Jacobians of these curves have rank zero; and using the command Chabauty0, one finds that each has two rational points. In each case, the rational points are cusps.
The fourth curve, with minimal Weierstrass model
has no
![]() $3$
-adic points. The file genus-2-analysis.m in [Reference Rouse, Sutherland and Zureick-BrownRSZB21] verifies these computations.
$3$
-adic points. The file genus-2-analysis.m in [Reference Rouse, Sutherland and Zureick-BrownRSZB21] verifies these computations.
8.3 Genus 3
The curves corresponding to the labels
have genus 3 and are not hyperelliptic. The first has canonical model
Since X is a Picard curve (which is clear from the y coordinate), we can use Magma’s RankBound command to compute that the rank of
![]() $J_X(\mathbb {Q})$
is zero. In principle, one can now simply compute
$J_X(\mathbb {Q})$
is zero. In principle, one can now simply compute
![]() $J_X(\mathbb {Q}) = J_X(\mathbb {Q})_{{\operatorname {tors}}}$
and then compute
$J_X(\mathbb {Q}) = J_X(\mathbb {Q})_{{\operatorname {tors}}}$
and then compute
![]() $X(\mathbb {Q})$
as the preimage of an Abel–Jacobi map
$X(\mathbb {Q})$
as the preimage of an Abel–Jacobi map
![]() $X(\mathbb {Q}) \hookrightarrow J_X(\mathbb {Q})$
; see [Reference Derickx, Etropolski, van Hoeij, Morrow and Zureick-BrownDEvH+, Subsection 5.2] for a longer discussion of such computations.
$X(\mathbb {Q}) \hookrightarrow J_X(\mathbb {Q})$
; see [Reference Derickx, Etropolski, van Hoeij, Morrow and Zureick-BrownDEvH+, Subsection 5.2] for a longer discussion of such computations.
In practice, we were not able to compute
![]() $J_X(\mathbb {Q})_{{\operatorname {tors}}}$
exactly. By [Reference KatzKat81, Appendix], reduction modulo an odd prime p gives an injection
$J_X(\mathbb {Q})_{{\operatorname {tors}}}$
exactly. By [Reference KatzKat81, Appendix], reduction modulo an odd prime p gives an injection
![]() $J_X(\mathbb {Q})_{{\operatorname {tors}}} \hookrightarrow J_X({\mathbb F}_p)$
. We compute (using Magma’s ClassGroup command) that
$J_X(\mathbb {Q})_{{\operatorname {tors}}} \hookrightarrow J_X({\mathbb F}_p)$
. We compute (using Magma’s ClassGroup command) that
![]() $J_X({\mathbb F}_5) \simeq \mathbb {Z}/198\mathbb {Z}$
and
$J_X({\mathbb F}_5) \simeq \mathbb {Z}/198\mathbb {Z}$
and
![]() $J_X({\mathbb F}_{13}) \simeq \mathbb {Z}/45\mathbb {Z} \times \mathbb {Z}/45\mathbb {Z}$
. (See [Reference Derickx, Etropolski, van Hoeij, Morrow and Zureick-BrownDEvH+, Subsection 4.1] for a longer discussion of computing torsion on modular Jacobians). On the other hand, X has two visible rational points with coordinates
$J_X({\mathbb F}_{13}) \simeq \mathbb {Z}/45\mathbb {Z} \times \mathbb {Z}/45\mathbb {Z}$
. (See [Reference Derickx, Etropolski, van Hoeij, Morrow and Zureick-BrownDEvH+, Subsection 4.1] for a longer discussion of computing torsion on modular Jacobians). On the other hand, X has two visible rational points with coordinates
![]() $[0 : 1 : 0]$
,
$[0 : 1 : 0]$
,
![]() $[1 : 0 : 0]$
whose difference is a point of order 3 in
$[1 : 0 : 0]$
whose difference is a point of order 3 in
![]() $J_X(\mathbb {Q})$
. Thus the only two possibilities for
$J_X(\mathbb {Q})$
. Thus the only two possibilities for
![]() $J_X(\mathbb {Q})$
are
$J_X(\mathbb {Q})$
are
![]() $\mathbb {Z}/3\mathbb {Z}$
and
$\mathbb {Z}/3\mathbb {Z}$
and
![]() $\mathbb {Z}/9\mathbb {Z}$
. A long search for low-degree points on X does not produce a point of order 9 on
$\mathbb {Z}/9\mathbb {Z}$
. A long search for low-degree points on X does not produce a point of order 9 on
![]() $J_X(\mathbb {Q})$
, nor do further local computations (including refined techniques such as [Reference Ozman and SiksekOS19, Section 4]) give a better local bound than
$J_X(\mathbb {Q})$
, nor do further local computations (including refined techniques such as [Reference Ozman and SiksekOS19, Section 4]) give a better local bound than
![]() $\mathbb {Z}/9\mathbb {Z}$
. This suggests a local to global failure for
$\mathbb {Z}/9\mathbb {Z}$
. This suggests a local to global failure for
![]() $J_X(\mathbb {Q})_{{\operatorname {tors}}}$
.
$J_X(\mathbb {Q})_{{\operatorname {tors}}}$
.
We circumvent this as follows. We enumerate
![]() $X({\mathbb F}_2)$
and find that for any
$X({\mathbb F}_2)$
and find that for any
![]() $P,Q \in X({\mathbb F}_2)$
, the order of
$P,Q \in X({\mathbb F}_2)$
, the order of
![]() $P - Q$
is not equal to 9. Since
$P - Q$
is not equal to 9. Since
![]() $J_X(\mathbb {Q})$
has rank 0 and odd order, the reduction map
$J_X(\mathbb {Q})$
has rank 0 and odd order, the reduction map
![]() $J_X(\mathbb {Q})_{{\operatorname {tors}}} \hookrightarrow J_X({\mathbb F}_2)$
is injective by [Reference KatzKat81, Appendix]. Thus, there also do not exist points
$J_X(\mathbb {Q})_{{\operatorname {tors}}} \hookrightarrow J_X({\mathbb F}_2)$
is injective by [Reference KatzKat81, Appendix]. Thus, there also do not exist points
![]() $P,Q \in X(\mathbb {Q})$
such that the order of
$P,Q \in X(\mathbb {Q})$
such that the order of
![]() $P - Q$
is equal to 9 (but note that this does not exclude the possibility that
$P - Q$
is equal to 9 (but note that this does not exclude the possibility that
![]() $J_X(\mathbb {Q}) \simeq \mathbb {Z}/9\mathbb {Z}$
).
$J_X(\mathbb {Q}) \simeq \mathbb {Z}/9\mathbb {Z}$
).
Finally, we compute the preimage of the remaining points under an Abel–Jacobi map. Fix
![]() $P = [0 : 1 : 0]$
,
$P = [0 : 1 : 0]$
,
![]() $P' = [1 : 0 : 0]$
and
$P' = [1 : 0 : 0]$
and
![]() $D = P'-P$
. Let
$D = P'-P$
. Let
![]() $\iota _P \colon X \hookrightarrow J_X$
be the map
$\iota _P \colon X \hookrightarrow J_X$
be the map
![]() $Q \mapsto Q-P$
. By the previous paragraph, for any
$Q \mapsto Q-P$
. By the previous paragraph, for any
![]() $Q \in X(\mathbb {Q})$
,
$Q \in X(\mathbb {Q})$
,
![]() $\iota _P(Q)$
has order 1 or 3. By definition,
$\iota _P(Q)$
has order 1 or 3. By definition,
![]() $\iota _P(P) = 0\cdot D$
, and
$\iota _P(P) = 0\cdot D$
, and
![]() $\iota _P(Q) = 1\cdot D$
. Using Magma’s RiemannRoch command, we find that the linear system
$\iota _P(Q) = 1\cdot D$
. Using Magma’s RiemannRoch command, we find that the linear system
![]() $|2\cdot D + P|$
is empty, so there is no
$|2\cdot D + P|$
is empty, so there is no
![]() $Q \in X(\mathbb {Q})$
such that
$Q \in X(\mathbb {Q})$
such that
![]() $\iota _P(Q) = 2\cdot D$
. Since this exhausts
$\iota _P(Q) = 2\cdot D$
. Since this exhausts
![]() $J_X(\mathbb {Q})_{{\operatorname {tors}}}$
, we have computed
$J_X(\mathbb {Q})_{{\operatorname {tors}}}$
, we have computed
![]() $X(\mathbb {Q})$
. Using our equations for the j-map, we determine that the two known points are both CM points with
$X(\mathbb {Q})$
. Using our equations for the j-map, we determine that the two known points are both CM points with
![]() $j = 0$
.
$j = 0$
.
The second curve has canonical model
and is also a Picard curve (which is clear from the z coordinate). It has an automorphism
![]() $\iota \colon X \to X$
that swaps x and y. The quotient is the elliptic curve
$\iota \colon X \to X$
that swaps x and y. The quotient is the elliptic curve
![]() $E\colon y^{2} + y = x^{3} + 20$
, which has rank one and corresponding newform 243.2.a.a. Applying Magma’s RankBound command reveals that the rank of
$E\colon y^{2} + y = x^{3} + 20$
, which has rank one and corresponding newform 243.2.a.a. Applying Magma’s RankBound command reveals that the rank of
![]() $J_X(\mathbb {Q})$
is also one. In particular,
$J_X(\mathbb {Q})$
is also one. In particular,
![]() $J_X$
is isogenous to
$J_X$
is isogenous to
![]() $E \times A$
, where A is the abelian surface A corresponding to the newform 243.2.a.d; see Example 6.2. The analytic rank of
$E \times A$
, where A is the abelian surface A corresponding to the newform 243.2.a.d; see Example 6.2. The analytic rank of
![]() $A(\mathbb {Q})$
is zero; by Corollary A.8, the algebraic rank is also zero.
$A(\mathbb {Q})$
is zero; by Corollary A.8, the algebraic rank is also zero.
One could in principle apply Chabauty’s method, but this is not directly implemented in Magma for nonhyperelliptic curves. We present an alternative argument. For any point
![]() $P \in X(\mathbb {Q})$
, P and
$P \in X(\mathbb {Q})$
, P and
![]() $\iota (P)$
have the same image in
$\iota (P)$
have the same image in
![]() $E(\mathbb {Q})$
, so
$E(\mathbb {Q})$
, so
![]() $P - \iota (P)$
has trivial image in
$P - \iota (P)$
has trivial image in
![]() $E(\mathbb {Q})$
. Thus, since
$E(\mathbb {Q})$
. Thus, since
![]() $A(\mathbb {Q})$
is torsion, the image of
$A(\mathbb {Q})$
is torsion, the image of
![]() $P - \iota (P)$
in
$P - \iota (P)$
in
![]() $E(\mathbb {Q}) \times A(\mathbb {Q})$
is also torsion; since the map
$E(\mathbb {Q}) \times A(\mathbb {Q})$
is also torsion; since the map
![]() $J(\mathbb {Q}) \to E(\mathbb {Q}) \times A(\mathbb {Q})$
is finite, we conclude that
$J(\mathbb {Q}) \to E(\mathbb {Q}) \times A(\mathbb {Q})$
is finite, we conclude that
![]() $P - \iota (P)$
is an element of
$P - \iota (P)$
is an element of
![]() $J_X(\mathbb {Q})_{{\operatorname {tors}}}$
.
$J_X(\mathbb {Q})_{{\operatorname {tors}}}$
.
It thus suffices to compute
![]() $J_X(\mathbb {Q})_{{\operatorname {tors}}}$
and the preimage of the map
$J_X(\mathbb {Q})_{{\operatorname {tors}}}$
and the preimage of the map
 $$ \begin{align*} \tau\colon X(\mathbb{Q}) &\to J_X(\mathbb{Q})_{{\operatorname{tors}}}\\ P &\mapsto P - \iota(P). \end{align*} $$
$$ \begin{align*} \tau\colon X(\mathbb{Q}) &\to J_X(\mathbb{Q})_{{\operatorname{tors}}}\\ P &\mapsto P - \iota(P). \end{align*} $$
Local computations show that
![]() $J_X(\mathbb {Q})_{{\operatorname {tors}}}$
is isomorphic to a subgroup of
$J_X(\mathbb {Q})_{{\operatorname {tors}}}$
is isomorphic to a subgroup of
![]() $\left (\mathbb {Z}/3\mathbb {Z}\right )^2$
, and differences of rational points generate a group of order 9.
$\left (\mathbb {Z}/3\mathbb {Z}\right )^2$
, and differences of rational points generate a group of order 9.
To compute the preimage of
![]() $\tau $
, we first note that the
$\tau $
, we first note that the
![]() $\tau $
is injective away from the fixed points of
$\tau $
is injective away from the fixed points of
![]() $\iota $
. Indeed, if
$\iota $
. Indeed, if
![]() $P - \iota (P) = Q - \iota (Q)$
as divisors, then either
$P - \iota (P) = Q - \iota (Q)$
as divisors, then either
![]() $P = Q$
, or
$P = Q$
, or
![]() $P = \iota (P)$
and
$P = \iota (P)$
and
![]() $Q = \iota (Q)$
. Now suppose that
$Q = \iota (Q)$
. Now suppose that
![]() $P - \iota (P) \neq Q - \iota (Q)$
as divisors, but
$P - \iota (P) \neq Q - \iota (Q)$
as divisors, but
![]() $P - \iota (P) \sim Q - \iota (Q)$
. If
$P - \iota (P) \sim Q - \iota (Q)$
. If
![]() $P = \iota (P)$
but
$P = \iota (P)$
but
![]() $Q \neq \iota (Q)$
, this equivalence gives a
$Q \neq \iota (Q)$
, this equivalence gives a
![]() $g^1_1$
, which is a contradiction since X is not rational (and similarly if
$g^1_1$
, which is a contradiction since X is not rational (and similarly if
![]() $Q = \iota (Q)$
but
$Q = \iota (Q)$
but
![]() $P \neq \iota (P)$
). If
$P \neq \iota (P)$
). If
![]() $Q \neq \iota (Q)$
and
$Q \neq \iota (Q)$
and
![]() $P \neq \iota (P)$
, then instead this gives a
$P \neq \iota (P)$
, then instead this gives a
![]() $g^1_2$
on a nonhyperelliptic curve, which is also a contradiction. Thus
$g^1_2$
on a nonhyperelliptic curve, which is also a contradiction. Thus
![]() $\tau $
is injective away from the fixed points of
$\tau $
is injective away from the fixed points of
![]() $\iota $
.
$\iota $
.
Next, differences of rational points give an explicit basis
![]() $D_1, D_2$
for
$D_1, D_2$
for
![]() $J_X(\mathbb {Q})_{{\operatorname {tors}}}$
. For each
$J_X(\mathbb {Q})_{{\operatorname {tors}}}$
. For each
![]() $a,b \in \mathbb {Z}/3\mathbb {Z}$
such that
$a,b \in \mathbb {Z}/3\mathbb {Z}$
such that
![]() $(a,b) \neq (0,0)$
, we either find an explicit point P for which we have
$(a,b) \neq (0,0)$
, we either find an explicit point P for which we have
![]() $P - \iota (P) = aD_1 + bD_2$
, or we find a prime p such that there is no
$P - \iota (P) = aD_1 + bD_2$
, or we find a prime p such that there is no
![]() $P \in X({\mathbb F}_p)$
such that
$P \in X({\mathbb F}_p)$
such that
![]() $P - \iota (P) = aD_1 + bD_2$
in
$P - \iota (P) = aD_1 + bD_2$
in
![]() $J_X({\mathbb F}_p)$
(essentially, ‘sieving’) and thus no such
$J_X({\mathbb F}_p)$
(essentially, ‘sieving’) and thus no such
![]() $P \in X(\mathbb {Q})$
. If
$P \in X(\mathbb {Q})$
. If
![]() $(a,b) = (0,0)$
, then
$(a,b) = (0,0)$
, then
![]() $P - \iota (P) = aD_1 + bD_2$
if and only if
$P - \iota (P) = aD_1 + bD_2$
if and only if
![]() $P = \iota (P)$
: that is, if and only if P is a fixed point of the involution
$P = \iota (P)$
: that is, if and only if P is a fixed point of the involution
![]() $\iota $
; there are finitely many such points, and they are straightforward to compute. Using our equations for the j-map, we find that two of the known points are cusps and one is a CM point with
$\iota $
; there are finitely many such points, and they are straightforward to compute. Using our equations for the j-map, we find that two of the known points are cusps and one is a CM point with
![]() $j = 0$
.
$j = 0$
.
The third curve is isomorphic to the first, which is easy to verify with the explicit models. The 2 rational points are not exceptional; they are both CM points with
![]() $j = 0$
.
$j = 0$
.
The files 9.108.3.1.m, 27.36.3.1.m, 27.108.3.1.m in [Reference Rouse, Sutherland and Zureick-BrownRSZB21] verify these computations.
8.4 Genus 4
The curves corresponding to the labels
have genus 4. The fourth curve (with label 27.108.4.5) has no
![]() ${\mathbb F}_7$
points (see Section 5), and computations with Magma show that the other 3 are all isomorphic. Using the method of [Reference van Hoeij and NovocinvHN05], we find that they are all isomorphic to the Picard curve
${\mathbb F}_7$
points (see Section 5), and computations with Magma show that the other 3 are all isomorphic. Using the method of [Reference van Hoeij and NovocinvHN05], we find that they are all isomorphic to the Picard curve
(We note that while [Reference van Hoeij and NovocinvHN05] is unpublished and thus has not been refereed, in our example it is straightforward to verify that our curve is isomorphic to this one.) The Jacobian of the curve X is isogenous to the modular abelian variety 81.2.c.b, which has analytic rank 0.
From here the argument is identical to those in Subsection 8.3. Local computations show that
![]() $J_X(\mathbb {Q})_{{\operatorname {tors}}}$
is isomorphic to a subgroup of
$J_X(\mathbb {Q})_{{\operatorname {tors}}}$
is isomorphic to a subgroup of
![]() $\left (\mathbb {Z}/3\mathbb {Z}\right )^2$
, and differences of rational points generate a group of order 9. Using Magma’s RiemannRoch command, we compute the preimage of
$\left (\mathbb {Z}/3\mathbb {Z}\right )^2$
, and differences of rational points generate a group of order 9. Using Magma’s RiemannRoch command, we compute the preimage of
![]() $J(\mathbb {Q})$
under an Abel–Jacobi map and find that
$J(\mathbb {Q})$
under an Abel–Jacobi map and find that
![]() $\#X(\mathbb {Q}) = 3$
; via Section 5, we compute a priori that for each of the 3 curves, there are 3 rational cusps.
$\#X(\mathbb {Q}) = 3$
; via Section 5, we compute a priori that for each of the 3 curves, there are 3 rational cusps.
The files 9.108.4.1.m, 27.108.4.1.m, and 27.108.4.3.m in [Reference Rouse, Sutherland and Zureick-BrownRSZB21] verify these computations.
8.5 Genus 6
Let H be the subgroup labeled 27.108.6.1. The curve
![]() $X_H$
has genus
$X_H$
has genus
![]() $6$
; it is a Picard curve and admits an automorphism
$6$
; it is a Picard curve and admits an automorphism
![]() $\iota $
of order
$\iota $
of order
![]() $2$
defined over
$2$
defined over
![]() $\mathbb {Q}$
. The quotient curve Y has genus
$\mathbb {Q}$
. The quotient curve Y has genus
![]() $3$
and appears to have
$3$
and appears to have
![]() $11$
rational points; its Jacobian
$11$
rational points; its Jacobian
![]() $J_Y$
is geometrically simple and is isogenous to the modular abelian variety 243.2.a.f, which has analytic ran 3. The Jacobian
$J_Y$
is geometrically simple and is isogenous to the modular abelian variety 243.2.a.f, which has analytic ran 3. The Jacobian
![]() $J_H$
of
$J_H$
of
![]() $X_H$
is isogenous to
$X_H$
is isogenous to
![]() $J_Y \times A$
, where A is the geometrically simple modular abelian variety 243.2.a.e, which has analytic rank 0.
$J_Y \times A$
, where A is the geometrically simple modular abelian variety 243.2.a.e, which has analytic rank 0.
We are thus in a similar situation to the group with label 27.36.3.1 from Subsection 8.3: every rational point
![]() $P \in X_H(\mathbb {Q})$
has the property that
$P \in X_H(\mathbb {Q})$
has the property that
![]() $P - \iota (P)$
is torsion in
$P - \iota (P)$
is torsion in
![]() $J(X_H)$
. Local computations show that
$J(X_H)$
. Local computations show that
![]() $J_H(\mathbb {Q})_{{\operatorname {tors}}}$
is isomorphic to a subgroup of
$J_H(\mathbb {Q})_{{\operatorname {tors}}}$
is isomorphic to a subgroup of
![]() $\left (\mathbb {Z}/3\mathbb {Z}\right )^2$
. (In fact, we can show that
$\left (\mathbb {Z}/3\mathbb {Z}\right )^2$
. (In fact, we can show that
![]() $J_H(\mathbb {Q})_{{\operatorname {tors}}} \simeq \left (\mathbb {Z}/3\mathbb {Z}\right )^2$
, but we will not need this fact.)
$J_H(\mathbb {Q})_{{\operatorname {tors}}} \simeq \left (\mathbb {Z}/3\mathbb {Z}\right )^2$
, but we will not need this fact.)
As in Subsection 8.3, the map
 $$ \begin{align*} \tau\colon X(\mathbb{Q}) &\to J_H(\mathbb{Q})_{{\operatorname{tors}}}\\ P &\mapsto P - \iota(P). \end{align*} $$
$$ \begin{align*} \tau\colon X(\mathbb{Q}) &\to J_H(\mathbb{Q})_{{\operatorname{tors}}}\\ P &\mapsto P - \iota(P). \end{align*} $$
is injective away from the fixed points of
![]() $\iota $
. Additionally, since
$\iota $
. Additionally, since
![]() $\#J_H(\mathbb {Q})_{{\operatorname {tors}}}$
is odd, the reduction map
$\#J_H(\mathbb {Q})_{{\operatorname {tors}}}$
is odd, the reduction map
is injective [Reference KatzKat81, Appendix]. The involution
![]() $\iota $
has two fixed points P and Q, both of which are rational. Let
$\iota $
has two fixed points P and Q, both of which are rational. Let
![]() $U = X_H - \{P,Q\}$
, and consider the commutative diagram
$U = X_H - \{P,Q\}$
, and consider the commutative diagram

Since
![]() $\tau $
and
$\tau $
and
![]() ${\operatorname {red}}_{J,2}$
are injective,
${\operatorname {red}}_{J,2}$
are injective,
![]() ${\operatorname {red}}_{U,2}$
is also injective. We compute in Magma that
${\operatorname {red}}_{U,2}$
is also injective. We compute in Magma that
![]() $\#U({\mathbb F}_2) = 2$
and that both points lift to
$\#U({\mathbb F}_2) = 2$
and that both points lift to
![]() $\mathbb {Q}$
. We conclude that
$\mathbb {Q}$
. We conclude that
![]() $\#X(\mathbb {Q}) = 4$
.
$\#X(\mathbb {Q}) = 4$
.
Finally, using our equations for the j-map, we compute that the four known points are CM with
![]() $j = 0$
and
$j = 0$
and
![]() $j=54000$
.
$j=54000$
.
The file 27.108.6.1.m in [Reference Rouse, Sutherland and Zureick-BrownRSZB21] verifies these computations.
8.6 Genus 36 and 43
Let H be the group with label 27.729.43.1. The curve
![]() $X_H$
has genus
$X_H$
has genus
![]() $43$
and is a degree
$43$
and is a degree
![]() $27$
cover of the curve with label 9.27.0.1, the modular curve that is the subject of the paper [Reference ElkiesElk06]. If
$27$
cover of the curve with label 9.27.0.1, the modular curve that is the subject of the paper [Reference ElkiesElk06]. If
![]() $E/\mathbb {Q}$
is an elliptic curve and the image of
$E/\mathbb {Q}$
is an elliptic curve and the image of
![]() $\rho _{E,3^{\infty }}$
is contained in H, then
$\rho _{E,3^{\infty }}$
is contained in H, then
![]() $\mathbb {Q}(E[27]) = \mathbb {Q}(E[3],\zeta _{27})$
. This remarkable situation is incompatible with most known possibilities for
$\mathbb {Q}(E[27]) = \mathbb {Q}(E[3],\zeta _{27})$
. This remarkable situation is incompatible with most known possibilities for
![]() $\rho _{E,3^{\infty }}(G_{\mathbb {Q}_3})$
, which suggests that
$\rho _{E,3^{\infty }}(G_{\mathbb {Q}_3})$
, which suggests that
![]() $X_H$
has no
$X_H$
has no
![]() $3$
-adic points.
$3$
-adic points.
We verify this as follows. Using the methods described in Section 7, we compute the canonical model for
![]() $X_H$
in
$X_H$
in
![]() $\mathbb {P}^{42}$
. We successfully compute a basis for the space of weight
$\mathbb {P}^{42}$
. We successfully compute a basis for the space of weight
![]() $6$
and weight
$6$
and weight
![]() $8$
modular forms for H (which have dimensions
$8$
modular forms for H (which have dimensions
![]() $318$
and
$318$
and
![]() $438$
, respectively). In general, a nonhyperelliptic curve of genus g contains
$438$
, respectively). In general, a nonhyperelliptic curve of genus g contains
![]() $\binom {g-2}{2}$
quadrics as generators for the canonical ideal, and these generate the canonical ideal provided
$\binom {g-2}{2}$
quadrics as generators for the canonical ideal, and these generate the canonical ideal provided
![]() $g \geq 4$
, the curve is not trigonal, and, if
$g \geq 4$
, the curve is not trigonal, and, if
![]() $g = 6$
, the curve is not a smooth plane quintic [Reference PetriPet23], [Reference Green and LazarsfeldGL85, Corollary 1.7, Remark 1.9]. Indeed, the curve
$g = 6$
, the curve is not a smooth plane quintic [Reference PetriPet23], [Reference Green and LazarsfeldGL85, Corollary 1.7, Remark 1.9]. Indeed, the curve
![]() $X_H$
is not trigonal, so our canonical model is given by the vanishing of
$X_H$
is not trigonal, so our canonical model is given by the vanishing of
![]() $\binom {41}{2} = 820$
quadrics in
$\binom {41}{2} = 820$
quadrics in
![]() $\mathbb {P}^{42}$
.
$\mathbb {P}^{42}$
.
The model computation takes about 10 hours. We are able to represent
![]() $E_{4}$
as a ratio of a degree
$E_{4}$
as a ratio of a degree
![]() $4$
and a degree
$4$
and a degree
![]() $2$
element in the canonical ring and represent
$2$
element in the canonical ring and represent
![]() $E_{6}$
as a ratio of a degree
$E_{6}$
as a ratio of a degree
![]() $5$
and a degree
$5$
and a degree
![]() $2$
element in the canonical ring. However, memory limitations do not allow us to use these to represent j as a ratio of elements in the canonical ring. Using the expressions for
$2$
element in the canonical ring. However, memory limitations do not allow us to use these to represent j as a ratio of elements in the canonical ring. Using the expressions for
![]() $E_{4}$
and
$E_{4}$
and
![]() $E_{6}$
to compute j gives a ratio of elements each of degree
$E_{6}$
to compute j gives a ratio of elements each of degree
![]() $18$
. Note that a generic homogeneous degree
$18$
. Note that a generic homogeneous degree
![]() $18$
polynomial in
$18$
polynomial in
![]() $43$
variables is a linear combination of
$43$
variables is a linear combination of
![]() $\binom {60}{18} = 925029565741050$
monomials.
$\binom {60}{18} = 925029565741050$
monomials.
We use this model to show that
![]() $X_H$
has no
$X_H$
has no
![]() $3$
-adic points using a suggestion of David Zywina. First we find that the reduction mod
$3$
-adic points using a suggestion of David Zywina. First we find that the reduction mod
![]() $3$
of our model has
$3$
of our model has
![]() $19$
points over
$19$
points over
![]() ${\mathbb F}_{3}$
; this reduction is not one-dimensional. For each point
${\mathbb F}_{3}$
; this reduction is not one-dimensional. For each point
![]() $(a_{0} : \cdots : a_{42})$
on
$(a_{0} : \cdots : a_{42})$
on
![]() $X_{H}({\mathbb F}_{3})$
, we plug
$X_{H}({\mathbb F}_{3})$
, we plug
![]() $a_{i} + 3x_{i}$
into the defining equations for
$a_{i} + 3x_{i}$
into the defining equations for
![]() $X_{H}/\mathbb {Z}$
; here
$X_{H}/\mathbb {Z}$
; here
![]() $a_{i}$
and
$a_{i}$
and
![]() $x_{i}$
represent the first two digits in the
$x_{i}$
represent the first two digits in the
![]() $3$
-adic expansion of the ith coordinate. Dividing by
$3$
-adic expansion of the ith coordinate. Dividing by
![]() $3$
and reducing modulo
$3$
and reducing modulo
![]() $3$
represents the mod
$3$
represents the mod
![]() $9$
lifts of
$9$
lifts of
![]() $(a_{0} : \cdots : a_{42})$
as a system of linear equations in
$(a_{0} : \cdots : a_{42})$
as a system of linear equations in
![]() $x_{0}, \ldots , x_{42}$
. We find that in all cases, this system of linear equations has no solutions, so
$x_{0}, \ldots , x_{42}$
. We find that in all cases, this system of linear equations has no solutions, so
![]() $X_{H}(\mathbb {Z}/9\mathbb {Z})$
is empty. The total running time to verify this is approximately 20 seconds. This technique computes the fibres of the map
$X_{H}(\mathbb {Z}/9\mathbb {Z})$
is empty. The total running time to verify this is approximately 20 seconds. This technique computes the fibres of the map
![]() $\mathrm {Gr}_{2}(X_{H})({\mathbb F}_{p}) \to X_{H}({\mathbb F}_{p})$
, where
$\mathrm {Gr}_{2}(X_{H})({\mathbb F}_{p}) \to X_{H}({\mathbb F}_{p})$
, where
![]() $\mathrm {Gr}_{2}$
denotes the level 2 Greenberg functor. For a short introduction to the Greenberg transform, see [Reference PoonenPoo01, Section 3].
$\mathrm {Gr}_{2}$
denotes the level 2 Greenberg functor. For a short introduction to the Greenberg transform, see [Reference PoonenPoo01, Section 3].
The group H with label 25.625.36.1 is similarly remarkable and has the following properties:
![]() $\#H(25) = 5\cdot \#H(5) = \#\operatorname {GL}_2({\mathbb F}_5)$
(i.e., the kernel reduction map
$\#H(25) = 5\cdot \#H(5) = \#\operatorname {GL}_2({\mathbb F}_5)$
(i.e., the kernel reduction map
![]() $H(25)\to H(5)$
has order
$H(25)\to H(5)$
has order
![]() $5$
), the image of
$5$
), the image of
![]() $H(5)$
in
$H(5)$
in
![]() $\operatorname {PGL}_{2}({\mathbb F}_5)$
is
$\operatorname {PGL}_{2}({\mathbb F}_5)$
is
![]() $S_4$
, and if
$S_4$
, and if
![]() $E/\mathbb {Q}$
is an elliptic curve such that
$E/\mathbb {Q}$
is an elliptic curve such that
![]() $\rho _{E,5^{\infty }}(G_{\mathbb {Q}}) \leq H$
, then
$\rho _{E,5^{\infty }}(G_{\mathbb {Q}}) \leq H$
, then
![]() $\mathbb {Q}(E[25]) = \mathbb {Q}(E[5], \zeta _{25})$
or
$\mathbb {Q}(E[25]) = \mathbb {Q}(E[5], \zeta _{25})$
or
![]() $\zeta _{25} \in \mathbb {Q}(E[5])$
. The procedure described above for the group 27.729.43.1 also works here and shows that
$\zeta _{25} \in \mathbb {Q}(E[5])$
. The procedure described above for the group 27.729.43.1 also works here and shows that
![]() $X_H(\mathbb {Z}/25\mathbb {Z})$
is empty.
$X_H(\mathbb {Z}/25\mathbb {Z})$
is empty.
The files 27.729.43.1.m and 25.625.36.1.m in [Reference Rouse, Sutherland and Zureick-BrownRSZB21] verify these computations.
8.7 Genus 41: an equationless Mordell–Weil sieve
Let H be the subgroup with label 121.605.41.1. The associated curve
![]() $X_H$
has genus 41, and its Jacobian has analytic rank 41. We were unable to compute a model for
$X_H$
has genus 41, and its Jacobian has analytic rank 41. We were unable to compute a model for
![]() $X_H$
but will show that
$X_H$
but will show that
![]() $X_H(\mathbb {Q})$
is empty by Mordell–Weil sieving without using equations (in other words, sieving ‘via moduli’).
$X_H(\mathbb {Q})$
is empty by Mordell–Weil sieving without using equations (in other words, sieving ‘via moduli’).
The reduction
![]() $H(11)$
mod 11 is a subgroup of
$H(11)$
mod 11 is a subgroup of
![]() $N_{\operatorname {\mathrm {ns}}}(11)$
, so there is a map
$N_{\operatorname {\mathrm {ns}}}(11)$
, so there is a map
![]() $\pi \colon X_H \to X_{\operatorname {\mathrm {ns}}}^+(11)$
. The curve
$\pi \colon X_H \to X_{\operatorname {\mathrm {ns}}}^+(11)$
. The curve
![]() $X_{\operatorname {\mathrm {ns}}}^+(11)$
is an elliptic curve with Mordell–Weil group
$X_{\operatorname {\mathrm {ns}}}^+(11)$
is an elliptic curve with Mordell–Weil group
![]() $X_{\operatorname {\mathrm {ns}}}^+(11)(\mathbb {Q}) \simeq \mathbb {Z}$
. We will perform a Mordell–Weil sieve (see [Reference Bruin and StollBS10]) in the following sense: for a set S of primes of good reduction (i.e.,
$X_{\operatorname {\mathrm {ns}}}^+(11)(\mathbb {Q}) \simeq \mathbb {Z}$
. We will perform a Mordell–Weil sieve (see [Reference Bruin and StollBS10]) in the following sense: for a set S of primes of good reduction (i.e.,
![]() $11 \not \in S$
), the diagram
$11 \not \in S$
), the diagram

is commutative. We claim that for
![]() $S = \{13, 307\}$
, the intersection of the images of the maps
$S = \{13, 307\}$
, the intersection of the images of the maps
![]() $\pi _S$
and
$\pi _S$
and
![]() $\beta $
is empty, and in particular
$\beta $
is empty, and in particular
![]() $X_H(\mathbb {Q})$
is empty.
$X_H(\mathbb {Q})$
is empty.
In principle, this is a straightforward computation to implement. In practice, we do not have explicit equations for the map
![]() $\pi \colon X_H \to X_{\operatorname {\mathrm {ns}}}^+(11)$
. Nonetheless, for
$\pi \colon X_H \to X_{\operatorname {\mathrm {ns}}}^+(11)$
. Nonetheless, for
![]() $p \neq 11$
, we can determine whether a point
$p \neq 11$
, we can determine whether a point
![]() $P \in X_{\operatorname {\mathrm {ns}}}^+(11)({\mathbb F}_p)$
is the image under
$P \in X_{\operatorname {\mathrm {ns}}}^+(11)({\mathbb F}_p)$
is the image under
![]() $\pi $
of some point of
$\pi $
of some point of
![]() $X_H({\mathbb F}_p)$
by working directly with the (generalised) elliptic curve E corresponding to P, as follows. The mod 11 image
$X_H({\mathbb F}_p)$
by working directly with the (generalised) elliptic curve E corresponding to P, as follows. The mod 11 image
![]() $\rho _{E,11}(G_{{\mathbb F}_p})$
is a subgroup of
$\rho _{E,11}(G_{{\mathbb F}_p})$
is a subgroup of
![]() $N_{\operatorname {\mathrm {ns}}}^+(11)$
. To prove there does not exist a point
$N_{\operatorname {\mathrm {ns}}}^+(11)$
. To prove there does not exist a point
![]() $Q \in X_H({\mathbb F}_p)$
such that
$Q \in X_H({\mathbb F}_p)$
such that
![]() $\pi (Q) = P$
, it suffices to show that the mod 121 image
$\pi (Q) = P$
, it suffices to show that the mod 121 image
![]() $\rho _{E,121}(G_{{\mathbb F}_p})$
is not a subgroup of H. These images are cyclic groups generated by the image of Frobenius.
$\rho _{E,121}(G_{{\mathbb F}_p})$
is not a subgroup of H. These images are cyclic groups generated by the image of Frobenius.
The reduction mod N of the matrix
![]() $A_{\pi }$
from equation 5.2 is the matrix of Frobenius acting on
$A_{\pi }$
from equation 5.2 is the matrix of Frobenius acting on
![]() $E[N](\overline {{\mathbb F}}_p)$
(with respect to some basis) and is computed by the function GL2nTorsionFrobenius in the file gl2.m in [Reference Rouse, Sutherland and Zureick-BrownRSZB21]. We compute this and check whether it (or a conjugate) is contained in H; if not, then P is not in the image of
$E[N](\overline {{\mathbb F}}_p)$
(with respect to some basis) and is computed by the function GL2nTorsionFrobenius in the file gl2.m in [Reference Rouse, Sutherland and Zureick-BrownRSZB21]. We compute this and check whether it (or a conjugate) is contained in H; if not, then P is not in the image of
![]() $\pi $
(mod p).
$\pi $
(mod p).
We can thus perform the Mordell–Weil sieve ‘at the level of moduli’. For our chosen generator R of
![]() $X_{\operatorname {\mathrm {ns}}}^+(11)(\mathbb {Q})$
, we find that, for
$X_{\operatorname {\mathrm {ns}}}^+(11)(\mathbb {Q})$
, we find that, for
![]() $p = 13$
, a hypothetical point of
$p = 13$
, a hypothetical point of
![]() $X_H(\mathbb {Q})$
maps to
$X_H(\mathbb {Q})$
maps to
![]() $n\cdot R$
, where n is 1 or 5 mod 7; and for
$n\cdot R$
, where n is 1 or 5 mod 7; and for
![]() $p = 307$
, any point of
$p = 307$
, any point of
![]() $X_H(\mathbb {Q})$
maps to
$X_H(\mathbb {Q})$
maps to
![]() $n\cdot R$
, where n is 2, 3, 4, 7, 10 or 13 mod 14; we conclude that
$n\cdot R$
, where n is 2, 3, 4, 7, 10 or 13 mod 14; we conclude that
![]() $X_H(\mathbb {Q})$
is empty.
$X_H(\mathbb {Q})$
is empty.
The file 121.605.41.1.m in [Reference Rouse, Sutherland and Zureick-BrownRSZB21] verifies these computations.
9 Comments on the remaining cases
In this section, we discuss our (unsuccessful) efforts to determine the rational points on the six curves marked with asterisks in Table 5, which also appear in Table 2. Each of these curves has no rational cusps and at least one rational CM point; our analysis suggests that there are no exceptional points on any of these curves, but we are unable to prove this.
9.1
 $X_{\mathrm {ns}}^{+}(27)$
$X_{\mathrm {ns}}^{+}(27)$
While we are not able to determine the rational points on
![]() $X = X_{\mathrm {ns}}^{+}(27)$
(labeled 27.243.12.1), we will describe our attempts. As described in Section 7, we compute the canonical model of
$X = X_{\mathrm {ns}}^{+}(27)$
(labeled 27.243.12.1), we will describe our attempts. As described in Section 7, we compute the canonical model of
![]() $X_{\mathrm {ns}}^{+}(27)$
, which has genus
$X_{\mathrm {ns}}^{+}(27)$
, which has genus
![]() $12$
.
$12$
.
Rather than try to work directly with X, we work with a modular curve
![]() $X_{H}$
for which
$X_{H}$
for which
![]() $\det H$
is not surjective and whose geometric connected components are defined over
$\det H$
is not surjective and whose geometric connected components are defined over
![]() $\mathbb {Q}(\zeta _{3})$
rather than
$\mathbb {Q}(\zeta _{3})$
rather than
![]() $\mathbb {Q}$
. Although
$\mathbb {Q}$
. Although
![]() $N_{\mathrm {ns}}(27)$
is a maximal subgroup of index
$N_{\mathrm {ns}}(27)$
is a maximal subgroup of index
![]() $9$
in
$9$
in
![]() $N_{\mathrm {ns}}(9)$
, if we let
$N_{\mathrm {ns}}(9)$
, if we let
![]() $D = \{ g \in \operatorname {GL}_{2}(\mathbb {Z}_{3}) \colon \det (g) \equiv 1 \pmod {3} \}$
, then there is a nontrivial subgroup between
$D = \{ g \in \operatorname {GL}_{2}(\mathbb {Z}_{3}) \colon \det (g) \equiv 1 \pmod {3} \}$
, then there is a nontrivial subgroup between
![]() $N_{\mathrm {ns}}(27) \cap D$
and
$N_{\mathrm {ns}}(27) \cap D$
and
![]() $N_{\mathrm {ns}}(9) \cap D$
. This is the subgroup
$N_{\mathrm {ns}}(9) \cap D$
. This is the subgroup
![]() $H = \left \langle \left [\begin {smallmatrix} 0 & 26 \\ 4 & 6 \end {smallmatrix}\right ], \left [\begin {smallmatrix} 10 & 1 \\ 25 & 26 \end {smallmatrix}\right ]\right \rangle \le \operatorname {GL}_{2}(27)$
with label 3.2.1-27.81.3.1. Let
$H = \left \langle \left [\begin {smallmatrix} 0 & 26 \\ 4 & 6 \end {smallmatrix}\right ], \left [\begin {smallmatrix} 10 & 1 \\ 25 & 26 \end {smallmatrix}\right ]\right \rangle \le \operatorname {GL}_{2}(27)$
with label 3.2.1-27.81.3.1. Let
![]() $X_{H}'$
denote one of the connected components of
$X_{H}'$
denote one of the connected components of
![]() $X_{H, \mathbb {Q}(\zeta _{3})}$
(the components are all isomorphic). The curve
$X_{H, \mathbb {Q}(\zeta _{3})}$
(the components are all isomorphic). The curve
![]() $X_{H}'$
has genus
$X_{H}'$
has genus
![]() $3$
, and we use a variant of the method from Section 7 to compute a model. We find that
$3$
, and we use a variant of the method from Section 7 to compute a model. We find that
![]() $X_{H}'$
is the smooth plane quartic
$X_{H}'$
is the smooth plane quartic
 $$ \begin{align*} a^{4} &+ (\zeta_{3} - 1) a^{3} b + (3 \zeta_{3} + 2) a^{3} c - 3a^{2}c^{2} + (2 \zeta_{3} + 2) ab^{3} - 3 \zeta_{3} ab^{2} c\\ &+ 3 \zeta_{3} abc^{2} - 2 \zeta_{3} ac^{3} - \zeta_{3} b^{3} c + 3 \zeta_{3} b^{2} c^{2} + (-\zeta_{3} + 1) bc^{3} + (\zeta_{3} + 1) c^{4} = 0. \end{align*} $$
$$ \begin{align*} a^{4} &+ (\zeta_{3} - 1) a^{3} b + (3 \zeta_{3} + 2) a^{3} c - 3a^{2}c^{2} + (2 \zeta_{3} + 2) ab^{3} - 3 \zeta_{3} ab^{2} c\\ &+ 3 \zeta_{3} abc^{2} - 2 \zeta_{3} ac^{3} - \zeta_{3} b^{3} c + 3 \zeta_{3} b^{2} c^{2} + (-\zeta_{3} + 1) bc^{3} + (\zeta_{3} + 1) c^{4} = 0. \end{align*} $$
There is a degree
![]() $3$
morphism
$3$
morphism
![]() $X \to X_{H}'$
defined over
$X \to X_{H}'$
defined over
![]() $\mathbb {Q}(\zeta _{3})$
, so every
$\mathbb {Q}(\zeta _{3})$
, so every
![]() $\mathbb {Q}(\zeta _{3})$
point of X maps to a
$\mathbb {Q}(\zeta _{3})$
point of X maps to a
![]() $\mathbb {Q}(\zeta _{3})$
point of
$\mathbb {Q}(\zeta _{3})$
point of
![]() $X_{H}'$
. There are at least
$X_{H}'$
. There are at least
![]() $13$
points in
$13$
points in
![]() $X_{H}'(\mathbb {Q}(\zeta _{3}))$
. These include the images of the
$X_{H}'(\mathbb {Q}(\zeta _{3}))$
. These include the images of the
![]() $8$
rational points on
$8$
rational points on
![]() $X_{\mathrm {ns}}^{+}(27)$
, a CM point with discriminant
$X_{\mathrm {ns}}^{+}(27)$
, a CM point with discriminant
![]() $-43$
, three more CM points with discriminant
$-43$
, three more CM points with discriminant
![]() $-4$
and a non-CM point corresponding to an elliptic curve with j-invariant
$-4$
and a non-CM point corresponding to an elliptic curve with j-invariant
![]() $2^{3} \cdot 5^{3} \cdot 19^{-27} \cdot (-15-2 \zeta _{3})^{3} \cdot (452 + 431\zeta _{3})^{3} \cdot (53515427 + 41314914 \zeta _{3})^{3}$
. The restriction of scalars
$2^{3} \cdot 5^{3} \cdot 19^{-27} \cdot (-15-2 \zeta _{3})^{3} \cdot (452 + 431\zeta _{3})^{3} \cdot (53515427 + 41314914 \zeta _{3})^{3}$
. The restriction of scalars
![]() $\operatorname {\mathrm {Res}}_{\mathbb {Q}(\zeta _{3})/\mathbb {Q}} J(X^{\prime }_H)$
is isogenous to
$\operatorname {\mathrm {Res}}_{\mathbb {Q}(\zeta _{3})/\mathbb {Q}} J(X^{\prime }_H)$
is isogenous to
![]() $J_H$
, and Theorem A.7 shows that
$J_H$
, and Theorem A.7 shows that
![]() $J_{H}$
is isogenous to the
$J_{H}$
is isogenous to the
![]() $\mathbb {Q}$
-simple abelian variety associated to 729.2.a.c with analytic rank
$\mathbb {Q}$
-simple abelian variety associated to 729.2.a.c with analytic rank
![]() $6$
.
$6$
.
We searched for points on
![]() $X_{\mathrm {ns}}^{+}(27)$
by enumerating rational points on
$X_{\mathrm {ns}}^{+}(27)$
by enumerating rational points on
![]() $X_{\mathrm {ns}}^{+}(9) \cong \mathbb {P}^{1}$
and seeing if they lift to
$X_{\mathrm {ns}}^{+}(9) \cong \mathbb {P}^{1}$
and seeing if they lift to
![]() $X_{H}'$
. We tested all points on
$X_{H}'$
. We tested all points on
![]() $X_{\mathrm {ns}}^{+}(9)$
with height
$X_{\mathrm {ns}}^{+}(9)$
with height
![]() $\leq 1000$
, and the only points we found that lifted were
$\leq 1000$
, and the only points we found that lifted were
![]() $8$
CM points (two with discriminant
$8$
CM points (two with discriminant
![]() $D=-4$
and one each for
$D=-4$
and one each for
![]() $D=-7 -16, -19, -28, -67, -163$
). The computation takes approximately two hours.
$D=-7 -16, -19, -28, -67, -163$
). The computation takes approximately two hours.
It is not hard to find a divisor D supported at
![]() $4$
of the
$4$
of the
![]() $\mathbb {Q}(\zeta _{3})$
points of
$\mathbb {Q}(\zeta _{3})$
points of
![]() $X_{H}'$
whose image in
$X_{H}'$
whose image in
![]() $J(X_{H}')$
has order
$J(X_{H}')$
has order
![]() $3$
. Using this point, one can construct a family
$3$
. Using this point, one can construct a family
![]() $\{ D_{\delta } \}$
of 9 étale triple covers of
$\{ D_{\delta } \}$
of 9 étale triple covers of
![]() $X_{H}'$
. Counting points on these genus
$X_{H}'$
. Counting points on these genus
![]() $7$
curves over finite fields strongly suggests that each of these genus
$7$
curves over finite fields strongly suggests that each of these genus
![]() $7$
curves
$7$
curves
![]() $D_{\delta }$
maps to an elliptic curve
$D_{\delta }$
maps to an elliptic curve
![]() $E/\mathbb {Q}(\zeta _{3})$
. One can search for elliptic curves defined over
$E/\mathbb {Q}(\zeta _{3})$
. One can search for elliptic curves defined over
![]() $\mathbb {Q}(\zeta _{3})$
with bad reduction only at
$\mathbb {Q}(\zeta _{3})$
with bad reduction only at
![]() $\langle 1 - \zeta _{3} \rangle $
and use this to predict, for each twist
$\langle 1 - \zeta _{3} \rangle $
and use this to predict, for each twist
![]() $D_{\delta }$
, which elliptic curve it maps to. For
$D_{\delta }$
, which elliptic curve it maps to. For
![]() $8$
of the
$8$
of the
![]() $9$
twists
$9$
twists
![]() $D_{\delta }$
, the elliptic curve in question has rank
$D_{\delta }$
, the elliptic curve in question has rank
![]() $0$
or
$0$
or
![]() $1$
, which should in principle make an elliptic curve Chabauty computation feasible.
$1$
, which should in principle make an elliptic curve Chabauty computation feasible.
Six of the
![]() $13$
known
$13$
known
![]() $\mathbb {Q}(\zeta _{3})$
points of
$\mathbb {Q}(\zeta _{3})$
points of
![]() $X_{H}'$
lift to the final twist
$X_{H}'$
lift to the final twist
![]() $D_{1}$
. Since the cover
$D_{1}$
. Since the cover
![]() $D_{1} \to X_{H}'$
is étale, each of those six points on
$D_{1} \to X_{H}'$
is étale, each of those six points on
![]() $X_{H}'$
has
$X_{H}'$
has
![]() $3 \ \mathbb {Q}(\zeta _{3})$
-rational preimages on
$3 \ \mathbb {Q}(\zeta _{3})$
-rational preimages on
![]() $X_{K}$
, so
$X_{K}$
, so
![]() $D_{1}$
has at least
$D_{1}$
has at least
![]() $18 \ \mathbb {Q}(\zeta _{3})$
-rational points. For
$18 \ \mathbb {Q}(\zeta _{3})$
-rational points. For
![]() $D_{1}$
, the elliptic curve in question is
$D_{1}$
, the elliptic curve in question is
![]() $E : y^{2} = x^{3} - 48$
, and for this curve
$E : y^{2} = x^{3} - 48$
, and for this curve
![]() $E(\mathbb {Q}(\zeta _{3})) \simeq \mathbb {Z}/3\mathbb {Z}\times \mathbb {Z}^{2}$
. We explicitly compute the map from
$E(\mathbb {Q}(\zeta _{3})) \simeq \mathbb {Z}/3\mathbb {Z}\times \mathbb {Z}^{2}$
. We explicitly compute the map from
![]() $D_{1} \to E$
over
$D_{1} \to E$
over
![]() $\mathbb {Q}(\zeta _{3})$
as follows. We attempt to find the composition
$\mathbb {Q}(\zeta _{3})$
as follows. We attempt to find the composition
![]() $D_{1} \to E \to \mathbb {P}^{1}$
given by the x-coordinate map. If the degree of the map from
$D_{1} \to E \to \mathbb {P}^{1}$
given by the x-coordinate map. If the degree of the map from
![]() $D_{1} \to E$
is d, then the map
$D_{1} \to E$
is d, then the map
![]() $x \colon D_{1} \to \mathbb {P}^{1}$
has degree
$x \colon D_{1} \to \mathbb {P}^{1}$
has degree
![]() $2d$
and each pole of x has even multiplicity. First we pick
$2d$
and each pole of x has even multiplicity. First we pick
![]() $\mathfrak {p} = \langle 1 - 2\zeta _{3} \rangle $
to be one of the prime ideals above
$\mathfrak {p} = \langle 1 - 2\zeta _{3} \rangle $
to be one of the prime ideals above
![]() $7$
in
$7$
in
![]() $\mathbb {Q}(\zeta _{3})$
, and we enumerate effective divisors D of degree d on
$\mathbb {Q}(\zeta _{3})$
, and we enumerate effective divisors D of degree d on
![]() $D_{1}/{\mathbb F}_{7}$
. We search for divisors such that the Riemann–Roch space of
$D_{1}/{\mathbb F}_{7}$
. We search for divisors such that the Riemann–Roch space of
![]() $2D$
is nontrivial. If
$2D$
is nontrivial. If
![]() $f \in L(2D)$
is nonconstant, then we build the function field of
$f \in L(2D)$
is nonconstant, then we build the function field of
![]() $D_{1}/{\mathbb F}_{7}$
as an extension of
$D_{1}/{\mathbb F}_{7}$
as an extension of
![]() ${\mathbb F}_{7}(f)$
and search to see if there are intermediate fields. If so, this produces a nontrivial morphism from
${\mathbb F}_{7}(f)$
and search to see if there are intermediate fields. If so, this produces a nontrivial morphism from
![]() $D_{1}$
to a lower genus curve. This technique succeeds for
$D_{1}$
to a lower genus curve. This technique succeeds for
![]() $d = 3$
, and we find a map from
$d = 3$
, and we find a map from
![]() $D_{1} \to E$
defined over
$D_{1} \to E$
defined over
![]() ${\mathbb F}_{7}$
. The x-coordinate map can be written as a ratio of degree
${\mathbb F}_{7}$
. The x-coordinate map can be written as a ratio of degree
![]() $1$
elements of the canonical ring for
$1$
elements of the canonical ring for
![]() $D_{1}$
, and the y-coordinate map can be written as a ratio of degree
$D_{1}$
, and the y-coordinate map can be written as a ratio of degree
![]() $2$
elements.
$2$
elements.
From here, we write down a scheme X that parametrises maps from
![]() $D_{1} \to E$
of the form we found, with the additional constraint that one particular
$D_{1} \to E$
of the form we found, with the additional constraint that one particular
![]() $\mathbb {Q}(\zeta _{3})$
-rational point on
$\mathbb {Q}(\zeta _{3})$
-rational point on
![]() $D_{1}$
maps to
$D_{1}$
maps to
![]() $(0 : 1 : 0)$
. The map from
$(0 : 1 : 0)$
. The map from
![]() $D_{1} \to E$
gives rise to a point on X, and we use Hensel’s lemma to lift this point to a point modulo
$D_{1} \to E$
gives rise to a point on X, and we use Hensel’s lemma to lift this point to a point modulo
![]() $\langle 1 - 2 \zeta _{3} \rangle ^{512}$
. We then use Magma’s Reconstruct function to find simple elements of
$\langle 1 - 2 \zeta _{3} \rangle ^{512}$
. We then use Magma’s Reconstruct function to find simple elements of
![]() $\mathbb {Q}(\zeta _{3})$
that reduce modulo
$\mathbb {Q}(\zeta _{3})$
that reduce modulo
![]() $\langle 1-2 \zeta _{3} \rangle ^{512}$
to the point found on X. This yields the desired map to E.
$\langle 1-2 \zeta _{3} \rangle ^{512}$
to the point found on X. This yields the desired map to E.
Using the map
![]() $\phi \colon D_{1} \to E$
, we can create an étale triple cover of
$\phi \colon D_{1} \to E$
, we can create an étale triple cover of
![]() $D_{1}$
via the fibre product
$D_{1}$
via the fibre product

where
![]() $\psi \colon E \to E$
is a cyclic
$\psi \colon E \to E$
is a cyclic
![]() $3$
-isogeny defined over
$3$
-isogeny defined over
![]() $\mathbb {Q}(\zeta _{3})$
(which exists because E has complex multiplication). The
$\mathbb {Q}(\zeta _{3})$
(which exists because E has complex multiplication). The
![]() $18$
known
$18$
known
![]() $\mathbb {Q}(\zeta _{3})$
rational points become equidistributed among the nine twists of
$\mathbb {Q}(\zeta _{3})$
rational points become equidistributed among the nine twists of
![]() $D_{1} \times _{E} E$
. Our hope was that we could find a map from
$D_{1} \times _{E} E$
. Our hope was that we could find a map from
![]() $D_{1} \times _{E} E$
, which has genus
$D_{1} \times _{E} E$
, which has genus
![]() $19$
, to a lower genus curve. We can compute the zeta function of
$19$
, to a lower genus curve. We can compute the zeta function of
![]() $D_{1} \times _{E} E$
over
$D_{1} \times _{E} E$
over
![]() ${\mathbb F}_{4}$
by counting points on it over
${\mathbb F}_{4}$
by counting points on it over
![]() ${\mathbb F}_{4^{k}}$
for
${\mathbb F}_{4^{k}}$
for
![]() $1 \leq k \leq 12$
, since we already know a
$1 \leq k \leq 12$
, since we already know a
![]() $7$
-dimensional factor (namely
$7$
-dimensional factor (namely
![]() $J(D_{1})$
) of
$J(D_{1})$
) of
![]() $J(D_{1} \times _{E} E)$
. We find that the dimension
$J(D_{1} \times _{E} E)$
. We find that the dimension
![]() $12$
‘new’ part of the Jacobian of
$12$
‘new’ part of the Jacobian of
![]() $D_{1} \times _{E} E$
is irreducible. We have not been able to provably determine
$D_{1} \times _{E} E$
is irreducible. We have not been able to provably determine
![]() $D_{1}(\mathbb {Q}(\zeta _{3}))$
or
$D_{1}(\mathbb {Q}(\zeta _{3}))$
or
![]() $X_{\mathrm {ns}}^{+}(27)(\mathbb {Q})$
.
$X_{\mathrm {ns}}^{+}(27)(\mathbb {Q})$
.
9.2
 $X_{\mathrm {ns}}^{+}(\ell ^2)$
,
$X_{\mathrm {ns}}^{+}(\ell ^2)$
,
 $\ell = 5,7,11$
$\ell = 5,7,11$
Using the techniques of Section 7, we have computed the canonical model of
![]() $X_{\mathrm {ns}}^{+}(25)$
, which has genus
$X_{\mathrm {ns}}^{+}(25)$
, which has genus
![]() $14$
. We searched for points on
$14$
. We searched for points on
![]() $X_{\mathrm {ns}}^{+}(25)$
by enumerating points on
$X_{\mathrm {ns}}^{+}(25)$
by enumerating points on
![]() $X_{\mathrm {ns}}^{+}(5) \cong \mathbb {P}^{1}$
with height
$X_{\mathrm {ns}}^{+}(5) \cong \mathbb {P}^{1}$
with height
![]() $\leq 1000$
, writing down the corresponding elliptic curve E and testing if the pairs
$\leq 1000$
, writing down the corresponding elliptic curve E and testing if the pairs
![]() $(p+1-\# E({\mathbb F}_{p}) \mod 25, p \mod 25)$
are in
$(p+1-\# E({\mathbb F}_{p}) \mod 25, p \mod 25)$
are in
![]() $\{ (\operatorname {\mathrm {tr}} g, \det g) : g \in N_{\mathrm {ns}}(25) \}$
. This process rules out all non-CM j-invariants in the range we tested and takes approximately 6 hours.
$\{ (\operatorname {\mathrm {tr}} g, \det g) : g \in N_{\mathrm {ns}}(25) \}$
. This process rules out all non-CM j-invariants in the range we tested and takes approximately 6 hours.
Point searching finds
![]() $8$
rational points, all of which are CM with discriminants
$8$
rational points, all of which are CM with discriminants
![]() $-3$
,
$-3$
,
![]() $-7$
,
$-7$
,
![]() $-12$
,
$-12$
,
![]() $-27$
,
$-27$
,
![]() $-28$
,
$-28$
,
![]() $-43$
,
$-43$
,
![]() $-67$
and
$-67$
and
![]() $-163$
. The Jacobian has three
$-163$
. The Jacobian has three
![]() $2$
-dimensional factors, and this raises the possibility that
$2$
-dimensional factors, and this raises the possibility that
![]() $X_{\mathrm {ns}}^{+}(25)$
might map to a genus
$X_{\mathrm {ns}}^{+}(25)$
might map to a genus
![]() $2$
hyperelliptic curve; two genus
$2$
hyperelliptic curve; two genus
![]() $2$
curves
$2$
curves
![]() $X_H$
whose Jacobians are factors of
$X_H$
whose Jacobians are factors of
![]() $J(X_{\mathrm { ns}}^{+}(25))$
are those with labels 25.50.2.1 and 25.75.2.1. The automorphism group of
$J(X_{\mathrm { ns}}^{+}(25))$
are those with labels 25.50.2.1 and 25.75.2.1. The automorphism group of
![]() $X_{\mathrm { ns}}^{+}(25)$
is trivial over
$X_{\mathrm { ns}}^{+}(25)$
is trivial over
![]() $\mathbb {Q}$
.
$\mathbb {Q}$
.
If
![]() $f \colon X_{\mathrm {ns}}^{+}(25) \to C$
were a map to a genus
$f \colon X_{\mathrm {ns}}^{+}(25) \to C$
were a map to a genus
![]() $2$
curve, it seems plausible that the induced map on differentials
$2$
curve, it seems plausible that the induced map on differentials
![]() $\Omega _{C} \to \Omega _{X_{\mathrm {ns}}^{+}(25)}$
should respect the action of the Hecke operators. We have identified the two-dimensional Hecke stable subspaces of
$\Omega _{C} \to \Omega _{X_{\mathrm {ns}}^{+}(25)}$
should respect the action of the Hecke operators. We have identified the two-dimensional Hecke stable subspaces of
![]() $\Omega _{X_{\mathrm {ns}}^{+}(25)}$
(canonically identified with weight
$\Omega _{X_{\mathrm {ns}}^{+}(25)}$
(canonically identified with weight
![]() $2$
cusp forms) and checked that these do not give rise to a map to a genus
$2$
cusp forms) and checked that these do not give rise to a map to a genus
![]() $2$
curve.
$2$
curve.
For
![]() $X_{\mathrm {ns}}^{+}(49)$
, we applied the same technique to search for points as for
$X_{\mathrm {ns}}^{+}(49)$
, we applied the same technique to search for points as for
![]() $X_{\mathrm {ns}}^{+}(25)$
and found no non-CM rational points.
$X_{\mathrm {ns}}^{+}(25)$
and found no non-CM rational points.
For
![]() $X_{\mathrm {ns}}^{+}(121)$
with genus
$X_{\mathrm {ns}}^{+}(121)$
with genus
![]() $511$
, we did not compute a model. However,
$511$
, we did not compute a model. However,
![]() $X_{\mathrm {ns}}^{+}(11)$
is isomorphic to the elliptic curve
$X_{\mathrm {ns}}^{+}(11)$
is isomorphic to the elliptic curve
![]() $E\colon $
$E\colon $
![]() $y^{2} + y = x^{3} - x^{2} - 7x + 10$
with Mordell–Weil group
$y^{2} + y = x^{3} - x^{2} - 7x + 10$
with Mordell–Weil group
![]() $E(\mathbb {Q}) \cong \mathbb {Z}$
generated by
$E(\mathbb {Q}) \cong \mathbb {Z}$
generated by
![]() $P = (4 : 5 : 1)$
. We use the isomorphism computed in [Reference Chen and CumminsCC04]. We used this to Mordell–Weil sieve (as in Section 8.7). As a result, if
$P = (4 : 5 : 1)$
. We use the isomorphism computed in [Reference Chen and CumminsCC04]. We used this to Mordell–Weil sieve (as in Section 8.7). As a result, if
![]() $Q \in X_{\mathrm {ns}}^{+}(121)$
is a rational point and its image on
$Q \in X_{\mathrm {ns}}^{+}(121)$
is a rational point and its image on
![]() $X_{\mathrm {ns}}^{+}(11)$
is
$X_{\mathrm {ns}}^{+}(11)$
is
![]() $kP$
, then either
$kP$
, then either
![]() $k \in \{ -5, -4, -3, -2, -1, 0, 1 \}$
, which implies that Q is CM, or
$k \in \{ -5, -4, -3, -2, -1, 0, 1 \}$
, which implies that Q is CM, or
![]() $|k| \geq \operatorname {\mathrm {lcm}}(1,2,3,\ldots ,233)$
. This implies that if Q is a non-CM point on
$|k| \geq \operatorname {\mathrm {lcm}}(1,2,3,\ldots ,233)$
. This implies that if Q is a non-CM point on
![]() $X_{\mathrm {ns}}^{+}(121)$
, then the height of
$X_{\mathrm {ns}}^{+}(121)$
, then the height of
![]() $j(Q)$
would need to be roughly on the order of
$j(Q)$
would need to be roughly on the order of
![]() $10^{7.92 \cdot 10^{202}}$
(or larger).
$10^{7.92 \cdot 10^{202}}$
(or larger).
9.3 The curves
 $\mathrm {\texttt {49.147.9.1}}$
and
$\mathrm {\texttt {49.147.9.1}}$
and
 $\mathrm {\texttt {49.196.9.1}}$
$\mathrm {\texttt {49.196.9.1}}$
The curve 49.147.9.1 is a degree
![]() $7$
cover of
$7$
cover of
![]() $X_{\mathrm {ns}}^{+}(7)$
, which has genus zero. Using this, we have a singular degree
$X_{\mathrm {ns}}^{+}(7)$
, which has genus zero. Using this, we have a singular degree
![]() $7$
plane model of the modular curve. We searched for points on our plane model with height up to
$7$
plane model of the modular curve. We searched for points on our plane model with height up to
![]() $10^{7}$
and found a unique rational point (above
$10^{7}$
and found a unique rational point (above
![]() $j = 0$
). The Jacobian is irreducible and has trivial torsion subgroup over
$j = 0$
). The Jacobian is irreducible and has trivial torsion subgroup over
![]() $\mathbb {Q}$
. The automorphism group of the modular curve is also trivial over
$\mathbb {Q}$
. The automorphism group of the modular curve is also trivial over
![]() $\mathbb {Q}$
. We have not made any further progress with this curve.
$\mathbb {Q}$
. We have not made any further progress with this curve.
The modular curve 49.196.9.1 is a degree
![]() $7$
cover of
$7$
cover of
![]() $X_{\mathrm {s}}^{+}(7)$
, which also has genus zero. We likewise have a singular degree
$X_{\mathrm {s}}^{+}(7)$
, which also has genus zero. We likewise have a singular degree
![]() $7$
plane model for it and searched for points with height up to
$7$
plane model for it and searched for points with height up to
![]() $10^{7}$
. Again, it appears to have a unique rational point (above
$10^{7}$
. Again, it appears to have a unique rational point (above
![]() $j = 0$
) on it. The curve does not have any nontrivial automorphisms over
$j = 0$
) on it. The curve does not have any nontrivial automorphisms over
![]() $\mathbb {Q}$
, and the torsion subgroup of its Jacobian is trivial. We have not made any further progress with this curve.
$\mathbb {Q}$
, and the torsion subgroup of its Jacobian is trivial. We have not made any further progress with this curve.
10 The cases with
 $-I \not \in H$
$-I \not \in H$
We now suppose that
![]() $H \leq \operatorname {GL}_{2}(N)$
has genus 0,
$H \leq \operatorname {GL}_{2}(N)$
has genus 0,
![]() $-I \not \in H$
and
$-I \not \in H$
and
![]() $X_{\langle H, -I \rangle } \cong \mathbb {P}^{1}$
. Let U be the complement of the cusps and preimages on
$X_{\langle H, -I \rangle } \cong \mathbb {P}^{1}$
. Let U be the complement of the cusps and preimages on
![]() $X_{H}$
of
$X_{H}$
of
![]() $j = 0, 1728$
. Then
$j = 0, 1728$
. Then
![]() $U \subseteq \operatorname {\mathrm {Spec}} \mathbb {Q}[t]$
is an affine scheme, and the moduli problem of H-level structures is rigid. Therefore, by [Reference Katz and MazurKM85, Scholie 4.7.0, page 111], the moduli problem there is representable and there is a universal curve
$U \subseteq \operatorname {\mathrm {Spec}} \mathbb {Q}[t]$
is an affine scheme, and the moduli problem of H-level structures is rigid. Therefore, by [Reference Katz and MazurKM85, Scholie 4.7.0, page 111], the moduli problem there is representable and there is a universal curve
![]() $\mathscr {E} \to U$
such that an elliptic curve
$\mathscr {E} \to U$
such that an elliptic curve
![]() $E/K$
with
$E/K$
with
![]() $j(E) \ne 0, 1728$
has
$j(E) \ne 0, 1728$
has
![]() $\operatorname {\mathrm {im}} \rho _{E,N} \leq H$
if and only if
$\operatorname {\mathrm {im}} \rho _{E,N} \leq H$
if and only if
![]() $E \simeq \mathscr {E}_{t}$
for some (possibly more than one)
$E \simeq \mathscr {E}_{t}$
for some (possibly more than one)
![]() $t \in U(K)$
. The following is [Reference Rouse and Zureick-BrownRZB15, Lemma 2.4].
$t \in U(K)$
. The following is [Reference Rouse and Zureick-BrownRZB15, Lemma 2.4].
Lemma 10.1. Let
![]() $f \colon {\mathscr E} \to U$
be as above, and assume that
$f \colon {\mathscr E} \to U$
be as above, and assume that
![]() $U \subset \mathbb {A}^1$
. Then there exists a closed immersion
$U \subset \mathbb {A}^1$
. Then there exists a closed immersion
![]() ${\mathscr E} \hookrightarrow \mathbb {P}^2_U$
given by a homogeneous polynomial
${\mathscr E} \hookrightarrow \mathbb {P}^2_U$
given by a homogeneous polynomial
where
![]() $a,b \in \mathbb {Z}[t]$
.
$a,b \in \mathbb {Z}[t]$
.
In [Reference Rouse and Zureick-BrownRZB15, Section 5.2], the authors proved [Reference Rouse and Zureick-BrownRZB15, Lemma 5.1] that if
![]() $E/K$
is an elliptic curve for which
$E/K$
is an elliptic curve for which
![]() $\operatorname {\mathrm {im}} \rho _{E,N} \leq \langle H, -I \rangle $
, then there is a unique quadratic twist
$\operatorname {\mathrm {im}} \rho _{E,N} \leq \langle H, -I \rangle $
, then there is a unique quadratic twist
![]() $E_{d}$
of E so that the image of
$E_{d}$
of E so that the image of
![]() $\rho _{E_{d},N}$
is contained in H (where
$\rho _{E_{d},N}$
is contained in H (where
![]() $\rho _{E_{d},N}$
is defined using a basis for
$\rho _{E_{d},N}$
is defined using a basis for
![]() $E_{d}[N]$
that is compatible with the choice for E). See also [Reference SutherlandSut16, Section 5.6]. It follows that if E has
$E_{d}[N]$
that is compatible with the choice for E). See also [Reference SutherlandSut16, Section 5.6]. It follows that if E has
![]() $\ell $
-adic image
$\ell $
-adic image
![]() $\langle H, -I \rangle $
, then the number of quadratic twists
$\langle H, -I \rangle $
, then the number of quadratic twists
![]() $E_{d}$
for which the
$E_{d}$
for which the
![]() $\ell $
-adic image is H is equal to the number of index two subgroups of
$\ell $
-adic image is H is equal to the number of index two subgroups of
![]() $\langle H, -I \rangle $
that are
$\langle H, -I \rangle $
that are
![]() $\operatorname {GL}_{2}(\mathbb {Z}_{\ell })$
-conjugate to H. It is straightforward to see that this is
$\operatorname {GL}_{2}(\mathbb {Z}_{\ell })$
-conjugate to H. It is straightforward to see that this is
![]() $[N_{\operatorname {GL}_{2}(\mathbb {Z}_{\ell })}(\langle H, -I \rangle ) : N_{\operatorname {GL}_{2}(\mathbb {Z}_{\ell })}(H)]$
. If
$[N_{\operatorname {GL}_{2}(\mathbb {Z}_{\ell })}(\langle H, -I \rangle ) : N_{\operatorname {GL}_{2}(\mathbb {Z}_{\ell })}(H)]$
. If
![]() $j \ne 1728$
, then
$j \ne 1728$
, then
![]() $E_{d} \cong E_{d'}$
if and only if
$E_{d} \cong E_{d'}$
if and only if
![]() $d/d' \in (K^{\times })^{2}$
.
$d/d' \in (K^{\times })^{2}$
.
The authors of [Reference Rouse and Zureick-BrownRZB15] gave a procedure (based on a general theory of resolvent polynomials from [Reference Dokchitser and DokchitserDD13]) to represent
![]() $\mathscr {E} \to U$
as an elliptic curve over
$\mathscr {E} \to U$
as an elliptic curve over
![]() $\mathbb {Q}(t)$
.
$\mathbb {Q}(t)$
.
This technique works in general, and the same techniques are used to compute models for the universal elliptic curves over
![]() $X_{H}$
for all arithmetically maximal H for which
$X_{H}$
for all arithmetically maximal H for which
![]() $X_{\langle H, -I \rangle }(\mathbb {Q})$
is infinite. In all such cases,
$X_{\langle H, -I \rangle }(\mathbb {Q})$
is infinite. In all such cases,
![]() $X_{\langle H, -I \rangle } \simeq \mathbb {P}^{1}$
. As an example, if
$X_{\langle H, -I \rangle } \simeq \mathbb {P}^{1}$
. As an example, if
![]() $E/\mathbb {Q}$
is an elliptic curve with
$E/\mathbb {Q}$
is an elliptic curve with
![]() $E[5] \simeq \mathbb {Z}/5\mathbb {Z} \times \mu _{5}$
as Galois modules, then there is a
$E[5] \simeq \mathbb {Z}/5\mathbb {Z} \times \mu _{5}$
as Galois modules, then there is a
![]() $t \in \mathbb {Q}$
with
$t \in \mathbb {Q}$
with
![]() $t \ne 0$
so that
$t \ne 0$
so that
![]() $E \simeq E_{t}$
, where
$E \simeq E_{t}$
, where
 $$ \begin{align*} E_{t} \colon y^{2} = x^{3} &+ (-27t^{20} - 6156t^{15} - 13338t^{10} + 6156t^{5} - 27) x\\ & + (54t^{30} - 28188t^{25} - 540270t^{20} - 540270t^{10} + 28188t^{5} + 54). \end{align*} $$
$$ \begin{align*} E_{t} \colon y^{2} = x^{3} &+ (-27t^{20} - 6156t^{15} - 13338t^{10} + 6156t^{5} - 27) x\\ & + (54t^{30} - 28188t^{25} - 540270t^{20} - 540270t^{10} + 28188t^{5} + 54). \end{align*} $$
This corresponds to the
![]() $5$
-adic image with label 5.120.0.1.
$5$
-adic image with label 5.120.0.1.
These models allow us to efficiently compute the
![]() $\ell $
-adic image of Galois for non-CM elliptic curves
$\ell $
-adic image of Galois for non-CM elliptic curves
![]() $E/\mathbb {Q}$
; see Section 11 for details.
$E/\mathbb {Q}$
; see Section 11 for details.
11 Computing
 $\ell $
-adic images of non-CM elliptic curves over
$\ell $
-adic images of non-CM elliptic curves over
 $\mathbb {Q}$
$\mathbb {Q}$
In this section, we present the algorithm promised in the introduction, which takes as input an elliptic curve
![]() $E/\mathbb {Q}$
without complex multiplication and outputs a list of labels that identify all groups of nontrivial index that arise as
$E/\mathbb {Q}$
without complex multiplication and outputs a list of labels that identify all groups of nontrivial index that arise as
![]() $\rho _{E,\ell ^{\infty }}(G_{\mathbb {Q}})$
for some prime
$\rho _{E,\ell ^{\infty }}(G_{\mathbb {Q}})$
for some prime
![]() $\ell $
. Serre’s open image theorem guarantees that this list is finite, and we use an extension of an algorithm due to Zywina [Reference ZywinaZyw20, Algorithm 1.1] to compute a finite set S that is guaranteed to contain all the primes
$\ell $
. Serre’s open image theorem guarantees that this list is finite, and we use an extension of an algorithm due to Zywina [Reference ZywinaZyw20, Algorithm 1.1] to compute a finite set S that is guaranteed to contain all the primes
![]() $\ell $
, we must consider. The set S consists of the primes
$\ell $
, we must consider. The set S consists of the primes
![]() $\ell =2,3,5,7,13$
, any prime
$\ell =2,3,5,7,13$
, any prime
![]() $\ell =11,17,37$
for which
$\ell =11,17,37$
for which
![]() $j(E)$
is exceptional and listed in Table 1, and possibly a small number of additional primes. While this ‘small number’ can be arbitrarily large, it is typically zero unless E has bad or supersingular reduction at many small primes, and in fact it is zero for all non-CM
$j(E)$
is exceptional and listed in Table 1, and possibly a small number of additional primes. While this ‘small number’ can be arbitrarily large, it is typically zero unless E has bad or supersingular reduction at many small primes, and in fact it is zero for all non-CM
![]() $E/\mathbb {Q}$
of conductor up to 500000. The function PossiblyNonsurjectivePrimes in the file gl2.m in [Reference Rouse, Sutherland and Zureick-BrownRSZB21] implements this computation.
$E/\mathbb {Q}$
of conductor up to 500000. The function PossiblyNonsurjectivePrimes in the file gl2.m in [Reference Rouse, Sutherland and Zureick-BrownRSZB21] implements this computation.
11.1 Computing Frobenius matrices
The next step of the algorithm is to compute a sequence of matrices
![]() $A_p \in \mathbb {Z}^{2\times 2}$
for primes
$A_p \in \mathbb {Z}^{2\times 2}$
for primes
![]() $p\le B$
of good reduction for E whose reductions modulo any integer N coprime to p give the action of the Frobenius endomorphism
$p\le B$
of good reduction for E whose reductions modulo any integer N coprime to p give the action of the Frobenius endomorphism
![]() $\pi $
of
$\pi $
of
![]() $E_p:=E\bmod p$
on a basis for
$E_p:=E\bmod p$
on a basis for
![]() $E_p[N]$
. From equation (5.2), we may take
$E_p[N]$
. From equation (5.2), we may take
![]() $A_p=A_{\pi }=A(a,b,\Delta )$
, where a is the trace of Frobenius,
$A_p=A_{\pi }=A(a,b,\Delta )$
, where a is the trace of Frobenius,
![]() $\Delta $
is the discriminant of the ring
$\Delta $
is the discriminant of the ring
![]() $R_{\pi }=\operatorname {\mathrm {End}}(E_p)\cap \mathbb {Q}[\pi ]$
and
$R_{\pi }=\operatorname {\mathrm {End}}(E_p)\cap \mathbb {Q}[\pi ]$
and
![]() $b=[R_{\pi }:\mathbb {Z}[\pi ]]$
when
$b=[R_{\pi }:\mathbb {Z}[\pi ]]$
when
![]() $\mathbb {Z}[\pi ]\ne \mathbb {Z}$
, and
$\mathbb {Z}[\pi ]\ne \mathbb {Z}$
, and
![]() $b=0$
otherwise.
$b=0$
otherwise.
In [Reference CentelegheCen16], Centeleghe gives an algorithm to compute
![]() $A(a,b,\Delta )$
using Hilbert class polynomials that is implemented in the Magma package IntegralFrobenius. The time and space complexity of this algorithm are both superlinear in p, which means the cost of computing
$A(a,b,\Delta )$
using Hilbert class polynomials that is implemented in the Magma package IntegralFrobenius. The time and space complexity of this algorithm are both superlinear in p, which means the cost of computing
![]() $A_p$
for good primes
$A_p$
for good primes
![]() $p\le B$
grows quadratically with B, making the algorithm unsuitable for our intended application. Here we describe a more efficient approach whose complexity is subexponential in
$p\le B$
grows quadratically with B, making the algorithm unsuitable for our intended application. Here we describe a more efficient approach whose complexity is subexponential in
![]() $\log p$
under the generalised Riemann hypothesis (GRH), meaning that in practice, we can compute
$\log p$
under the generalised Riemann hypothesis (GRH), meaning that in practice, we can compute
![]() $A_p$
for all good primes
$A_p$
for all good primes
![]() $p\le B$
in quasi-linear time.
$p\le B$
in quasi-linear time.
For
![]() $j(E_p)=0,1728$
, the matrix
$j(E_p)=0,1728$
, the matrix
![]() $A(a,b,\Delta )$
can be read from Table 6 after computing
$A(a,b,\Delta )$
can be read from Table 6 after computing
![]() $\operatorname {\mathrm {Aut}}(E_p)$
and
$\operatorname {\mathrm {Aut}}(E_p)$
and
![]() $\#E_p[2]$
, which takes time
$\#E_p[2]$
, which takes time
![]() $(\log p)^{2+o(1)}$
. If
$(\log p)^{2+o(1)}$
. If
![]() $j(E_p)\ne 0,1728$
and
$j(E_p)\ne 0,1728$
and
![]() $E_p$
is supersingular (which can be determined in expected time
$E_p$
is supersingular (which can be determined in expected time
![]() $(\log p)^{3+o(1)}$
and heuristically in time
$(\log p)^{3+o(1)}$
and heuristically in time
![]() $(\log p)^{2+o(1)}$
on average for
$(\log p)^{2+o(1)}$
on average for
![]() $p\le B$
via [Reference SutherlandSut12b]), then
$p\le B$
via [Reference SutherlandSut12b]), then
![]() $a=0$
, and
$a=0$
, and
![]() $D=a^2-4p=-4p$
implies that either
$D=a^2-4p=-4p$
implies that either
![]() $b=1$
and
$b=1$
and
![]() $\Delta =-4p$
(which must occur if
$\Delta =-4p$
(which must occur if
![]() $p\equiv 1\bmod 4$
) or
$p\equiv 1\bmod 4$
) or
![]() $b=2$
and
$b=2$
and
![]() $\Delta =-p$
, which occurs precisely when
$\Delta =-p$
, which occurs precisely when
![]() $E_p$
is on the surface of its 2-volcano (the connected components of its 2-isogeny graph over
$E_p$
is on the surface of its 2-volcano (the connected components of its 2-isogeny graph over
![]() ${\mathbb F}_p$
; see [Reference SutherlandSut13] for details). We can determine which case applies in
${\mathbb F}_p$
; see [Reference SutherlandSut13] for details). We can determine which case applies in
![]() $(\log p)^{2+o(1)}$
time by checking whether
$(\log p)^{2+o(1)}$
time by checking whether
![]() $\#E_p[2]=4$
.
$\#E_p[2]=4$
.
In all remaining cases,
![]() $E_p$
is ordinary and
$E_p$
is ordinary and
![]() $j(E_p)\ne 0,1728$
, which occurs for 100 percent of the primes
$j(E_p)\ne 0,1728$
, which occurs for 100 percent of the primes
![]() $p\le B$
asymptotically. In this situation, our first step is to compute the trace of Frobenius
$p\le B$
asymptotically. In this situation, our first step is to compute the trace of Frobenius
![]() , which can be accomplished using Schoof’s algorithm [Reference SchoofSch85] in
, which can be accomplished using Schoof’s algorithm [Reference SchoofSch85] in
![]() $(\log p)^{5+o(1)}$
time [Reference Shparlinski and SutherlandSS15, Corollary 11]. Alternatively, one can apply the Schoof-Elkies-Atkin (SEA) algorithm [Reference SchoofSch95, Reference ElkiesElk98], which takes
$(\log p)^{5+o(1)}$
time [Reference Shparlinski and SutherlandSS15, Corollary 11]. Alternatively, one can apply the Schoof-Elkies-Atkin (SEA) algorithm [Reference SchoofSch95, Reference ElkiesElk98], which takes
![]() $(\log p)^{4+o(1)}$
expected time on average under the generalised Riemann hypothesis (GRH) [Reference Shparlinski and SutherlandSS15, Corollary 14], or the average polynomial-time algorithm of [Reference Harvey and SutherlandHS16], which takes
$(\log p)^{4+o(1)}$
expected time on average under the generalised Riemann hypothesis (GRH) [Reference Shparlinski and SutherlandSS15, Corollary 14], or the average polynomial-time algorithm of [Reference Harvey and SutherlandHS16], which takes
![]() $(\log p)^{4+o(1)}$
time on average unconditionally. For small values of p, it is practically faster to use Mestre’s algorithm (see [Reference SchoofSch95, Sections 2–3]); the Magma function TraceOfFrobenius switches between Mestre’s algorithm and the SEA algorithm depending on the size of p.
$(\log p)^{4+o(1)}$
time on average unconditionally. For small values of p, it is practically faster to use Mestre’s algorithm (see [Reference SchoofSch95, Sections 2–3]); the Magma function TraceOfFrobenius switches between Mestre’s algorithm and the SEA algorithm depending on the size of p.
Having computed a, it suffices to compute
![]() $b=\bigl [\operatorname {\mathrm {End}}(E_p):\mathbb {Z}[\pi ]\bigr ]$
, since
$b=\bigl [\operatorname {\mathrm {End}}(E_p):\mathbb {Z}[\pi ]\bigr ]$
, since
![]() $\Delta = (a^2-4p)/b^2$
. The integer b is computed by the algorithm in [Reference Bisson and SutherlandBS11] in subexponential expected time
$\Delta = (a^2-4p)/b^2$
. The integer b is computed by the algorithm in [Reference Bisson and SutherlandBS11] in subexponential expected time
![]() $\exp ((\log p)^{1/2+o(1)})$
under heuristic assumptions that can be reduced to GRH via [Reference BissonBis11]. The first step of this algorithm involves an isogeny volcano computation to determine the
$\exp ((\log p)^{1/2+o(1)})$
under heuristic assumptions that can be reduced to GRH via [Reference BissonBis11]. The first step of this algorithm involves an isogeny volcano computation to determine the
![]() $\ell $
-adic valuation of b at any small primes
$\ell $
-adic valuation of b at any small primes
![]() $\ell $
that divide
$\ell $
that divide
![]() $v:=[{\mathcal O}_K:\mathbb {Z}[\pi ]]$
, where
$v:=[{\mathcal O}_K:\mathbb {Z}[\pi ]]$
, where
![]() ${\mathcal O}_K$
is the ring of integers of
${\mathcal O}_K$
is the ring of integers of
![]() $K:=\mathbb {Q}(\sqrt {a^2-4p})\simeq \operatorname {\mathrm {End}}(E)\otimes \mathbb {Q}$
. To compute v and its prime divisors
$K:=\mathbb {Q}(\sqrt {a^2-4p})\simeq \operatorname {\mathrm {End}}(E)\otimes \mathbb {Q}$
. To compute v and its prime divisors
![]() $\ell $
, we factor
$\ell $
, we factor
![]() $D:=a^2-4p$
to determine the fundamental discriminant
$D:=a^2-4p$
to determine the fundamental discriminant
![]() for which
for which
![]() $D=v^2D_0$
, which can be accomplished in subexponential expected time
$D=v^2D_0$
, which can be accomplished in subexponential expected time
![]() $\exp ((\log p)^{1/2+o(1)})$
via [Reference Lenstra and PomeranceLJP92] (there are also heuristically faster algorithms).
$\exp ((\log p)^{1/2+o(1)})$
via [Reference Lenstra and PomeranceLJP92] (there are also heuristically faster algorithms).
The
![]() $\ell $
-adic valuation of b is equal to the distance from
$\ell $
-adic valuation of b is equal to the distance from
![]() $j(E)$
to the floor of its
$j(E)$
to the floor of its
![]() $\ell $
-volcano, which can be computed using the FindShortestPathToFloor algorithm in [Reference SutherlandSut13]. In the typical case where D is not divisible by
$\ell $
-volcano, which can be computed using the FindShortestPathToFloor algorithm in [Reference SutherlandSut13]. In the typical case where D is not divisible by
![]() $\ell ^4$
, this amounts to checking whether the instantiated modular polynomial
$\ell ^4$
, this amounts to checking whether the instantiated modular polynomial
![]() $\Phi _{\ell }(j(E),x)\in {\mathbb F}_p[x]$
splits completely in
$\Phi _{\ell }(j(E),x)\in {\mathbb F}_p[x]$
splits completely in
![]() ${\mathbb F}_p[x]$
. Typically v will be quite small. Indeed, for a random integer
${\mathbb F}_p[x]$
. Typically v will be quite small. Indeed, for a random integer
![]() $-D\in [1,4p]$
, the average size of the positive v for which
$-D\in [1,4p]$
, the average size of the positive v for which
![]() $D=v^2D_0$
with
$D=v^2D_0$
with
![]() $D_0$
squarefree is
$D_0$
squarefree is
![]() $\frac {3}{\pi ^2}\log (4p)$
, and when v is
$\frac {3}{\pi ^2}\log (4p)$
, and when v is
![]() $O(\log p)$
, we are happy to compute the
$O(\log p)$
, we are happy to compute the
![]() $\ell $
-adic valuation of b for every prime
$\ell $
-adic valuation of b for every prime
![]() $\ell |v$
in this fashion. This yields
$\ell |v$
in this fashion. This yields
![]() $b\in \mathbb {Z}$
in expected time bounded by
$b\in \mathbb {Z}$
in expected time bounded by
![]() $(\log p)^{5+o(1)}$
, a bound that includes the time to compute the modular polynomial
$(\log p)^{5+o(1)}$
, a bound that includes the time to compute the modular polynomial
![]() $\Phi _{\ell }(x,y)$
via [Reference Bröoker, Lauter and SutherlandBLS12]. We may gain a large constant factor speedup (up to 1728 in the best case) by using alternative modular polynomials such as those provided by the AtkinModularPolynomial function in Magma or one of the modular polynomials considered in [Reference Bröoker, Lauter and SutherlandBLS12]. This complexity bound can be improved to
$\Phi _{\ell }(x,y)$
via [Reference Bröoker, Lauter and SutherlandBLS12]. We may gain a large constant factor speedup (up to 1728 in the best case) by using alternative modular polynomials such as those provided by the AtkinModularPolynomial function in Magma or one of the modular polynomials considered in [Reference Bröoker, Lauter and SutherlandBLS12]. This complexity bound can be improved to
![]() $(\log p)^{4+o(1)}$
via [Reference KohelKoh96, Lemma 25], but with the constant factor improvements noted above, it is typically not worth doing this when v is
$(\log p)^{4+o(1)}$
via [Reference KohelKoh96, Lemma 25], but with the constant factor improvements noted above, it is typically not worth doing this when v is
![]() $O(\log p)$
(in [Reference KohelKoh96] v may be as large as
$O(\log p)$
(in [Reference KohelKoh96] v may be as large as
![]() $p^{1/6}$
).
$p^{1/6}$
).
Even if v is not small, as long as its prime factors
![]() $\ell $
are all small, say
$\ell $
are all small, say
![]() $\ell =O(\log p)$
, we can achieve the same complexity bound for computing b, which is comparable to the time required to compute a. In the uncommon case that v is divisible by a large prime
$\ell =O(\log p)$
, we can achieve the same complexity bound for computing b, which is comparable to the time required to compute a. In the uncommon case that v is divisible by a large prime
![]() $\ell $
, we instead use the volcano climbing algorithm of [Reference SutherlandSut11, Section 4.1] to obtain an isogenous elliptic curve
$\ell $
, we instead use the volcano climbing algorithm of [Reference SutherlandSut11, Section 4.1] to obtain an isogenous elliptic curve
![]() $E_p'$
whose endomorphism ring is typically isomorphic to
$E_p'$
whose endomorphism ring is typically isomorphic to
![]() ${\mathcal O}_K$
or a suborder of index
${\mathcal O}_K$
or a suborder of index
![]() $\ell $
(when there are multiple large prime divisors of v, one needs to consider additional suborders). These cases can be distinguished by searching for smooth relations in the ideal class group of
$\ell $
(when there are multiple large prime divisors of v, one needs to consider additional suborders). These cases can be distinguished by searching for smooth relations in the ideal class group of
![]() ${\mathcal O}$
and testing them in the isogeny graph of
${\mathcal O}$
and testing them in the isogeny graph of
![]() $E_p$
as described in [Reference Bisson and SutherlandBS11]. As an additional optimisation, when
$E_p$
as described in [Reference Bisson and SutherlandBS11]. As an additional optimisation, when
![]() $|D_0|$
is particularly small, one may instead simply test whether
$|D_0|$
is particularly small, one may instead simply test whether
![]() $j(E_p)$
is a root of the Hilbert class polynomial
$j(E_p)$
is a root of the Hilbert class polynomial
![]() $H_{D_0}(x)$
modulo p (or, better, use the class polynomials provided by the WeberClassPolynomial function in Magma or one of the class polynomials considered in [Reference Enge and SutherlandES10]).
$H_{D_0}(x)$
modulo p (or, better, use the class polynomials provided by the WeberClassPolynomial function in Magma or one of the class polynomials considered in [Reference Enge and SutherlandES10]).
The function EndomorphismRingData in gl2.m in [Reference Rouse, Sutherland and Zureick-BrownRSZB21] computes the triple
![]() $(a,b,\Delta )$
using a simple Magma implementation of the algorithm described above that is optimised for the case where v is small and provides reasonably good performance in the range
$(a,b,\Delta )$
using a simple Magma implementation of the algorithm described above that is optimised for the case where v is small and provides reasonably good performance in the range
![]() $p \in [1,2^{30}]$
, which is more than sufficient for our intended application. This is used by the function GL2FrobeniusMatrices in gl2.m in [Reference Rouse, Sutherland and Zureick-BrownRSZB21] to compute the matrices
$p \in [1,2^{30}]$
, which is more than sufficient for our intended application. This is used by the function GL2FrobeniusMatrices in gl2.m in [Reference Rouse, Sutherland and Zureick-BrownRSZB21] to compute the matrices
![]() $A_p$
for primes p of good reduction for a given elliptic curve
$A_p$
for primes p of good reduction for a given elliptic curve
![]() $E/\mathbb {Q}$
up to a specified bound B. An asymptotically fast implementation of the algorithm in [Reference Bisson and SutherlandBS11] is available in the C library smoothrelation.
$E/\mathbb {Q}$
up to a specified bound B. An asymptotically fast implementation of the algorithm in [Reference Bisson and SutherlandBS11] is available in the C library smoothrelation.
Table 8 compares the times to compute the Frobenius trace
![]() $a_p$
and the Frobenius matrix
$a_p$
and the Frobenius matrix
![]() $A_p$
for all primes
$A_p$
for all primes
![]() $p\le B$
of good reduction for a non-CM elliptic curve
$p\le B$
of good reduction for a non-CM elliptic curve
![]() $E/\mathbb {Q}$
using the function GL2FrobeniusMatrices described above, and using the Magma package IntegralFrobenius, which implements the algorithm in [Reference CentelegheCen16]; both algorithms use the built-in Magma function TraceOfFrobenius to compute
$E/\mathbb {Q}$
using the function GL2FrobeniusMatrices described above, and using the Magma package IntegralFrobenius, which implements the algorithm in [Reference CentelegheCen16]; both algorithms use the built-in Magma function TraceOfFrobenius to compute
![]() $a_p$
.
$a_p$
.
Table 8 Time to compute
![]() $a_p$
and
$a_p$
and
![]() $A_p$
for non-CM
$A_p$
for non-CM
![]() $E/\mathbb {Q}$
at good
$E/\mathbb {Q}$
at good
![]() $p\le 2^n$
. Times in CPU-seconds on a 4.40GHz Intel i9-9960X core, averaged over the first 100 nonisogenous elliptic curves of conductor greater than 250000 (just the first 10 curves for times over 100s and just the first curve for times over 1000s)
$p\le 2^n$
. Times in CPU-seconds on a 4.40GHz Intel i9-9960X core, averaged over the first 100 nonisogenous elliptic curves of conductor greater than 250000 (just the first 10 curves for times over 100s and just the first curve for times over 1000s)

In Table 8, one sees the quasi-linear time complexity of the functions TracesOfFrobenius and FrobeniusMatrices versus the super-quadratic time complexity of IntegralFrobenius. In fact, the running times for FrobeniusMatrices grows sublinearly up to
![]() $B=2^{26}$
, and its performance relative to TracesOfFrobenius continues to improve even up to
$B=2^{26}$
, and its performance relative to TracesOfFrobenius continues to improve even up to
![]() $B=2^{30}$
.
$B=2^{30}$
.
11.2 Proving surjectivity
Having computed an initial set of primes
![]() $\ell \in S$
, where
$\ell \in S$
, where
![]() $\rho _{E,\ell ^{\infty }}$
might be nonsurjective via PossiblyNonsurjectivePrimes, we use FrobeniusMatrices to compute Frobenius matrices
$\rho _{E,\ell ^{\infty }}$
might be nonsurjective via PossiblyNonsurjectivePrimes, we use FrobeniusMatrices to compute Frobenius matrices
![]() $A_p$
for good primes p up to an initial bound
$A_p$
for good primes p up to an initial bound
![]() $B_{\mathrm {min}}$
(we used
$B_{\mathrm {min}}$
(we used
![]() $B_{\mathrm {min}}=256$
in our computations). Let
$B_{\mathrm {min}}=256$
in our computations). Let
![]() $e_{\ell }=3,2$
for
$e_{\ell }=3,2$
for
![]() $\ell =2,3$
, respectively, and let
$\ell =2,3$
, respectively, and let
![]() $e_{\ell }=1$
for all
$e_{\ell }=1$
for all
![]() $\ell \ge 5$
. Then
$\ell \ge 5$
. Then
![]() $\rho _{E,\ell ^{\infty }}$
is surjective if and only if
$\rho _{E,\ell ^{\infty }}$
is surjective if and only if
![]() $\rho _{E,\ell ^{e_{\ell }}}$
is surjective; for
$\rho _{E,\ell ^{e_{\ell }}}$
is surjective; for
![]() $\ell =2,3$
this follows from [Reference Sutherland and ZywinaSZ17, Lemma 3.7] and for
$\ell =2,3$
this follows from [Reference Sutherland and ZywinaSZ17, Lemma 3.7] and for
![]() $\ell \ge 5$
, we may apply [Reference SerreSer98, Lemma 3, p. IV-23]. By reducing each
$\ell \ge 5$
, we may apply [Reference SerreSer98, Lemma 3, p. IV-23]. By reducing each
![]() $A_p$
modulo
$A_p$
modulo
![]() $\ell ^{e_{\ell }}$
, we obtain a set of
$\ell ^{e_{\ell }}$
, we obtain a set of
![]() $\operatorname {GL}_2(\ell ^{e_{\ell }})$
-conjugacy classes
$\operatorname {GL}_2(\ell ^{e_{\ell }})$
-conjugacy classes
![]() $C_{\ell }$
that we can typically use to prove that
$C_{\ell }$
that we can typically use to prove that
![]() $\rho _{E,\ell ^{\infty }}$
is surjective in any case where this is true. For every maximal subgroup
$\rho _{E,\ell ^{\infty }}$
is surjective in any case where this is true. For every maximal subgroup
![]() $H\le \operatorname {GL}_2(\ell ^{e_{\ell }})$
, there are several
$H\le \operatorname {GL}_2(\ell ^{e_{\ell }})$
, there are several
![]() $\operatorname {GL}_2(\ell ^{e_{\ell }})$
-conjugacy classes that do not intersect H. If any of these lie in
$\operatorname {GL}_2(\ell ^{e_{\ell }})$
-conjugacy classes that do not intersect H. If any of these lie in
![]() $C_{\ell }$
, then
$C_{\ell }$
, then
![]() $\rho _{E,\ell ^{e_{\ell }}}(G_{\mathbb {Q}})$
cannot lie in H; and if this holds for every maximal subgroup H, then
$\rho _{E,\ell ^{e_{\ell }}}(G_{\mathbb {Q}})$
cannot lie in H; and if this holds for every maximal subgroup H, then
![]() $\rho _{E,\ell ^{\infty }}$
must be surjective. By precomputing sets of conjugacy classes for the maximal subgroups of
$\rho _{E,\ell ^{\infty }}$
must be surjective. By precomputing sets of conjugacy classes for the maximal subgroups of
![]() $\operatorname {GL}_2(\ell ^{e_{\ell }})$
for
$\operatorname {GL}_2(\ell ^{e_{\ell }})$
for
![]() $\ell \le 13$
, this test can be performed very efficiently (the set S typically contains no primes
$\ell \le 13$
, this test can be performed very efficiently (the set S typically contains no primes
![]() $\ell>13$
). We remove from S any primes
$\ell>13$
). We remove from S any primes
![]() $\ell $
for which we can prove
$\ell $
for which we can prove
![]() $\rho _{E,\ell ^{\infty }}$
is surjective using the sets of conjugacy classes
$\rho _{E,\ell ^{\infty }}$
is surjective using the sets of conjugacy classes
![]() $C_{\ell }$
.
$C_{\ell }$
.
11.3 Determining nonsurjective
 $\ell $
-adic images
$\ell $
-adic images
Having reduced S to a set of primes
![]() $\ell $
for which we expect
$\ell $
for which we expect
![]() $\rho _{E,\ell ^{\infty }}$
to be nonsurjective, we first check whether
$\rho _{E,\ell ^{\infty }}$
to be nonsurjective, we first check whether
![]() $j(E)$
is one of the 20 exceptional j-invariants listed in Table 1, and if so, whether E is isomorphic to any of the corresponding exceptional models listed in Table 1. Whenever this applies, we can read the image of
$j(E)$
is one of the 20 exceptional j-invariants listed in Table 1, and if so, whether E is isomorphic to any of the corresponding exceptional models listed in Table 1. Whenever this applies, we can read the image of
![]() $\rho _{E,\ell ^{\infty }}$
from the appropriate row of the table.
$\rho _{E,\ell ^{\infty }}$
from the appropriate row of the table.
Otherwise, we expect that
![]() $j(E)$
is not exceptional (we conjecture that this is always true), in which case it corresponds to a point on a modular curve
$j(E)$
is not exceptional (we conjecture that this is always true), in which case it corresponds to a point on a modular curve
![]() $X_H$
for which
$X_H$
for which
![]() $j(X_H(\mathbb {Q}))$
is infinite (possibly more than one such H). Except for the four 2-adic groups with labels
$j(X_H(\mathbb {Q}))$
is infinite (possibly more than one such H). Except for the four 2-adic groups with labels
which were shown to have no noncuspidal rational points in [Reference Rouse and Zureick-BrownRZB15], there is no open subgroup
![]() $H\le \operatorname {GL}_2({\widehat {\mathbb {Z}}})$
of prime power level for which
$H\le \operatorname {GL}_2({\widehat {\mathbb {Z}}})$
of prime power level for which
![]() $j(X_H(\mathbb {Q}))$
is infinite that has a maximal subgroup
$j(X_H(\mathbb {Q}))$
is infinite that has a maximal subgroup
![]() $H'\le H$
for which
$H'\le H$
for which
![]() $j(X_{H'}(\mathbb {Q}))$
is finite that contains the same set of
$j(X_{H'}(\mathbb {Q}))$
is finite that contains the same set of
![]() $\operatorname {GL}_2(\ell ^e)$
-conjugacy classes as H, where
$\operatorname {GL}_2(\ell ^e)$
-conjugacy classes as H, where
![]() $\ell ^e$
is the level of
$\ell ^e$
is the level of
![]() $H'$
. It follows that if we compute sufficiently many Frobenius matrices
$H'$
. It follows that if we compute sufficiently many Frobenius matrices
![]() $A_p$
, for each
$A_p$
, for each
![]() $\ell \in S$
, we should be able to prove that
$\ell \in S$
, we should be able to prove that
![]() $j(E)$
is not exceptional and obtain a small list of groups H of
$j(E)$
is not exceptional and obtain a small list of groups H of
![]() $\ell $
-power level for which
$\ell $
-power level for which
![]() $j(E)$
is one of infinitely many elements of
$j(E)$
is one of infinitely many elements of
![]() $j(X_H(\mathbb {Q}))$
. Typically, the initial set of Frobenius matrices
$j(X_H(\mathbb {Q}))$
. Typically, the initial set of Frobenius matrices
![]() $A_p$
for good
$A_p$
for good
![]() $p\le B=B_{\mathrm {min}}$
is already sufficient; but if not, we successively double B and compute more Frobenius matrices
$p\le B=B_{\mathrm {min}}$
is already sufficient; but if not, we successively double B and compute more Frobenius matrices
![]() $A_p$
until this condition holds or we reach a preset maximum
$A_p$
until this condition holds or we reach a preset maximum
![]() $B_{\mathrm {max}}$
(we used
$B_{\mathrm {max}}$
(we used
![]() $B_{\mathrm {max}}=2^{20}$
in our computations), at which point we are convinced that we must have found a new exceptional point and compute
$B_{\mathrm {max}}=2^{20}$
in our computations), at which point we are convinced that we must have found a new exceptional point and compute
![]() $\rho _{E,\ell ^{\infty }}(G_{\mathbb {Q}})$
directly by explicitly computing the torsion fields
$\rho _{E,\ell ^{\infty }}(G_{\mathbb {Q}})$
directly by explicitly computing the torsion fields
![]() $\mathbb {Q}(E[\ell ^n])$
for sufficiently many powers of
$\mathbb {Q}(E[\ell ^n])$
for sufficiently many powers of
![]() $\ell $
(we must eventually have
$\ell $
(we must eventually have
![]() $[\mathbb {Q}(E[\ell ^{n+1}]):\mathbb {Q}(E[\ell ^n])]=\ell ^4$
with
$[\mathbb {Q}(E[\ell ^{n+1}]):\mathbb {Q}(E[\ell ^n])]=\ell ^4$
with
![]() $\ell>2$
or
$\ell>2$
or
![]() $n>1$
, at which point we can stop, by [Reference Sutherland and ZywinaSZ17, Lemma 3.7]). We conjecture that this will never happen, and it has not happened for any non-CM elliptic curve
$n>1$
, at which point we can stop, by [Reference Sutherland and ZywinaSZ17, Lemma 3.7]). We conjecture that this will never happen, and it has not happened for any non-CM elliptic curve
![]() $E/\mathbb {Q}$
whose
$E/\mathbb {Q}$
whose
![]() $\ell $
-adic Galois images we have computed; as described in Section 11.4, this includes more than 380 million elliptic curves.
$\ell $
-adic Galois images we have computed; as described in Section 11.4, this includes more than 380 million elliptic curves.
Assuming we do not reach
![]() $B=B_{\mathrm {max}}$
, for each remaining prime
$B=B_{\mathrm {max}}$
, for each remaining prime
![]() $\ell \in S$
, we have a small list of candidate groups H of
$\ell \in S$
, we have a small list of candidate groups H of
![]() $\ell $
-power level for which
$\ell $
-power level for which
![]() $j(X_H(\mathbb {Q}))$
is infinite that we know includes the image of
$j(X_H(\mathbb {Q}))$
is infinite that we know includes the image of
![]() $\rho _{E,\ell ^{\infty }}$
. These groups H can have genus at most 1, and we have precomputed explicit models (
$\rho _{E,\ell ^{\infty }}$
. These groups H can have genus at most 1, and we have precomputed explicit models (
![]() $\mathbb {P}^1$
or a positive rank elliptic curve over
$\mathbb {P}^1$
or a positive rank elliptic curve over
![]() $\mathbb {Q}$
) and maps
$\mathbb {Q}$
) and maps
![]() $j_H\colon X_H\to X(1)$
for each of them, as described in Sections 7 and 10. There is necessarily a unique H of maximal index containing
$j_H\colon X_H\to X(1)$
for each of them, as described in Sections 7 and 10. There is necessarily a unique H of maximal index containing
![]() $-I$
for which
$-I$
for which
![]() $j(E)\in j_H(X_H(\mathbb {Q}))$
, which we can determine by testing whether
$j(E)\in j_H(X_H(\mathbb {Q}))$
, which we can determine by testing whether
![]() $j(E)$
lies in the image of
$j(E)$
lies in the image of
![]() $j_H\colon X_H\to X(1)$
. If H has genus 0, then
$j_H\colon X_H\to X(1)$
. If H has genus 0, then
![]() $j_H\in \mathbb {Q}(t)$
and
$j_H\in \mathbb {Q}(t)$
and
![]() $j(E)$
lies in
$j(E)$
lies in
![]() $j_H(X_H(\mathbb {Q}))$
if and only if the numerator of
$j_H(X_H(\mathbb {Q}))$
if and only if the numerator of
![]() $j_H(t)-j(E)\in \mathbb {Q}(t)$
has a rational root or
$j_H(t)-j(E)\in \mathbb {Q}(t)$
has a rational root or
![]() $j_H(1/t)(0) = j(E)$
. When H has genus 1, we have a plane Weierstrass model
$j_H(1/t)(0) = j(E)$
. When H has genus 1, we have a plane Weierstrass model
![]() $X_H\colon y^2+h(x)y=f(x)$
and a rational map
$X_H\colon y^2+h(x)y=f(x)$
and a rational map
![]() $j_H(x,y):X_H\to X(1)$
, and we can use the equations
$j_H(x,y):X_H\to X(1)$
, and we can use the equations
![]() $j_H(x,y)=j(E)$
and
$j_H(x,y)=j(E)$
and
![]() $y^2+h(x)=f(x)$
to solve for y as a function
$y^2+h(x)=f(x)$
to solve for y as a function
![]() $g(x)$
of x; for each root
$g(x)$
of x; for each root
![]() $x_0$
of
$x_0$
of
![]() $j_H(x,g(x))=j(E)$
, we then check whether
$j_H(x,g(x))=j(E)$
, we then check whether
![]() $g(x_0)^2+h(x_0)=f(x_0)$
holds. These computations are implemented in the functions OnGenusZeroCurve, OnGenusOneCurve in the file gl2data.m in [Reference Rouse, Sutherland and Zureick-BrownRSZB21].
$g(x_0)^2+h(x_0)=f(x_0)$
holds. These computations are implemented in the functions OnGenusZeroCurve, OnGenusOneCurve in the file gl2data.m in [Reference Rouse, Sutherland and Zureick-BrownRSZB21].
It may happen that the unique H of maximal index containing
![]() $-I$
with
$-I$
with
![]() $j(E)\in j_H(X_H(\mathbb {Q}))$
actually has index 1, in which case we have proved that the Galois representation
$j(E)\in j_H(X_H(\mathbb {Q}))$
actually has index 1, in which case we have proved that the Galois representation
![]() $\rho _{E,\ell ^{\infty }}$
is surjective; this is rare but may occasionally happen when the initial set of Frobenius matrices
$\rho _{E,\ell ^{\infty }}$
is surjective; this is rare but may occasionally happen when the initial set of Frobenius matrices
![]() $A_p$
for
$A_p$
for
![]() $p\le B_{\mathrm {min}}$
are not sufficient to rule out every maximal subgroup of
$p\le B_{\mathrm {min}}$
are not sufficient to rule out every maximal subgroup of
![]() $\operatorname {GL}_2(\ell ^{e_{\ell }})$
as described in Section 11.2. When we encounter this case, we remove
$\operatorname {GL}_2(\ell ^{e_{\ell }})$
as described in Section 11.2. When we encounter this case, we remove
![]() $\ell $
from S and continue.
$\ell $
from S and continue.
Having determined
![]() $H=\langle \rho _{E,\ell ^{\infty }}(G_{\mathbb {Q}}),-I\rangle $
, it remains only to check the index-2 subgroups
$H=\langle \rho _{E,\ell ^{\infty }}(G_{\mathbb {Q}}),-I\rangle $
, it remains only to check the index-2 subgroups
![]() $H'\le H$
for which
$H'\le H$
for which
![]() $\langle H',-I\rangle =H$
. For each
$\langle H',-I\rangle =H$
. For each
![]() $H'$
, we need to test whether E is isomorphic to the universal elliptic curve
$H'$
, we need to test whether E is isomorphic to the universal elliptic curve
![]() $E_t$
for
$E_t$
for
![]() $H'$
instantiated at a value of t for which
$H'$
instantiated at a value of t for which
![]() $j(E_t)=j(E)$
(there are no such
$j(E_t)=j(E)$
(there are no such
![]() $H'$
for any H of genus 1, so we may assume the universal elliptic curve has a single parameter). This amounts to finding the rational roots of an integer polynomial and checking the isomorphism of elliptic curves over
$H'$
for any H of genus 1, so we may assume the universal elliptic curve has a single parameter). This amounts to finding the rational roots of an integer polynomial and checking the isomorphism of elliptic curves over
![]() $\mathbb {Q}$
, a computation that is implemented in the function OnGenusZeroCurveTwist in gl2data.m in [Reference Rouse, Sutherland and Zureick-BrownRSZB21]. There will necessarily be at most one subgroup
$\mathbb {Q}$
, a computation that is implemented in the function OnGenusZeroCurveTwist in gl2data.m in [Reference Rouse, Sutherland and Zureick-BrownRSZB21]. There will necessarily be at most one subgroup
![]() $H'$
for which this holds. If there is one, then we have proved that
$H'$
for which this holds. If there is one, then we have proved that
![]() $\rho _{E,\ell ^{\infty }}(G_{\mathbb {Q}})=H'$
, and if not, we have proved that
$\rho _{E,\ell ^{\infty }}(G_{\mathbb {Q}})=H'$
, and if not, we have proved that
![]() $\rho _{E,\ell ^{\infty }}(G_{\mathbb {Q}})=H$
.
$\rho _{E,\ell ^{\infty }}(G_{\mathbb {Q}})=H$
.
The function GL2EllAdicImages in gl2data.m in [Reference Rouse, Sutherland and Zureick-BrownRSZB21] implements the algorithm we have described in this section. It takes as input a non-CM elliptic curve
![]() $E/\mathbb {Q}$
and a collection of precomputed data for the relevant subgroups H, models
$E/\mathbb {Q}$
and a collection of precomputed data for the relevant subgroups H, models
![]() $X_H$
and maps
$X_H$
and maps
![]() $j_H$
that can be loaded using the function GL2Load in gl2data.m in [Reference Rouse, Sutherland and Zureick-BrownRSZB21]. It outputs a list of labels that uniquely identify (up to conjugacy) all of the groups H corresponding to the image of a nonsurjective
$j_H$
that can be loaded using the function GL2Load in gl2data.m in [Reference Rouse, Sutherland and Zureick-BrownRSZB21]. It outputs a list of labels that uniquely identify (up to conjugacy) all of the groups H corresponding to the image of a nonsurjective
![]() $\ell $
-adic Galois representation
$\ell $
-adic Galois representation
![]() $\rho _{E,\ell ^{\infty }}\colon G_{\mathbb {Q}}\to \operatorname {GL}_2(\mathbb {Z}_{\ell })$
attached to E.
$\rho _{E,\ell ^{\infty }}\colon G_{\mathbb {Q}}\to \operatorname {GL}_2(\mathbb {Z}_{\ell })$
attached to E.
11.4 Database computations
We used the function GL2EllAdicImages to compute
![]() $\ell $
-adic images of Galois for the non-CM elliptic curves over
$\ell $
-adic images of Galois for the non-CM elliptic curves over
![]() $\mathbb {Q}$
in three large databases:
$\mathbb {Q}$
in three large databases:
-
○ The L-functions and Modular Forms Database (LMFDB) [LMF], which includes all elliptic curves
 $E/\mathbb {Q}$
of conductor up to 500000, of which approximately 3 million do not have complex multiplication (the LMFDB contains additional
$E/\mathbb {Q}$
of conductor up to 500000, of which approximately 3 million do not have complex multiplication (the LMFDB contains additional
 $E/\mathbb {Q}$
whose
$E/\mathbb {Q}$
whose
 $\ell $
-adic images we also computed, but the results are not included in Table 9).
$\ell $
-adic images we also computed, but the results are not included in Table 9).Table 9 Summary of
 $\ell $
-adic image data for non-CM elliptic curves
$\ell $
-adic image data for non-CM elliptic curves
 $E/\mathbb {Q}$
in the LMFDB, Stein–Watkins (SW) and Balakrishnan–Ho–Kaplan–Spicer–Stein–Weigandt (BHKSSW) databases. Nonsurjective counts are inclusive and may include curves that are also nonsurjective at another prime.
$E/\mathbb {Q}$
in the LMFDB, Stein–Watkins (SW) and Balakrishnan–Ho–Kaplan–Spicer–Stein–Weigandt (BHKSSW) databases. Nonsurjective counts are inclusive and may include curves that are also nonsurjective at another prime.
-
○ The Stein–Watkins Database [Reference Stein and WatkinsSW02], which consists of a nearly complete set of elliptic curves
 $E/\mathbb {Q}$
of absolute discriminant at most
$E/\mathbb {Q}$
of absolute discriminant at most
 $10^{12}$
that have conductor at most
$10^{12}$
that have conductor at most
 $10^8$
or prime conductor at most
$10^8$
or prime conductor at most
 $10^{10}$
, which has been filtered to include just one representative of each isogeny class and each class of quadratic twists; it contains more than 148 million elliptic curves without complex multiplication.
$10^{10}$
, which has been filtered to include just one representative of each isogeny class and each class of quadratic twists; it contains more than 148 million elliptic curves without complex multiplication. -
○ The Balakrishnan–Ho–Kaplan–Spicer–Stein–Weigandt Database [Reference Balakrishnan, Ho, Kaplan, Spicer, Stein and WeigandtBHK+16], which includes all elliptic curves
 $E/\mathbb {Q}$
of naive height up to
$E/\mathbb {Q}$
of naive height up to
 $2.7\times 10^{10}$
, including nearly 239 million elliptic curves without complex multiplication.
$2.7\times 10^{10}$
, including nearly 239 million elliptic curves without complex multiplication.
The total time to compute all
![]() $\ell $
-adic Galois images of every non-CM elliptic curve over
$\ell $
-adic Galois images of every non-CM elliptic curve over
![]() $\mathbb {Q}$
in the LMFDB was less than 45 hours, an average of about 42 milliseconds per curve. Most of this time is spent on elliptic curves whose
$\mathbb {Q}$
in the LMFDB was less than 45 hours, an average of about 42 milliseconds per curve. Most of this time is spent on elliptic curves whose
![]() $\ell $
-adic Galois representation is nonsurjective for one or more primes
$\ell $
-adic Galois representation is nonsurjective for one or more primes
![]() $\ell $
. The method given in Section 11.2 for proving nonsurjectivity is very efficient, and for elliptic curves whose
$\ell $
. The method given in Section 11.2 for proving nonsurjectivity is very efficient, and for elliptic curves whose
![]() $\ell $
-adic Galois representations are surjective at every prime, it typically takes less than a millisecond to prove this. As can be seen in Table 9, such curves make up almost all of the Balakrishnan–Ho–Kaplan–Spicer–Stein–Weigandt database, and it did not take much longer to compute the
$\ell $
-adic Galois representations are surjective at every prime, it typically takes less than a millisecond to prove this. As can be seen in Table 9, such curves make up almost all of the Balakrishnan–Ho–Kaplan–Spicer–Stein–Weigandt database, and it did not take much longer to compute the
![]() $\ell $
-adic image data for this dataset than it did for the LMFDB. The Stein–Watkins database took substantially longer, nearly two core-years (about five days of parallel computation on 128 cores).
$\ell $
-adic image data for this dataset than it did for the LMFDB. The Stein–Watkins database took substantially longer, nearly two core-years (about five days of parallel computation on 128 cores).
12 Computing
 $\ell $
-adic images of CM elliptic curves over
$\ell $
-adic images of CM elliptic curves over
 $\mathbb {Q}$
$\mathbb {Q}$
Let E be an elliptic curve over the number field
![]() $F=\mathbb {Q}(j(E))$
with potential CM by
$F=\mathbb {Q}(j(E))$
with potential CM by
![]() ${\mathcal O}$
, by which we mean that
${\mathcal O}$
, by which we mean that
![]() $\operatorname {\mathrm {End}}(E_{\overline {F}})\simeq {\mathcal O}$
is an order in an imaginary quadratic field K. The possible images of
$\operatorname {\mathrm {End}}(E_{\overline {F}})\simeq {\mathcal O}$
is an order in an imaginary quadratic field K. The possible images of
![]() $\rho _{E,\ell ^{\infty }}$
are determined by Lozano-Robledo in [Reference Lozano-RobledoLR]. In this section, we give an efficient algorithm to compute these images. We are primarily interested in the case
$\rho _{E,\ell ^{\infty }}$
are determined by Lozano-Robledo in [Reference Lozano-RobledoLR]. In this section, we give an efficient algorithm to compute these images. We are primarily interested in the case
![]() $F=\mathbb {Q}$
, where
$F=\mathbb {Q}$
, where
![]() ${\mathcal O}$
is one of the 13 imaginary quadratic orders of class number one, but we shall treat the more general case of a CM elliptic curve defined over its minimal field of definition, as this requires little additional effort.
${\mathcal O}$
is one of the 13 imaginary quadratic orders of class number one, but we shall treat the more general case of a CM elliptic curve defined over its minimal field of definition, as this requires little additional effort.
12.1 Adelic Cartan groups
For each imaginary quadratic order
![]() ${\mathcal O}$
, we define
${\mathcal O}$
, we define
where N varies over positive integers ordered by divisibility. We embed
![]() $C_{{\mathcal O}}$
in
$C_{{\mathcal O}}$
in
![]() $\operatorname {GL}_2({\widehat {\mathbb {Z}}})$
as follows. Let
$\operatorname {GL}_2({\widehat {\mathbb {Z}}})$
as follows. Let
, let
, and let
if D is odd, with
otherwise. Let
so that
![]() ${\mathcal O}=\mathbb {Z}[1,\omega ]$
with
${\mathcal O}=\mathbb {Z}[1,\omega ]$
with
![]() $\omega ^2-\phi \omega -\delta =0$
. We now define the Cartan subgroup
$\omega ^2-\phi \omega -\delta =0$
. We now define the Cartan subgroup
as the inverse limit of the groups

It is a closed subgroup of
![]() $\operatorname {GL}_2({\widehat {\mathbb {Z}}})$
that is isomorphic to
$\operatorname {GL}_2({\widehat {\mathbb {Z}}})$
that is isomorphic to
![]() $C_{\mathcal O}$
via the map induced by
$C_{\mathcal O}$
via the map induced by
 $$ \begin{align} a+b\omega \mapsto \begin{bmatrix}a+b\phi & b\\ \delta b & a\end{bmatrix}. \end{align} $$
$$ \begin{align} a+b\omega \mapsto \begin{bmatrix}a+b\phi & b\\ \delta b & a\end{bmatrix}. \end{align} $$
It follows from the theory of complex multiplication that if the CM field
lies in the field of definition of an elliptic curve E with CM by
![]() ${\mathcal O}$
, then the image of
${\mathcal O}$
, then the image of
![]() $\rho _E$
lies in
$\rho _E$
lies in
![]() ${\mathcal C}_{\mathcal O}\le \operatorname {GL}_2({\widehat {\mathbb {Z}}})$
(recall that we view subgroups of
${\mathcal C}_{\mathcal O}\le \operatorname {GL}_2({\widehat {\mathbb {Z}}})$
(recall that we view subgroups of
![]() $\operatorname {GL}_2({\widehat {\mathbb {Z}}})$
as defined only up to conjugation); see [Reference Serre and TateST68, Theorem 5], for example. This is not true when E is defined over its minimal field of definition
$\operatorname {GL}_2({\widehat {\mathbb {Z}}})$
as defined only up to conjugation); see [Reference Serre and TateST68, Theorem 5], for example. This is not true when E is defined over its minimal field of definition
![]() $F=\mathbb {Q}(j(E))$
or over any field that does not contain K. In this case, the image of
$F=\mathbb {Q}(j(E))$
or over any field that does not contain K. In this case, the image of
![]() $\rho _E$
lies in the group
$\rho _E$
lies in the group
![]() ${\mathcal N}_{\mathcal O}\le \operatorname {GL}_2({\widehat {\mathbb {Z}}})$
, which we define as the inverse limit of the groups
${\mathcal N}_{\mathcal O}\le \operatorname {GL}_2({\widehat {\mathbb {Z}}})$
, which we define as the inverse limit of the groups
The group
![]() ${\mathcal N}_{\mathcal O}$
is nonabelian and contains the abelian group
${\mathcal N}_{\mathcal O}$
is nonabelian and contains the abelian group
![]() ${\mathcal C}_{\mathcal O}$
with index 2. We shall use
${\mathcal C}_{\mathcal O}$
with index 2. We shall use
![]() ${\mathcal C}_{\mathcal O}(\mathbb {Z}_{\ell })$
and
${\mathcal C}_{\mathcal O}(\mathbb {Z}_{\ell })$
and
![]() ${\mathcal N}_{\mathcal O}(\mathbb {Z}_{\ell })$
to denote the images of these groups in
${\mathcal N}_{\mathcal O}(\mathbb {Z}_{\ell })$
to denote the images of these groups in
![]() $\operatorname {GL}_2(\mathbb {Z}_{\ell })$
under the projection from
$\operatorname {GL}_2(\mathbb {Z}_{\ell })$
under the projection from
![]() $\operatorname {GL}_2({\widehat {\mathbb {Z}}})\simeq \prod _{\ell } \operatorname {GL}_2(\mathbb {Z}_{\ell })$
.
$\operatorname {GL}_2({\widehat {\mathbb {Z}}})\simeq \prod _{\ell } \operatorname {GL}_2(\mathbb {Z}_{\ell })$
.
Remark 12.1. Our definition of
![]() ${\mathcal C}_{\mathcal O}$
above differs slightly from that in [Reference Lozano-RobledoLR] for odd N when
${\mathcal C}_{\mathcal O}$
above differs slightly from that in [Reference Lozano-RobledoLR] for odd N when
![]() $D\equiv 1\bmod 4$
, but the groups are conjugate. This difference simplifies our presentation here and has no impact on our results or those in [Reference Lozano-RobledoLR] on which we rely.
$D\equiv 1\bmod 4$
, but the groups are conjugate. This difference simplifies our presentation here and has no impact on our results or those in [Reference Lozano-RobledoLR] on which we rely.
Remark 12.2. The group
![]() ${\mathcal N}_{\mathcal O}$
is sometimes referred to as the ‘normaliser’ of the Cartan subgroup
${\mathcal N}_{\mathcal O}$
is sometimes referred to as the ‘normaliser’ of the Cartan subgroup
![]() ${\mathcal C}_{\mathcal O}$
in the literature. The group
${\mathcal C}_{\mathcal O}$
in the literature. The group
![]() ${\mathcal N}_{\mathcal O}(\mathbb {Z}_{\ell })$
is the normaliser of
${\mathcal N}_{\mathcal O}(\mathbb {Z}_{\ell })$
is the normaliser of
![]() ${\mathcal C}_{\mathcal O}(\mathbb {Z}_{\ell })$
in
${\mathcal C}_{\mathcal O}(\mathbb {Z}_{\ell })$
in
![]() $\operatorname {GL}_2(\mathbb {Z}_{\ell })$
, by [Reference Lozano-RobledoLR, Proposition 5.6(2)], but
$\operatorname {GL}_2(\mathbb {Z}_{\ell })$
, by [Reference Lozano-RobledoLR, Proposition 5.6(2)], but
![]() ${\mathcal N}_{\mathcal O}$
is not the normaliser of
${\mathcal N}_{\mathcal O}$
is not the normaliser of
![]() ${\mathcal C}_{\mathcal O}$
in
${\mathcal C}_{\mathcal O}$
in
![]() $\operatorname {GL}_2({\widehat {\mathbb {Z}}})$
; indeed,
$\operatorname {GL}_2({\widehat {\mathbb {Z}}})$
; indeed,
![]() ${\mathcal C}_{\mathcal O}$
has infinite index in its normaliser. The group
${\mathcal C}_{\mathcal O}$
has infinite index in its normaliser. The group
![]() ${\mathcal N}_{\mathcal O}(N)$
is properly contained in the normaliser of
${\mathcal N}_{\mathcal O}(N)$
is properly contained in the normaliser of
![]() ${\mathcal C}_{\mathcal O}(N)$
in
${\mathcal C}_{\mathcal O}(N)$
in
![]() $\operatorname {GL}_2(N)$
for most values of N. This can occur even when N is a prime (if it divides
$\operatorname {GL}_2(N)$
for most values of N. This can occur even when N is a prime (if it divides
![]() $\operatorname {\mathrm {disc}} {\mathcal O}$
) and for infinitely many powers of the same prime; see [Reference Lozano-RobledoLR, Proposition 5.6] for examples.
$\operatorname {\mathrm {disc}} {\mathcal O}$
) and for infinitely many powers of the same prime; see [Reference Lozano-RobledoLR, Proposition 5.6] for examples.
Proposition 12.3. Let E be a elliptic curve over
![]() $F=\mathbb {Q}(j(E))$
with potential CM by
$F=\mathbb {Q}(j(E))$
with potential CM by
![]() ${\mathcal O}$
. There is a choice of
${\mathcal O}$
. There is a choice of
![]() $\iota _E\colon \operatorname {\mathrm {Aut}}(E_{\mathrm {tor}}({\overline {F}}))\overset {\sim }{\to } \operatorname {GL}_2({\widehat {\mathbb {Z}}})$
for which the induced Galois representation
$\iota _E\colon \operatorname {\mathrm {Aut}}(E_{\mathrm {tor}}({\overline {F}}))\overset {\sim }{\to } \operatorname {GL}_2({\widehat {\mathbb {Z}}})$
for which the induced Galois representation
![]() $\rho _E\colon G_F\to \operatorname {GL}_2({\widehat {\mathbb {Z}}})$
satisfies the following:
$\rho _E\colon G_F\to \operatorname {GL}_2({\widehat {\mathbb {Z}}})$
satisfies the following:
-
(i)
 $\rho _E(G_F)$
is an open subgroup of
$\rho _E(G_F)$
is an open subgroup of
 ${\mathcal N}_{\mathcal O}$
,
${\mathcal N}_{\mathcal O}$
, -
(ii)
 $[{\mathcal N}_{\mathcal O}:\rho _E(G_F)]$
divides
$[{\mathcal N}_{\mathcal O}:\rho _E(G_F)]$
divides
 $\#{\mathcal O}^{\times }$
,
$\#{\mathcal O}^{\times }$
, -
(iii)
 $[\rho _E(G_F):\rho _E(G_F)\cap {\mathcal C}_{\mathcal O}]=2$
.
$[\rho _E(G_F):\rho _E(G_F)\cap {\mathcal C}_{\mathcal O}]=2$
.
Proof. Parts (i) and (ii) follow from [Reference Lozano-RobledoLR, Theorem 1.1]. For (iii), we note that, as in [Reference ZywinaZyw15a, Lemma 7.2], if we pick
![]() $\beta \in {\mathcal O}-\mathbb {Z}$
with
$\beta \in {\mathcal O}-\mathbb {Z}$
with
![]() $\beta ^2\in \mathbb {Z}$
squarefree, then for any
$\beta ^2\in \mathbb {Z}$
squarefree, then for any
![]() $\sigma \in G_F-G_{FK}$
, we have
$\sigma \in G_F-G_{FK}$
, we have
![]() $\sigma (\beta P)=\sigma (\beta )\sigma (P)=-\beta \sigma (P)$
for all
$\sigma (\beta P)=\sigma (\beta )\sigma (P)=-\beta \sigma (P)$
for all
![]() $P\in E[N]$
and all
$P\in E[N]$
and all
![]() $N\ge 1$
. It follows that
$N\ge 1$
. It follows that
![]() $\rho _E(\sigma )\pi (\beta )=-\pi (\beta )\rho _E(\sigma )$
, where
$\rho _E(\sigma )\pi (\beta )=-\pi (\beta )\rho _E(\sigma )$
, where
![]() $\pi $
is the natural map
$\pi $
is the natural map
![]() ${\mathcal O}\to C_{\mathcal O}\overset {\sim }{\rightarrow } {\mathcal C}_{\mathcal O}$
, thus
${\mathcal O}\to C_{\mathcal O}\overset {\sim }{\rightarrow } {\mathcal C}_{\mathcal O}$
, thus
![]() $\rho _E(G_F)$
is nonabelian. It therefore contains the abelian group
$\rho _E(G_F)$
is nonabelian. It therefore contains the abelian group
![]() $\rho _E(G_G)\cap {\mathcal C}_{\mathcal O}$
with index at least 2, and (i) implies that the index is at most 2, since
$\rho _E(G_G)\cap {\mathcal C}_{\mathcal O}$
with index at least 2, and (i) implies that the index is at most 2, since
![]() $[{\mathcal N}_{\mathcal O}:{\mathcal C}_{\mathcal O}]=2$
.
$[{\mathcal N}_{\mathcal O}:{\mathcal C}_{\mathcal O}]=2$
.
Proposition 12.4. Let E be an elliptic curve over
![]() $F=\mathbb {Q}(j(E))$
with potential CM by
$F=\mathbb {Q}(j(E))$
with potential CM by
![]() ${\mathcal O}$
, let
${\mathcal O}$
, let
![]() $\ell $
be a prime, and let
$\ell $
be a prime, and let
 $$\begin{align*}e = \begin{cases} 4&\text{if }\ell=2,\\ 3&\text{if }\ell=3,\\ 1&\text{otherwise}. \end{cases} \end{align*}$$
$$\begin{align*}e = \begin{cases} 4&\text{if }\ell=2,\\ 3&\text{if }\ell=3,\\ 1&\text{otherwise}. \end{cases} \end{align*}$$
Then
![]() $\rho _{E,\ell ^{\infty }}(G_F)$
is the inverse image of
$\rho _{E,\ell ^{\infty }}(G_F)$
is the inverse image of
![]() $\rho _{E,\ell ^e}(G_{\ell })$
under the projection
$\rho _{E,\ell ^e}(G_{\ell })$
under the projection
![]() ${\mathcal N}_{\mathcal O}(\mathbb {Z}_{\ell })\to {\mathcal N}_{\mathcal O}(\ell ^e)$
.
${\mathcal N}_{\mathcal O}(\mathbb {Z}_{\ell })\to {\mathcal N}_{\mathcal O}(\ell ^e)$
.
Proof. This follows from Theorems 1.2, 1.4, 1.5, 1.6, 1.7 in [Reference Lozano-RobledoLR] once one notes that for every imaginary quadratic order
![]() ${\mathcal O}$
(including
${\mathcal O}$
(including
![]() $\mathbb {Z}[\zeta _3],\mathbb {Z}[i]$
), the possibilities for
$\mathbb {Z}[\zeta _3],\mathbb {Z}[i]$
), the possibilities for
![]() $\rho _{E,\ell ^{\infty }}(G_F)\le {\mathcal N}_{\mathcal O}(\mathbb {Z}_{\ell })$
enumerated in these theorems are nonconjugate modulo
$\rho _{E,\ell ^{\infty }}(G_F)\le {\mathcal N}_{\mathcal O}(\mathbb {Z}_{\ell })$
enumerated in these theorems are nonconjugate modulo
![]() $\ell ^e$
.
$\ell ^e$
.
Remark 12.5. The values of e in Proposition 12.4 are best possible, even if one restricts to
![]() $F=\mathbb {Q}$
. If one excludes
$F=\mathbb {Q}$
. If one excludes
![]() ${\mathcal O}=\mathbb {Z}[\zeta _3]$
, one can take
${\mathcal O}=\mathbb {Z}[\zeta _3]$
, one can take
![]() $e=1$
for
$e=1$
for
![]() $\ell =3$
, but
$\ell =3$
, but
![]() $e=4$
is necessary for
$e=4$
is necessary for
![]() $\ell =2$
and infinitely many imaginary quadratic orders
$\ell =2$
and infinitely many imaginary quadratic orders
![]() ${\mathcal O}$
.
${\mathcal O}$
.
Proposition 12.4 implies that to identify
![]() $\rho _{E,\ell ^{\infty }}(G_F)$
, it suffices to specify the order
$\rho _{E,\ell ^{\infty }}(G_F)$
, it suffices to specify the order
![]() ${\mathcal O}$
(via its discriminant) and the subgroup
${\mathcal O}$
(via its discriminant) and the subgroup
![]() $\rho _{E,\ell ^e}(G_F)\le {\mathcal N}_{\mathcal O}(\ell ^e)\le \operatorname {GL}_2(\ell ^e)$
(via its label defined in Section 2.4). Note that in the CM setting, these labels identify the inverse image of a subgroup of
$\rho _{E,\ell ^e}(G_F)\le {\mathcal N}_{\mathcal O}(\ell ^e)\le \operatorname {GL}_2(\ell ^e)$
(via its label defined in Section 2.4). Note that in the CM setting, these labels identify the inverse image of a subgroup of
![]() ${\mathcal N}_{\mathcal O}(\ell ^e)\le \operatorname {GL}_2(\ell ^e)$
in
${\mathcal N}_{\mathcal O}(\ell ^e)\le \operatorname {GL}_2(\ell ^e)$
in
![]() ${\mathcal N}_{\mathcal O}(\mathbb {Z}_{\ell })$
rather than in
${\mathcal N}_{\mathcal O}(\mathbb {Z}_{\ell })$
rather than in
![]() $\operatorname {GL}_2(\mathbb {Z}_{\ell })$
.
$\operatorname {GL}_2(\mathbb {Z}_{\ell })$
.
Remark 12.6. For each prime
![]() $\ell $
, there are infinitely many nonconjugate
$\ell $
, there are infinitely many nonconjugate
![]() ${\mathcal N}_{\mathcal O}(\mathbb {Z}_{\ell })\le \operatorname {GL}_2(\mathbb {Z}_{\ell })$
as
${\mathcal N}_{\mathcal O}(\mathbb {Z}_{\ell })\le \operatorname {GL}_2(\mathbb {Z}_{\ell })$
as
![]() ${\mathcal O}$
varies, even though there are only finitely many possibilities for
${\mathcal O}$
varies, even though there are only finitely many possibilities for
![]() ${\mathcal N}_{\mathcal O}(\ell ^e)$
. It is the pair
${\mathcal N}_{\mathcal O}(\ell ^e)$
. It is the pair
![]() $({\mathcal O},\rho _{E,\ell ^e}(G_F))$
that uniquely determines
$({\mathcal O},\rho _{E,\ell ^e}(G_F))$
that uniquely determines
![]() $\rho _{E,\ell ^{\infty }}(G_F)\le {\mathcal N}_{\mathcal O}(\mathbb {Z}_{\ell })\le \operatorname {GL}_2(\mathbb {Z}_{\ell })$
. We should note that
$\rho _{E,\ell ^{\infty }}(G_F)\le {\mathcal N}_{\mathcal O}(\mathbb {Z}_{\ell })\le \operatorname {GL}_2(\mathbb {Z}_{\ell })$
. We should note that
![]() ${\mathcal N}_{\mathcal O}(Z_{\ell })$
and
${\mathcal N}_{\mathcal O}(Z_{\ell })$
and
![]() ${\mathcal N}_{\mathcal O}'(\mathbb {Z}_{\ell })$
may be conjugate even when
${\mathcal N}_{\mathcal O}'(\mathbb {Z}_{\ell })$
may be conjugate even when
![]() ${\mathcal O}\ne {\mathcal O}'$
; this happens when
${\mathcal O}\ne {\mathcal O}'$
; this happens when
![]() $\operatorname {\mathrm {disc}}{\mathcal O}/\operatorname {\mathrm {disc}}{\mathcal O}'=u^2$
with
$\operatorname {\mathrm {disc}}{\mathcal O}/\operatorname {\mathrm {disc}}{\mathcal O}'=u^2$
with
![]() $u\in \mathbb {Z}_{\ell }^{\times }$
(to see this, conjugate equation (12.1) by
$u\in \mathbb {Z}_{\ell }^{\times }$
(to see this, conjugate equation (12.1) by
![]() $\left [\begin {smallmatrix} u & 0 \\ 0 & u^{-1} \end {smallmatrix}\right ]$
).
$\left [\begin {smallmatrix} u & 0 \\ 0 & u^{-1} \end {smallmatrix}\right ]$
).
For any number field F, we say that an elliptic curve
![]() $E/F$
with potential CM by
$E/F$
with potential CM by
![]() ${\mathcal O}$
has maximal
${\mathcal O}$
has maximal
![]() $\ell $
-adic image if
$\ell $
-adic image if
![]() $\rho _{E,\ell ^{\infty }}(G_F)$
contains
$\rho _{E,\ell ^{\infty }}(G_F)$
contains
![]() $\operatorname {SL}_2(\mathbb {Z}_{\ell })\cap {\mathcal C}_{\mathcal O}(\mathbb {Z}_{\ell })$
.
$\operatorname {SL}_2(\mathbb {Z}_{\ell })\cap {\mathcal C}_{\mathcal O}(\mathbb {Z}_{\ell })$
.
Proposition 12.7. Let E be an elliptic curve over
![]() $F=\mathbb {Q}(j(E))$
with potential CM by
$F=\mathbb {Q}(j(E))$
with potential CM by
![]() ${\mathcal O}\ne \mathbb {Z}[\zeta _3]$
. Then E has maximal
${\mathcal O}\ne \mathbb {Z}[\zeta _3]$
. Then E has maximal
![]() $\ell $
-adic image for all primes
$\ell $
-adic image for all primes
![]() $\ell \nmid 2\operatorname {\mathrm {disc}}{\mathcal O}$
.
$\ell \nmid 2\operatorname {\mathrm {disc}}{\mathcal O}$
.
Proof. This is [Reference Lozano-RobledoLR, Theorem 1.2(4)].
The following lemma allows us to immediately compute the label of
![]() $\rho _{E,\ell }(G_F)$
when E has maximal
$\rho _{E,\ell }(G_F)$
when E has maximal
![]() $\ell $
-adic image at a prime
$\ell $
-adic image at a prime
![]() $\ell>3$
not dividing
$\ell>3$
not dividing
![]() $\operatorname {\mathrm {disc}}{\mathcal O}$
.
$\operatorname {\mathrm {disc}}{\mathcal O}$
.
Lemma 12.8. Let E be an elliptic curve over
![]() $F=\mathbb {Q}(j(E))$
with potential CM by
$F=\mathbb {Q}(j(E))$
with potential CM by
![]() ${\mathcal O}$
and maximal
${\mathcal O}$
and maximal
![]() $\ell $
-adic image at a prime
$\ell $
-adic image at a prime
![]() $\ell>3$
not dividing
$\ell>3$
not dividing
![]() $D:=\operatorname {\mathrm {disc}}{\mathcal O}$
. Then
$D:=\operatorname {\mathrm {disc}}{\mathcal O}$
. Then
![]() has index
has index
![]() $i=2\ell (\ell +(\frac {D}{\ell }))$
in
$i=2\ell (\ell +(\frac {D}{\ell }))$
in
![]() $\operatorname {GL}_2(\ell )$
and genus
$\operatorname {GL}_2(\ell )$
and genus
 $$\begin{align*}g = \begin{cases} (11+(\ell-8)\ell-4(\frac{-3}{\ell}))/24&\text{if } (\frac{D}{\ell})=+1,\\ (23+(\ell-10)\ell+6(\frac{-1}{\ell})+4(\frac{-3}{\ell}))/24&\text{if } (\frac{D}{\ell})=-1. \end{cases} \end{align*}$$
$$\begin{align*}g = \begin{cases} (11+(\ell-8)\ell-4(\frac{-3}{\ell}))/24&\text{if } (\frac{D}{\ell})=+1,\\ (23+(\ell-10)\ell+6(\frac{-1}{\ell})+4(\frac{-3}{\ell}))/24&\text{if } (\frac{D}{\ell})=-1. \end{cases} \end{align*}$$
The subgroup H has label
![]() $\ell .i.g.1$
under the labeling system defined in §2.4.
$\ell .i.g.1$
under the labeling system defined in §2.4.
Proof. When E has maximal
![]() $\ell $
-adic, image
$\ell $
-adic, image
![]() $\rho _{E,\ell }(G_F)$
contains an index-2 Cartan subgroup of
$\rho _{E,\ell }(G_F)$
contains an index-2 Cartan subgroup of
![]() $\operatorname {GL}_2(\ell )$
that is split if
$\operatorname {GL}_2(\ell )$
that is split if
![]() $(\frac {D}{\ell })=+1$
and nonsplit if
$(\frac {D}{\ell })=+1$
and nonsplit if
![]() $(\frac {D}{\ell })=-1$
. We have
$(\frac {D}{\ell })=-1$
. We have
![]() $({\mathcal O}/\ell {\mathcal O})^{\times }\simeq {\mathbb F}_{\ell }^{\times } \times {\mathbb F}_{\ell }^{\times }$
of order
$({\mathcal O}/\ell {\mathcal O})^{\times }\simeq {\mathbb F}_{\ell }^{\times } \times {\mathbb F}_{\ell }^{\times }$
of order
![]() $(\ell -1)^2$
in the split case and
$(\ell -1)^2$
in the split case and
![]() $({\mathcal O}/\ell {\mathcal O})^{\times }\simeq {\mathbb F}_{\ell ^2}^{\times }$
of order
$({\mathcal O}/\ell {\mathcal O})^{\times }\simeq {\mathbb F}_{\ell ^2}^{\times }$
of order
![]() $\ell ^2-1$
in the nonsplit case, which implies the index formula, since
$\ell ^2-1$
in the nonsplit case, which implies the index formula, since
![]() $\#\operatorname {GL}_2(\ell )=\ell (\ell -1)(\ell ^2-1)$
. The genus formulas for these groups appear on page 117 of [Reference MazurMaz77a]. For
$\#\operatorname {GL}_2(\ell )=\ell (\ell -1)(\ell ^2-1)$
. The genus formulas for these groups appear on page 117 of [Reference MazurMaz77a]. For
![]() $\ell> 31$
, there is a unique conjugacy class of subgroups of index
$\ell> 31$
, there is a unique conjugacy class of subgroups of index
![]() $i=2(\ell -1)(\ell \pm 1)$
in
$i=2(\ell -1)(\ell \pm 1)$
in
![]() $\operatorname {GL}_2(\ell )$
(this follows from Dickson’s classification [Reference DicksonDic58]), and this implies that the last number in the label of H must be
$\operatorname {GL}_2(\ell )$
(this follows from Dickson’s classification [Reference DicksonDic58]), and this implies that the last number in the label of H must be
![]() $1$
. A direct calculation shows that this is also true for
$1$
. A direct calculation shows that this is also true for
![]() $3\le \ell \le 31$
.
$3\le \ell \le 31$
.
12.2 CM twists
For each imaginary quadratic order
![]() ${\mathcal O}$
, we define
${\mathcal O}$
, we define

so that
![]() $\langle z_{\mathcal O}\rangle $
is the image of
$\langle z_{\mathcal O}\rangle $
is the image of
![]() ${\mathcal O}^{\times }\le C_{\mathcal O}$
under the isomorphism defined in equation (12.1). We note that
${\mathcal O}^{\times }\le C_{\mathcal O}$
under the isomorphism defined in equation (12.1). We note that
![]() $\operatorname {\mathrm {Aut}}(E_{\overline {F}})\simeq {\mathcal O}^{\times }\simeq \langle z_{\mathcal O}\rangle $
via the restriction of
$\operatorname {\mathrm {Aut}}(E_{\overline {F}})\simeq {\mathcal O}^{\times }\simeq \langle z_{\mathcal O}\rangle $
via the restriction of
![]() $\iota _E\colon \operatorname {\mathrm {Aut}}(E_{\mathrm {tor}}(\overline {F}))\simeq \operatorname {GL}_2({\widehat {\mathbb {Z}}})$
in Proposition 12.3. We also note that
$\iota _E\colon \operatorname {\mathrm {Aut}}(E_{\mathrm {tor}}(\overline {F}))\simeq \operatorname {GL}_2({\widehat {\mathbb {Z}}})$
in Proposition 12.3. We also note that
![]() $\langle z_{\mathcal O}\rangle $
is a normal subgroup of
$\langle z_{\mathcal O}\rangle $
is a normal subgroup of
![]() ${\mathcal N}_{\mathcal O}$
.
${\mathcal N}_{\mathcal O}$
.
Recall that a twist of an elliptic curve
![]() $E/F$
is an elliptic curve
$E/F$
is an elliptic curve
![]() $E'/F$
for which
$E'/F$
for which
![]() $E^{\prime }_{\overline {F}}\simeq E_{\overline {F}}$
, equivalently, for which
$E^{\prime }_{\overline {F}}\simeq E_{\overline {F}}$
, equivalently, for which
![]() $j(E')=j(E)$
.
$j(E')=j(E)$
.
Proposition 12.1. Let E be a elliptic curve over
![]() $F=\mathbb {Q}(j(E))$
with potential CM by
$F=\mathbb {Q}(j(E))$
with potential CM by
![]() ${\mathcal O}$
. There is a choice of
${\mathcal O}$
. There is a choice of
![]() $\iota _E\colon \operatorname {\mathrm {Aut}}(E_{\mathrm {tor}}({\overline {F}}))\overset {\sim }{\to } \operatorname {GL}_2({\widehat {\mathbb {Z}}})$
for which the induced Galois representation
$\iota _E\colon \operatorname {\mathrm {Aut}}(E_{\mathrm {tor}}({\overline {F}}))\overset {\sim }{\to } \operatorname {GL}_2({\widehat {\mathbb {Z}}})$
for which the induced Galois representation
![]() $\rho _E\colon G_F\to \operatorname {GL}_2({\widehat {\mathbb {Z}}})$
has image
$\rho _E\colon G_F\to \operatorname {GL}_2({\widehat {\mathbb {Z}}})$
has image
![]() $H=\rho _E(G_F)$
satisfying
$H=\rho _E(G_F)$
satisfying
![]() ${\mathcal N}_{\mathcal O} = \langle H,z_{\mathcal O}\rangle $
. Moreover, every
${\mathcal N}_{\mathcal O} = \langle H,z_{\mathcal O}\rangle $
. Moreover, every
![]() $H\le {\mathcal N}_{\mathcal O}$
with
$H\le {\mathcal N}_{\mathcal O}$
with
![]() $\langle H,z_{\mathcal O}\rangle ={\mathcal N}_{\mathcal O}$
occurs as
$\langle H,z_{\mathcal O}\rangle ={\mathcal N}_{\mathcal O}$
occurs as
![]() $\rho _{E'}(G_F)$
for some twist
$\rho _{E'}(G_F)$
for some twist
![]() $E'$
of E and choice of
$E'$
of E and choice of
![]() $\iota _E'$
.
$\iota _E'$
.
In particular, for every positive integer N, the images
![]() $\rho _{E',N}(G_F)\le {\mathcal N}_{\mathcal O}(N)$
realised by twists
$\rho _{E',N}(G_F)\le {\mathcal N}_{\mathcal O}(N)$
realised by twists
![]() $E'$
of E are the subgroups
$E'$
of E are the subgroups
![]() $H\le {\mathcal N}_{\mathcal O}(N)$
for which
$H\le {\mathcal N}_{\mathcal O}(N)$
for which
![]() $\langle H,z_{\mathcal O}\rangle = {\mathcal N}_{\mathcal O}(N)$
.
$\langle H,z_{\mathcal O}\rangle = {\mathcal N}_{\mathcal O}(N)$
.
Proof. It follows from [Reference Lozano-RobledoLR, Corollary 4.3] that if we choose
![]() $\iota _E$
as in Proposition 12.3, then
$\iota _E$
as in Proposition 12.3, then
![]() $\langle H,z_{\mathcal O}\rangle = {\mathcal N}_{\mathcal O}$
, which proves the first statement in the proposition.
$\langle H,z_{\mathcal O}\rangle = {\mathcal N}_{\mathcal O}$
, which proves the first statement in the proposition.
By [Reference Lozano-RobledoLR, Theorem 6.5], we may assume
![]() $\rho _{E}(G_F)={\mathcal N}_{\mathcal O}$
(replace E by an appropriate twist and choose
$\rho _{E}(G_F)={\mathcal N}_{\mathcal O}$
(replace E by an appropriate twist and choose
![]() $\iota _E\colon \operatorname {\mathrm {Aut}}(E_{\mathrm {tor}}(\overline F))\to \operatorname {GL}_2({\widehat {\mathbb {Z}}})$
as above) with
$\iota _E\colon \operatorname {\mathrm {Aut}}(E_{\mathrm {tor}}(\overline F))\to \operatorname {GL}_2({\widehat {\mathbb {Z}}})$
as above) with
![]() $\iota _E(\operatorname {\mathrm {Aut}}(E_{\overline F}))=\langle z_{\mathcal O}\rangle \triangleleft {\mathcal N}_{\mathcal O}$
. Let H be any subgroup of
$\iota _E(\operatorname {\mathrm {Aut}}(E_{\overline F}))=\langle z_{\mathcal O}\rangle \triangleleft {\mathcal N}_{\mathcal O}$
. Let H be any subgroup of
![]() ${\mathcal N}_{\mathcal O}$
for which
${\mathcal N}_{\mathcal O}$
for which
![]() $\langle H,z_{\mathcal O}\rangle ={\mathcal N}_{\mathcal O}$
. Let
$\langle H,z_{\mathcal O}\rangle ={\mathcal N}_{\mathcal O}$
. Let
![]() $A=\langle a\rangle $
be the cyclic subgroup of
$A=\langle a\rangle $
be the cyclic subgroup of
![]() $\langle z_{\mathcal O}\rangle $
of order
$\langle z_{\mathcal O}\rangle $
of order
![]() so that
so that
![]() ${\mathcal N}_{\mathcal O}=A\rtimes H$
(note that A is a subgroup of a cyclic normal subgroup, hence normal), and define the character
${\mathcal N}_{\mathcal O}=A\rtimes H$
(note that A is a subgroup of a cyclic normal subgroup, hence normal), and define the character
![]() $\chi \colon G_F\twoheadrightarrow \mu _m={\mathcal O}^{\times }[m]$
by
$\chi \colon G_F\twoheadrightarrow \mu _m={\mathcal O}^{\times }[m]$
by
![]() $\sigma \mapsto \zeta _m^{e_{\sigma }}$
, where
$\sigma \mapsto \zeta _m^{e_{\sigma }}$
, where
![]() $e_{\sigma }\in [0,\ldots ,m-1]$
is uniquely determined by
$e_{\sigma }\in [0,\ldots ,m-1]$
is uniquely determined by
![]() $\rho _E(\sigma )\in h_{\sigma }a^{e_{\sigma }}$
, with
$\rho _E(\sigma )\in h_{\sigma }a^{e_{\sigma }}$
, with
![]() $h_{\sigma }\in H$
. Now consider the twist
$h_{\sigma }\in H$
. Now consider the twist
![]() $E'$
of E by
$E'$
of E by
![]() $\chi ^{-1}$
; it is isomorphic to E over the fixed field of the kernel of
$\chi ^{-1}$
; it is isomorphic to E over the fixed field of the kernel of
![]() $\chi $
, which is a cyclic extension of F of degree m. For all
$\chi $
, which is a cyclic extension of F of degree m. For all
![]() $\sigma \in G_F$
, we have
$\sigma \in G_F$
, we have
![]() $\rho _{E'}(\sigma )=\rho _{E}(\sigma )\iota _E(\chi (\sigma ))=h_{\sigma } a^{e_{\sigma }}a^{-e_{\sigma }}=h_{\sigma }$
, and it follows that
$\rho _{E'}(\sigma )=\rho _{E}(\sigma )\iota _E(\chi (\sigma ))=h_{\sigma } a^{e_{\sigma }}a^{-e_{\sigma }}=h_{\sigma }$
, and it follows that
![]() $\rho _{E'}(G_F)=H$
.
$\rho _{E'}(G_F)=H$
.
In view of Proposition 12.1, we shall call the subgroups
![]() $H\le {\mathcal N}_{\mathcal O}$
for which
$H\le {\mathcal N}_{\mathcal O}$
for which
![]() $\langle H,z_{\mathcal O}\rangle = {\mathcal N}_{\mathcal O}$
twists of
$\langle H,z_{\mathcal O}\rangle = {\mathcal N}_{\mathcal O}$
twists of
![]() ${\mathcal N}_{\mathcal O}$
, and similarly for
${\mathcal N}_{\mathcal O}$
, and similarly for
![]() ${\mathcal N}_{\mathcal O}(\mathbb {Z}_{\ell })$
and
${\mathcal N}_{\mathcal O}(\mathbb {Z}_{\ell })$
and
![]() ${\mathcal N}_{\mathcal O}(N)$
. The proposition states that the images of Galois that arise among the twists of an elliptic curve
${\mathcal N}_{\mathcal O}(N)$
. The proposition states that the images of Galois that arise among the twists of an elliptic curve
![]() $E/\mathbb {Q}(j(E))$
with potential CM by
$E/\mathbb {Q}(j(E))$
with potential CM by
![]() ${\mathcal O}$
are precisely the twists of
${\mathcal O}$
are precisely the twists of
![]() ${\mathcal N}_{\mathcal O}$
. It will also be convenient to distinguish twists H of
${\mathcal N}_{\mathcal O}$
. It will also be convenient to distinguish twists H of
![]() ${\mathcal N}_{\mathcal O}$
for which
${\mathcal N}_{\mathcal O}$
for which
![]() $\langle H,-I\rangle = {\mathcal N}_{\mathcal O}$
as quadratic twists, and similarly for
$\langle H,-I\rangle = {\mathcal N}_{\mathcal O}$
as quadratic twists, and similarly for
![]() ${\mathcal N}_{\mathcal O}(N)$
. If
${\mathcal N}_{\mathcal O}(N)$
. If
![]() ${\mathcal O} \ne \mathbb {Z}[\zeta _3],\mathbb {Z}[i]$
, then every twist of
${\mathcal O} \ne \mathbb {Z}[\zeta _3],\mathbb {Z}[i]$
, then every twist of
![]() ${\mathcal N}_{\mathcal O}$
is a quadratic twist.
${\mathcal N}_{\mathcal O}$
is a quadratic twist.
Proposition 12.2. Let E be an elliptic curve over
![]() $F=\mathbb {Q}(j(E))$
with potential CM by
$F=\mathbb {Q}(j(E))$
with potential CM by
![]() ${\mathcal O}$
, and let
${\mathcal O}$
, and let
![]() $\ell>3$
be a prime divisor of
$\ell>3$
be a prime divisor of
![]() $\operatorname {\mathrm {disc}} {\mathcal O}$
. All but two F-isomorphism classes of quadratic twists of E have maximal
$\operatorname {\mathrm {disc}} {\mathcal O}$
. All but two F-isomorphism classes of quadratic twists of E have maximal
![]() $\ell $
-adic image
$\ell $
-adic image
![]() ${\mathcal N}_{\mathcal O}(\ell ^{\infty })$
. The two that do not have mod-
${\mathcal N}_{\mathcal O}(\ell ^{\infty })$
. The two that do not have mod-
![]() $\ell $
image equal to one of the two index-
$\ell $
image equal to one of the two index-
![]() $2$
subgroups
$2$
subgroups
![]() $H_1,H_2\le {\mathcal N}_{\mathcal O}(\ell )$
that do not contain
$H_1,H_2\le {\mathcal N}_{\mathcal O}(\ell )$
that do not contain
![]() $-1$
. These three possibilities are distinguished by their orbit signatures as follows:
$-1$
. These three possibilities are distinguished by their orbit signatures as follows:
-
○
 ${\mathcal N}_{\mathcal O}(\ell )$
has two nontrivial
${\mathcal N}_{\mathcal O}(\ell )$
has two nontrivial
 $\ell $
-torsion orbits, one of size
$\ell $
-torsion orbits, one of size
 $\ell -1$
and one of size
$\ell -1$
and one of size
 $\ell (\ell -1)$
;
$\ell (\ell -1)$
; -
○
 $H_1$
has three nontrivial
$H_1$
has three nontrivial
 $\ell $
-torsion orbits, one of size
$\ell $
-torsion orbits, one of size
 $\ell -1$
and two of size
$\ell -1$
and two of size
 $\ell (\ell -1)/2$
;
$\ell (\ell -1)/2$
; -
○
 $H_2$
has three nontrivial
$H_2$
has three nontrivial
 $\ell $
-torsion orbits, two of size
$\ell $
-torsion orbits, two of size
 $(\ell -1)/2$
and one of size
$(\ell -1)/2$
and one of size
 $\ell (\ell -1)$
.
$\ell (\ell -1)$
.
The cases
![]() $H_1$
and
$H_1$
and
![]() $H_2$
each arise for a quadratic twist of E that is unique up to F-isomorphism.
$H_2$
each arise for a quadratic twist of E that is unique up to F-isomorphism.
Proof. This follows from [Reference Lozano-RobledoLR, Theorem 1.5], [Reference SutherlandSut16, Corollary 5.25] and an analysis of the
![]() $\ell $
-torsion orbits of
$\ell $
-torsion orbits of
![]() ${\mathcal N}_{\mathcal O}(\ell ),H_1,H_2$
, which are explicitly described in [Reference Lozano-RobledoLR, Theorem 1.5].
${\mathcal N}_{\mathcal O}(\ell ),H_1,H_2$
, which are explicitly described in [Reference Lozano-RobledoLR, Theorem 1.5].
In practice, we can quickly determine when we are in the typical case
![]() $\rho _{E,\ell }(G_F)={\mathcal N}_{\mathcal O}(\ell )$
of Proposition 12.2 by sampling Frobenius elements at small primes of good reduction, since
$\rho _{E,\ell }(G_F)={\mathcal N}_{\mathcal O}(\ell )$
of Proposition 12.2 by sampling Frobenius elements at small primes of good reduction, since
![]() ${\mathcal N}_{\mathcal O}(\ell )$
contains many elements that are not
${\mathcal N}_{\mathcal O}(\ell )$
contains many elements that are not
![]() $\operatorname {GL}_2(\ell )$
-conjugate to any element in
$\operatorname {GL}_2(\ell )$
-conjugate to any element in
![]() $H_i$
for
$H_i$
for
![]() $i=1,2$
. But if we do not find such an element, we cannot rule out the possibility that
$i=1,2$
. But if we do not find such an element, we cannot rule out the possibility that
![]() $\rho _{E,\ell }(G_F)={\mathcal N}_{\mathcal O}(\ell )$
, nor can we hope to distinguish
$\rho _{E,\ell }(G_F)={\mathcal N}_{\mathcal O}(\ell )$
, nor can we hope to distinguish
![]() $H_1$
from
$H_1$
from
![]() $H_2$
by sampling Frobenius elements; since these groups are Gassmann equivalent subgroups of
$H_2$
by sampling Frobenius elements; since these groups are Gassmann equivalent subgroups of
![]() $\operatorname {GL}_2(\ell )$
, they contain the same number of elements in each
$\operatorname {GL}_2(\ell )$
, they contain the same number of elements in each
![]() $\operatorname {GL}_2(\ell )$
-conjugacy class.
$\operatorname {GL}_2(\ell )$
-conjugacy class.
However, we can use the
![]() $\ell $
-division polynomial of E to compute the orbit-signature of
$\ell $
-division polynomial of E to compute the orbit-signature of
![]() $\rho _{E,\ell }(G_F)$
and thereby uniquely determine which of the three cases in Proposition 12.2 applies. Let
$\rho _{E,\ell }(G_F)$
and thereby uniquely determine which of the three cases in Proposition 12.2 applies. Let
![]() $y^2=f(x)$
be an integral model for E with
$y^2=f(x)$
be an integral model for E with
![]() $f\in {\mathcal O}_F[x]$
a cubic polynomial, and let
$f\in {\mathcal O}_F[x]$
a cubic polynomial, and let
![]() $h\in {\mathcal O}_F[x]$
be the
$h\in {\mathcal O}_F[x]$
be the
![]() $\ell $
-division polynomial of degree
$\ell $
-division polynomial of degree
![]() $(\ell ^2-1)/2$
, which can be efficiently computed using well known recursive formulas [Reference McKeeMcK94]; the roots of h are the distinct x-coordinates of the nontrivial points in
$(\ell ^2-1)/2$
, which can be efficiently computed using well known recursive formulas [Reference McKeeMcK94]; the roots of h are the distinct x-coordinates of the nontrivial points in
![]() $E[\ell ](\overline F)$
. Each irreducible factor g of h in
$E[\ell ](\overline F)$
. Each irreducible factor g of h in
![]() $F[x]$
corresponds to a Galois orbit of the set
$F[x]$
corresponds to a Galois orbit of the set
![]() $\{x(P):P\in E[\ell ](\overline F) \text { of order }\ell \}$
, each of which corresponds to either two Galois orbits of
$\{x(P):P\in E[\ell ](\overline F) \text { of order }\ell \}$
, each of which corresponds to either two Galois orbits of
![]() $E[\ell ](\overline F)$
of the same size or a single Galois orbit of
$E[\ell ](\overline F)$
of the same size or a single Galois orbit of
![]() $E[\ell ](\overline F)$
of twice the size. These two possibilities can be distinguished by checking whether f is a square in the field
$E[\ell ](\overline F)$
of twice the size. These two possibilities can be distinguished by checking whether f is a square in the field
![]() $F[x]/(g(x))$
. This computation is implemented by the function TorsionOrbits in the file gl2.m in [Reference Rouse, Sutherland and Zureick-BrownRSZB21], which can be used to compute the Galois orbit signature of
$F[x]/(g(x))$
. This computation is implemented by the function TorsionOrbits in the file gl2.m in [Reference Rouse, Sutherland and Zureick-BrownRSZB21], which can be used to compute the Galois orbit signature of
![]() $E[N](\overline F)$
for any positive integer N.
$E[N](\overline F)$
for any positive integer N.
The algorithm sketched above runs in polynomial-time (we can factor polynomials over number fields in polynomial time [Reference LenstraLen83, Reference LandauLan85] and then compute square-roots by Hensel lifting), but it is time-consuming for large values of
![]() $\ell $
, including
$\ell $
, including
![]() $\ell =163$
, which is a necessary case to consider for
$\ell =163$
, which is a necessary case to consider for
![]() $F=\mathbb {Q}$
. A more expedient approach is to determine once and for all the finite set of F-isomorphism classes of elliptic curves
$F=\mathbb {Q}$
. A more expedient approach is to determine once and for all the finite set of F-isomorphism classes of elliptic curves
![]() $E/F$
with potential CM by an imaginary quadratic order
$E/F$
with potential CM by an imaginary quadratic order
![]() ${\mathcal O}$
that have nonmaximal
${\mathcal O}$
that have nonmaximal
![]() $\ell $
-adic image a prime
$\ell $
-adic image a prime
![]() $\ell>3$
that divides
$\ell>3$
that divides
![]() $\operatorname {\mathrm {disc}} {\mathcal O}$
. For
$\operatorname {\mathrm {disc}} {\mathcal O}$
. For
![]() $F=\mathbb {Q}$
, this is done by Zywina in [Reference ZywinaZyw15a, Proposition 1.14]. Table 10 lists the LMFDB labels of these elliptic curves and the label of their mod-
$F=\mathbb {Q}$
, this is done by Zywina in [Reference ZywinaZyw15a, Proposition 1.14]. Table 10 lists the LMFDB labels of these elliptic curves and the label of their mod-
![]() $\ell $
image
$\ell $
image
![]() $H_i$
. With this table in hand, determining which case in Proposition 12.2 applies is reduced to an isomorphism test.
$H_i$
. With this table in hand, determining which case in Proposition 12.2 applies is reduced to an isomorphism test.
Table 10 Nonmaximal
![]() $\ell $
-adic images of
$\ell $
-adic images of
![]() $E/\mathbb {Q}$
with potential CM by
$E/\mathbb {Q}$
with potential CM by
![]() ${\mathcal O}$
of discriminant D divisible by a prime
${\mathcal O}$
of discriminant D divisible by a prime
![]() $\ell>3$
.
$\ell>3$
.

Proposition 12.3. Let E be an elliptic curve over
![]() $\mathbb {Q}$
with integral model
$\mathbb {Q}$
with integral model
![]() $y^2=x^3+a$
and potential CM by
$y^2=x^3+a$
and potential CM by
![]() ${\mathcal O}=\mathbb {Z}[\zeta _3]$
, and let
${\mathcal O}=\mathbb {Z}[\zeta _3]$
, and let
![]() $\ell> 3$
be prime. Then E has maximal
$\ell> 3$
be prime. Then E has maximal
![]() $\ell $
-adic image unless
$\ell $
-adic image unless
![]() $4a\ell ^e$
is an integer cube, where
$4a\ell ^e$
is an integer cube, where
![]() $e\in \{1,2\}$
satisfies
$e\in \{1,2\}$
satisfies
![]() $\ell \equiv \pm 2e\bmod 9$
, in which case
$\ell \equiv \pm 2e\bmod 9$
, in which case
![]() $\rho _{E,\ell }(G_{\mathbb {Q}})$
is the unique index-
$\rho _{E,\ell }(G_{\mathbb {Q}})$
is the unique index-
![]() $3$
subgroup of
$3$
subgroup of
![]() ${\mathcal N}_{\mathcal O}(\ell )$
that does not contain
${\mathcal N}_{\mathcal O}(\ell )$
that does not contain
![]() $z_{\mathcal O}^2$
.
$z_{\mathcal O}^2$
.
Proof. This follows from [Reference ZywinaZyw15a, Proposition 1.16] and Proposition 12.1 above.
Corollary 12.4. Let
![]() $E/\mathbb {Q}$
be an elliptic curve with potential CM by
$E/\mathbb {Q}$
be an elliptic curve with potential CM by
![]() ${\mathcal O}=\mathbb {Z}[\zeta _3]$
that has nonmaximal
${\mathcal O}=\mathbb {Z}[\zeta _3]$
that has nonmaximal
![]() $\ell $
-adic image with
$\ell $
-adic image with
![]() $\ell>3$
. Then
$\ell>3$
. Then
![]() has index
has index
![]() $i=2\ell (\ell -(\frac {-3}{\ell }))/3$
in
$i=2\ell (\ell -(\frac {-3}{\ell }))/3$
in
![]() $\operatorname {GL}_2(\ell )$
and genus
$\operatorname {GL}_2(\ell )$
and genus
![]() $g=3g'-3+(\ell -(\frac {-1}{\ell }))/4+2$
, where
$g=3g'-3+(\ell -(\frac {-1}{\ell }))/4+2$
, where
![]() $g'$
is the genus of
$g'$
is the genus of
![]() ${\mathcal N}_{\mathcal O}(\ell )$
.
${\mathcal N}_{\mathcal O}(\ell )$
.
The subgroup H has label
![]() $\ell .i.g.1$
under the labeling system defined in §2.4 .
$\ell .i.g.1$
under the labeling system defined in §2.4 .
Proof. The index formula follows immediately from Proposition 12.3, since
![]() ${\mathcal N}_{\mathcal O}(\ell )$
contains an index-2 Cartan subgroup of order
${\mathcal N}_{\mathcal O}(\ell )$
contains an index-2 Cartan subgroup of order
![]() $(\ell -1)(\ell -(\frac {-3}{\ell }))$
, and the genus formula follows from a calculation similar to [Reference BaranBar10, Proposition 7.10].
$(\ell -1)(\ell -(\frac {-3}{\ell }))$
, and the genus formula follows from a calculation similar to [Reference BaranBar10, Proposition 7.10].
For
![]() $\ell>37$
, the group
$\ell>37$
, the group
![]() $\operatorname {GL}_2(\ell )$
contains a unique conjugacy class of index i (this follows from Dickson’s classification [Reference DicksonDic58]), which implies that the label for H is as claimed, and a direct computation verifies that this is also true for
$\operatorname {GL}_2(\ell )$
contains a unique conjugacy class of index i (this follows from Dickson’s classification [Reference DicksonDic58]), which implies that the label for H is as claimed, and a direct computation verifies that this is also true for
![]() $3<\ell \le 37$
.
$3<\ell \le 37$
.
12.3
 $\ell $
-adic CM images for
$\ell $
-adic CM images for
 $\ell =2,3$
$\ell =2,3$
With Propositions 12.7, 12.2, 12.3 in hand, the problem of computing
![]() $\rho _{E,\ell ^{\infty }}(G_F)$
for an elliptic curve E over
$\rho _{E,\ell ^{\infty }}(G_F)$
for an elliptic curve E over
![]() $F=\mathbb {Q}(j(E))$
with potential CM is reduced to the case
$F=\mathbb {Q}(j(E))$
with potential CM is reduced to the case
![]() $\ell =2,3$
, where we must distinguish the subgroups of
$\ell =2,3$
, where we must distinguish the subgroups of
![]() $\operatorname {GL}_2(16)$
and
$\operatorname {GL}_2(16)$
and
![]() $\operatorname {GL}_2(27)$
that can arise for an elliptic curve with potential CM.
$\operatorname {GL}_2(27)$
that can arise for an elliptic curve with potential CM.
Proposition 12.1. There are
![]() $59$
subgroups of
$59$
subgroups of
![]() $\operatorname {GL}_2(16)$
that arise as the reduction of a twist of
$\operatorname {GL}_2(16)$
that arise as the reduction of a twist of
![]() ${\mathcal N}_{\mathcal O}$
for some imaginary quadratic order
${\mathcal N}_{\mathcal O}$
for some imaginary quadratic order
![]() ${\mathcal O}$
, of which
${\mathcal O}$
, of which
![]() $14$
arise as maximal
$14$
arise as maximal
![]() $2$
-adic images (the reduction of some
$2$
-adic images (the reduction of some
![]() ${\mathcal N}_{\mathcal O}$
); if one restricts to imaginary quadratic orders
${\mathcal N}_{\mathcal O}$
); if one restricts to imaginary quadratic orders
![]() ${\mathcal O}$
of class number
${\mathcal O}$
of class number
![]() $1$
, there are
$1$
, there are
![]() $28$
, of which
$28$
, of which
![]() $7$
are maximal.
$7$
are maximal.
There are
![]() $26$
subgroups of
$26$
subgroups of
![]() $\operatorname {GL}_2(27)$
that arise as the reduction of a twist of
$\operatorname {GL}_2(27)$
that arise as the reduction of a twist of
![]() ${\mathcal N}_{\mathcal O}$
for some imaginary quadratic order
${\mathcal N}_{\mathcal O}$
for some imaginary quadratic order
![]() ${\mathcal O}$
, of which
${\mathcal O}$
, of which
![]() $7$
are maximal; if one restricts to imaginary quadratic orders
$7$
are maximal; if one restricts to imaginary quadratic orders
![]() ${\mathcal O}$
of class number
${\mathcal O}$
of class number
![]() $1$
, there are
$1$
, there are
![]() $17$
, of which
$17$
, of which
![]() $4$
are maximal.
$4$
are maximal.
Proof. It is clear from the definition of
![]() ${\mathcal N}_{\mathcal O}$
that
${\mathcal N}_{\mathcal O}$
that
![]() ${\mathcal N}_{\mathcal O}(16)$
depends only on the residue class of D modulo
${\mathcal N}_{\mathcal O}(16)$
depends only on the residue class of D modulo
![]() $64$
. It thus suffices to enumerate a representative list of 32 imaginary quadratic discriminants D that realise the residue classes modulo 64 that are squares modulo 4, compute
$64$
. It thus suffices to enumerate a representative list of 32 imaginary quadratic discriminants D that realise the residue classes modulo 64 that are squares modulo 4, compute
![]() ${\mathcal N}_{\mathcal O}(16)$
for each D, and then reduce this collection to a set of nonconjugate subgroups of
${\mathcal N}_{\mathcal O}(16)$
for each D, and then reduce this collection to a set of nonconjugate subgroups of
![]() $\operatorname {GL}_2(16)$
. This yields 14 distinct subgroups of
$\operatorname {GL}_2(16)$
. This yields 14 distinct subgroups of
![]() $\operatorname {GL}_2(16)$
that arise as maximal twists, and it then suffices to compute the quadratic twists of these subgroups, along with all twists of
$\operatorname {GL}_2(16)$
that arise as maximal twists, and it then suffices to compute the quadratic twists of these subgroups, along with all twists of
![]() ${\mathcal N}_{\mathcal O}(16)$
for
${\mathcal N}_{\mathcal O}(16)$
for
![]() ${\mathcal O}=\mathbb {Z}[i],\mathbb {Z}[\zeta _3]$
to obtain a complete list of 59 nonconjugate subgroups of
${\mathcal O}=\mathbb {Z}[i],\mathbb {Z}[\zeta _3]$
to obtain a complete list of 59 nonconjugate subgroups of
![]() $\operatorname {GL}_2(16)$
. Repeating this process for the 13 discriminants of class number 1 yields the first statement of the theorem. The second statement is proved similarly, but now
$\operatorname {GL}_2(16)$
. Repeating this process for the 13 discriminants of class number 1 yields the first statement of the theorem. The second statement is proved similarly, but now
![]() ${\mathcal N}_{\mathcal O}(27)$
depends only on the residue class of D modulo 27. The function GL2CMTwists in the file gl2.m in [Reference Rouse, Sutherland and Zureick-BrownRSZB21] was used to perform these computations.
${\mathcal N}_{\mathcal O}(27)$
depends only on the residue class of D modulo 27. The function GL2CMTwists in the file gl2.m in [Reference Rouse, Sutherland and Zureick-BrownRSZB21] was used to perform these computations.
Remark 12.2. That 28 subgroups of
![]() $\operatorname {GL}_2(16)$
arise as reductions of twists of
$\operatorname {GL}_2(16)$
arise as reductions of twists of
![]() ${\mathcal N}_{\mathcal O}$
with
${\mathcal N}_{\mathcal O}$
with
![]() ${\mathcal O}$
of class number
${\mathcal O}$
of class number
![]() $1$
is also noted in [Reference Lozano-RobledoLR, p. 2].
$1$
is also noted in [Reference Lozano-RobledoLR, p. 2].
Corollary 12.3. Let E be an elliptic curve with potential CM by an imaginary quadratic order
![]() ${\mathcal O}$
of discriminant D defined over
${\mathcal O}$
of discriminant D defined over
![]() $F=\mathbb {Q}(j(E))$
. If
$F=\mathbb {Q}(j(E))$
. If
![]() $D\ge -4$
, then
$D\ge -4$
, then
![]() $\rho _{E,16}(G_F)$
is listed in Table 18 and
$\rho _{E,16}(G_F)$
is listed in Table 18 and
![]() $\rho _{E,27}(G_F)$
is listed in Table 19. If
$\rho _{E,27}(G_F)$
is listed in Table 19. If
![]() $D<-4$
, then
$D<-4$
, then
![]() $\rho _{E,16}(G_F)$
is listed in Table 20 or Table 21 and
$\rho _{E,16}(G_F)$
is listed in Table 20 or Table 21 and
![]() $\rho _{E,27}(G_F)$
is listed in Table 22. Moreover, every group listed in these tables arises for some elliptic curve with potential CM defined over its minimal field of definition.
$\rho _{E,27}(G_F)$
is listed in Table 22. Moreover, every group listed in these tables arises for some elliptic curve with potential CM defined over its minimal field of definition.
As can be seen in Tables 18–22, for any given imaginary quadratic order
![]() ${\mathcal O}$
, the 4-orbits and 8-orbits of the possible subgroups
${\mathcal O}$
, the 4-orbits and 8-orbits of the possible subgroups
![]() $H\le \operatorname {GL}_2(16)$
that arise as twists of
$H\le \operatorname {GL}_2(16)$
that arise as twists of
![]() ${\mathcal N}_{\mathcal O}(16)$
are sufficient to determine
${\mathcal N}_{\mathcal O}(16)$
are sufficient to determine
![]() $\rho _{E,16}(G_F)$
except for 11 pairs of subgroups. For each of these 11 pairs, there are many conjugacy classes of
$\rho _{E,16}(G_F)$
except for 11 pairs of subgroups. For each of these 11 pairs, there are many conjugacy classes of
![]() $\operatorname {GL}_2(16)$
that arise in one element of the pair and not the other. We can thus compute
$\operatorname {GL}_2(16)$
that arise in one element of the pair and not the other. We can thus compute
![]() $\rho _{E,16}(G_F)$
by using division polynomials to compute the 4-torsion and 8-torsion orbits of E as described at the end of the previous subsection and then sampling Frobenius elements to eliminate any remaining ambiguity. Similar comments apply to
$\rho _{E,16}(G_F)$
by using division polynomials to compute the 4-torsion and 8-torsion orbits of E as described at the end of the previous subsection and then sampling Frobenius elements to eliminate any remaining ambiguity. Similar comments apply to
![]() ${\mathcal N}_{\mathcal O}(27)$
using 3-orbits and 9-orbits to distinguish all but three pairs of subgroups that can then be distinguished by sampling Frobenius elements. The script CMImages.m in [Reference Rouse, Sutherland and Zureick-BrownRSZB21] verifies these claims. This yields the following algorithm, which is implemented in the function GL2CMEllAdicImages in the file gl2.m in [Reference Rouse, Sutherland and Zureick-BrownRSZB21].
${\mathcal N}_{\mathcal O}(27)$
using 3-orbits and 9-orbits to distinguish all but three pairs of subgroups that can then be distinguished by sampling Frobenius elements. The script CMImages.m in [Reference Rouse, Sutherland and Zureick-BrownRSZB21] verifies these claims. This yields the following algorithm, which is implemented in the function GL2CMEllAdicImages in the file gl2.m in [Reference Rouse, Sutherland and Zureick-BrownRSZB21].
Algorithm 12.4. Given an elliptic curve E with potential CM defined over its minimal field of definition F = ℚ(j(E)), we may compute ρ E, ℓ ∞ (G F ) for all primes ℓ as follows:
-
1. Compute the discriminant D of O≃End(E F¯).Footnote 7
-
2. Compute ρ E, 16(G F ) and ρ E, 27(G F ) using Tables 18-22 as described above.
-
3. Compute ρ E, ℓ (G F ) for ℓ > 3 dividing D via Proposition 12.2 (Table 10 if F = ℚ).
-
4. If j(E) = 0, compute ρ E, ℓ (G F ) for ℓ of bad reduction via Proposition 12.3.
-
5. ρ E, ℓ (G F ) = NO(ℓ) for all ℓ not addressed in steps (1) to (4), by Proposition 12.7.
Having determined ρ E, ℓ e (G F ) for all primes ℓ = 2, 3, 7, … with e = 4, 3, 1, 1, …, ρ E, ℓ ∞ (G F ) is the inverse image of ρ E, ℓ e (G F ) under the projection NO(ℤ ℓ ) →NO(ℓ e ), by Proposition 12.4.
Acknowledgements
We thank Jennifer Balakrishnan, Maarten Derickx, Wei Ho, Álvaro Lozano-Robledo, Jackson Morrow, Pierre Parent, Bjorn Poonen, William Stein, Mark van Hoeij, John Voight and David Zywina for useful conversations. We also thank the referee for helpful comments. The second author was supported by NSF grant DMS-1522526 and Simons Foundation grant 550033. The third author was supported in part by NSF grant DMS-1555048. We are grateful to the organisers of ‘Modular Forms, Arithmetic, and Women in Mathematics (Atlanta 2019)’, ‘Rational Points (Lichtenfels 2019)’, ‘Simons Collaboration on Arithmetic Geometry, Number Theory, and Computation Annual Meeting (New York City 2019)’, ‘Torsion groups and Galois representations of elliptic curves (Zagreb 2018)’ and ‘Arithmetic Aspects of Explicit Moduli Problems (Banff 2017)’ for providing stimulating environments where progress was made; and the Simons Collaboration on Arithmetic Geometry, Number Theory, and Computation for funding a visit hosted by MIT.
A Jacobians of arbitrary modular curves (with John Voight)
Ribet [Reference RibetRib04, Section 3] observed that the simple abelian varieties attached to newforms on
![]() $\Gamma _1(N)$
are of
$\Gamma _1(N)$
are of
![]() $\operatorname {GL}_2$
-type over
$\operatorname {GL}_2$
-type over
![]() $\mathbb {Q}$
. In this appendix, we generalise this to any modular curve. One may anticipate this result from the fact that
$\mathbb {Q}$
. In this appendix, we generalise this to any modular curve. One may anticipate this result from the fact that
![]() $\Gamma (N)$
is
$\Gamma (N)$
is
![]() $\operatorname {GL}_2(\mathbb {Q})$
-conjugate to a subgroup of
$\operatorname {GL}_2(\mathbb {Q})$
-conjugate to a subgroup of
![]() $\Gamma _1(N^2)$
, but the proof requires attention to descent. As a corollary, we show that if A is an isogeny factor of
$\Gamma _1(N^2)$
, but the proof requires attention to descent. As a corollary, we show that if A is an isogeny factor of
![]() $J_H$
with
$J_H$
with
![]() $r_{{\operatorname {an}}}(A) = 0$
, then
$r_{{\operatorname {an}}}(A) = 0$
, then
![]() $r_{\operatorname {\mathrm {alg}}}(A) = 0$
.
$r_{\operatorname {\mathrm {alg}}}(A) = 0$
.
By a curve over a perfect field k in this appendix, we mean a smooth, nonsingular scheme of finite type over k, possibly disconnected, but with all components of dimension
![]() $1$
. Isogenies of abelian varieties are by definition defined over the ground field of the objects, but we will sometimes remind the reader of this convention for clarity.
$1$
. Isogenies of abelian varieties are by definition defined over the ground field of the objects, but we will sometimes remind the reader of this convention for clarity.
Let A be a simple abelian variety over a number field F, and let
![]() $\operatorname {\mathrm {End}}(A)_{\mathbb {Q}}$
be the
$\operatorname {\mathrm {End}}(A)_{\mathbb {Q}}$
be the
![]() $\mathbb {Q}$
-algebra of endomorphisms of A (defined over F). We say A is of
$\mathbb {Q}$
-algebra of endomorphisms of A (defined over F). We say A is of
![]() $\operatorname {GL}_2$
-type if there exists a subfield
$\operatorname {GL}_2$
-type if there exists a subfield
![]() $E \subseteq \operatorname {\mathrm {End}}(A)_{\mathbb {Q}}$
such that
$E \subseteq \operatorname {\mathrm {End}}(A)_{\mathbb {Q}}$
such that
![]() $[E:\mathbb {Q}]=\dim A$
. Evidently, if A is of
$[E:\mathbb {Q}]=\dim A$
. Evidently, if A is of
![]() $\operatorname {GL}_2$
-type over F, then so is
$\operatorname {GL}_2$
-type over F, then so is
![]() $A_K$
for any field extension
$A_K$
for any field extension
![]() $K \supseteq F$
(taking the same subfield E): in fact,
$K \supseteq F$
(taking the same subfield E): in fact,
![]() $A_K$
is isogenous over K to a power of a simple abelian variety of
$A_K$
is isogenous over K to a power of a simple abelian variety of
![]() $\operatorname {GL}_2$
-type over K (called a building block), by Pyle [Reference PylePyl04, Proposition 1.3].
$\operatorname {GL}_2$
-type over K (called a building block), by Pyle [Reference PylePyl04, Proposition 1.3].
Let
![]() $N \in \mathbb {Z}_{\geq 3}$
. Let
$N \in \mathbb {Z}_{\geq 3}$
. Let
![]() $X(N)$
be the modular curve over
$X(N)$
be the modular curve over
![]() $\mathbb {Q}$
attached to the trivial subgroup of
$\mathbb {Q}$
attached to the trivial subgroup of
![]() $\operatorname {GL}_2(N)$
, parametrising generalised elliptic curves with ‘full level N structure’ in the sense of Katz–Mazur [Reference Katz and MazurKM85, 3.1]. (When
$\operatorname {GL}_2(N)$
, parametrising generalised elliptic curves with ‘full level N structure’ in the sense of Katz–Mazur [Reference Katz and MazurKM85, 3.1]. (When
![]() $N=1,2$
, in fact
$N=1,2$
, in fact
![]() $X(N)$
is a stack not a scheme, but its components are of genus
$X(N)$
is a stack not a scheme, but its components are of genus
![]() $0$
and our applications – for example, Proposition A.6 – hold trivially.) Then
$0$
and our applications – for example, Proposition A.6 – hold trivially.) Then
![]() $X(N)$
is connected over
$X(N)$
is connected over
![]() $\mathbb {Q}$
but becomes disconnected over
$\mathbb {Q}$
but becomes disconnected over
![]() $\mathbb {Q}(\zeta _N)$
, with geometrically connected components indexed by
$\mathbb {Q}(\zeta _N)$
, with geometrically connected components indexed by
![]() $\operatorname {\mathrm {Gal}}(\mathbb {Q}(\zeta _N)\,|\,\mathbb {Q}) \simeq (\mathbb {Z}/N\mathbb {Z})^{\times }$
(see also the proof of Lemma A.2). More precisely, the group
$\operatorname {\mathrm {Gal}}(\mathbb {Q}(\zeta _N)\,|\,\mathbb {Q}) \simeq (\mathbb {Z}/N\mathbb {Z})^{\times }$
(see also the proof of Lemma A.2). More precisely, the group
![]() $(\mathbb {Z}/N\mathbb {Z})^{\times }$
acts geometrically by diamond operators, letting
$(\mathbb {Z}/N\mathbb {Z})^{\times }$
acts geometrically by diamond operators, letting
![]() $d \in (\mathbb {Z}/N\mathbb {Z})^{\times }$
act via
$d \in (\mathbb {Z}/N\mathbb {Z})^{\times }$
act via
![]() $\left [\begin {smallmatrix} 1 & 0 \\ 0 & d \end {smallmatrix}\right ]$
, which on moduli problems sends
$\left [\begin {smallmatrix} 1 & 0 \\ 0 & d \end {smallmatrix}\right ]$
, which on moduli problems sends
![]() $[(E,P,Q)] \mapsto [(E,P,dQ)]$
. Each connected component of
$[(E,P,Q)] \mapsto [(E,P,dQ)]$
. Each connected component of
![]() $X(N)_{\mathbb {C}}$
is attached to the congruence subgroup
$X(N)_{\mathbb {C}}$
is attached to the congruence subgroup
![]() $\Gamma (N) \leq \operatorname {SL}_2(\mathbb {Z})$
. Since these diamond automorphisms are defined on the moduli problem, they are defined over
$\Gamma (N) \leq \operatorname {SL}_2(\mathbb {Z})$
. Since these diamond automorphisms are defined on the moduli problem, they are defined over
![]() $\mathbb {Q}$
, giving
$\mathbb {Q}$
, giving
![]() $(\mathbb {Z}/N\mathbb {Z})^{\times } \hookrightarrow \operatorname {\mathrm {Aut}}(X(N))$
.
$(\mathbb {Z}/N\mathbb {Z})^{\times } \hookrightarrow \operatorname {\mathrm {Aut}}(X(N))$
.
Let
![]() $J(N)$
be the Jacobian of
$J(N)$
be the Jacobian of
![]() $X(N)$
. Let
$X(N)$
. Let
![]() $\operatorname {\mathrm {Pic}}^0 X(N)$
be the functor of line bundles whose restriction to each geometric component of
$\operatorname {\mathrm {Pic}}^0 X(N)$
be the functor of line bundles whose restriction to each geometric component of
![]() $X(N)$
has degree
$X(N)$
has degree
![]() $0$
. Although
$0$
. Although
![]() $X(N)$
is geometrically disconnected, the functor
$X(N)$
is geometrically disconnected, the functor
![]() $\operatorname {\mathrm {Pic}}^0 X(N)$
is representable by an abelian variety
$\operatorname {\mathrm {Pic}}^0 X(N)$
is representable by an abelian variety
![]() $J(N)$
over
$J(N)$
over
![]() $\mathbb {Q}$
: see, for example, Kleiman [Reference KleimanKle05, Remark 5.6]. (We note that even though
$\mathbb {Q}$
: see, for example, Kleiman [Reference KleimanKle05, Remark 5.6]. (We note that even though
![]() $X(N)$
does not admit a degree one divisor,
$X(N)$
does not admit a degree one divisor,
![]() $\operatorname {\mathrm {Pic}}^0$
is representable as long as one sheafifies [Reference PoonenPoo17, Warning 5.7.10]). The formation of the Jacobian is functorial, so
$\operatorname {\mathrm {Pic}}^0$
is representable as long as one sheafifies [Reference PoonenPoo17, Warning 5.7.10]). The formation of the Jacobian is functorial, so
![]() $J(N)_{\mathbb {Q}(\zeta _N)}$
is isomorphic over
$J(N)_{\mathbb {Q}(\zeta _N)}$
is isomorphic over
![]() $\mathbb {Q}(\zeta _N)$
to the product of the Jacobians of the geometric connected components of
$\mathbb {Q}(\zeta _N)$
to the product of the Jacobians of the geometric connected components of
![]() $X(N)$
.
$X(N)$
.
Next, let
![]() , where
, where
![]() $H_0 \leq \operatorname {GL}_2({\widehat {\mathbb {Z}}})$
is the preimage of
$H_0 \leq \operatorname {GL}_2({\widehat {\mathbb {Z}}})$
is the preimage of
![]() $\left \{\left [\begin {smallmatrix} * & 0 \\ 0 & 1 \end {smallmatrix}\right ]\right \}\le \operatorname {GL}_2(\mathbb {Z}/N\mathbb {Z})$
. (In Derickx–Sutherland [Reference Derickx and SutherlandDS17, Section 2],
$\left \{\left [\begin {smallmatrix} * & 0 \\ 0 & 1 \end {smallmatrix}\right ]\right \}\le \operatorname {GL}_2(\mathbb {Z}/N\mathbb {Z})$
. (In Derickx–Sutherland [Reference Derickx and SutherlandDS17, Section 2],
![]() $X(N)'$
is denoted
$X(N)'$
is denoted
![]() $X_{0,1}(N,N)$
.) We have
$X_{0,1}(N,N)$
.) We have
![]() $X(N)'=X(N)/H_0(N)$
, and the moduli problem attached to
$X(N)'=X(N)/H_0(N)$
, and the moduli problem attached to
![]() $X(N)'$
has several equivalent descriptions. Directly from the description as a quotient, we see that
$X(N)'$
has several equivalent descriptions. Directly from the description as a quotient, we see that
![]() $X(N)'$
parametrises triples
$X(N)'$
parametrises triples
![]() $(E, \phi , P)$
, where E is a generalised elliptic curve, P is a point of exact order N and
$(E, \phi , P)$
, where E is a generalised elliptic curve, P is a point of exact order N and
![]() $\phi $
is a cyclic N-isogeny such that
$\phi $
is a cyclic N-isogeny such that
![]() $E[N]$
is generated by P and
$E[N]$
is generated by P and
![]() $\ker \phi $
. The curve
$\ker \phi $
. The curve
![]() $X(N)'$
is geometrically connected and attached to the congruence subgroup
$X(N)'$
is geometrically connected and attached to the congruence subgroup
![]() $\Gamma (N) \leq \operatorname {SL}_2(\mathbb {Z})$
. The diamond operators above are defined by the same formula and their image
$\Gamma (N) \leq \operatorname {SL}_2(\mathbb {Z})$
. The diamond operators above are defined by the same formula and their image
![]() $(\mathbb {Z}/N\mathbb {Z})^{\times } \hookrightarrow \operatorname {\mathrm {Aut}}(X(N)')$
gives a subgroup C.
$(\mathbb {Z}/N\mathbb {Z})^{\times } \hookrightarrow \operatorname {\mathrm {Aut}}(X(N)')$
gives a subgroup C.
Remark A.1. See also Poonen–Schaefer–Stoll [Reference Poonen, Schaefer and StollPSS07, Sections 4.1–4.2], who describe
![]() $X(N)'$
(for
$X(N)'$
(for
![]() $N=7$
and away from the cusps) as parametrising isomorphism classes of pairs
$N=7$
and away from the cusps) as parametrising isomorphism classes of pairs
![]() $(E,\psi )$
, where E is a generalised elliptic curve and
$(E,\psi )$
, where E is a generalised elliptic curve and
![]() $\psi \colon \mu _N \times \mathbb {Z}/N\mathbb {Z} \xrightarrow {\sim } E[N]$
is a symplectic isomorphism.
$\psi \colon \mu _N \times \mathbb {Z}/N\mathbb {Z} \xrightarrow {\sim } E[N]$
is a symplectic isomorphism.
Lemma A.2. The curve
![]() $X(N)$
over
$X(N)$
over
![]() $\mathbb {Q}$
is isomorphic to
$\mathbb {Q}$
is isomorphic to
![]() $X(N)^{\prime }_{\mathbb {Q}(\zeta _N)}$
as a curve over
$X(N)^{\prime }_{\mathbb {Q}(\zeta _N)}$
as a curve over
![]() $\mathbb {Q}$
.
$\mathbb {Q}$
.
By as a curve over
![]() $\mathbb {Q}$
, we mean the composition
$\mathbb {Q}$
, we mean the composition
![]() $X(N)^{\prime }_{\mathbb {Q}(\zeta _N)} \to \operatorname {\mathrm {Spec}} \mathbb {Q}(\zeta _N) \to \operatorname {\mathrm {Spec}} \mathbb {Q}$
as structure morphism: that is, the product
$X(N)^{\prime }_{\mathbb {Q}(\zeta _N)} \to \operatorname {\mathrm {Spec}} \mathbb {Q}(\zeta _N) \to \operatorname {\mathrm {Spec}} \mathbb {Q}$
as structure morphism: that is, the product
![]() $X(N)' \times _{\operatorname {\mathrm {Spec}} \mathbb {Q}} \operatorname {\mathrm {Spec}} \mathbb {Q}(\zeta _N)$
viewed as a scheme over
$X(N)' \times _{\operatorname {\mathrm {Spec}} \mathbb {Q}} \operatorname {\mathrm {Spec}} \mathbb {Q}(\zeta _N)$
viewed as a scheme over
![]() $\mathbb {Q}$
.
$\mathbb {Q}$
.
Proof. Let
![]() $Y(N) \subseteq X(N)$
and
$Y(N) \subseteq X(N)$
and
![]() $Y(N)' \subseteq X(N)'$
denote the affine curves obtained by restricting the moduli problem to elliptic curves. In the terminology of Katz–Mazur [Reference Katz and MazurKM85, 5.6], for a point
$Y(N)' \subseteq X(N)'$
denote the affine curves obtained by restricting the moduli problem to elliptic curves. In the terminology of Katz–Mazur [Reference Katz and MazurKM85, 5.6], for a point
![]() $[(E,P,Q)] \in Y(N)(R)$
over a
$[(E,P,Q)] \in Y(N)(R)$
over a
![]() $\mathbb {Q}$
-algebra R, where E is an elliptic curve, we have its determinant
$\mathbb {Q}$
-algebra R, where E is an elliptic curve, we have its determinant
![]() $e_N(P,Q)$
(obtained equivalently by the Weil pairing), an element of
$e_N(P,Q)$
(obtained equivalently by the Weil pairing), an element of
![]() , where
, where
![]() $\Phi _N(x)$
is the Nth cyclotomic polynomial. Refining the natural assignment above, we have a map
$\Phi _N(x)$
is the Nth cyclotomic polynomial. Refining the natural assignment above, we have a map
![]() $[(E,P,Q)] \mapsto [(E,\phi ,P;e_N(P,Q))]$
on points which induces a map
$[(E,P,Q)] \mapsto [(E,\phi ,P;e_N(P,Q))]$
on points which induces a map
![]() $Y(N) \to Y(N)^{\prime }_{\mathbb {Q}[\zeta _N]}$
of nonsingular curves over
$Y(N) \to Y(N)^{\prime }_{\mathbb {Q}[\zeta _N]}$
of nonsingular curves over
![]() $\mathbb {Q}$
. Over any geometric point, this map is bijective, so as a map of nonsingular curves it is an isomorphism. Thus we obtain a (unique) map
$\mathbb {Q}$
. Over any geometric point, this map is bijective, so as a map of nonsingular curves it is an isomorphism. Thus we obtain a (unique) map
![]() $X(N) \to X(N)^{\prime }_{\mathbb {Q}(\zeta _N)}$
of projective, nonsingular curves over
$X(N) \to X(N)^{\prime }_{\mathbb {Q}(\zeta _N)}$
of projective, nonsingular curves over
![]() $\mathbb {Q}$
.
$\mathbb {Q}$
.
For a Dirichlet character
![]() $\chi \colon (\mathbb {Z}/N\mathbb {Z})^{\times } \to \mathbb {C}^{\times }$
of modulus N, let
$\chi \colon (\mathbb {Z}/N\mathbb {Z})^{\times } \to \mathbb {C}^{\times }$
of modulus N, let
![]() $X(N)^{\prime }_{\chi }$
be the twist of
$X(N)^{\prime }_{\chi }$
be the twist of
![]() $X(N)'$
attached to
$X(N)'$
attached to
![]() $\chi $
(with respect to
$\chi $
(with respect to
![]() $C \leq \operatorname {\mathrm {Aut}}(X(N)')$
) and let
$C \leq \operatorname {\mathrm {Aut}}(X(N)')$
) and let
![]() $J(N)^{\prime }_{\chi }$
be its Jacobian. For a precise description of this twisting operation; see Kida [Reference KidaKid95, Section 2].
$J(N)^{\prime }_{\chi }$
be its Jacobian. For a precise description of this twisting operation; see Kida [Reference KidaKid95, Section 2].
Corollary A.3. Up to isogeny over
![]() $\mathbb {Q}$
, we have
$\mathbb {Q}$
, we have
where
![]() $\operatorname {\mathrm {Res}}_{\mathbb {Q}(\zeta _N)|\mathbb {Q}}$
is a restriction of scalars and
$\operatorname {\mathrm {Res}}_{\mathbb {Q}(\zeta _N)|\mathbb {Q}}$
is a restriction of scalars and
![]() $\chi $
ranges over Dirichlet characters of modulus N.
$\chi $
ranges over Dirichlet characters of modulus N.
Proof. By the universal property of the restriction of scalars, the Jacobian of
![]() $X(N)^{\prime }_{\mathbb {Q}(\zeta _N)}$
as a curve over
$X(N)^{\prime }_{\mathbb {Q}(\zeta _N)}$
as a curve over
![]() $\mathbb {Q}$
is the restriction of scalars
$\mathbb {Q}$
is the restriction of scalars
![]() $\operatorname {\mathrm {Res}}_{\mathbb {Q}(\zeta _N)|\mathbb {Q}}(J(N)')$
, a line bundle on
$\operatorname {\mathrm {Res}}_{\mathbb {Q}(\zeta _N)|\mathbb {Q}}(J(N)')$
, a line bundle on
![]() $X(N)^{\prime }_{\mathbb {Q}(\zeta _N)}$
as a curve over
$X(N)^{\prime }_{\mathbb {Q}(\zeta _N)}$
as a curve over
![]() $\mathbb {Q}$
is just a line bundle on
$\mathbb {Q}$
is just a line bundle on
![]() $X(N)^{\prime }_{\mathbb {Q}(\zeta _N)}$
, so the first isogeny follows from Lemma A.2. The second isogeny follows from a result of Kida [Reference KidaKid95, Theorem, p. 53].
$X(N)^{\prime }_{\mathbb {Q}(\zeta _N)}$
, so the first isogeny follows from Lemma A.2. The second isogeny follows from a result of Kida [Reference KidaKid95, Theorem, p. 53].
Let
, and let

To prove our main result, we study the effect of conjugating H-level structures by
![]() $\varpi $
, when this is defined. Conjugation by
$\varpi $
, when this is defined. Conjugation by
![]() $\varpi $
in
$\varpi $
in
![]() $\operatorname {GL}_2({\widehat {\mathbb {Q}}})$
is given by the formula
$\operatorname {GL}_2({\widehat {\mathbb {Q}}})$
is given by the formula
 $$\begin{align*}\varpi \begin{bmatrix} a & b \\ c & d \end{bmatrix} \varpi^{-1} = \begin{bmatrix} d & N^{-1}c \\ Nb & a \end{bmatrix}. \end{align*}$$
$$\begin{align*}\varpi \begin{bmatrix} a & b \\ c & d \end{bmatrix} \varpi^{-1} = \begin{bmatrix} d & N^{-1}c \\ Nb & a \end{bmatrix}. \end{align*}$$
Let
![]() $H \leq \operatorname {GL}_2({\widehat {\mathbb {Z}}})$
be an open subgroup, and suppose that its reduction
$H \leq \operatorname {GL}_2({\widehat {\mathbb {Z}}})$
be an open subgroup, and suppose that its reduction
![]() $H(N) \in \operatorname {GL}_2(\mathbb {Z}/N\mathbb {Z})$
is contained in the Borel subgroup
$H(N) \in \operatorname {GL}_2(\mathbb {Z}/N\mathbb {Z})$
is contained in the Borel subgroup
![]() $B(N)$
of upper-triangular matrices. Then the level of H is divisible by N. We define
$B(N)$
of upper-triangular matrices. Then the level of H is divisible by N. We define
The group
![]() $H^{\varpi }$
is again an open subgroup. If H has level
$H^{\varpi }$
is again an open subgroup. If H has level
![]() $MN$
, then visibly
$MN$
, then visibly
![]() $H^{\varpi }$
has level dividing
$H^{\varpi }$
has level dividing
![]() $MN^2$
, and this bound is in general sharp: for example, if H is the level N preimage of
$MN^2$
, and this bound is in general sharp: for example, if H is the level N preimage of
![]() $\left \{\left [\begin {smallmatrix} * & 0 \\ 0 & * \end {smallmatrix}\right ]\right \} \leq \operatorname {GL}_2(\mathbb {Z}/N\mathbb {Z})$
, then
$\left \{\left [\begin {smallmatrix} * & 0 \\ 0 & * \end {smallmatrix}\right ]\right \} \leq \operatorname {GL}_2(\mathbb {Z}/N\mathbb {Z})$
, then
![]() $H^{\varpi }=\{\left [\begin {smallmatrix} * & * \\ 0 & * \end {smallmatrix}\right ]\} \leq \operatorname {GL}_2(\mathbb {Z}/N^2\mathbb {Z})$
, which has level
$H^{\varpi }=\{\left [\begin {smallmatrix} * & * \\ 0 & * \end {smallmatrix}\right ]\} \leq \operatorname {GL}_2(\mathbb {Z}/N^2\mathbb {Z})$
, which has level
![]() $N^2$
.
$N^2$
.
Lemma A.4. Suppose that
![]() $H(N) \leq B(N)$
. Then the modular curves
$H(N) \leq B(N)$
. Then the modular curves
![]() $X_H$
and
$X_H$
and
![]() $X_{H^{\varpi }}$
are isomorphic over
$X_{H^{\varpi }}$
are isomorphic over
![]() $\mathbb {Q}$
.
$\mathbb {Q}$
.
Proof. We apply a result of Deligne–Rapoport [Reference Deligne and RapoportDR73, Propositions IV-3.16 and IV-3.19] with
![]() $K=H$
and
$K=H$
and
![]() $g=\varpi $
: the isomorphism provided is defined on the (open) moduli problem and extends to an isomorphism of curves over
$g=\varpi $
: the isomorphism provided is defined on the (open) moduli problem and extends to an isomorphism of curves over
![]() $\mathbb {Q}$
.
$\mathbb {Q}$
.
The preceding lemma explains in many cases why modular curves are in fact isomorphic over
![]() $\mathbb {Q}$
(even though they may look like twists!). The following example illustrates how conjugation by
$\mathbb {Q}$
(even though they may look like twists!). The following example illustrates how conjugation by
![]() $\varpi $
transforms one moduli problem into an isomorphic moduli problem (over
$\varpi $
transforms one moduli problem into an isomorphic moduli problem (over
![]() $\mathbb {Q}$
).
$\mathbb {Q}$
).
Example A.5. Let
Then
![]() $\Gamma _{H_1} = \Gamma _1(N)$
(following the conventions in Section 2.2), and the points of
$\Gamma _{H_1} = \Gamma _1(N)$
(following the conventions in Section 2.2), and the points of
![]() $X_{H_1}$
are given by classes
$X_{H_1}$
are given by classes
![]() $[(E,P)]$
, where E is a generalised elliptic curve and
$[(E,P)]$
, where E is a generalised elliptic curve and
![]() $P \in E[N]$
is a point of order N.
$P \in E[N]$
is a point of order N.
We compute that
![]() $H_1^{\varpi } = \{\left [\begin {smallmatrix} * & * \\ 0 & 1 \end {smallmatrix}\right ]\} \leq \operatorname {GL}_2(\mathbb {Z}/N\mathbb {Z})$
has level N. (Swapping basis vectors transforms
$H_1^{\varpi } = \{\left [\begin {smallmatrix} * & * \\ 0 & 1 \end {smallmatrix}\right ]\} \leq \operatorname {GL}_2(\mathbb {Z}/N\mathbb {Z})$
has level N. (Swapping basis vectors transforms
![]() $H_1^{\varpi }$
to the transpose
$H_1^{\varpi }$
to the transpose
![]() $H_1^T = \{\left [\begin {smallmatrix} 1 & 0 \\ * & * \end {smallmatrix}\right ]\} \leq \operatorname {GL}_2(\mathbb {Z}/N\mathbb {Z})$
.) The points of
$H_1^T = \{\left [\begin {smallmatrix} 1 & 0 \\ * & * \end {smallmatrix}\right ]\} \leq \operatorname {GL}_2(\mathbb {Z}/N\mathbb {Z})$
.) The points of
![]() $X_{H_1^T}$
are classes
$X_{H_1^T}$
are classes
![]() $[(E,\upsilon )]$
, where E is a generalised elliptic curve and
$[(E,\upsilon )]$
, where E is a generalised elliptic curve and
![]() $\upsilon \colon \mu _N \hookrightarrow E[N]$
is an inclusion. We have
$\upsilon \colon \mu _N \hookrightarrow E[N]$
is an inclusion. We have
![]() $\Gamma _{H_1^{\varpi }}=\Gamma ^1(N)$
(conjugate to
$\Gamma _{H_1^{\varpi }}=\Gamma ^1(N)$
(conjugate to
![]() $\Gamma _1(N)$
in
$\Gamma _1(N)$
in
![]() $\operatorname {SL}_2(\mathbb {Z})$
), but of course the moduli interpretation is different for the two cases.
$\operatorname {SL}_2(\mathbb {Z})$
), but of course the moduli interpretation is different for the two cases.
Lemma A.4 shows that in fact we have an isomorphism
![]() $X_{H_1} \xrightarrow {\sim } X_{H_1^{\varpi }}$
defined over
$X_{H_1} \xrightarrow {\sim } X_{H_1^{\varpi }}$
defined over
![]() $\mathbb {Q}$
. In terms of the moduli problems above, this isomorphism is defined as follows: the point
$\mathbb {Q}$
. In terms of the moduli problems above, this isomorphism is defined as follows: the point
![]() $[(E,\upsilon )]$
over a base ring R maps to the pair
$[(E,\upsilon )]$
over a base ring R maps to the pair
![]() $[(E',Q')]$
over R, where
$[(E',Q')]$
over R, where
![]() and
and
![]() $Q' \in E'[N]$
is the image of any point
$Q' \in E'[N]$
is the image of any point
![]() $Q \in E[N]$
such that
$Q \in E[N]$
such that
![]() $e_N(\upsilon (\zeta _N), Q) = \zeta _N$
under the Weil pairing
$e_N(\upsilon (\zeta _N), Q) = \zeta _N$
under the Weil pairing
![]() $e_N$
. This isomorphism was observed by Poonen–Schaefer–Stoll [Reference Poonen, Schaefer and StollPSS07, Remark 5.1] in the case
$e_N$
. This isomorphism was observed by Poonen–Schaefer–Stoll [Reference Poonen, Schaefer and StollPSS07, Remark 5.1] in the case
![]() $N=7$
, where they write
$N=7$
, where they write
![]() $X_{\mu }(N)$
for
$X_{\mu }(N)$
for
![]() $X_{H_1^T}$
.
$X_{H_1^T}$
.
With this setup, we can prove our first main result.
Proposition A.6. For all Dirichlet characters
![]() $\chi $
, every simple isogeny factor of
$\chi $
, every simple isogeny factor of
![]() $J(N)^{\prime }_{\chi }$
over
$J(N)^{\prime }_{\chi }$
over
![]() $\mathbb {Q}$
is an isogeny factor of
$\mathbb {Q}$
is an isogeny factor of
![]() $J_1(N^2)$
and of
$J_1(N^2)$
and of
![]() $\operatorname {GL}_2$
-type over
$\operatorname {GL}_2$
-type over
![]() $\mathbb {Q}$
. More precisely, each such factor is isogenous to a modular abelian variety of the form
$\mathbb {Q}$
. More precisely, each such factor is isogenous to a modular abelian variety of the form
![]() $A_f$
, where f is a Galois orbit of newforms of level dividing
$A_f$
, where f is a Galois orbit of newforms of level dividing
![]() $N^2$
and conductor of modulus N.
$N^2$
and conductor of modulus N.
Proof. Let

Then
![]() $\Gamma _H = \Gamma _0(N^2) \cap \Gamma _1(N)$
; in particular, there is a natural surjective map
$\Gamma _H = \Gamma _0(N^2) \cap \Gamma _1(N)$
; in particular, there is a natural surjective map
![]() $X_1(N^2) \to X_H$
.
$X_1(N^2) \to X_H$
.
By Lemma A.4, we have an isomorphism of modular curves
![]() $X_H \xrightarrow {\sim } X_{H^{\varpi }}$
. We compute directly that
$X_H \xrightarrow {\sim } X_{H^{\varpi }}$
. We compute directly that
![]() $H^{\varpi }=H_0$
is the preimage of
$H^{\varpi }=H_0$
is the preimage of
![]() $\{\left [\begin {smallmatrix} * & 0 \\ 0 & 1 \end {smallmatrix}\right ]\}\le \operatorname {GL}_2(\mathbb {Z}/N\mathbb {Z})$
, so
$\{\left [\begin {smallmatrix} * & 0 \\ 0 & 1 \end {smallmatrix}\right ]\}\le \operatorname {GL}_2(\mathbb {Z}/N\mathbb {Z})$
, so
![]() $X_{H^{\varpi }}=X(N)'$
.
$X_{H^{\varpi }}=X(N)'$
.
Ribet [Reference RibetRib04, Section 3] observed that every isogeny factor of
![]() $J_1(N^2)$
is of
$J_1(N^2)$
is of
![]() $\operatorname {GL}_2$
-type over
$\operatorname {GL}_2$
-type over
![]() $\mathbb {Q}$
: more precisely, we have a decomposition
$\mathbb {Q}$
: more precisely, we have a decomposition
![]() $J_1(N^2)$
into a product of simple abelian varieties
$J_1(N^2)$
into a product of simple abelian varieties
![]() $A_f$
over
$A_f$
over
![]() $\mathbb {Q}$
, possibly with multiplicity, where f is a Galois orbit of newforms of level dividing
$\mathbb {Q}$
, possibly with multiplicity, where f is a Galois orbit of newforms of level dividing
![]() $N^2$
. In fact, the natural quotient map
$N^2$
. In fact, the natural quotient map
![]() $X_1(N^2) \to X_H$
is defined by the subgroup of the diamond operators
$X_1(N^2) \to X_H$
is defined by the subgroup of the diamond operators
![]() $\{\langle d\rangle :d \in (\mathbb {Z}/N^2\mathbb {Z})^{\times } \text { with } d\equiv 1\bmod N\}$
, so the cusp forms on
$\{\langle d\rangle :d \in (\mathbb {Z}/N^2\mathbb {Z})^{\times } \text { with } d\equiv 1\bmod N\}$
, so the cusp forms on
![]() $X_H$
are precisely those with conductor dividing N (so of modulus N). Finally, the isomorphism
$X_H$
are precisely those with conductor dividing N (so of modulus N). Finally, the isomorphism
![]() $X_H \xrightarrow {\sim } X(N)'$
over
$X_H \xrightarrow {\sim } X(N)'$
over
![]() $\mathbb {Q}$
transports Ribet’s observation to the Jacobian
$\mathbb {Q}$
transports Ribet’s observation to the Jacobian
![]() $J(N)'$
, as claimed.
$J(N)'$
, as claimed.
To finish, we consider the twist: from the decomposition in the previous paragraph,
 $$\begin{align*}J(N)^{\prime}_{\chi} \sim \prod_f A_{f \otimes \chi}^{e_f}, \end{align*}$$
$$\begin{align*}J(N)^{\prime}_{\chi} \sim \prod_f A_{f \otimes \chi}^{e_f}, \end{align*}$$
where
![]() $f \otimes \chi $
is the twist of f by the character
$f \otimes \chi $
is the twist of f by the character
![]() $\chi $
. Let
$\chi $
. Let
![]() $\psi $
be the character of f, of modulus N and conductor
$\psi $
be the character of f, of modulus N and conductor
![]() $\operatorname {\mathrm {cond}}(\psi )$
. By Shimura [Reference ShimuraShi94, Proposition 3.64], the level of
$\operatorname {\mathrm {cond}}(\psi )$
. By Shimura [Reference ShimuraShi94, Proposition 3.64], the level of
![]() $f \otimes \chi $
divides
$f \otimes \chi $
divides
and moreover,
![]() $f \otimes \chi $
has character
$f \otimes \chi $
has character
![]() $\psi \chi ^2$
still of modulus N. Thus
$\psi \chi ^2$
still of modulus N. Thus
![]() $A_{f \otimes \chi }$
is an isogeny factor over
$A_{f \otimes \chi }$
is an isogeny factor over
![]() $\mathbb {Q}$
of
$\mathbb {Q}$
of
![]() $J_1(N^2)$
, and the result follows as in the previous case.
$J_1(N^2)$
, and the result follows as in the previous case.
Theorem A.7. Let
![]() $H \leq \operatorname {GL}_2({\widehat {\mathbb {Z}}})$
be an open subgroup of level N, let
$H \leq \operatorname {GL}_2({\widehat {\mathbb {Z}}})$
be an open subgroup of level N, let
![]() $X_H$
be the modular curve attached to H, and let
$X_H$
be the modular curve attached to H, and let
![]() $J_H$
be its Jacobian. Then each simple factor of
$J_H$
be its Jacobian. Then each simple factor of
![]() $J_H$
is isogenous to a simple factor of
$J_H$
is isogenous to a simple factor of
![]() $J_1(N^2)$
. In particular, every simple factor of
$J_1(N^2)$
. In particular, every simple factor of
![]() $J_H$
is of
$J_H$
is of
![]() $\operatorname {GL}_2$
-type.
$\operatorname {GL}_2$
-type.
Proof. Let A be a simple factor of
![]() $J_H$
. We have a map
$J_H$
. We have a map
![]() $X(N) \to X_H$
, realising
$X(N) \to X_H$
, realising
![]() $J_H$
as an isogeny factor of
$J_H$
as an isogeny factor of
![]() $J(N)$
, so A is a simple isogeny factor of
$J(N)$
, so A is a simple isogeny factor of
![]() $J(N)$
. Corollary A.3 implies that A is a simple isogeny factor of
$J(N)$
. Corollary A.3 implies that A is a simple isogeny factor of
![]() $J(N)^{\prime }_{\chi }$
for some Dirichlet character
$J(N)^{\prime }_{\chi }$
for some Dirichlet character
![]() $\chi $
. By Proposition A.6, every simple factor of
$\chi $
. By Proposition A.6, every simple factor of
![]() $J(N)^{\prime }_{\chi }$
is an isogeny factor of
$J(N)^{\prime }_{\chi }$
is an isogeny factor of
![]() $J_1(N^2)$
, hence of
$J_1(N^2)$
, hence of
![]() $\operatorname {GL}_2$
-type.
$\operatorname {GL}_2$
-type.
Corollary A.8. Let A be an isogeny factor of
![]() $J_H$
of analytic rank
$J_H$
of analytic rank
![]() $0$
. Then
$0$
. Then
![]() $A(\mathbb {Q})$
is finite.
$A(\mathbb {Q})$
is finite.
Proof. Apply Kato [Reference KatoKat04, Corollary 14.3].
Remark A.9. Assaf [Reference AssafAss21] has given a method for computing Hecke operators on arbitrary congruence subgroups. According to Theorem A.7, the Galois orbits of cusp forms appearing can be matched with classical modular forms according to the corresponding system of Hecke eigenvalues (forms with level dividing
![]() $N^2$
and character of modulus N), thereby explicitly providing the isotypic decomposition of
$N^2$
and character of modulus N), thereby explicitly providing the isotypic decomposition of
![]() $J_H$
up to isogeny over
$J_H$
up to isogeny over
![]() $\mathbb {Q}$
.
$\mathbb {Q}$
.
This method is indeed sensitive to the group H! For example, the groups 16.24.1.6, 16.24.1.7, 16.24.1.8 (numbered
![]() $163$
,
$163$
,
![]() $162$
,
$162$
,
![]() $164$
by Rouse–Zureick-Brown [Reference Rouse and Zureick-BrownRZB15]) have the same intersection with
$164$
by Rouse–Zureick-Brown [Reference Rouse and Zureick-BrownRZB15]) have the same intersection with
![]() $\operatorname {SL}_2(\mathbb {Z}/16\mathbb {Z})$
, with Cummins-Pauli label
$\operatorname {SL}_2(\mathbb {Z}/16\mathbb {Z})$
, with Cummins-Pauli label
![]() $\mathrm {16D}^1$
, as can be seen in Table 17; but the associated modular Jacobians are nonisogenous elliptic curves 128.c2, 128.b2, 128.d2 with j-invariant 128 (so isomorphic over
$\mathrm {16D}^1$
, as can be seen in Table 17; but the associated modular Jacobians are nonisogenous elliptic curves 128.c2, 128.b2, 128.d2 with j-invariant 128 (so isomorphic over
![]() $\mathbb {C}$
but not even isogenous over
$\mathbb {C}$
but not even isogenous over
![]() $\mathbb {Q}$
).
$\mathbb {Q}$
).
Remark A.10. The same proof works for an arbitrary (possibly geometrically disconnected) Jacobian of a Shimura curve attached to a quaternion algebra over a totally real field with a unique real split place. The step that generalises Ribet’s observation (there are Hecke operators and degeneracy operators) is given by Hida [Reference HidaHid81, Proposition 4.8].
Acknowledgements
The authors would like to thank Asher Auel and Bjorn Poonen for helpful conversations. Voight was supported by a Simons Collaboration Grant (550029).
Appendix B. Tables
The tables that follow provide data for various subgroups H of
![]() $\ell $
-power level that include:
$\ell $
-power level that include:
-
○ the label
 $\texttt {N.i.g.n}$
of H as defined in Section 2.4;
$\texttt {N.i.g.n}$
of H as defined in Section 2.4; -
○ a list of generators for H in
 $\operatorname {GL}_2(N)$
(which we believe is minimal);
$\operatorname {GL}_2(N)$
(which we believe is minimal); -
○ for
 $g(H)\le 24$
, the label of
$g(H)\le 24$
, the label of
 $H\cap \operatorname {SL}_2(\mathbb {Z})$
assigned by Cummins and Pauli [Reference Cummins and PauliCP03, Reference Campagna and PengoCP];
$H\cap \operatorname {SL}_2(\mathbb {Z})$
assigned by Cummins and Pauli [Reference Cummins and PauliCP03, Reference Campagna and PengoCP]; -
○ the number of cusps
 $\#X_H^{\infty }({\overline {\mathbb {Q}}})$
and rational cusps
$\#X_H^{\infty }({\overline {\mathbb {Q}}})$
and rational cusps
 $\#X_H^{\infty }(\mathbb {Q})$
, as described in Section 2;
$\#X_H^{\infty }(\mathbb {Q})$
, as described in Section 2; -
○ the analytic rank r of
 $J_H:=\operatorname {\mathrm {Jac}}(X_H)$
, whose computation is described in Section 6;
$J_H:=\operatorname {\mathrm {Jac}}(X_H)$
, whose computation is described in Section 6; -
○ the genus g of
 $X_H$
;
$X_H$
; -
○ the dimensions and LMFDB labels of the Galois orbits of newforms
 $[f]$
whose modular abelian varieties
$[f]$
whose modular abelian varieties
 $A_f$
are isogeny factors of
$A_f$
are isogeny factors of
 $J_H$
(exponents denote multiplicities).
$J_H$
(exponents denote multiplicities).
Table 11 Subgroups H of
![]() $\ell $
-power level that have rational noncuspidal non-CM points but do not arise as
$\ell $
-power level that have rational noncuspidal non-CM points but do not arise as
![]() $\rho _{E,\ell ^{\infty }}(G_{\mathbb {Q}})$
for any non-CM elliptic curve
$\rho _{E,\ell ^{\infty }}(G_{\mathbb {Q}})$
for any non-CM elliptic curve
![]() $E/\mathbb {Q}$
(the noncuspidal non-CM points in
$E/\mathbb {Q}$
(the noncuspidal non-CM points in
![]() $X_H(\mathbb {Q})$
all correspond to elliptic curves
$X_H(\mathbb {Q})$
all correspond to elliptic curves
![]() $E/\mathbb {Q}$
with
$E/\mathbb {Q}$
with
![]() $\rho _{E,\ell ^{\infty }}(\mathbb {Q})$
properly contained in H).
$\rho _{E,\ell ^{\infty }}(\mathbb {Q})$
properly contained in H).

Table 12 Arithmetically maximal subgroups of
![]() $3$
-power level.
$3$
-power level.

Table 13 Arithmetically maximal subgroups of
![]() $5$
-power level.
$5$
-power level.

Table 14 Arithmetically maximal subgroups of
![]() $\ell $
-power level for
$\ell $
-power level for
![]() $\ell =7,11$
.
$\ell =7,11$
.

Table 15 Arithmetically maximal subgroups of
![]() $\ell $
-power level for
$\ell $
-power level for
![]() $\ell =13,17,19$
.
$\ell =13,17,19$
.

Table 16 Arithmetically maximal subgroups of
![]() $\ell $
-power level for
$\ell $
-power level for
![]() $\ell =23,29,31,37$
.
$\ell =23,29,31,37$
.

Table 17 Arithmetically maximal subgroups of
![]() $2$
-power level.
$2$
-power level.

Table 18 Twists H of
![]() ${\mathcal N}_{\mathcal O}(16)$
for
${\mathcal N}_{\mathcal O}(16)$
for
![]() ${\mathcal O}=\mathbb {Z}[i],\mathbb {Z}[\zeta _3]$
and
${\mathcal O}=\mathbb {Z}[i],\mathbb {Z}[\zeta _3]$
and
![]() $E/\mathbb {Q}$
with potential CM by
$E/\mathbb {Q}$
with potential CM by
![]() ${\mathcal O}$
and
${\mathcal O}$
and
![]() $\rho _{E,2^{\infty }}(G_{\mathbb {Q}})=H$
.
$\rho _{E,2^{\infty }}(G_{\mathbb {Q}})=H$
.

Table 19 Twists H of
![]() ${\mathcal N}_{\mathcal O}(27)$
for
${\mathcal N}_{\mathcal O}(27)$
for
![]() ${\mathcal O}=\mathbb {Z}[\zeta _3]$
and
${\mathcal O}=\mathbb {Z}[\zeta _3]$
and
![]() $E/\mathbb {Q}$
with potential CM by
$E/\mathbb {Q}$
with potential CM by
![]() ${\mathcal O}$
and
${\mathcal O}$
and
![]() $\rho _{E,3^{\infty }}(G_{\mathbb {Q}})=H$
.
$\rho _{E,3^{\infty }}(G_{\mathbb {Q}})=H$
.

Table 20 Subgroups
![]() ${\mathcal N}_{\mathcal O}(16)$
of determinant index 1 that arise for imaginary quadratic orders
${\mathcal N}_{\mathcal O}(16)$
of determinant index 1 that arise for imaginary quadratic orders
![]() ${\mathcal O}$
of discriminant D and their quadratic twists (noted by asterisks), along with elliptic curves that realise them, identified by LMFDB label or an element
${\mathcal O}$
of discriminant D and their quadratic twists (noted by asterisks), along with elliptic curves that realise them, identified by LMFDB label or an element
![]() $a\in \mathbb {Q}(j(E))$
to twist by, where
$a\in \mathbb {Q}(j(E))$
to twist by, where
![]() $a^4-2a^3-13a^2+14a+19=0$
.
$a^4-2a^3-13a^2+14a+19=0$
.

Table 21 Subgroups
![]() ${\mathcal N}_{\mathcal O}(16)$
of determinant index
${\mathcal N}_{\mathcal O}(16)$
of determinant index
![]() $i>1$
for imaginary quadratic orders
$i>1$
for imaginary quadratic orders
![]() ${\mathcal O}$
of discriminant D and their quadratic twists (noted by asterisks), along with elliptic curves that realise them, identified by LMFDB label except for the curve
${\mathcal O}$
of discriminant D and their quadratic twists (noted by asterisks), along with elliptic curves that realise them, identified by LMFDB label except for the curve
![]() $E_1:y^2 + axy + y = x^3 + \frac {a^2}{2}x^2 + \frac {48a^3 + 45a^2 - 250a - 246}{2}x + (144a^3 + 121a^2 - 752a - 638),$
where
$E_1:y^2 + axy + y = x^3 + \frac {a^2}{2}x^2 + \frac {48a^3 + 45a^2 - 250a - 246}{2}x + (144a^3 + 121a^2 - 752a - 638),$
where
![]() $a^4-6a^2+4=0$
.
$a^4-6a^2+4=0$
.

Table 22 Subgroups
![]() ${\mathcal N}_{\mathcal O}(27)$
that arise for imaginary quadratic orders
${\mathcal N}_{\mathcal O}(27)$
that arise for imaginary quadratic orders
![]() ${\mathcal O}$
of discriminant D and their quadratic twists (noted by asterisks), along with elliptic curves that realise them, identified by LMFDB label.
${\mathcal O}$
of discriminant D and their quadratic twists (noted by asterisks), along with elliptic curves that realise them, identified by LMFDB label.

Conflicts of Interest
None.
Financial support
Sutherland was supported by NSF grant DMS-1522526 and Simons Foundation grant 550033; Zureick-Brown was supported by NSF grant DMS-1555048; Voight was supported by Simons Foundation grant 550029.