Hostname: page-component-8448b6f56d-c4f8m Total loading time: 0 Render date: 2024-04-24T08:13:12.622Z Has data issue: false hasContentIssue false
  • English
  • Français

INFORMATION IN PROPOSITIONAL PROOFS AND ALGORITHMIC PROOF SEARCH

Part of: Theory of computing Proof theory and constructive mathematics

Published online by Cambridge University Press:  27 September 2021

JAN KRAJÍČEK Open the ORCID record for JAN KRAJÍČEK [Opens in a new window]
JAN KRAJÍČEK*
Affiliation:
FACULTY OF MATHEMATICS AND PHYSICS CHARLES UNIVERSITY SOKOLOVSKÁ 83, PRAGUE 186 75, THE CZECH REPUBLICE-mail:krajicek@karlin.mff.cuni.cz
Get access Rights & Permissions [Opens in a new window]

Abstract

We study from the proof complexity perspective the (informal) proof search problem (cf. [17, Sections 1.5 and 21.5]):

  • • Is there an optimal way to search for propositional proofs?

We note that, as a consequence of Levin’s universal search, for any fixed proof system there exists a time-optimal proof search algorithm. Using classical proof complexity results about reflection principles we prove that a time-optimal proof search algorithm exists without restricting proof systems iff a p-optimal proof system exists.

To characterize precisely the time proof search algorithms need for individual formulas we introduce a new proof complexity measure based on algorithmic information concepts. In particular, to a proof system P we attach information-efficiency function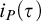 $i_P(\tau )$ assigning to a tautology a natural number, and we show that:

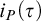  • • $i_P(\tau )$ characterizes time any P-proof search algorithm has to use on 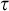$\tau $ ,

  • • for a fixed P there is such an information-optimal algorithm (informally: it finds proofs of minimal information content),

  • • a proof system is information-efficiency optimal (its information-efficiency function is minimal up to a multiplicative constant) iff it is p-optimal,

  • • for non-automatizable systems P there are formulas $\tau $ with short proofs but having large information measure 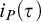$i_P(\tau )$ .

We isolate and motivate the problem to establish unconditional super-logarithmic lower bounds for 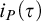$i_P(\tau )$ where no super-polynomial size lower bounds are known. We also point out connections of the new measure with some topics in proof complexity other than proof search.

Keywords

propositional proof systemsalgorithmic informationproof search

MSC classification

Primary: 03F20: Complexity of proofs
Secondary: 68Q30: Algorithmic information theory (Kolmogorov complexity, etc.)
Type
Article
Information
The Journal of Symbolic Logic , Volume 87 , Issue 2 , June 2022 , pp. 852 - 869
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Atserias, A. and Müller, M., Automating resolution is NP-hard . Journal of the ACM , vol. 67 (2020), no. 5, Article no. 31.CrossRefGoogle Scholar
Bonet, M. L., Pitassi, T. and Raz, R., On interpolation and automatization for Frege proof systems . SIAM Journal of Computing , vol. 29 (2000), no. 6, pp. 1939–1967.CrossRefGoogle Scholar
Buss, S. R. and Nordström, J., Proof complexity and SAT solving , Handbook of Satisfiability , second ed. (A. Biere, M. Heule, H. van Maaren and T. Walsh, editors), IOS Press, Amsterdam, 2021, pp. 233–350.Google Scholar
Chaitin, G. J., Information-theoretic limitations of formal systems . Journal of the ACM , vol. 21 (1974), pp. 403–424.10.1145/321832.321839CrossRefGoogle Scholar
Cook, S. A., Feasibly constructive proofs and the propositional calculus , Proceedings of the Seventh Annual ACM Symposium on Theory of Computing (STOC) (W. C. Rounds, N. Martin, J. W. Carlyle, and M. A. Harrison, editors), ACM Press, New York, 1975, pp. 83–97.CrossRefGoogle Scholar
Cook, S. A. and Krajíček, J., Consequences of the provability of NP ⊂ P/poly, this Journal, vol. 72 (2007), no. 4, pp. 1353–1371.Google Scholar
Cook, S. A. and Reckhow, R. A., The relative efficiency of propositional proof systems, this Journal, vol. 44 (1979), no. 1, pp. 36–50.Google Scholar
Feige, U., Kim, J. H. and Ofek, E., Witnesses for nonsatisfiability of dense random 3 CNF formulas. Proceedings of the IEEE 47th Annual Symposium on Foundations of Computer Science (FOCS) , IEEE, Washington, DC, 2006, pp. 497–508.CrossRefGoogle Scholar
Haken, A., The intractability of resolution . Theoretical Computer Science , vol. 39 (1985), pp. 297–308.CrossRefGoogle Scholar
Kolmogorov, A. N., Three approaches to the quantitative definition of information . Problems of Information Transmission , vol. 1 (1965), no. 1, pp. 1–7.Google Scholar
Kolmogorov, A. N., Logical basis for information theory and probability theory . IEEE Transactions on Information Theory , vol. 14 (1968), no. 5, pp. 662–664.CrossRefGoogle Scholar
Krajíček, J., Dual weak pigeonhole principle, pseudo-surjective functions, and provability of circuit lower bounds, this Journal, vol. 69 (2004), no. 1, pp. 265–286.Google Scholar
Krajíček, J., Implicit proofs, this Journal, vol. 69 (2004), no. 2, pp. 387–397.Google Scholar
Krajíček, J., Diagonalization in proof complexity . Fundamenta Mathematicae , vol. 182 (2004), pp. 181–192.CrossRefGoogle Scholar
Krajíček, J., Forcing with Random Variables and Proof Complexity , London Mathematical Society Lecture Note Series, vol. 382, Cambridge University Press, Cambridge, 2011.Google Scholar
Krajíček, J., A note on SAT algorithms and proof complexity . Information Processing Letters , vol. 112 (2012), pp. 490–493.CrossRefGoogle Scholar
Krajíček, J., Proof Complexity , Encyclopedia of Mathematics and Its Applications, vol. 170, Cambridge University Press, Cambridge, 2019.CrossRefGoogle Scholar
Krajíček, J., Proof search problem (ext. abstract), Mathematical Logic: Proof Theory, Constructive Mathematics (9–13 November 2020) , Oberwolfach Reports, Report No. 34/2020, 2020, pp. 45–46. Available at https://www.karlin.mff.cuni.cz/~krajicek/mfo2020.pdf.Google Scholar
Krajíček, J. and Pudlák, P., Propositional proof systems, the consistency of first-order theories and the complexity of computations, this Journal, vol. 54 (1989), no. 3, pp. 1063–1079.Google Scholar
Krajíček, J. and Pudlák, P., Some consequences of cryptographical conjectures for $\ {S}_2^1\ {}$ and EF . Information and Computation , vol. 140 (1998), no. 1, pp. 82–94.CrossRefGoogle Scholar
van Lambalgen, M., Algorithmic information theory, this Journal, vol. 54 (1989), pp. 1389–1400.Google Scholar
Levin, L. A., Universal sequential search problems . Problems of Information Transmission , vol. 9 (1973), pp. 265–266.Google Scholar
Levin, L. A., Randomness conservation inequalities; information and independence in mathematical theories . Information and Control , vol. 61 (1984), pp. 15–37.10.1016/S0019-9958(84)80060-1CrossRefGoogle Scholar
Müller, S. and Tzameret, I., Short propositional refutations for dense random 3CNF formulas . Annals of Pure and Applied Logic , vol. 165 (2014), no. 12, pp. 1864–1918.10.1016/j.apal.2014.08.001CrossRefGoogle Scholar
Papadimitriou, C., Computational Complexity , Addison Wesley, Reading, MA, 1994.Google Scholar
Pich, J. and Santhanam, R., Why are proof complexity lower bounds hard? IEEE 60th Annual Symposium on Foundations of Computer Science (FOCS) (D. Zuckerman, editor), IEEE, Washington, DC, 2019, pp. 1305–1324.CrossRefGoogle Scholar