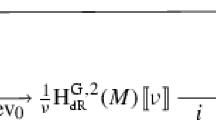Skip to main content
SpringerLink
Log in

Morita Equivalence of Fedosov Star Products and Deformed Hermitian Vector Bundles

  • Published:
Letters in Mathematical Physics Aims and scope Submit manuscript

Abstract

Based on the usual Fedosov construction of star products for a symplectic manifold M, we give a simple geometric construction of a bimodule deformation for the sections of a vector bundle over M starting with a symplectic connection on M and a connection for E. In the case of a line bundle, this gives a Morita equivalence bimodule, and the relation between the characteristic classes of the Morita equivalent star products can be found very easily within this framework. Moreover, we also discuss the case of a Hermitian vector bundle and give a Fedosov construction of the deformation of the Hermitian fiber metric.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Bayen, F., Flato, M., Frønsdal, C., Lichnerowicz, A. and Sternheimer, D.: Deformation theory and quantization, Ann. Phys. 111 (1978), 61–151.

    Google Scholar 

  2. Bertelson, M., Cahen, M. and Gutt, S.: Equivalence of star products, Classical Quantum Gravity 14 (1997), A93-A107.

    Google Scholar 

  3. Bordemann, M., Neumaier, N. and Waldmann, S.: Homogeneous Fedosov star products on cotangent bundles II: GNS representations, the WKB expansion, traces, and applications, J. Geom. Phys. 29 (1999), 199–234.

    Google Scholar 

  4. Bordemann, M. and Waldmann, S.: A Fedosov star product of Wick type for Kähler manifolds, Lett. Math. Phys. 41 (1997), 243–253.

    Google Scholar 

  5. Bordemann, M. and Waldmann, S.: Formal GNS construction and states in deformation Quantization, Comm. Math. Phys. 195 (1998), 549–583.

    Google Scholar 

  6. Bursztyn, H. and Waldmann, S.: Deformation quantization of Hermitian vector bundles, Lett. Math. Phys. 53 (2000), 349–365.

    Google Scholar 

  7. Bursztyn, H. and Waldmann, S.: Algebraic Rieffel induction, formal Morita equivalence and applications to deformation quantization, J. Geom. Phys. 37 (2001), 307–364.

    Google Scholar 

  8. Bursztyn, H. and Waldmann, S.: The characteristic classes of Morita equivalent star products on symplectic manifolds, Preprint Freiburg FR-THEP 2001/09, math.QA/0106178, To appear in Comm. Math. Phys.

  9. Cattaneo, A. S., Felder, G. and Tomassini, L.: Fedosov connections on jet bundles and deformation quantization, Preprint math.QA/0111290.

  10. DeWilde, M. and Lecomte, P. B. A.: Existence of star-products and of formal deformations of the Poisson lie algebra of arbitrary symplectic manifolds, Lett. Math. Phys. 7 (1983), 487–496.

    Google Scholar 

  11. Dito, G. and Sternheimer, D.: Deformation quantization: genesis, developments and metamorphoses, Preprint math.QA/0201168. To appear in the Proc. of the meeting between mathematicians and theoretical physicists, Strasbourg, 2001, IRMA Lectures in Math. Theoret. Phys. 1, De Gruyter, Berlin, 2002, pp. 9–54.

    Google Scholar 

  12. Fedosov, B. V.: Deformation Quantization and Index Theory, Akademie Verlag, Berlin, 1996.

    Google Scholar 

  13. Gutt, S.: Variations on deformation quantization, In: G. Dito and D. Sternheimer (eds), Confèrence Moshè Flato 1999. Quantization, Deformations, and Symmetries, Math. Phys. Stud. 22, Kluwer Acad. Publ. Dordrecht, 2000, pp. 217–254.

    Google Scholar 

  14. 14. Jurco, B., Schupp, P. and Wess, J.: Noncommutative line bundle and Morita equivalence, Preprint hep-th/0106110.

  15. Karabegov, A. V.: Deformation quantization with separation of variables on a Kähler manifold, Comm. Math. Phys. 180 (1996), 745–755.

    Google Scholar 

  16. Karabegov, A. V.: On Fedosov's approach to deformation quantization with separation of variables, In: G. Dito and D. Sternheimer (eds), Confèrence Moshè Flato 1999. Quantization, Deformations, and Symmetries, Math. Phys. Stud. 22, Kluwer Acad. Publ. Dordrecht, 2000 22

    Google Scholar 

  17. Karabegov, A. V. and Schlichenmaier, M.: Almost-Kähler deformation quantization, Lett. Math. Phys. 57 (2001), 135–148.

    Google Scholar 

  18. Kontsevich, M.: Deformation quantization of poisson manifolds, I. Preprint q-alg/ 9709040.

  19. Nest, R. and Tsygan, B.: Algebraic index theorem, Comm. Math. Phys. 172 (1995), 223–262.

    Google Scholar 

  20. Neumaier, N.: Local ?-Euler derivations and Deligne's characteristic class of Fedosov star products, Preprint Freiburg FR-THEP-99/3, math.QA/9905176.

  21. Omori, H., Maeda, Y. and Yoshioka, A.: Weyl manifolds and deformation quantization, Adv. Math. 85 (1991), 224–255.

    Google Scholar 

  22. Rieffel, M. A.: Morita equivalence for C*-algebras and W*-algebras, J. Pure. Appl. Math. 5 (1974), 51–96.

    Google Scholar 

  23. Waldmann, S.: On the representation theory of deformation quantization, Preprint Freiburg FR-THEP 2001/10, math.QA/0107112. To appear in the Proc. of the meeting between mathematicians and theoretical physicists, Strasbourg, 2001, IRMA Lectures in Math. Theoret. Phys., 1, De Gruyter, Berlin, 2002.

    Google Scholar 

  24. Weinstein, A.: Deformation quantization, Séminaire Bourbaki 46ème année 789 (1994).

Download references

Author information

Authors and Affiliations

  1. Fakultät für Physik, Albert-Ludwigs-Universität Freiburg, Hermann Herder Straße 3, D 79104, Freiburg, Germany

    Stefan Waldmann

Authors
  1. Stefan Waldmann
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Waldmann, S. Morita Equivalence of Fedosov Star Products and Deformed Hermitian Vector Bundles. Letters in Mathematical Physics 60, 157–170 (2002). https://doi.org/10.1023/A:1016109723843

Download citation

  • Issue Date:

  • DOI: https://doi.org/10.1023/A:1016109723843

Search

Navigation