Introduction

Quantum computers offer computational power fundamentally different from classical computers. A universal quantum computer may solve classically intractable problems within areas ranging from many-body physics to quantum chemistry1. There has been impressive experimental progress in developing quantum computers on different architectures2,3,4. Although achieving fault-tolerant computation remains a challenge, noisy intermediate-scale quantum (NISQ) devices are expected to be available in the near future5. These are devices containing a few hundred qubits with small error rates but without error-correction. An outstanding question is what kind of computations such devices may facilitate.

Algorithms designed for NISQ devices should run on a moderate number of qubits and be resilient to noise. The specific hardware may also pose further restrictions regarding the connectivity of the device, as not all qubits can interact directly with each other2,4. Promising frameworks that fulfill these conditions are the quantum approximate optimization algorithm6 and the quantum variational eigensolver (VQE)7,8. In these frameworks, the task of the quantum computer is roughly speaking to compute the expectation value of local Hamiltonians on some many-body quantum state. Recent work has characterized a number of conditions for which this can be done in a noise-robust way9,10,11,12,13. Due to the limited resources of NISQ devices, it is also important to run such algorithms as efficiently as possible in terms of circuit size and number of qubits.

We address this outstanding problem by developing a general framework for computing physical properties of quantum many-body states efficiently on NISQ devices. In particular, we upper bound the circuit size and number of qubits necessary to estimate the expectation values of local observables. Importantly, these bounds can significantly decrease the resource requirements compared to previous works for a number of circuit topologies and sizes. Specifically, we are able to show that the energy of a many-body quantum state can be estimated with a constant-sized quantum circuit if the correlation functions exhibit an exponential decay. This is the case for non-trivial states such as ground states of gapped Hamiltonians, surface codes and quantum states described by a multiscale entanglement renormalization ansatz (MERA) or the larger class of deep MERA (DMERA)12,13. The latter is believed to capture Chern insulators.

Our framework is akin to sequentially generated14,15,16 or finitely correlated states17. This enables us to control the size of the past causal cone18,19,20 of local observables. Combined with the notion of mixing rate of local observables under the circuit12,13 we determine after how many layers of the circuit, expectation values stabilize. To estimate these expectation values, it suffices to implement the potentially small subset of the circuit under which they stabilize instead of producing the entire many-body state or its past causal cone. Consequently, the necessary number of qubits and quantum gates can be reduced significantly from scaling with the size of the many-body state to even a constant number.

Results

Basic setup

We consider three basic operations, which are iterated T times to generate a many-body quantum state. The first operation adds qubits to the existing system. The second operation lets them interact with each other and a bath via a constant depth circuit. In the third operation, some of the existing qubits may be discarded. By introducing a separate bath, we allow for situations where a fixed sized quantum processor (the bath) iteratively prepares a quantum state on the system qubits. This allows e.g. the construction of arbitrary matrix product states (MPS) (see Example 1 below).

More specifically, we will start with a system S0 consisting of n0 qubits initialized in some fixed state ρ0 and a bath system B consisting of sB qubits initialized in some fixed state ρB. At each iteration t, we introduce new subsystems St with nt qubits and ancillary states At with at qubits, all initialized in some fixed quantum state. These new subsystems then interact with the existing ones and finally, the ancillary system is discarded, which concludes the iteration. The procedure is iterated for a total of T iterations to produce the entire state.

Interaction scheme

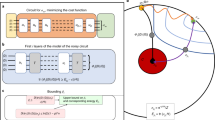
The structure of the final quantum state is determined by the allowed interactions between qubits during the iterative preparation. In order to get a handle on how the correlations of the final state evolve during the preparation, we will fix the allowed interactions according to a given interaction scheme. Our construction of such an interaction scheme is inspired by so-called graph states21. These can be visualized by letting the vertices of a graph denote qubits and edges denoting correlations between them. In a similar way, we define an interaction scheme as a sequence of T graphs {Gt = (Vt, Et)} where a vertex (Vt) denotes a qubit and an edge (Et) implies that it is possible to implement unitary gates between these two qubits in that time step. We further restrict this unitary gate such that at most D rounds of two-qubit operations are applied with the condition that on each round at most one unitary acts on each qubit. Figure 1 showcases a simple example of one iteration of the procedure illustrating all aspects of the framework. While such a simple interaction scheme serves the purpose of illustration, our framework encompasses arbitrary interaction graphs in each iteration step. This allows it to capture a number of widely studied tensor networks states, as illustrated in the two examples below.

Fig. 1: Generation procedure.
figure 1

Example of one iteration of the generation procedure broken down into five steps. The first line (1) represents the initial system before the iteration. We start with two system qubits (orange circles) and a bath (blue triangles). The first operation (line 1–2) is to add two new system qubits and two auxiliary qubit (red diamond). The new qubits are placed to the right of the old ones. The second operation (line 2–3) is to act with a unitary \({\mathcal{U}}\) between the indicated qubits and from (3) to (4) we apply another layer of unitaries and, thus, D = 2 for this example. Finally, in line (4)–(5) we discard the auxiliary systems.

Full size image

Definition 1 (MPS and higher dimensional versions) MPS have been studied in a sequential interaction picture22,23 and adapt naturally to our framework. The initial system S0 consists of one qubit and the dimension of the bath gives the bond dimension. At each iteration t, we add a system consisting of one qubit St to the system. The graph Gt only has edges between the qubits in the bath and the newest added qubit St. Note that we are considering a proper subset of MPS since we restrict to unitaries implementable with D two-qubit gates for each edge. Nevertheless, the bond dimension of the resulting MPS scales exponentially with the number of qubits in the bath. It is straightforward to generalize such sequentially generated states by considering the case in which a bath interacts with a subsystem of dimension d rather than a single qubit at each iteration12,15.

Definition 2 (Deep multiscale entanglement renormal-ization ansatz) The DMERA, introduced in ref. 13, is a variation of the MERA19 tailored for NISQ devices. In our framework, the initial system S0 consists of one qubit and there is no bath. We then define the graphs Gt recursively: at each iteration we add one qubit in between every existing qubit and nearest neighbors interact, resulting in a tree structure.

Past causal cone

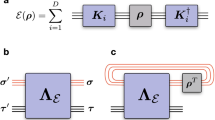
Formally, the final state of the system can always be written as

$$\rho ={\text{tr}}_{B}\left[\left({{{\Phi }}}_{[0,T]}\right)\left({\rho }_{0}\otimes {\rho }_{B}\right)\right],$$
(1)

where Φ[0, T] = ΦT∘ΦT−1∘…∘Φ0 and Φt are quantum channels of the form \({{{\Phi }}}_{t}={{\mathcal{D}}}_{t}\circ {{\mathcal{U}}}_{t}\circ {{\mathcal{A}}}_{t}\). Here \({{\mathcal{A}}}_{t}\) adds the new subsystems and auxiliary qubits, \({{\mathcal{U}}}_{t}\) is a unitary channel that consists of D two-qubit gates for each edge in Gt and \({{\mathcal{D}}}_{t}\) traces out the ancillary systems. An important property of our framework is that it allows to bound the number of qubits that can influence the value of a local observable, referred to as the causal cone of an observable18,19. The growth of the casual cone depends on the geometry of the graph Gt. To see this, consider an observable OT on the final state ρ. According to Eq. (1), the expectation value is

$$\,{\mathrm{tr}}\,\left(\rho {O}_{T}\right)=\,{\mathrm{tr}}\,\left(\left[{{{\Phi }}}_{[0,T]}^{* }\left({O}_{T}\otimes {{\mathbb{1}}}_{B}\right)\right]{\rho }_{0}\otimes {\rho }_{B}\right)$$

where \({{{\Phi }}}_{[t,T]}^{* }={{{\Phi }}}_{t}^{* }\circ {{{\Phi }}}_{t+1}^{* }\circ \cdots \circ {{{\Phi }}}_{T}^{* }\). Here \({{{\Phi }}}_{t}^{* }\) is the evolution in the Heisenberg picture.

We can use our framework to bound the size of the radius of the support of OT on the final state i.e. the number of qubits on the final state that OT involves. Going back to the t’th iteration, we denote the observable \({O}_{t}={{{\Phi }}}_{[t,T]}^{* }\left({O}_{T}\otimes {{\mathbb{1}}}_{B}\right)\). Let R(Ot) be the radius of the smallest ball in Gt containing the support of Ot. That is, Ot differs from the identity on qubits that are at most 2R(Ot) edges away in the graph Gt. To analyze the growth of the support and its past causal cone we consider the action of \({{{\Phi }}}_{T}^{* }={{\mathcal{A}}}_{T}^{* }\circ {{\mathcal{U}}}_{T}^{* }\circ {{\mathcal{D}}}_{T}^{* }\). First, \({{\mathcal{D}}}_{T}^{* }\) acts by tensoring the identity operator on the auxiliary qubits, not increasing the support. In the next step, \({{\mathcal{U}}}_{T}^{* }\) increases the support. As OT has radius R(OT), it will be mapped to an observable with radius at most R(OT) + D by \({{\mathcal{U}}}_{T}^{* }\) according to the locality assumptions of \({{\mathcal{U}}}_{T}^{* }\) (i.e. the restriction of D two-qubit gates for each edge). The map \({{\mathcal{A}}}_{T}^{* }\) will then map this observable to OT−1 supported on qubits that correspond to vertices in GT−1, as it traces out all the qubits added at iteration T. This can potentially decrease the support of the observable, as in DMERA.

Given the graphs Gt and a constant D, it is straightforward to track the support of the observable and the past causal cone with the above procedure. This allows us to find the maximum number of unitaries (NU(t, r)) and qubits (NQ(t, r)) in the past causal cone of an observable with radius of support of r on the final state going back to iteration t. Note that NQ(t, r) keeps track of the total number of qubits necessary to implement the past causal cone and thus also includes those that were discarded at a previous step.

Estimating local observables

So far we have devised a way of keeping track of the unitaries in the past causal cone of local observables. However, we are also interested in quantifying how much each iteration of the past causal cone contributes to the expectation value. In case the expectation value of the observable stabilizes after a couple of iterations, we can find smaller quantum circuits than the entire causal cone that will approximate the desired expectation value.

Inspired by refs. 12,13, we assume that the maps \({{{\Phi }}}_{[t,T]}^{* }\) are locally mixing. To this end, let us define the mixing rate as:

$$\delta (t,r) \equiv \mathop {{{\mathrm{sup}}}}\limits_{R(O_T) \le r,||O_T||_\infty \le 1} \mathop {{{\mathrm{inf}}}}\limits_{c \in {\mathbb{R}}} ||\Phi _{[t,T]}^ \ast \left( {O_T} \right) - {c{\mathbb{1}}}||_\infty .$$

Here ∥⋅∥∞ is the operator norm. The mixing rate, δ(t, r), quantifies how close observables on the final state, whose support is contained in a ball of radius r, are to the identity after going back to the t’th iteration of the evolution in the Heisenberg picture (Fig. 2). Intuitively speaking, δ(t, r) measures how many steps of the circuit contribute to the expectation value of local observables before it stabilizes, as we are interested in the regime in which c approaches \(\,{\mathrm{tr}}\,\left(\rho O\right)\) for large enough t. This is also connected to the memory of the evolution24. The next lemma formalizes this intuition (see “Methods” for a proof):

Fig. 2: Mixing and support growth in the Heisenberg picture.
figure 2

Evolution in the Heisenberg picture of an observable initially supported on the last two incoming qubits in the lower right corner (filled orange corner) at the fourth time step. The U indicates that we apply a unitary between the involved qubits and the dashed arrows indicate that old qubits are shifted to the left. Note that we suppressed the unitaries that do not contribute to the expectation value. The distance of the observables to the identity is indicated by how filled the element, i.e., empty shapes indicate that the observable is proportional to the identity on that system. Note that as in the Heisenberg picture we discard qubits, this causes the observables to mix. Moreover, we see that after two iterations the observables are essentially proportional to the identity and it suffices to implement that part of the circuit to estimate it.

Full size image

Lemma Let OT be an observable supported in a ball of radius r. Then

$$\left|\,{\mathrm{tr}}\,\left({{{\Phi }}}_{[t,T]}\left(\rho ^{\prime} \right){O}_{T}\right)-\,{\mathrm{tr}}\,\left(\rho {O}_{T}\right)\right|\le 2\delta (t,r)\parallel {O}_{T}{\parallel }_{\infty },$$
(2)

where \(\rho ={\text{tr}}_{B}\left[{{{\Phi }}}_{[0,T]}\left({\rho }_{0}\otimes {\rho }_{B}\right)\right]\), which holds for all \(\rho ^{\prime}\).

In other words, only the last T − t steps of the circuit are necessary to approximately compute the expectation value of OT up to an error of 2δ(t, r)∥OT∥∞. Note that the expectation value is independent of the initial state \(\rho ^{\prime}\), which we furthermore may restrict to the qubits that are in the support of Ot. We may further reduce the size of the circuit that needs to be implemented by restricting to the past causal cone. Combining these two observations leads to the statement of our main result:

Theorem Let OT be an observable supported in a ball of radius r and \(\rho ^{\prime}\) be a state on the qubits that are in the support of Ot. It is possible to compute \(\,{\text{tr}}\,\left(\rho {O}_{T}\right)\) up to an additive error 2δ(t, r) by implementing a circuit consisting of NU(t, r) two-qubit gates on NQ(t, r) qubits.

The theorem implies a way of performing VQE given bounds on δ(t, r) using a potentially smaller NISQ device than preparing the whole state. This is because implementing the smaller, effective circuit, requires fewer qubits and gates.

Robustness to noise

Consider the objective of calculating the ground state energy of a two local Hamiltonian H, in the sense that it only acts on nearest neighbors in GT, with each local term Hi satisfying ∥Hi∥∞ ≤ 1. It suffices to estimate all Hi individually to obtain an estimate of the global energy of the state by adding up the energy terms. Now suppose that we can implement each 2-qubit gate with an error ϵU in operator norm and can prepare each initial qubit up to an error ϵP. This implies that the total error of implementing the causal cone and measuring each Hi is bounded by ϵUNU(t, 2) + ϵPNQ(t, 2). Thus, by only implementing the circuit from iteration t to T, it is possible to estimate the energy of each term with an error of

$$2\delta (t,2)+{\epsilon }_{U}{N}_{U}(t,2)+{\epsilon }_{P}{N}_{Q}(t,2).$$
(3)

This generalizes to observables with arbitrary radius r and can be improved to by exploiting the fact that :

$$\begin{array}{ll}2\delta (t,r)+\mathop{\sum }\limits_{k=t+1}^{T}\delta (k-1,r){\epsilon }_{U}\left({N}_{U}(k,r)-{N}_{U}(k-1,r)\right)\\ \qquad\quad\;+\mathop{\sum }\limits_{k=t+1}^{T}\delta (k-1,r){\epsilon }_{P}\left({N}_{Q}(k,r)-{N}_{Q}(k-1,r)\right).\end{array}$$
(4)

To see this, recall that δ(k, r) measures how close the operator Ok is to being proportional to the identity, as there exists an operator Ak with the same support as Ok such that Ok can be decomposed into Ok = \({c{\mathbb{1}}}\) + δ(k, r)Ak. At the k’th iteration, any evolution in the Heisenberg picture only acts non-trivially on Ak and changes the expectation value of the observable w.r.t. to any state by at most δ(k, r)∥OT∥. Thus, if we actually implement a noisy version of the original evolution which is ϵU close to it, then we can only notice the effect of the noise in the part given by δ(k, r)Ak. We conclude that each noisy unitary contributes with an error at most ϵUδ(t, r), i.e., the effect of noise decreases in time if δ(t, r) decays. As there are NU(k, r) − NU(k − 1, r) new unitaries in the causal cone at the iteration, we obtain the bound. We note that the noise robustness we obtain is of the same order as the one obtained implementing the whole circuit, as in refs. 12,13, and refer to Supplementary Information for a detailed discussion.

These results are related with the fact that δ(t, r) and the geometry of the interactions govern the correlations present in the state produced. For ET, FT two observables of disjoint support of radius r and t be the largest t such that Et and Ft have supports that intersect we can show that:

$$\left|\,\text{tr}\,\left(\rho {E}_{T}\otimes {F}_{T}\right)-\,\text{tr}\,\left(\rho {E}_{T}\right)\,\text{tr}\,\left(\rho {F}_{T}\right)\right|\le 6\delta (t,r).$$

As the decay of δ(t, r) also governs the noise robustness, we see that there is a trade-off between the correlation length and the robustness to noise. For instance, one should expect δ(t, r) to be exponentially decaying for states with finite correlation length.

Estimating convergence

It is necessary to bound δ(t, r) in our approach in order to bound the error. Thus, it is important to find conditions that guarantee the decay of the mixing rate and to develop protocols to estimate the mixing rate on a NISQ device. In the translationally invariant case, one can apply the large toolbox available to estimate mixing time bounds25,26,27,28,29, as further explained in Supplementary Information.

However, it is important to acknowledge that obtaining rigorous mixing time bounds is notoriously difficult even for classical systems30. But this has not kept Markov Chain Monte Carlo algorithms from being one of the most successful methods to simulate physical systems31. There exist many heuristic methods for classical systems32 and here we also discuss a heuristic method to determine when the circuit has stabilized. As made transparent by Eq. (2), whenever the circuit has converged, the output of the circuit is independent of the initial state \(\rho ^{\prime}\). Thus, one possible way of checking that the circuit has indeed converged is testing several different initial states and making sure that the expectation value of the output with respect to the observable does not depend on the input. This can be done by picking a set of initial states that is overcomplete, i.e., spans the space of all states as detailed in the “Methods” section.

In short, the approach is to pick random initial product states on the support of the observable Ot and compare the value of the expectation value to that of the initial state where all qubits in the support are in state \(\left|0\right\rangle\). If the expectation value with respect to different initial states all coincide, we build confidence that the computation has indeed converged. On the other hand, if the expectation values differ for two different initial states, then we have not converged and must go deeper and decrease t. We denote the maximal difference of the expectation value for the several different choices of initial state by Δz and refer to the “Methods” section for a precise definition. An example of the approach is shown in Fig. 3 for a matrix product states with both fast and slow convergence.

Fig. 3: Convergence check.
figure 3

Illustration of convergence check for MPS in a rapid and slow mixing scenario. We consider a bath of 9 qubits arranged on a line. In each iteration a new system qubit is added and a fixed circuit is run between the bath and the new system qubit. In the rapid mixing case, we perform a depth 3 circuit between the system qubit and the bath such that each gate is followed by a depolarizing channel with probability 5%. The complete state was evolved for 50 time steps and, thus, consists of total of 50 qubits, and we measured Pauli observables on the last two qubits. In the slow mixing we perform a depth 2 circuit instead. If we denote by Xt the expectation value of the state evolved by t steps, we define the relative error to the true value to be ∣1 − Xt/X50∣, as X50 corresponds to preparing the whole state. To generate each plot, we have generated 50 instances where the gates in the circuits were picked at random for each instance. The figures display the logarithm in base 10 of the average of the quantities. Even with moderate levels of noise, we can faithfully reproduce the expectation value up to a relative error of 10−2 after 5 iterations, giving an order of magnitude saving in the number of qubits in the rapid mixing scenario, while in the slow mixing, we required around 13. Moreover, we have picked 20 random initial states to estimate Δz, as more initial states did not seem to improve the estimate. As we can see, Δz is a good proxy for the relative distance to the true expectation value.

Full size image

As we can see from the figures, estimating Δz gives reliable convergence diagnostics. Importantly, this is obtained with only a modest number of randomly selected input states. This suggests that estimating the convergence does not outweigh the overall advantage of bounding the circuit size for estimating local observables with our framework. We do note, however, that this is a heuristic and not rigorous approach. For rigorously establishing convergence, it would in general require a sample complexity increasing exponentially with the support. We refer to the supplementary information for more details.

Discussion

To demonstrate the implications of our results, we summarize the noise robustness and required number of gates and qubits in Table 1 for some interaction schemes. We are able to significantly decrease the number of unitaries and qubits compared to the approach of refs. 12,13. This is because we only require the circuit corresponding to the past causal cone until it stabilizes to be implemented, in contrast to the the whole causal cone. Clearly, these results also imply that it is possible to approximate these expectation values classically if the resulting effective circuits are of a classically simulatable size.

Table 1 Summary of resources.
Full size table

Our results provide an intuitive understanding of the stability of these computations. Each iteration contributes less to the value of expectation values, which implies that there is a small effective quantum circuit underlying the computation. Furthermore, the size of this circuit is related to the correlation length of the state and the effect of noise decreases proportionally to the correlations between regions.

Although rigorously testing at which iteration the circuit has converged might require exponential resources, we see that chosing a few random initial states and comparing the different expectation values provides useful guidance to check wether convergence has occurred. This shows that it is feasible to build confidence in the convergence and required depth with moderate resources using such heuristics. However, it would still be interesting to establish more rigorous protocols under suitable additional assumptions.

There are significant challenges in scaling up current qubit technologies33,34,35. The reduction in the number of qubits that we have shown above means that it may be possible to explore many-body quantum states with NISQ devices with substantially fewer qubits, potentially bringing such tasks into reach for current technology3,4. The possible reduction in the number of gates also reduces the necessary runtime of the circuits, which is important for hardware subject to qubit loss over time such as trapped atoms36. Note that the objective of this method is to expand the simulating capabilities of NISQ devices subject to strict hardware limitations. This is in contrast to other techniques, like measurement regrouping8,37,38,39,40,41, that focus on optimizing resources given the ability to implement the whole circuit that prepares a given state.

Methods

Proofs and checking mixing

The main result of our work is based on the lemma in the main text. In order to prove this lemma, we have used a method based on viewing the generation as a quantum channel in the Heisenberg picture. The formal proof is given below.

Proof By the definition of δ(t, r), we see that

$${{{\Phi }}}_{[t,T]}^{* }({O}_{T})={O}_{t}=c{\mathbb{1}}+\delta (t,r)A,$$
(5)

where A is some observable supported on supp(Ot) satisfying ∥A∥∞ ≤ ∥OT∥∞. As \({{{\Phi }}}_{[0,t-1]}^{* }\) is a quantum channel in the Heisenberg picture, \({{{\Phi }}}_{[0,t-1]}^{* }({\mathbb{1}})={\mathbb{1}}\) and \(\parallel {{{\Phi }}}_{[0,t-1]}^{* }{\parallel }_{\infty \to \infty }\le 1\)42. Thus,

$${{{\Phi }}}_{[0,t-1]}^{* }\circ {{{\Phi }}}_{[t,T]}^{* }({O}_{T})=c{\mathbb{1}}+\delta (t,r){{{\Phi }}}_{[0,t-1]}^{* }\left(A\right),$$
(6)

where \(\parallel {{{\Phi }}}_{[0,t-1]}^{* }\left(A\right){\parallel }_{\infty }\,\le \,\parallel {O}_{T}{\parallel }_{\infty }\). We conclude that

$$\begin{array}{ll}\left|\,{\mathrm{tr}}\,\left({{{\Phi }}}_{[t,T]}\left(\rho ^{\prime} \right){O}_{T}\right)-\,{\mathrm{tr}}\,\left(\rho {O}_{T}\right)\right| =\left|\,{\mathrm{tr}}\,\left(\rho ^{\prime} {{{\Phi }}}_{[t,T]}^{* }\left({O}_{T}\right)\right)-\,{\mathrm{tr}}\,\left({\rho }_{0}\otimes {\rho }_{B}{{{\Phi }}}_{[0,T]}^{* }\left({O}_{T}\right)\right)\right|\\ \qquad\qquad\qquad\qquad\qquad\qquad\quad\,\,\,=\delta (t,r)\left|\,{\mathrm{tr}}\,\left(\rho ^{\prime} A\right)-\,{\mathrm{tr}}\,\left({\rho }_{0}\otimes {\rho }_{B}{{{\Phi }}}_{[0,t-1]}^{* }\left(A\right)\right)\right|\\ \qquad\qquad\qquad\qquad\qquad\qquad\quad\,\,\,\le 2\delta (t,r)\parallel {O}_{T}{\parallel }_{\infty }\end{array}$$

by combining (5) and (6).□

Our results show that having an estimate for the mixing rate δ(t, r) allows to bound the number of qubits and circuit size needed to estimate local observable on a many-body quantum state. While certain classes of states are known to have rapid mixing leading to fast convergence of the observables (like ground states of gapped Hamiltonians), we have developed a heuristic method for estimating the convergence of local observables. The method relies on the observation that we can expand any density matrix using a basis of single qubit states. Let ρt = Φ[0, t](ρ0 ⊗ ρb) be the state we obtain by evolving from time 0 to t and OT be defined as usual. Moreover, let m = NQ(r, t) be the number of qubits in the support of Ot. To check the convergence of the circuit, we prepare input states \(\left|{\psi }_{z}\right\rangle { = \bigotimes }_{i = 1}^{m}\left|{z}_{i}\right\rangle\), where \(\left|{z}_{i}\right\rangle \in \{\left|0\right\rangle ,\left|1\right\rangle ,\left|+\right\rangle ,\left|-\right\rangle \}\). The states \(\left|{\psi }_{x}\right\rangle\) thus corresponds to various product state combinations of the states \(\left|0\right\rangle ,\left|1\right\rangle ,\left|+\right\rangle\) and \(\left|-\right\rangle\) on the support of the observable Ot. It is well-known that these states form a basis of the space of Hermitian matrices. We can therefore expand ρt as

$${\rho }_{t}=\sum _{z}{a}_{z}\left|{\psi }_{z}\right\rangle \left\langle {\psi }_{z}\right|,$$

where \({a}_{z}\in {\mathbb{C}}\). Furthermore, it is easy to see that ∑zaz = 1 by taking the trace. Now define Δz to be given by:

$${{{\Delta }}}_{z}=\,\text{tr}\,((\left|{\psi }_{z}\right\rangle \left\langle {\psi }_{z}\right|-\left|0\right\rangle {\left\langle 0\right|}^{\otimes m}){O}_{t}).$$

From this, we immediately obtain that:

$$\,{\mathrm{tr}}\,({\rho }_{t}{O}_{t})=\,{\mathrm{tr}}\,\left(\left|0\right\rangle {\left\langle 0\right|}^{\otimes m}{O}_{t}\right)+\mathop {\sum}\limits_{z}{a}_{z}{{{\Delta }}}_{z}.$$
(7)

Equation (7) suggests the simple protocol of picking random initial product states \(\left|{\psi }_{z}\right\rangle\) and comparing the expectation value with the outcome for initial state \({\left|0\right\rangle }^{\otimes m}\) to estimate the convergence. If the expectation value with respect to different initial states\(\left|{\psi }_{z}\right\rangle\) all coincide with the one of \({\left|0\right\rangle }^{\otimes m}\), we build confidence that all Δz are small, thus ensuring that the expectation value is similar as picking the initial state to be \({\left|0\right\rangle }^{\otimes m}\).