Introduction

Currently, the researchers and scientists have been focussed on the study of non-Newtonian fluid flow induced by stretched geometry, due to everyday desires of these assets in chemical and manufacturing practice. Corn flour, mud, syrups, dilatant, glue, chilli sauce, gypsum paste, body lotions, shampoo, toxoid vaccines, pasteurized milk, and soapy water are some industrial products included into this category. Various models are available in the data to review the flows of non-Newtonian fluids according to their adoptable essence. In which, the furthermost tackled liquids are micropolar shear thickening liquids. In 1964, the concept of micropolar shear thickening fluid was originated by Eringen1. Keeping this into mind, Rao and Rao2 explored the characteristics of micropolar liquid past a spherical geometry. Some notable information about the motion of non-Newtonian liquids via stretchable surface can be view in the earlier literature3,4,5. They acquired the problem solutions numerically with the aid of various finite difference schemes. The investigation on the problem of micropolar shear thickening fluid over a convectively heated surface can be view in ref.6. Waqas et al.7 scrutinized the essence of Biot number on forced convective non-Newtonian fluid flow induced by nonlinear stretchable surface. They stated that the micropolar constant has a propensity to regulate the rate of thermal transport. Recently, Lu et al.8 reported numerical scrutiny of the magnetohydrodynamic flow of shear thickening liquid across a stretched sheet in the attendance of radiation and chemical reaction.

The Phenomenon of stretching plays a decisive task in the examination of boundary layer flow owing to its incredible consequences in engineering applications such as polymer engineering, wire drawing, metallic beds cooling, glass forming approaches, hot rolling, plastic sheets extraction, paper production, etc. Based upon these applications the feature of the desired products will be controlled by the measure of thermal transfer. In 1970, the first study on the motion over a stretching surface was scrutinized by Crane9. Micropolar fluid motion induced by a strained surface was described by Chiam10. Hayat et al.11 reported the impact of Nusselt number on non-Newtonian liquid motion via a non-linear surface. The influence of organic response on the stagnated motion of Newtonian liquid across a cylinder was reported by Najib et al.12 and presented dual solutions for shrinking and stretching cases. Later, the work of Hayat et al.11 was then extended by Babu et al.13 with injection/suction. Soid et al.14 analyzed the heat transport attribute on time-dependent flow of Newtonian liquid induced by a shrinking sheet.

The analysis of magnetohydrodynamics has ample significances in the fields of cooling of the reactor, astrophysics, accelerators, design of heat exchangers, power generators, geophysics, plasma studies, and cancer research. Micropolar fluid motion across a nonlinear stretchable sheet under the impact of drag force was scrutinized by Hayat et al.15 and concluded that angular velocity has an inverse relationship with material parameter. Nadeem and Hussain16 explored the Lorentz force essence on viscous Newtonian fluid through the porous stretched surface. The MHD flow driven by a wedge or a cone with the aid of non-Fourier heat conduction was reported by Kumar et al.17 and concluded that temperature field is suppresses with a hike in the magnitude of relaxation parameter but enhances with magnetic field parameter. Impact of Lorentz force on forced convection Jeffery fluid through a permeable surface was reported by Ahmad and Ishak18. They implemented the finite difference numerical scheme to obtain the solution. The influence of thermophoresis and Brownian motion on MHD flow of nanoliquid across a solid surface in the attendance of linear Rossland approximation was investigated by Mabood et al.19. Mabood et al.20 presented an analytical solution for the problem of time-dependent flow of nanoliquid past a convectively heated surface in the attendance of Lorentz force and concluded that the magnetic field parameter has a proclivity to enhance the curves of heat function. The influence of variable viscosity on conducting flow of nanoliquid across a rotating surface in the presence of a porous medium was reported by Mabood et al.21. Recently, Kumar et al.22 investigated the flow characteristics of micropolar with radiation and frictional heating. They found that friction factor has an inverse relationship with the magnetic field parameter.

The impact of heat transport has sufficient significance in the sub-disciplines of paramedical and some engineering. Power creation, Oceanography, heat exchangers, magnetic drug targeting, thermal conduction in tissues, convection in earth’s mantle, electronic devices, boilers, missiles, fuel cells, etc are some applications of heat transfer. Polymer processing, gas turbines, production of paper, space vehicles, hypersonic fights, space technology, production of glass, gas cooled nuclear reactors are certain beneficial claims of radiation. Ziabakhsh et al.23 examined the heat generation and microrotation impacts on non-Newtonian liquid motion past a surface and concluded that a rise in blowing constant origins an improvement in the thermal fields. The influence of Newtonian heating on micropolar fluid motion driven by a stretched geometry was described by Qasim et al.24 and established that an augmentation in both the local Nusselt number and temperature distribution with larger Newtonian parameter. Cortell25 discussed the influence of the rate of heat transport on radiative liquid over a solid surface. Brownian motion influence on magnetohydrodynamic radiative flow of shear thickening liquid via stretchable geometry was reported by Farooq et al.26. Recently, the authors27,28 have paid their attention to investigate heat transport with nonlinear radiation.

The phenomenon of uneven heat sink/source has countless solicitations in medicine and many engineering happenings like cooling of metallic sheets, the intention of a thrust bearing, unpolished oil retrieval, etc. Pal29 studied the thermal transport attributes of time-dependent fluid flow across a stretched sheet with irregular heat sink/source. Some notable data about the irregular heat fall or raise effect on electrically conducting liquid flow due to stretching surface can be view in the ref.30. It was founded that uneven heat constraints have done a key character in the performance of thermal transport. RamReddy et al.31 numerically reported the behavior of Biot and Soret numbers on the forced convective motion of viscous liquid through a vertical plate and finalized that all the physical quantities have an inverse relationship. Patil et al.32 bestowed an inexact result for the forced convective motion subjected to the convective sheet. Kumar et al.33 presented the features of thermal transport on ferrofluid motion past a convective sheet with radiation. Impact of variable heat source/sink on MHD flow of micropolar liquid across a stretching surface with thermo-diffusion was reported by Mabood et al.34. The influence of heat source/sink and radiation on MHD flow of nanofluid past a nonlinear surface was scrutinized by Makinde et al.35 and Mabood et al.36 and concluded that the heat source/sink parameter has a tendency to enhance the temperature.

In the aforesaid investigations the impact of no slip condition is presumed. Mainly first order slip is important when the fluid is particulate like bubbles, mixtures (grease, egg yolk, the combination of oil and liquid), and polymer solutions. Many years ago, Navier37 recommended the momentum slip condition to liquid motion across a sheet. Behavior of secondary slip on Newtonian fluid flow due to a convective surface was analyzed by Fang et al.38. The impact of radiation on magnetohydrodynamic mixed convective slip motion was reported by Beg et al.39. Martin and Boyd40 investigated the influence of velocity slip on viscous liquid over a stretching sheet. With the aid of self-similar transformations, the flow equations are mutated and hence numerical results for the flow fields are presented. Attributes of slip motion and heat transport on magnetohydrodynamic micropolar liquid due to stretched sheet was reported by Ibrahim41. Recently, Mabood et al.42 scrutinized the influence of primary slip on boundary layer motion of radiative liquid across a melting surface. They noticed that higher values of the slip parameter cause an increment in the fluid temperature but the friction factor is inversely proportional to the slip parameter. Ibrahim et al.43 presented numerical scrutiny to examine the influence of chemical reaction and velocity slip on electrically conduction flow of non-Newtonian liquid across a convectively heated surface and found that Biot number has a propensity to heighten the heat transfer rate.

All the afore believed studies, the scientists put their struggles to gain the knowledge in the heat transfer of MHD flows under distinct physical aspects such as heat source/sink, linear Rossland approximation and slip effects, etc. but every few researchers deliberated the flow of micropolar shear thickening fluid in the appearance of nonlinear radiation and variable heat rise/fall effects. Most percentage of the research articles specified above, the authors used no slip or slip boundary conditions. But in the present study, we applied the second-order velocity slip condition to the boundary. Yet, no author delineated second-order velocity slip effects on MHD motion of micropolar liquid across a stretched surface with irregular heat sink/source. In the present article, we sighted at examining the nature of nonlinear radiation on MHD shear thickening fluid to fulfill the pre averred gap. R. K. based shooting application is applied to get the solution of higher ordered coupled ODEs. Results are divulged pictorially and presented numerical values for stipulated physical parameters.

Mathematical Formulation

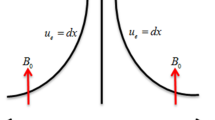
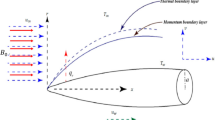
Flow geometry of the model is exposed in Fig. 1. Let us imagine the two-dimensional flow of an incompressible, electrically accompanying micropolar fluid past a stretching sheet with the influence of secondary velocity slip. The fluid motion is laminar and time independent. Simultaneous solutions are presented for first and second order slips. The stretching sheet is pondered along the x route and y axis is perpendicular to it. Consider the velocities us = px and ue = qx, where p, q are positive constants. The strength of the magnetic force B0 is exploited normal to the flow way as shown in Fig. 1. The following are some conventions on the present model.

  • Micropolar liquid model.

  • The impacts of uneven heat sink/source, nonlinear radiation are deemed.

  • Influence of viscous dissipation is neglected.

  • Convective and second-order velocity slip boundary conditions are employed.

Figure 1
figure 1

Flow Geometry.

Full size image

With the above-declared assumptions, the flow equations will be (See refs24,26,41),

$$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0,$$
(1)
$$\rho (u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y})=\mu \frac{{\partial }^{2}u}{\partial {y}^{2}}-\kappa (\frac{\partial N}{\partial y}+\frac{{\partial }^{2}u}{\partial {y}^{2}})-\sigma {{B}_{0}}^{2}u,$$
(2)
$$\rho j(u\frac{\partial N}{\partial x}+v\frac{\partial N}{\partial y})=\varGamma \frac{{\partial }^{2}N}{\partial {y}^{2}}-\kappa (\frac{\partial u}{\partial y}+2N),$$
(3)
$$(\rho {C}_{P})(u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y})=k\frac{{\partial }^{2}T}{\partial {y}^{2}}+q\prime\prime\prime -\frac{\partial {q}_{f}}{\partial y}$$
(4)

Here (u, v) are the constituents of velocity in the ways of (x, y) correspondingly, (μ, ρ) correspondingly, the viscosity (dynamic) and density, κ is the vortex viscosity, N is the microrotation velocity, electrical conductivity and micro-inertia density are \((\sigma ,j=\frac{\upsilon }{p})\) respectively, (Cp, k) correspondingly, the heat capacitance and conductivity (thermal).

Consider

$$\Gamma =(\mu +\frac{\kappa }{2})j=\mu j(1+\frac{\alpha }{2})$$
(5)

where \(\alpha =\frac{\kappa }{\mu }\) is the material parameter.

In Eq. (4) the second term in the R.H.S, \(q\prime\prime\prime \) is defined as (See ref.26)

$$q\prime\prime\prime =\frac{k({T}_{s}-{T}_{\infty })\,{u}_{s}}{x\,\upsilon }({A}^{\ast }f^{\prime} +{B}^{\ast }\frac{(T-{T}_{\infty })}{({T}_{s}-{T}_{\infty })}),$$
(6)

Here Ts and T∞ are the nearby and ambient temperatures of the sheet correspondingly, the lessening and swelling values of A* and B* corresponds to heat fall or raise.

Consider

$${q}_{f}=\frac{-4{\sigma }^{\ast }}{3{k}^{\ast }}\frac{\partial {T}^{4}}{\partial y}=\frac{-16{\sigma }^{\ast }}{3{k}^{\ast }}{T}^{3}\frac{\partial T}{\partial y}$$
(7)

From Eqs (6 and 7), Eq. (4) converts as

$$(\rho {C}_{P})(u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y})=k\frac{{\partial }^{2}T}{\partial {y}^{2}}+\frac{16{\sigma }^{\ast }}{3{k}^{\ast }}\frac{\partial }{\partial y}({T}^{3}\frac{\partial T}{\partial y})+\frac{k({T}_{s}-{T}_{\infty })\,{u}_{s}}{x\,\upsilon }({A}^{\ast }f^{\prime} +{B}^{\ast }\frac{(T-{T}_{\infty })}{({T}_{s}-{T}_{\infty })}),$$
(8)

Consider (See refs28,41),

$$v=0,u={u}_{s}+{u}_{{\rm{Slip}}},N=-\,{M}_{r}\frac{\partial u}{\partial y},\frac{\partial T}{\partial y}=\frac{{h}_{f}}{k}({T}_{s}-T),\,\,{\rm{at}}\,y=0,$$
(9)
$$u\to {u}_{e},N\to 0,T\to {T}_{\infty },\,\,{\rm{as}}\,y\to \infty ,$$
(10)

Consider the second-order velocity slip model (Ibrahim41)

$${u}_{{\rm{Slip}}}=\frac{2}{3}(\frac{3-a{l}^{2}}{a}-\frac{3}{2}\frac{1-{l}^{2}}{{K}_{n}})\lambda \frac{\partial u}{\partial y}-\frac{1}{4}({l}^{4}+\frac{2}{{K}_{n}^{2}}(1-{l}^{2})){\lambda }^{2}\frac{{\partial }^{2}u}{\partial {y}^{2}}=P\frac{\partial u}{\partial y}+Q\frac{{\partial }^{2}u}{\partial {y}^{2}},$$
(11)
$$l=\,\min (\frac{1}{{K}_{n}},1),$$
(12)

here P, Q are the constants, Kn is the Knudsen number, λ is the molecular free mean path, a is the coefficient of the momentum accommodation (0 ≤ a ≤ 1), Mr is a micro rotation parameter. From Eq. (12), we have 0 ≤ l ≤ 1, ∀Kn. So λ is always non-negative. i.e., Q < 0 and hence the last term on R.H.S. of Eq. (11) is a positive number.

Here Knudsen number is the pivotal factor, which is a rate of the molecular free mean path of characteristic length. For very small Kn no-slip is noticed between the surface and fluid. However, Kn lies between 10−3 to 0.1, first order slip arises near the fluid-surface interaction.

Consider the transformations in order to get the dimensional less expressions of the flow equations: (See refs24,26,41),

$$\chi =\sqrt{p\upsilon }xf,\eta =\sqrt{\frac{p}{\upsilon }}y,N=px\,\sqrt{\frac{p}{\upsilon }}g,u=\frac{\partial \chi }{\partial y},v=-\frac{\partial \chi }{\partial x},T={T}_{\infty }(1+({\theta }_{w}-1)\theta ),{\theta }_{w}=\frac{{T}_{s}}{{T}_{\infty }},$$
(13)

Here χ is the stream function and η is the similarity variable, \(f^{\prime} (\eta ),g(\eta )\& \theta (\eta )\) are the dimensionless flow fields and θw is the temperature ratio parameter.

From Eq. (13), Eq. (1) satisfied trivially and the Eqs (2), (3) and (8) becomes

$$(1+\alpha )\frac{{d}^{3}f}{d{\eta }^{3}}+f\frac{{d}^{2}f}{d{\eta }^{2}}-{(\frac{df}{d\eta })}^{2}+\alpha \frac{dg}{d\eta }-M\frac{df}{d\eta }=0,$$
(14)
$$(1+\frac{\alpha }{2})\frac{{d}^{2}g}{d{\eta }^{2}}+f\frac{dg}{d\eta }-g\frac{df}{d\eta }-\alpha (2g+\frac{{d}^{2}f}{d{\eta }^{2}})=0,$$
(15)
$$\begin{array}{c}\frac{{d}^{2}\theta }{d{\eta }^{2}}+f\Pr \frac{d\theta }{d\eta }+({A}^{\ast }\frac{df}{d\eta }+{B}^{\ast }\theta )+\\ {N}_{r}(\begin{array}{c}\frac{{d}^{2}\theta }{d{\eta }^{2}}+{(\theta )}^{3}\frac{{d}^{2}\theta }{d{\eta }^{2}}{({\theta }_{w}-1)}^{3}+3{(\theta )}^{2}{(\frac{d\theta }{d\eta })}^{2}{({\theta }_{w}-1)}^{3}+\\ 3{(\theta )}^{2}\frac{{d}^{2}\theta }{d{\eta }^{2}}{({\theta }_{w}-1)}^{2}+6\theta {(\frac{d\theta }{d\eta })}^{2}{({\theta }_{w}-1)}^{2}+3\theta \frac{{d}^{2}\theta }{d{\eta }^{2}}({\theta }_{w}-1)+3{(\frac{d\theta }{d\eta })}^{2}({\theta }_{w}-1)\end{array})=0,\end{array}$$
(16)

The corresponding mutated boundary conditions are

$$\frac{df}{d\eta }=1+\gamma \frac{{d}^{2}f}{d{\eta }^{2}}+\delta \frac{{d}^{3}f}{d{\eta }^{3}},f=0,g=-\,{M}_{r}\frac{{d}^{2}f}{d{\eta }^{2}},\frac{d\theta }{d\eta }=-\,Bi(1-\theta )\,\,at\,\,\eta =0,$$
(17)
$$\frac{df}{d\eta }\to \lambda ,g\to 0,\theta \to 0\,\,as\,\,\eta \to \infty ,$$
(18)

here \(\alpha ,M,\Pr ,{N}_{r},Bi,\lambda ,\gamma \& \delta \) are the micropolar parameter, magnetic field parameters, Prandtl number, nonlinear radiation parameter, Biot number, stretching ratio parameter, first and second order slip parameter respectively and these are defined by

$$M=\frac{\sigma {B}_{0}^{2}}{p\,\rho },\Pr =\frac{\mu {C}_{p}}{k},{N}_{r}=\frac{16{\sigma }^{\ast }{T}_{\infty }^{3}}{3k{k}^{\ast }},\gamma =P\sqrt{\frac{p}{\upsilon }}( > 0),\delta =Q\frac{p}{\upsilon }( < 0),Bi=\frac{{h}_{f}}{k}\sqrt{\frac{\upsilon }{p}},\lambda =\frac{q}{p},$$
(19)

Calculated friction factor, couple stress coefficient and heat transfer rate are

$$\begin{array}{c}{\mathrm{Re}}_{x}^{1/2}{C}_{F}=2(1+\alpha (1-{M}_{r})){(\frac{{d}^{2}f}{d{\eta }^{2}})}_{\eta =0},{C}_{S}=(1+\frac{\alpha }{2}){(\frac{dg}{d\eta })}_{\eta =0},\\ {\mathrm{Re}}_{x}^{-1/2}Nu=-\,(1+{N}_{r}{({\theta }_{w})}^{3}){(\frac{d\theta }{d\eta })}_{\eta =0},\end{array}\}$$
(20)

where \({\mathrm{Re}}_{x}=\frac{p\,{x}^{2}}{\upsilon }\) is the confined Reynolds number.

Deliberation of Results

This section sightsees the inspiration of flow variable parameters on the flow fields. The scheme of nonlinear and coupled ODEs (14)–(16) with the restrictions of the boundary (17)–(18) have resolved numerically with the sequential solicitation of shooting and R.K. methods. The effect of varied dimensionless parameters on the fluid temperature, micro-rotation, and velocity field is exposed via plots. Further, we scrutinize the influence of the same variables on the physical quantities and the consequences are exhibited in the table. We prescribed the values of \(\alpha =2,M=1,{\theta }_{w}=0.5,{N}_{r}=0.3,{A}^{\ast }={B}^{\ast }=0.2,\Pr =7,Bi=0.5,\gamma =1.0\) and λ = 0.2 for computation purpose. In the pictures, solid lines stipulate the impact of first-order slip and dashed lines stipulates the impact of second-order slip.

For the verification of accuracy, the present results of friction factor (CF) are compared with the results obtained by Ibrahim41 through Table 1. This table shows that the present results are in good agreement with the results reported by Ibrahim41 for \({N}_{r}=0,{\theta }_{w}=0,\) \({A}^{\ast }=0,{B}^{\ast }=0,\gamma =1,\delta =-\,1,Bi=0,\Pr =1\) and \({M}_{r}=0.5\).

Table 1 Comparison of friction factor (CF) for different values of α and M when \({N}_{r}=0,\) \({\theta }_{w}=0,{A}^{\ast }=0,\)\({B}^{\ast }=0,\gamma =1,\delta =-\,1,Bi=0,\Pr =7\) and \({M}_{r}=0.5\).
Full size table

The influence of relevant parameters on \(f^{\prime\prime} (0),g^{\prime} (0)\) and \(-\theta ^{\prime} (0)\) for first and second order slips of micropolar shear-thickening liquid flow through a stretched surface is sightseen by Tables 2 and 3. From the table, it is noticed that a rise in the values of Lorentz force results a drop in all the quantities (\(f^{\prime\prime} (0),g^{\prime} (0)\) and \(-\theta ^{\prime} (0)\)) however a reverse consequence is perceived for material parameter. Swelling values of micropolar constant upshots a hike in \(g^{\prime} (0)\) but a reduction is noticed for a larger magnetic field parameter. Larger Mr yields an increment in the couple stress coefficient, friction factor, and the measure of heat transport. Also, the measure of thermal transport is supreme for larger Bi for both the cases. Heat generation or absorption and temperature ratio parameters cause a reduction in heat transfer rate while an opposite outcome is noticed with nonlinear radiative energy for both the slips (first and second order) cases. From Table 3 it is noticed that an increase in γ results a hike in both \(f^{\prime\prime} (0),g^{\prime} (0)\) but a contrary development is noticed for second order slip parameter. Also, the thermal transport rate is a cumulative function of second order slip parameter but an inverse outcome is discerned for γ.

Table 2 Influence of sundry flow parameters on CF, CS and Nu for δ = 0 and δ = 1.
Full size table
Table 3 Impact of second and first order slip parameters on CF, CS and Nu.
Full size table

Figure 2 renders for the variation of magnetic field parameter (M) on the velocity, microrotation and thermal fields. Figure 2(a),(b) divulge that, both the distributions of linear and angular momentum suppresses as the values of magnetic field variable enhances. This contest the physical interpretation on hiring the magnetic force to an electrically conducting fluid, and this provides an elevation in the drag force, which consequences in the decelerating strength on velocities. Owing to this, a reduction in the fields of velocity and microrotation is noticed. But in case of thermal fields, it’s quite reverse to fluid velocities as exposed in Fig. 2(c). From the plots, it is spotted that both the velocity and the angular velocity are attained maximum due to second order slip and the maximum temperature is noticed for first order slip.

Figure 2
figure 2

Impact of M on (a) velocity (b) microrotation (c) temperature.

Full size image

Figure 3 is plotted to know the essence of the micropolar parameter (α) on the velocity, microrotation and thermal fields. It is interesting to note that, an enhancement in the values of α boosts the linear velocity, however, a contrary consequence is detected for microrotation and thermal fields. The results specify that the momentum transfer layer-by-layer is boosted expressively owing to the escalation of viscosity caused by the collective micro-rotation of particles, i.e., large values of the micropolar parameter; on the other hand, the thermal diffusions are weakened slightly. Hence, there is a reduction in both the micro-rotation and thermal fields are noticed for larger material constant.

Figure 3
figure 3

Impact of α on (a) velocity (b) microrotation (c) temperature.

Full size image

Figure 4(a) is deliberate to discuss the influence of radiation parameter (Nr) on the distribution of temperature. From the figure, it is noticed that the impression of radiation parameter Nr on θ(η) is increasing. It is familiar that the mechanism of radiation and is the heat transference phenomenon which releases the energy via fluid particles such that some additional heat is produced in the flow. It is worth mention that the influence of radiation becomes more significant as \({N}_{r}\to \infty \) and the influence of radiation can be neglected when \({N}_{r}=0\). Moreover, high heat transfer is attained in the presence of first-order slip than that of second-order slip.

Figure 4
figure 4

Curves of temperature with the variant in (a) Nr (b) θw (c) Bi.

Full size image

The essence of the temperature ratio parameter on fluid temperature is investigated through Fig. 4(b). It is worth mention that thermal field enhances with increasing values of θw. Mathematically, \({\theta }_{w}=\frac{{T}_{w}}{{T}_{\infty }}\) is the ratio of temperature at the surface to the temperature at a free stream. The value of θw must be greater than 1 for the nonlinear radiation. Also, an increase in temperature ratio parameter causes a hike in the temperature along the surface. As a result, the distribution of thermal field and the corresponding layer thickness enhances. It is significant to remark that as \({\theta }_{w}\to 1\), the temperature of nonlinear Rosseland and linear Rosseland approximation are the same. We observed an interesting result that the distribution of temperature (\(\theta (\eta )\)) is high for \(\delta =0\) when compared to that of \(\delta \ne 0\).

The influence of Biot number (Bi) on the fluid temperature is investigated through Fig. 4(c). We see that the ascending values of the Biot number improve the fluid temperature. Biot number occurs in the current investigation owing to the assumption of convective boundary condition and signifies the ratio of diffusive resistance within the sheet to the convective resistance at the surface of the sheet. Thus smaller values of the Biot number provides high convective resistance at the surface, which leads to low heat transfer rate from the sheet to the fluid. Hence the fluid temperature is an increasing function of Biot number. We observed a motivating consequence that the distribution of temperature (θ(η)) is high for δ = 0 when compared that of δ ≠ 0.

Figure 5 is sketched to know the influence of microrotation parameter on the velocity, microrotation and thermal fields. From Fig. 5(a), it is spotted that fluid velocity is an increasing function of the microrotation parameter. As a result, we glimpse a decrement in temperature and microrotation profiles from Fig. 5(b),(c) respectively.

Figure 5
figure 5

Impact of Mr on (a) velocity (b) microrotation (c) temperature.

Full size image

Figures 6 and 7 are drawn to see the influence of γ and δ on \(f^{\prime} (\eta ),g(\eta )\) and \(\theta (\eta )\) respectively. From Fig. 6(a),(b), we eye that an accelerating values of δ results a hike in dimensionless velocity but the thermal field is a decelerating function of δ. Hence Fig. 6(c) says that the distribution of angular momentum increases with an increment in δ. The impression of γ on \(\theta (\eta ),g(\eta )\) and \(f^{\prime} (\eta )\) is investigated via Fig. 7(a)–(c) respectively. For increasing values of γ results a hike in both the thermal field and the corresponding boundary thickness. Moreover, the fluid velocity and microrotation profiles are decelerating functions of γ. So we conclude that the primary and the secondary slip parameters are proportional to each other. Hence the maximum temperature is noticed for second-order slip and maximum velocity is noticed for first-order slip parameter.

Figure 6
figure 6

Impact of δ on (a) velocity (b) microrotation (c) temperature.

Full size image
Figure 7
figure 7

Impact of γ on (a) velocity (b) microrotation (c) temperature.

Full size image

Figure 8(a),(b) reveal the nature of fluid temperature for different values of non-uniform heat source/sink parameters (A*, B*). It is detected that swelling values of irregular heat source/sink parameters results a hike in the fluid temperature. Actually, an increasing values of irregular heat parameters act as an agent to produce temperature in the flow. Due to this, we observed that a rise in the fluid temperature for swelling values of A*, B*. It is prominent that the more heat transfer is attained in the absence of second-order slip.

Figure 8
figure 8

Curves of temperature with the variant in (a) A* (b) B*.

Full size image

Findings of the Problem

This paper narrates the flow and thermal transport attributes of shear thinking fluid across a stretching surface with Biot number and drag force. Simultaneous solutions were presented for first and second order slips. The principal outcomes are listed below

  • Microrotation profile is a decelerating function of micropolar parameter.

  • A rise in the microrotation parameter causes the same in g(η) and θ(η) but a reverse trend is noticed for \(f^{\prime} (\eta )\).

  • Fluid temperature is enhanced due to an increment in the values of both Nr and θw.

  • The Velocity distribution upturns for rising values of magnetic field parameter.

  • In all the figures supreme velocity is achieved due to second order velocity slip however the supreme temperature is achieved due to first order slip.

  • The irregular heat raise/fall parameters plays key role in the heat transfer performance.

  • The nature of all the physical quantities is reverse for slip parameters.