Introduction

The enrichment of heat transfer performance for the working fluid in cooling/heating appliances with optimum use of cost and energy has been the main concern for industrial and societal benefits. The addition of a single nanoparticle into a host working fluid is originated by Choi1 to enhance the base fluid’s thermal conductivity. Since then, many investigations were conducted through experimental works or fundamental studies (computational boundary layer flow) with less cost and time consumption. The model by Buongiorno2 which related to the effects of Brownian motion and thermopheresis as well as the model by Tiwari and Das3, are widely used by many researchers in the computational analysis of the nanofluid’s flow. Using the spectral relaxation method, Oyelakin et al.4 solved the Buongiorno’s model of Casson nanofluid flow with the inclusion of slip and convective conditions, magnetic field and thermal radiation. Further, Oyelakin et al.5 discussed the three-dimensional flow of unsteady magnetohydrodynamics (MHD) Casson nanofluid utilizing the Buongiorno’s model. Another interesting works regarding the Buongiorno’s model of nanofluid can be read from these papers6,7,8,9,10,11. Meanwhile, Karmakar et al.12 scrutinized the stagnation point flow of carbon nanotubes (CNT)-water nanofluid towards a stretching sheet with convective boundary condition. In recent times, the combination of a base fluid with suspended dissimilar nanoparticles is experimentally conducted to create a superior nanocomposite liquid known as hybrid nanofluid. The hybrid nanofluid’s correlations by Takabi and Salehi13 and Devi and Devi14 were extensively used in the estimation of the thermophysical properties. The advantages of hybrid nanofluid in augmenting the heat transfer performance could also be found in these references15,16,17,18,19,20,21. For the distant future of the cooling/heating applications, there are tremendous demands in the investigation of both internal and external hybrid nanofluid flows. Acharya et al.22 observed the temperature profile of working fluid with Cu-TiO2 nanosuspension was greater than single nanofluids when it was streaming over a revolving disk. The inclined magnetic field with a suitable inclination angle was shown as one of the potential factors in augmenting the thermal rate of the hybrid nanofluid23. Further assessment of the nonlinear radiation and magnetic field effects have been conducted by Acharya et al.24 for hybrid Ag-Fe3O4/kerosene nanofluid flow over a permeable stretching sheet. The Cu-Al2O3/water hybrid nanofluid flow past an exponentially stretching/shrinking surface was recently studied by Wahid et al.25,26.

The squeezing flow which emerged from the moving boundaries is significant in polymer processing, lubrication equipment, molding’s injection, and compression including the hydrodynamical machines. The connection between the squeezing flow and the loaded bearings’ performance in engines including the phenomenon of adhesion has been highlighted by Jackson27. Stefan28 used lubrication approximation to initiate his work on squeezing flow. Meanwhile, other early works considering numerical schemes on the squeezing flow were studied by Verma29 and Singh et al.30. Hamza31 inspected the squeezing flow and highlighted the impact of the suction and injection parameters. Other interesting papers reflecting the squeezing viscous flow have been debated in Ahmad et al.32, Shah et al.33, Khan et al.34, Magalakwe et al.35 and Basha36. Later, the analysis of squeezing flow in nanofluids was also considered by a few of researchers. The time-dependent bioconvection flow containing motile gyrotactic microorganisms was solved by Raees et al.37 using Buongiorno’s model of nanofluid. Hayat et al.38 analyzed the unsteady squeezed flow of nanofluid with the presence of magnetic field while Hayat et al.39 scrutinized the effect of couple stress due to time-dependent applied magnetic field. Both Hayat et al.38,39 implemented the Buongiorno nanofluid model which indirectly examined any specific nanoparticles. Recently, Acharya et al.40 analyzed the simultaneous effects of chemical reaction, magnetic field, and second-order slip on the bioconvection nanofluid squeezing flow between two parallel plates. Meanwhile, interesting work of the squeezing hybrid nanofluid with Fe3O4-MoS2 and the combination of water and ethylene glycol for the base fluid was conducted by Salehi et al.41. The impact of radiation from the solar energy on the Cu-Al2O3/water hybrid nanofluid inside a channel was deliberated by Acharya42. Another interesting aspect of the internal hybrid nanofluid flow inside a channel also has been scrutinized by Ikram et al.43 and Islam et al.44. Detail description of previous works37,38,39,40,41,42,43,44 concerning the internal flow between two plates is presented in Table 1 which highlights the gap between previous works and the present study.

Table 1 Detail description of references concerning the internal flow between two plates.
Full size table

Inspired from the existing literature while fulfilling the available research gaps, this work aims to analyze the time-dependent squeezing flow of hybrid Cu-Al2O3/water nanofluid in a horizontal channel (between two parallel plates) with the magnetic field effect. The physical geometry of the lower plate is presumed as permeable and stretchable. Our main focus is to analyze the features of hybrid nanofluid flow like distribution of velocity, skin friction, temperature, and thermal rate for several physical parameters such as suction/injection, stretching, unsteadiness squeezing, the magnetic and volumetric concentration of the nanoparticles. In long term, this study is can be applied in designing an optimum thermal process for example in refrigeration systems and heat pumps using relevant physical sources. To accomplish the objectives, the single-phase mathematical model of Cu-Al2O3/water is formulated based on this physical problem and then, transformed into reduced differential equations via the similarity transformation. The bvp4c application is completely used for the results’ generation and validated based on the available numerical values from the previous works. This study is novel and original which considers a time-dependent Cu-Al2O3/water hybrid nanofluid flow with different boundary conditions as compared to the existing references in Table 1.

Mathematical model

Physical assumptions and thermophysical correlations

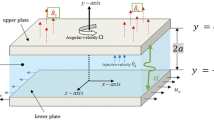
Cu-Al2O3/water formation is considered to flow between two infinite parallel plates, as shown in Fig. 1. The upper plate is placed at \(y = h\left( t \right) = \sqrt {\frac{{\nu _{f} \left( {1 - \alpha t} \right)}}{b}}\) from the lower plate, while the upper plate with velocity \(V_{h} = \frac{{dh\left( t \right)}}{{dt}} = - \frac{\alpha }{2}\sqrt {\frac{{\nu _{f} }}{{b\left( {1 - \alpha t} \right)}}}\) is moving towards (squeezing) the lower plate. Further assumption is the lower and upper plates are maintained at fixed temperatures \(T_{1}\) and \(T_{2}\), respectively. Meanwhile, the porous lower plate is included in the physical illustration for the possible fluid suction/injection with the wall mass velocity is denoted as \(v_{w} = - \frac{{V_{0} }}{{1 - \alpha t}}\); \(V_{0} > 0\) for suction, \(V_{0} < 0\) for injection and \(V_{0} = 0\) corresponds to an impermeable plate. Also, the lower plate is stretchable with linear velocity \(u_{w} = \frac{{bx}}{{1 - \alpha t}};t < {1 \mathord{\left/ {\vphantom {1 \alpha }} \right. \kern-\nulldelimiterspace} \alpha }\) while the inclusion of time-dependent magnetic field is formulated with \(B\left( t \right) = \frac{{B_{0} }}{{1 - \alpha t}}\) (see Hayat et al.38,39).

Figure 1
figure 1

Physical illustration with coordinate system.

Full size image

Under these assumptions and using the hybrid nanofluid model proposed by Takabi and Salehi13, the governing conservation equations are37,38,39.

$$ \frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial y}} = 0, $$
(1)
$$ \frac{{\partial V}}{{\partial t}} + u\frac{{\partial V}}{{\partial x}} + v\frac{{\partial V}}{{\partial y}} = \frac{{\mu _{{hnf}} }}{{\rho _{{hnf}} }}\frac{{\partial ^{2} V}}{{\partial y^{2} }} - \frac{{\sigma _{{hnf}} }}{{\rho _{{hnf}} }}B\left( t \right)^{2} V, $$
(2)
$$ \frac{{\partial T}}{{\partial t}} + u\frac{{\partial T}}{{\partial x}} + v\frac{{\partial T}}{{\partial y}} = \frac{{k_{{hnf}} }}{{(\rho C_{p} )_{{hnf}} }}\frac{{\partial ^{2} T}}{{\partial y^{2} }}, $$
(3)

where \(V = \frac{{\partial v}}{{\partial x}} - \frac{{\partial u}}{{\partial y}}\). The associate conditions at the lower and upper plates are (see Raees et al.37 and Hayat et al.38,39)

$$ \begin{gathered} u = \lambda \frac{{bx}}{{1 - \alpha t}},{\text{ }}v = - \frac{{V_{0} }}{{1 - \alpha t}},{\text{ }}T = T_{1} {\text{ at }}y = 0{\text{ (lower plate)}} \hfill \\ u = 0,{\text{ }}v = \frac{{dh\left( t \right)}}{{dt}},{\text{ }}T = T_{2} {\text{ at }}y = h\left( t \right){\text{ (upper plate)}} \hfill \\ \end{gathered} $$
(4)

Here \(u\) and \(v\) are the velocities along \(x\) and \(y\) directions and \(T\) is the hybrid nanofluid temperature. For the evaluation of the thermophysical properties (see Table 2), we adopt the correlations by Takabi and Salehi13 which are feasible and correct based on the experimental validation. These correlations are built based on the physical assumptions. Meanwhile, Table 3 display the the physical properties of the pure water and nanoparticles.

Table 2 Hybrid nanofluid’s correlations13.
Full size table
Table 3 Thermophysical properties for pure water and nanoparticles45,46.
Full size table

Reduced differential equations

According to Raees et al.37 and Hayat et al.38,39, the suitable dimensionless variables are

$$ \left. \begin{gathered} \psi = \sqrt {\frac{{b\nu _{f} }}{{1 - \alpha t}}} xf\left( \eta \right),{\text{ }}u = \frac{{bx}}{{1 - \alpha t}}f^{\prime}\left( \eta \right),{\text{ }}v = - \sqrt {\frac{{b\nu _{f} }}{{1 - \alpha t}}} f\left( \eta \right),{\text{ }} \hfill \\ \eta = \sqrt {\frac{b}{{\nu _{f} \left( {1 - \alpha t} \right)}}} y,{\text{ }}\theta \left( \eta \right) = \frac{{T - T_{0} }}{{T_{2} - T_{0} }} \hfill \\ \end{gathered} \right\} $$
(5)

Hence, substituting (5) into Eqs. (2)-(4), the ODEs and boundary conditions are

$$ \left( {\frac{{{{\mu _{{hnf}} } \mathord{\left/ {\vphantom {{\mu _{{hnf}} } {\mu _{f} }}} \right. \kern-\nulldelimiterspace} {\mu _{f} }}}}{{{{\rho _{{hnf}} } \mathord{\left/ {\vphantom {{\rho _{{hnf}} } {\rho _{f} }}} \right. \kern-\nulldelimiterspace} {\rho _{f} }}}}} \right)f^{{iv}} + ff^{\prime\prime\prime} - f^{\prime}f^{\prime\prime} - \frac{{Sq}}{2}\left( {3f^{\prime\prime} + \eta f^{\prime\prime\prime}} \right) - \left( {\frac{{{{\sigma _{{hnf}} } \mathord{\left/ {\vphantom {{\sigma _{{hnf}} } {\sigma _{f} }}} \right. \kern-\nulldelimiterspace} {\sigma _{f} }}}}{{{{\rho _{{hnf}} } \mathord{\left/ {\vphantom {{\rho _{{hnf}} } {\rho _{f} }}} \right. \kern-\nulldelimiterspace} {\rho _{f} }}}}} \right)Mf^{\prime\prime} = 0, $$
(6)
$$ \frac{1}{{\Pr }}\frac{{{{k_{{hnf}} } \mathord{\left/ {\vphantom {{k_{{hnf}} } {k_{f} }}} \right. \kern-\nulldelimiterspace} {k_{f} }}}}{{{{\left( {\rho C_{p} } \right)_{{hnf}} } \mathord{\left/ {\vphantom {{\left( {\rho C_{p} } \right)_{{hnf}} } {\left( {\rho C_{p} } \right)_{f} }}} \right. \kern-\nulldelimiterspace} {\left( {\rho C_{p} } \right)_{f} }}}}\theta ^{\prime\prime} + f\theta ^{\prime} - \frac{{Sq}}{2}\eta \theta ^{\prime} = 0, $$
(7)
$$ \begin{gathered} f^{\prime}\left( 0 \right) = \lambda ,{\text{ }}f\left( 0 \right) = S,{\text{ }}\theta \left( 0 \right) = \delta , \hfill \\ f^{\prime}\left( 1 \right) = 0,{\text{ }}f\left( 1 \right) = \frac{{Sq}}{2},{\text{ }}\theta \left( 1 \right) = 1. \hfill \\ \end{gathered} $$
(8)

where \(\lambda > 0\) refers to the stretching lower plate and \(\lambda = 0\) denotes the fixed/static lower plate. Another dimensionless parameters are the unsteadiness squeezing parameter \(Sq\), magnetic parameter \(M\), suction parameter \(S\), Prandtl number \(\Pr\) and constant \(\delta\). These parameters are defined as37,38,39

$$ \Pr = \frac{{\left( {\rho C_{p} } \right)_{f} }}{{k_{f} }},{\text{ }}Sq = \frac{\alpha }{b},{\text{ }}M = \frac{{\sigma _{f} B_{0} }}{{b\rho _{f} }},{\text{ }}S = \frac{{V_{0} }}{{bh}},{\text{ }}\delta = \frac{{T_{1} - T_{0} }}{{T_{2} - T_{0} }},{\text{ }} $$
(9)

In this work, we set \(\delta = 0\) which in accordance with Hayat et al.38,39. Further, we notice that Eq. (6) is compatible with the reduced momentum equation in Hayat et al.38 and Hayat et al.39 (if the couple stress parameter is zero) with the exclusion of the hybrid nanoparticles or \(\phi _{1} ,\phi _{2} \approx 0\) (regular fluid). The reduced skin friction coefficients and local Nusselt numbers at lower and upper plates are37,38,39

$$ {\text{Lower: }}\text{Re} _{x} ^{{1/2}} C_{{f1}} = \frac{{\mu _{{hnf}} }}{{\mu _{f} }}f^{\prime\prime}\left( 0 \right){\text{, Upper: }}\text{Re} _{x} ^{{1/2}} C_{{f2}} = \frac{{\mu _{{hnf}} }}{{\mu _{f} }}f^{\prime\prime}\left( 1 \right){\text{, }} $$
(10)
$$ {\text{Lower: }}\text{Re} _{x} ^{{ - 1/2}} Nu_{{x1}} = - \frac{{k_{{hnf}} }}{{k_{f} }}\theta ^{\prime}\left( 0 \right){\text{, }}\text{Re} _{x} ^{{ - 1/2}} Nu_{{x2}} = - \frac{{k_{{hnf}} }}{{k_{f} }}\theta ^{\prime}\left( 1 \right){\text{, }} $$
(11)

where \(\text{Re} _{x} = \frac{{xU_{w} }}{{\nu _{f} }}.\)

Numerical methods and validation test

In solving the boundary layer equations, there are many methods proposed by the researchers such as homotopy analysis method (HAM), shooting technique, Keller-box method, Runge–Kutta method, Laplace transform and many others. A concise review of the numerical methods which used to solve the boundary layer equations specifically for Casson fluid was discussed by Verma and Mondal47. Meanwhile, Rai and Mondal48 reviewed spectral methods like spectral relaxation method, spectral homotopy analysis method, spectral quasi-linearization method and spectral local linearization method in solving fluid flow problem. Another interesting technique namely multi domain bivariate quasi-linearization method was used by Oyelakin et al.49 in solving mixed convection flow of Casson nanofluid. Meanwhile, the bvp4c solver procurable in the Matlab software was also widely used by many researchers to solve the nonlinear ODEs. It is validated that the results of limiting cases using bvp4c is in accordance with the previously published results that used another methods (i.e., analytical, shooting, Keller-box method). The finite difference method under subclass 3-stage Lobatto IIIa scheme was programmed into the bvp4c solver through a general syntax sol = bvp4c (@OdeBVP, @OdeBC, solinit, options). For the completion of the numerical solutions in this study, Eqs. (6) to (8) are solved by transforming it first into the language of the bvp4c code as follows:

$$ f = y1,{\text{ }}f^{\prime} = y2,{\text{ }}f^{\prime\prime} = y3,{\text{ }}f^{\prime\prime\prime} = y4,{\text{ }} $$
(12)
$$ \begin{gathered} f^{{iv}} = \left( {\frac{{{{\rho _{{hnf}} } \mathord{\left/ {\vphantom {{\rho _{{hnf}} } {\rho _{f} }}} \right. \kern-\nulldelimiterspace} {\rho _{f} }}}}{{{{\mu _{{hnf}} } \mathord{\left/ {\vphantom {{\mu _{{hnf}} } {\mu _{f} }}} \right. \kern-\nulldelimiterspace} {\mu _{f} }}}}} \right)\left( {f^{\prime}f^{\prime\prime} - ff^{\prime\prime\prime} + \frac{{Sq}}{2}\left( {3f^{\prime\prime} + \eta f^{\prime\prime\prime}} \right) + \left( {\frac{{{{\sigma _{{hnf}} } \mathord{\left/ {\vphantom {{\sigma _{{hnf}} } {\sigma _{f} }}} \right. \kern-\nulldelimiterspace} {\sigma _{f} }}}}{{{{\rho _{{hnf}} } \mathord{\left/ {\vphantom {{\rho _{{hnf}} } {\rho _{f} }}} \right. \kern-\nulldelimiterspace} {\rho _{f} }}}}} \right)Mf^{\prime\prime}} \right), \hfill \\ {\text{ }} = \left( {\frac{{{{\rho _{{hnf}} } \mathord{\left/ {\vphantom {{\rho _{{hnf}} } {\rho _{f} }}} \right. \kern-\nulldelimiterspace} {\rho _{f} }}}}{{{{\mu _{{hnf}} } \mathord{\left/ {\vphantom {{\mu _{{hnf}} } {\mu _{f} }}} \right. \kern-\nulldelimiterspace} {\mu _{f} }}}}} \right)\left( {y2y3 - y1y4 + \frac{{Sq}}{2}\left( {3y3 + \eta y4} \right) + \left( {\frac{{{{\sigma _{{hnf}} } \mathord{\left/ {\vphantom {{\sigma _{{hnf}} } {\sigma _{f} }}} \right. \kern-\nulldelimiterspace} {\sigma _{f} }}}}{{{{\rho _{{hnf}} } \mathord{\left/ {\vphantom {{\rho _{{hnf}} } {\rho _{f} }}} \right. \kern-\nulldelimiterspace} {\rho _{f} }}}}} \right)My3} \right), \hfill \\ \end{gathered} $$
(13)
$$ \theta = y5,{\text{ }}\theta ^{\prime} = y6,{\text{ }} $$
(14)
$$ \begin{gathered} \theta ^{\prime\prime} = \Pr \left( {\frac{{{{\left( {\rho C_{p} } \right)_{{hnf}} } \mathord{\left/ {\vphantom {{\left( {\rho C_{p} } \right)_{{hnf}} } {\left( {\rho C_{p} } \right)_{f} }}} \right. \kern-\nulldelimiterspace} {\left( {\rho C_{p} } \right)_{f} }}}}{{{{k_{{hnf}} } \mathord{\left/ {\vphantom {{k_{{hnf}} } {k_{f} }}} \right. \kern-\nulldelimiterspace} {k_{f} }}}}} \right)\left( {\frac{{Sq}}{2}\eta \theta ^{\prime} - f\theta ^{\prime}} \right), \hfill \\ {\text{ }} = \Pr \left( {\frac{{{{\left( {\rho C_{p} } \right)_{{hnf}} } \mathord{\left/ {\vphantom {{\left( {\rho C_{p} } \right)_{{hnf}} } {\left( {\rho C_{p} } \right)_{f} }}} \right. \kern-\nulldelimiterspace} {\left( {\rho C_{p} } \right)_{f} }}}}{{{{k_{{hnf}} } \mathord{\left/ {\vphantom {{k_{{hnf}} } {k_{f} }}} \right. \kern-\nulldelimiterspace} {k_{f} }}}}} \right)\left( {\frac{{Sq}}{2}\eta y6 - y1y6} \right), \hfill \\ \end{gathered} $$
(15)
$$ \begin{gathered} f^{\prime}\left( 0 \right) = \lambda ,{\text{ }}f\left( 0 \right) = S,{\text{ }}\theta \left( 0 \right) = \delta , \hfill \\ f^{\prime}\left( 1 \right) = 0,{\text{ }}f\left( 1 \right) = \frac{{Sq}}{2},{\text{ }}\theta \left( 1 \right) = 1, \hfill \\ \hfill \\ ya2 - \lambda ,{\text{ }}ya1 - S,{\text{ }}ya5 - \delta , \hfill \\ yb2,{\text{ }}yb1 - \frac{{Sq}}{2},{\text{ }}yb5 - 1. \hfill \\ \end{gathered} $$
(16)

where \(ya\) and \(yb\) implies the boundary conditions at lower and upper plates, respectively. The bvp4c solver will code Eqs. (13) and (15) into @OdeBVP while the condition (16) is coded into @OdeBC. Generally, the solinit function refers to the initial mesh point and guesses at the mesh points. However, modifications are necessary for the solinit and options functions in the bvp4c syntax to solve the present internal flow problem which affirms the novelty of this work. The asymptotical profile (for usual boundary layer flow) is necessary when the problem is dealing with the external flow over an infinite surface where these profiles must satisfy the free stream condition. However, in this work, the validation part is based on the comparison with previous similar works as presented in Tables 4 and 5. The validation is important to highlight the precision of the present model and code. Hence, the numerical values are compared with Hayat et al.38,39 (main references) as displayed in Tables 4 and 5 which shows identical results when suction and magnetic parameters are considered.

Table 4 Comparative values of \(f^{\prime\prime}\left( 0 \right)\)-lower plate and \(f^{\prime\prime}\left( 1 \right)\)-upper plate when \(Sq = 0\), \(\lambda = 1\), \(\phi _{1} ,\phi _{2} = 0\) with various \(S\) and \(M\).
Full size table
Table 5 Comparative values of \(f^{\prime\prime}\left( 1 \right)\)-upper plate when \(\lambda = 1\) and \(\phi _{1} ,\phi _{2} \approx 0\) with various \(S\), \(Sq\) and \(M\).
Full size table

Results and discussion

The results are generated and graphically presented for the distribution of the skin friction coefficients, velocity, heat transfer rates, and temperature of both upper and lower plates. The value of the Prandtl number is fixed to 6.2 which indicates the use of water at 25 °C while the initial temperature at the lower plate’s wall is represented by \(\delta = 0\) so that \(\theta \left( 0 \right) = 0\). Other parameters are controlled within the ranges of \(0 \le Sq \le 1\) (unsteadiness squeezing parameter), \(- 1.2 \le S \le 1.2\) (suction/injection parameter), \(0 \le \lambda \le 2\) (stretching parameter), and \(0 \le M \le 3\) (magnetic parameter).

Table 6 shows the variety of \(\text{Re} _{x} ^{{1/2}} C_{{f1}}\), \(\text{Re} _{x} ^{{1/2}} C_{{f2}}\), \(- \text{Re} _{x} ^{{ - 1/2}} Nu_{{x1}}\) and \(- \text{Re} _{x} ^{{ - 1/2}} Nu_{{x2}}\). With the consideration of viscous fluid, lower static plate, and the exclusion of magnetic, suction/injection, and squeezing parameters, the internal flow has zero frictions and equal heat transfer rates at both plates. The observation in Table 6 shows that as the stretching parameter increases from \(\lambda = 0\) to \(\lambda = 1\), \(- \text{Re} _{x} ^{{ - 1/2}} Nu_{{x1}}\) increases, but the stretching lower plate tends to increase \(\text{Re} _{x} ^{{1/2}} C_{{f1}}\). Further, we analyze four types of fluids: viscous/water \(\left( {\phi _{1} ,\phi _{2} = 0} \right)\), Al2O3-water \(\left( {\phi _{1} = 0.01,\phi _{2} = 0} \right)\), Cu-water \(\left( {\phi _{1} = 0,\phi _{2} = 0.01} \right)\) , and Cu-Al2O3/water \(\left( {\phi _{1} ,\phi _{2} = 0.01} \right)\) which reveals that the Cu-Al2O3/water has the highest heat transfer coefficients at both plates followed by the Cu-water, Al2O3-water, and water. This implies the suitability of Cu-Al2O3/water hybrid nanofluid as an effective coolant in engineering and technology appliances. Since the inclusion of the squeezing parameter can reduce the heat transfer rate at both plates, it is useful to know the exact parameters which can assist the heat transfer performance for this situation. In Table 7, we analyze the difference percentage of the heat transfer rate at both upper and lower plate which can be used for future assessment by other engineers or researchers. This analysis also can help in determining the preferable strength of the parameters either in the augmentation or reduction of the heat transfer in both locations.

Table 6 Numerical values of \(\text{Re} _{x} ^{{1/2}} C_{{f1}}\), \(\text{Re} _{x} ^{{1/2}} C_{{f2}}\), \(- \text{Re} _{x} ^{{ - 1/2}} Nu_{{x1}}\) and \(- \text{Re} _{x} ^{{ - 1/2}} Nu_{{x2}}\) with various values of the control parameters.
Full size table
Table 7 Heat transfer analysis with the addition of the control parameters.
Full size table

The exploration of pertinent parameters’ impact such as squeezing, suction/injection, and stretching parameters is continued with the observation on \(f^{\prime}\left( \eta \right)\) and \(\theta \left( \eta \right)\) as displayed in Figs. 2–7. In Fig. 2, the velocity distribution enhances with the addition of the unsteadiness squeezing parameter. As the squeezing parameter’s magnitude increases up to \(Sq = 1\), the velocity distribution is depreciated at the upper plate. This is due to the squeezing effect which originated from the upper plate. However, the temperature profile in Fig. 3 slightly reduces near to the lower plate \(\left( {\eta < 0.5} \right)\) while increases near to the upper plate \(\left( {\eta > 0.5} \right)\).

Figure 2
figure 2

Effect of squeezing parameter on \(f^{\prime}\left( \eta \right)\) when \(S = 0.2\), \(\lambda = 0\), \(M = 1\) and \(\phi _{1} = \phi _{2} = 0.01\).

Full size image
Figure 3
figure 3

Effect of squeezing parameter on \(\theta \left( \eta \right)\) when \(S = 0.2\), \(\lambda = 0\), \(Sq = M = 1\) and \(\phi _{1} = \phi _{2} = 0.01\).

Full size image

Further, the impact of the suction/injection parameter on both profiles is visualized in Figs. 4 and 5. As the suction/injection parameter increases from injection to suction \(\left( {S = - 1.2, - 0.2,0,0.2,1.2} \right)\), the velocity profile decreases which reflects the higher magnitude of suction strength can reduce the velocity distribution. Since the suction is applied through the lower permeable plate, the velocity lessens while increases near to the upper plate. The temperature profile augments at both locations (lower and upper plate). Figures 6 and 7 present the plots of velocity and temperature distribution with variety values of the stretching parameter. The velocity gradually increases when \(\eta < 0.3\) while a contrary observation is obtained for \(\eta > 0.3\). The temperature profile increases for both lower and upper plates.

Figure 4
figure 4

Effect of suction/injection parameter on \(f^{\prime}\left( \eta \right)\) when \(\lambda = 0\), \(Sq = M = 1\) and \(\phi _{1} = \phi _{2} = 0.01\).

Full size image
Figure 5
figure 5

Effect of suction/injection parameter on \(\theta \left( \eta \right)\) when \(\lambda = 0\), \(Sq = M = 1\) and \(\phi _{1} = \phi _{2} = 0.01\).

Full size image
Figure 6
figure 6

Effect of stretching parameter on \(f^{\prime}\left( \eta \right)\) when \(S = 0.2\), \(Sq = M = 1\) and \(\phi _{1} = \phi _{2} = 0.01\).

Full size image
Figure 7
figure 7

Effect of stretching parameter on \(\theta \left( \eta \right)\) when \(S = 0.2\), \(Sq = M = 1\) and \(\phi _{1} = \phi _{2} = 0.01\).

Full size image

Conclusion

This novel work presents a numerical study of Cu-Al2O3/water inside two plates (parallel lower and upper) with the appearance of the magnetic field. The lower plate is permeable for the suction/injection processes and also can be stretched. Meanwhile, the upper plate can move towards the lower plate and creates the squeezing flow phenomenon. The mathematical model which suits this physical phenomenon follows the usual approximations of boundary layer flow while the bvp4c programme is fully utilized for the generation of the results. The distribution of \(\text{Re} _{x} ^{{1/2}} C_{{f1}}\), \(\text{Re} _{x} ^{{1/2}} C_{{f2}}\), \(- \text{Re} _{x} ^{{ - 1/2}} Nu_{{x1}}\) and \(- \text{Re} _{x} ^{{ - 1/2}} Nu_{{x2}}\) are examined. The heat transfer rate of the lower plate reduces with the increase of magnetic, squeezing, and injection parameters. However, about 30.35% of \(- \text{Re} _{x} ^{{ - 1/2}} Nu_{{x1}}\) is developed with the inclusion of suction. Meanwhile, the enhancement of magnetic and injection parameters can lead to the development of the upper plate’s heat transfer performance. Another observation is conducted for the distribution of the velocity and temperature profiles. The addition of squeezing and stretching parameters can increase the velocity profile whereas high suction’s magnitude shows the opposite trend.