RETRACTED ARTICLE: A numerical study of chemical reaction in a nanofluid flow due to rotating disk in the presence of magnetic field

Abstract

In this paper, a numerical study of MHD steady flow due to a rotating disk with mixed convection, Darcy Forchheimer’s porous media, thermal radiation, and heat generation/absorption effects are explored. A strong magnetic field is applied in perpendicular direction to the flow which governs the Hall current effects. Homogeneous and heterogeneous reactions are also taken into account. For the simplification of partial differential equations (PDEs) into the nonlinear ordinary differential equations (ODEs), the method of generalized Von Karman similarity transformations is employed, and the resulting non-dimensional ordinary differential equations are solved by using the homotopy analysis method (HAM). Effects of different parameters on the axial, radial and tangential velocity profiles, temperature and concentration of chemical reaction profiles are analyzed and discussed. The present work’s remarkable finding is that with the expansion of nanoparticles size, dimensionless constant parameter, local Grashof number, porosity parameter, Hall current, and suction parameter, the nanofluid radial velocity is enhanced. For the higher values of magnetic field parameter, the tangential velocity and nanofluid temperature are enhanced. The magnetic field parameter and the disk thickness coefficient parameter have similar impacts on the axial velocity profile. Heterogeneous chemical reaction parameter decreases the concentration of chemical reaction profile. The nanoparticles volume fraction increases the concentration of chemical reaction profile. Furthermore, the present results are found to be in excellent agreement with previously published work in tabulated form.

Introduction

The flow problem due to rotating disk is much interest for scientists over the last few years because of its vast applications in industrial and engineering process such as spin coating, centrifugal pumps, rotor-stator system, electronic device, turbomachinery and multi-power distributor manipulative, etc. The nonlinear radiated MHD flow of nanofluids due to rotating disk with heat flux conditions and irregular heat source is studied by Mahanthesh et al.¹. They used the Runge–Kutta Fehlberg method to find the solution of their problem numerically and also discussed the different results of velocities and temperature graphically. By using partial slip conditions over a rotating disk, the magnetohydrodynamic flow of Cu-water nanofluid is investigated by Hayat et al.² where homotopy analysis technique is used to find the numerical results of the flow and heat transfer model. Yin et al.³ analyzed the occurrence of a uniform stretching rate in the radial direction of the heat and flow transfer of a nanofluid over the disk. To find the solution of their mathematical model numerically, they engaged the homotopy analysis method (HAM). Their research work shows that the velocity in axial and radial directions, coefficient of skin friction and local Nusselt number are enhanced with the increasing of stretching parameter, while the velocity in tangential direction and thickness of thermal boundary layer is decreased. In the presence of slip conditions over a rotating disk, the magnetohydrodynamic flow of nanofluid is explored by Hayat et al.⁴. In their research work, they performed the computation for Sherwood and Nusselt numbers and also noted the impacts of different parameters on the temperature, concentration, and velocity profiles. The properties of a magnetohydrodynamic slip flow with variable thickness toward the rotating disk is initiated by Imtiaz et al.⁵ with the application of homotopy analysis technique for the solution, obtaining the convergent series solution for the model. Their conclusions show that for the variable thickness of a rotating disk, the effects of radial and axial velocities are opposite where for Hartman number and drag forces have a direct relationship with each other. In the presence of variable thickness, the slip flow and entropy generation in magnetohydrodynamic on a rotating porous disk is presented by Rashidi et al.⁶. To obtain the numerical solution of their model, Von Karman approach is employed and also discussed the impacts of different parameters namely relative temperature difference, suction injection parameter. By the impact of partial slip, the MHD nanofluid over rotating disk through the use of the Buongiorno model is proposed by Mustafa⁷ through the applications of the shooting technique. Turkyilmazoglu⁸ scrutinized the heat transfer and nanofluid flow with the implementation of spectral Chebyshev collection numerical integration scheme. For various values of nanoparticles volume fraction, the properties of heat transfer and shear stress as well as flow and temperature fields are calculated by him and found that with the increment of Cu-nanofluid the heat transfer rate is enhanced. Lin et al.⁹ demonstrated the Marangoni boundary layer flow of copper-water nanofluid and heat transfer toward the porous medium disk. For the conversion of partial differential equations into ordinary differential equations, they used generalized Karman transformations. Sheikholeslami et al.¹⁰ analyzed the nanofluid model for the cooling process on the rotating disk with the help of the fourth-order Runge-Kutta method. They found that the thermophoretic parameter and Schmidt number have increasing effects. Turkyilmazoglu and Senel¹¹ explained the heat and mass transfer flow due to the rotating disk. Their results show that for heat and mass transfer, the roughness of the surface and slip parameters are decreased but suction and injection are in opposite behavior. Devi and Devi¹² described the hydromagnetic flow past a rotating disk with the effects of radiation and magnetic field parameters through the use of Runge–Kutta method with shooting technique. Osalusi¹³ discussed the magnetohydrodynamic and slip flow through the variable thickness in the presence of thermal radiation over the rotating disk. Khan et al.¹⁴ investigated the analytical modeling for heat transfer of the couple stress and unsteady MHD flow due to the rotating disk in which they explained the variation of physical parameters for pressure, temperature, and velocity profiles. Arikoglu and Ozkol¹⁵ pointed out the study of MHD and slip flow with the occurrence of heat transfer through the rotating disk. They noticed that the velocity of the fluid in radial, axial and tangential directions are decreased with magnetic flux and slip parameters. Nadeem et al.¹⁶ used the Optimal Homotopy Asymptotic Method (OHAM) to find the exact solution of the third-grade nanofluid model for a rotating vertical cone with Brownian motion and thermophoresis effects. They used the Buongiorno nanofluid model and detected that for increasing values of the buoyancy forces and unsteadiness parameter, the rate of heat transfer and Sherwood number are enhanced. Hafeez et al.¹⁷ considered the 3D Oldroyd-B nanofluid over a rotating disk under the effect of stagnation point flow via the BVP Midrich technique. They concluded that the temperature distribution of the Oldroyed-B nanofluid is rising for higher values of disk convection parameter and radiative heat flux. Abbasi et al.¹⁸ examined the non-Newtonian viscoelastic nanofluid over a rotating disk in the presence of heat source through the utilization of the Keller box scheme. They observed that both the temperature and the concentration profiles of the nanofluid are increased for the thermophoresis parameter. Recent additions considering nanofluids with heat and mass transfer in various physical situations are given by Refs.^{19,20,21,22,23}.

The nanofluids have various applications in numerous crucial areas such as microelectronics, manufacturing, power saving, transportation, medical, and microfluidics. All these elements enhance the heating rate and decrease the processing time as well as extend the life span of machinery. In the automotive and nuclear reactor, heat exchange systems, nanofluids are utilized as coolants. Nanofluids are described as nanoparticles embedded inside the fluid with a size of less than 100 nm. Nanofluids have wide applications in cooling towers, in cancer patient detection of drugs, the efficiency of the hybrid-powered engine, and transportation. Abbasi et al.²⁴ employed the Keller box method for the description of the bioconvection nanofluid model toward the rotting disk along with zero mass flux and convective conditions. Tiwari et al.²⁵ discussed the water and multi-walled carbon nanotubes based hybrid nanofluid with the thermal conductivity of $\hbox {CeO}_{{2}}$ where their study contains the 4S consideration (synthesis, sonication, surfactant, stability). For the preparation of the nanofluid, they used the two-step method and a broad range of ultrasonication time (30, 60, 90, 120, 150, and 180 min). Finally, a correlation has been evaluated from the experimental data to estimate the experimental values of thermal conductivity, which could be useful in a variety of heat transfer applications. Ahmad et al.²⁶ described the mathematical modeling of nanofluid with the base fluid water and kerosene through the porous medium. Acharya²⁷ explored the idea of the unsteady ferrous-water nano liquid flow with the existence of a magnetic field over the rotating disk and discoursed the effects of nanolayer and nanoparticle diameter. The spectral quasilinearization method is adopted for the numerical solution of his model. Li et al.²⁸ investigated the chemical reaction and irreversibility phenomena in a nanofluid past a rotating sheet along with entropy behavior. Tiwari et al.²⁹ analyzed the viscosity and stability of hybrid nanoparticle with different base fluid in the presence of surfactants such as cetrimonium chloride (CTAC), ammonium lauryl sulphate (ALS), PLS (pottasium lauryl sulphate), benzalkonium chloride (BAC), sonication time (30–240 min), and temperature (55 $^\circ$C $\thicksim$ 80 $^\circ$C). Their outcomes indicate that the stability of the prepared hybrid nanofluid through the use of different base fluid. Acharya³⁰ investigated the ferrofluid flow toward the spinning disk by considering the solid–liquid interfacial layer and nanoparticles diameter with the oscillating magnetic effect and found that the heat transfer is intensified for base liquid nanolayer conductivity ratio but decreases for nanoparticles diameter. Ahmed et al.³¹ examined the SWCNT-MWCNT hybrid nanofluid problem due to the moving wedge by the occurrence of temperature-dependent viscosity in which their experiment shows that for both nanofluid and hybrid nanofluid temperature profiles are declined but the axial velocity is increased for viscosity parameter. Acharya³² described the study of radiative nanofluid over the curved surface. He transformed the higher-order partial differential equations into the system of nonlinear ordinary differential equations with the help of suitable similarity variables and solved these resulting ordinary differential equations by using the spectral quasilinearization technique. An increment in the mass transfer rate is noted for thermal and Biot number but Lewis number and curvature parameter decrease the mass transfer rate. Acharya and Mabood³³ inspected the existence of thermal radiation and heat source/sink with hydrothermal features of both hybrid nanofluid and mono nanofluid flow toward the bent curve. The graphene and ferrous nanoparticles are also taken into account in which the fluid temperature and velocity are raised for nanoparticles concentration. Acharya et al.³⁴ investigated the nanofluid model for a spinning disk with a Hall current and radiation effects. Their conclusions show that the Hall current and nanoparticles volume fraction amplifies the radial velocity. Acharya et al.³⁵ explained the unsteady chemically reactive nanofluid flow by applying the Brownian motion and thermophoresis impacts on the bidirectional stretching surface which proved that the Brownian motion and thermophoresis diminish the concentration of the nanofluid. Acharya et al.³⁶ reported the significance of water-based hybrid nanofluid $\hbox {TiO}_{{2}}$–$\hbox {CoFe}_{{204}}$ through the revolving disk.

The present study is related to Hall current effect, variable thickness and homogeneous–heterogenous chemical reactions of the nanofluid to examine the heat transfer and magnetically driven nanofluid flow over a rotating disk. The partial differential equations of the model are converted into ordinary differential equations with the help of similarity transformations and solved by using the homotopy analysis method (HAM). The effects of different parameters are analyzed and discussed.

Methods

Basic equations

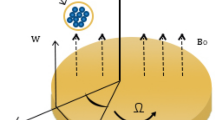
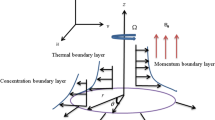
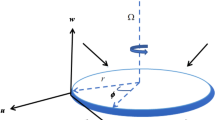
The steady, axially symmetric laminar flow of nanofluid with heat generation/absorption past a porous rotating disk is explored. Strong magnetic field which is responsible to generate the Hall current effects is applied normally to the flow by ignoring the induced magnetic field. The fluid motion is produced due to the rotation and stretching of the disk. The disk is rotated at $z =0$ with a uniform angular velocity $\Omega$. Imagine the disk of variable thickness is at $z = d ( 1+\frac{r}{R_{0}})^{-p_{1}}$. The thermal radiation effect is also taken in the present study. Due to the rotational symmetry, the derivatives in the azimuthal direction may be neglected. Heat transportation modeling is computed with the addition of viscous dissipation. The z-axis is taken perpendicularly to the surface of the rotating disk while in $r$, $\vartheta$ and $z$ directions the velocities are denoted by $u$, $v$ and $w$ in the cylindrical coordinate system. ${T_{w}}$ is the temperature of the disk and ambient temperature of the fluid is ${T_{\infty }}$. The temperature ${T_{w}}$ at the surface of the disk is higher than the fluid ambient temperature ${T_{\infty }}$. A simple model is considered for the interaction between a homogeneous (or bulk) reaction and a heterogeneous (or surface) reaction involving two chemical species $A$ and $B$. Figure 1 shows the physical model of the problem.

Figure 1

Physical model of the problem.

Under the above assumptions, the governing equations^37,41,42,43 for the present heat and mass transfer nanofluid flow model is given below

$$\begin{aligned}\frac{\partial u}{\partial r} + \frac{u}{r} + \frac{\partial w}{\partial z} = 0, \end{aligned}$$

(1)

$$\begin{aligned} \left( u \frac{\partial u}{\partial r}- \frac{v^{2}}{r} + w \frac{\partial u}{\partial z}\right)&=-\frac{1}{\rho _{nf}}\frac{\partial P}{\partial r} +{\nu _{nf}}\left(\frac{\partial ^2 u}{\partial r^{2}} + \frac{\partial ^2 u}{\partial z^{2}}\right)+\frac{{g_{1}}(\rho \beta _{T})_{nf}(T-T_{\infty })}{\rho _{nf}}-\frac{\sigma _{nf}{{B_{0}}}^{2}}{\rho _{nf}{(1+m^{2})}}( u+mw)\nonumber \\&\quad -\frac{\nu _{nf}}{k^{*}}{} u - {{F}_{{1}}}{u^{2}}, \end{aligned}$$

(2)

$$\begin{aligned}\left( u \frac{\partial v}{\partial r}+ \frac{uv}{r} + w \frac{\partial v}{\partial z} \right) ={\nu _{nf}}\left(\frac{\partial ^2 v}{\partial r^{2}} + \frac{\partial ^2 v}{\partial z^{2}}\right)-\frac{\sigma _{nf}{{B_{0}}}^{2}}{\rho _{nf}{(1+m^{2})}}( v+mu)-F_{1} {} v^{2} , \end{aligned}$$

(3)

$$\begin{aligned}\left( u \frac{\partial T}{\partial r} + w \frac{\partial T}{\partial z}\right) =\frac{k_{nf}}{(\rho {C}_{P})_{nf}}\left(\frac{\partial ^2 T}{\partial r^{2}} + \frac{\partial ^2 T}{\partial z^{2}}\right)+Q_{0} -\frac{1}{{(\rho {C}_{P})_{nf}}}\frac{\partial q_{r}}{\partial z}, \end{aligned}$$

(4)

$$\begin{aligned}\left( u \frac{\partial a}{\partial r} + w \frac{\partial a}{\partial z}\right) =D_{A} \left(\frac{\partial ^2 a}{\partial z^{2}}\right)-k_{c} {} a {} b^{2} , \end{aligned}$$

(5)

$$\begin{aligned}\left( u \frac{\partial b}{\partial r} + w \frac{\partial b}{\partial z}\right) =D_{B} \left(\frac{\partial ^2 b}{\partial z^{2}}\right)+k_{c} {} a {} b^{2} . \end{aligned}$$

(6)

The boundary conditions for the present problem are

$$\begin{aligned}{u} = 0,\quad {v} = {r}\Omega ,\quad {w} = {w_{0}},\quad {T} = {T_{w}}, \quad {D_{A}}\frac{\partial a}{\partial z}={{k_{s}}{a}},\quad {D_{B}}\frac{\partial b}{\partial z}=-{{k_{s}}{a}},\quad at \quad {z} = {d}(1+r^{*})^{-p_{1}}, \end{aligned}$$

(7)

$$\begin{aligned}{{u} \rightarrow 0,\quad {v} \rightarrow 0,\quad {w} \rightarrow 0,\quad {T} \rightarrow {T}_{\infty }, \quad {a} \rightarrow {a}_{0}, \quad {b} \rightarrow {b}_{0},\quad at \quad {z} \rightarrow {\infty }}, \end{aligned}$$

(8)

where the components of velocity are u(r, $\vartheta$, z), v(r, $\vartheta$, z) and w(r, $\vartheta$, z), $Q _{0}$ is used for the heat generation/absorption and property of the nanofluid is denoted by the subscript $nf$. $P$ is used for pressure, ${p_{1}}$ is the disk thickness index parameter, $T$ is used for temperature, Hall current parameter is $m$, the density of the nanofluid is $\rho _{nf}$, $\nu _{nf}$ is the kinematic viscosity of the nanofluid, ${(\rho {C}_{P})_{nf}}$ is the heat capacitance of the nanofluid, the nanolfuid thermal conductivity is ${k_{nf}}$, the gravitational acceleration is denoted by ${{g_{1}}}$, $\beta _{T}$ is the thermal expansion coefficient, the electric conductivity is $\sigma _{nf}$, ${{B_{0}}}$ is used for magnetic induction, the permeability of porous medium is ${k^{*}}$, the inertia coefficient of porous medium is ${F_{1}}$, the radiation heat flux is expressed by ${{q_{r}}}$, $a$ is the concentration of chemical species $A$, $b$ is the concentration of chemical species $B$, ${{D_{A}}}$ and ${{D_{B}}}$ are the diffusion coefficients, the rates of homogeneous and heterogeneous chemical reactions are denoted by ${{k_{c}}}$ and ${{k_{s}}}$ respectively.

For radiative heat flux the expression is given by

$$\begin{aligned} {q_{r}}=-\left(\frac{16\sigma ^{*}{T_{\infty }}^{3}}{3k_{e}}\frac{\partial T}{\partial z} \right), \end{aligned}$$

(9)

where Stefan–Boltzmann constant is $\sigma ^{*}$ and the mean absorption coefficient ${k_{e}}$. With the help of Eq. (9), the temperature equation (4) becomes as

$$\begin{aligned} \left( u \frac{\partial T}{\partial r} + w \frac{\partial T}{\partial z}\right) =\frac{k_{nf}}{(\rho {C}_{P})_{nf}}\left(\frac{\partial ^2 T}{\partial r^{2}} + \frac{\partial ^2 T}{\partial z^{2}}\right)+{Q_{0}} +\frac{1}{{(\rho {C}_{P})_{nf}}}\left(\frac{16\sigma ^{*}{T_{\infty }}^{3}}{3k_{e}}\right)\frac{\partial ^{2} T}{\partial z^{2}}. \end{aligned}$$

(10)

Nanofluid properties

The properties of the nanofluid^37,38 are given by

$$\begin{aligned} \rho _{nf}=\left(\frac{1}{\phi {\rho _{P}}+(1-\phi ){\rho _{f}}}\right), {(\rho {C}_{P})_{nf}}=\left(\frac{1}{\phi {(\rho {C}_{P})_{P}}+(1-\phi ){(\rho {C}_{P})_{f}}}\right), {\sigma _{nf}={\sigma _{f}}\left(1+\frac{3(\sigma -1)\phi }{(\sigma +2)-(\sigma -1){\phi }}\right),\quad where \quad {\sigma = \frac{\sigma _{p}}{\sigma _{f}}}}, \end{aligned}$$

(11)

where $p$ denote the nanoparticles, to analyze the suitable model for effective thermal conductivity and efficient viscosity, the role of nanoparticles concentration, nano thermal layer, nanoparticles size lead to maintain the theoretical validity of the nanofluid with thermophysical characteristics.

The nanofluid viscosity³⁹ is specified through

$$\begin{aligned} \mu _{nf}=\left(\frac{\mu _{f}}{1.3487(\frac{d_{p}}{d_{f}})^{-0.3}{(\phi )}^{1.03}}\right), \end{aligned}$$

(12)

where ${d_{f}}$ represents the diameter of base fluid molecule, ${d_{p}}$ is the diameter of the nanoparticles, the dynamic viscosity of the nanofluid is $\mu _{nf}$, $\phi$ is the nanoparticles concentration, the base fluid mass density is expressed by the $\rho _{f_{0}}$. For water $\rho _{f_{0}}$ = 998.2. The effective nanofluids thermal conductivity⁴⁰ is defined as below

$$\begin{aligned}\frac{{k_{nf}}}{{k_{f}}}=\left[\frac{{k_{pe}}+2{k_{f}}+2({k_{pe}}-{k_{f}})(1-\beta )^{3}\phi }{{k_{pe}}+2{k_{f}}-2({k_{pe}}-{k_{f}})(1-\beta )^{3}\phi }\right], \end{aligned}$$

(13)

$$\begin{aligned}\frac{{k_{p}}}{{k_{f}}}=\gamma \left[\frac{2(1-\gamma )+(1-\beta )^{3}(1+2\gamma )}{-(1-\gamma )+(1-\beta )^{3}(1+2\gamma )}\right],\quad \gamma =\frac{k_{layer}}{{k_{p}}} \quad and \quad \beta =\frac{h}{{r_{p}}}, \end{aligned}$$

(14)

where $\gamma$ is the ratio of nanolayer thermal conductivity to the particle thermal conductivity, $\beta$ is the ratio of nanolayer thermal thickness to the original particle radius, base fluid thermal conductivity is designed by ${k_{f}}$, ${r_{p}}$ is used for radius of nano atom, nano atom thermal conductivity is denoted by ${k_{p}}$, around the nanoparticles, the thickness of nanolayer is denoted by $h$. It is noted from the experimental results that ${k_{layer}} = 100{k_{f}}$.

The thermophysical properties of base fluid and nanoparticles are given in Table 1.

Table 1 Thermophysical properties of base fluid and nanoparticles.

The similarity transformations are used as⁴²

$$\begin{aligned}{u}&={r^{*}}{R_{0}}\Omega {F}(\zeta ),\quad {v}={r^{*}}{R_{0}}\Omega {G}(\zeta ),\quad {w}=\frac{{R_{0}}\Omega }{(1+r^{*})^{p_{1}}}\left(\frac{{\Omega {R_{0}}^{2}}{\rho _{f}}}{\mu _{f}}\right)^{\frac{-1}{1+n}}{B}(\zeta ),\quad \theta (\zeta ) =\frac{T-T_{\infty }}{T_{w}-T_{\infty }}, \\&\quad {J}(\zeta )=\frac{a}{a_{0}}, \quad {S}(\zeta )=\frac{b}{b_{0}},\quad {P-P_{\infty }}=2\mu _{nf}\Omega {P}(\zeta ),\quad \zeta =\frac{z}{R_{0}}(1+r^{*})^{p_{1}}\left(\frac{{\Omega {R_{0}}^{2}}{\rho _{f}}}{\mu _{f}}\right)^{\frac{1}{1+n}}. \end{aligned}$$

(15)

With the help of similarity transformations in Eq. (15), the obtained dimensionless governing equations are

$$\begin{aligned}F +B ^{\prime }+\zeta \epsilon p_{1}{} F ^{\prime }=0, \end{aligned}$$

(16)

$$\begin{aligned}&{A_{1}}\left(\frac{\zeta ^{2}{{p_{1}}^{2}}\epsilon }{Re{r^{*}}{(1+r^{*})}}+(1+r^{*})^{2p_{1}}({Re})^\frac{1-n}{1+n} \right){F}^{\prime \prime }+{A_{1}}\frac{\zeta {{p_{1}}^{2}}\epsilon }{Re{r^{*}}{(1+r^{*})}}{F}^{\prime } -{p_{1}}\epsilon \zeta {F}{F}^{\prime }+{G}^{2}-{B}{F}^{\prime }+{Gr}\theta \\&\quad \quad -\frac{M}{1+m^{2}}\left[{F}+\frac{m}{{r^{*}}(1+r^{*})^{p_{1}}}({Re})^\frac{-1}{1+n}{B}\right]-{A_{1}}\lambda {F}-{Fr}{F^{2}}=0, \end{aligned}$$

(17)

$$\begin{aligned}&{A_{1}}\left(\frac{\zeta ^{2}{{p_{1}}^{2}}\epsilon }{Re{(1+r^{*})}}+{r^{*}}(1+r^{*})^{2p_{1}}({Re})^\frac{1-n}{1+n} \right){G}^{\prime \prime }+{A_{1}}{\frac{\zeta {{p_{1}}^{2}}\epsilon }{Re{(1+r^{*})}}}{G}^{\prime } -{r^{*}}{p_{1}}\epsilon \zeta {F}{G}^{\prime }-{r^{*}}{F}{G}-{r^{*}}{B}{G}^{\prime } \\& \quad -\frac{M{r^{*}}}{(1+m^{2})}\left({G}+{m}{F}\right)-{r^{*}}{Fr}{G}^{2}=0, \end{aligned}$$

(18)

$$\begin{aligned}&{A_{2}}\frac{1}{Pr}\left(\frac{k_{nf}}{k_{f}}\frac{\zeta ^{2}{{p_{1}}^{2}}}{Re{(1+r^{*})^{2}}}+\frac{k_{nf}}{k_{f}}{(1+r^{*})^{2p_{1}}}({Re})^\frac{1-n}{1+n} +\frac{4}{3}{Rd}{(1+r^{*})^{2p_{1}}}({Re})^\frac{1-n}{1+n}\right)\theta ^{\prime \prime } +{A_{2}}\frac{k_{nf}}{k_{f}}\frac{1}{Pr}\frac{\zeta {{p_{1}}^{2}}}{Re{(1+r^{*})^{2}}}\theta ^{\prime } \\&\quad -\epsilon \zeta {p_{1}}{F}\theta ^{\prime }-{B}\theta ^{\prime }-{Q}=0, \end{aligned}$$

(19)

$$\begin{aligned}\frac{1}{Sc}({Re})^\frac{1-n}{1+n}{(1+r^{*})^{2p_{1}}}{J}^{\prime \prime }-{K_{ho}}{J}{S^{2}}- \epsilon \zeta {p_{1}}{F}{J}^{\prime }-{B}{J}^{\prime }=0, \end{aligned}$$

(20)

$$\begin{aligned}\frac{\delta }{Sc}({Re})^\frac{1-n}{1+n}{(1+r^{*})^{2p_{1}}}{S}^{\prime \prime }+{K_{ho}}{J}{S^{2}}- \epsilon \zeta {p_{1}}{F}{S}^{\prime }-{B}{S}^{\prime }=0, \end{aligned}$$

(21)

with the transformed boundary conditions

$$\begin{aligned}{B} = {ws}, \quad {F} = 0, \quad {G} = 1,\quad \theta = 1,\quad {J}^{\prime }{(0)} = {K_{he}}{J}{(0)},\quad \delta {S}^{\prime }{(0)}= -{K_{he}}{J}{(0)}, \quad at \quad \zeta = \alpha , \end{aligned}$$

(22)

$$\begin{aligned}{F} = 0, \quad \quad {G} = 0, \quad \theta = 0,\quad {J} = 1,\quad {S} = 0, \quad at \quad \zeta = \infty , \end{aligned}$$

(23)

where $\zeta$ is the similarity variable, ${r^{*}}$ is the dimensionless radius, ${R_{0}}$ is the feature radius, the positive dimensional constants are ${a_{0}}$, ${b_{0}}$, the nanofluid constants are A$_{1}$ = $\left(\frac{1}{(1.3487(\frac{d_{p}}{d_{f}})^{-0.3}{(\phi )}^{1.03})(\phi (\frac{\rho _{p}}{\rho _{f}})+(1-\phi ))}\right)$, A$_{2}$ = $\left(\frac{1}{\phi \left(\frac{{{(\rho {C_{P}})_{P}}}}{{(\rho {C_{P}})_{f}}}\right)+(1-\phi )}\right)$. $\epsilon$ = $\frac{r^{*}}{1+r^{*}}$ is the dimensionless constant parameter, the Reynolds number is Re = $\frac{\Omega {R_{0}}}{\nu _{f}}$, the dimensionless radius is indicated by r$^{*}$ = $\frac{r}{R_{0}}$, local Grashof number is Gr = $\frac{{g_{1}}(\beta _{T})_{nf}(T_{w}-T_{}\infty )}{r\Omega ^{2}}$, the magnetic field parameter is M = $\frac{\sigma _{nf}{{B_{0}}}^{2}}{\Omega \rho _{nf}}$, the homogeneous chemical reaction parameter is symbolized by K$_{ho}$ = $\frac{a^{2}{k_{c}}}{\Omega }$, heterogeneous chemical reaction parameter is designed by K$_{he}$ = $\frac{{R_{0}}k_{s}}{{D_{A}}{(1+r^{*})^{p_{1}}}\left(\frac{{\Omega {R_{0}}^{2}}{\rho _{f}}}{\mu _{f}}\right)^{\frac{1}{1+n}}}$, the Schmidt number is Sc = $\frac{\nu _{f}}{D_{A}}$, $\delta$ = $\frac{D_{B}}{D_{A}}$ is the ratio of diffusion coefficients, the Darcy Forchheimer parameter is Fr = $\frac{C_{b}}{\sqrt{k^{*}}}$, Rd = $\frac{4\sigma ^{*}{{T_{\infty }}^{3}}}{k_{e}{k_{f}}}$ is the radiation parameter, $\lambda$ = $\frac{\nu _{f}}{k^{*}\Omega }$ stands for the porosity parameter, the Prandtl number is signified by Pr = $\frac{\nu _{f}(\rho {C}_{P})_{f}}{k_{f}}$, the disk thickness coefficient is $\alpha$ = $\frac{d}{R_{0}}\left(\frac{{\Omega {R_{0}}^{2}}{\rho _{f}}}{\mu _{f}}\right)^{\frac{1}{1+n}}$ and ws = $\frac{\left(\frac{{\Omega {R_{0}}^{2}}{\rho _{f}}}{\mu _{f}}\right)^{\frac{1}{1+n}}{(1+r^{*})^{p_{1}}}}{\Omega {R_{0}}}{w_{0}}$ is the suction/injection parameter. For injection, ws>0 and for suction, ws<0.

In most of the applications, it is expected that the diffusion coefficient of the chemical reaction species $A$ and $B$ to be in comparable size. This leads to make an assumption that the diffusion coefficients ${D_{A}}$ and ${D_{B}}$ are of similar size, then the ratio of diffusion coefficients are assumed to be one ($\delta$ = $1$) so

$$\begin{aligned} J {(\zeta )}+S {(\zeta )} = 1. \end{aligned}$$

(24)

By using Eqs. (20–21), it is obtained that

$$\begin{aligned} \frac{1}{Sc}({Re})^\frac{1-n}{1+n}{(1+r^{*})^{2p_{1}}}{J}^{\prime \prime }-{K_{ho}}{J}(1-{J})^{2} -\epsilon \zeta {p_{1}}{F}{J}^{\prime }-{B}{J}^{\prime }=0, \end{aligned}$$

(25)

with boundary conditions

$$\begin{aligned} J ^{\prime }{(0)}={K_{he}}{} J {(0)},\quad J (\infty ) = 1. \end{aligned}$$

(26)

Furthermore, various physical quantities of interests are being discussed such as skin friction coefficients, local Nusselt number as

$$\begin{aligned}{C_{Fx}}=\frac{\sqrt{{\tau ^{2}_{zr}}+\tau ^{2}_{z\vartheta }}}{\rho _{f}{(r\Omega )^{2}}}, \end{aligned}$$

(27)

$$\begin{aligned}{Nu_{x}}=\frac{R_{0}q_{w}}{{k_{f}}{(T_{w}-T_{\infty })}}, \end{aligned}$$

(28)

where $\tau _{zr}$ and $\tau _{z\vartheta }$ are the total shear stress in radial and tangential directions respectively, ${q_{w}}$ is the heat flux at the surface of the disk which are introduced as follows⁴²,

$$\begin{aligned} \tau _{zr}= & {} \mu _{nf}\begin{bmatrix}\frac{\partial u}{\partial z}\end{bmatrix}_{z=0}, \end{aligned}$$

(29)

$$\begin{aligned} \tau _{z\vartheta }= & {} \mu _{nf}\begin{bmatrix}\frac{\partial v}{\partial z}\end{bmatrix}_{z=0}, \end{aligned}$$

(30)

$$\begin{aligned} {q_{w}}= & {} -k _{nf}\begin{bmatrix}\frac{\partial T}{\partial z}\end{bmatrix}_{z=0}. \end{aligned}$$

(31)

Implementation of quantities in Eq. (15), provides dimensionless mathematical interpretations for the coefficient of skin friction and Nusselt number as

$${C_{Fx}}{(R_{e})^{\frac{n-1}{n+1}}}=\frac{1}{(1-\phi )^{2.5}{r^{*}}}(1+r^{*})^{p_{1}}\left( \sqrt{({F}^{\prime })^{2}+({G}^{\prime })^{2}}\right),$$

(32)

$$\begin{aligned}{Nu_{x}}{(R_{e})^{\frac{-1}{n+1}}}=-\frac{k_{nf}}{k_{f}}(1+r^{*})^{p_{1}}{\theta ^{\prime }}(0). \end{aligned}$$

(33)

Solution of the problem

The present problem is solved via Mathematica 10 computer-based programming with the help of homotopy analysis method (HAM). The HAM approach is chosen to tackle the problem. Without linearization and discretization of the nonlinear differential equations, this method is useful to any system of nonlinear differential equations. This method can be used with systems that have small or large natural parameters. This method yields a convergent solution to the problem. This method is free from a set of base functions and linear operators.

By following the procedure of HAM, initial guesses and linear operators are taken as

$$\begin{aligned} {B_{0}}(\zeta ) = {ws},\quad {F_{0}}(\zeta )=0, \quad {G_{0}}(\zeta ) =\exp (-\zeta +\alpha ),\quad \theta _{0}(\zeta ) = \frac{1-{k_{he}}\exp (-\zeta )+{k_{he}}}{1+{k_{he}}}, \\& {J_{0}}(\zeta ) =\exp (-\zeta +\alpha ), \end{aligned}$$

(34)

$$\begin{aligned}{{\varvec{L}}}_{{\varvec{B}}} = {B^{\prime }},\quad {{\varvec{L}}}_{{\varvec{F}}} = {F^{\prime \prime }}-{F},\quad {{\varvec{L}}}_{{\varvec{G}}} = {G^{\prime \prime }}-{G},\quad {{\varvec{L}}}_{\theta } = \theta ^{\prime \prime }-\theta ,\quad {{\varvec{L}}}_{{\varvec{J}}} = {J^{\prime \prime }}-{J}, \end{aligned}$$

(35)

then

$$\begin{aligned} &{{\varvec{L}}}_{B}\left[{C_{1}}\right] = 0,\quad {{\varvec{L}}}_{F}\left[{C_{2}}\exp (\zeta ) + {C_{3}}\exp (-\zeta ) \right] = 0,\quad {{\varvec{L}}}_{G}\left[{C_{4}}\exp (\zeta ) + {C_{5}}\exp (-\zeta ) \right] = 0, \\& {{\varvec{L}}}_{\theta }\left[{C_{6}}\exp (\zeta ) + {C_{7}}\exp (-\zeta ) \right] = 0, \quad {{\varvec{L}}}_{J}\left[{C_{8}}\exp (\zeta ) + {C_{9}}\exp (-\zeta ) \right] = 0, \end{aligned}$$

(36)

and C$_{i}$(i = 1–9) are the arbitrary constants.

Zeroth order deformation problems

Zeroth order form of the present problem is

$$\begin{aligned}(1 - q ) {{\varvec{L}}_{{\varvec{B}}}} [B (\zeta , q ) - {B_{0}}(\zeta )] = q h _{B} N _{B} [F (\zeta , q ),B (\zeta , q)], \end{aligned}$$

(37)

$$\begin{aligned}(1 - q ) {{\varvec{L}} _{{\varvec{F}}}} [F (\zeta , q ) - {F_{0}}(\zeta )] = q h _{F} N _{F} [F (\zeta , q ),G (\zeta , q),B (\zeta , q),\theta (\zeta , q) ], \end{aligned}$$

(38)

$$\begin{aligned}(1 - q ) {{\varvec{L}} _{{\varvec{G}}} } [G (\zeta , q ) - G _{0}(\zeta )] = q h _{G } N _{G } [F (\zeta , q ), G (\zeta , q ),B (\zeta , q)], \end{aligned}$$

(39)

$$\begin{aligned}(1 - q ) {{\varvec{L}}_{{\varvec{\theta }}} } [\theta (\zeta , q ) - \theta _{0}(\zeta )] = q h _{\theta } N _{\theta } [F (\zeta , q ),B (\zeta , q), \theta (\zeta , q )], \end{aligned}$$

(40)

$$\begin{aligned}(1 - q ) {{\varvec{L}}_{{\varvec{J}}} } [J (\zeta , q ) - J _{0}(\zeta )] = q h _{J } N _{J } [F (\zeta , q ),B (\zeta , q), J (\zeta , q )], \end{aligned}$$

(41)

where $q$ is the embedding parameter, the non-zero auxiliary parameters are $h _{B}$, $h _{F}$, $h _{G }$, $h _{\theta }$, and $h _{J }$. The nonlinear operators in the leading equations of the present problem are denoted by $N _{B}$, $N _{F}$, $N _{G }$, $N _{\theta }$, $N _{J }$, and are given as

$$\begin{aligned}N _{B}[F(\zeta , q ), B (\zeta , q)]=F (\zeta , {q})+\frac{\partial B(\zeta , q)}{\partial \zeta }+\zeta \epsilon p _{1}\frac{\partial F(\zeta , q)}{\partial \zeta }, \end{aligned}$$

(42)

$$\begin{aligned}{N}_{F}[F(\zeta , {q}), {G}(\zeta , q),{B}(\zeta , q), \theta (\zeta , q)] &={A_{1}}\left(\frac{{{p_{1}}^{2}}\epsilon }{Re{r^{*}}{(1+r^{*})}}\zeta ^{2}+(1+r^{*})^{2p_{1}}({Re})^\frac{1-n}{1+n} \right)\frac{\partial ^{2}F(\zeta , q)}{\partial \zeta ^{2}}\nonumber \\&\quad +{A_{1}}\frac{{{p_{1}}^{2}}\epsilon }{Re{r^{*}}{(1+r^{*})}}\zeta \frac{\partial F(\zeta , q)}{\partial \zeta } -{p_{1}}\epsilon \zeta {F(\zeta , {q})}\frac{\partial F(\zeta , q)}{\partial \zeta } +({G(\zeta , {q})})^{2}-{B}(\zeta , q)\frac{\partial F(\zeta , q)}{\partial \zeta } +{Gr}\theta (\zeta ,q)\nonumber \\&\quad -\frac{M}{1+m^{2}}\begin{bmatrix}{F(\zeta , {q})}+ \frac{m}{{r^{*}}(1+r^{*})^{p_{1}}}({Re})^\frac{-1}{1+n}{B}(\zeta , q)\end{bmatrix} -{A_{1}}\lambda {F(\zeta , {q})}-{Fr}({F(\zeta , {q})})^{2}, \end{aligned}$$

(43)

$$\begin{aligned} {N}_{G}[F(\zeta , {q}), {G}(\zeta , q),{B}(\zeta , q)] &={A_{1}}\left(\frac{{{p_{1}}^{2}}\epsilon }{Re{(1+r^{*})}}\zeta ^{2}+{r^{*}}(1+r^{*})^{2p_{1}}({Re})^\frac{1-n}{1+n} \right)\frac{\partial ^{2}G(\zeta , q)}{\partial \zeta ^{2}} +{A_{1}}\frac{{{p_{1}}^{2}}\epsilon }{Re{(1+r^{*})}}\zeta \frac{\partial G(\zeta , q)}{\partial \zeta } \\& \quad -{r^{*}}{p_{1}}\epsilon \zeta {F(\zeta , {q})}\frac{\partial G(\zeta , q)}{\partial \zeta }-{r^{*}}{F(\zeta , {q})}{G(\zeta , {q})}-{r^{*}}{B}(\zeta , q)\frac{\partial G(\zeta , q)}{\partial \zeta } -\frac{M{r^{*}}}{(1+m^{2})}\left({G(\zeta , {q})}+{m}{F(\zeta , {q})}\right) \\& \quad -{r^{*}}{Fr}({G(\zeta , {q})})^{2}, \end{aligned}$$

(44)

$$\begin{aligned}{N}_{\theta }[F(\zeta , {q}),{B}(\zeta , q), \theta (\zeta , q)] &={A_{2}}\frac{1}{Pr}\begin{pmatrix}\frac{k_{nf}}{k_{f}}\frac{{{p_{1}}^{2}}}{Re{(1+r^{*})^{2}}}\zeta ^{2}+\frac{k_{nf}}{k_{f}}{(1+r^{*})^{2p_{1}}}({Re})^\frac{1-n}{1+n}\\ +\frac{4}{3}{Rd}{(1+r^{*})^{2p_{1}}}({Re})^\frac{1-n}{1+n}\end{pmatrix} \frac{\partial ^{2} \theta (\zeta , q)}{\partial \zeta ^{2}} \\&\quad +{A_{2}}\frac{k_{nf}}{k_{f}}\frac{1}{Pr}\frac{{{p_{1}}^{2}}}{Re{(1+r^{*})^{2}}}\zeta \frac{\partial \theta (\zeta , q)}{\partial \zeta }-\epsilon {p_{1}}\zeta {F(\zeta , {q})}\frac{\partial \theta (\zeta , q)}{\partial \zeta }-{B}(\zeta , q)\frac{\partial \theta (\zeta , q)}{\partial \zeta }-{Q}, \end{aligned}$$

(45)

$$\begin{aligned}{N}_{J}[F(\zeta , {q}),{B}(\zeta , q), {J}(\zeta , q)] & =\frac{1}{Sc}({Re})^\frac{1-n}{1+n}{(1+r^{*})^{2p_{1}}}\frac{\partial ^{2}J(\zeta , q)}{\partial \zeta ^{2}} -{K_{ho}}{J(\zeta , {q})}(1-{J(\zeta , {q})})^{2} - \epsilon {p_{1}}\zeta {F(\zeta , {q})}\frac{\partial J(\zeta , q)}{\partial \zeta } \\&\quad - {B}(\zeta , q)\frac{\partial J(\zeta , q)}{\partial \zeta }, \end{aligned}$$

(46)

$$\begin{aligned}{B} (0, q) = {ws}, \end{aligned}$$

(47)

$$\begin{aligned}{F} (0, q) = 1,\quad {F} (\infty , q) = 0, \end{aligned}$$

(48)

$$\begin{aligned}{G} (0, q) = 1,\quad {G} (\infty , q) = 0, \end{aligned}$$

(49)

$$\begin{aligned}\theta (0, q) = 1,\quad {\theta } (\infty , q) = 0, \end{aligned}$$

(50)

$$\begin{aligned}{J^{\prime }} (0, q) ={k_{he}}{J}(0) ,\quad {J} (\infty , q) = 0. \end{aligned}$$

(51)

For ${q} = 0$ and ${q} = 1$, Eqs. (37–41) provide

$$\begin{aligned}{q} = 0 \Rightarrow {B} (\zeta , 0) = B_{0}(\zeta ) \quad and \quad {q} = 1 \Rightarrow {B}(\zeta , 1) = B(\zeta ), \end{aligned}$$

(52)

$$\begin{aligned}{q} = 0 \Rightarrow {F} (\zeta , 0) = F_{0}(\zeta ) \quad and \quad {q} = 1 \Rightarrow {F}(\zeta , 1) = F(\zeta ), \end{aligned}$$

(53)

$$\begin{aligned}{q} = 0 \Rightarrow {G} (\zeta , 0) = G_{0}(\zeta ) \quad and \quad {q} = 1 \Rightarrow {G}(\zeta , 1) = G(\zeta ), \end{aligned}$$

(54)

$$\begin{aligned}{q} = 0 \Rightarrow \theta (\zeta , 0) = \theta _{0}(\zeta ) \quad and \quad {q} = 1 \Rightarrow \theta (\zeta , 1) = \theta (\zeta ), \end{aligned}$$

(55)

$$\begin{aligned}{q} = 0 \Rightarrow {J} (\zeta , 0) = J_{0}(\zeta ) \quad and \quad {q} = 1 \Rightarrow {J}(\zeta , 1) = J(\zeta ). \end{aligned}$$

(56)

By using Taylor expansion series on Eqs. (52–56), it is obtained that

$$\begin{aligned}{B}(\zeta , {q}) = {B_{0}}(\zeta ) + \sum ^{\infty }_{m = 1} {B_{m}}(\zeta ){q^{m}}, \quad {B_{m}}(\zeta ) = \frac{1}{m!} \frac{\partial ^{m} {B}(\zeta , {q})}{\partial \zeta ^{m}}\mid _{q=0}, \end{aligned}$$

(57)

$$\begin{aligned}{F}(\zeta , {q}) = {F_{0}}(\zeta ) + \sum ^{\infty }_{m = 1} {F_{m}}(\zeta ){q^{m}}, \quad {F_{m}}(\zeta ) = \frac{1}{m!} \frac{\partial ^{m} {F}(\zeta , {q})}{\partial \zeta ^{m}}\mid _{q=0}, \end{aligned}$$

(58)

$$\begin{aligned}{G}(\zeta , {q}) = {G_{0}}(\zeta ) + \sum ^{\infty }_{m = 1} {G_{m}}(\zeta ){q^{m}}, \quad {G_{m}}(\zeta ) = \frac{1}{m!} \frac{\partial ^{m} {G}(\zeta , {q})}{\partial \zeta ^{m}}\mid _{q=0}, \end{aligned}$$

(59)

$$\begin{aligned}\theta (\zeta , {q}) = {\theta _{0}}(\zeta ) + \sum ^{\infty }_{m = 1} {\theta _{m}}(\zeta ){q^{m}}, \quad {\theta _{m}}(\zeta ) = \frac{1}{m!} \frac{\partial ^{m} \theta (\zeta , {q})}{\partial \zeta ^{m}}\mid _{q=0}, \end{aligned}$$

(60)

$$\begin{aligned}{J}(\zeta , {q}) = {J_{0}}(\zeta ) + \sum ^{\infty }_{m = 1} {J_{m}}(\zeta ){q^{m}}, \quad {J_{m}}(\zeta ) = \frac{1}{m!} \frac{\partial ^{m} {J}(\zeta , {q})}{\partial \zeta ^{m}}\mid _{q=0}. \end{aligned}$$

(61)

From Eqs. (57–61), the convergence of the series is obtained by taking q = 1 on the convenient values of $h _{B}$, $h _{F}$, $h _{G}$, $h _{\theta }$ and $h _{J}$ as

$$\begin{aligned}{B}(\zeta ) = {B_{0}}(\zeta ) + \sum ^{\infty }_{m = 1}{B_{m}}(\zeta ), \end{aligned}$$

(62)

$$\begin{aligned}{F}(\zeta ) = {F_{0}}(\zeta ) + \sum ^{\infty }_{m = 1}{F_{m}}(\zeta ) , \end{aligned}$$

(63)

$$\begin{aligned}{G}(\zeta ) = {G_{0}}(\zeta ) + \sum ^{\infty }_{m = 1}{G_{m}}(\zeta ) , \end{aligned}$$

(64)

$$\begin{aligned}\theta (\zeta ) = {\theta _{0}}(\zeta ) + \sum ^{\infty }_{m = 1}{\theta _{m}}(\zeta ) , \end{aligned}$$

(65)

$$\begin{aligned}{J}(\zeta ) = {J_{0}}(\zeta ) + \sum ^{\infty }_{m = 1}{J_{m}}(\zeta ). \end{aligned}$$

(66)

mth order deformation problems

The mth order deformation problem is

$$\begin{aligned}{{\varvec{L}}_{{B}}}[{B_{m}}(\zeta ) - \eta _{m}{B_{m-1}}(\zeta )] = \hslash _{B} {\mathfrak {R}}^{B}_{m}(\zeta ), \end{aligned}$$

(67)

$$\begin{aligned}{{\varvec{L}}_{{F}}}[{F_{m}}(\zeta ) - \eta _{m}{F_{m-1}}(\zeta )] = \hslash _{F} {\mathfrak {R}}^{F}_{m}(\zeta ), \end{aligned}$$

(68)

$$\begin{aligned}{{\varvec{L}}_{{G}}}[{G_{m}}(\zeta ) - \eta _{m}{G_{m-1}}(\zeta )] = \hslash _{G} {\mathfrak {R}}^{G}_{m}(\zeta ), \end{aligned}$$

(69)

$$\begin{aligned}{{\varvec{L}}_{{{\theta }}}}[{\theta _{m}}(\zeta ) - \eta _{m}{\theta _{m-1}}(\zeta )] = \hslash _{\theta } {\mathfrak {R}}^{\theta }_{m}(\zeta ), \end{aligned}$$

(70)

$$\begin{aligned}{{\varvec{L}}_{{J}}}[{J_{m}}(\zeta ) - \eta _{m}{J_{m-1}}(\zeta )] = \hslash _{J} {\mathfrak {R}}^{J}_{m}(\zeta ), \end{aligned}$$

(71)

$$\begin{aligned}B_{m}(0) = 0, \end{aligned}$$

(72)

$$\begin{aligned}F_{m}(0) = 0,\quad F_{m}(\infty ) = 0, \end{aligned}$$

(73)

$$\begin{aligned}G_{m}(0) = 0,\quad G_{m}(\infty ) = 0, \end{aligned}$$

(74)

$$\begin{aligned}\theta _{m}(0) = 0,\quad \theta _{m}(\infty ) = 0, \end{aligned}$$

(75)

$$\begin{aligned}J_{m}(0) = 0,\quad J_{m}(\infty ) = 0, \end{aligned}$$

(76)

where $R _{m}^{B}(\zeta )$, $R _{m}^{F}(\zeta )$, $R _{m}^{G}(\zeta )$, $R _{m}^{\theta }(\zeta )$ and $R _{m}^{J}(\zeta )$ are defined as

$$\begin{aligned}{\mathfrak {R}}_{m}^{B}(\zeta )={F}_{m}+B^{\prime }_{m-1}+\zeta \epsilon {p_{1}}F^{\prime }_{m-1}, \end{aligned}$$

(77)

$$\begin{aligned} {\mathfrak {R}}_{m}^{F}(\zeta )&={A_{1}}\left(\frac{{{p_{1}}^{2}}\epsilon }{Re{r^{*}}{(1+r^{*})}}\zeta ^{2}+(1+r^{*})^{2p_{1}}({Re})^\frac{1-n}{1+n} \right)F^{\prime \prime }_{m-1}+{A_{1}}\zeta \frac{{{p_{1}}^{2}}\epsilon }{Re{r^{*}}{(1+r^{*})}}F^{\prime }_{m-1} -{p_{1}}\epsilon \zeta \sum ^{m - 1}_{k = o}F_{m - 1 - k} F^{\prime }_{k}\nonumber \\&\quad +\sum ^{m - 1}_{k = o}G_{m - 1 - k} G_{k}-\sum ^{m - 1}_{k = o}B_{m - 1 - k} F^{\prime }_{k} +{Gr}\theta _{m} -\frac{M}{1+m^{2}}\begin{bmatrix}{F}_{m}+ \frac{m}{{r^{*}}(1+r^{*})^{p_{1}}}({Re})^\frac{-1}{1+n}{B_{m}}\end{bmatrix}\nonumber \\&\quad -{A_{1}}\lambda {F}_{m} -{Fr}\sum ^{m - 1}_{k = o}F_{m - 1 - k} F_{k}, \end{aligned}$$

(78)

$$\begin{aligned} {\mathfrak {R}}_{m}^{G}(\zeta )&={A_{1}}\left(\frac{{{p_{1}}^{2}}\epsilon }{Re{(1+r^{*})}}\zeta ^{2}+{r^{*}}(1+r^{*})^{2p_{1}}({Re})^\frac{1-n}{1+n} \right)G^{\prime \prime }_{m-1}\nonumber \\&\quad +{A_{1}}{\frac{{{p_{1}}^{2}}\epsilon }{Re{(1+r^{*})}}\zeta }G^{\prime }_{m-1} -{r^{*}}{p_{1}}\epsilon \zeta {\sum ^{m - 1}_{k = o}F_{m - 1 - k} G^{\prime }_{k}}\nonumber \\&\quad -{r^{*}}{\sum ^{m - 1}_{k = o}F_{m - 1 - k} G_{k}}-{r^{*}}{\sum ^{m - 1}_{k = o}B_{m - 1 - k} G^{\prime }_{k}}-\frac{M{r^{*}}}{(1+m^{2})} \left({G}_{m}+{m}{F}_{m}\right) -{r^{*}}{Fr}{\sum ^{m - 1}_{k = o}G_{m - 1 - k} G_{k}}, \end{aligned}$$

(79)

$$\begin{aligned} {\mathfrak {R}}_{m}^{\theta }(\zeta )&={A_{2}}\frac{1}{Pr}\left(\frac{k_{nf}}{k_{f}}\frac{{{p_{1}}^{2}}}{Re{(1+r^{*})^{2}}}\zeta ^{2}+\frac{k_{nf}}{k_{f}}{(1+r^{*})^{2p_{1}}}({Re})^\frac{1-n}{1+n} +\frac{4}{3}{Rd}{(1+r^{*})^{2p_{1}}}({Re})^\frac{1-n}{1+n}\right)\theta ^{\prime \prime }_{m-1}\nonumber \\&\quad +{A_{2}}\frac{k_{nf}}{k_{f}}\frac{1}{Pr}\frac{\zeta {{p_{1}}^{2}}}{Re{(1+r^{*})^{2}}}\theta ^{\prime }_{m-1}-\epsilon \zeta {p_{1}}{\sum ^{m - 1}_{k = o}F_{m - 1 - k} \theta ^{\prime }_{k}}-{\sum ^{m - 1}_{k = o}B_{m - 1 - k} \theta ^{\prime }_{k}}-{Q}, \end{aligned}$$

(80)

$$\begin{aligned} {\mathfrak {R}}_{m}^{J}(\zeta )&=\frac{1}{Sc}({Re})^\frac{1-n}{1+n}{(1+r^{*})^{2p_{1}}}J^{\prime \prime }_{m-1}-{K_{ho}}\left(\sum ^{m - 1}_{k = o}\left(\sum ^{k}_{r = o}J_{m - 1 - k} J_{k-r}\right){J}_{r}\right)\nonumber \\&\quad -\epsilon {p_{1}}\zeta {\sum ^{m - 1}_{k = o}F_{m - 1 - k} j^{\prime }_{k}}-{\sum ^{m - 1}_{k = o}B_{m - 1 - k} J^{\prime }_{k}}, \end{aligned}$$

(81)

$$\begin{aligned}\eta _{m} = \left\{ \begin{array}{ll} 0, &{} \hbox {m} \le 1 \\ 1, &{} \hbox {m} > 1. \end{array} \right. \end{aligned}$$

(82)

With the help of particular solutions, the general solution is

$${B_{m}}(\zeta ) = {B^{*}_{m}}(\zeta ) + {C_{1}},$$

(83)

$${F_{m}}(\zeta ) = {F^{*}_{m}}(\zeta ) + {C_{2}}\exp (\zeta ) + {C_{3}}\exp (-\zeta ),$$

(84)

$${G_{m}}(\zeta ) = {G^{*}_{m}}(\zeta ) + {C_{4}}\exp (\zeta ) + {C_{5}}\exp (-\zeta ),$$

(85)

$$\theta _{m}(\zeta ) = \theta ^{*}_{m}(\zeta ) + {C_{6}}\exp (\zeta ) + {C_{7}}\exp (-\zeta ),$$

(86)

$${J_{m}}(\zeta ) = {J^{*}_{m}}(\zeta ) + {C_{8}}\exp (\zeta ) + {C_{9}}\exp (-\zeta ).$$

(87)

Validation of the current work

The numerical validation is assessed and compared from the results of existing literature^{44,45,46,47,48,49}. The comparative solution of the proposed nanofluid model with the results of the existing literature is produced by using the finite difference method (FDM). The comparison shown in Tables 2 and 3 seems to be in strong accordance. However, the outcomes of the present study are highly accurate. The authors have found the best percentage accuracy for each validation, as shown in Tables 2 and 3. The percentage accuracy between the present results and the Ishak et al.⁴⁴ results are given as 0.02001113, 0, 0.00653948, 0.02755298, 0.00391610, and the percentage accuracy of Ishak et al.⁴⁵ results and the present results are 0.02001113, 0, 0.00134124, 0.02755298, 0.53921769, when we fix up the nanoparticles concentration $\phi =0$, heat generation/absorption parameter $Q = 0$, disk thickness index $p = 0$, dimensionless constant parameter $\epsilon = 0$, Hall current parameter $m = 0$, Forchheimer parameter $Fr = 0$, local Grashof number $Gr = 0$, power law exponent of fluid $n = 0$ and porosity parameter $\lambda =0$. For the same fixed values of parameters, the percentage accuracy between present results and Jamshed et al.⁴⁸ and Jamshed⁴⁹ results are 0, 0, 0, 0, 0, which means that present results show 100 percent accuracy.

Table 2 Comparative variation of $-\theta ^{\prime }(0)$ with Prandtl number showing percentage accuracy.

Table 3 Comparative variation of $-\theta ^{\prime }(0)$ with Prandtl number showing percentage accuracy.

Results and discussion

The homotopy analysis method (HAM) in MATHEMATICA-10 is applied for the complete solution of the present problem. The effects of the emerging parameters on the axial, radial and tangential velocity profiles, temperature and concentration of chemical reaction profiles are computed and discussed through the graphical form in Figs. 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35.

Table 4 describes the numerical values of different parameters such as nanoparticles concentration $\phi$ and magnetic field parameter $M$ for shear stress ${F ^{\prime \prime }(0)}$ and heat transfer rate $\theta ^{\prime }$(0). It is observed that heat transfer rate is increased but shear stress is reduced with the increase of nanoparticles concentration. Also, it is noticed that the shear stress is enhanced but the heat transfer rate is diminished with the enhancement of the magnetic field parameter. For different values of the suction parameter $ws$, Prandtl number $Pr$ and heat generation/absorption parameter $Q$, the variance of the shear stress ${F ^{\prime \prime }(0)}$ and heat transfer rate $\theta ^{\prime }$(0) are presented in Table 5. Table 5 explained that the suction parameter has the same effects over the shear stress and heat transfer rate, which means for higher values of suction parameter, the values of all these parameters are decreased. It is also observed that the heat transfer rate is increased due to the increase in the Prandtl number values. Also, it is detected that the values of heat transfer rate is increased with the increment of heat absorption/gneration parameter.

Table 4 Shear stress ${F ^{\prime \prime }(0)}$, heat transfer rate $\theta ^{\prime }$(0) for different values of nanoparticles concentration $\phi$ and magnetic field parameter $M$.

Table 5 Shear stress ${F ^{\prime \prime }(0)}$, heat transfer rate $\theta ^{\prime }$(0) for different values of suction parameter $ws$, Prandtl number $Pr$ and heat generation/absoprtion $Q$.

Axial velocity profile

Figures 2, 3, 4 and 5 presents the flow analysis of the axial velocity profile for different parameters. Figure 2 depicts the influence of the disk thickness coefficient $\alpha$ on the axial velocity profile. It is noted that the axial velocity profile is decayed for increasing values of disk thickness coefficient $\alpha$. Figure 3 illustrates the behavior of the axial velocity profile against a dimensionless constant parameter $\epsilon$. Axial velocity is enhanced for larger values of the dimensionless constant parameter $\epsilon$. The effects of magnetic field parameter $M$ on axial velocity profile are shown in Fig. 4. The axial velocity profile is diminished with the enhancement of the magnetic field parameter $M$. Figure 5 is drawn to show the variation of an axial velocity profile for disk thickness index ${p_{1}}$. From this graph, it is concluded that with the intensification of the disk thickness index ${p_{1}}$, the axial velocity profile is also rising.

Figure 2

Effect of $\alpha$ on axial velocity $B (\zeta )$.

Figure 3

Effect of $\epsilon$ on axial velocity $B (\zeta )$.

Figure 4

Effect of $M$ on axial velocity $B (\zeta )$.

Figure 5

Effect of ${p_{1}}$ on axial velocity $B (\zeta )$.

Radial velocity profile

The variation of radial velocity profile for distinct values of different parameters are discussed in Figs. 6, 7, 8, 9, 10, 11, 12, 13, 14 and 15. Figure 6 displays the variation of a radial velocity profile for different values of nanoparticles size ${d_{p}}$. It is noted that for higher values of nanoparticles size ${d_{p}}$, the radial velocity of the nanofluid increases. The increment in radial velocity profile is observed for various values of dimensionless constant parameter $\epsilon$ in Fig. 7. Figure 8 demonstrates the influence of Forchheimer parameter $Fr$ on the radial velocity profile which describes that due to the enhancement of Forchheimer parameter $Fr$, the velocity in radial direction decreases. In the fluid motion, the resistive force is produced due to the increase of Forchheimer parameter. Figure 9 explains that the local Grashof number $Gr$ enhances the radial velocity of the nanofluid. The porosity parameter $\lambda$ increases the radial velocity profile due to the presence of the porous medium which decreases the resistance as shown in Fig. 10. The effect of magnetic field parameter $M$ on the radial velocity profile can be visualized in Fig. 11. It is clear that when the magnetic field parameter $M$ is rising, the velocity in the radial direction is decreased. It is due to the fact that a drag-like Lorentz force is created by the presence of the vertical magnetic field on the electrically conducting fluid. This force tends to slow down the flow around the disk. Therefore, the velocity in the radial direction is reduced. Variation of radial velocity profile against Hall current parameter $m$ is shown in Fig. 12. The increasing effect is noted in the radial velocity profile with the intensification of the Hall current parameter $m$. Figure 13 shows that the radial velocity profile falls due to the rise of nanoparticles concentrations $\phi$. In Fig. 14, the radial velocity tends to decrease when the Reynolds number $Re$ becomes higher and higher. Reynolds number $Re$ is defined as the ratio between the inertial and viscous forces. When the Reynolds number increases, the inertial forces become dominant compared to the viscous forces. Both boundary layer thickness and velocity decrease with the rise of the Reynolds number. Figure 15 depicts the role of the suction parameter $ws$ on the radial velocity. It is observed that radial velocity is increased for the rising values of the suction parameter $ws$.

Figure 6

Effect of ${d_{p}}$ on radial velocity $F (\zeta )$.

Figure 7

Effect of $\epsilon$ on radial velocity $F (\zeta )$.

Figure 8

Effect of $Fr$ on radial velocity $F (\zeta )$.

Figure 9

Effect of $Gr$ on radial velocity $F (\zeta )$.

Figure 10

Effect of $\lambda$ on radial velocity $F (\zeta )$.

Figure 11

Effect of $M$ on radial velocity $F (\zeta )$.

Figure 12

Effect of $m$ on radial velocity $F (\zeta )$.

Figure 13

Effect of $\phi$ on radial velocity $F (\zeta )$.

Figure 14

Effect of $Re$ on radial velocity $F (\zeta )$.

Figure 15

Effect of $ws$ on radial velocity $F (\zeta )$.

Tangential velocity profile

Figures 16, 17, 18, 19, 20, 21, 22 and 23 describe the influence of different parameters on the tangential velocity profile. The analysis of the tangential velocity for nanopartilces size ${d_{p}}$ is detected in Fig. 16. In this analysis, the tangential velocity profile is hiking with the expansion of nanoparticles size ${d_{p}}$. The dimensionless constant parameter $\epsilon$ effect is shown in Fig. 17 which shows that the tangential velocity profile increases with the high values of $\epsilon$. The effect of the Forchheimer parameter $Fr$ on tangential velocity is illustrated in Fig. 18. When the Forchheimer parameter $Fr$ is increased, the tangential velocity increases as well. Drag force is increased with the enhancement of the Forchheimer parameter $Fr$, therefore the tangential velocity is also increased. Figure 19 shows the disparity of tangential velocity for the magnetic field parameter $M$. The augmentation in the tangential velocity graph is seen for various values of the magnetic field parameter $M$. Figure 20 is used to present the efficiency of Hall current parameter $m$ on the tangential velocity profile. It is disclosed that the tangential velocity profile becomes minimum for increasing values of the Hall current parameter $m$. Figure 21 shows the impact of disk thickness index parameter ${p_{1}}$ on the tangential velocity profile. The flow profile accelerates for different values of disk thickness index parameter ${p_{1}}$. The feature of nanoparticles concentration $\phi$ for the tangential velocity profile is represented in Fig. 22. It is shown that the tangential velocity profile is a decreasing function of the nanoparticles concentration $\phi$. This is because solid nanoparticles lead to further thinning of the velocity boundary layer. Figure 23 presents the behavior of tangential velocity profile for various values of Reynolds number $Re$. The tangential velocity profile is decayed for the increasing values Reynolds number $Re$. This is due to the fact that rise in Reynolds number $Re$, the inertial forces are implemented which are dominant compared to the viscous forces.

Figure 16

Effect of ${d_{p}}$ on tangential velocity $G (\zeta )$.

Figure 17

Effect of $\epsilon$ on tangential velocity $G (\zeta )$.

Figure 18

Effect of $Fr$ on tangential velocity $G (\zeta )$.

Figure 19

Effect of $M$ on tangential velocity $G (\zeta )$.

Figure 20

Effect of $m$ on tangential velocity $G (\zeta )$.

Figure 21

Effect of ${p_{1}}$ on tangential velocity $G (\zeta )$.

Figure 22

Effect of $\phi$ on tangential velocity $G (\zeta )$.

Figure 23

Effect of $Re$ on tangential velocity $G (\zeta )$.

Temperature profile

In this section temperature profile is discussed for various parameters. Figure 24 reveals that the temperature profile is reduced for the increasing values of nanoparticles size parameter ${d_{p}}$. The temperature profile of the nanofluid is declined for the prescribed values of dimensionless constant parameter $\epsilon$ as shown in Fig. 25. Figure 26 demonstrates the effect of local Grashof number $Gr$ on the temperature profile. It is detected that the higher values of local Grashof number $Gr$ decreases the temperature of the fluid. Intensifying local Grashof number $Gr$ reduces the thickness of the boundary layer. The relation between the temperature profile and porosity parameter $\lambda$ of the nanofluid is plotted in Fig. 27. It is found that the temperature profile is an increasing function of the porosity parameter $\lambda$. Figure 28 is exposed to the behavior of temperature profile for distinct values of magnetic field parameter $M$. The Lorentz forces are increased as the magnetic field is intensified which increases the resistance of the liquid particles, therefore the temperature of the fluid increases. Figure 29 is drawn to check the influence of disk thickness index parameter ${p_{1}}$ on the temperature profile. The temperature profile is shown to be an increasing function of the disk thickness index parameter ${p_{1}}$. Figure 30 shows the temperature profile trend for the different nanoparticles concentration $\phi$ values. Nanoparticles concentration $\phi$ increases the temperature of the nanofluid. Physically, greater nanoparticles concentration $\phi$ make the fluid dense. The thermal conductivity of nanofluids is enhanced due to a rise in the volume fraction of nanoparticles. Thus the momentum boundary layer shows an upward trend due to the enhancement of thermal conductivity. With the increment of volume fraction parameter, the thermal conductivity of fluid is increased therefore the temperature is increased. The consequence of Reynolds number $Re$ for the temperature profile is presented in Fig. 31. It is shown that when the Reynolds number $Re$ is upsurging then the temperature profile is lessened. Figure 32 shows that the temperature profile of the nanofluid is decreased for larger values of the suction parameter $ws$. This phenomenon occurs because applying injection leads to inject the number of nanoparticles into the nanofluid and consequently the boundary layers thickness is decreased. The usual decay of temperature occurs for the larger values of the injection parameter $ws$.

Figure 24

Effect of ${d_{p}}$ on temperature $\theta (\zeta )$.

Figure 25

Effect of $\epsilon$ on temperature $\theta (\zeta )$.

Figure 26

Effect of $Gr$ on temperature $\theta (\zeta )$.

Figure 27

Effect of $\lambda$ on temperature $\theta (\zeta )$.

Figure 28

Effect of $M$ on temperature $\theta (\zeta )$.

Figure 29

Effect of ${p_{1}}$ on temperature $\theta (\zeta )$.

Figure 30

Effect of $\phi$ on temperature $\theta (\zeta )$.

Figure 31

Effect of $Re$ on temperature $\theta (\zeta )$.

Figure 32

Effect of $ws$ on temperature $\theta (\zeta )$.

Concentration of chemical reactions profile

Figure 33, 34, 35 are plotted for the concentration of chemical reaction through the variation of different parameters. Figure 33 is sketched to see the influence of dimensionless constant parameter $\epsilon$ on the concentration of chemical reaction. The greater values of the dimensionless constant parameter $\epsilon$ increase the concentration of chemical reaction. Figure 34 is drawn for the heterogeneous chemical reaction parameter ${k_{he}}$ and concentration of chemical reaction of the nanofluid. This figure elucidates that the magnitude of the concentration of chemical reaction is reduced for the larger values of heterogeneous reaction parameters ${k_{he}}$. Figure 35 shows the behavior of concentration of chemical reaction for the nanoparticles concentration $\phi$. It is perceived that increasing values of nanoparticles concentration enhance the concentration of chemical reaction.

Figure 33

Effect of $\epsilon$ on concentration of chemical reaction $J (\zeta )$.

Figure 34

Effect of ${k_{he}}$ on concentration of chemical reaction $J (\zeta )$.

Figure 35

Effect of $\phi$ on concentration of chemical reaction $J (\zeta )$.

Conclusions

A numerical study of heat and mass transfer nanofluid flow with homogeneous–heterogeneous chemical reactions over the rotating disk in the existence of Hall current and heat generation/absorption effects are analyzed. The homotopy analysis technqiue is employed to obtain the solution analytically. The influence of various physical parameters on the non-dimensional velocities, temperature and concentration of chemical reactions profiles are shown graphically. After a thorough investigation, the following concluding observations are obtained

• (1) The heat transfer rate is increased for nanoparticles volume fraction but is decreased for a magnetic field parameter.

• (2) The nanoparticles volume fraction reduces the shear stress but the magnetic field parameter has the opposite effect on shear stress.

• (3) Both shear stress and heat transfer rate have decreasing effects on suction parameter.

• (4) The heat transfer rate is diminished for Prandtl number but rises for the heat generation/absorption parameter.

• (5) Increasing the dimensionless constant and disk thickness index parameters show the increasing behaviors for the axial velocity profile.

• (6) The disk thickness coefficient and magnetic field parameters have decreasing effects on the axial velocity profile.

• (7) For higher values of nanoparticles size, dimensionless constant, local Grashof number, porosity, Hall current, and injection parameters, the radial velocity is increased but the opposite behavior is seen for the Forchheimer, and magnetic field parameters, nanoparticles volume fraction and Reynolds number.

• (8) The nanoparticles size, dimensionless constant, Forchheimer, magnetic field and disk thickness index parameters have increasing effects on the tangential velocity profile.

• (9) The tangential velocity profile is reduced with the enhancement of Hall current parameter, nanoparticles volume fraction and Reynolds number.

• (10) The temperature profile is the increasing function of the porosity, magnetic field and disk thickness index parameters as well as nanoparticles volume fraction.

• (11) The decreasing performance of temperature profile is evaluated for nanoparticles size, dimensionless constant, local Grashof and Reynolds numbers as well as injection parameter.

• (12) The homogenous/heterogenous chemical reaction profile is amplified for the dimensionless constant parameter and nanoparticles volume fraction but decreases for the heterogeneous chemical reaction parameter.