Intrinsic optimization using stochastic nanomagnets

Abstract

This paper draws attention to a hardware system which can be engineered so that its intrinsic physics is described by the generalized Ising model and can encode the solution to many important NP-hard problems as its ground state. The basic constituents are stochastic nanomagnets which switch randomly between the ±1 Ising states and can be monitored continuously with standard electronics. Their mutual interactions can be short or long range, and their strengths can be reconfigured as needed to solve specific problems and to anneal the system at room temperature. The natural laws of statistical mechanics guide the network of stochastic nanomagnets at GHz speeds through the collective states with an emphasis on the low energy states that represent optimal solutions. As proof-of-concept, we present simulation results for standard NP-complete examples including a 16-city traveling salesman problem using experimentally benchmarked models for spin-transfer torque driven stochastic nanomagnets.

Introduction

The use of Ising computers to solve NP-hard problems has a rich heritage in both theory¹ and practice. These computers seek to solve a wide range of optimization problems by encoding the solution to the problem as the ground-state of an Ising energy expression. Many diverse systems have been proposed to solve NP-hard optimization problems such as those based on simulated annealing², DNA^3,4, quantum annealing^5,6, Cellular Neural Networks^7,8,9, CMOS¹⁰, trapped ions¹¹, electromechanics¹², optics^{13,14,15,16,17,18,19,20}, and magnets^21,22,23. A common objective of many of the Ising-based approaches is the identification of hardware configurations that can efficiently solve optimization problems of interest.

In this letter, we demonstrate the possibility of a hardware implementation that does not just mimic the Ising model, but embodies it as a part of its natural physics^21,22,23. It uses a network of N “soft” nanomagnets operating in a stochastic manner²⁴, each with an energy barrier Δ comparable to k_BT so that they switch between the two Ising states, ±1, on time scales where τ₀ ~ 0.1–1 ns. The natural laws of statistical mechanics guide the network through the 2^N collective states at GHz rates, with an emphasis on low energy states. We show how an optimization problem of interest is solved by engineering the spin-mediated magnet-magnet interactions to encode the problem solution and to simulate annealing without any change in temperature simply by continuously adjusting their overall strength. As proof-of-concept for the potential applications of this natural Ising computer, we present detailed simulation results for standard NP-complete examples, including a 16-city traveling salesman problem. This involves using experimentally benchmarked modules to simulate a suitably designed network of 225 stochastic nanomagnets and letting the hardware itself rapidly identify solutions within the 2²²⁵ possibilities. It should be possible to integrate such hardware into standard solid state circuits, which will govern the scalability of the solution.

The Ising Hamiltonian for a collection of spins, S_i, which can take on one of two values, ±1,

was originally developed to describe ferromagnetism where the J_ij are positive numbers representing an exchange interaction between neighboring spins S_i and S_j, while h_i represents a local magnetic field for spin S_i. Classically, different spin configurations σ{S_i} have a probability proportional to , T being the temperature, and k_B, the Boltzmann constant. At low temperatures, the system should be in its ground state σ_G, the state with the lowest energy H(σ). With h_i = 0, and positive J_ij, it is easy to see that the ground state is the ferromagnetic configuration σ_F with all spins parallel.

Much of the interest in the Ising Hamiltonian arises from the demonstration of many direct mappings of NP-complete and NP-hard problems to the model^1,25,26 such that the desired solution is represented by the spin configuration σ corresponding to the ground state. However, in general this mapping may require a large number of spins, and may require the parameters J_ij and h_i to take on a wide range of values, both positive and negative. Finding the ground state of this artificial spin glass is the essence of Ising computing, and broadly speaking it involves abstractly representing an array of spins, their coupling, and thermal noise through software and hardware that attempts to harness the efficiencies of physical equivalence²⁷. These representations may take the form of abstract models of the spins, the use of random number generators to produce noise, and logical or digital adders for the weighted summing. If enough layers of abstraction can be eliminated, the underlying hardware will inherently solve a given problem as part of its natural, intrinsic operation and this should be reflected in increased speed and efficiency.

Engineering Correlations Through Spin Currents

Here we describe a natural hardware for an Ising computer based on the representation of an Ising spin S_k by the magnetization m of a stochastic nanomagnet (SNM), which we believe will compare well with other alternative representations. These SNMs are in the “telegraphic” switching regime^24,28 requiring the existence of a small barrier in the magnetic energy (Δ ≈ k_BT), that gives a small, but definite preference for a given axis, with two preferred states ±1. In the absence of currents, these SNMs continually switch between +1 and −1 on the order of nanoseconds, and can be physically realized by a reduction of the magnetic grain volume²⁹ or by designing weak perpendicular magnetic anisotropy (PMA) magnets³⁰. Figure 1 shows the response of such a monodomain PMA magnet in the presence of an external spin current in the direction of the magnet’s easy axis.

Figure 1: Response of stochastic nanomagnet to spin current.

(a) The magnetization of a stochastic nanomagnet is shown for varying spin currents. The five number summary of the magnetization is shown throughout the simulation. (b) Obtaining stochastic operation for a magnet can be accomplished with a reduction of the energy barrier of the magnet E_B through device geometry or by increasing its temperature. The response of the magnet to thermal noise under these conditions is modeled using a stochastic Landau-Lifshitz-Gilbert (LLG) circuit element based on the input spin current I_S and magnetic field H. (c) Sample time slices are shown at various set points along the sigmoid in order to visualize the magnetization dynamics.

How do we couple the SNMs to implement the Ising Hamiltonian of Equation (1)? The usual forms of coupling involve dipolar or exchange interactions that are too limited in range and weightability. Instead, one possibility is an architecture²³ that uses charge currents which can be readily converted locally into spin currents through the spin Hall effect (SHE). These charge currents can be arbitrarily long-range and the total number of cross-couplings is only limited by considerations of routing congestion and delay. The couplings may also be confined to nearest-neighbors, simplifying the hardware design complexity while promoting scalability and retaining universality²⁶.

The Ising Hamiltonian of Equation (1) can be implemented by exposing each SNM m_k to a spin current I_k

which has a constant bias determined by h_k together with a term proportional to the magnetization of the j^th SNM m_j. The future state of magnet m_k at time (t + Δt) is related to the state of the other magnets at time t through the current I_k. This expression is derived analytically in the following section using the Fokker-Planck equation for the system³¹.

The spin current I_k can be generated using well-established phenomena and the prospects for physical realization of such a system are discussed later in this paper. The distinguishing feature of the present proposal arises from the intrinsic stochasticity of SNMs and their biasing through the use of weighted spin currents (Fig. 1(a)). How the SNMs are interconnected to implement Equation (2) can evolve as the field progresses.

Getting a large system to reach its true ground state is non-trivial as it tends to get stuck in local minima³². It is common to guide the system towards the ground state through a process of “annealing”² which is carried out differently in different hardware implementations. For example, systems based on superconducting flux qubits make use of quantum tunneling, which is referred to as quantum annealing³³, whereas classical CMOS approaches make use of random number generators³⁴ to produce random transitions out of local minima.

For our system of coupled SNMs, random noise is naturally present and can be easily controlled (Fig. 1(a)), causing the system of SNMs coupled according to Equation (2) to explore the configuration space of the problem on a nanosecond timescale. Annealing could be performed through a controlled lowering of the actual temperature, or equivalently through a controlled increase in the magnitude of the current I_k, even at room temperature. It has been noted that certain annealing schedules can guarantee convergence to the true ground state, but these schedules may be too slow to be used in practice³⁵. This paper only presents a straightforward annealing process and does not seek out optimal annealing schedules. Consequently, as we show in one of our combinatorial optimization examples, we may find only an approximate solution which, however, may be adequate for many practical problems.

Steady-State Fokker-Planck Description

Our goal is to interconnect magnets such that their equilibrium state is governed by Boltzmann statistics with thermal noise as an inherent characteristic of the system. To see that this is possible, consider a system of N magnets where we want

and

where m_k represents the z-component of the magnets.

Suppose each magnet is driven by a spin current derived from the others. We start with the Fokker-Planck equation³¹ for the N-magnet system:

where and i_k = I_k/I₀ with I₀ as the critical switching spin current . At equilibrium, yielding from (3) and (5):

respectively. Comparing equations (6) and (7) while assuming symmetric coupling, , for the system we find

and arrive at (2):

Stochastic Landau-Lifshitz-Gilbert (LLG) Model

In this section we briefly describe the simulation framework and stochastic LLG model used throughout this paper. We start with the LLG equation³¹ for a monodomain magnet with magnetization m_i in the presence of a spin current

The magnetic thermal noise enters the equation through the effective field of the magnet, H_i = H₀ + H_n, as an uncorrelated external magnetic field in three dimensions with the following mean and variance:

The numerical model is implemented as an equivalent circuit for SPICE-like simulators and reproduces the equilibrium (Boltzmann) distribution from a Fokker-Planck Equation³¹.

A given system of magnets is simulated using a collection of independent, though current-coupled, stochastic LLG models. Delays associated with the communication from one magnet to the next are neglected assuming that the response time of the nanomagnets is much greater than associated wire-delays. Presently, the attempt time τ of experimental nanomagnets is on the order of ∼μs to ∼ms^28,29,36. With additional scaling, the response times of these magnets will continue to improve³⁷ and should approach the ∼ns times discussed in this paper. With response times ∼ns, our simulations show that even routing delays on the order of 100s of ps do not affect the results materially. Using nearest-neighbor Ising approaches or other constraining design decisions it should be possible to limit routing delays to shorter values. However, if the routing delay is comparable to the intrinsic response time of the nanomagnets then it would be important to include their effect in the simulation.

Many options exist, please see the final section, for physical realization of the proposed system of stochastic nanomagnets. For the simulations in this paper we simply use Equation (2) without assuming any specific hardware to implement it, since it is likely that better alternatives will emerge in the near future, given the rapid pace of discovery in the field of spintronics, see for example^38,39,40,41.

Combinatorial Optimization

We will focus on two specific examples to demonstrate the ability of such an engineered spin glass to solve problems of interest⁴²: an instructive example based on the satisfiability problem (SAT), and a representative example based on the traveling salesman problem (TSP). The first known NP-complete problem is the problem of Boolean satisfiability⁴³, namely, deciding if some assignment of boolean variables {x_i} exists that satisfies a given conjunctive normal form (CNF) expression. Finding the collection of inputs that makes the clauses of the CNF expression true is computationally difficult, but easy to verify.

It is known that any given CNF expression can be mapped to a collection of Ising contraints using the fundamental building blocks of NOT (), AND (), and OR () each subject to the Ising constraints given by⁴⁴:

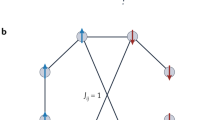
Using these building blocks, a network capable of finding the truth table for XOR was prepared (Fig. 2). For simplicity, the solution uses a naive method to construct the network and leverages the use of ancillary spins to represent and respectively (note that four spins could have been used⁴⁵). The array of spins from Fig. 2(b) are connected as specified by equations (11, 12, 13), driven by a reference current I₀. As the magnets explore the configuration space, their outputs are digitized and used to compute the overall energy of the system (Fig. 2(c)). The regions of zero energy correspond to solutions of the problem. The digitized outputs are aggregated to determine their probability of occurrence. By looking at the first three bits of the most probable outputs, the solution to the problem can be directly found (Fig. 2(d,e)). While this problem helps convey the essence of the approach, a more demonstrative application is worth considering.

Figure 2: Boolean satisfiability with stochastic magnets.

(a) The coupling between individual magnets is represented using abstract write and read units. Each magnet is influenced by problem specific on-site bias, B_i, and weighted, W_(ji), coupling to magnet . In turn, magnet influences magnet through weight W_(ij). (b) The magnetization response of the five magnets during a small time slice is digitized in order to compute the overall energy of the system as a function of time. (c) The truth table of the exclusive or operation is found by decomposing the operation into an expression involving only NOT, OR, and AND. The energy of this expression is found using the Ising model with two additional ancilla bits. The logical bits are represented by magnets mi that are coupled and biased as specified by the Ising energy expression. (d) Each digitized magnetization is used to represent the logical bits x_i. (e) Steady-State Fokker-Planck equation analytical solution using thresholding, demonstrating a qualitative match to the stochastic LLG solution of (d).

The decision form of the TSP is NP-complete, that is, for a collection of N cities, does there exist a closed path for which each city is visited exactly once that has a tour length less than some value d? Finding tours that satisfy this problem is computationally challenging and also of great practical interest. There are well-known mappings that translate the TSP to the Ising model^25,46. Here we adopt the following:

where x_i,j is a Boolean variable that is TRUE when city i is stop number j and FALSE otherwise, and W_(uv) are directed weights based on the distance between cities u and v. This Hamiltonian is mapped to a spin system by replacing each x_ij with 1/2(m_ij + 1) and weights W_(uv) with i_(uv) given by Equation (2).

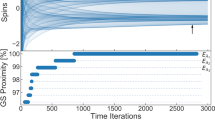
If the interconnections between each city are symmetric, then a Boltzmann machine⁴⁷ with each of the 2^N×N states associated with an effective energy H is realized, and the probability of the system visiting a particular state is proportional to . In order to find low-energy, optimized states, direct annealing of the glass can be performed. Using the ulysses16 reference dataset⁴⁸, annealing of a problem specific magnetic array through control of the effective temperature was performed (Fig. 3). Two specific traits of interest arise, namely the energy decays in a sigmoidal relationship with the ln T, and the specific heat of the system, , shows a defined peak about a critical temperature. At high temperatures, the system is disordered and corresponds to high energy states (Fig. 3(c)). As the temperature is reduced, the system continues to explore the energy landscape on a nanosecond timescale while gradually converging to a low-energy solution. For the given annealing profile and simulation duration, a low-energy, though not ideal, solution is found to the problem, highlighting the heuristic nature of the optimization⁴⁶. Note that in principle these simulation results could be obtained directly from actual hardware. For example, Figs 2(d) and 3(d) could be obtained by continuously monitoring the states of the individual SNMs using spin valves.

Figure 3: Annealing stochastic nanomagnets for heuristic optimization of the traveling salesman problem.

(a) An N = 16 city traveling salesman problem based on the ulyssess16 data set⁴⁸ was simulated using an array of (N − 1)² = 225 stochastic magnets, assuming a fixed starting city. Each magnet represents if city i was stop j using m_z = +1 or was skipped m_z = −1 (insets). The magnets are prepared in a random initial configuration and gradually annealed until eventually frozen in a low-energy configuration. The normalized average energy of the system at each temperature is shown as the system is gradually annealed. (b) The specific heat of the array versus temperature is shown along with insets of the array configuration at early and late temperatures. (c) The state of the array is shown as a TSP graph at various temperatures, shown as green diamonds in (a), during the annealing process with the ideal configuration shown on the top left. (d) Average magnetization shown at the temperatures of (c). (Map imagery data: Google, TerraMetrics).

Considerations for Physical Realization

Physical realization of these engineered spin glasses requires the integration of multiple functional elements as highlighted in Fig. 2(a). The magnetization of each magnet m_i is first sensed with a read unit. The signal produced by this read unit is then propagated to all of the magnets with couplings dependent on the read magnetization m_i. Each of these connections is independently weighted with weights W_(ij) and provided as input, along with an on-site bias B_i to the write units. The write units in turn influence and control the state of magnet m_j.

There are a number of design options available for each functional unit as shown in Table 1. Write-control of the magnets can be affected through a number of means including the spin Hall effect (SHE)³⁹ or perhaps through voltage control⁴⁰. The use of the SHE effect provides a convenient mechanism with which to sum several, independently weighted, input currents. Readout of the magnetization can be accomplished using well-established tunnel junctions⁴⁹ which have been demonstrated for stochastic nanomagnets²⁹. Alternatively, readout could perhaps be accomplished using the inverse SHE³⁹. Assuming the use of a SHE material and tunnel junction stack, care must be given to accomodate the simultaneous use of write and read currents. One approach would be to introduce the use of a time-multiplexed scheme that disassociates the write and read operations⁵⁰. Alternatively, structures that provide write and read isolation may be used⁵¹.

Table 1 Options for Physical Realization.

The ability to write and read the magnetization is of fundamental importance, however, once read, the likely weak signal must be amplified to satisfy the fanout requirements of the network. This transistor-like gain can be realized using all-spin based approaches^23,51 or perhaps with the use of a hybrid-CMOS design^52,53. These proposed approaches may introduce power dissipation challenges during the read operation, e.g. the short-circuit current produced with the use of amplifying inverters. Power dissipation considerations must be carefully evaluated to assess the viability of scaling the proposed system.

The output from the amplification stage can be selectively weighted so that a wide range of problems based on (1) can be encoded onto the network. The weighting of inputs can be based on an approach using re-programmable floating-gate voltages⁵⁴ that would enable the use of analog weights for the circuit. While floating-gate regulation would enable convenient re-programmability, the design would be complicated with the requirement for peripheral drivers to control the floating-gate array. Others proposals have suggested the use of memristors^24,53,55 or other programmable elements in a cross-bar like configuration^50,56, though with constrained fanout. Note that one weighting scheme that still retains the ability to encode NP-hard problems onto the network is with the use of {−1, 0, 1} weights¹. Using this simple approach removes the necessity for tunable weights and instead relegates the problem to one of routing, connectivity, and area.

All of the simulations used in this paper assume a fully connected network of magnets in which each magnet talks to all other magnets. For small networks this is reasonable, however, such an assumption is invalid for large networks as the number of routes grows rapidly. Instead, different topologies⁵⁷ and routing considerations must be made to account for congestion and long-distance communication. By limiting the connections to local-neighbors^9,10, the network may still be used to perform NP-hard optimization while also simplifying routing complexity. One design possibility is to leverage the lessons learned from the advances in the design of Field-Programmable Gate Array (FPGA) interconnects⁵⁸. FPGAs are designed with routing topologies that facilitate both short and long-range interconnections while also providing re-programmability.

The fidelity of the programmed weights and number of high-fanout signals needed for robust solutions may impose challenges on the selected weighting and routing schemes. Additionally, the propagation delay of these high-fanout signals must be balanced with the response time of the magnets in order for the system to be governed by (1). While flexibility in the allowed weights and number of couplings is convenient for encoding problems onto the model²⁵, it is important to note that discrete nearest-neighbor couplings still retain NP-hardness¹ and may greatly simplify the hardware design, improving scalability at the expense of increased encoding complexity and area.

The main point of this paper is the remarkable high-speed search through Fock space enabled by the intrinsic physics of a network of stochastic nanomagnets interacting via spin-mediated interactions. We hope this work fosters an interest in the physical realization and exploration of stochastic nanomagnets as a viable Ising computer.

Methods

Simulations based on the modular framework for spintronics³⁸ were used to produce the results in this work. Within the framework, a stochastic Landau-Lifshitz-Gilbert (LLG) model was used to simulate each nanomagnet. The magnetic parameters for the telegraphic PMA magnets used in the simulations are: effective anisotropy of PMA, , saturation magnetization, , damping coefficient, α = 0.01, and PMA diameter, Φ = 45 nm, amounting to a barrier height of Δ = 1 kT. In all simulations, the initial state of the magnetic array was randomly selected. Figure 1 was produced using a modular stochastic LLG simulation element with the input current swept from −2 μA to 2 μA in increments of 800 nA. At each current, the response of the magnet is observed for 10 μs. Figure 2 was simulated for 100 μs using the coupling depicted in the Figure and a reference current I₀ of 2 μA. Figure 3 used an annealing schedule of T_i+1 = 0.9 T_i and Lagrange multiplier of . At each temperature the magnets were allowed to randomly walk for 1 μs and were measured every 200 ps. The SAT and TSP magnetic networks were simulated using coupled stochastic LLG models with the intermagnet-coupling and on-site biases produced via the spin current term of the LLG equation. The magnetization of each magnet was digitized using Schmitt trigger based thresholds. HSPICE was used to solve the simultaneous coupled differential equations of the magnetic network.