Composable end-to-end security of Gaussian quantum networks with untrusted relays

Abstract

Gaussian networks are fundamental objects in network information theory. Here many senders and receivers are connected by physically motivated Gaussian channels, while auxiliary Gaussian components, such as Gaussian relays, are entailed. Whilst the theoretical backbone of classical Gaussian networks is well established, the quantum analog is yet immature. Here, we theoretically tackle composable security of arbitrary Gaussian quantum networks, with generally untrusted nodes, in the finite-size regime. We put forward a general methodology for parameter estimation, which is only based on the data shared by the remote end-users. Taking a chain of identical quantum links as an example, we further demonstrate our study. Additionally, we find that the key rate of a quantum amplifier-assisted chain can ideally beat the fundamental repeaterless limit with practical block sizes. However, this objective is practically questioned leading the way to future network/chain designs.

Introduction

$-{\log }_{2}(1-\eta )$, where η is the channel’s transmissivity, is the maximum fundamental rate, in bits, at which two distant parties can distribute quantum bits, entanglement bits, or secret bits. This is known as the Pirandola-Laurenza-Ottaviani-Banchi (PLOB) bound and holds for any point-to-point protocol of quantum communication¹. Since the discovery of PLOB, vast efforts have been made to break its hindrance, e.g., by using quantum repeater chains^2,3. In fact to outclass the PLOB bound, it is necessary to insert in-the-middle quantum stations, which can also be set out in a non-chain configuration to build a quantum network withal. Thus, one ultimate goal is not only to surpass the PLOB bound, but also to branch out a network of quantum links that would enable simultaneous secure communication or key distribution between more than just a few pairs of users⁴. Such telecommunication networks can further develop to provide us with a future quantum internet for quantum-secure communications^2,3 and distributing quantum computing^5,6,7,8.

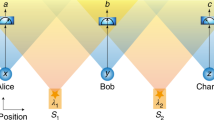
Gaussian networks, inter alia, are at the core of classical information theory, upon which concepts of communication networks have been developed⁹. Such networks, e.g., a large network of optical fiber links, have been studied and evolved in response to our continuous demand for data communications. They, as the name suggests, enjoy Gaussian signal assumptions and Gaussian links, where random variables with Gaussian probability density functions describe the channel noise. In addition, any other component, e.g., repeater relays, that makes the process of data communications possible or alleviates it is Gaussian, such that none of the shared variables/distributions between users of the network becomes non-Gaussian. In this work, we put our focus on Gaussian quantum networks that benefit from Gaussian input signals, Gaussian quantum channels, and auxiliary Gaussian quantum devices. In particular, we study end-to-end security between two arbitrary users of a Gaussian quantum network who are generally linked via untrusted nodes (see Fig. 1). More weakly, as we explain later, we also admit some post-selection operations that are conditionally Gaussian, i.e., projecting into a Gaussian state when they are successful (discarding their output otherwise).

Fig. 1: Quantum communication network.

Two arbitrary end-users, Alice (A) and Bob (B), can communicate through diverse, not necessarily direct, routes that extend across intermediate untrusted sender-receiver pairs that act as relays (yellow nodes). Two possible routes are highlighted in red. The quantum network is Gaussian if the operations at the nodes and the channels associated with links are all Gaussian, so that the final state shared by Alice and Bob is Gaussian. More weakly, we also include the possibility of non-Gaussian post-selection operations which however project into a Gaussian state when they are successful (see text for more details).

While examining a quantum network, not only is it fundamental to compute the relevant communication rates between arbitrary users, namely upper, lower and achievable rates, but it is crucial to evaluate composable key rates with a finite number of uses of the network. Evaluating the rate is possible by analyzing the data statistics that the parties would obtain through the so-called parameter estimation (PE)^10,11,12. For a typical single link, PE analysis, which commonly refers to estimating channel parameters (loss and noise), is relatively straightforward^13,14. However, PE can become very challenging in large-scale quantum networks. For these reasons, we do not consider estimating channel parameters; instead, we use PE in a more general sense by directly estimating measurable quantities, e.g., the covariance matrix (CM) of the end parties.

In the context of continuous-variable (CV) quantum key distribution (QKD), we show that any two users of a Gaussian quantum network can successfully extract composable secret keys from their local shared data, together with any classical public data that they might receive from other stations of the network. As mentioned above, an important point to remark is that we allow the network to deviate from being Gaussian, including the possibility to be conditionally Gaussian, i.e., described by a Gaussian state only after the success of a non-Gaussian, post-selection mechanism (feature which is needed for effective entanglement distillation^{15,16,17,18,19}). In particular, this happens when non-deterministic quantum amplifiers are in use, where they sporadically fail to amplify^{20,21,22,23,24,25}. We further investigate the use of such amplifiers in a linear quantum chain.

Results and discussion

Gaussian quantum networks

We consider the scenario where Alice and Bob are two arbitrary users of a quantum network, as sketched in Fig. 1; their objective is to remotely share a secret key. Let us assume that there are M − 1 stations that relay signals from Alice to Bob through a specific route that is made of M basic links. As Fig. 2a schematically illustrates, an arbitrary route can be seen as a chain of quantum links. It is also assumed that a powerful eavesdropper (Eve) may operate the intermediate stations and also store all the lost portion of the signals into her quantum memories (QMs). The relay stations may consist of several components. For instance, they can be equipped with entanglement sources, such as two-mode squeezed vacuum (TMSV), quantum amplifiers, QMs, and a classical communication system; see Fig. 2b. Nonetheless, the key role of the relays is to connect adjacent links via joint Bell measurements, whose outcomes γ_i (for i = 1, …, M − 1) are aired to Alice and Bob for local data processing. Note that, in case the relays operate differently from expected, this would reflect in high amount of noise in Alice and Bob’s shared data.

Fig. 2: Quantum communication chain within a network.

a An arbitrary route between Alice and Bob can be seen as a linear chain between them that consists of M links and M − 1 stations (R_i's). b Each station can encompass a noiseless linear amplifier (NLA, g), a bipartite entanglement TMSV source (μ), a couple of QMs, and a non-ideal Bell detection, whose loss is simulated by a couple of beam splitters with transmissivity η_B. c A Gaussian quantum network provides the end parties with a Gaussian bipartite state, called the network state ${\rho }_{{A}^{\prime}{B}^{\prime}}$. Displacement operations need to be applied according to the information received form the stations, as shown in a. d The effect of the Gaussian quantum network in c can be simulated via a one-way Gaussian protocol with an equivalent source ${\mu }^{\prime}$, and an equivalent channel, ${{{\mathcal{E}}}}^{\prime}$, with loss ${\eta }^{\prime}$ and excess noise ${\xi }^{\prime}$.

Figure 2c captures the role of the network in terms of quantum teleportation-stretching formalism¹. The network provides end-parties, Alice and Bob, with a bipartite (entangled) Gaussian state, which we call the network state ${\rho }_{{A}^{\prime}{B}^{^{\prime\prime} }| \{{\gamma }_{i}\}}$, before γ_i’s corrections are applied. We conventionally assume that the initial single links are of zero mean. However, execution of a relay, e.g., R₁, displaces the mean value of the state by an amount f(γ₁) proportional to γ₁. In order to “correct” this a displacement operation, e.g., ${\widehat{D}}_{1}$, should be applied accordingly. Similar displacement operations are applied due to other relay outcomes that can all be postponed to one end. Thus, in this way, the mean value of the network state after γ_i corrections, now described by ${\rho }_{{A}^{\prime}{B}^{\prime}}$, becomes independent of the γ_i’s (in fact we balance it to zero). Further, since displacements are local operations, the network state will have a CM ${{{{\bf{V}}}}}_{{A}^{\prime}{B}^{\prime}}={{{{\bf{V}}}}}_{{A}^{\prime}{B}^{^{\prime\prime} }| \{{\gamma }_{i}\}}$, which is described in the normal form:

$${{{{\bf{V}}}}}_{{A}^{\prime}{B}^{\prime}}=\left(\begin{array}{cc}{\mathsf{a}}{{{\bf{I}}}}&{\mathsf{c}}{{{\bf{Z}}}}\\ {\mathsf{c}}{{{\bf{Z}}}}&{\mathsf{b}}{{{\bf{I}}}}\end{array}\right),\,\left\{\begin{array}{l}{{{\bf{I}}}}:={{{\rm{diag}}}}(1,1),\\ {{{\bf{Z}}}}:={{{\rm{diag}}}}(1,-1).\end{array}\right.$$

(1)

Therefore, the network state supplies Alice and Bob with an overall two-mode Gaussian state that can be used to implement different one-way-like communication protocols.

We remark that the Gaussianity assumption can be weakened because of conditioning, or post-selection, where relays can actually impose non-Gaussianity on the entire network, yet the system can be assumed conditionally Gaussian. This situation occurs because measurable quantities, such as CM elements, depend on relay measurement outcomes, which may vary for different sets of {γ_i}. This is similar to post-selection^26,27 or discrete-alphabet protocols^28,29 where, for example, the outcome set #1 gives ${{{{\bf{V}}}}}_{{A}^{\prime}{B}^{\prime}}^{\#1}$, while the outcome set #2 gives ${{{{\bf{V}}}}}_{{A}^{\prime}{B}^{\prime}}^{\#2}$ that differs from the CM associated to that of set #1. Thus, one needs to build an average rate over all possible outcome sets. Therefore, the average state/CM would be non-Gaussian. Nevertheless, if in such situations we choose to discard the unsuccessful events, then the post-selected state between Alice and Bob is Gaussian.

Security reduction

It is conceivable that the types of attack that eavesdroppers may apply on a multi-link quantum network can be more complex than the way they would attack conventional one-link protocols. For instance, in a quantum network a subset of the links that form the route from Alice to Bob may have correlations. In fact, Eve may adapt her attack on a link based on the information she has gained while attacking other, previous links. This generally defines a collective network attack, which has memory between the links but is memory-less between different uses of the network. Such inter-link correlations are taken into account in the network state or, alternatively, its corresponding CM. This is due to the fact that we consider only the end-to-end Gaussian CM for the analysis. As a requirement for our analysis, it is important to note that the CM of the network state is in normal form of Eq. (1). Note that we assume that the route is fixed. In the case it changes use-by-use, a more general attack would involve correlations between all the links that are overall used over multiple uses of the network.

Nevertheless, there may also be correlations between subsequent uses of a route, which defines an even more powerful and general, coherent attack. Hence, we need to prove the security when the eavesdroppers develop inter-use correlations, i.e., when they apply a coherent attack. Our solution is to tackle this problem by reducing the Gaussian quantum network security to that of one-way protocols, for which optimality of collective Gaussian attacks has been proven³⁰. In this way, we reduce the complexity of the problem and extend the security analysis under collective attacks to coherent attacks.

Assume that the end-nodes of the network, $A^{\prime}$ and $B^{\prime}$, remain in the Gaussian regime. We can seek for equivalent parameters of a single Gaussian channel that does the same job. In fact, the overall function of a Gaussian quantum network can be reduced to, and modeled by, a one-way Gaussian channel, with loss ${\eta }^{\prime}$ and excess noise ${\xi }^{\prime}$, applied to an equivalent source with modulation ${\mu }^{\prime}$. See Fig. 2d, where we have that such equivalent parameters builds up a CM in normal form:

$${{{{\bf{V}}}}}_{{A}^{\prime}{B}^{\prime}}^{{{{\rm{eqv}}}}}=\left(\begin{array}{cc}{\mu }^{\prime}{{{\bf{I}}}}&\sqrt{{\eta }^{\prime}({\mu }^{^{\prime} 2}-1)}{{{\bf{Z}}}}\\ \sqrt{{\eta }^{\prime}({\mu }^{^{\prime} 2}-1)}{{{\bf{Z}}}}&{\eta }^{\prime}{\mu }^{\prime}+1-{\eta }^{\prime}+{\xi }^{\prime}{{{\bf{I}}}}\end{array}\right).$$

(2)

It is straightforward to find the elements of the CM of the equivalent state, given by Eq. (2), in the terms of the triplet (a, b, c) in Eq. (1) that describes the network state ${\rho }_{{A}^{\prime}{B}^{\prime}}$; one can obtain:

$$\left\{\begin{array}{l}{\mu }^{\prime}={\mathsf{a}},\quad \\ {\eta }^{\prime}={{\mathsf{c}}}^{2}{\left({{\mathsf{a}}}^{2}-1\right)}^{-1},\quad \\ {\xi }^{\prime}=({\mathsf{a}}+1)({\mathsf{b}}-1)-{{\mathsf{c}}}^{2}.\quad \end{array}\right.$$

(3)

Note that ${{{{\bf{V}}}}}_{{A}^{\prime}{B}^{\prime}}^{{{{\rm{eqv}}}}}$ is bona fide, i.e., ${\mu }^{\prime}\ge 1$, ${\eta }^{\prime}\le 1$, and ${\xi }^{\prime}\ge 0$, when the CM in Eq. (1) is bona fide, i.e., a, b ≥ 1 and ${\mathsf{c}}\le \min \{\sqrt{{{\mathsf{a}}}^{2}-1},\sqrt{({\mathsf{a}}+1)({\mathsf{b}}-1)}\}$³¹.

This means that the original collective network attacks can be extended to coherent network attacks where correlations could happen between different uses of the network. Consequently, the optimality of Gaussian attacks in typical one-way Gaussian protocols is extended to Gaussian quantum networks. It is therefore a reasonable assumption to consider Gaussian eavesdropping which is the optimal strategy in the presence of protocols based on Gaussian resources. For this reason, for our security analysis and composable study we consider network attacks that are collective and Gaussian.

Emulation of sending- and receiving-only relays

It is conceivable that a node in a quantum network is exploited to only send/share or only receive/measure quantum signals. In order to keep our study as general as possible, especially when it comes to PE, we shall simulate such specific relays that include either a relay with some outcome γ or a source with some variance μ to feed its adjacent relays; see Fig. 3a1. Assume three single links that are connected via two Bell detection modules. The emulation can be performed by (1) applying the second relay on modes B and c, which produces the outcome γ₂, (2) applying a correction/displacement, ${\widehat{D}}_{2}$, at the first relay on mode b, which subsequently teleports mode c to $b^{\prime}$, and (3) taking the limit ν → ∞. As sketched in Fig. 3a2, we show that the above steps would reduce the two “full” relays, which include a Bell measurement as well as a TMSV source, to a receiving-only and a sending-only relays.

Fig. 3: Emulation of specific nodes of a quantum network.

a1, a2 We emulate receiving-only and sending-only nodes. b1, b2 We sketch the teleportation stretching form of a1 and a2, respectively. c1, c2 We show that all displacement operations can be postponed to one, receiver end (see main text). Here, ${{{\mathcal{E}}}}$ and $\widehat{D}$ represent a thermal-loss channel and single-mode displacement operation, respectively. (see main text for explanation).

For convenience, let us describe the situation in terms of the teleportation-stretching technique, developed in ref. ¹, as shown in Fig. 3b1, b2. We shall show that in both cases, after taking the limit ν → ∞, the resultant CM for modes ${b}^{\prime}{C}^{\prime}$ is the same. By assuming that ${{{\mathcal{E}}}}$ is a thermal-loss with transmissivity η and noise at channel output ξ, we see that the scheme in Fig. 3b2 gives:

$${{{{\bf{V}}}}}_{{b}^{\prime}{C}^{\prime}}^{{{{\rm{b}}}}2}=\left(\begin{array}{cc}\mu {{{\bf{I}}}}&\sqrt{\eta ({\mu }^{2}-1)}{{{\bf{Z}}}}\\ \sqrt{\eta ({\mu }^{2}-1)}{{{\bf{Z}}}}&\eta \mu +1-\eta +\xi {{{\bf{I}}}}\end{array}\right).$$

(4)

With a bit of math one can show that the execution of the relay in Fig. 3b1 gives:

$$\begin{array}{l}{{{{\bf{V}}}}}_{{b}^{\prime}{C}^{\prime}}^{{{{\rm{b1}}}}}=\left(\begin{array}{ll}\mu -\frac{{\mu }^{2}-1}{\mu +\nu }{{{\bf{I}}}}&\frac{\sqrt{\eta ({\mu }^{2}-1)({\nu }^{2}-1)}}{\mu +\nu }{{{\bf{Z}}}}\\ \frac{\sqrt{\eta ({\mu }^{2}-1)({\nu }^{2}-1)}}{\mu +\nu }{{{\bf{Z}}}}& F{{{\bf{I}}}}\end{array}\right),\\ F\quad\,\,\,=\,\displaystyle\frac{\mu (\eta \mu +1-\eta +\xi )+(1-\eta +\xi )+\eta }{\mu +\nu }.\end{array}$$

(5)

One can then verify that ${{{{\bf{V}}}}}_{{b}^{\prime}{C}^{\prime}}^{{{{\rm{b1}}}}}$ equals the CM in Eq. (4) in the limit ν → ∞.

In Fig. 3c1, c2, we further verify that corrections based on broadcasted γ_i’s can be postponed to one end (here to the end-mode “a”). We do so by checking the equivalence when the displacement operator ${\widehat{D}}_{2}$ can be postponed and performed along with ${\widehat{D}}_{1}$. The equivalence can be verified through checking both CMs and mean values. From upper and lower panels in Fig. 3c, it is clear that the equality holds for CMs since both scenarios start with the same resources and channels, on which only local displacement operations, which do not change the CMs, are applied.

For mean values, we start by the fact that initial mean value vector for the four involved modes is zero, i.e., ${\overline{{{{\bf{x}}}}}}_{{B}^{\prime}bAa}={{{\bf{0}}}}$. Let us start from Fig. 3c1. The displacement ${\gamma }_{2}:=({q}_{{\gamma }_{2}}+i{p}_{{\gamma }_{2}})/\sqrt{2}$ implies that $\overline{{{{\bf{x}}}}}^{\prime} ={(0\,0\,{q}_{{\gamma }_{2}}\,{p}_{{\gamma }_{2}}\,0\,0\,0\,0)}^{{\mathrm{T}}}$, which after applying the balanced beam splitter of the Bell detection varies to:

$${\overline{{{{\bf{x}}}}}}_{{B}^{\prime}bAa}^{^{\prime\prime} }={\left(0\,0\frac{{q}_{{\gamma }_{2}}}{\sqrt{2}}\,\frac{{p}_{{\gamma }_{2}}}{\sqrt{2}}\,\frac{-{q}_{{\gamma }_{2}}}{\sqrt{2}}\,\frac{-{p}_{{\gamma }_{2}}}{\sqrt{2}}\,0\,0\right)}^{{\mathrm{T}}}.$$

(6)

Next, it can be shown that the execution of homodyne detection modules, with the outcomes ${q}_{{\gamma }_{1}}$ and ${p}_{{\gamma }_{1}}$ that forms ${\gamma }_{1}:={q}_{{\gamma }_{1}}+i{p}_{{\gamma }_{1}}$, gives the mean value vector for the mode a:

$${\overline{{\mathbf{x}}}}_{a}^{\prime\prime\prime}=\Gamma \left(\begin{array}{c}{q}_{\gamma_{2}}+\sqrt{2}q_{\gamma_{1}}\\ p_{\gamma_{2}}-\sqrt{2}p_{\gamma_{1}}\end{array}\right),{\mathrm{with}}\,\Gamma :=\frac{\sqrt{\eta ({\mu}^{2}-1)}}{\nu +\eta (\mu -1)+1+\xi }.$$

(7)

Then the parties apply the following displacement dependent on the outcomes:

$${D}_{1}({q}_{{\gamma }_{1}},{p}_{{\gamma }_{1}})=\Gamma \left(\begin{array}{c}-\sqrt{2}{q}_{{\gamma }_{1}}\\ +\sqrt{2}{p}_{{\gamma }_{1}}\end{array}\right),$$

(8)

and obtain the mean of mode b (rescaled by the factor Γ):

$${\overline{{{{\bf{x}}}}}}_{a}^{{{{\rm{up}}}}}=\Gamma \left(\begin{array}{c}{q}_{{\gamma }_{2}}\\ {p}_{{\gamma }_{2}}\end{array}\right).$$

(9)

In Fig. 3c2, after applying the Bell detection module, with outcomes ${q}_{{\gamma }_{1}}^{\prime}$ and ${p}_{{\gamma }_{1}}^{\prime}$, we have that:

$${\overline{{{{\bf{x}}}}}}_{a}=\sqrt{2}\Gamma \left(\begin{array}{c}{q}_{{\gamma }_{1}}^{\prime}\\ {p}_{{\gamma }_{1}}^{\prime}\end{array}\right);$$

(10)

hence, we apply the displacement ${D}_{1}^{\prime}({q}_{{\gamma }_{1}}^{\prime},{p}_{{\gamma }_{1}}^{\prime})$ to obtain:

$${\overline{{{{\bf{x}}}}}}_{a}^{\prime}=\left(\begin{array}{c}0\\ 0\end{array}\right).$$

(11)

One can show that the mean value vector for the mode a after the displacement ${D}_{2}^{\prime}({q}_{{\gamma }_{2}}^{\prime},{p}_{{\gamma }_{2}}^{\prime})$ is given by:

$${\overline{{{{\bf{x}}}}}}_{a}^{{{{\rm{down}}}}}=\left(\begin{array}{c}{q}_{{\gamma }_{2}}^{\prime}\\ {p}_{{\gamma }_{2}}^{\prime}\end{array}\right),$$

(12)

whose entries can be tuned so that ${\overline{{{{\bf{x}}}}}}_{a}^{{{{\rm{down}}}}}={\overline{{{{\bf{x}}}}}}_{a}^{{{{\rm{up}}}}}$.

Note that we can define a “network number,” S_net, which tells us how a generic network is different from a fully designed network whose nodes are all sending-receiving. Precisely, the number S_net accounts for the number of only-receiving plus only-sending nodes. A fully designed network then has S_net = 0. Note also that, as described in Fig. 3, such nodes always appear in pairs, such that S_net is an even number, the reason being directionality of the generated signals as well as network’s symmetry. In fact, like an entanglement source that feeds the two ends of a single link, the function of the network is to distribute entanglement toward both far-ends. Installing nodes that result in S_net being an odd number, would break the directionality, and the symmetry, which therefore breaks off the links of the network.

Parameter estimation

The outcomes of the relays are bi-dimensional Gaussian variables ${\gamma }_{i}={({q}_{{\gamma }_{i}},{p}_{{\gamma }_{i}})}^{T}$, which are taken into account by Alice and Bob to post-process their local variables. Let us focus on the q-quadrature for the next derivations since equivalent steps hold for the p-variable. To simplify the derivations, we in fact assume that q and p quadratures are not mixed by the eavesdropper so that they can be treated as independent variables. (This is a reasonable protocol assumption; extension is just a matter of technicalities).

In this work we assume that both Alice and Bob apply heterodyne measurements on the end-to-end modes $A^{\prime}$ and $B^{\prime}$ with outcomes z_A: = (q_A, p_A) and z_B: = (q_B, p_B), respectively, to establish a secure key. By assuming that the relays work properly and that the quadratures follow a normal distribution, we can write the variables that build the raw key for Alice and Bob, respectively, as:

$${q}_{x}={q}_{A}-\mathop{\sum }\limits_{i=1}^{M-1}{u}_{i}{q}_{{\gamma }_{i}},$$

(13)

$${q}_{y}={q}_{B}-\mathop{\sum }\limits_{i=1}^{M-1}{v}_{i}{q}_{{\gamma }_{i}},$$

(14)

where u_i’s and v_i’s are real numbers. In a prepare and measure variant, where Alice prepares coherent states, she generates variable ${\bar{z}}_{A}=\left(\sqrt{\frac{\mu -1}{\mu +1}}{q}_{A},\sqrt{\frac{\mu -1}{\mu +1}}{p}_{A}\right)$, with $\mu ={\sigma }_{A}^{2}-1$, where ${\sigma }_{A}^{2}$ is the variance of the Gaussian modulation of ${\bar{z}}_{A}$. Hence, before applying Eqs. (13) and (14), one needs to apply a transformation, ${{{\bf{L}}}}=\sqrt{\frac{\mu -1}{\mu +1}}{{{\bf{I}}}}$, on ${\bar{z}}_{A}$ in order to obtain z_A.

For security reasons, we require q_x and q_y to be uncorrelated with the public variables ${q}_{{\gamma }_{i}}$’s that are known to Eve, i.e., $\langle {q}_{x}{q}_{{\gamma }_{i}}\rangle =0$, which imposes the following constraints:

$$\left\langle {q}_{A}{q}_{{\gamma }_{i}}\right\rangle =\mathop{\sum }\limits_{k=1}^{M-1}{u}_{k}\langle {q}_{{\gamma }_{i}}{q}_{{\gamma }_{k}}\rangle ,$$

(15)

from which one can calculate the weights u_i’s (similar relations hold for q_y, q_B and v_i’s).

Now, let us consider and study the sampled data ${[{q}_{A}]}_{j}$ and ${[{q}_{{\gamma }_{i}}]}_{j}$, for j = 1, …, N, associated with variables q_A and ${q}_{{\gamma }_{i}}$, respectively. From these, Alice can calculate the corresponding maximum likelihood estimators:

$${\widehat{\langle {q}_{A}{q}_{{\gamma }_{i}}\rangle }}={N}^{-1}\mathop{\sum }\limits_{j=1}^{N}{\left[{q}_{A}\right]}_{j}{\left[{q}_{{\gamma }_{i}}\right]}_{j},$$

(16)

$${\widehat{\langle {q}_{{\gamma }_{i}}{q}_{{\gamma }_{k}}\rangle }}={N}^{-1}\mathop{\sum }\limits_{j=1}^{N}{\left[{q}_{{\gamma }_{i}}\right]}_{j}{\left[{q}_{{\gamma }_{k}}\right]}_{j}.$$

(17)

Next, to obtain values of the weights u_i’s, she replaces these values in the set of M equalities in Eq. (15). She then continues with calculating ${[{q}_{x}]}_{j}$ by replacing the u_i’s, and the data points ${[{q}_{A}]}_{j}$ and ${[{q}_{{\gamma }_{i}}]}_{j}$, in Eq. (13). Indeed, Bob obtains similar relations for q_y and v_i’s.

At this stage the parties are in a position to compute the classical CM associated to their post-processed data:

$$\widehat{{{{\boldsymbol{\Sigma }}}}}=\left(\begin{array}{cc}{\widehat{{{{\bf{V}}}}}}_{x}&{\widehat{{{{\bf{C}}}}}}_{xy}\\ {\widehat{{{{\bf{C}}}}}}_{xy}&{\widehat{{{{\bf{V}}}}}}_{y}\end{array}\right),$$

(18)

where ${\widehat{{{{\bf{V}}}}}}_{x}={{{\rm{diag}}}}\left(\widehat{\langle {q}_{x}^{2}\rangle },\widehat{\langle {p}_{x}^{2}\rangle }\right)$, ${\widehat{{{{\bf{V}}}}}}_{y}={{{\rm{diag}}}}\left(\widehat{\langle {q}_{y}^{2}\rangle },\widehat{\langle {p}_{y}^{2}\rangle }\right)$, and ${\widehat{{{{\bf{C}}}}}}_{xy}={{{\rm{diag}}}}\left(\widehat{\langle {q}_{x}{q}_{y}\rangle },\widehat{\langle {p}_{x}{p}_{y}\rangle }\right)$.

For the q-quadrature we have that (not to mention that the parties repeat the same process for the p-quadrature):

$$\widehat{\langle {q}_{x}^{2}\rangle }={m}_{{{{\rm{pe}}}}}^{-1}\mathop{\sum }\limits_{j=1}^{{m}_{{{{\rm{pe}}}}}}{\left[{q}_{x}\right]}_{j}^{2},$$

(19)

$$\widehat{\langle {q}_{y}^{2}\rangle }={m}_{{{{\rm{pe}}}}}^{-1}\mathop{\sum }\limits_{j=1}^{{m}_{{{{\rm{pe}}}}}}{\left[{q}_{y}\right]}_{j}^{2},$$

(20)

$${\widehat{\langle {q}_{x}{q}_{y}\rangle }}={m}_{{{{\rm{pe}}}}}^{-1}\mathop{\sum }\limits_{j=1}^{{m}_{{{{\rm{pe}}}}}}{\left[{q}_{x}\right]}_{j}{\left[{q}_{y}\right]}_{j},$$

(21)

when m_pe is the number of signals sacrificed for PE.

Note that, in principle, the parties can locally calculate the values from the estimators ${\widehat{{{{\bf{V}}}}}}_{x}$ and ${\widehat{{{{\bf{V}}}}}}_{y}$ using N data points while $\widehat{\langle {q}_{x}{q}_{y}\rangle }$ demands sharing m_pe data points through the public classical channel. These data can be easily acquired by Eve and thus must not contribute to the key generation. In general, the parties optimize the amount of shared data, m_pe, so as to limit the uncertainty of terms such as $\widehat{\langle {q}_{x}{q}_{y}\rangle }$ while still keeping as many samples as possible for the secret key.

The parties can compute an interval, with confidence 1 − ε_pe, for the estimated CM from which they derive the worst-case scenario CM, i.e., the CM that minimizes the key rate according to the sampled data with a probability larger than 1 − ε_pe. This CM is given by:

$${{{{\boldsymbol{\Sigma }}}}}_{{{{\rm{wc}}}}}=\widehat{{{{\boldsymbol{\Sigma }}}}}+\sqrt{\frac{4\kappa }{{m}_{{{{\rm{pe}}}}}}}\left(\begin{array}{cc}{\widehat{{{{\bf{V}}}}}}_{x}&-\frac{{\widehat{{{{\bf{V}}}}}}_{x}+{\widehat{{{{\bf{V}}}}}}_{y}}{2}{{{\bf{Z}}}}\\ -\frac{{\widehat{{{{\bf{V}}}}}}_{x}+{\widehat{{{{\bf{V}}}}}}_{y}}{2}{{{\bf{Z}}}}&{\widehat{{{{\bf{V}}}}}}_{y}\end{array}\right),$$

(22)

with $\kappa ={{{\rm{\ln }}}}(8{\varepsilon }_{{{{\rm{pe}}}}}^{-1})$. This is calculated by using suitable tail bounds for the chi-squared distribution (see Methods). It is valid for any CM of two correlated systems even if the entries are given theoretically via a model, e.g., $y=\sqrt{\tau }x+\epsilon$, with scale factor $\sqrt{\tau }$ and variance ${\sigma }_{\epsilon }^{2}$ for the normal variable ϵ.

Asymptotic key rate

We define the asymptotic secret key rate of sharing a key between two arbitrary users of a quantum network based on the Devetak-Winter rate³²:

$$K=\beta I({z}_{A}:{z}_{B}| \{{\gamma }_{i}\})-\chi (E:{z}_{r}| \{{\gamma }_{i}\}),$$

(23)

where I(z_A: z_B∣{γ_i}) is the mutual information between z_A and z_B and S(E: z_r) is the Holevo information between Eve’s system and the reconciliation variable z_r, with r = A(B) indicating direct (reverse) reconciliation. In this work, we focus on the reverse reconciliation r = B. By definition, we have:

$$\chi (E:{z}_{B}| \{{\gamma }_{i}\})=S(E| \{{\gamma }_{i}\})-S(E| {z}_{B}\{{\gamma }_{i}\}),$$

(24)

where:

$$S(E| \{{\gamma }_{i}\})=-{{{\rm{tr}}}}\left({\rho }_{E| \{{\gamma }_{i}\}}{\log }_{2}{\rho }_{E| \{{\gamma }_{i}\}}\right)$$

(25)

is the von Neumann entropy of Eve’s state, ρ_E (conditioned on the knowledge of the γ’s), and:

$$\begin{array}{l}S(E| {z}_{B}\{{\gamma }_{i}\})=\displaystyle{\int} {{{\rm{d}}}}{z}_{B}p({z}_{B}| \{{\gamma }_{i}\})\\\qquad\qquad\qquad\quad\times \left[-{{{\rm{tr}}}}\left({\rho }_{E| {z}_{B}\{{\gamma }_{i}\}}{\log }_{2}{\rho }_{E| {z}_{B}\{{\gamma }_{i}\}}\right)\right],\end{array}$$

(26)

where ${\rho }_{E| {z}_{B}{\gamma }_{i}}$ is the state conditioned on Bob’s variable z_B (after the γ’s).

With this in mind, the parties neither know the explicit description of Eve’s system nor how she interacts with the links. However, by assuming that Eve purifies the system between Alice and Bob, such that ${\rho }_{ABE| \{{\gamma }_{i}\}}$ is a pure state, it holds that S(E∣{γ_i}) = S(AB∣{γ_i}) and S(E∣z_B{γ_i}) = S(A∣z_B{γ_i})³³, where the later equality also exploits the fact that Bob performs a rank-1 measurement (like heterodyne detection) therefore projecting the global pure state ${\rho }_{ABE| \{{\gamma }_{i}\}}$ into a reduced pure state ${\rho }_{AB| {z}_{B}\{{\gamma }_{i}\}}$. Since the state ${\rho }_{AB| \{{\gamma }_{i}\}}$ is Gaussian, it is characterized by its CM, ${{{{\bf{V}}}}}_{AB| \{{\gamma }_{i}\}}$. In practice, this can be estimated by the worst-case quantum CM, V_wc (compatible with the classical data shared by the parties):

$${{{{\bf{V}}}}}_{AB| \{{\gamma }_{i}\}}\simeq {{{{\bf{V}}}}}_{{{{\rm{wc}}}}}={{{{\boldsymbol{\Sigma }}}}}_{{{{\rm{wc}}}}}-{{{\bf{I}}}}\oplus {{{\bf{I}}}}.$$

(27)

By setting:

$${{{{\bf{V}}}}}_{AB| \{{\gamma }_{i}\}}:=\left(\begin{array}{cc}{{{{\bf{V}}}}}_{A| \{{\gamma }_{i}\}}&{{{{\bf{C}}}}}_{AB| \{{\gamma }_{i}\}}\\ {{{{\bf{C}}}}}_{AB| \{{\gamma }_{i}\}}&{{{{\bf{V}}}}}_{B| \{{\gamma }_{i}\}}\end{array}\right),$$

(28)

we have that the conditional CM after Bob’s heterodyne is given by:

$${{{{\bf{V}}}}}_{A| {z}_{B}\{{\gamma }_{i}\}}={{{{\bf{V}}}}}_{A| \{{\gamma }_{i}\}}-{{{{\bf{C}}}}}_{AB| \{{\gamma }_{i}\}}^{\top }{\left[{{{{\bf{V}}}}}_{B| \{{\gamma }_{i}\}}+{{{\bf{I}}}}\right]}^{-1}{{{{\bf{C}}}}}_{AB| \{{\gamma }_{i}\}}.$$

(29)

Next, from the symplectic spectra ${{{{\boldsymbol{\nu }}}}}_{AB| \{{\gamma }_{i}\}}$ and ${{{{\boldsymbol{\nu }}}}}_{A| {z}_{B}\{{\gamma }_{i}\}}$, of ${{{{\bf{V}}}}}_{AB| \{{\gamma }_{i}\}}$ and ${{{{\bf{V}}}}}_{A| {z}_{B}\{{\gamma }_{i}\}}$, we compute the Holevo information:

$$\chi (E:{z}_{B}| {\gamma }_{i})=\mathop{\sum}\limits_{l}h({[{{{{\boldsymbol{\nu }}}}}_{AB| \{{\gamma }_{i}\}}]}_{l})-\mathop{\sum}\limits_{k}h({[{{{{\boldsymbol{\nu }}}}}_{A| {z}_{B}\{{\gamma }_{i}\}}]}_{k}),$$

(30)

where $h(x)=\frac{x+1}{2}{\log }_{2}\frac{x+1}{2}-\frac{x-1}{2}{\log }_{2}\frac{x-1}{2}$. In addition, the mutual information is given by³⁴:

$$I({z}_{A}:{z}_{B}| \{{\gamma }_{i}\})=\frac{1}{2}{\log }_{2}\frac{1+\det {{{{\bf{V}}}}}_{A| \{{\gamma }_{i}\}}+{{{\rm{tr}}}}{{{{\bf{V}}}}}_{A| \{{\gamma }_{i}\}}}{1+\det {{{{\bf{V}}}}}_{A| {z}_{B}\{{\gamma }_{i}\}}+{{{\rm{tr}}}}{{{{\bf{V}}}}}_{A| {z}_{B}\{{\gamma }_{i}\}}}.$$

(31)

Therefore, the parties have calculated a modified asymptotic key rate that encompasses the worst-case scenario given the sampled data. This is correct up to an error ε_pe and is calculated from Alice’s and Bob’s remote, shared, data that account for the relay outputs γ_i’s without any assumption on the structure of the intermediate channels. To put it more precisely, the rate should be re-scaled in a way to account for the number of uses sacrificed for PE. We discuss this and other aspects in detail shortly.

Let us also remark that in all the derivation above, we assume that the conditioning associated with the γ_i’s create the same conditional CM for the shared state regardless of the actual values of γ_i’s. This makes sense only under the Gaussian assumptions for the network, but this is still true even in the presence of NLAs, where the network is conditionally Gaussian.

Composable finite-size key rate

The security of Gaussian quantum networks can be further extended by considering finite-size correction terms dependent on small failure probabilities of different processes of the protocol. Over a chosen route of the network, Alice and Bob would share the following classical-quantum state between themselves and Eve, who is assumed to perform a collective Gaussian attack:

$${\rho }_{ABE}=\mathop{\sum}\limits_{k,l}p(k,l){\left|k\right\rangle }_{A}\left\langle k\right|\otimes {\left|l\right\rangle }_{B}\left\langle l\right|\otimes {\rho }_{E}(k,l),$$

(32)

where E ≡ E₁E₂ … E_M are Eve’s systems; see Fig. 2a. Thus, at the end of the error correction (EC), Alice and Bob possess correlated discretized variables kⁿ and lⁿ respectively associated with ${\rho }_{ABE}^{\otimes n}$.

As we discussed, the end-to-end CM, either built from sampled data or given by means of a proper model, would suffice to derive the secret key rate or suitable bounds by using the notions of coherent information and reverse coherent information of bosonic channels^35,36, as well as the relative entropy of entanglement³⁷. Since in a real-world scenario the parties exchange only a finite number of signal states, here the focus is put on composable finite-size analysis, which has become the touchstone for QKD security, rather than the ultimate bounds. The security of a QKD protocol is desired to be composable, i.e., the protocol must not be distinguished from an ideal protocol which is secure by construction². Mathematically, a composable security proof can be provided by incorporating proper error parameters, ε’s, for each segment of the protocol, namely, EC, privacy amplification, smoothing, and hashing^10,11.

We assume that a total number of N Gaussian signals are measured by Alice and Bob. An amount n of these would be used for key extraction, while the rest m_pe = N − n are left for PE, i.e., the evaluation of the CM. Upon successful completion of the EC procedure, with probability p_ec, the composable finite-size secret key rate is given by³⁸:

$$K\ge \frac{n{p}_{{{{\rm{ec}}}}}}{N}\left({K}_{{{{\rm{pe}}}}}-\frac{{\Delta }_{{{{\rm{aep}}}}}}{\sqrt{n}}+\frac{\Theta }{n}\right),$$

(33)

where the higher-order terms read:

$${\Delta }_{{{{\rm{aep}}}}}:=4\,{\log }_{2}(\sqrt{d}+2)\sqrt{{\log }_{2}(18{p}_{{{{\rm{ec}}}}}^{-2}{\varepsilon }_{{{{\rm{s}}}}}^{-4})},$$

(34)

$$\Theta :={\log }_{2}\left[{p}_{{{{\rm{ec}}}}}\left(1-\frac{{\varepsilon }_{{{{\rm{s}}}}}^{2}}{3}\right)\right]+2{\log }_{2}(\sqrt{2}{\varepsilon }_{{{{\rm{h}}}}}),$$

(35)

The above equation is valid for a protocol with overall security ε = ε_cor + ε_s + ε_h + p_ecε_pe, where ε_pe is the total error probability associated with PE. Assuming reverse reconciliation, the hash comparison stage of the finite-key analysis requires Bob sending $\lceil {\log }_{2}(1-{\varepsilon }_{{{{\rm{cor}}}}})\rceil$ bits to Alice for some proper ε_cor (called ε_cor-correctness) and bounds the probability that Alice’s and Bob’s sequences are different even if their hashes coincide. ε_h(s) is the hashing (smoothing) parameter. Conveniently one can also define the frame error rate FER = 1 − p_ec. It is also assumed that by using an analog-to-digital conversion, each CV symbol is encoded with d bits of precision.

The value of K_pe in Eq. (33) can be computed in different ways depending on the level of reliability. In practice, one would use the sampled data to compute K_pe using Eq. (23) and the worst-case CM shared by the end-users. Remarkably this is practically the most appropriate choice in the case of multi-hop quantum networks with untrusted relays. In the presence of a conditionally Gaussian network, the rate in Eq. (33) modifies by setting m → mp_s where p_s is the probability of successful post-selection. As an example, in the following, we study a quantum repeater chain and compute the composable finite-size key rate considering the worst-case parameters for the end-to-end shared CM.

Numerical results

As we mentioned earlier, a route between two nodes in a quantum network can be seen as a chain of quantum links. We here apply our general techniques for quantum networks to study a quantum chain of identical links and generally-untrusted stations. We note that this is a mere example and that our methodology is generic that can be applied to any chain. Subsequently, by assuming the illustration in Fig. 2, we find the end-to-end CM and compute the composable finite-size key rate.

Let us assume the chain is made of M = 2^m identical links (we call m the repeater depth), each described by a standard CM:

$${{{{\bf{V}}}}}_{0}=\left(\begin{array}{cc}{{\mathsf{a}}}_{0}{{{\bf{I}}}}&{{\mathsf{c}}}_{0}{{{\bf{Z}}}}\\ {{\mathsf{c}}}_{0}{{{\bf{Z}}}}&{{\mathsf{b}}}_{0}{{{\bf{I}}}}\end{array}\right).$$

(36)

For a typical link (without an NLA), with a TMSV source μ, channel loss η and excess noise ϵ (referred to the channel’s input), we have that a₀ = μ, b₀ = ημ + 1 − η + ηϵ, and ${{\mathsf{c}}}_{0}=\sqrt{\eta ({\mu }^{2}-1)}$. By using similar techniques introduced in ref. ³⁹, the end-to-end CM between Alice and Bob, in the case of non-ideal Bell measurements, is found to have the standard form:

$${{{{\bf{V}}}}}_{AB}=\left(\begin{array}{cc}{{\mathsf{a}}}_{m}{{{\bf{I}}}}&{{\mathsf{c}}}_{m}{{{\bf{Z}}}}\\ {{\mathsf{c}}}_{m}{{{\bf{Z}}}}&{{\mathsf{b}}}_{m}{{{\bf{I}}}}\end{array}\right),$$

(37)

with the following parameters:

$$\left\{\begin{array}{l}{{\mathsf{a}}}_{m}={{\mathsf{a}}}_{m-1}-\frac{{\eta }_{{{{\rm{B}}}}}{{\mathsf{c}}}_{m-1}^{2}}{{\eta }_{{{{\rm{B}}}}}({{\mathsf{a}}}_{m-1}+{{\mathsf{b}}}_{m-1})+1-{\eta }_{{{{\rm{B}}}}}},\quad \\ {{\mathsf{b}}}_{m}={{\mathsf{b}}}_{m-1}-\frac{{\eta }_{{{{\rm{B}}}}}{{\mathsf{c}}}_{m-1}^{2}}{{\eta }_{{{{\rm{B}}}}}({{\mathsf{a}}}_{m-1}+{{\mathsf{b}}}_{m-1})+1-{\eta }_{{{{\rm{B}}}}}},\quad \\ {{\mathsf{c}}}_{m}=\frac{{\eta }_{{{{\rm{B}}}}}{{\mathsf{c}}}_{m-1}^{2}}{{\eta }_{{{{\rm{B}}}}}({{\mathsf{a}}}_{m-1}+{{\mathsf{b}}}_{m-1})+1-{\eta }_{{{{\rm{B}}}}}}.\quad \end{array}\right.$$

(38)

As expected, for η_B = 1 the above equations reduce to the previous results in ref. ³⁹. Next, we can apply the formula for finite-size key rate, given in Eq. (33).

In Fig. 4, we plot the secret key rate versus the overall distance between Alice and Bob. Assuming the CV QKD protocol with heterodyne detection, we compute K_pe for the worst-case scenario CM. The links are thermal-loss channels, which we simulate by considering optical fibers with the loss factor of 0.2 dB/km and noise parameter ϵ. Here, we choose an initial modulation at the input of each link, μ, such that the maximum distance is achieved. It was observed that the composable rate is highly sensitive to the relay loss, η_B, as well as channel excess noise, ϵ. This can be seen in Fig. 4 where we compare the rates for m = 1 and m = 2 with that of ideal chain, with η_B = 1 and ϵ = 0.

Fig. 4: Composable key rate per chain use.

We consider a heterodyne-based CV-QKD protocol implemented over a quantum chain with depths m = 1 and m = 2. Here, we assume non-ideal Bell detection modules with η_B = 0.95 and excess noise ϵ = 0.005 SNU for each single link. Other parameters are β = 0.98, N = 10¹⁰, m_pe = 0.1N, d = 2⁵, FER = 0.1, ε_s = ε_h = ε_pe = 10⁻¹⁰, w = 6.34 and ε = 4.5 × 10⁻¹⁰. Rates are compared with an ideal chain (with η_B = 1, ϵ = 0 and β = 1) and the repeaterless capacity, i.e., PLOB bound¹.

It is known that Gaussian-only nodes cannot act as quantum repeaters^40,41. Expectedly, Fig. 4 verifies that the end-to-end rate cannot reach/beat the repeaterless PLOB limit. This is because, in our example, the relays are Gaussian operation and as such they cannot do so. That being said, we emphasize that references^40,41 are more about entanglement distribution than QKD. The quantum repeater chain in our paper has an element of non-Gaussianity in the concept of being post-selectively Gaussian, e.g., via NLAs.

One can also compare a part of our results to the well-studied measurement-device-independent (MDI) QKD protocols⁴². In the case where m = 1 our chain includes two links and one intermediate node, which very much resembles a MDI setup. It is known that the so-called symmetric MDI, wherein the links are identical and the node sits exactly at the middle, is poor in delivering a secret key at long distances, especially for non-zero excess noise and non-ideal relay⁴³. Whereas an asymmetric MDI, wherein the node is closer to one end, can reach longer distances. In our example, we assumed identical links and as such, comparing with symmetric MDI, we do not expect to reach longer distances.

Now let us revamp the quantum chain to design a quantum repeater. Considering the class of CV quantum repeaters^{39,44,45,46,47,48}, several proposals have been suggested to increase the reach of single-link CV QKD protocols, e.g., by utilizing NLAs⁴⁹, which nevertheless can improve the secure distance for only a few tens of kilometers^49,50,51. One idea is that a quantum repeater can essentially be built by a concatenation of such NLA-improved links. Key elements of any repeater chain include entanglement distribution, entanglement distillation or purification, and entanglement swapping. An NLA-based quantum repeater uses TMSV sources as an entanglement distribution source and CV Bell measurements as entanglement swapper device. Other components such as QMs^52,53 can help to improve the performance of quantum repeaters, though they are not essential^54,55,56. But due to the non-deterministic nature of NLAs, using QMs in the structure of amplifier-based repeaters seems indispensable.

To continue, we shall first account for the probabilistic (post-selection) nature of the NLAs. Take that in total N signals are transmitted, i.e., assume N runs. The meaning of “run” is well understood in a single-link protocol. It however may be slightly more complex in a repeater setup with essentially probabilistic links. Here, by each run we mean that TMSV sources at all stations simultaneously transmit a signal. Each signal then has the chance to be successfully amplified by an NLA placed at the other end of the link. In the following, we account for the post-selection effect of the NLAs by referring to ref. ⁵⁷, which has studied a similar post-selection problem in the scope of free-space quantum communications.

Of the overall N runs of the protocol p_sN, where p_s is success probability of the repeater system, will be post-selected by NLAs. In other words, they post-select a portion p_sN of the signals. Hence, assuming that EC is successful with probability p_ec, an average number of np_sp_ec signals contribute to the final key and, therefore, Eq. (33) takes the form:

$$K\ge \frac{n{p}_{{{{\rm{s}}}}}{p}_{{{{\rm{ec}}}}}}{N}\left({K}_{{{{\rm{pe}}}}}-\frac{{\Delta }_{{{{\rm{aep}}}}}}{\sqrt{n{p}_{{{{\rm{s}}}}}}}+\frac{\Theta }{n{p}_{{{{\rm{s}}}}}}\right).$$

(39)

Before we present numerical results, let us briefly weigh up the action of NLAs. Firstly, to see if such devices can be practically useful, we allow some weakening of the Gaussian assumption. This is because the NLA-assisted relays can actually impose non-Gaussianity, which as pointed out earlier, is necessary to (possibly) outdistance the PLOB. As a well-known realization, we can take the action of quantum scissors (QSs), as non-deterministic NLAs, as a guide. QSs were introduced in ref. ²⁰, and were studied further in refs. ^24,25. While the ideal NLA operation is unphysical, in the sense that it works only with zero probability of success, QSs can act as almost-ideal NLAs under weak signal assumptions. More precisely, it has been shown that a QS can almost-noiselessly amplify an input coherent state $\left|\alpha \right\rangle$ to $\left|g\alpha \right\rangle$ with the success probability of a QS p_s = 1/g², assuming that g²∣α∣² ≪ 1^21,22,24. In the prepare-and-measure (P&M) protocol, where each link has an initial Gaussian modulation variance V_A, a similar assumption holds: ηg²V_A ≪ 1, where we have also take into account the channel loss (We note that the P&M and entanglement-based protocols are related via μ = V_A + 1).

In Fig. 5, by using the recursive equations, we plot the asymptotic secret key rate versus the overall distance between Alice and Bob. Here we have assumed that an ideal chain with η_B = 1 and ϵ = 0. We encounter a dual optimization problem, which we solve numerically by optimizing over input modulation μ and amplification gain g, while making sure that ηg²V_A < 10⁻².

Fig. 5: Asymptotic key rate per use of quantum repeater chain.

We consider a heterodyne-based CV-QKD protocol implemented over a quantum repeater chain with depths m = 1 and m = 2. Here, we assume reconciliation efficiency β = 0.98, ideal Bell detection modules with η_B = 1.0, and zero excess noise ϵ = 0 for each single link. Rates are compared with the repeaterless capacity, i.e., PLOB bound¹, and the single-repeater capacity⁴.

We interpret the results as follows. The curves show that a quantum repeater chain with m = 1 (m = 2) can outperform the ultimate benchmarks at about 300 km (500 km), before which the optimized amplification gain is g = 1, meaning that no amplification in needed. Although these results look interesting, when we deviate from the ideal case, i.e., relay loss η < 1 and excess noise ϵ > 0 (specifically we could not find a positive rate for, e.g., η_B = 0.999 and ϵ = 0.001 SNU). As discussed for a chain without NLAs, this is partly due to the absolutely symmetric (MDI-like) design that we assumed through our example. With a different, possibly asymmetric, design of the repeater links, it may be possible that one can obtain positive rates (nevertheless, the methodology remains the same as presented in this manuscript). From this prospective, our results are the starting point for future studies on NLA-based quantum repeaters.

In summary, we have analyzed the composable end-to-end security of Gaussian quantum networks in the presence of generally-untrusted nodes. Assuming two arbitrary end-users of the network, we established a methodology that enables them to complete the crucial task of PE based only on the data remotely possessed. We have further investigated how they can use the estimated parameters and compute the composable key rate in the finite-size regime. Our study does not need to estimate channel parameters of the individual links that make the route between the two users. In fact, other than being Gaussian, it does not make any assumptions about the communication links, stations, and/or any other components involved.

Furthermore, we backed up our theory by considering the specific case of a chain of identical quantum links, both with and without NLAs. In our NLA-assisted design, we assumed ideal NLAs for two reasons. Firstly, under weak signal assumptions, they can be assumed Gaussian operations^20,24,25 (a good example of these NLAs are QSs²⁰). Secondly, since they are ideal, in the sense that they do not add extra noise to the system, they help to obtain the ultimate performance that can be achieved by means of such designs. While we could show that an NLA-assisted chain can beat the repeaterless limit, we question its practicality. Compared with MDI protocols, we conclude that, apart from noise and loss, this is mostly due to symmetric design of the chain. In addition, for achieving a real-world analysis one can replace the ideal NLAs with realistic ones. This can nevertheless obsolete the Gaussianity of the network so this next step will have to be investigated cautiously.

Methods

The worst-case scenario covariance matrix

In the following, we discuss the confidence intervals for $\widehat{{{{\boldsymbol{\Sigma }}}}}$. Despite the fact that this procedure is based on the shared data, it can have a direct application on a theoretical CM as in Eq. (37) defined through a specific model of the links between the parties. Our analysis relies on tail bounds for the chi-squared distribution. Assume that random data variables [q]₁, …, [q]_N from the variable q which follows a normal distribution with unit variance and zero mean value. Then, the random variable:

$$Q=\mathop{\sum }\limits_{i=1}^{{m}_{{{{\rm{pe}}}}}}{\left[q\right]}_{i}^{2} \sim {\chi }^{2}({m}_{{{{\rm{pe}}}}},0)$$

(40)

follows a chi-squared distribution and allows for the following tail bounds [ref. ⁵⁸, Lemma 6]:

$$P[Q\ge {m}_{{{{\rm{pe}}}}}+2\sqrt{{m}_{{{{\rm{pe}}}}}\kappa }+2\kappa ]\le \exp (-\kappa ),$$

(41)

$$P[Q\le {m}_{{{{\rm{pe}}}}}-2\sqrt{{m}_{{{{\rm{pe}}}}}\kappa }]\le \exp (-\kappa ),$$

(42)

where κ is related to the error of PE, ε_pe, as we shall see shortly.

From the samples ${[{q}_{x}]}_{i}$ and ${[{q}_{y}]}_{i}$, one can define standard normal variables ${[{{\mathsf{q}}}_{x}]}_{i}={[{q}_{x}]}_{i}/\sqrt{{\sigma }_{x}^{2}}$ and ${[{{\mathsf{p}}}_{{\mathsf{y}}}]}_{i}={[{p}_{y}]}_{i}/\sqrt{{\sigma }_{y}^{2}}$ so the estimators of $\langle {q}_{x}^{2}\rangle$ and $\langle {q}_{y}^{2}\rangle$ can be expressed as:

$$\widehat{\langle {q}_{x}^{2}\rangle }:={m}_{{{{\rm{pe}}}}}^{-1}\mathop{\sum }\limits_{i=1}^{{m}_{{{{\rm{pe}}}}}}{\left[{q}_{x}\right]}_{i}^{2}={\sigma }_{x}^{2}{m}_{{{{\rm{pe}}}}}^{-1}\mathop{\sum }\limits_{i=1}^{{m}_{{{{\rm{pe}}}}}}{\left[{{\mathsf{q}}}_{x}\right]}_{i}^{2},$$

(43)

$$\widehat{\langle {q}_{y}^{2}\rangle }:={m}_{{{{\rm{pe}}}}}^{-1}\mathop{\sum }\limits_{i=1}^{{m}_{{{{\rm{pe}}}}}}{\left[{q}_{y}\right]}_{i}^{2}={\sigma }_{x}^{2}{m}_{{{{\rm{pe}}}}}^{-1}\mathop{\sum }\limits_{i=1}^{{m}_{{{{\rm{pe}}}}}}{\left[{{\mathsf{q}}}_{y}\right]}_{i}^{2},$$

(44)

where $\mathop{\sum }\nolimits_{i = 1}^{{m}_{{{{\rm{pe}}}}}}{[{{\mathsf{q}}}_{x}]}_{i}^{2}$ and $\mathop{\sum }\nolimits_{i = 1}^{{m}_{{{{\rm{pe}}}}}}{[{{\mathsf{q}}}_{y}]}_{i}^{2}$ are chi-square variables following the tail bounds:

$$\min \left[\sum \limits_{i=1}^{{m}_{{\rm{pe}}}}\left[{{\mathsf{q}}}_{x}\right]^{2}_{i},\,\sum\limits_{i=1}^{{m}_{{{{\rm{pe}}}}}}\left[{{\mathsf{q}}}_{y}\right]^{2}_{i}\right] \,>\, {m}_{{{{\rm{pe}}}}}+2\sqrt{{m}_{{{{\rm{pe}}}}}\kappa }+2\kappa .$$

(45)

This guarantees that maximum noise is considered based on the data, and implies that:

$$\widehat{\langle {q}_{x}^{2}\rangle }\ge {\langle {q}_{x}^{2}\rangle }_{{{{\rm{wc}}}}},\,\widehat{\langle {q}_{y}^{2}\rangle }\ge {\langle {q}_{y}^{2}\rangle }_{{{{\rm{wc}}}}},$$

(46)

with probability:

$$\Pr \left[\widehat{\langle {q}_{x}^{2}\rangle }\ge {\langle {q}_{x}^{2}\rangle }_{{{{\rm{wc}}}}}\right]\le \exp (-\kappa ),$$

(47)

$$\Pr \left[\widehat{\langle {q}_{y}^{2}\rangle }\ge {\langle {q}_{y}^{2}\rangle }_{{{{\rm{wc}}}}}\right]\le \exp (-\kappa ),$$

(48)

for the worst-case scenario values:

$$\begin{array}{l}{\langle {q}_{x}^{2}\rangle }_{{{{\rm{wc}}}}}={\sigma }_{x}^{2}{{m}_{{{{\rm{pe}}}}}}^{-1}({m}_{{{{\rm{pe}}}}}+2\sqrt{{m}_{{{{\rm{pe}}}}}\kappa })+{{{\mathcal{O}}}}(1/{m}_{{{{\rm{pe}}}}})\\ \qquad\quad={\sigma }_{x}^{2}(1+2\sqrt{\kappa /{m}_{{{{\rm{pe}}}}}}),\end{array}$$

(49)

$$\begin{array}{rcl}{\langle {q}_{y}^{2}\rangle }_{{{{\rm{wc}}}}}&=&{\sigma }_{y}^{2}{{m}_{{{{\rm{pe}}}}}}^{-1}({m}_{{{{\rm{pe}}}}}+2\sqrt{{m}_{{{{\rm{pe}}}}}\kappa })+{{{\mathcal{O}}}}(1/{m}_{{{{\rm{pe}}}}})\\ &=&{\sigma }_{y}^{2}(1+2\sqrt{\kappa /{m}_{{{{\rm{pe}}}}}}).\end{array}$$

(50)

To find the worst-case scenario values for the covariance term 〈xy〉 we make the following calculations: Combining the samples [x]_i and [y]_i accordingly, we have that:

$${({[{q}_{y}]}_{i}-{[{q}_{x}]}_{i})}^{2}={[{q}_{y}]}_{i}^{2}+{[{q}_{x}]}_{i}^{2}-2{[{q}_{y}]}_{i}{[{q}_{x}]}_{i},$$

(51)

$${({[{q}_{y}]}_{i}+{[{q}_{x}]}_{i})}^{2}={[{q}_{y}]}_{i}^{2}+{[{q}_{x}]}_{i}^{2}+2{[{q}_{y}]}_{i}{[{q}_{x}]}_{i},$$

(52)

which leads to the relation:

$${[{q}_{y}]}_{i}{[{q}_{x}]}_{i}=\frac{1}{4}[{({[{q}_{y}]}_{i}+{[{q}_{x}]}_{i})}^{2}-{({[{q}_{y}]}_{i}-{[{q}_{x}]}_{i})}^{2}].$$

(53)

The variables ${[{q}_{y}]}_{i}\pm {[{q}_{x}]}_{i}$ are zero-mean Gaussian variables with variances V_± since ${[{q}_{x}]}_{i}$ and ${[{q}_{y}]}_{i}$ are assumed to be Gaussian. More specifically, the variables ${[{q}_{{z}_{\pm }}]}_{i}=({[{q}_{y}]}_{i}\pm {[{q}_{x}]}_{i})/\sqrt{{V}_{\pm }}$ are standard normal variables. Thus by summing over all the samples and dividing by m_pe, we may express the estimator of 〈q_xq_y〉 as:

$$\begin{array}{l}\widehat{\langle {q}_{x}{q}_{y}\rangle }:={{m}_{{{{\rm{pe}}}}}}^{-1}\mathop{\sum }\limits_{i=1}^{{m}_{{{{\rm{pe}}}}}}{\left[{q}_{y}\right]}_{i}{\left[{q}_{x}\right]}_{i}\\ \qquad\quad\,\,=\frac{1}{4}\left({V}_{+}{{m}_{{{{\rm{pe}}}}}}^{-1}\mathop{\sum }\limits_{i=1}^{{m}_{{{{\rm{pe}}}}}}{\left[{q}_{{z}_{+}}\right]}^{2}-{V}_{-}{{m}_{{{{\rm{pe}}}}}}^{-1}\mathop{\sum }\limits_{i=1}^{{m}_{{{{\rm{pe}}}}}}{\left[{q}_{{z}_{-}}\right]}^{2}\right),\end{array}$$

(54)

where $\mathop{\sum }\nolimits_{i = 1}^{{m}_{{{{\rm{pe}}}}}}{[{q}_{{z}_{\pm }}]}^{2}$ are chi-square distributions following the tail bounds of Eqs. (41) and (42).

We then impose that the estimator is smaller than its worst-case scenario value ${\langle {q}_{x}{q}_{y}\rangle }_{{{{\rm{wc}}}}}$, i.e.:

$$\widehat{\langle {q}_{x}{q}_{y}\rangle } < {\langle {q}_{x}{q}_{y}\rangle }_{{{{\rm{wc}}}}},$$

(55)

where ${\langle {q}_{x}{q}_{y}\rangle }_{{{{\rm{wc}}}}}$ is computed by replacing $\mathop{\sum }\nolimits_{i = 1}^{{m}_{{{{\rm{pe}}}}}}{[{q}_{{z}_{\pm }}]}^{2}$ with the tail bounds in Eqs. (41) and (42), i.e., using:

$$\mathop{\sum }\limits_{i=1}^{{m}_{{{{\rm{pe}}}}}}{\left[{q}_{{z}_{+}}\right]}^{2} \,<\, {m}_{{{{\rm{pe}}}}}-2\sqrt{{m}_{{{{\rm{pe}}}}}\kappa },$$

(56)

and:

$$\mathop{\sum }\limits_{i=1}^{{m}_{{{{\rm{pe}}}}}}{\left[{q}_{{z}_{-}}\right]}^{2} \,>\, {m}_{{{{\rm{pe}}}}}+2\sqrt{{m}_{{{{\rm{pe}}}}}\kappa }+2\kappa .$$

(57)

Therefore, up to ${{{\mathcal{O}}}}(1/{m}_{{{{\rm{pe}}}}})$, we have:

$$\begin{array}{l}{\left\langle {q}_{x}{q}_{y}\right\rangle }_{{{{\rm{wc}}}}}=\frac{1}{4}\left({V}_{+}\frac{1}{{m}_{{{{\rm{pe}}}}}}({m}_{{{{\rm{pe}}}}}-2\sqrt{{m}_{{{{\rm{pe}}}}}\kappa })\right.\\ \left.\qquad\qquad-{V}_{-}\frac{1}{{m}_{{{{\rm{pe}}}}}}({m}_{{{{\rm{pe}}}}}+2\sqrt{{m}_{{{{\rm{pe}}}}}\kappa }+2\kappa )\right)\\ \qquad\qquad=\frac{1}{4}\left(({V}_{+}-{V}_{-})-2\sqrt{\kappa /{m}_{{{{\rm{pe}}}}}}({V}_{+}+{V}_{-})\right)\\ \qquad\qquad=\langle {q}_{x}{q}_{y}\rangle -\sqrt{k/{m}_{{{{\rm{pe}}}}}}(\langle {q}_{x}^{2}\rangle +\langle {q}_{y}^{2}\rangle ).\end{array}$$

(58)

Note that a necessary condition for $\widehat{\langle {q}_{x}{p}_{y}\rangle } < {\langle {q}_{x}{q}_{y}\rangle }_{{{{\rm{wc}}}}}$ to be valid is that either Eq. (56) or Eq. (57) is valid. Therefore:

$$\begin{array}{l}\Pr \left[\widehat{\langle {q}_{x}{p}_{y}\rangle } < {\langle {q}_{x}{q}_{y}\rangle }_{{{{\rm{wc}}}}}\right]\\ \le \Pr \left[\left(\mathop{\sum }\limits_{i=1}^{{m}_{{{{\rm{pe}}}}}}{\left[{q}_{{z}_{+}}\right]}^{2} < {m}_{{{{\rm{pe}}}}}-2\sqrt{{m}_{{{{\rm{pe}}}}}\kappa }\right)\right.\\ \left.\vee \left(\mathop{\sum }\limits_{i=1}^{{m}_{{{{\rm{pe}}}}}}{\left[{q}_{{z}_{-}}\right]}^{2} > {m}_{{{{\rm{pe}}}}}+2\sqrt{{m}_{{{{\rm{pe}}}}}\kappa }+2\kappa \right)\right]\\ \le \Pr \left[\left(\mathop{\sum }\limits_{i=1}^{{{m}_{{{{\rm{pe}}}}}}_{{{{\rm{pe}}}}}}{\left[{q}_{{z}_{+}}\right]}^{2} < {m}_{{{{\rm{pe}}}}}-2\sqrt{{m}_{{{{\rm{pe}}}}}\kappa }\right)\right]\\ +\Pr \left[\left(\mathop{\sum }\limits_{i=1}^{{m}_{{{{\rm{pe}}}}}}{\left[{q}_{{z}_{-}}\right]}^{2} > {m}_{{{{\rm{pe}}}}}+2\sqrt{{m}_{{{{\rm{pe}}}}}\kappa }+2\kappa \right)\right]\\ \le 2\exp (-\kappa ).\end{array}$$

(59)

Similarly, the parties calculate equivalent relations for the data from the p-quadrature. They obtain corresponding equations for ${\langle {p}_{x}^{2}\rangle }_{{{{\rm{wc}}}}}$, ${\langle {p}_{y}^{2}\rangle }_{{{{\rm{wc}}}}}$, and ${\langle {p}_{x}{p}_{y}\rangle }_{{{{\rm{wc}}}}}$ following Eqs. (49), (50), and (58). In particular, since ${\langle {p}_{x}{p}_{y}\rangle }_{{{{\rm{wc}}}}}$ is a negative quantity, the corresponding probability of Eq. (59) will have as an argument an inequality with a different direction and the minus sign in the corresponding Eq. (58) will be replaced by a plus sign.

All the worst-case parameters 〈…〉_wc define the worst-case scenario CM Σ_wc which has the form of Eq. (18) of the main text but with the replacements 〈…〉 → 〈…〉_wc. From the previous derivations, we see that:

$${{{{\boldsymbol{\Sigma }}}}}_{{{{\rm{wc}}}}}=\widehat{{{{\boldsymbol{\Sigma }}}}}+\sqrt{\frac{4\kappa }{{m}_{{{{\rm{pe}}}}}}}\left(\begin{array}{cc}{\widehat{{{{\bf{V}}}}}}_{x}&-\frac{{\widehat{{{{\bf{V}}}}}}_{x}+{\widehat{{{{\bf{V}}}}}}_{y}}{2}{{{\bf{Z}}}}\\ -\frac{{\widehat{{{{\bf{V}}}}}}_{x}+{\widehat{{{{\bf{V}}}}}}_{y}}{2}{{{\bf{Z}}}}&{\widehat{{{{\bf{V}}}}}}_{y}\end{array}\right),$$

(60)

where $\widehat{{{{\boldsymbol{\Sigma }}}}}$ is exactly the one defined in Eq. (18) of the main text, together with the associated ${\widehat{{{{\bf{V}}}}}}_{x}$ and ${\widehat{{{{\bf{V}}}}}}_{y}$. As we see, the diagonal (noise) terms are increased whereas the off-diagonal (correlation) terms are decreased in modulus. This vanishes in the asymptotic case where m_pe → ∞.

Now, let us assume that at least one of the inequalities in Eqs. (46) or (55) is true which happens with total probability $\le 4\exp (-\kappa )$. Considering the p quadrature, the total probability of failure is $\le 8\exp (-\kappa )$. The latter is therefore a bound on the probability that the CM is worse than the worst-case expression Σ_wc (in which case the rate would be less than the worst-case value). The parties can only allow this to happen with a very small probability that is less than ε_pe. Therefore, by bounding the previous relation we have that:

$$8\exp (-\kappa )\le {\varepsilon }_{{{{\rm{pe}}}}},$$

(61)

which defines $\kappa ={{{\rm{\ln }}}}(8/{\varepsilon }_{{{{\rm{pe}}}}})$.

Finally, for calculating the secret key rate of Eq. (39) from the theoretical CM V in Eq. (37) we apply the inverse transformation of Eq. (27). In this way, we obtain a theoretical version of the classical CM:

$${{{{\boldsymbol{\Sigma }}}}}^{{{{\rm{thr}}}}}=\left[{{{\bf{V}}}}+({{{\bf{I}}}}\oplus {{{\bf{I}}}})\right]:=\left(\begin{array}{cc}{{{{\bf{V}}}}}_{x}^{{{{\rm{thr}}}}}&{{{{\bf{C}}}}}_{xy}^{{{{\rm{thr}}}}}\\ {{{{\bf{C}}}}}_{xy}^{{{{\rm{thr}}}}}&{{{{\bf{V}}}}}_{y}^{{{{\rm{thr}}}}}\end{array}\right).$$

(62)

By using this CM, we can calculate the worst-case scenario theoretical CM:

$${{{{\boldsymbol{\Sigma }}}}}_{{{{\rm{wc}}}}}^{{{{\rm{thr}}}}}={{{{\boldsymbol{\Sigma }}}}}^{{{{\rm{thr}}}}}+\sqrt{\frac{4\kappa }{{m}_{{{{\rm{pe}}}}}}}\left(\begin{array}{cc}{{{{\bf{V}}}}}_{x}^{{{{\rm{thr}}}}}&-\frac{{{{{\bf{V}}}}}_{x}^{{{{\rm{thr}}}}}+{{{{\bf{V}}}}}_{y}^{{{{\rm{thr}}}}}}{2}{{{\bf{Z}}}}\\ -\frac{{{{{\bf{V}}}}}_{x}^{{{{\rm{thr}}}}}+{{{{\bf{V}}}}}_{y}^{{{{\rm{thr}}}}}}{2}{{{\bf{Z}}}}&{{{{\bf{V}}}}}_{y}^{{{{\rm{thr}}}}}\end{array}\right).$$

(63)

Then, we calculate the worst-case scenario theoretical quantum CM using:

$${{{{\bf{V}}}}}_{{{{\rm{wc}}}}}^{{{{\rm{thr}}}}}={{{{\boldsymbol{\Sigma }}}}}_{{{{\rm{wc}}}}}^{{{{\rm{thr}}}}}-({{{\bf{I}}}}\oplus {{{\bf{I}}}}).$$

(64)

The latter is finally used to compute K_pe of the composable secret key rate in Eq. (39) by following the steps (28)–(31).