Introduction

The electronic behavior of metals is usually described using the standard Fermi liquid theory in terms of a single-particle spectral function of well-defined electron-like quasiparticles and a two-particle excitation spectrum dominated by long-lived collective charge excitations called plasmons.1,2 It is, however, generally agreed that Fermi liquid theory breaks down in the high-temperature superconducting cuprates and the search for a fully satisfactory replacement theory remains one of the most studied problems in condensed matter physics.3 Empirically, techniques such as angle-resolved photoemission spectroscopy (ARPES), scanning tunneling spectroscopy, and quantum oscillations have given us a detailed picture of the cuprates’ electronic band structure.4 Developing a comprehensive picture of the collective charge excitation in the cuprates has proved much more challenging. A key issue is limited \(\overrightarrow{q}\)-space access. Optical techniques are intrinsically limited to \(q\approx 0\).5,6 Although electron energy loss spectroscopy (EELS) has no such restriction in principle, accessing \(c\)-axis dispersion remains difficult.7,8,9,10 RIXS has recently observed dispersive charge excitations in electron-doped cuprates, opening new routes to characterize the charge dynamics of the high temperature superconductors.11,12,13,14,15 Importantly, RIXS also provides bulk sensitivity. A recent breakthrough in this area is the identification of these modes as acoustic plasmons,15 but the seeming agreement to a simple layered electron gas description is puzzling in view of the strongly correlated nature of the cuprates.

Here, we report RIXS measurements on electron doped LCCO at the Cu \({L}_{3}\)-edge, focusing on charge excitations around the two dimensional Brillouin zone (BZ) center. By using doping-concentration-gradient (combi) films,16 we are able to provide finer doping dependence than recent results published while this paper was under preparation.15 By measuring the incident energy dependence of the modes, we demonstrate that the charge excitations have mostly collective nature. As the electron doping increases from \(x=0.11\) to \(x=0.18\), the plasmon energy gently increases and the peak width gradually sharpens. The deviation of the doping dependent plasmon energy from the simple layered electron gas model prediction, as well as the increase of the plasmon life time indicated by the sharpening of excitation width upon increased doping, suggest that electron correlations have a crucial effect. We use dynamical mean field theory (DMFT) calculations to evaluate the evolution of the charge fluctuations with electron correlations. We find that a reduced effective mass and increased electronic quasiparticle coherence near the FS are the dominant effects and that electron correlations control the region of reciprocal space in which the layered electron gas model is applicable. All these effects are signs of a crossover from Mott physics to an itinerant picture, as doping drives the system from a high-temperature-superconducting to a metallic state.

Results

Charge excitation and its plasmon nature

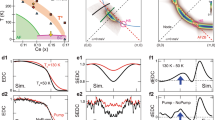
Figure 1a shows the experiment geometry and Fig. 1b plots Cu \({L}_{3}\)-edge RIXS measurements of LCCO \(x=0.17\). Distinct from measurements of hole-doped cuprates, where the low-energy excitations are dominated by spin excitations,17,18,19,20,21 two low-energy dispersive modes are seen.12,13,14,15 The excitation at lower energy with stronger intensity can be assigned as spin fluctuations, following previous studies of hole-doped cuprates.17,18,19,20,21 The other excitation with higher energy and weaker intensity was absent in RIXS measurements of hole-doped systems, and appears to be unique to electron-doped cuprates.12,13,14,15 This feature disperses much more steeply, and merges into the high-energy \(dd\) excitations above \(\sim\) 1.3 eV with in-plane wavevector \({q}_{\parallel }\ge 0.2\) reciprocal space unit (r.l.u.).

Fig. 1: Plasmon and paramagnon measurements of LCCO for \({\mathbf{x}}={\mathbf{0.17}}\).
figure 1

a Sketch of experimental geometry. b 2D color map of RIXS spectra with \(2\theta =14{6}^{\circ }\) and \(\sigma\) polarization. The elastic peak is subtracted for clarity. Red diamonds and black circles present the energies of the plasmon and paramagnon from fitting, respectively. The light pink line shows the fitting of the plasmon dispersion for a layered system (Eq. (2)) and the light black line arises from fitting a 2D antiferromagnetic Heisenberg model to the paramagnon. The inset shows the two-dimensional BZ and the red line presents the measured range of in-plane wavevectors along the \((H,0)\) direction.

Full size image

To characterize this excitation, we first examined its polarization dependence. In the RIXS process, the X-ray photon can exchange angular momentum \({m}_{J}\) with the sample, thus excitations of different characters can be enhanced or suppressed in different polarization channels.22,23 Figure 2a, b compares the excitation intensity with \(\sigma\)- and \(\pi\)-polarized incident beams at different \({q}_{\parallel }\) points. The strongly dispersive feature in Fig. 1b consistently shows stronger spectral intensity with a \(\sigma\)-polarized incident beam. Such polarization dependence indicates that the excitation is related to \(\Delta {m}_{J}=0\) or 2 processes, namely charge excitations or bimagnon excitations (see Supplementary Fig. 2 and Supplementary discussion). Bimagnon excitations, however, were suggested to disperse weakly near BZ center and appear as tails of the \(\Delta {m}_{J}=1\) paramagnon excitations.24,25 Therefore, the higher energy features are most likely to be charge excitations, consistent with previous interpretations.12,13,14,15

Fig. 2: Characterization of the plasmon nature of the charge excitation of LCCO.
figure 2

a, b Incident polarization dependent RIXS spectra at \({q}_{\parallel }\) = (0.06, 0) and (0.03, 0.03) for \(x=0.18\). c, d Out-of-plane momentum transfer dependence of RIXS spectra at \({q}_{\parallel }\) = (0.06, 0) and (0.11, 0) for \(x=0.17\) with \(\sigma\) polarization. The paramagnon is independent of \(L\) whereas the plasmon varies significantly with \(L\).

Full size image

Further characterization of this excitation was provided by examining its out-of-plane wavevector \({q}_{\perp }\) dependence, which probes the inter-CuO\({}_{2}\) plane coupling. In Fig. 2c, d, we compare spectra taken at different \({q}_{\perp }\) with \({q}_{\parallel }\) fixed at different points. In Fig. 2d, \({q}_{\parallel }=(0.11,0)\), where both the spin excitation and the higher energy excitation can be clearly observed, the spin excitation energy stays constant for different \({q}_{\perp }\), consistent with the quasi-two-dimensional (2D) nature of this layered compound. On the other hand, the higher energy excitation behaves differently with strong \({q}_{\perp }\) dependence.26 In Fig. 2c, with a \({q}_{\perp }\) variation from 1.68 to 1.78, its energy at \({q}_{\parallel }=(0.06,0)\) shifts by \(\sim\)90 meV. Conversely, spin-related excitations are expected to show 2D character. Thus the strong \({q}_{\perp }\) dependence supports the peak’s charge fluctuation origin. Considering the strong dispersion of the charge excitations which extends \(\sim\)1 eV in the observable \({q}_{\parallel }\) range, the natural choice of the leading interaction to host such excitations would be the long-range Coulomb interaction.15 With a reasonable-sized long-range Coulomb interaction coupling the electrons in different layers, plasmon excitations will become highly dispersive along the out-of-plane direction.27,28,29,30,31,32,33

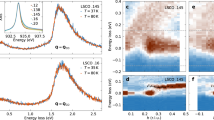
To check the RIXS resonance behavior of the observed charge excitation, spectra at various incident X-ray energies across the Cu-\({L}_{3}\) edge were collected, as shown in Fig. 3a. Collective excitations are expected to exist at constant energy loss regardless of incident energy, whereas incoherent X-ray processes tend to occur at constant final energy.34 As shown in Fig. 3b, both features from spin and charge excitations start to gain spectral weight at the rising edge of the Cu-\({L}_{3}\) white line, indicating they are stimulated by the same intermediate states, namely the ultra-fast transient double occupancy in the \(2{p}^{6}3{d}^{9}\underset{}{\overset{}{\to }}2{p}^{5}3{d}^{10}\underset{}{\overset{}{\to }}2{p}^{6}3{d}^{9* }\) RIXS process.21 The spin excitation spectral weight peaks at the maximum of the absorption curve, consistent with observations in hole-doped cuprates.35 Although both features share similar behaviors at the absorption rising edge, specifically increasing in spectral weight and constant energy loss, they behave quite differently at the falling edge on the higher X-ray energy side. The spin excitation quickly diminishes, but the charge excitation seems to survive longer into the tail. More importantly, the charge excitation spectral weight reaches its maximum at \(\sim\)0.3 eV above the energy of the white line peak and then gradually reduces, accompanied by a noticeable shift in its energy. We emphasize that, although the shift is obvious, the size of the shift is much smaller than the increase of the incident X-ray energy, so the data rule out constant final energy processes as shown in Fig. 3c. We assign the charge excitation as primarily a collective plasmon, but a small contribution of incoherent electron–hole processes appear to be present above the white line.35,36,37,38 It is worth noting that the observed \({q}_{\perp }\) dependence is only expected within a plasmon model; electron–hole excitations would be expected to be independent of \({q}_{\perp }\).39,40,41

Fig. 3: Incident energy dependence of the plasmon implies a primarily collective nature of the excitation.
figure 3

a XAS data in total fluorescence yield mode for \(x=0.17\). b RIXS spectra for \(x=0.17\) at \(Q=(0.08,0,1.75)\) with different incident energies marked in (a), from \({L}_{3}-0.6\) to \({L}_{3}+0.9\)eV with step of 0.3 eV. Dashed lines indicate the paramagnon and plasmon energies. \(\sigma\) polarization is used for XAS and RIXS measurements. c Plasmon and paramagnon energies extracted from fitting. The dashed line indicates the expected incident energy dependence of constant final energy processes, such as fluorescence emission. Error bars describe the standard deviation from the least-squares fitting.

Full size image

Plasmon doping dependence

With the charge excitation identified as a plasmon, we investigate its doping dependence. By using the LCCO combi films, we were able to obtain a fine doping dependence by simply translating the sample along its doping gradient direction while keeping the experimental conditions identical. Four \({q}_{\parallel }\) points at (0.06, 0), (0.11, 0), (0.04, 0.04), and (0.08, 0.08) were studied, which all show similar doping dependent behaviors. In Fig. 4, data at \({q}_{\parallel }=(0.06,0)\) and (0.04, 0.04) are shown as typical examples (see Supplementary Fig. 4 for \({q}_{\parallel }=(0.11,0)\) and (0.08, 0.08)).

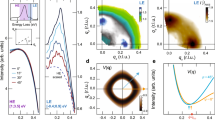
Fig. 4: Doping dependence of the plasmon.
figure 4

a RIXS spectra of LCCO at \({\boldsymbol{Q}}=(0.06,0,1.66)\) for \(x=0.11\) to 0.18. The vertical dashed line presents the plasmon energy for \(x=0.18\) and spectra are offset vertically for clarity. b, c RIXS spectra at \({\boldsymbol{Q}}=(0.06,0,1.68)\) and (0.04, 0.04, 1.68). In each panel, spectra for \(x=0.11\) and \(x=0.18\) are compared. The shaded peaks show the Gaussian profile representing the plasmon. Error bars describe the statistic error. d RIXS spectra measured at \({\boldsymbol{Q}}=(0.06,0,1.68)\) and (0.04, 0.04, 1.68) show same dispersion with different in-plane directions \((H,0)\) and \((H,H)\) for \(x=0.18\). e Plasmon energy for each doping. f Plasmon full-width at half maximum (FWHM). Error bars in (e) and (f) describe the standard deviation from the least-squares fitting. g \(L\) variation as a function of doping with fixed geometry.

Full size image
Fig. 5: Scaling of the plasmon energy vs. \({\mathbf{x}}\) and \(\sqrt{\mathbf{x}}\) for doping \({\mathbf{x}}={\mathbf{0.11}}\) to 0.18 at \({\mathbf{q}}_{\parallel}\) = (0.06, 0) and (0.11, 0).
figure 5

The dashed blue line present a fit to \({\omega }_{p}=a\sqrt{x}+b\) with \(a=1.19(7)\) and \(b=0.11(3)\). Note that the non-zero \(b\) value is inconsistent with simple fermi liquid model. Error bars describe the standard deviation from the least-squares fitting.

Full size image

Figure 4a shows a stacking plot of the RIXS spectra at \({q}_{\parallel }=(0.06,0)\). Two direct observations can be made before any quantitative analysis. From \(x=0.11\) to 0.18, the plasmon excitation evolves from a broad feature into a well-defined peak, and its energy gradually increases, consistent with studies of single phase samples.15 Since the spectra were measured with identical experimental geometry, there is actually a small variation in the momentum transfer due to possible variation in lattice constants at different doping levels. As shown in Fig. 2, the plasmon excitation energy strongly depends on \({q}_{\perp }\) values. With this concern, the variation in the momentum transfer was carefully considered. Figure 4g shows the converted \({q}_{\perp }\) values from the measured \(c\)-lattice constant variation of our combi film as a function of doping.16 From \(x=0.11\) to 0.18, the change in \(c\)-lattice constant is about 0.4\(\%\), leading to a variation in \({q}_{\perp }\) of 0.008. Importantly, Fig. 2 shows that, in the vicinity of these \({q}_{\perp }\) values, the plasmon excitation energy increases towards larger \({q}_{\perp }\). At higher doping level, towards which the measured plasmon energy increases, the \({q}_{\perp }\) actually reduces. Thus it is safe to conclude that the energy increase upon further doping is an intrinsic property of the plasmon excitation.

In Fig. 4b, c, RIXS spectra for two end doping levels, \(x=0.11\) and 0.18, are compared for clarity. The shaded peaks are the plasmon excitation components from our fitting (see Supplementary Fig. 3). The extracted energy and intrinsic, deconvolved peak width are shown in Fig. 4e, f. At both \({q}_{\parallel }\) points, the plasmon energy increases by \(\sim 20 \%\) and the width sharpens by \(\sim 20 \%\). A variation in \({q}_{\perp }\) of 0.1 at \({q}_{\parallel }=(0.06,0)\), as shown in Fig. 2c, leads to about 100 meV change in plasmon energy. A simple linear estimation suggests that the \(c\)-lattice constant reduction of 0.008 could lead to \(\sim\)8 meV softening in the measured doping range, which is far smaller than the energy variation in Fig. 4e and can be neglected compared to the much larger doping induced plasmon energy increase.

We emphasize that the two \({q}_{\parallel }\) points we compare were specifically chosen such that their amplitudes of in-plane and out-of-plane momentum transfers are the same, although (0.06, 0) is along the in-plane \((H,0)\) direction and (0.04, 0.04) is along the \((H,H)\) direction. The similarity of their RIXS response is further shown in Fig. 4d. At the same doping level, the charge excitation features for both \({q}_{\parallel }\) points almost overlap. Such \((H,0)-(H,H)\) symmetry is confirmed at another \(\overrightarrow{q}\) pair, namely (0.11, 0, 1.65) and (0.08, 0.08, 1.65). The connection of such observations to the band structure of LCCO will be discussed.

Microscopic consideration of the collective excitations

A plasmon is an emergent collective mode in many-body physics arising due to the materials’ electronic structure and Coulomb interactions, including both the short-range interaction and the screened long-range interactions respectively.1,2 The dispersion of the plasmon is given by the zero of dielectric function

$$\epsilon (\overrightarrow{q},\omega )=1-v(\overrightarrow{q})\Pi (\overrightarrow{q},\omega ),$$
(1)

where \(v(\overrightarrow{q})\) is the Fourier transformation of Coulomb interaction, and \(\Pi (\overrightarrow{q},\omega )\) is the polarizability function.

Exact calculations of the plasmon dispersion in strongly correlated metals is challenging, partially due to the lack of knowledge on the vertex contribution which is needed to derive the polarizability function.2 Progress has been made in studying the 2D extended Hubbard model42 and the large-\(N\) expansion of the layered \(t-J-V\) model.39 In particular, the plasmon excitation energy was suggested to be closely related to the single-particle density distribution. The spectral weight and the renormalization of its dispersion reflect the evolution of the on-site Coulomb repulsion \(U\) and the long-range screened Coulomb interaction \(V\). Thus RIXS could serve as a good bulk sensitive tool to probe the electronic structures of the cuprates, complimentary to other spectroscopic techniques.

Although the plasmon excitation in strongly correlated systems involves complicated processes, Hafermann et al.43 pointed out that the polarizability \(\Pi (\overrightarrow{q},\omega )\) shares similar \(\Pi (\overrightarrow{q},\omega ) \sim {\alpha }^{2}\frac{{\overrightarrow{q}}^{2}}{{\omega }^{2}}\) behavior as the Lindhard function in random phase approximation (RPA) calculations, in the long-wavelength limit. Such a property of the polarization function in the long-wavelength limit, even for the correlated system, is a consequence of gauge invariance and local charge conservation, regardless of the interaction strength.42,43 Thus for small \({q}_{\parallel }\), to leading order, the electronic correlations only modify the scaling factor \(\alpha\). This was numerically confirmed by the consistency of RPA and Dual-Boson calculations, where the vertex corrections from the DMFT local contribution was taken into account only in the latter.42,43 Applying this approach, we investigate the dispersion of the observed charge excitation with \(\Pi (q,\omega ) \sim {\alpha }^{2}\frac{{q}^{2}}{{\omega }^{2}}\) in the low \({q}_{\parallel }\) regime that we focus on here, and treating the Coulomb potential as that from charge on a lattice.39,44 As a result the plasmon dispersion for a layered correlated system in the long wave-length limit can be approximated as

$${\omega }_{p}(\overrightarrow{q})=\alpha A{q}_{\parallel }{\left[\frac{{\epsilon }_{\parallel }}{{a}^{2}}(2-{\rm{cos}}a{q}_{x}-{\rm{cos}}a{q}_{y})+\frac{{\epsilon }_{\perp }}{{d}^{2}}(1-{\rm{cos}}d{q}_{z})\right]}^{-1/2}.$$
(2)

This includes material parameters \(a\)(\(d\)) representing in-plane (inter-plane) lattice constant, \({\epsilon }_{\parallel }\)(\({\epsilon }_{\perp }\)) the dielectric constants parallel (perpendicular) to the plane, and \(A=\sqrt{\frac{{e}^{2}}{2{a}^{2}d}}\). Equation (2) was used to fit the measured plasmon dispersion with free parameters \({p}_{1}=\alpha /\sqrt{{\epsilon }_{\parallel }}\) and \({p}_{2}={\epsilon }_{\parallel }/{\epsilon }_{\perp }\). The fitting for \(x=0.17\) is plotted as the light pink line in Fig. 1c, which agrees with the RIXS measurements quite well. With the fitted \({p}_{1}\) and \({p}_{2}\), the plasmon energy for \(x=0.17\) at \(\overrightarrow{q}=0\) is calculated to be 1.24 eV, which is consistent with infrared optical and EELS measurements.9,24,45

Within Eq. (2), the doping dependence of the plasmon excitation is parameterized by \(\alpha\), which encapsulates the electron correlation effects. It is interesting to compare this coefficient with the naive expectation that the plasmon energy scales like the square root of the carrier concentration, as predicted from the free electron model. In Fig. 5, the extracted plasmon excitation energies are plotted as function of both \(x\) and \(\sqrt{x}\). At a lower \({q}_{\parallel }\) value of (0.06, 0), the plasmon excitation could be described to be linear with \(x\) or \(\sqrt{x}\), with similar degree of agreement. Such ambiguity lies in the fact that the measured doping range is not large enough to clearly resolve any power law behavior (see Methods). At a higher \({q}_{\parallel }\) value of (0.11, 0), it is obvious that the plasmon excitation does not scale with either \(x\) or \(\sqrt{x}\). The disagreement with a simple free electron model comes as no surprise, and the degree of the disagreement serves as an indication of the electron correlation effect in defining the electronic structures in the cuprates.

Discussion

To help understand our observations, we examine the charge susceptibility via the Lindhard–Ehrenreich–Cohen expression for the charge dynamical susceptibility

$${\chi }_{0}(\overrightarrow{q},\omega ) \sim \sum _{\overrightarrow{k}}{n}_{\overrightarrow{k}}(1-{n}_{\overrightarrow{k}+\overrightarrow{q}})\frac{{E}_{\overrightarrow{k}-\overrightarrow{q}}}{{\omega }^{2}-{E}_{\overrightarrow{k}-\overrightarrow{q}}^{2}},$$
(3)

where \({n}_{\overrightarrow{k}}\) is the Fermi–Dirac distribution function, and \({E}_{\overrightarrow{k}-\overrightarrow{q}}\) is the excitation energy for a \(| \overrightarrow{k}>\underset{}{\overset{}{\to }}| \overrightarrow{k}+\overrightarrow{q}>\) transition. This equation can model the elements of our results that are consistent with an effective quasiparticle picture, such as how Eq. (2) can provide a reasonable description of the data. At low \(\overrightarrow{q}\), bounded by \({n}_{\overrightarrow{k}}(1-{n}_{\overrightarrow{k}+\overrightarrow{q}})\), electron–hole pairs involving electrons deeply under the FS do not contribute to \({\chi }_{0}(\overrightarrow{q},\omega )\). Thus the low \({q}_{\parallel }\) plasmon we probe here is governed by the dynamics of the electrons near the FS, which are most relevant to the conducting behavior including superconductivity. In the low \({q}_{\parallel }\) limit, we can approximate \({E}_{\overrightarrow{k}-\overrightarrow{q}}\approx \overrightarrow{v}\cdot \overrightarrow{q}\) where \(\overrightarrow{v}={\nabla }_{\overrightarrow{k}}{E}_{\overrightarrow{k}}\). The effective summation area in 2D reciprocal space, which contains electrons that contribute to the summation, is proportional to \(\overrightarrow{q}\cdot {\overrightarrow{k_{F}}}\). Thus \({\chi }_{0}(\overrightarrow{q},\omega )\) is expected to be proportional to \(\overrightarrow{v}\cdot {\overrightarrow{k_{F}}}\). It is worthwhile to clarify such FS sensitivity by considering the simple 2D electron gas case. Here, the conducting band is defined as \(E(\overrightarrow{k})=\frac{{k}^{2}}{2m}\), \(\overrightarrow{v}={\overrightarrow{k_{F}}}/m\), and \({k}_{F}^{2}\) is proportional to total carrier density \(n\). Thus, the low \(\overrightarrow{q}\) plasmon intensity scales with \(\frac{n}{m}\) consistent with general expectations.

The above argument shows that the plasmon in LCCO measures the dot product of the Fermi velocity \(\overrightarrow{v}\) with the Fermi wavevector \({\overrightarrow{k_{F}}}\), combined with the \(\alpha\) factor (i.e., the prefactor in Eq. (2)) from the correlation effects. To appreciate the applicability of the quasiparticle description to the plasmon excitation and the doping dependent evolution of \(\overrightarrow{v}\), the one particle spectrum for LCCO was calculated with DMFT combined with density functional theory (DFT).46 The main results are shown in Fig. 6 (see more details in the Supplementary Methods).

Fig. 6: Spectral function of LCCO from DMFT+DFT calculation.
figure 6

a \(x=0.1\), b \(x=0.2\). The square boxes highlight the electron and hole states that can be connected by momentum transfer \({q}_{\parallel }=(0.06,0)\).

Full size image

In the calculated spectrum, the electron correlation effects significantly reduce the quasiparticle lifetime away from the Fermi energy, while the states near the FS are of good coherent character. With increased electron itinerancy from \(x=0.1\) to 0.2, the near-FS region that hosts long lived quasiparticles extends out to larger momentum space, as shown in Fig. 6 (see Supplementary Fig. 5 and Supplementary Discussion). This is consistent with the sharpening of the plasmon peak with increasing doping as observed in our RIXS data. As the plasmon excitation at low \({q}_{\parallel }\) originates from the dynamics of the electrons near the FS, its width measures the life time of the quasi-particles near the FS in the region accessible with \({q}_{\parallel }\). Upon increasing \({q}_{\parallel }\), the plasmon excitation starts to probe the incoherent states that suffer more from the electron correlation effect (reduced lifetime and increased vertex corrections). Thus the excitation quickly broadens and become hard to identify in the RIXS spectrum as observed.

Plasmons are collective electron–hole quasiparticle pair excitations, and Fig. 7 gives a 2D view of the portion of the single particle spectrum where electrons can be excited into unoccupied hole states under momentum conservation constraints, as required in Eq. (3). Although the plasmon is a collective excitation involving a large number of electrons, plasmon excitation along different \(\overrightarrow{q}\) directions selectively probes different portion of the electron states near the FS. The almost overlapping plasmon excitations at \({q}_{\parallel }=(0.06,0)\) and \({q}_{\parallel }=(0.04,0.04)\), as shown in Fig. 4, may suggest that the FS is more isotropic as a functionof in-plane momentum than that from our DMFT+DFT calculations, consistent with ARPES reports.47

Fig. 7: Portions of the quasiparticle states that contribute to plasmon excitations at \({\mathbf{q}}_{\parallel}\) = (0.06, 0) and \({\mathbf{q}}_{\parallel}\) = (0.04, 0.04).
figure 7

The black circle shows the FS for \(x=0.1\) from DMFT+DFT calculations. The blue and red contours show FSs shifted by \({q}_{\parallel }=(0.06,0)\) and \({q}_{\parallel }=(0.04,0.04)\), respectively. The shaded blue and red regions show the electron states that can be excited into unoccupied hole states under momentum conservation constraints.

Full size image

Following the above reasoning, we can discuss about the absence of plasmon excitations in Cu \({L}_{3}\)-edge RIXS measurement of hole-doped cuprates, despite extensive studies of these materials.17,18,19,20,21,35,36,48 The correlation effects could be still significant in the studied doping range, and coherent particles only live in a very small region in reciprocal space. Thus the plasmon excitation is expected to be weaker and broader, making it difficult to identify in the RIXS spectrum. Further, carriers in the hole-doped cuprates are known to have primarily oxygen rather than copper character, so O \(K\)-edge RIXS might be insightful.49 Another consideration is the weaker intensity for charge excitations in hole-doped cuprates than electron-doped cuprates caused by the RIXS process and the asymmetric electronic states.50

The increase of the plasmon excitation upon increased doping is a combined effect from multiple factors. In the standard Fermi liquid model, the plasmon excitation is expected to increase upon doping an electron pocket, as both \({\overrightarrow{k_{F}}}^{2}\) and \(\overrightarrow{v}\) are expected to increase. On the other hand, as discussed in the above section, our observed plasmon energy increase does not follow a simple \(\sqrt{x}\) relation, emphasizing the contribution from the local correlation effect. It would be interesting to compare the RIXS measured plasmon spectrum to that from the 2D extended Hubbard model.42 From the doping dependent evolution of the plasmon excitation lifetime and energy, the two major observations we made here, a full picture of crossing over from a strongly correlated Mott system to itinerant electron liquid could be obtained.

As a conclusion, our RIXS measurements of combi films support the collective nature of the charge excitations in LCCO, which evolve into long lifetime plasmons in a large region of reciprocal space at higher doping. The cuprate electronic structure and Coulomb interactions determine the charge excitation behavior, and both effects are expressed in different ways in different \(\overrightarrow{q}\) regions. The doping-dependent energy increase and width sharpening of the charge excitations are in good agreement with our theoretical interpretation from extended DMFT calculations with nonlocal vertex corrections. Our results are consistent with the theoretical idea that the emergence of collective charge excitations in the long wave limit is ensured by gauge invariance and local charge conservation even with strong electron correlations, and such collective coherent excitations extend to finite momentum transfers with higher doping where the electron correlation effect is reduced. The merits of appreciable momentum range and being bulk sensitive distinguish RIXS from other conventional techniques in probing the two-particle charge dynamics in the cuprates. With improved energy resolution to probe even smaller regions close to the FS, future RIXS measurements could provide unprecedented bulk sensitive information on the evolution of the electronic states in the electron doped cuprates.

Methods

Sample preparation

A LCCO doping-concentration-gradient film was fabricated on a SrTiO\({}_{3}\) substrate by pulsed laser deposition equipped with a continuous moving mask setup at the Institute of Physics, Chinese Academy of Sciences. Moving masks were used to control the deposition of well-defined fractions of La\({}_{2-x}\)Ce\({}_{x}\)CuO\({}_{4}\) (\(x=0.10\)) and La\({}_{2-x}\)Ce\({}_{x}\)CuO\({}_{4}\) (\(x=0.19\)) targets with respect to translation along the film. The final composition was confirmed by \(c\)-axis lattice constant measurements on the film and \({T}_{c}\) measurement on a film patterned into small chips.16 In our measured sample, \(x\) varies from 0.10 to 0.19 along the chosen direction from edge to edge. The high quality of the sample was also evidenced by the smooth evolution of the measured X-ray absorption spectroscopy spectrum during our experiments (see Supplementary Fig. 1). The choice of such gradient film allows a careful doping dependent survey in fine doping steps. More importantly, changing the doping concentration was done by simply translating the film along the doping gradient direction while keeping the experimental condition identical. Thus experimental error is largely minimized, and data for different dopings can be compared with great confidence. To avoid possible non-intrinsic edge effects from the growth, our experiments were focused on the doping range of 0.11–0.18, covering the optimal superconducting state to the non-superconducting metallic phase.16,51,52 The wave vectors used in our paper are indexed using the tetragonal (\(I4/mmm\)) space group with \(a=b=4.01\)Å, \(c\) continuously changes from 12.46 Å for \(x=0.10\) to 12.40 Å for \(x=0.19\).

Experimental setup

Our experiments were carried out at the ADRESS beamline of the Swiss Light Source at the Paul Scherrer Institute53,54 and beamline I21 of the Diamond Light Source. The experimental geometry is sketched in Fig. 1a. Most of the data were taken with \(\sigma\)-polarized incident light, unless mentioned otherwise. The RIXS stations work at fixed scattered angle, thus the total momentum transfer is fixed and the in-plane and out-of-plane momentum transfers vary with relation as \({q}_{\parallel }^{2}+{q}_{\perp }^{2}={\rm{const}}\). In order to compare RIXS spectra at different \({q}_{\perp }\) with the in-plane \({q}_{\parallel }\) fixed, data in Fig. 2c, d was first collected at ADRESS with a fixed scattered angle of 130°, and compared to data collected at Diamond beamline I21 where the scattered angle is fixed at 146°. For figures containing data only from one experimental station, the \({q}_{\perp }\) indexing is omitted for plotting purpose. At each station, the momentum transfer was varied by rocking the sample. Most of the RIXS spectra were collected with the incident X-ray photon energies at the maximum of the absorption curve near the Cu \({L}_{3}\)-edge (see Supplementary Fig. 1), unless mentioned otherwise.

Along the gradient direction, the doping level \(x\) varies from 0.10 to 0.19 in an 8 mm range, which is 0.011 per mm. The experiments were performed at the ADRESS beamline of the Swiss Light Source using the SAXES spectrometer and the I21 beamline of Diamond Light Source, with beamspots at the sample of \(50({\rm{H}})\times 4({\rm{V}})\)µm2 and \(30({\rm{H}})\times 10({\rm{V}})\) µm2, respectively. Thus, the variation of doping level \(x\) of the sample within the beamspot is less than 0.0006, after considering beam footprint effects and can be regarded as homogeneous. The instrumental resolution is about 120 meV at the ADRESS beamline and 50 meV at I21 beamline at the Cu \({L}_{3}\) edge, estimated from the full-width at half maximum (FWHM) of the elastic scattering from carbon tape. All data presented were collected at a temperature of 20 K.

Plasmon dispersion fitting

The total RIXS spectrum is fitted with five components: A pseudo-Voigt function for the elastic line, an anti-symmetrized Lorentzian function multiplied by Bose-Factor and convoluted with resolution function for the paramagnon, a Gaussian function convoluted with the resolution function for the plasmon and a Gaussian function for the \(dd\) excitations. Background scattering is treated with a polynominal function. Similar approaches have been used extensively in the RIXS literature.13,15,18,20,35

Linearity

Assuming \({\omega }_{p}\) follows a linear relation to \(x\) as

$${\omega }_{p}=ax+b\underset{}{\overset{}{\to }}\Delta {\omega }_{p}=a(x-{x}_{0})$$
(4)

Replace \(x\) with \({\sqrt{x}}^{2}\), we have

$$\Delta {\omega }_{p}=a(\sqrt{x}-\sqrt{{x}_{0}})(\sqrt{x}+\sqrt{{x}_{0}})$$
(5)

The variation of \((\sqrt{x}+\sqrt{{x}_{0}})\) in the measured range measures the error if a \({\omega }_{p} \sim \sqrt{x}\) relation is enforced. Over \(x\) from 0.11 to 0.18, \(\sqrt{x}+\sqrt{{x}_{0}}\) varies from 0.7125 to 0.8051 with ±\(6 \%\) variation from the averaged value, which is not big enough to be well resolved from the experimental data.