Introduction

In higher-order topological insulators, the ingap states can be found in (d−n)-dimensional edges (n > 1), such as the corner states of two-dimensional (2D) systems or the hinge states of three-dimensional systems1,2,3,4,5,6,7,8,9,10,11,12. Different from topological insulators with (d−1)-dimensional edge states, the Chern numbers or \({{\mathbb{Z}}}_{2}\) numbers in higher-order topological insulators are zero. The higher-order topology can be captured by topological quantum chemistry13,14,15,16,17,18, nested Wilson-loop method1,8 and second Stiefel–Whitney (SW) class19,20,21,22,23,24,25. Using topological quantum chemistry13, the higher-order topological insulator can be diagnosed by the decomposition of atomic band representations (aBRs) as an unconventional insulator (or obstructed atomic insulator) with mismatching of electronic charge centers and atomic positions16,17,18,26. In contrast to dipoles (Berry phase) for topological insulators, the higher-order topological insulators can be understood by multipole moments1. In a 2D system, the second-order topology corresponds to the quadrupole moment, which can be diagnosed by the nested Wilson-loop method1,8,23. When the system contains space-time inversion symmetries, such as PT and C2zT, where the P and T represent inversion and time-reversal symmetries, the second-order topology can be described by the second SW number (w2)23,27. The second SW number w2 is a well-defined 2D topological invariant of an insulator only when the first SW number w1 = 0. Usually, a 2D quadrupole topological insulator (QTI) with w1 = 0, w2 = 1 has gapped edge states and degenerate localized corner states, which are pinned at zero energy (being topological) in the presence of chiral symmetry. When the degenerate corner states are in the energy gap of bulk and edge states, the fractional corner charge can be maintained due to filling anomaly28.

So far, various 2D systems are proposed to be SW insulators with second-order topology, such as monolayer graphdiyne29,30, liganded Xenes25,31, β-Sb monolayer18 and Bi/EuO32. However, no compound has been proposed to be a QTI with Mx and My symmetries. After considering many-body interactions in transition-metal compounds, superconductivity, exciton condensation and Luttinger liquid could emerge in a transition-metal QTI. In recent years, van der Waals layered materials of A2M1,3X5 (A = Ta, Nb; M = Pd, Ni; X = Se, Te) family have attracted attentions because of their special properties, such as quantum spin Hall effect in Ta2Pd3Te5 monolayer33,34, excitons in Ta2NiSe535,36,37, and superconductivity in Nb2Pd3Te5 and doped Ta2Pd3Te538. In particular, the monolayers of A2M1,3X5 family can be exfoliated easily, serving as a good platform for studying topology and interactions in lower dimensions.

In this work, we predict that based on first-principles calculations, Ta2Ni3Te5 monolayer is a 2D QTI. Using the Wilson-loop method, we show that its SW numbers are w1 = 0 and w2 = 1, corresponding to the second-order topology. We also solve the aBR decomposition for Ta2Ni3Te5 monolayer, and find that it is unconventional with an essential band representation (BR) at an empty Wykoff position (WKP), Ag@4c, which origins from the remarkable double-band inversion on Y–Γ line. To verify the QTI phase, we compute the energy spectrum of Ta2Ni3Te5 monolayer with open boundary conditions in both x and y directions and obtain four degenerate corner states. Then, we construct an eight-band quadrupole model with Mx and My successfully. The double-band-inversion picture widely happens in the band structures of A2M1,3X5 family. The Ta2M3Te5 monolayers are 2D QTI candidates for experimental realization in electronic systems.

Results

Band structures

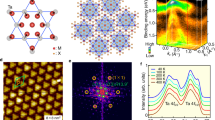
The band structure of Ta2Ni3Te5 monolayer suggests that it is an insulator with a band gap of 65 meV. We have checked that spin–orbit coupling (SOC) has little effect on the band structure (Supplementary Fig. 2b). We also checked the band structures using GW method and SCAN method, and we find that the band gap remains using these methods (the corresponding band structures are shown in Supplementary Note 1). As shown in the orbital-resolved band structures of Fig. 3a–c, although low-energy bands near the Fermi level (EF) are mainly contributed by Ta-\({d}_{{z}^{2}}\) orbitals (two conduction bands) and NiA-dxz orbitals (two valence bands), the inverted bands of {Y2; GM1−, GM3−} come from Te-px orbitals. The irreducible representations (irreps)39 at Y and Γ are denoted for the inverted bands in Fig. 1b. We notice that the double-band inversion between {Y2; GM1−, GM3−} bands and {Y1; GM1+, GM3+} bands is remarkable, about 1 eV.

Fig. 1: Crystal structures and electronic structures of Ta2Ni3Te5 monolayer.
figure 1

a The crystal structure, Wyckoff positions and Brillouin zone (BZ) of Ta2Ni3Te5 monolayer. b Band structure and irreps at Y and Γ of Ta2Ni3Te5 monolayer. c The 1D ky-direct Wilson bands as a function of kx calculated in the DFT code. d Close-up of the green region in (c), with one crossing of Wilson bands at θ = π indicating the second SW class w2 = 1.

Full size image

Atomic band representations

To analyze the band topology, the decomposition of aBR is performed. In a unit cell of Ta2Ni3Te5 monolayer in Fig. 1a, four Ta atoms, four NiB atoms and eight Te atoms are located at different 4e WKPs. The rest two Te atoms and two NiA atoms are located at 2a and 2b WKPs, respectively. The aBRs are obtained from the crystal structure by pos2aBR16,17,18, and irreps of occupied states are calculated by IRVSP39 at high-symmetry k-points. Then, the aBR decomposition is solved online—http://tm.iphy.ac.cn/UnconvMat.html. The results are listed in Supplementary Table 2 of Supplementary Note 2. Instead of being a sum of aBRs, we find that the aBR decomposition of the occupied bands has to include an essential BR at an empty WKP, i.e., Ag@4c. As illustrated in Fig. 1a, the charge centers of the essential BR are located at the middle of NiB-NiB bonds (i.e., the 4c WKP), indicating that the Ta2Ni3Te5 monolayer is a 2D unconventional insulator with second-order topology.

Double-band inversion

In an ideal atomic limit, Te-p orbitals and Ni-d orbitals are occupied, while Ta-d orbitals are fully unoccupied. Thus, all the occupied bands are supposed to be the aBRs of Te-p and Ni-d orbitals, as shown in the left panel of Fig. 2a. However, in the monolayers of A2M1,3X5 family (see their band structures in Supplementary Note 1), a double-band inversion happens between the occupied aBR A″@4e (Te-px and Ni-d) and unoccupied aBR \(A^{\prime} @4e\) (Ta-\({d}_{{z}^{2}}\)), as shown in the right two panels of Fig. 2a. When the double-band inversion happens between {Y2; GM1−, GM3−} and {Y1; GM2−, GM4−} on Y–Γ line, it results in a semimetal for Ta2NiSe5 monolayer (215-type; Fig. 2b). When it happens between {Y2; GM1−, GM3−} and {Y1; GM1+, GM3+} in Fig. 2c, the system becomes a 2D QTI for Ta2Ni3Te5 monolayer (235-type), resulting in the essential BR of Ag@4c.

Fig. 2: The double-band inversion process.
figure 2

a The diagram of double-band inversion along Y–Γ line. The schematic band structures of (b) 215-type semimetal and (c) 235-type insulator. The double-band inversion happens in both cases. The crossing points on the Γ–X line are part of the nodal line.

Full size image

Second Stiefel–Whitney class w 2 = 1

To identify the second-order topology of the monolayers, we compute the second SW number by the Wilson-loop method. The first SW class (w1) is

$${w}_{1}{\left|\right.}_{C}=\frac{1}{\pi }{\oint }_{C}{{{\rm{d}}}}{{{\boldsymbol{k}}}}\cdot {{{\rm{Tr}}}}{{{\mathcal{A}}}}({{{\boldsymbol{k}}}})$$
(1)

where \({{{{\mathcal{A}}}}}_{mn}({{{\boldsymbol{k}}}})=\left\langle {u}_{m}({{{\boldsymbol{k}}}})\right|{{{\rm{i}}}}{{{{\boldsymbol{\nabla }}}}}_{{{{\boldsymbol{k}}}}}\left|{u}_{n}({{{\boldsymbol{k}}}})\right\rangle\)22. The second SW class (w2) can be computed by the nested Wilson-loop method, or simply by m module 2, where m is the number of crossings of Wilson bands at θ = π. It should be noted that w2 is well-defined only when w1 = 0. With w1 = 0, w2 can be unchanged when choosing the unit cell shifting a half lattice constant. The 1D Wilson-loops are computed along ky. The computed phases of the eigenvalues of Wilson-loop matrices Wy(kx) (Wilson bands) are shown in Fig. 1c as a function of kx. The results show that the first SW class is w1 = 0. In addition, there is one crossing of Wilson bands at θ = π [Fig. 1d], indicating the second SW class w2 = 1. The quadruple moment qxy = e/2 calculated by the nested Wilson-loop method in Supplementary Note 3. Therefore, the Ta2Ni3Te5 monolayer is a QTI with a nontrivial second SW number.

Edge spectrum and corner states

From the orbital-resolved band structures (Fig. 3), the maximally localized Wannier functions of Ta-\({d}_{{z}^{2}}\), NiA-dxz and Te-px orbitals are extracted, to construct a 2D tight-binding (TB) model of Ta2Ni3Te5 monolayer. As shown in Fig. 3d, the obtained TB model fits the density functional theory (DFT) band structure well. First, we compute the (01)-edge spectrum with open boundary condition along y. Instead of gapless edge states for a 2D \({{\mathbb{Z}}}_{2}\)-nontrivial insulator, gapped edge states are obtained for the 2D QTI [Fig. 3e]. Then, we explore corner states as the hallmark of the 2D QTI. We compute the energy spectrum for a nanodisk. For concreteness, we take a rectangular-shaped nanodisk with 50 × 10 unit cells, preserving both Mx and My symmetries in the 0D geometry. The obtained discrete spectrum for this nanodisk is plotted in the inset of Fig. 3f. Remarkably, one observes four degenerate states near EF. The spatial distribution of these four-fold modes can be visualized from their charge distribution, as shown in Fig. 3f. Clearly, they are well localized at the four corners, corresponding to isolated corner states.

Fig. 3: The band structures and corner states of Ta2Ni3Te5 monolayer.
figure 3

The orbital-resolved band structures of a \({d}_{{z}^{2}}\) orbitals of Ta atoms, b dxz orbitals of NiA atoms, and c px orbitals of Te atoms. d The comparison between band structures of maximally localized Wannier functions and DFT results. e (01)-edge states around Γ. f The charge distribution of four corner states. The insert shows the energy spectrum of the tight-binding model with open boundaries in x and y directions.

Full size image

Minimum model for the 2D QTI

As shown in Fig. 2, the minimum model for the 2D QTI should be consisted of two BRs of \(A^{\prime} @4e\) and A″@4e. Based on the situation of Ta2Ni3Te5 monolayer in Fig. 2c, the minimum effective model is derived as below:

$${H}_{{{{\rm{TB}}}}}({{{\boldsymbol{k}}}})=\left(\begin{array}{cc}{H}_{{{{\rm{Ta}}}}}({{{\boldsymbol{k}}}})&{H}_{{{{\rm{hyb}}}}}({{{\boldsymbol{k}}}})\\ {{H}_{{{{\rm{hyb}}}}}({{{\boldsymbol{k}}}})}^{{\dagger} }&{H}_{{{{\rm{Ni}}}}}({{{\boldsymbol{k}}}})\end{array}\right)$$
(2)

The terms of HTa(k), HNi(k) and Hint(k) are 4 × 4 matrices, which read

$$\begin{array}{rcl}{H}_{{{{\rm{Ta}}}}}({{{\boldsymbol{k}}}})&=&[{\varepsilon }_{s}+2{t}_{s1}\cos ({k}_{x})]{\sigma }_{0}{\tau }_{0}+{t}_{s2}{\gamma }_{1}({{{\boldsymbol{k}}}})+{t}_{s3}{\sigma }_{0}{\tau }_{x},\\ {H}_{{{{\rm{Ni}}}}}({{{\boldsymbol{k}}}})&=&[{\varepsilon }_{p}+2{t}_{p1}\cos ({k}_{x})]{\sigma }_{0}{\tau }_{0}+{t}_{p2}{\gamma }_{2}({{{\boldsymbol{k}}}})+{t}_{p3}{\sigma }_{0}{\tau }_{x},\\ {H}_{{{{\rm{hyb}}}}}({{{\boldsymbol{k}}}})&=&2{{{\rm{i}}}}{t}_{sp}\sin ({k}_{x}){\gamma }_{3}({{{\boldsymbol{k}}}}).\end{array}$$
(3)

The γ1,2,3(k) matrices are given explicitly in Supplementary Note 4.

We find that ts1 < 0 and tp1, tp2 > 0 for the A2M1,3X5 family (ts3 and tp3 are small). When εs + 2ts1 − 2∣ts2∣ < εp + 2tp1 + 2tp2, the double-band inversion happens in the monolayers of this family. By fitting the DFT bands, we obtain ts2 > 0 for the 215-type, while ts2 < 0 for the 235-type. When εp = − εs and tpi = − tsi(i = 1, 2, 3), the model is chiral symmetric (i.e., δ = 0 in Table 1). Since the second SW insulator or QTI is topological in the presence of chiral symmetry, we would focus on the model (almost respecting chiral symmetry) in the following discussion.

Table 1 Parameters of the TB model for the QTI with chiral symmetry when δ = 0.
Full size table

Analytic solution of (01)-edge states

As the remnants of the QTI phase, the localized edge states can be solved analytically for the minimum model. For the (01)-edge, one can treat the model HTB(k) as two parts, H0(k) and \(H^{\prime} ({{{\boldsymbol{k}}}})\),

$$\begin{array}{rcl}{H}_{0}({{{\boldsymbol{k}}}})&=&\left(\begin{array}{cc}{t}_{s2}{\gamma }_{1}({{{\boldsymbol{k}}}})+{t}_{s3}{\sigma }_{0}{\tau }_{x}&0\\ 0&{t}_{p2}{\gamma }_{2}({{{\boldsymbol{k}}}})+{t}_{p3}{\sigma }_{0}{\tau }_{x}\end{array}\right)\\ H^{\prime} ({{{\boldsymbol{k}}}})&=&\left(\begin{array}{cc}[{\varepsilon }_{s}+2{t}_{s1}\cos ({k}_{x})]{\sigma }_{0}{\tau }_{0}&{H}_{{{{\rm{hyb}}}}}({{{\boldsymbol{k}}}})\\ {{H}_{{{{\rm{hyb}}}}}({{{\boldsymbol{k}}}})}^{{\dagger} }&[{\varepsilon }_{p}+2{t}_{p1}\cos ({k}_{x})]{\sigma }_{0}{\tau }_{0}\end{array}\right)\end{array}$$
(4)

Note that there is a pair of Dirac points \((\pm {k}_{x}^{D},0)\), with \({k}_{x}^{D}=\arccos \left[\frac{1}{2}{(\frac{{t}_{s3}}{{t}_{s2}})}^{2}-1\right]\). Since kx is still a good quantum number on the (01)-edge, expanding ky to the second order, the zero-mode equation H0(kx, − i∂y)Ψ(kx, y) = 0 can be solved for y ∈ [0, +∞). Taking the trial solution of Ψ(kx, y) = ψ(kx)eλy, we obtain the secular equation and the solution of λ = ±λ±, where

$${\lambda }_{\pm }=1\pm \sqrt{\frac{{t}_{s3}^{2}}{(1+\cos ({k}_{x})){t}_{s2}^{2}}-1}$$
(5)

With the boundary conditions Ψ(kx, 0) = Ψ(kx, +∞) = 0, only − λ± are permitted.

In the kx regime of \(\left[-{{{{\boldsymbol{k}}}}}_{x}^{D},{{{{\boldsymbol{k}}}}}_{x}^{D}\right]\), the edge zero-mode states are Ψ(kx, y) = [C1(kx)ϕ1(kx) + C2(kx)ϕ2(kx)]\(({e}^{-{\lambda }_{+}y}-{e}^{-{\lambda }_{-}y})\) with

$$\begin{array}{l}{\phi }_{1}({k}_{x})={\left(\begin{array}{cccccccc}-\frac{(1+{{\rm{e}}}^{-{{{\rm{i}}}}{k}_{x}}){t}_{s2}}{{t}_{s3}}\quad0\quad1\quad0\quad0\quad0\quad0\quad0\end{array}\right)}^{{{{\rm{T}}}}}\\ {\phi }_{2}({k}_{x})={\left(\begin{array}{cccccccc}0\quad0\quad0\quad0\quad-\frac{{t}_{p3}}{(1+{{\rm{e}}}^{{{{\rm{i}}}}{k}_{x}}){t}_{p2}}\quad0\quad1\quad0\end{array}\right)}^{{{{\rm{T}}}}}\end{array}$$
(6)

The edge zero states are Fermi arcs that linking the pair of projected Dirac points \((\!\pm {k}_{x}^{D},0)\). Once \(H^{\prime} ({{{\boldsymbol{k}}}})\) included, the effective (01)-edge Hamiltonian is,

$$\begin{array}{rcl}{H}_{{{{\rm{01}}}}}^{eff}&=&\left\langle {{\Phi }}\right|H({{{\boldsymbol{k}}}})\left|{{\Phi }}\right\rangle \\ &=&\left(\begin{array}{cc}{\varepsilon }_{s}+2{t}_{s1}\cos ({k}_{x})&0\\ 0&{\varepsilon }_{p}+2{t}_{p1}\cos ({k}_{x})\end{array}\right)\end{array}$$
(7)

where \(\left|{{\Phi }}\right\rangle \equiv \left|{\phi }_{1}({k}_{x}),{\phi }_{2}({k}_{x})\right\rangle\). Two edge spectra are obtained in Fig. 4a.

Fig. 4: The corner states of minimum model.
figure 4

Energy spectrum for a the (01)-edge, b the (10)-edge, and c a Mx- and My-symmetric disk of 80 × 20 unit cells of the minimum model with chiral symmetry slightly broken (δ = −0.1). d The spatial distribution of four degenerate in-gap states in c. e The diverse properties of A2M1,3X5 (A = Ta, Nb; M = Pd, Ni; X = Se, Te) family.

Full size image

Effective Su–Schrieffer–Heeger model on (10)-edge and corner states

Similarly, we derive the (10)-edge modes as \([{F}_{1}({k}_{y}){\varphi }_{1}({k}_{y})+{F}_{2}({k}_{y}){\varphi }_{2}({k}_{y})]\left({{\rm{e}}}^{-{{{\Lambda }}}_{+}x}-{{\rm{e}}}^{-{{{\Lambda }}}_{-}x}\right)\) with

$$\begin{array}{r}{\varphi }_{1}=\left(\begin{array}{c}0\\ 1-{{{\Delta }}}_{s}\\ 1-{{{\Delta }}}_{s}{{\rm{e}}}^{{\rm{i}}{k}_{y}}\\ 0\\ -1+{{{\Delta }}}_{p}\\ 0\\ 0\\ -1+{{{\Delta }}}_{p}{{\rm{e}}}^{-{\rm{i}}{k}_{y}}\end{array}\right),{\varphi }_{2}=\left(\begin{array}{c}{{\rm{e}}}^{-{\rm{i}}{k}_{y}}\left(1-{{{\Delta }}}_{s}\right)\\ 0\\ 0\\ 1-{{{\Delta }}}_{s}{{\rm{e}}}^{-{\rm{i}}{k}_{y}}\\ 0\\ -1+{{{\Delta }}}_{p}\\ -{{\rm{e}}}^{-{\rm{i}}{k}_{y}}+{{{\Delta }}}_{p}\\ 0\end{array}\right).\end{array}$$
(8)

Here, \({{{\Lambda }}}_{\pm }=\frac{2{t}_{sp}\pm \sqrt{4{t}_{sp}^{2}-2(2{t}_{s1}+{t}_{s2})(2{t}_{s1}+2{t}_{s2}+{\varepsilon }_{s})}}{2{t}_{s1}+{t}_{s2}}\), \({{{\Delta }}}_{s}={\left(\frac{{t}_{s3}}{2{t}_{s2}}\right)}^{2}\), and \({{{\Delta }}}_{p}={\left(\frac{{t}_{p3}}{2{t}_{p2}}\right)}^{2}\). Then we obtain the effective Hamiltonian on (10) edge below,

$$\begin{array}{rcl}{H}_{{{{\rm{10}}}}}^{{\rm{eff}}}&=&\left(\begin{array}{cc}0&v+w{{\rm{e}}}^{-{\rm{i}}{k}_{y}}\\ v+w{{\rm{e}}}^{{\rm{i}}{k}_{y}}&0\end{array}\right),\\ w&=&{t}_{s3}+{t}_{p3}-4{t}_{s3}{{{\Delta }}}_{s},\\ v&=&{t}_{s3}+{t}_{p3}-4{t}_{p3}{{{\Delta }}}_{p}\end{array}$$
(9)

When δ = 0, the minimum QTI model is chiral symmetric and it is gapless on the (10) edge (preserving My symmetry). When the chiral symmetry is slightly broken (δ ≠ 0), the \({H}_{10}^{{\rm{eff}}}\) becomes an Su–Schrieffer–Heeger model (δ < 0 nontrivial; δ > 0 trivial), as presented in Fig. 4b–d. As a result, we obtain a solution state on the end of the edge mode, i.e., the corner. As long as the energy of the corner state is located in the gap of bulk and edge states, the corner state is well localized at the corners, as shown in Fig. 4c, d.

Discussion

In Ta2NiSe5 monolayer, the double-band inversion has also happened between Ta-\({d}_{{z}^{2}}\) and Te-px states, about 0.4 eV, resulting in a semimetal with a pair of nodal lines in the 215-type. The highest valence bands on Y–Γ are from the inverted Ta-\({d}_{{z}^{2}}\) states. However, in Ta2Ni3Te5 monolayer, the double-band inversion strength becomes remarkable, ~1 eV, which is ascribed to the filled B-type voids and more extended Te-p states. On the other hand, the highest valence bands become NiA-dxz states (slightly hybridized with Te-px states). It is insulating with a small gap of 65 meV. When it comes to A2Pd3Te5 monolayer, the remarkable inversion strength is similar to that of Ta2Ni3Te5. But the PdA-dxz states go upwards further due to more expansion of the d orbitals and the energy gap becomes almost zero in Ta2Pd3Te5. In short, the double-band inversion happens in all these monolayers, while the band gap of the 235-type changes from positive (Ta2Ni3Te5), to nearly zero (Ta2Pd3Te5 with a tiny band overlap), to negative (Nb2Pd3Te5), as shown in Supplementary Fig. 1. Although the band structure of Ta2Pd3Te5 bulk is metallic without SOC33,34,38, the monolayer could become a QSH insulator upon including SOC in ref. 33. Since their bulk materials are van der Waals layered compounds, the bulk topology and properties strongly rely on the band structures of the monolayers in the A2M1,3X5 family.

As we find in ref. 33, the band topology of Ta2Pd3Te5 monolayer is lattice sensitive. By applying >1% uniaxial compressive strain along b, it becomes a \({{\mathbb{Z}}}_{2}\)-trivial insulator, being a QTI. On the other hand, due to the quasi-1D crystal structure, the screening effect of carriers is relatively weak and the electron-hole Coulomb interaction may be substantial for exciton condensation. The 1D in-gap edge states as remnants of the QTI are responsible for the observed Luttinger-liquid behavior.

In conclusion, we predict that Ta2M3Te5 monolayers can be QTIs by solving aBR decomposition and computing SW numbers. Through aBR analysis, we conclude that the second-order topology comes from an essential BR at the empty site (Ag@4c), and it origins from the remarkable double-band inversion. The double-band inversion also happens in the band structure of Ta2NiSe5 monolayer. The second SW number of Ta2Ni3Te5 monolayer is w2 = 1, corresponding to a QTI. Therefore, we obtain edge states and corner states of the monolayer. The eight-band quadrupole model with Mx and My has been constructed successfully for electronic materials. With the large double-band inversion and small band energy gap/overlap, these transition-metal materials of A2M1,3X5 family provide a good platform to study the interplay between the topology and interactions (Fig. 4e).

Methods

Calculation method

Our first-principles calculations were performed within the framework of the DFT using the projector augmented wave method40,41, as implemented in Vienna ab-initio simulation package (VASP)42,43. The Perdew–Burke–Ernzerhof (PBE) generalized gradient approximation exchange-correlations functional44 was used. SOC was neglected in the calculations except in Supplementary Fig. 2b. We also used SCAN45 and GW46 method when checking the band gap. In the self-consistent process, 16 × 4 × 1 k-point sampling grids were used, and the cut-off energy for plane wave expansion was 500 eV. The irreps were obtained by the program IRVSP39. The maximally localized Wannier functions were constructed by using the Wannier90 package47. The edge spectra are calculated using surface Green’s function of semi-infinite system48,49.