Main

By the end of May 2020, the number of confirmed COVID-19 cases exceeded 6 million and the pandemic had claimed nearly 400,000 lives worldwide1,2 (https://www.arcgis.com/apps/opsdashboard/index.html#/bda7594740fd40299423467b48e9ecf6). Although some countries are past their (first) epidemic peak, infections continue to rise in others. In the absence of a vaccine or effective antiviral treatments (which will most likely not be available any time soon3,4), several countries imposed strict lockdown measures to curb the spread of the disease. For countries such as China, an initial evaluation of mobility restrictions has resulted in important reductions in case incidence5. At the time of writing, several countries that initially imposed strict lockdown measures are in the process of lifting them or considering doing so—but there are substantial differences in policy approach. The fact that the 1918 influenza pandemic had a second deadly epidemic wave, presumably caused by strain mutations6, has also stimulated a vigorous debate on whether actions taken now should incorporate this possibility. However, data on the last pandemic of similar scale more than one century ago remain limited, despite aftermath reports7. Currently, optimal interventions against the COVID-19 pandemic aiming at a relaxation of strict social distancing enforcement are hard to identify8,9. This is further complicated by the fact that the extent of pre-symptomatic and asymptomatic infections is not narrowly constrained (for example, may be up to 86% (ref. 10)) and basic SARS-CoV-2 and coronaviruses characteristics are not yet known11,12,13,14,15. Test–trace–isolate strategies might indeed be an effective approach if combined with social distancing and individual protection measures16,17. With respect to the role of social distancing specifically, Japan’s mild restrictions appear to have had a marked containment effect by the end of May, due to social distancing18. This is despite the fact that Japan conducted only 2.2 tests per 1,000 people (as compared to 16 in South Korea and in the United States, for example). At the time of writing, Europe’s first worst-hit countries, Italy and Spain, are experiencing a flattening of their respective death tolls.

On 29 March, the government of Spain published a decree that affected all sectors considered non-essential in a strict lockdown19. The objective was to take advantage of Easter holidays to extend the low level of mobility from Saturdays and Sundays to the rest of the days of the week, thereby reducing new infections and managing healthcare capacity. Under an impending economic crisis, the Spanish executive government believed that it was time two weeks later (14 April 2020) for the economy to recover a certain dynamism20 and lifted the extreme lockdown conditions. However, the decisions to impose restrictions and on when and how to optimally ease those is at the centre of international debate21,22. This decision unfortunately presents two related problems: first, the risk that the return to activity might cause a spike in infections that could aggravate capacity-limited healthcare systems at a time when the situation appears still precarious; and second, there is no way to assess this risk, given the lack of reliable information on the actual number of people infected or the extent of immunity developed among the population. The lifting of lockdown restrictions makes the risk of a flare-up in cases again a serious threat.

On 19 March 2020, the World Health Organization issued an interim guidance report stating how and when to best proceed with the lifting of confinement measures, given the high number of active cases and the not yet fully controlled situation in some of the countries approaching deconfinement policies23,24. On the other hand, strict lockdown conditions during the COVID-19 epidemic peak appeared to be effective in Italy and later Spain, given that the number of new infections and fatalities was decreasing. Re-allowing the mobility of a large number of the confined population might increase the risk that these figures will rise again25. In China, for instance, suspending intracity public transport, closing entertainment venues and banning public gatherings were associated with reductions in case incidence26. The first evaluation studies seem to indicate that the national emergency response appeared to have delayed the growth and limited the size of the COVID-19 epidemic in China, averting hundreds of thousands of cases24,27.

In this study, we present projections based on a modified SEIR model that allows us to simulate both the degree of population confinement and the different post-confinement strategies. Our study intends to evaluate the effects of different actionable scenarios and inform countries of the risk that each of these scenarios may entail. However, although steps to curb the spread of SARS-CoV-2 have already been taken in many countries (for example, behavioural changes, social distancing and use of face masks), assessing how effective each of these is from the standpoint of disease epidemiology remains an open challenge. Although we do not yet have a full understanding of the principles governing SARS-CoV-2 transmission and the most efficient behavioural interventions to implement, so far the use of face masks and gloves, hand hygiene and ‘shelter in place’ mandates have already demonstrated benefits in decreasing the transmissibility and the number of active contacts.26. We aimed to quantitatively evaluate their relevance as containment strategies.

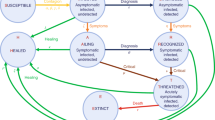
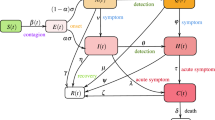
Our model framework is based on the work of Peng et al.27 and Gumel et al.28, it enables testing of control interventions, and we recently also implemented it for Spain and Italy29 (see those studies and the Methods for mathematical details). As an important difference, we added a return function with τ to simulate the return of people from the C (confined) compartment to the S (susceptible) compartment, through which the effect of population deconfinement with different scenarios can be explored. Our model framework, unlike previous studies28, does not treat confined people as coming from the population of exposed individuals (E), who are then quarantined, as the large (and unknown) proportion of asymptomatic undiagnosed individuals would, in this case, make this compartment extremely unstable. Instead, we essentially defined as confined (C) those individuals coming from the susceptible compartment, and we assumed that, by being there, they are entirely ‘protected’ from infection. We made the same assumption in ref. 29, to be less alarmist in our projections. However, this assumption is not realistic and we are fully aware that a significant, but unspecified, number of contagions can come from household infections. As for hospital-acquired infections (which we did not consider either), having these numbers to initialize any model is unfeasible for an ongoing and unique epidemic such as COVID-19. These datasets are not currently available and will be prone to uncertainties related to large reporting discrepancies and errors. They also tend to be highly country-specific as they depend largely on public health protocols and notification systems that vary widely among countries. Owing to our assumption that confined individuals cannot become infected, our simulations therefore represent an underestimation of the actual burden of disease. Nonetheless, given the significant debate on the use and misuse of epidemiological models to inform policy, we opted for a less alarmist approach. Additionally, we dynamically included behavioural interventions and people’s awareness as modulating functions of some relevant model’s parameters (Methods). The general description of the model is provided in equation (1):

$$\frac{{{\rm{d}}S}}{{{\rm{d}}t}} = \mu N_{\rm{T}} + \tau C\left( t \right) - \alpha S\left( t \right) - \beta \frac{{S\left( t \right)I\left( t \right)}}{{N_{\rm{T}}}} - \mu S\left( t \right)$$
$$\frac{{{\rm{d}}E}}{{{\rm{d}}t}} = \beta \frac{{S\left( t \right)I\left( t \right)}}{{N_{\rm{T}}}} - \gamma E\left( t \right) - \mu E\left( t \right)$$
$$\frac{{{\rm{d}}I}}{{{\rm{d}}t}} = \gamma E\left( t \right) - \delta I\left( t \right) - \mu I\left( t \right)$$
$$\frac{{{\rm{d}}Q}}{{{\rm{d}}t}} = \delta I\left( t \right) - Q\left( t \right)\left( {\lambda \left( t \right) + k\left( t \right) + \mu } \right)$$
$$\frac{{{\rm{d}}R}}{{{\rm{d}}t}} = \lambda \left( t \right)Q\left( t \right) - \mu R\left( t \right)$$
$$\frac{{{\rm{d}}D}}{{{\rm{d}}t}} = k\left( t \right)Q\left( t \right)$$
$$\frac{{{\rm{d}}C}}{{{\rm{d}}t}} = \alpha S\left( t \right) - \tau C\left( t \right) - \mu C\left( t \right)$$
(1)

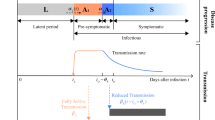
where S(t) is the susceptible population, C(t) is the confined susceptible population, E(t) is the exposed population, I(t) is the infectious population, Q(t) is the population under quarantine (infected reported cases), R(t) is the recovered population, D(t) is the population deceased because of the virus and NT is the total population. As COVID-19 exhibits a mild or even ‘preclinical but communicable’ period of viral shedding and spread of infection30, the differentiation between the I and Q classes is relevant. The parameters λ(t) and k(t) are time-dependent functions shown in equation (2):

$$\begin{array}{l}k\left( t \right) = k_0\exp\left( { - k_1t} \right)\\ \lambda \left( t \right) = \lambda _0\left( {1 - \exp\left( { - \lambda _1t} \right)} \right)\end{array}$$
(2)

where k0, k1, λ0 and λ1 are the fitted coefficients.

The main parameters of the model are the protection rate (α), the infection rate (β), the incubation rate (γ), the quarantine rate (δ), the natural death and birth rates (μ) (1/(80 × 365)), the recovery rate (λ(t)), the mortality rate by the virus (k(t)) and finally τ is the deconfinement rate. The model parameters are all listed in Table 1.

Table 1 Model fitted parameters for Spain
Full size table

The implemented model is expanded from Peng et al.27, but it differs in a number of respects, as the main objective of our study was to help generate robust and objective projections of a suite of public-health-relevant scenarios important for the current COVID-19 crisis. The main structural modifications are: the deconfinement process, which is explicitly simulated here; the incorporation of a time-delay parameter to mimic the loss of acquired immunity to other coronaviruses; and the addition of a time-decaying parameter modulating the infection rate β. These modifications were carried out to mimic and study the effect on transmissibility of non-pharmaceutical interventions (NPIs) and human behaviour (for example, hand hygiene, face masks, public education about personal protection and increases in home-/teleworking). The influence of this time-decaying parameter on β decays with time, aiming at reproducing the likely time-evolving relaxation in population awareness in response to an alarming situation30,31 (see Methods).

Another main difference is that we moved to a probabilistic framework and generated a large number of simulations from the exploration of variations in parameter values. The probabilistic framework enables us to more reliably explore the uncertainty associated with parameter estimates and provides additional strength when evaluating potential projections.

The proportion of people released in all scenarios was 50% higher than the population confined, with the released proportion being equivalent to roughly the active population in Spain at the end of 2019 (58.18%)32. The two gradual release protocols evaluated differed in that, in the first strategy (Fig. 1), there is a monotonic gradual return of people to work (for example, people are progressively being integrated again into the susceptible population, following a decaying function defined in equation (4); see Methods). The second scenario attempts to mimic the delayed release of the susceptible portions of the population being more at risk (for example, older people and people with existing co-morbidities, among others). All simulations were generated with observed data from Spain up to the peak in active cases (circa 29 April) and for 30, 60 and 90 d after this date, corresponding here to 28 May, 27 June and 27 July, respectively (Figs. 1 and 2 and Extended Data Fig. 1). In the case of Fig. 2 and the lower panel of Extended Data Fig. 1, a mixed scenario is generated in which abrupt deconfinement of 50% of the protected population is simulated after 45, 60 and 75 d from 13 March, corresponding to 27 April, 13 May and 27 May, respectively. Then, gradual deconfinement of the population is simulated 30, 45 and 60 d after the first deconfinement date (therefore corresponding to 28 May, 29 June and 28 July, respectively), with the remainder of the confined population being released gradually with the same function as that defined in equation (1) and for τ following equation (4). The reason for this approach is to be able, to the extent possible, to generate results for application elsewhere in the world. To this end, we locked all simulations in Figs. 1 and 2 and Extended Data Fig. 1 (with simulations extended up to the end of 2021), to be generated with data up to the date of the peak in active cases in Spain (29 April). A fixed lockdown time of 30 d (15-d semi-lockdown and 15-d total lockdown conditions) had taken place in the country by the time Spain reached the peak in active cases. In all scenarios, 50% of the population was released either gradually (Fig. 1) or suddenly (Fig. 2, and as specifically stated in each of the figure captions). For comparison with Fig. 1, a benchmark situation with the sudden release of 100% of the people was simulated at the same 30-, 60- and 90-d periods. In this benchmark situation, all of the confined population is abruptly released from confinement once the lockdown is lifted (Extended Data Fig. 2). This approach enables the estimation of what a country would expect for a large COVID-19 incidence at the peak in active cases when lifting lockdowns after 30, 60 and 90 d of confinement. Longer lockdowns were not considered to be realistic. We present also as a benchmark situation what the evolution of the epidemics would be if, instead of the above scenario design, we run the model with the most updated observations at this time (up to 25 May 2020). This is the scenario named ‘current’ represented in Figs. 1 and 2 and Extended Data Fig. 1 for Spain. The number of infected people (I) shown in all of the figures corresponds to the number of active cases (not new cases), representing those people who are diagnosed with COVID-19 and whose status is not yet resolved. As a consequence, these individuals take some time to move into the recovered (R) or deceased (D) compartments, as on average a patient remains hospitalized for 10 to 13 d before recovering or dying from the disease33. It is clear from Fig. 1a that the ‘current’ scenario of an implemented (complete) lockdown of only 15 d is well simulated by the model, with the earlier appearance of the peak in I than in the 30-d scenario (black line).

Fig. 1: Gradual deconfinement scenario for Spain from the peak in active cases.
figure 1

This scenario implements a gradual deconfinement rate of 50% higher than the confinement rate. a,b,d–f, Temporal dynamics for Spain for the active cases (a), recovered population (b), deaths (d), susceptible population (e) and confined population (f) after 30 (black), 60 (blue) and 90 (red) d of confinement. The simulations in a–f were generated with data up to 30 April. The ‘current’ scenario denotes the epidemic evolution simulated in Spain with the updated observed data (I, D, R) up to 25 May. c, A zoom visualization of the initial epidemic evolution in a; red circles in a and c are the reported data. The lockdown duration was 30 d since the peak in active cases (29 April 2020). Gradual deconfinement took place from 30 May, 30 June and 30 July, respectively; red arrows indicate the lockdown dates and black arrow denotes the lockdown lift. The ‘current’ scenario liberates the population on 14 May, exactly a month after the lifting of the established lockdown. 95% CI is plotted as a light blue shaded area for each population.

Full size image
Fig. 2: Abrupt–gradual deconfinement scenario for Spain from the peak in active cases.
figure 2

This scenario combines an abrupt deconfinement of 50% of the confined population and a subsequent gradual rate of deconfinement (10% higher than the confinement rate). a,b,d–f, The dynamics estimated for Spain in terms of the active cases (red circles are the reported data) (a), recovered population (b), deaths (d), susceptible population (e) and protected population (f) after 45 (black), 60 (blue) and 75 (red) d of confinement. c, A zoomed-in visualization of the initial epidemic evolution in a; red arrows indicate the lockdown (partial, total) dates and black arrow denotes the lockdown lift. The data used in all simulations are up to 29 April 2020 (25 May 2020 for the ‘current’ scenario), the date from which the sudden deconfinement of 50% of the confined population is made. Gradual deconfinement release of the population is on 30 May, 30 June and 30 July, respectively. The lockdown time is counted from 14 March, the date when the first mobility restrictions in Spain were imposed.

Full size image

We also extended the study further to explore the behaviour of the model deconfinement scenarios in other countries currently observing contrasting epidemiological situations and located in different latitudes (Fig. 3). These countries include Japan (Fig. 3a; which on 25 May 2020 ended its COVID-19 state of emergency18) and New Zealand (Extended Data Fig. 3; in which, after 52 d of complete lockdown, from Thursday 14 May, main businesses, hairdressers, cafes, gyms, cinemas, malls and playgrounds were free to open, and from Monday 18 May, also schools resumed classes as usual34). We also generated scenarios for the United States (Fig. 3b), as the world’s most affected country at the time of writing; Indonesia for its location in tropical latitudes, and therefore not subject to large seasonal temperature fluctuations (Fig. 3c); and finally, Argentina (Fig. 3d). The last of these is approaching wintertime conditions, and it is currently unclear whether the virus will exhibit seasonal patterns (for example, Northern Hemisphere winter) due to changing air temperatures (or humidity), which might potentially affect epidemic progression in 2020. In all of these cases, the temporal scenarios simulated were for 45-d, 75-d and 100-d lockdowns.

Fig. 3: Gradual deconfinement scenarios for other countries in different geographical regions and epidemiological states.
figure 3

a–d, Gradual deconfinement scenarios (50% of the confined population) for Japan (a), the United States (b), Indonesia (c) and Argentina (d). The dynamics were estimated for active cases, recovered population, deaths, susceptible population and protected population after 45 (black), 75 (blue) and 100 (red)d of confinement. The observed data up to 25 May 2020 used in the simulations are shown as red circles.

Full size image

Finally, we explored a generic scenario of varying confinement/deconfinement ratios testing for the effects of a variable proportion of people deconfined (Fig. 4a–c), as well as for the effects of the use of social distancing and NPIs (Fig. 4d–f). This is achieved by simulating a decaying effect (for example, decaying awareness in time and therefore relaxation of individual prevention measures; see Methods). We eventually also introduced a time-delay parameter simulating a variable temporal loss of acquired immunity (Fig. 4g–i). We also provide ranges of the sensitivity in parameter estimates and a diagnostic test of the robustness of these results (Fig. 5 and Extended Data Fig. 4).

Fig. 4: Generic scenarios for Spain.
figure 4

a–c, Variable \(\frac{\alpha }{\tau }\) ratio (confinement/deconfinement) (0.9, 0.5 and 0.1, respectively). d–f, β (infection rate) reduction in a variable range (0.1, 0.3 and 0.5, respectively). g–i, ϕ (loss of immunity) in a variable range (120, 240 and 360 d, respectively).

Full size image
Fig. 5: Parameter distribution of the adjusted model for Spain.
figure 5

a, A box-and-whisker plot of the average distribution for each of the fitted parameters and their respective 95% CI (blue outline), with crosses denoting outliers and red line denoting the median. The distribution of the parameters was obtained by successive model fitting (100 fittings) using larger datasets in each iteration, from 5 data points in the full dataset (113 data points, from 1 February to 25 May) to 113 points in the dataset. A space of around 10,000 elements was generated for each parameter. b, The distribution of 10,000 realizations for each of the fitted model’s parameters. Note the near-normal shape of all the distributions.

Full size image

Results

A gradual deconfinement scenario in which the population is released with a τ rate 50% higher than the confinement rate α is displayed in Fig. 1. The figure shows how this scenario evolves for all lockdown durations, to resume growth to a second peak that appears more delayed as the lockdown time increases. For the ‘current’ epidemic scenario—followed now in Spain—a second peak would occur earlier, in mid-August (Fig. 1a). Figure 1c shows the fitting of the model to observations for all temporal scenarios, tracking the peak in active cases occurring by the end of April 2020. Obviously, this is an idealized simulation, where all released individuals are considered fully susceptible, and therefore they are assumed not to be using any social distancing measures or other protective NPIs. As stated, no seasonality has been assumed either (that is, the potential effect of climate is therefore not considered). The main difference among the three temporal lockdown durations is the earlier arrival of a second peak for the shorter lockdown (30 d), peaking in mid-September with over 10 million infected (including individuals, both diagnosed and undiagnosed, with COVID-19). Longer lockdowns imposed since the peak in active cases produce second peaks later in the year (for example, December 2020 for the 60-d lockdown and well into 2021 for the 90-d lockdown; Extended Data Fig. 1). In terms of magnitude, the current scenario is the one yielding the higher number of deaths if considered up to the end of 2021, with 30% more deaths when compared to the 60- and 90-d confinement scenarios.

Conversely, Fig. 2 shows a mixed scenario in which the confined population is released in two stages, trying to mimic a selective post-confinement in which certain types of worker are freed to return to work earlier, while others are not (for example, schools, gyms, restaurants and so on are still closed at this time). In this mixed scenario, first, 50% of the population is released in a single step and then a gradual strategy is adopted in which the deconfinement rate is set to be 50% higher than the confinement rate, mimicking a slow incorporation of (risk) segments of the population. For the 45-d sudden release (for example, counted since the first lockdown date on 14 March, black line), epidemic growth is resumed (Fig. 2c), yielding a large peak that scales up to 6 million active cases, appearing earlier, towards mid-August (Fig. 2a). The extended temporal versions of the simulations shown in Figs. 1 and 2 up to the end of 2021 can be found in Extended Data Fig. 2. Interestingly, shorter lockdown times in the gradual scenarios result in secondary peaks appearing later in the year than in the sudden ones, albeit with double the amount of infected individuals (for example, compare 45-d in Fig. 2 to 30-d in Fig. 1). In this situation of sudden release of a similar portion of people as in Fig. 1, all peaks for the different lockdown times occur, instead, within 2020. Within the mixed scenarios, up to the end of 2020, in addition to a delay in the occurrence of the second peak, there is an important increase in the number of active cases. This increase goes from 30% in the shorter lockdown durations to over 50% in the longer lockdown durations. Similarly, the number of deaths increases, doubling by the end of 2020, when we compare the outcomes of the 45-d and the 75-d scenarios.

For countries located in different latitudes and continents, Fig. 3 shows a deconfinement scenario using a rate τ 50% higher than the confinement rate α (that is, similar to the gradual scenario proposed for Spain in Fig. 1). Again, the progressive release of the confined population is carried out after 45, 75 and 100 d (that is, on 9 July 2020 for the 45-d scenario) with the model fitted for observations in each country up to 25 May 2020. The simulations were carried out until 31 December 2021 to fully visualize all possible peaks occurring. For Japan (Fig. 3a), a country that moved swiftly to control the early outbreak of the disease towards the end of 2019 and the beginning of 2020 and that lifted the state emergency after seven weeks of restrictions, the fitting to the first wave is not optimal (Fig. 3a(iii)). All temporal scenarios produced second waves delayed to 2021, with a one-month separation between each and slightly smaller numbers of infected for the longest lockdown. A related situation occurred in New Zealand (Extended Data Fig. 3), where similar containment of COVID-19 seems to have been achieved and lockdown restrictions were also lifted by mid-May 2020. Despite the fact that the results are almost identical to those in Japan, the fitting to the observed epidemic curve is significantly better (Extended Data Fig. 3c). The case of the United States (Fig. 3b), instead, shows that a relaxation at this point (25 May) of the control measures leads to more immediate consequences. The model tracks the observations very well (Fig. 3b(iii)), and except for the shortest temporal scenario (45-d), it always simulates a protracted first peak and instead a much delayed second epidemic wave (that is, one-fifth smaller in size than for the 45-d scenario). We can observe a first peak of active cases of the order of 10 million I and a second one of about 40–50 million I (recall that I refers to all individuals with active infections, both diagnosed and undiagnosed). This large peak is delayed towards the beginning of 2021 if the duration of lockdown is 90 d. Simulations for Indonesia (Fig. 3c) show a situation similar to those for Japan and Argentina (Fig. 3d), with all cases having a delayed peak compared to Spain. This peak is of the order of 40 million I for the scenario of 45-d lockdown and 32 million for the 100-d lockdown scenario. Once again, this peak is delayed until the first part of 2021 for the 100-d scenario and the reduction in the number of deaths with the longest scenario is around 10%. Finally, Fig. 3d shows the dynamics generated for Argentina. As for Indonesia, the relaxation of confinement leads to the appearance of a delayed peak, observed from December 2020 for the 45-d lockdown scenario to February 2021 for the 100-d lockdown scenario. In all cases, the magnitude attained is similar, as are the number of deaths at the end of the epidemics (that is, approximately 20,000).

Finally, we explored different generic scenarios for Spain (Fig. 4). In the first scenario, we studied the potential impact in terms of epidemic size and timings of different confinement/deconfinement ratios. We explored three different α/τ ratios (0.9, 0.5 and 0.1). In terms of τ, this is equivalent to the rate of deconfinement being 10% more than, twice and 10 times more than the rate of confinement, respectively. When the ratio is 0.1, this is equivalent to releasing between 25 and 30 million people during the deconfinement. A ratio of 0.5 (Fig. 4b) displays no major difference compared with the 0.1 ratio (Fig. 4a), neither on the timing nor on the size of the second wave. Conversely, release at a rate ten times higher (Fig. 4c) produces a larger second peak for all scenarios that is equal in magnitude irrespective of lockdown duration. In this case, the only difference among the scenarios is the timing of the arrival of the second peak. A very fast deconfinement process (Fig. 4c) increases the size and shortens the arrival time of the second wave when compared to slow deconfinements (Fig. 4a). This may be because delaying the release of a high percentage of the population can lead to an increase in the number of effective contacts when the release occurs.

We also investigated the effects of individual NPI measures and of social distancing on disease transmissibility (β). The perception of danger—exemplified by a smaller or larger impact on β—typically shows a decrease in time, mimicking a decay of people’s awareness as time passes (Fig. 4d–f; see Methods). The infection rate β was therefore only moderately reduced (a 10% reduction in β in Fig. 4d, representing a limited use of NPIs due to low awareness of COVID-19 dangers; Fig. 4d), or alternatively we imposed a drastic reduction in transmissibility due to high awareness of COVID-19 threats (for example, 0.50β in Fig. 4f). The simulations show dramatic differences in terms of the number of infected people between the different β values (Fig. 4d–f) and in all three temporal scenarios, with also a complete absence of a second COVID-19 wave when awareness is high (Fig. 4f). If the transmissibility parameter β is not so affected due to the lack of danger awareness, and people do not act in a way (that is, through widespread use of NPIs) that reduces effective transmission (only 10% reduction in Fig. 4d), then second much larger epidemic waves occur as early as before the end of 2020. Interestingly, although they do not prevent new outbreaks, even moderate reductions in transmissibility (by 30% in Fig. 4e) yield much smaller returning waves (60% reduction in Fig. 4e compared to Fig. 4d). Large reductions in transmissibility seem to act strongly on reducing (and eventually interrupting) COVID-19 infections, as they not only prevent further recurrence of the disease, but also result in drastic decreases in the overall disease burden. As can be seen in Fig. 4f, as β decreases, effective contacts do as well. Decreasing the intensity of the eventual second peaks or eliminating them appears to be possible even without complete lockdowns.

Finally, we explored the effects of a potential loss of acquired immunity on subsequent epidemics. We simulated long (one year), medium (six months) and short (four months) durations of immunity, by imposing a decaying function on ϕ. Our simulations indicate how a longer extent of immunity has the largest effect in the 60-d scenario by reducing the burden of cases in the second wave by around 25% (compare Fig. 4i to Fig. 4g). The change from four-month to one-year duration in immunity also divides by half the period or recurrence in epidemic waves (for example, from one year to six months).

Our results present robust estimates, further reinforced by the uncertainty analysis (Fig. 5) and the assessment of the model’s predictive ability (Extended Data Fig. 4). However, as in all COVID-19 studies, a noticeable degree of uncertainty remains due to concerns associated with COVID-19 data quality. To further assess the degree of robustness in our simulations, we plotted variability ranges in the fitted parameter estimates (see Fig. 5a). Estimated ranges from all 500 simulations support consistency for the vast majority of parameters, with the parameters β, γ and δ being those that exhibit larger variability. Figure 5b shows also the distribution of errors for all parameters and remarkably indicates near-normality. These distributions were obtained by fitting the model 100 times with random initial conditions (see Extended Data Fig. 5) for successively larger datasets (for example, ranging from only 10% to 90% of the full dataset). On the other hand, Extended Data Fig. 4 shows the mean of all model fits, with a 95% confidence interval (CI), either using 80% (Fig. 5a) or 90% (Fig. 5b) of the total dataset. The predictive ability of the model seems clear in both cases (80% and 90%) as new data lie within the CI envelope, therefore precluding overfitting concerns.

Discussion

Our study shows the importance of taking prompt and efficient actions to both limit the epidemic spread and prevent disease recurrence, in contrast to other approaches35. Gradual deconfinement strategies always result in a lower number of infections and deaths, when compared to the sudden release of moderate to large portions of the population. If, conversely, sudden deconfinement is unavoidable due to the economic stress imposed by persistent lockdowns, a mixed deconfinement framework (Fig. 2) can be considered36, whereby those individuals most susceptible to the disease would still need to be shielded from potential infection for a longer period of time. Those not at high risk would be able to exit full lockdown, as long as they keep following some social distancing and other NPI measures. It would still be vital to keep transmission rates as low as possible through testing and contact tracing. Our results are in line with others showing that, in the absence of other control measures (for example, increases in case detection, isolation, and/or contact tracing), widespread relaxation of social distancing will result in a resurgence of cases, which will most likely overwhelm healthcare capacity37. Our mixed framework (sudden plus gradual deconfinement strategy) could also mimic potential quarantine lifts made in two stages according to age or risk classes. Our results indicate lower cumulative mortalities with a difference of up to 50% of the total number of deaths between the 30-d and 90-d scenarios (100,000 and 200,000 people, respectively; Fig. 2d). A higher number of total cases is also seen for the 90-d scenario (of the order of 20 million people more), but with lower mortality, as shown elsewhere for other locations38.

Our simulations suggest that, in the absence of a vaccine or effective antiviral treatments, recurring epidemic waves may occur and longer lockdowns lead to more delayed returning waves. Gradual deconfinement appears to be the best scenario in terms of disease burden, and the temporal extension of restrictions for the more susceptible groups results in a significant reduction in death counts. The use of social distancing, face masks, gloves and other individual protection measures has a massive impact in reducing the current peak of active cases, but diminished awareness over time of the threats of the pandemic may result in a new larger second epidemic wave. Interestingly, even moderate reductions in transmissibility (30%), despite the fact that they do not manage to prevent returning waves, much reduce its associated burden. In a generic scenario, a longer duration of immunity reduces the size of the second wave by approximately 30%, and if it lasts for one year, it would also cut by half the period or recurrence of epidemic waves (from one year to six months). Application to other countries in different latitudes is feasible and it can similarly inform policies for optimal and tailored lockdown release strategies.

Our results indicate that, in terms of successful containment, early enforcement of lockdowns and effective implementation of social distancing measures38 and personal protection are the most effective interventions37. In the near future, however, combining strategies might be an optimal approach, as promising improvements have been made in the sensitivity and specificity of both the saliva-sample real-time PCR tests39 and the new enzyme-linked immunosorbent assay serology tests40. Nonetheless, although widespread test–trace–isolate strategies may be equally or locally more effective and may minimize the economic and social costs of lockdowns, these are outside the reach of most countries (and are not modelled in this work). Our results show that a delayed and more gradual return to previous conditions by partially lifting lockdowns when the number of active cases is still high may lead to continued epidemic growth if the lockdown time is less than 45 d. Instead, shorter but stricter mobility restrictions, enforcement of social distancing and the adoption of appropriate personal protective measures (for example, hand-washing, face masks) appear to be highly successful in containing epidemic spread. Masks may provide a much more effective barrier than previously thought41, much reducing the number of infectious viruses in exhaled breath and protecting uninfected individuals from SARS-CoV-2 aerosols42. This is especially true for both asymptomatic people and those with mild symptoms43.

Reductions in transmissibility by early social distancing and the personal use of NPI measures can therefore have important outcomes in terms of reducing the disease burden. They could potentially even help halt the re-emergence of the COVID-19 disease during 2021, when applied in combination with much shorter lockdowns. Public campaigns by policymakers and health agencies should therefore keep alerting the public of the risks of new epidemics and emphasize the need for personal protective behaviours and social distancing.

Our study has several limitations. First, as noted earlier in the text, our modelling assumes that confined individuals cannot become infected, which underestimates the potential burden of disease. We also do not model the potential effectiveness of test–trace–isolate strategies and how they may reduce the burden of disease in combination with other NPIs44. Additionally, as for any other COVID-19 modelling study, the quantitative estimates we provide become substantially less reliable the longer the time window of modelling is—our findings must therefore be interpreted primarily in qualitative terms. The continuous nature of our modelling framework could result in the prediction of new epidemic waves occurring even in the presence of very marginal numbers of infected individuals. While this may be seen as a limitation in the simulation of fade-outs, in the case of non-disappearing seasonal epidemics (for example, flu), it gives a useful and timely indication on how easily new epidemics can occur just by external seeding from other regions in the world where the virus might still be circulating. There are at present still important gaps in our knowledge of the current COVID-19 pandemic due to its uniqueness that are key to improve all modelling attempts8,45. For instance, the potential impact of different SARS-CoV-2 genetic variants isolated in different regions and population densities is unknown; the effects of increased daily commuting in a post-confinement phase (especially, but not only, due to workforce movement) are also difficult to estimate; the variable close-contact interactions and the actual extent of the effects on the epidemic de-escalating stages of other individual actions—such as the ones explored above—are equally difficult to estimate. These limitations prevent the development of more accurate and comprehensive mathematical models that include complex pathogen-related and societal variables46. Incorporating age-dependent structure into more complex COVID-19 models also remains a challenge, given the large disparities existing among countries, despite initial attempts made in simpler structural frameworks17. Moreover, specific knowledge of age-dependent transmission and infection is yet largely uncertain47. The rigorous collection of population-scale data to address this global health crisis (for example, the COVID-19 Symptom Tracker mobile application successfully launched in the United Kingdom and the United States)48 might help improve mathematical modelling efforts by enabling rapidly scalable epidemiological data collection and analysis. Important uncertainties in our simulations—as in any other study—remain, mainly due to the limited quality of the current COVID-19 data. To be able to accurately anticipate the type, timing and magnitude of a second and further epidemic waves, high-quality, reliable data are necessary. Current models clearly simulate these returning wintertime epidemic waves, mostly if—in addition—immunity to SARS-CoV-2 wanes in the same manner as for related coronaviruses49. Additionally, the role of environmental modulators (for example, temperature and humidity) in COVID-19 transmission is not clear at this time and more research is needed to fully understand their potential seasonal modulation50.

Methods

The ordinary differential equation (ODE) system was solved in a stochastic framework by using a nonlinear data-fitting approach that minimizes a least-squares error function, by using the lsqcurvefit function of the Matlab optimization toolbox. The problem to minimize is shown in equation (3):

$${\rm{min}}_x\left\| {F\left( {x,x_{{\rm{data}}}} \right) - y_{{\rm{data}}}} \right\|_2^2 = {\rm{min}}_x\mathop {\sum}\nolimits_i^N {\left( {F\left( {x,x_{{\rm{data}}}} \right) - y_{{\rm{data}}}} \right)} ^2$$
(3)

where given input data xdata (Q, R and D), provided by the integration of the ODE system (equation (1)), ydata is the observed output (active reported cases, recovered and deaths) sourced from public repositories51,52 (https://github.com/datadista/datasets). Confirmed cases may include presumptive positive cases and probable cases. Death totals in the United States, for instance, include confirmed and probable. Finally, recovered cases outside China are estimates based on local media reports, and state and local reporting when available, and therefore may be substantially lower than the true number of cases.

The ODE system (equation (1)) was integrated by using a fourth-order Runge–Kutta method. The main advantages of Runge–Kutta methods are that they are easy to implement and very stable. For straightforward dynamical systems, this method can converge fast if we use an integration step of the order of 1 × 103. Although from the computational point of view this method is expensive compared to simpler methods such as Euler’s, the error of approximation is considerably less. On the other hand, this type of method has greater stability, especially when applied to nonlinear systems53.

The fitted parameters are the confinement rate α, the infection rate β, the incubation rate γ, the quarantine rate δ, the coefficients λ0 and λ1 that determine the recovery rate and the coefficients k0 and k1 that determine the mortality rate. Thus, the optimization problem described in equation (2) is subject to the constraints specified by the vectors lb = [0; 0; 0; 0; 0; 0; 0; 0] and ub = [1; 2; 2; 2; 1; 1; 1; 1] (lower bound and upper bound, respectively). A trust-region algorithm54 was chosen to minimize the problem because this type of algorithm is especially useful for solving nonlinear constrained optimization problems.

To obtain a representative measure of the optimal set of parameters, 500 iterations of the method were performed taking the initial values for the parameters, randomly within a uniform distribution. Extended Data Fig. 5 shows the initial values and the fitting results for each parameter. The same procedure was performed for each of the countries shown in Fig. 3. Extended Data Fig. 6 shows the parameters fitted for Japan, Extended Data Fig. 7 shows the parameters for Indonesia and Extended Data Figs. 8 and 9 show the resulting fitted parameters for Argentina and the United States, respectively. An extra parameter table is included for New Zealand (Extended Data Fig. 10).

The same algorithm was run using incremental dataset sizes (from 10 points to 54 points, the equivalent of 90% of the dataset). This procedure was carried out point by point 100 times with stochastic initial conditions in order not to always fall into the same local minimum. In this way, as shown in Fig. 5, a convergence of the adjusted parameters can be seen and the distributions can be assumed normal. Finally, Extended Data Fig. 5 shows a measure of the uncertainties of the fit using both a dataset of 80% and 90% of the total values and how the remaining values (not used in the training of the model) were correctly predicted. The mean error is of the order of \(3\times10^{ - 3 }\pm 6\times10^{ - 4}\) (CI 95%).

The deconfinement parameter τ is modelled as a time-dependent function modulated by the τd value as indicated below.

$$\tau \left( t \right) = 0,ift < T_{\rm{C}}$$
$$\alpha + \alpha \tau ^d,ift \ge T_{\rm{C}}$$
(4)

where TC is the confinement time in days, and τd is a value inside the interval [0; 1] representing the deconfinement proportion according with the confinement rate α.

For the immunity loss scenario (Fig. 4g–i), a parameter ϕ that modifies the R and S compartments is added to equation (1) as shown below.

$$\frac{{{\rm{d}}S}}{{{\rm{d}}t}} = \mu N_{\rm{T}} + \tau C\left( t \right) + \phi R\left( t \right) - \alpha S\left( t \right) - \beta \frac{{S\left( t \right)I\left( t \right)}}{{N_{\rm{T}}}} - \mu S\left( t \right)$$
$$\frac{{{\rm{d}}R}}{{{\rm{d}}t}} = \lambda \left( t \right)Q\left( t \right) - R\left( t \right)\left( {\mu + \phi } \right),$$
(5)

where ϕ is the loss of immunity after n days \(\left( {\frac{1}{n}} \right)\). Finally, to model the decay of the infection rate β (Fig. 4d–f), a β(t) was used where β = k, constant if t < TC (before the end of confinement), and β = β − cβ, with \(c \in \left[ {0.1} \right]\), in the opposite case (after the confinement).

Reporting Summary

Further information on research design is available in the Nature Research Reporting Summary linked to this article.