Main

Realizing isolated Majorana modes (MMs) as zero-energy excitations in solid-state systems has been an immense quest in the past two decades, being motivated by their possible use for fault-tolerant topological quantum computing1,2,3. Theoretical proposals combine superconductivity, magnetism and Rashba spin–orbit coupling (SOC)4,5,6,7,8,9,10. One-dimensional (1D) experimental platforms featuring these effects include semiconducting nanowires in proximity to superconductors with an externally applied Zeeman magnetic field11,12 or atomic spin chains with ferromagnetic13,14,15,16 or spin-helical order17,18 on superconducting substrates. MMs on the system’s boundaries are the consequence of a topologically non-trivial band structure in the chain’s bulk. This makes them immune to perturbations sufficiently local compared with the size of the system. Atomic spin chains studied so far are short, consisting of only tens of atoms13,17,18. Here MMs on both ends of the chain may still interact, thereby splitting in energy away from zero in an oscillatory fashion as a function of the chain length, one of the key signatures of the so-called precursors of MMs (PMMs) in short chains19,20,21. Indeed, Coulomb blockade spectroscopy in InAs nanowires coupled to Al has provided evidence for an oscillatory splitting of near-zero-energy states as a function of the Zeeman field, which decreased for longer devices20. However, the length could not be continuously varied in these measurements and they were done for only one of the wires’ ends. Another indication for MMs, the quantized zero-bias conductance, has been detected only on one of the ends of InSb nanowires coupled to NbTiN, whereas the other simultaneously measured end showed a different signature22. Zero-bias peaks as indications for MMs or their precursors have also been observed at the ends of atomic spin chains13,14,15,16. However, such peaks were only found for some of the chains and were not detected on both ends of the same defect-free chain, whereas other chains in the same system did not display this signature at all13,14,15,16. Also, it was not possible to continuously vary the length of the chains. In this work, we measure the energy oscillations of PMMs in Mn chains on Nb(110), along the entire chain, including both ends, and as a function of the chain length that we continuously vary in an atom-by-atom manner. Using this extensive dataset, we can determine all the parameters of a low-energy model9,23, except for an effective Rashba SOC whose order is deduced from first-principles calculations. We predict the chain length above which isolated and topologically protected MMs will evolve from these PMMs.

Topological phase diagram of Shiba chains

Topological superconductivity and the resulting MMs can be engineered in 1D ferromagnets with an odd number of spin-polarized bands crossing the Fermi energy EF (refs. 4,5,9). The low-energy bands may be formed by hybridizing the Yu–Shiba–Rusinov (YSR)9,10,23 states locally induced by magnetic impurities on superconducting substrates24,25,26,27. This has led to the intense investigation of YSR states in the past years24,28,29,30,31,32. Recently, it has been shown that the dispersions of emergent YSR bands can be measured in Mn spin chains along the [001] direction on Nb(110) (ref. 23). Experimental evidence for p-wave correlations in this system was found, leading to gap Δp exceeding the energy splittings of the states due to finite-size quantization. However, the multiband nature of the YSR chain prevented the identification of its total topological phase. In the following, we exploit this microscopic insight into the low-energy band formation to design an effective one-band system from single, hybridizing YSR states in a bottom-up approach. In this scenario, the system is topologically non-trivial in the presence of any finite p-wave pairing, as shown below.

We use scanning tunnelling microscopy (STM) and scanning tunnelling spectroscopy (STS) with a superconducting tip to probe the local density of states (LDOS) at subgap energies (Methods). Single Mn atoms on clean Nb(110) induce multiple YSR states (Fig. 1a)23,33. Their spatial anisotropy facilitates different hybridizations of the YSR states stemming from neighbouring Mn atoms by tailoring the directionality of nanostructures on the Nb(110) surface, as it has been shown for dimers of Mn atoms33. In particular, the lowest-energy YSR state (referred to as δ hereafter) extends along the [\(1\bar 10\)] direction (Fig. 1b–d). Thus, we construct chains along the [\(1\bar 10\)] direction (Fig. 2a). We expect this orientation to lead to a dominant hybridization of the lowest-energy δ-YSR states compared with the weaker coupling of all the other higher-energy YSR states, such as the state labelled as α+/– in Fig. 1a. This is reasonable, especially because the interatomic distance in this configuration is large (d = 0.467 nm) compared with the interatomic distances for chains along [001] or \([1\bar 11]\). Similarly, Mn is in the centre of the transition metal series and its d states are energetically located at very high energies away from EF. Even when hybridizing, the bandwidth of the emerging d bands is expected to be too small to reach EF. Thus, ideally, the low-energy band structure would be reduced to an effective one-YSR-band system around EF, in contrast to the case elsewhere23 (Extended Data Fig. 1b and Supplementary Note 1). In this case, sufficient hybridization between the δ states results in a topologically non-trivial band structure irrespective of the model parameters, strongly reminiscent of the seminal Kitaev chain model for topological superconductivity1. The magnetic moments in Mn chains along the [\(1\bar 10\)] direction are ferromagnetically aligned (Extended Data Fig. 2 and Supplementary Note 2), thus providing all the necessary ingredients for topological superconductivity in the presence of any non-vanishing effective Rashba SOC kh. With the use of model calculations approximating the effective low-energy theory of a 1D chain of dilute YSR impurities9 (Methods and Supplementary Notes 3 and 4), we discuss the expected topological properties of chains crafted from single YSR atoms. Within this model, the chain is embedded in a three-dimensional superconductor. We additionally find very similar results using a tight-binding model for a chain on the surface (Supplementary Note 5). We start by modelling the δ-YSR states of a single Mn impurity23,33 (Methods and Fig. 1a) and use the same parameters to extrapolate to the case of a YSR chain. The resulting phase diagram shown in Fig. 1e demonstrates that the chain is indeed almost always in a topologically non-trivial phase9. This holds as long as the chain is sufficiently dilute to remain in an effective one-band scenario where only the hybridizing δ-YSR states are relevant and as long as the effective coherence length ξ of the substrate is not unrealistically small or its Fermi wavevector kF,0 has a very specific size. Experimentally, we can determine kF,0 to be (0.6 ± 0.1)π/d (Extended Data Fig. 3 and Supplementary Note 6), which is far from these critical points.

Fig. 1: YSR states of single Mn atoms on Nb(110) and resulting topological properties of a hybridized chain.
figure 1

a, Deconvoluted dI/dV spectra averaged around a single Mn atom on Nb(110) and on the bare substrate. Pairs of the most-intense YSR states, namely, δ+/– and α+/–, are highlighted by arrows. The weak resonances at ±0.8 meV are due to additional YSR states, which can be disregarded here (Supplementary Note 1). The measured coherence peaks are energetically located at the superconducting gap of bulk Nb (ΔNb = 1.52 meV). Both energy and particle–hole asymmetry of the δ-YSR states are well described by a YSR model with the magnetic and non-magnetic scattering parameters A = 1.1 and B = 0.2 (orange line; Methods). b, STM image of a single Mn atom. c,d, Spatially resolved dI/dV map around the atom at energies of δ– (c) and δ+ (d), showing the state’s lobes along [\(1\bar 10\)]—the direction of the chains (image sizes are 2 × 2 nm2). e, Topological phase diagram calculated for an infinite chain of interacting YSR states for different values of Fermi wavevector kF,0 and coherence length ξ of the substrate. The parameters for the YSR states (as derived in a) are used; a constant, weak effective Rashba SOC kh = 0.05π/d is added. The phase diagram does not qualitatively change for other small values of kh. The colour scale indicates the magnitude of the system’s gap Egap multiplied by the topological \({\Bbb Z}_2\) invariant, which is M = −1 (topologically non-trivial; blue) or M = +1 (trivial; red), compared with the superconducting pairing of the substrate, Δs. The dark dashed lines mark the parameters used in Fig. 4 that best describe the experimental data in Fig. 3.

Source data

Full size image
Fig. 2: In-gap states in Mn chains on Nb(110) along [\(1\bar 10\)].
figure 2

a, Geometry of the experimentally assembled Mn atoms (red spheres) on top of the atoms of the superconducting Nb host (brown spheres). b, Constant-current STM image (topography) of a Mn32 chain. Scale bar, 1 nm. c, Corresponding deconvoluted dI/dV maps at the indicated energies. The brown dashed lines mark the position of the chain. d, Single deconvoluted dI/dV spectra obtained on the chain’s end, in the centre and on the Nb substrate. The zero-energy peak is highlighted by the red arrow.

Source data

Full size image

End states and their energy splitting

To experimentally realize this concept, we construct MnN chains consisting of N atoms along the [\(1\bar 10\)] direction (Fig. 2a) by the controlled lateral manipulation of Mn atoms on the Nb surface using the STM tip (Methods). In Fig. 2b, we present an example of a Mn32 chain. In Fig. 2c, we show the spatially resolved deconvoluted differential conductance (dI/dV) maps around the chain. We find states at zero energy that are well localized at the chain’s ends with additional small LDOS oscillations in the interior of the chain. In contrast, energetically higher states (0.5 < |E| < 1.5 meV), which are most probably the bands derived from hybridizing α-YSR states, are distributed all over the chain (Extended Data Fig. 1a and Supplementary Note 1). Spectra from the dataset in Fig. 2c measured at the chain’s end and centre as well as on the bare Nb substrate (Fig. 2d) reveal a narrow zero-energy peak in the dI/dV signal localized on the chain’s end, corresponding to the zero-energy state of Fig. 2c. Peaks corresponding to the finite-energy states in Fig. 2c are distributed over the entire chain. Such a clearly resolved zero-energy end state is typically considered as an indication for MMs11,12,13,14,15,16,17,18.

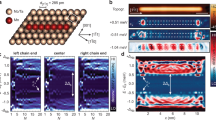
Since we construct the chains in an atom-by-atom manner, we are able to track changes in the low-energy states for each length N and to probe the robustness of the zero-energy end state. As an example, we show the deconvoluted dI/dV signal along the chain in a 1D line of spectra (called the dI/dV line profile hereafter) for N = 14–16 (Fig. 3a–f). Interestingly, we find similar zero-energy end states as in Fig. 2c for N = 14 and 16 (Fig. 3d,f, arrows), separated from the higher-energy states by a large gap ΔFS = 400 µeV. Instead, for N = 15, there are two states with a similarly strong localization on the chain’s ends (Fig. 3e, arrows) but split by Ehyb ≈ 300 µeV symmetrically around EF. Importantly, this shows that the two end modes on both sides are a single, coherent quantum state of the chain, since their energies on both ends of the chain are intertwined. As substantiated later, these states can be interpreted as PMMs with a residual MM coupling due to the finite length of the chain. If this is the case, their coupling will not only depend on the length of the chain but also on the wavefunction modulation of the PMMs.

Fig. 3: Chain-length dependence of in-gap states.
figure 3

a–c, STM images of MnN chains with N = 14 (a), 15 (b) and 16 (c). d–f, Corresponding deconvoluted dI/dV line profiles acquired along the longitudinal axis through the centre of the three chains (as indicated by the dashed line along the Mn14 chain). The STM images are aligned with the dI/dV line profiles and edge states are highlighted by white arrows. g, Sequence of dI/dV spectra obtained on the end of MnN chains for different N values located at a different sample position as the chains in a–f. The spectral features associated with the bands from hybridizing α- and δ-YSR states are marked on the right side (Extended Data Fig. 1). h, Dataset from g with chains of even and odd N plotted in separate panels.

Source data

Full size image

To investigate this effect, we show the deconvoluted dI/dV signal measured at the end of another, structurally identical chain with varying chain length N (Fig. 3g). With increasing N, we added Mn atoms to one chain end and measured the dI/dV spectra at the opposite end to trace the states’ energies. In accordance with Fig. 3d–f, we find that the energy of the state closest to EF, which corresponds to the end state, is modulated with a period of ΔN ≈ 2. This trend continues up to the longest chains built by us (N = 45). The remaining density of oxygen impurities on the surface limits the maximum length of ordered magnetic chains to this length, corresponding to 20–25 nm. The modulation effect is the most apparent when we separately plot the chains with even and odd N (Fig. 3h). Here the change in the subgap state energies appears to be continuously changing as a function of N. Most notably, for certain chain lengths, such as N = 12, 21, 32 and 42, the energy of the end state can be tuned to zero within the experimental peak width, which corresponds to ΔE = 50 µeV. In contrast to this observation, the hybridizing α-YSR states evolve into a comparably narrow band (Fig. 3g), which is irrelevant for the topological properties of the system (Extended Data Fig. 1b and Supplementary Note 1).

Theoretical modelling of length-tunable chains

To substantiate that the observed end states are indeed PMMs from the two ends of the chain, we performed the aforementioned model calculations9 to simulate the chains of N sites in contact with a superconducting host. We emphasize that within this model, we are unable to explain the experimental data in Fig. 3g,h when assuming a topologically trivial phase. Yet, we find regimes of the model in the topologically non-trivial phase qualitatively reproducing the experimental data on finite chains (Fig. 4). Using the parameters yielding the band structure of the YSR chain in Fig. 4a, we find end states at zero energy with a strong localization at the terminal sites for special lengths of the chain (Fig. 4b). Most notably, the ΔN ≈ 2 modulation of the low-energy states is in good agreement with the experiment (Figure 3g,h and Fig. 4c,d). The modulation turns out to be induced by a particular position of the Fermi points in the low-energy band structure: since the YSR band crosses EF at kF ≈ ±π/2d, the Fermi wavelength λF = 2π/kF ≈ 4d is specifically related to the lattice constant. This leads to a modulation of eigenenergies in chains of length N with ΔN ≈ 2. This type of beating effect in a quantum-size-limited system has been observed on other platforms, for example, quantum well states in thin films of Pb/Si(111) (refs. 34,35,36) or in predictions for Andreev-bound states in superconducting carbon nanotubes37. Equally, the effect can be understood in terms of PMMs: it has been shown that MMs feature an LDOS modulation with λF/2 (ref. 38) (Fig. 4b). Accordingly, the overlap, and thus the interaction of MM wavefunctions from both ends of the chain, is expected to oscillate with the total chain length with ΔN ≈ 2. Notably, the approximate zero energy of the MM for particular chain lengths is not protected by the topological properties of the electronic band structure but is tuned by the atomically precise experimental control of the chain length. Within the model, they evolve into isolated MMs for very long chains (Supplementary Notes 3 and 4) and can thus be seen as their precursors19,20,21. The large gap ΔFS to higher-energy excitations can be interpreted as a finite-size gap resulting from the steep YSR band (Fig. 4a).

Fig. 4: Theoretical model for PMMs derived from YSR bands.
figure 4

a, Band structure of an infinite chain of YSR impurities using parameters describing the experimentally measured energy and particle–hole asymmetry of the δ-YSR states. The topological index of the infinite chain is non-trivial (M = −1). b, Calculated LDOS of the state with least energy along a finite chain of 32 sites using the parameters from a. c, LDOS on the first site of a finite chain of length N. d, Dataset from c with chains of even and odd N plotted in separate panels. The arrows exemplarily show a position where weak anticrossings of the states are visible, indicating the presence of p-wave superconducting pairing (Supplementary Fig. 2). Parameters: A = 1.1, B = 0.2, kh = 0.05π/d, kF,0 = 0.53π/d, ξ = 4.67 nm, d = 0.467 nm and Δs = ΔNb = 1.5 meV (Methods and Supplementary Note 3).

Source data

Full size image

The agreement with our model calculations indicates that the relevant single band is indeed formed by hybridizing δ-YSR states of the single Mn atoms expanded along the [\(1\bar 10\)] direction, which have energies close to zero for isolated atoms (Fig. 1a)23,33.

Exclusion of other topologically trivial causes

The question is whether other topologically trivial explanations for the observed end states exist. The emergence of trivial zero-energy states due to disorder effects is frequently discussed for various Majorana platforms22,39,40,41. We can rule out this explanation because of the geometrically perfect structure of our chains. Most importantly, the fact that the end modes at both ends of the chain change equally when perturbing only one side (Fig. 3d–f and Supplementary Note 8) proves that the end state is a collective mode of the 1D structure. We can, therefore, rule out that the end states are zero-dimensional features induced by local defects or localized YSR states24,25,26,27. The observation of this correlation between both ends is a key advantage compared with previous experimental studies of potential topological superconductors, where only one end of a nanowire is probed11,12,13,14,15,16,20. It is possible that the localization of the wavefunction closest to EF is less pronounced than the experiment suggests (Supplementary Notes 3 and 4). Especially since both YSR states and MMs can be predominantly located in the superconducting host, the measurement of LDOS above the atomic chain could suppress the signal in the chain’s interior and amplify the intensity at the chain’s ends14. Note that the topological phase of the infinite system would still be non-trivial in this case. Topologically trivial phases could only be compatible with the experiment in the presence of additional low-energy bands. In this scenario, an even number of MMs from different bands would inevitably interact for arbitrarily long chains, thereby lifting their degeneracy and destroying topological protection. Experimentally, all the features from additional bands are well separated from EF (Fig. 3g, Extended Data Fig. 1b and Supplementary Note 1), providing strong evidence that our chains indeed realize an effective one-band model in the low-energy limit. As such, our model calculations reveal that the system is topologically non-trivial in the relevant parameter regime (Fig. 1e and Supplementary Note 3).

It is important to note, however, that the MMs in an infinite system only experience a topological protection of the size of the bulk topological gap Δp. The topological gap for the system at hand is calculated to be 50 µeV (Supplementary Note 7), which is considerably smaller than the observed energy splitting of the PMMs Ehyb and the finite-size gap ΔFS in our experimentally realized chains (Fig. 3, Supplementary Note 3 and Supplementary Fig. 1e). For systems with this sequence of orders of magnitude of the different parameters, the p-wave pairing Δp manifests as an emergent apparent avoided crossing of the lowest- and second-lowest-energy states at positions exemplarily indicated by the arrows in Fig. 4d, which is just too small to be detected within our experimental energy resolution (Supplementary Figs. 1 and 2 show the evolution of the avoided crossings in longer chains). The long-range extension of MMs has been shown to be inversely related to Δp (ref. 42). Our results indicate that the observation of a well-localized zero-energy end state in a finite-size topological superconductor does not directly imply that the corresponding MMs are non-interacting under the influence of small perturbations (Supplementary Note 4). We expect the energy of the end modes to converge to energies below Δp only for long chains with N > 70 corresponding to chain lengths of 35 nm (Supplementary Figs. 1 and 2). However, the interactions of the observed fine-tuned zero-energy PMMs with the continuum of 1D modes are strongly suppressed by the presence of a relatively large finite-size gap ΔFS.

Conclusions

One way to improve the localization further and to reduce the interactions of MMs would be to enhance the Rashba SOC in the system, either using a different superconducting host, heavy-material interlayers or artificial SOC5,43,44,45, all of which are expected to enhance Δp. However, as shown in the topological phase diagram in Fig. 1e using the parameters from Fig. 4 (black dashed lines), although the system is deep in the topological phase, it is near a gap closing at kF ≈ ±π/2d (Supplementary Note 3). Note that, uncommonly, this gap closing is between two topologically non-trivial regions9. Despite constant SOC, this gap closing adds a previously disregarded constraint for realizing strongly protected MMs in a hard gap Δp in future experiments. Moreover, even if the hard gap of the infinite system cannot be experimentally resolved, a gradual separation of the lowest-energy states from the continuum (Supplementary Fig. 2) could serve as an indicator for the magnitude of Δp and the degree of topological protection.

Owing to the atomic-scale control of nanostructure fabrication by single-atom manipulation, we can envision studies of MM interaction in artificially created networks of interacting chains46,47,48. An example for a junction of two Mn12 chains with varying interchain distance is shown in Fig. 5a,b. We can control the number of unoccupied adsorption sites N∅ with the precision of a single atom and analyse the energy of the state closest to EF (Fig. 5c, left, Extended Data Fig. 4 and Supplementary Note 8 show the full dataset). Its energy modulates with ΔN∅ ≈ 2 again, providing evidence that the two chains are coupled through long-range interactions of the YSR states with a strength oscillating with λF/2. This oscillatory change in the energy of the end state with interchain distance is qualitatively consistent with model calculations using the model and parameters from Fig. 4 and removing N∅ lattice sites of the YSR chain (Fig. 5c, right). However, a quantitative description of these interactions will require more advanced modelling. We emphasize that the observed energy splitting is an interplay of inter- and intrachain PMM interactions, where the latter is discussed above for single chains. Building similar networks of sufficiently long chains, where the MMs on each individual chain are initially at EF and topologically protected by gap Δp, may ultimately enable to explore the theoretically predicted robustness of such MMs under local perturbations acting only on one end of the chain.

Fig. 5: Junctions of interacting Mn12 chains.
figure 5

a, STM image (top) of two Mn12 chains with N∅ = 6 empty sites between the chains and a respective sketch of the geometric structure (bottom). Scale bar, 1 nm. b, dI/dV line profiles along the longitudinal axes through the centres of both chains in a aligned with the topography. c, Experimentally measured (left) and calculated (right) energy E0 of the lowest-energy state versus interchain spacing N∅. The same model parameters as in Fig. 4 are used. The error bars on the values of E0 are standard errors resulting from a least-square fit of two Gaussian peaks to the dI/dV spectra on the left end of the left chain.

Source data

Full size image

Methods

Experimental procedures

All the experiments were performed in a home-built STM facility operated at a temperature of T = 320 mK (ref. 49). We used a Nb(110) single crystal as a substrate, cleaned by high-temperature flashes to T > 2,700 K. Using this cleaning procedure, atomically clean surfaces with only few residual oxygen impurities on the surface can be obtained50. Subsequently, single Mn atoms were deposited onto the cold surface (T < 7 K), resulting in a statistical distribution of adatoms. Superconducting tips were created by indenting electrochemically etched W tips into the substrate, thereby picking up a large cluster of superconducting Nb. STM images were measured maintaining a constant tunnelling current I when applying a constant bias voltage Vd.c. across the tunnelling junction. For the measurement of the differential tunnelling conductance (dI/dV) spectra, the tip was stabilized at bias voltage Vstab and current Istab. Subsequently, the feedback loop was opened and the bias voltage was swept from –4 to +4 mV. The dI/dV signal was measured using a standard lock-in technique with a small modulation voltage Vmod (r.m.s.) of modulation frequency f = 4.142 kHz added to Vd.c.. The dI/dV line profiles and maps were acquired, recording multiple dI/dV spectra along a line or grid, respectively. All the datasets shown in the main manuscript were measured using Vstab = Vd.c. = −6 mV, Istab = 1 nA and Vmod = 20 µV. Note that at these stabilization parameters, the contribution of Andreev reflections can be neglected (Supplementary Note 9). Superconducting Nb tips have been chosen to increase the effective energy resolution. The measured differential tunnelling conductance dI/dV is, thus, proportional to the convolution of the LDOS of the sample and the density of states of the superconducting tip. We show the numerically deconvoluted STS data throughout the manuscript, resembling the sample’s LDOS (Supplementary Note 9). The chains were assembled using lateral atom manipulation51 at low tunnelling resistances of R ≈ 30–60 kΩ.

Model for single and hybridizing YSR states

The theoretical analysis of the single and hybridized YSR states follows ref. 23, adapting it to the material-specific parameters. We repeat the essential definitions here to be self-consistent. In the model of single YSR impurities embedded in a superconducting host (as described elsewhere9,52), the subgap states are characterized by a magnetic scattering term J and an additional non-magnetic scattering term V. Their energy E(A, B) and particle weight P(A, B) can be written in terms of the dimensionless parameters A = πν0J and B = πν0V, with the normal-phase density of states ν0 and the superconducting s-wave pairing Δs.

$$\begin{array}{*{20}{c}} {E\left( {A,B} \right) = \varDelta _{{{{s}}}}\frac{{1 - A^2 + B^2}}{{\sqrt {\left( {1 - A^2 + B^2} \right)^2 + 4A^2} }}} \end{array}$$
(1)
$$\begin{array}{*{20}{c}} {P\left( {A,B} \right) = \frac{{1 + \left( {A + B} \right)^2}}{{1 + \left( {A + B} \right)^2 + 1 + \left( {A - B} \right)^2}}} \end{array}$$
(2)

The particle weight P(A, B) determines the ratio between the observed peak heights of the positive- and negative-bias YSR peaks measured in the low-conductance regime of an STS experiment23,53. We find that the δ-YSR states of Mn atoms on Nb(110) (ref. 33) are well reproduced by choosing A = 1.1 and B = 0.2, leading to the correct energy and particle–hole asymmetry of the experimentally measured peaks in dI/dV (Fig. 1a shows the fit with two Gaussians). Accordingly, these parameters are used for the description of chains. Note that the choice of A = 0.94 and B = –0.20 also reproduces the YSR peaks well and leads to very similar topological phase diagrams.

To describe chains of weakly interacting YSR atoms, we use a model based on another work9, which is extended to include non-magnetic scattering at the YSR impurity (that is, the B term in equations (1) and (2)). For details on this model and its derivation, we refer to another study23. The low-energy Bogoliubov–de Gennes Hamiltonian for the YSR chain is characterized by the scattering parameters A and B of the single YSR states, the Fermi wavevector of the superconducting host in the metallic state kF,0, the effective coherence length in the YSR chain ξ and an effective Rashba SOC parameter kh. One can approximately relate kh to the usual definition of the Rashba SOC parameter via \(\hbar {\lambda} \approx \frac{{\Delta}_s {\xi} k_{\mathrm{h}}}{k_{{\mathrm{F}},0}}\), where ℏ is the reduced Planck constant. We compute the LDOS as a function of energy E and position x along a 1D lattice of N sites (Fig. 4) by diagonalizing the low-energy Hamiltonian (given elsewhere23) and summing over all the pairs of eigenvalues Ei and eigenvectors ψi:

$$\begin{array}{lll} {{\mathrm{LDOS}}\left( {E,x} \right)} &=& {\mathop {\sum }\limits_i \left[ {P(A,B)\left| {\psi _{i,\mathrm{e}}(x)} \right|^2 + (1 - P({{{\mathrm{A}}}},B))\left| {\psi _{i,\mathrm{h}}(x)} \right|^2} \right]} \\ & & \times{\left( { - \frac{{\partial f(E - E_i,\,T = 320\;{{{\mathrm{mK}}}})}}{{\partial E}}} \right)}, \end{array}$$
(3)

with the respective particle (e) and hole (h) components of the solutions and the Fermi–Dirac distribution function f(E, T) simulating the experimental thermal broadening. In order to accurately obtain the particle–hole asymmetry of all the states in terms of the physically original quasiparticles in equation (3) (which is measured in the experiment), P(A = 1.1, B = 0.2) is multiplied with the particle component of a state and (1 – P(A = 1.1, B = 0.2)) is multiplied with the hole component. We obtain the band structure for an infinite chain by Fourier transformation of the Hamiltonian with periodic boundary conditions applied9. For the numerical calculations shown in Fig. 4, we used the parameters A = 1.1, B = 0.2, kh = 0.05π/d, kF,0 = 0.53π/d, ξ = 4.670 nm, d = 0.467 nm and Δs = 1.5 meV. Using these values, we estimate a Rashba SOC parameter of \(\hbar {\lambda} \approx \frac{{\Delta}_s {\xi} k_{\mathrm{h}}}{k_{{\mathrm{F}},0}}\) = 0.0066 eV Å, which is in a reasonable range for the experimental system in this work compared with values in the literature54, considering the relatively weak SOC in Nb. The value for kF,0 is—within the error bar—compatible with the experimentally determined value (Supplementary Note 6). Note that the only free parameters that cannot be directly determined experimentally from single YSR states are kh and ξ (Supplementary Note 3).

The topological invariant M is calculated as

$$\begin{array}{*{20}{c}} {M = \mathrm{sgn}\left\{ {{{{\mathrm{Pf}}}}\left[ {\tilde H\left( 0 \right)} \right]{{{\mathrm{Pf}}}}\left[ {\tilde H\left( \uppi \right)} \right]} \right\}} \end{array},$$
(4)

where Pf denotes the Pfaffian and \(\tilde H\left( k \right)\) is the k-space Hamiltonian in the Majorana basis1.